Talk:Delta-sigma modulation
| This is the talk page for discussing improvements to the Delta-sigma modulation article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| Archives: 1Auto-archiving period: 365 days |
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
Original Research?
[edit]This section possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (June 2016)
There is no original research described in this section.
It is only a description of the mode of operation using block schematic diagrams and circuit diagrams which are description methods familiar to electronics engineers.
Since when has an encyclopedia not included tutorial material
It is an analysis of the operation of a circuit mentioned in the talk page at the time but cannot be found now. Puffingbilly (talk) 05:39, 3 August 2016 (UTC)
- Waveforms and some principles are not correlated with notable sources. ISBN: 0916550273 for example. Слишком похожий (talk) 08:55, 15 November 2016 (UTC)
- We don't know where this material came from. There are no citations. I haven't seen any improvements. Puffingbilly has made a lot of contributions to this article and respond to the WP:OR concerns above. Are you the one who added this material? If so, what were your sources? ~Kvng (talk) 21:52, 20 February 2018 (UTC)
I am a chartered engineer with many years (>50) experience in the design and analysis of electronic circuits. The analysis is mine. I chose the circuit to analyse because it was mentioned in the talk page and so must have been familiar to some of the editors. It does work as a delta-sigma modulator as the analysis shows. The analysis can be verified by any engineer competent in circuit analysis. The analysis must have been viewed by many competent engineers since it first appeared but no correction has appeared. The fact that the analysis does not sit easily with much of what follows in the article is my motivation for doing it. Puffingbilly (talk) 15:51, 12 January 2019 (UTC)Puffingbilly
I refer you to https://www.researchgate.net/publication/243767842_Asynchronous_Delta_Sigma_Modulation Puffingbilly (talk) 19:02, 19 February 2019 (UTC)
- What goes unsaid in this analysis is whether the loop is clocked. I believe it always is in delta-sigma converters, but in Puffingbilly's approach it appears to not be. His first edit in 2007 says "The method can be thought of as a voltage controlled oscillator...". I think this is misleading, and put us on a long wrong track. In the older diagrams, instead of the impulse at input to an integrator, there was a "1-bit DAC", which is implicitly clocked. I'd rather move toward making that approach more explicit than try to keep going with the asynchronous approach, which doesn't represent how these things actually work. Dicklyon (talk) 16:27, 12 January 2019 (UTC)
- By the way, I build pretty much exactly that VCO circuit in about 1972 using op-amp integrators to get good linearity for monitoring signals. Nothing wrong with it. But it's not a delta-sigma converter. Dicklyon (talk) 16:30, 12 January 2019 (UTC)
- Here, I found a book that distinguishes "asynchronous delta-sigma" from "conventional delta-sigma", the difference being a (clocked) sampling operation. Maybe we should cover both. Dicklyon (talk) 16:57, 12 January 2019 (UTC)
As indicated in Fig 1a clocking generates noise which may be critical at high output frequencies. As discussed:- If the ratio between the impulse interval and the summing interval is equal to the maximum (full scale) count, it is then possible for the impulse duration and the summing interval to be defined by the same clock with a suitable arrangement of logic and counters. This has the advantage that neither interval has to be defined with absolute precision as only the ratio is important. Then to achieve overall accuracy it is only necessary that the amplitude of the impulse be accurately defined.
For modulation no summing interval is required so clocking may be deleterious at high output frequencies due to the noise generated, Fig. 1a. It is quite possible to generate an accurately defined pulse without using a clock and this is what is shown in Fig. 1.
The circuit produces a frequency proportional to input voltage which is exactly what a voltage controlled oscillator does. Functionally they are near equivalent.Puffingbilly (talk) 18:30, 12 January 2019 (UTC)Puffingbilly
- Ah, yes, I see you did discuss clocking as "Implementations may...". But it's really much more fundamental than that. Clockless implementations simply not sigma-delta converters as usually understood; they do not generate a bit stream, such as could be used as input to a digital filter. The VCO/counter thing is not really what's meant by delta-sigma modulation. If you qualify as "asynchronous" them maybe, but that's a very different beast. Dicklyon (talk) 06:42, 13 January 2019 (UTC)
The object is to convey function to those unfamiliar with the topic. In my opinion it is helpful to the uninitiated to start with something very common which they may be familiar with. I think our differences are more of style than substance. The circuit analysed, fig 1b, is clocked and is shown to be clocked and does produce a frequency modulated pulse stream. Here the clock defines the duration of the impulse but the frequency is determine by the requirement that the integral of the pulse stream matches the integral of the input and so the frequency is proportional to input.The input shown, Fig.1c(a) is initially in the linear region (first 2 pulses) but is then taken to the limits, plus and minus, to illustrate the behaviour at the limits. Here I was constrained by the necessity to keep the drawing within bounds so it is difficult to discern the linear frequency conversion but it is there..Puffingbilly (talk) 17:01, 13 January 2019 (UTC)Puffingbilly
- Yes, I see now that you get there. But I think starting with the Fig. 1 clockless version confuses the issue. Maybe if it's first labeled as an asynschronous ideal, on the way to delta-sigma converter, it would be better. Dicklyon (talk) 17:58, 13 January 2019 (UTC)
A change has been made in the spirit of your suggestion.Puffingbilly (talk) 03:02, 14 January 2019 (UTC)Puffingbilly.
Verifiability and Original Research
[edit]Puffingbilly says:
- "Since when has an encyclopedia not included tutorial material?"
But WP:NOTGUIDE says:
- "Wikipedia is an encyclopedic reference, not an instruction manual, guidebook, or textbook. Wikipedia articles should not read like: Instruction manuals. While Wikipedia has descriptions of people, places and things, an article should not read like a "how-to" style owner's manual, cookbook, advice column (legal, medical or otherwise) or suggestion box. This includes tutorials, instruction manuals, game guides, and recipes." (Emphasis added)
Puffingbilly says:
- "There is no original research described in this section" [Analysis section].
But WP:VERIFY says:
- "All material in Wikipedia mainspace, including everything in articles, lists and captions, must be verifiable... Any material whose verifiability has been challenged or is likely to be challenged, must include an inline citation that directly supports the material. Any material that needs a source but does not have one may be removed." (Emphasis added)
I hereby challenge the verifiability of the material that Puffingbilly added. I await the addition of citations that directly support the material.
Puffingbilly says:
- "I am a chartered engineer with many years (>50) experience in the design and analysis of electronic circuits. The analysis is mine... It does work as a delta-sigma modulator as the analysis shows. The analysis can be verified by any engineer competent in circuit analysis." (Emphasis added)
But WP:NOR (No Original Research) says:
- "Wikipedia articles must not contain original research. The phrase "original research" (OR) is used on Wikipedia to refer to material—such as facts, allegations, and ideas—for which no reliable, published sources exist. This includes any analysis or synthesis of published material that serves to reach or imply a conclusion not stated by the sources. To demonstrate that you are not adding OR, you must be able to cite reliable, published sources that are directly related to the topic of the article, and directly support the material being presented... The prohibition against OR means that all material added to articles must be attributable to a reliable, published source." (Emphasis added)
BTW, I should mention (because many people don't understand this) that the question of whether something is verifiable is not the same thing as the question of whether it is true, and that I am not at this time expressing any opinion as to whether Puffingbilly's analysis is correct or incorrect. --Guy Macon (talk) 17:31, 19 February 2019 (UTC)
- I refer to https://www.researchgate.net/publication/243767842_Asynchronous_Delta_Sigma_Modulation Puffingbilly (talk) 19:02, 19 February 2019 (UTC)
- "Wikipedia articles must not contain original research. The phrase "original research" (OR) is used on Wikipedia to refer to material—such as facts, allegations, and ideas—for which no reliable, published sources exist. This includes any analysis or synthesis of published material that serves to reach or imply a conclusion not stated by the sources. To demonstrate that you are not adding OR, you must be able to cite reliable, published sources that are directly related to the topic of the article, and directly support the material being presented... The prohibition against OR means that all material added to articles must be attributable to a reliable, published source." (Emphasis added)
- It would save everyone a lot of wasted time if this emphasis was made for every new edit.
Now I find my work retained but altered incorrectly. I refer to https://www.researchgate.net/publication/243767842_Asynchronous_Delta_Sigma_Modulation. Delete it if you must but I believe many people have found it helpful. If you retain it at all I believe it should be restored to the form in which I put it since I have now demonsrated that it is factually correct. Puffingbilly (talk) 19:21, 19 February 2019 (UTC)
- Per Wikipedia:Ownership of content: "All Wikipedia content—articles, categories, templates, and other types of pages—is edited collaboratively. No one, no matter how skilled, or how high-standing in the community, has the right to act as though they are the owner of a particular page."
- It is now obvious that not only are you unwilling to follow our rules, you are not even willing to read them or discuss them. I am now going to delete your unsourced additions. Feel free to try again if you ever decide to provide citations that directly support the material you wish to add. --Guy Macon (talk) 20:13, 19 February 2019 (UTC)
I thought I had supplied the required citation: I refer to https://www.researchgate.net/publication/243767842_Asynchronous_Delta_Sigma_Modulation. In my opinion your judgement is your problem not mine. A deletion was all that was necessary, the unpleasant remarks are an abuse of your position. Because the objection raised was that it did not comply with Wikipedia rules I trust that if it is discovered to comply with the rules it will not be resurrected under another authors name. Because you chose not to invoke the rule but rather make a personal attack on me it is a possibility that that was the scenario you had in mind.Puffingbilly (talk) 01:28, 20 February 2019 (UTC)
You didn't indicate the specific claim that the above reference supports. If you had, and if the ref actualyy supports the claim, that claim would have been retained.
- Re: "I trust that if it is discovered to comply with the rules it will not be resurrected under another authors name." Every time you add anything to Wikipedia you agree to the following:
- By publishing changes, you agree to the Terms of Use, and you irrevocably agree to release your contribution under the CC BY-SA 3.0 License and the GFDL. You agree that a hyperlink or URL is sufficient attribution under the Creative Commons license.
- The edit history contains the URL that gives you the attribution required by the CC BY-SA 3.0 License. Nobody on Wikipedia has the power to change the edit history and thus nobody can take away the attribution. It is the only attribution you will get. In case you didn't notice, changes to Wikipedia articles are not signed.
- Once you hit that "publish changes" button you gave your permission for anyone and everyone to share, copy, distribute, re-use, remix and/or adapt the material. If you have any objection to this, I suggest that in the future you be more careful about the legally binding agreements you agree to. --Guy Macon (talk) 01:45, 20 February 2019 (UTC)
Quite so. I have absolutely no objection. The specific claim is that unclocked SDM do exist and https://www.researchgate.net/publication/243767842_Asynchronous_Delta_Sigma_Modulation supports that. I trust that if the item is resurrected It will be restored to the state it had before the dispute arose. Puffingbilly (talk) 02:20, 20 February 2019 (UTC)
- You can say "I trust..." as many times as you want, but the fact remains that any editor can and will modify it in any way they choose. They might even, you know, include sources. I'm just saying. You would be a lot less annoying if you stopped using the phrase "I trust..." to claim WP:OWNERSHIP. --Guy Macon (talk) 02:35, 20 February 2019 (UTC)
- Well you're not the only one who is annoyed. I'm the one in a hostile environment and you should not be surprised if I get annoying. Puffingbilly (talk) 02:50, 20 February 2019 (UTC)
- It is true that people who refuse to follow our rules often become annoyed with the reaction they get. As an engineer, can I interest you in a little experiment? Why not try following our rules? Those who have tried it generally report that they feel like they are treated very well. You never know unless you try... --Guy Macon (talk) 04:11, 20 February 2019 (UTC)
- In fact, I did modify that section before you removed it, Guy, and included a reference to that paper that Puffingbilly is linking, make makes it very clear that asynchronous delta-sigma modulation is not delta-sigma modulation, but rather an analog modulation technique. I agree with you that the section needs more sources and needs to be consistent with them, but I don't agree with just chucking out what we were working on. Dicklyon (talk) 06:11, 20 February 2019 (UTC)
- Fair enough. I have no problem with you reverting me and putting it all back in. --Guy Macon (talk) 07:10, 20 February 2019 (UTC)
What did I tell you. Don't throw the article away, just the independent minded author. It comes as absolutely no surprise, it was just what I asked for an assurance would not happen. Whatever I say and whatever I produce Guy Macon will insist on having his way. There is no doubt that Guy Macon is the industry specialist and by far the best qualified to describe in any way he sees fit current practice but I doubt if he can communicate to the general public even if he wants to. If he does not recognise that the phrase " sigma delta modulation" in its broadest definition means producing a series of pulses which , when integrated or low pass filtered, produces a reasonable facsimile of the originating waveform and forms a sufficient basis for informing the general public what the mystic phrase "sigma delta modulation" means in the simplest possible way then he rejects the whole point and purpose of constructing the section. He may well say this is not the dominant current practice and this is not how the dominant current practice works but he does the general public a disservice when not allowing the simplest possible meaning of the phrase to be conveyed to them. It is the modulation that is being described not the implementation.There are many ways of producing e.g FM but you would not seek to define FM in terms of any particular implementation.
Your ruling, taken with your definitions of the rules makes it absolutely clear that Wikipedia has no interest in informing the general public of anything other that the state of current technical understanding expressed in the standard technical way and rejects any attempt at clarification in simple terms. Given that fact and if you abide by your own rules you should not allow it to be reinstated by anyone.
Incidently fig 1b and fig 1c and the associated discussion are also in breach of the rules. It carries the warning:- This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (February 2019) (Learn how and when to remove this template message)
If your applying the rules you should delete them also. — Preceding unsigned comment added by Puffingbilly (talk • contribs) 20:36, 20 February 2019 (UTC) Puffingbilly (talk) 23:24, 20 February 2019 (UTC)
Anyway, farewell and welcome to the Humpty Dumpty world.
“When I use a word,’ Humpty Dumpty said in rather a scornful tone, ‘it means just what I choose it to mean — neither more nor less.’ Lewis Carroll, Through the Looking Glass. Puffingbilly (talk) 13:44, 20 February 2019 (UTC) — Preceding unsigned comment added by Puffingbilly (talk • contribs) 13:12, 20 February 2019 (UTC)
- To be fair, Guy Macon is just one more of us volunteer editors trying to do the right thing within the framework of the pillars of Wikipedia. Don't begrudge him that, and don't take his comments as some kind of judgement or final decision on how much your own input might be valued. Rather, try to learn how this enterprise works if you want to make a lasting contribution. If you don't, that's OK, too. Dicklyon (talk) 06:45, 21 February 2019 (UTC)
From hence, ye beauties, undeceived
Know one false step is ne'er retrieved
And be with caution bold.
Not all that tempts your wandering eyes
And heedless hearts is lawful prize,
Not all that glisters gold.
Tomas Gray, "Elegy To A Favourite Cat Drowned In A Bowl Of Goldfishes" Puffingbilly (talk) 13:33, 21 February 2019 (UTC)
You seem to be incapable of understanding that it is the modulation that is being described in this article not its implementation. I invented a simple implementation that illustrated what sigma delta modulation is and did not infringe any copyright. I have been emphatically, disrespectfully and insultingly informed that this breaches Wikipedia rules and so it will always breach the rules no matter how you modify it, and if you modify it to say it does not produce sigma delta modulation then you are mistaken. So far as your expertise in the topic is concerned, judging by your performance so far, you will be hard pressed to produce anything that meets requirement of Wikipedia that it must be understandable by the average reader and so if the average reader wants the information on a particular implementation I would recommend he reads the relevant patents. He will find an excellent History giving many references to relevant patents in "The Evolution of Oversampling Analog-to-Digital Converters" Bruce A. Wooley.
This article has been rated as C-Class on the project's quality scale. See top of page. This suggests you might want to bone up on your communication skills. Puffingbilly (talk) 17:49, 23 February 2019 (UTC)
Incidently, if I read you right, because I do not use high level mathematics to communicate with the average reader, in your ignorance of what a chartered engineer is, you seem to assume I am not familiar with the topic. Try looking it up. Puffingbilly (talk) 17:25, 23 February 2019 (UTC)
My contribution on a practical implementation is also in breach of the rules and if you respect the rules you will delete that also. Puffingbilly (talk) 15:07, 21 February 2019 (UTC)
- Again, why not try following our rules? Try to wrap your head around the concept that maybe, just maybe, 48,126,472 editors who have made 1,247,029,785 edits and created 61,664,317 encyclopedia pages just might know a few more things about creating an encyclopedia than an ineducable person who basically edits one page and refuses to even read the rules he keeps violating. I'm just saying. --Guy Macon (talk) 17:36, 21 February 2019 (UTC)
You still don't understand you are not free to be offensive. Puffingbilly (talk) 18:29, 21 February 2019 (UTC)
Avoid personal attacks. see top of page.
- Evasion noted. --Guy Macon (talk) 18:37, 21 February 2019 (UTC)
This whole mess started with my misunderstanding of the rules. Had I known that and the unpleasant people I would be working with I wouldn't have touched it with a specially disinfected bargepole. Puffingbilly (talk) 13:10, 22 February 2019 (UTC)
The following conversation was initiated by Dicklyon on my talk page. I reproduce it below so that it is easily accessible to everyone and probably represents closure of the interchange. Quote
Delta-sigma modulation issues
[edit]Puffingbilly, if you're willing, stick around and let's try to convert what you've done to a form that will meet Wikipedia's requirements of being WP:Verifiable. User:Guy Macon has agreed to back off while we try to work it out.
For starters, if you can point out any books or papers that approach the explanation or analysis as you do, using a charge-feedback integrator for voltage-to-pulse-rate conversion, we could cite that and make sure the analysis pretty much agrees with it. I find (with this Google book search) a few tantalizing snippets, but I don't have an easy way to get the original articles. For example:
- Electronic Design - Volume 36, Issues 8-12 - Page 54 [1] 1988 – "The basic delta-sigma converter contains two major blocks: a closed-loop modulator and a digital filter (see the figure). ... operates somewhat like a cross between a tracking a-d converter and a charge-balance voltage-to-frequency converter."
- Instruments & Control Systems - Volume 54 - Page 191 [2] – 1981 – ... and up to 10 MHz, outputs. Charge-balancing is a good method of converting voltage to frequency (Fig. ... 12: The "delta-sigma" method is used for voltage-to-frequency conversion when output pulse must be synched to a clock."
Most others contrast V-to-F with delta-sigma, but do not use an unclocked V-to-F circuit like you do to approach, analyze, or explain delta-sigma. I agree it's a valid clever analysis, but without a source it's not the way we should do it in Wikipedia.
Want to help? Dicklyon (talk) 03:15, 24 February 2019 (UTC)
- Given the Wikipedia rules, as I said, I devised it ab initio, and so there will be no reference available, unless you know better,or know of some appeal mechanism, we're stuck. Puffingbilly (talk) 05:54, 24 February 2019 (UTC)
The new caption for Fig. 1 closes the issue as far as I'm concerned. Puffingbilly (talk) 07:34, 6 August 2019 (UTC)
- There might be a somewhat cackhanded way around this problem, with a somewhat limited search, I found these two sites quote the article exactly.
- https://ipfs.io/ipfs/QmXoypizjW3WknFiJnKLwHCnL72vedxjQkDDP1mXWo6uco/wiki/Delta-sigma_modulation.html
- https://www.secret-bases.co.uk/wiki/Sigma-delta_modulation.
- We might quote those as sources or at least demonstrate that the article is well accepted. Puffingbilly (talk) 06:56, 24 February 2019 (UTC)
- No, that would be what we call WP:Citogenesis. Instead, let's look for good sources to help with a rewrite. I have a few books, and ordered the Candy and Temes 1991 edited volume of papers, which might have some older stuff about motivations, analysis, tutorial-ish stuff, etc. Dicklyon (talk) 16:26, 24 February 2019 (UTC)
I have no desire or intent to break the rules.
I've been thinking about the effect of the rules which, with this item as an example, prevents a simply worded tutorial, which would never qualify as a learned paper and was never intended to, nor was it expected to be contentious, being presented in Wikipedia. Because it was not of learned paper quality and deliberately so I think your chances of finding anything published are a good approximation for zero. Sorry I can't help further I don't have much time left and there are other things I need to finish. Best of luck.
If the effect achieved is the effect intended, is it possible that Wikipedia intends that only those who already have had very expensive access to further education may benefit from using Wikipedia? Just asking. Puffingbilly (talk) 09:01, 25 February 2019 (UTC)
Endquote. Puffingbilly (talk) 09:29, 28 February 2019 (UTC)
- No, that's not the intent. If you stick around, you'll learn how it works. Dicklyon (talk) 07:13, 2 March 2019 (UTC)
- OK, found it: a paper that uses the "asynchronous modulate" like Puffingbilly's to model the delta-sigma converter.
- J. Candy and O. Benjamin (September 1981). "The Structure of Quantization Noise from Sigma-Delta Modulation". IEEE Transactions on Communications. 29 (9): 1316–1323.
- Uncorrected quote snipped from OCR'd PDF:
"We now develop a model that is a convenient basis for analyzing the noise generated by sigma-delta modulation. First, consider the asynchronous modulator that uses no tim- ing clocks, as shown in Fig. 4. We let x represent the input level and z represent the integrated difference between the input and the output, y. An impulse of magnitude A is generated at the output whenever z becomes positive. Fig. 5 shows representative waveforms of signals in this modulator. When x is constant, the error z is a regular sawtooth waveform and y a regular stream of impulses, both of frequency x/A. Now modify the modulator to synchronize its output to a clock of period I- as in Fig. 1, where output impulses can occur only when the clock is present and z is positive. Waveforms in Fig. 6 show that the output impulses still occur at an average rate of xlA, (if 0 <x < A/r), but each impulse is delayed from the corresponding asynchronous pulse in order to be aligned with the next clock. The synchronous sawtooth waveform z overshoots positively but returns to its asynchronous value after the impulse occurs."
- So let's cite this and make sure Puffingbilly's development agrees with it. Dicklyon (talk) 04:57, 5 March 2019 (UTC)
- Working on it. Next I want to edit the figures to simplify and remove the figure numbers, which really shouldn't be in the figures. Dicklyon (talk) 01:16, 6 March 2019 (UTC)
- OK, did the figures, and copyedited equations and text some. Dicklyon (talk) 02:35, 7 May 2019 (UTC)
You have described to your own satisfaction what delta sigma modulation isn't. Your challenge must be to describe what delta sigma modulation is. The same as asynchronous delta sigma modulation but clocked? A trivial distinction? Puffingbilly (talk) 04:57, 6 April 2019 (UTC)— Preceding unsigned comment added by Puffingbilly (talk • contribs) 04:44, 6 April 2019 (UTC)
The difficulty, as I see it, is that various digital signal processing methods have been lumped with delta sigma modulation as if it were the same topic. Then clocking becomes important for the purposes of digital signal processing but is irrelevant to the topic of sigma delta modulation. If you can explain why clocking is important to delta sigma modulation, as narrowly defined independent of digital signal processing, and provide suitable references, I will be greatly appreciative and I am certain you will be doing the average reader a great service.Puffingbilly (talk) 08:23, 10 April 2019 (UTC)
- Yes, good ideas. I've been pretty busy, but may work on that. Fundamentally, delta-sigma is a technology for analog-to-digital conversion, and without clocking there's no discreteness, so it's not useful that way. As far as I know, nobody has ever referred to asynchronous delta-sigma modulation as "delta-sigma modulation", because that latter does not include the former. If you find otherwise, let us know. Dicklyon (talk) 23:10, 6 May 2019 (UTC)
If you examine figure 1 you will see that the waveform labelled 2 is the discreteness you assert is not present. It is these impulses which are transmitted as the sigma delta modulation stream with the frequency of impulses proportional to the input voltage. The introduction of clocking merely introduces noise as is discussed in association of Fig 1a. You state that "delta sigma modulation" does not include asynchronous delta-sigma modulation. What is your authority for that statement? Can you in turn cite a source. Fig 1 illustrates the full process of analogue to digital conversion in a form useful for instrumentation. In the form I first presented it this was made very clear. It was also made clear that it was the impulses that were transmitted for the modulation application. Subsequent editing by others has completely masked the original sense. I don't have either the time or the inclination to continually defend myself from idiots so you're stuck with what you've got.Puffingbilly (talk) 09:38, 31 July 2019 (UTC)
Incidently Fig 1 has been mutilated (By you?) so that the full waveform set formerly shown has been truncated which may make its interpretation difficult. So my remark above about Fig. 1 should be modified to read The original Fig. 1 illustrates.... Puffingbilly (talk) 10:24, 31 July 2019 (UTC)
The difficulty many people seem to have with my work may be that I use timing diagrams and block diagrams to illustrate the workings of the circuits under discussion rather than Transfer Functions with which they may be more familiar. I do that deliberately when addressing a relatively non-technical audience (as we do here in Wikipedia) because it does not require them to have a great knowledge of advanced mathematics but is nevertheless specific and accurate and better able to deal with transients and non-linearities and in my opinion is closer to the design process. Due to this unfamiliarity they simply don't read the description in conjunction with the diagrams but dismiss it out of hand. Because of your failure to recognise that fig.1 is a full analogue to digital converter and that the waveform 2 is the delta-sigma modulation stream I wonder if you fall into that category.Puffingbilly (talk) 21:00, 1 August 2019 (UTC)
- Hey, welcome back. Yes, I modified the figures. If I "mutilated" one or more, maybe you can produce what you think it should look like, but without the figure number legend embedded in the image as you had before, and we can discuss whether additional signals contribute to understanding; or just put the old figure here on the talk page for discussion before bothering to modify. I can try to put more time in to helping. As for the discreteness, what you're describing is a frequency, which is analog, not directly convertable to a sequence of discrete symbols as in a sigma-delta bitstream. The pulse frequency modulation is fine as far as it goes, but is not an A-to-D converter. Sigma-delta is an A-to-D strategy in all work that I've seen. Dicklyon (talk) 21:30, 1 August 2019 (UTC)
- Ah, you're referring to the modified SVG's bounding-box problem that I mentioned and asked for help on, in one of edit summaries, I think. The images look good on commons original file, but don't frame right when rendered to a size. I apologize for not figuring that out yet. Maybe there's an invisible box controlling that, that I could maybe find in Inkscape or something. Dicklyon (talk) 21:38, 1 August 2019 (UTC)
The impulses shown at 2 are a sequence of discrete symbols ie. standardised impulses and their frequency is proportional to the input voltage. The elements outside the feedback loop, Counter, Buffer Summing interval, convert the frequency to a number proportional to the average of the input voltage over the Summing Interval. By defining the duration of the impulse interval and the summing interval from the same clock an ADC of great accuracy is achieved. I've said it before but it has disappeared since in the editing. It is this inappropriate editing more than anything that makes me reluctant to persevere. It requires more time than I can spare.Puffingbilly (talk) 22:08, 1 August 2019 (UTC)
If the impulse and summing interval are derived from the same clock it follows they will be clocked and suffer the noise due to clocking.This noise is averaged out at the staticized output outside the feedback loop. If we are generating the sigma delta stream we will only use the elements within the loop,the other elements are then redundant. But this circuit appears under the heading analogue to digital converter and so the full circuit is given. If we are generating the sigma delta stream we can choose to make the impulse generator a triggered monostable which does not reference an external clock and so avoid the noise due to clocking. This is, in my opinion, a trivial difference but clocking may, in any case be necessary for external reasons such as being part of a time division multiplex system.Puffingbilly (talk) 23:10, 1 August 2019 (UTC)Puffingbilly (talk) 19:29, 2 August 2019 (UTC)
- A sequence of asynchronous standardized pulses does not count as what I mean by a discrete symbol sequence. In the asynchronous pulses, the information is all in the timing, primarily the rate. Whereas in a symbol sequence you can just write down the symbols in order and you have the information; sequence of 1s and 0s, typically. That latter is what an actual sigma-delta a-to-d converter produces. Subsequent processing to convert to "PCM" samples is generally much more elaborate than, and much better than, the simple counters you describe. That's how I see it, based on my reading of sources. If you find sources that call the unclocked thing a delta-sigma or sigma-delta converter, I'd like to hear about those. Dicklyon (talk) 22:02, 2 August 2019 (UTC)
As far as I'm concerned the difference between a sequence of 0's and 1's and a sequence of impulse is a distinction without a difference. Remember the object is to convey meaning to the layman in the simplest possible terms. If you're trying to teach a an advanced course the elements of communications technology your description will become clearer to them as the methods of signal processing are further developed but these are things the layman neither wants or needs to know. Puffingbilly (talk) 00:28, 4 August 2019 (UTC)
We have been through this before. Its called an Asynchronous Delta Sigma Modulator and references have been provided.
For the Fig. 1 problem try this link https://commons.wikimedia.org/wiki/File:Block_Diagram_Delta-Sigma_ADC.svg Puffingbilly (talk) 03:01, 3 August 2019 (UTC)
- That still has a figure number and unneeded caption inside the figure. Dicklyon (talk) 03:05, 4 August 2019 (UTC)
This link, at the time of posting, linked to a file dated 3 August, it doesn't now. and it was a reproduction of the file (as modified by you) further modified to convert properly to PDF. Puffingbilly (talk) 06:33, 4 August 2019 (UTC)
When I look at my file again it is dated 2014-02-20 21:23 but curiously it does not contain the unwanted caption. Puffingbilly (talk) 11:05, 4 August 2019 (UTC)
- It's where it always was; I didn't touch it. File:Block Diagram Delta-Sigma ADC(minor change).svg. Dicklyon (talk) 02:58, 4 August 2019 (UTC)
Before making the remark I had searched Wikimedia Commons for Puffingbilly and could not find. Today with the same search I can.Puffingbilly (talk) 06:07, 4 August 2019 (UTC)
- Conveying things simply to readers is good. But giving the impression that "asynchronous delta-sigma modulation" (a very uncommon concept) is a form of "delta-sigma modulation" is still not really supportable by sources. Dicklyon (talk) 03:05, 4 August 2019 (UTC)
I've already explained that the diagrams can refer to either clocked or asynchronous systems so that your implication that it only refers to asynchronous systems is misleading. Puffingbilly (talk) 07:27, 4 August 2019 (UTC)
- I see. I hadn't really grasped your point. But I don't like it, as the diagram doesn't show a clock, and the output is atypically periodic. Dicklyon (talk) 05:01, 5 August 2019 (UTC)
If you want to display the full figure you might find this works: open the svg file, select the entire figure, and shrink it relative to the page boundary. Puffingbilly (talk) 13:25, 4 August 2019 (UTC)
- Yes, that worked! I don't understand what's setting an implicit "page size" though; I see no box in Inkscape around there, but I shrunk it within a larger box. Is there another box invisible to me? Must be. Dicklyon (talk) 05:01, 5 August 2019 (UTC)
You can set page size in the document properties. There is always a page present. You can chose to display page boundaries or not. The object was a simple illustration for the layman. The new caption for Fig. 1 is a satisfactory compromise, thank you. Puffingbilly (talk) 07:25, 6 August 2019 (UTC)
Actually Fig. 1 illustrates an entire ADC. Remarks about the figure as if it were only a modulator will confuse the average reader and it would be nice if such remarks are removed. Puffingbilly (talk) 11:21, 6 August 2019 (UTC)
- See if you like how I fixed that. You're welcome to edit, too, you know. Also, if you have time to work on shrinking the other SVG images, feel free. Over at WP:AN/I they're working on blocking me, so maybe I won't get to them; or maybe I'll get to them later if commons is all I can edit. Dicklyon (talk) 03:16, 9 August 2019 (UTC)
I have uploaded rescaled svg files but I cannot persuade the conversion of these files to pdf to happen. Anyone know the method needed? — Preceding unsigned comment added by Puffingbilly (talk • contribs) 19:10, 26 December 2020 (UTC)
Invention
[edit]At the bottom of the article in the Naming section, there is a claim supported only by WP:PRIMARY sources that the technique was invented in Japan in 1961 by Yasuhiko Yasuda and team. Can someone help VERIFY this? ~Kvng (talk) 20:14, 30 January 2020 (UTC)
- I found one secondary source in the EL section that verifies this. I have promoted this to a reference. ~Kvng (talk) 20:26, 30 January 2020 (UTC)
Latest revision as of 14:18, 29 December 2020 (edit) (undo) (thank)
[edit]Kvng - I made the revisions to correct the impression given that all of fig.1 was devoted to modulation when it is only the closed loop that is needed for that. I've no intention of repeating the correction, I leave you stuck with the incomprehension illustrated by your reversion and your tolerance of the error for the previous many months. As I originated the diagrams Fig 1,a,b.c and the relevant discussion I feel you might have had more respect for my opinion. Fig 1b and 1c are mutilated by careless editing and try as I might I cannot clear the errors.Puffingbilly (talk) 00:28, 31 December 2020 (UTC)
In order to make it plain to the interested observer, if any, I give below the original text.
For the purpose of introduction, Figure 1 illustrates the concept of voltage-to-frequency conversion, in an unclocked form that resembles delta-sigma modulation, and is called asynchronous modulation,[2] asynchronous delta-sigma modulation,[3][4] or free-running modulators.[5]
It will be seen that the whole of Figure 1 is referred to in this original text. The modifications I made to make it clear exactly what part of Figure 1 is devoted to asynchronous delta-sigma modulation, etc. are given below with an explanation of what the rest of Figure 1 is for.
For the purpose of introduction,the closed loop running from points 1 to 5 and back through 2, Figure 1 illustrates the concept of voltage-to-frequency conversion, If it is in an unclocked form it is called asynchronous modulation,[2] asynchronous delta-sigma modulation,[3][4] or free-running modulators.[5]However if the same diagram is clocked, it becomes Sigma-Delta Modulation without question. The effect of clocking as a source of noise is discussed later with reference to Fig. 1a. The remainder of the diagram, the Counter, Buffer and Summing Interval illustrate the extra components necessary to convert the variable frequency signal at 5 into a digital number presentation stored in the Buffer for the full implementation of an Analogue to Digital converter, which, if the same clock is used to time the pulses at 5 and the define the duration of the Summing Interval, will produce a conversion for which the accuracy is only dependant on the precision of the threshold.
Puffingbilly (talk) 02:03, 31 December 2020 (UTC)
- You have left us before. If you'd stay and try to collaborate, we might get somewhere better. Respect for your opinions will increase if you can explain them. If there are errors, explain to us so we can try to go along with you. Your recent edits were not convincing, nor very interpretable. Dicklyon (talk) 02:22, 31 December 2020 (UTC)
It has been plain all along that you do not understand or comprehend circuit analysis, block diagrams or timing diagrams and so your rejection springs from ignorance and is not in the least surprising.Puffingbilly (talk) 03:57, 31 December 2020 (UTC)
- If that's directed at me, I'm pretty sure you're wrong. I've had a pretty successful career involving all those things, including a recent invention involving adaptive sigma-delta conversion in a MEMS microphone. Dicklyon (talk) 02:19, 2 January 2021 (UTC)
Ignorance was the kindest interpretation of your actions, I've told you of the corrections needed, I've even written the the corrections needed, your stubborn refusal to accept them indicates to me that you are deliberately misinforming the general reader.Puffingbilly (talk) 09:05, 9 January 2021 (UTC)
is Asynchronous Delta-Sigma Modulation tangent necessary? Can it be cut and pasted into its own Wikipedia page?
[edit]The "Analog to digital conversion" section starts off with a description which turns out to be of a "freerunning"/"asynchronous"/"unclocked" DSM, and goes into a somewhat lengthy analysis. But the rest of the article seems to be talking specifically about *clocked* DSMs. And every time I've looked at a datasheet for an actually-existing delta-sigma converter chip, it is always a clocked device. I don't think the asynchronous explanation really helps new readers' understanding of clocked DSM. And I'm afraid it may do more harm than good by loosing readers' attention. Can that whole async DSM discussion be cut out of this article and pasted into a new article for "asynchronous delta-sigma modulation"? Or at the very least, can it be moved to the very bottom of this article? Em3rgent0rdr (talk) 00:17, 1 July 2023 (UTC)
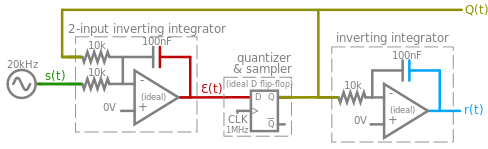
- I've dramatically shortened the Analog-to-digital conversion section, by using a much simpler circuit:Figure 1a: Schematic of simple delta-sigma converter.Figure 1b: Simulated scope view of key voltage signals over time. Each minor vertical division is 1 μs, which corresponds to a sampling event of the 1 MHz clock.
- I removed counting of pulses, and instead just gave a quick note in a "Subsequent Decimation" subheading and referred readers to Decimation (signal processing), Sinc filter, etc., because those steep digital filters are what is really used (not counting of pulses), and requires a longer discussion that may be out of scope of this article.
- My circuit and simulation also use nice colors with simple 1-letter names which makes referring to them much easier than previously. Em3rgent0rdr (talk) 06:17, 2 July 2023 (UTC)