Trapezoidal rule

In calculus, the trapezoidal rule (also known as the trapezoid rule or trapezium rule)[a] is a technique for numerical integration, i.e., approximating the definite integral:
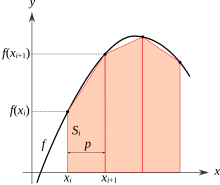
The trapezoidal rule works by approximating the region under the graph of the function as a trapezoid and calculating its area. It follows that

The trapezoidal rule may be viewed as the result obtained by averaging the left and right Riemann sums, and is sometimes defined this way. The integral can be even better approximated by partitioning the integration interval, applying the trapezoidal rule to each subinterval, and summing the results. In practice, this "chained" (or "composite") trapezoidal rule is usually what is meant by "integrating with the trapezoidal rule". Let be a partition of such that and be the length of the -th subinterval (that is, ), then When the partition has a regular spacing, as is often the case, that is, when all the have the same value the formula can be simplified for calculation efficiency by factoring out:.
The approximation becomes more accurate as the resolution of the partition increases (that is, for larger , all decrease).
As discussed below, it is also possible to place error bounds on the accuracy of the value of a definite integral estimated using a trapezoidal rule.
History
[edit]A 2016 Science paper reports that the trapezoid rule was in use in Babylon before 50 BCE for integrating the velocity of Jupiter along the ecliptic.[1]
Numerical implementation
[edit]Non-uniform grid
[edit]When the grid spacing is non-uniform, one can use the formula wherein
Uniform grid
[edit]For a domain discretized into equally spaced panels, considerable simplification may occur. Let the approximation to the integral becomes
Error analysis
[edit]
The error of the composite trapezoidal rule is the difference between the value of the integral and the numerical result:
There exists a number ξ between a and b, such that[2]
It follows that if the integrand is concave up (and thus has a positive second derivative), then the error is negative and the trapezoidal rule overestimates the true value. This can also be seen from the geometric picture: the trapezoids include all of the area under the curve and extend over it. Similarly, a concave-down function yields an underestimate because area is unaccounted for under the curve, but none is counted above. If the interval of the integral being approximated includes an inflection point, the sign of the error is harder to identify.
An asymptotic error estimate for N → ∞ is given by Further terms in this error estimate are given by the Euler–Maclaurin summation formula.
Several techniques can be used to analyze the error, including:[3]
It is argued that the speed of convergence of the trapezoidal rule reflects and can be used as a definition of classes of smoothness of the functions.[7]
Proof
[edit]First suppose that and . Let be the function such that is the error of the trapezoidal rule on one of the intervals, . Then and
Now suppose that which holds if is sufficiently smooth. It then follows that which is equivalent to , or
Since and , and
Using these results, we find and
Letting we find
Summing all of the local error terms we find
But we also have and
so that
Therefore the total error is bounded by
Periodic and peak functions
[edit]The trapezoidal rule converges rapidly for periodic functions. This is an easy consequence of the Euler-Maclaurin summation formula, which says that if is times continuously differentiable with period where and is the periodic extension of the th Bernoulli polynomial.[8] Due to the periodicity, the derivatives at the endpoint cancel and we see that the error is .
A similar effect is available for peak-like functions, such as Gaussian, Exponentially modified Gaussian and other functions with derivatives at integration limits that can be neglected.[9] The evaluation of the full integral of a Gaussian function by trapezoidal rule with 1% accuracy can be made using just 4 points.[10] Simpson's rule requires 1.8 times more points to achieve the same accuracy.[10][11]
Although some effort has been made to extend the Euler-Maclaurin summation formula to higher dimensions,[12] the most straightforward proof of the rapid convergence of the trapezoidal rule in higher dimensions is to reduce the problem to that of convergence of Fourier series. This line of reasoning shows that if is periodic on a -dimensional space with continuous derivatives, the speed of convergence is . For very large dimension, the shows that Monte-Carlo integration is most likely a better choice, but for 2 and 3 dimensions, equispaced sampling is efficient. This is exploited in computational solid state physics where equispaced sampling over primitive cells in the reciprocal lattice is known as Monkhorst-Pack integration.[13]
"Rough" functions
[edit]For functions that are not in C2, the error bound given above is not applicable. Still, error bounds for such rough functions can be derived, which typically show a slower convergence with the number of function evaluations than the behaviour given above. Interestingly, in this case the trapezoidal rule often has sharper bounds than Simpson's rule for the same number of function evaluations.[14]
Applicability and alternatives
[edit]The trapezoidal rule is one of a family of formulas for numerical integration called Newton–Cotes formulas, of which the midpoint rule is similar to the trapezoid rule. Simpson's rule is another member of the same family, and in general has faster convergence than the trapezoidal rule for functions which are twice continuously differentiable, though not in all specific cases. However, for various classes of rougher functions (ones with weaker smoothness conditions), the trapezoidal rule has faster convergence in general than Simpson's rule.[14]
Moreover, the trapezoidal rule tends to become extremely accurate when periodic functions are integrated over their periods, which can be analyzed in various ways.[7][11] A similar effect is available for peak functions.[10][11]
For non-periodic functions, however, methods with unequally spaced points such as Gaussian quadrature and Clenshaw–Curtis quadrature are generally far more accurate; Clenshaw–Curtis quadrature can be viewed as a change of variables to express arbitrary integrals in terms of periodic integrals, at which point the trapezoidal rule can be applied accurately.
Example
[edit]The following integral is given:
- Use the composite trapezoidal rule to estimate the value of this integral. Use three segments.
- Find the true error for part (a).
- Find the absolute relative true error for part (a).
Solution
- The solution using the composite trapezoidal rule with 3 segments is applied as follows.
Using the composite trapezoidal rule formula
- The exact value of the above integral can be found by integration by parts and is So the true error is
- The absolute relative true error is
See also
[edit]- Gaussian quadrature
- Newton–Cotes formulas
- Rectangle method
- Romberg's method
- Simpson's rule
- Volterra integral equation § Numerical Solution using Trapezoidal Rule
Notes
[edit]- ^ Ossendrijver, Mathieu (Jan 29, 2016). "Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph". Science. 351 (6272): 482–484. doi:10.1126/science.aad8085. PMID 26823423. S2CID 206644971.
- ^ Atkinson (1989, equation (5.1.7))
- ^ (Weideman 2002, p. 23, section 2)
- ^ Atkinson (1989, equation (5.1.9))
- ^ Atkinson (1989, p. 285)
- ^ Burden & Faires (2011, p. 194)
- ^ a b (Rahman & Schmeisser 1990)
- ^ Kress, Rainer (1998). Numerical Analysis, volume 181 of Graduate Texts in Mathematics. Springer-Verlag.
- ^ Goodwin, E. T. (1949). "The evaluation of integrals of the form". Mathematical Proceedings of the Cambridge Philosophical Society. 45 (2): 241–245. doi:10.1017/S0305004100024786. ISSN 1469-8064.
- ^ a b c Kalambet, Yuri; Kozmin, Yuri; Samokhin, Andrey (2018). "Comparison of integration rules in the case of very narrow chromatographic peaks". Chemometrics and Intelligent Laboratory Systems. 179: 22–30. doi:10.1016/j.chemolab.2018.06.001. ISSN 0169-7439.
- ^ a b c (Weideman 2002)
- ^ "Euler-Maclaurin Summation Formula for Multiple Sums". math.stackexchange.com.
- ^ Thompson, Nick. "Numerical Integration over Brillouin Zones". bandgap.io. Retrieved 19 December 2017.
- ^ a b (Cruz-Uribe & Neugebauer 2002)
References
[edit]- Atkinson, Kendall E. (1989), An Introduction to Numerical Analysis (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50023-0
- Rahman, Qazi I.; Schmeisser, Gerhard (December 1990), "Characterization of the speed of convergence of the trapezoidal rule", Numerische Mathematik, 57 (1): 123–138, doi:10.1007/BF01386402, ISSN 0945-3245, S2CID 122245944
- Burden, Richard L.; Faires, J. Douglas (2011), Numerical Analysis (9th ed.), Brooks/Cole
- Weideman, J. A. C. (January 2002), "Numerical Integration of Periodic Functions: A Few Examples", The American Mathematical Monthly, 109 (1): 21–36, doi:10.2307/2695765, JSTOR 2695765
- Cruz-Uribe, D.; Neugebauer, C. J. (2002), "Sharp Error Bounds for the Trapezoidal Rule and Simpson's Rule" (PDF), Journal of Inequalities in Pure and Applied Mathematics, 3 (4)
External links
[edit]- Trapezium formula. I.P. Mysovskikh, Encyclopedia of Mathematics, ed. M. Hazewinkel
- Notes on the convergence of trapezoidal-rule quadrature
- An implementation of trapezoidal quadrature provided by Boost.Math





![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)












![{\displaystyle {\begin{aligned}\int _{a}^{b}f(x)\,dx&\approx {\frac {\Delta x}{2}}\sum _{k=1}^{N}\left(f(x_{k-1})+f(x_{k})\right)\\[1ex]&={\frac {\Delta x}{2}}{\Biggl (}f(x_{0})+2f(x_{1})+2f(x_{2})+2f(x_{3})+\dotsb +2f(x_{N-1})+f(x_{N}){\Biggr )}\\[1ex]&=\Delta x\left({\frac {f(x_{N})+f(x_{0})}{2}}+\sum _{k=1}^{N-1}f(x_{k})\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbf262ab114addeef44142cbc4afc1286fcceeaa)


![{\displaystyle {\text{E}}=\int _{a}^{b}f(x)\,dx-{\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69bbf6fd3feca24e5b54d2648875a66b554edce8)

![{\displaystyle {\text{E}}=-{\frac {(b-a)^{2}}{12N^{2}}}{\big [}f'(b)-f'(a){\big ]}+O(N^{-3}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd5ac77d42c690b44c7f4e0046485375e36abae)


![{\displaystyle g_{k}(t)={\frac {1}{2}}t[f(a_{k})+f(a_{k}+t)]-\int _{a_{k}}^{a_{k}+t}f(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f7adf3c2fb86c683193757c4143af68d348ff66)

![{\displaystyle [a_{k},a_{k}+h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4278d1e363fde482a2cf9e04b012205776c5a9a3)
![{\displaystyle {dg_{k} \over dt}={1 \over 2}[f(a_{k})+f(a_{k}+t)]+{1 \over 2}t\cdot f'(a_{k}+t)-f(a_{k}+t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0340ea2941deffa7beed8c8595a4aaf897d797bd)














![{\displaystyle \sum _{k=1}^{N}g_{k}(h)={\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]-\int _{a}^{b}f(x)dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99801ff97304978cf8907920a96c7c8e777d9b84)


![{\displaystyle -{\frac {f''(\xi )h^{3}N}{12}}\leq {\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]-\int _{a}^{b}f(x)dx\leq {\frac {f''(\xi )h^{3}N}{12}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2f3d6ee982441634a1ba4a23b22400f4f8f532e)
![{\displaystyle {\text{error}}=\int _{a}^{b}f(x)\,dx-{\frac {b-a}{N}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{N-1}f\left(a+k{\frac {b-a}{N}}\right)\right]={\frac {f''(\xi )h^{3}N}{12}}={\frac {f''(\xi )(b-a)^{3}}{12N^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3499f9b1f021ad0084174d2d3a0deec83f5885ce)


















