Wikipedia:Reference desk/Archives/Mathematics/2008 June 26
| Mathematics desk | ||
|---|---|---|
| < June 25 | << May | June | Jul >> | June 27 > |
| Welcome to the Wikipedia Mathematics Reference Desk Archives |
|---|
| The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
June 26
[edit]what is the solution to this
[edit]x^x = y^y
Where x < y
202.147.44.80 (talk) 03:09, 26 June 2008 (UTC)
- There are an infinite number of solutions. If you have a graphing calculator, zoom in to see that the function xx is initially decreasing near x = 0. As a hint for an exact solution, look at the number 0.5 (think about it). 76.238.8.4 (talk) 04:13, 26 June 2008 (UTC)
- I guess the question should be read as 'What function f it is, such that for any x from properly chosen domain its output y=f(x) satisfies xx=yy?' Of course f not being Identity function. --CiaPan (talk) 10:03, 26 June 2008 (UTC)
- For 0 < x < e-1
- where W is the Lambert W function. Note that for x in the given range, we have −e-1 < x ln(x) < 0 and W(x ln(x)) has two values, one of which is ln(x). Take the other value of W(x ln(x)), for which |W(x ln(x))| < |ln(x)|, and you have y > x such that yy = xx. Gandalf61 (talk) 13:01, 26 June 2008 (UTC)
- For 0 < x < e-1
Fractional Coloring
[edit]Is the fractional chromatic number of a graph necessarily close to the regular chromatic number, or can they be extremely different? Black Carrot (talk) 04:49, 26 June 2008 (UTC)
They are within a logarithmic factor of each other according to [[1]]. 84.239.133.47 (talk) 11:23, 26 June 2008 (UTC)
Logic
[edit]I have a (subsequent, follow-up) question, but must first begin with a preliminary clarifying question ... it's about logic. I have heard / read / studied that ... you can never prove a negative statement ... you can only prove a positive statement. Thus, for example, one cannot prove "I did not visit Hawaii" ... but one can prove "I did visit Hawaii." That is, it is logically impossible to prove the negative statement. In fact, in criminal trials (in the USA), this is why the government can prove that the defendant is "guilty" (he did commit the crime) ... but the defense can never prove that the defendant is "innocent" (he did not commit the crime) ... at the very best, the defense can merely conclude that the defendant is "not guilty" (meaning, there is not enough evidence to prove that he did commit the crime). So, is my understanding correct? That one can logically prove that an event happened, but one cannot logically prove that an event did not happen? That it is logically impossible to prove a negative statement? Thanks. (Joseph A. Spadaro (talk) 10:55, 26 June 2008 (UTC))
- Do you mean one can prove that, say, 'two is less than three', but can't prove that 'two is not greater than three'...? --CiaPan (talk) 11:10, 26 June 2008 (UTC)
- No, I don't think that's what I mean. "Two is less than three" is a factual statement ... it is a statement of being or existence, no? It is either true or false, period. I am referring to proving events ... like I did not go to Hawaii ... I did not commit the murder ... I did not eat an apple. Etc. I think "events occuring" are different than "states of being" or factual statements like "2 is less than three" or "Bush is the current President". I think? (Joseph A. Spadaro (talk) 12:37, 26 June 2008 (UTC))
- This isn't really a matter of logic, at least as the term is used in mathematics. As CiaPan points out, any statement is logically equivalent to a negative statement (can you prove that you didn't not visit Hawaii?). In any case, in the sense of 'prove' used in mathematics, nothing about the real world can be proved. It's more about the amount of evidence needed to establish certain claims about the real world. Thus if you had lots of pictures of yourself in Hawaii, eyewitness reports, etc, we would probably be forced to admit that you'd been to Hawaii. On the other hand, far more evidence would be required to prove that you'd never been there: a reliable account of all your movements from birth, a totally reliable list of everyone who's ever made it to Hawaii, including (somehow) people using false names or illegal channels, or somesuch thing. It is in this sense that the existence of (for example) Russell's teapot cannot be disproved. Algebraist 11:19, 26 June 2008 (UTC)
- Forgot to say: I believe this sort of thing is part of what philosophers call 'logic', so you might want to try the humanities desk. And I don't think your second example is really applicable: one could establish beyond reasonable doubt that someone had not committed a crime, for example by showing that they were on another continent at the time. The point in criminal trials is that the burden of proof rests with the prosecution, so the defence doesn't have to prove innocence. Algebraist 11:23, 26 June 2008 (UTC)
- Algebraist ... you are convoluting the (real) issue by adding in standards such as "beyond reasonable doubt". That is merely an artificial legal concept that man has injected into legal proceedings. Of course, we can prove "beyond reasonable doubt" that Johnny did not kill Jimmy. But can it be proven absolutely (that is, wthout the limiting qualification or reduced standard of "beyond reasonable doubt"?) I thought that I had heard / read / studied that the negative can never be proved ( or is it, "proven" )? (Joseph A. Spadaro (talk) 12:45, 26 June 2008 (UTC))
- I agree the humanities desk might be better suited for this type of logic problem. However I agree mostly with your first point..
- It is easy to proove A (ie A=I've been to paris) because all I need is a single example of proof (and a level of trust) and there you go.
- However to proove (not A) (ie I've not been to paris) is more difficult because it requires proof by exhaustion - however it's not logically impossible - but it is much more difficult to proove.87.102.86.73 (talk) 12:25, 26 June 2008 (UTC)
- So, "User 87" ... you are saying that to prove "I have never been to Paris" would be the logical equivalent of taking every other moment in my life (all 8 zillion of them) and "proving that I was in Spain / USA / Japan / etc. (anywhere that is non-Paris)" ...? And adding up all those (hypothetical) 8 zillion proofs logicallys amounts to the equivalent proof that "I have never been to Paris" ... yes? (Joseph A. Spadaro (talk) 12:51, 26 June 2008 (UTC))
- Yes, that's what proof by exhaustion involves, hence it's name. In a purely mathematical sense it's possible, obviously it's easier to do this for the last week rather than you whole life..87.102.86.73 (talk) 12:59, 26 June 2008 (UTC)
- I think you are getting to the heart of the issue here, which is dealing with an issue of quantification. While universal quantification is possible is mathematics where the domain of quantification can be appropriately axiomaticly controlled, it isn't feasible (and certainly isn't practical) in the physical world. The issue of not being able to prove a negative boils down to the equivalence . What you really can't do is prove universally quantified propositions unless you have some suitable controls on the universality. -- Leland McInnes (talk) 16:20, 26 June 2008 (UTC)
- Yes, that's what proof by exhaustion involves, hence it's name. In a purely mathematical sense it's possible, obviously it's easier to do this for the last week rather than you whole life..87.102.86.73 (talk) 12:59, 26 June 2008 (UTC)
- So, "User 87" ... you are saying that to prove "I have never been to Paris" would be the logical equivalent of taking every other moment in my life (all 8 zillion of them) and "proving that I was in Spain / USA / Japan / etc. (anywhere that is non-Paris)" ...? And adding up all those (hypothetical) 8 zillion proofs logicallys amounts to the equivalent proof that "I have never been to Paris" ... yes? (Joseph A. Spadaro (talk) 12:51, 26 June 2008 (UTC))
- To the OP:I used 'beyond reasonable doubt', because that's the highest standard we can expect in 'proofs' of statements about the real world. If we admit unreasonable doubts (as we do in mathematics), then you can't prove either positive or negative statements: you say you've been to Hawaii, and I say neither you nor Hawaii exist, and I'm just a brain in a vat orbiting the third planet of Betelgeuse. Algebraist 13:31, 26 June 2008 (UTC)
- Generally, when we want to "prove" (in the legal sense) a negative, we do so by proving a contradictory positive. For example, I can't direct prove "I did not shoot the deputy", but I can directly prove "I was busy shooting the sheriff at the time the deputy was shot", which means I can't have shot the deputy. In other words, I have an alibi. --Tango (talk) 14:14, 26 June 2008 (UTC)
- Yes, of course you can prove a negative statement ! If I prove that this horse is dead, then I have also proved that this horse is not alive. If I prove that this cow has exactly four legs, then I have also proved that this cow does not have exactly three legs; does not have exactly five legs etc. etc. Even simpler, if I prove that any statement X is true, then I have also proved that X is not false - and vice versa. See this essay for a readable analysis by a professional philosopher. (Perhaps you were thinking of the negative proof fallacy ??). Gandalf61 (talk) 14:19, 26 June 2008 (UTC)
- Proving a negative statement (X does not exist, I never went to Hawaii) needs the whole domain of potential instances to be proven empty (X exists nowhere, my name is not on any hotel register in Hawaii), which may be difficult but not impossible. It is easy if a contradictory proved positive statement preempts the whole domain (Y exists everywhere, Hawaiians would certainly remember my face if I had ever shown it there but they don't). Proving a positive statement (an X exists, I visited Hawaii) needs no consideration of domain (look at this X here!, look at this pic of me with a hula girl!). In legal trials the defence does not have to prove the defendent never committed a crime, only that the positive assertion by the prosecutor is insufficiently proven. Cuddlyable3 (talk) 14:53, 26 June 2008 (UTC)
- From a mathematical perspective, negation is a relationship between two logical statements, not a property of a single logical statement. For example, the statement "This jar is open." is the negation of the statement "This jar is closed.", and vice versa. However, it's not the case that one of these statements is "the negative" and the other is "the positive". So from a mathematical perspective, there is no (meaningful) way to categorize statements into two categories, "positive statements" and "negative statements". The question, "Can I prove a negative statement?" doesn't have any mathematical meaning.
- From a non-mathematical perspective, we have an intuitive notion that some statements (e.g., "I have been to Hawaii.") are vaguely "positive" and that other statements (e.g., "I have not been to Hawaii.") are vaguely negative. It frequently is easier to find convincing evidence supporting a true positive-feeling statement than supporting a true negative-feeling statement; but this general tendency has nothing to do with mathematics. Eric. 86.153.207.223 (talk) 01:45, 27 June 2008 (UTC)
- I think this definition of "negative" means "prove that a specific event didn't occur" (prove you were never in Hawaii, didn't commit the murder, etc.). This definition doesn't apply to states, like "open" and "closed", where, as just stated, neither is any more negative than the other. StuRat (talk) 04:46, 3 July 2008 (UTC)
Straightness
[edit]What is the best way to measure the straightness of a line? For example, if I wanted to objectively compare 2 roads in terms of their relative straightness, how would I do this? 12.147.18.2 (talk) 18:48, 26 June 2008 (UTC)
- You could take a sum of the a function of the deviation (at right angles) from a central straight line, measured at regular intervals, and then divide by the distance.. A suitable function would be the absolute value, |x| or x squared amongst others.
- In general some sort of statistical analysis of the deviation from straightness would be required.87.102.86.73 (talk) 19:03, 26 June 2008 (UTC)
- "Best" is a little vague. For a somewhat mathematically rigorous idea, try measuring the mathematical curvature of the centerline at various points, and proceed as the anon suggests (sum them). For a practical method, try comparing the mileage on a car driving the road versus the distance from start to finish as the crow flies. The shortest path between two points is a straight line, and if the roads are approximately straight this should work, though it obviously fails for two loops around a city. JackSchmidt (talk) 19:20, 26 June 2008 (UTC)
- "Straight" is a vague term. 87.102's definition is "proximity to a straight line", which isn't bad, but leads to some counterintuitive results. For example: say Trip A involves driving 10 miles north, then 10 miles east. Trip B involves driving 1 mile north, then 1 mile east, then repeating that 10 times. By this definition, Trip B would be much straighter than Trip A. If I were driving it, I'd certainly consider Trip A straighter.
- Instead, I'd suggest a measure of the ratio between a straight line and a non-straight line, with the same endpoints. If it's 8 miles as the crow flies between points R and S, and your route takes 10 miles, you have a straightness of 0.8. jeffjon (talk) 19:20, 26 June 2008 (UTC)
- Your metric wouldn't support the conclusion that Trip A in your example is straighter. It would rate Trip A and Trip B the same (). --Prestidigitator (talk) 19:51, 26 June 2008 (UTC)
- Perhaps some angle turned per unit length metric might be what you wish?87.102.86.73 (talk) 19:58, 26 June 2008 (UTC)
- Your metric wouldn't support the conclusion that Trip A in your example is straighter. It would rate Trip A and Trip B the same (). --Prestidigitator (talk) 19:51, 26 June 2008 (UTC)
- You may even calculate the sum (or integral) of absolute values of all turns your road takes. However this may be misleading, too. Say you go straight from point X to Y, but you take a little loop (like the lowercase phi letter) at the halfway. The loop does not make a big change in your trip, however it adds from 2π up to about 3π radians to the 'total direction change'. Another counterexample are piecewise straight lines with a single right angle turn on the picture below:
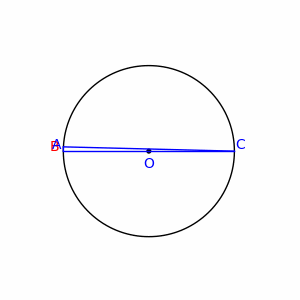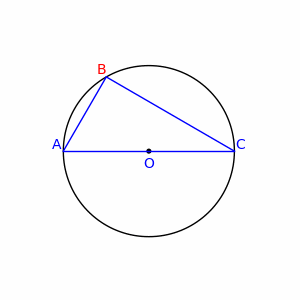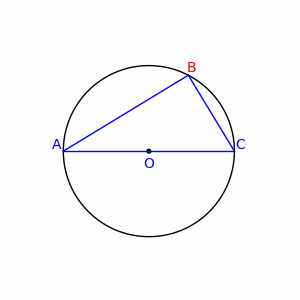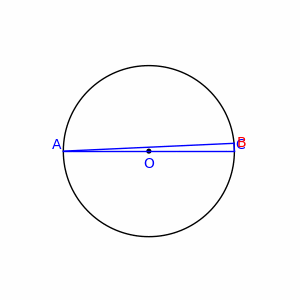
They all have the same 'total direction change' equal 90°, however those for B close to A or to C seem more 'straight' than those wih B far apart from AC line. CiaPan (talk) 09:04, 27 June 2008 (UTC)
CiaPan (talk) 09:04, 27 June 2008 (UTC)
- You may even calculate the sum (or integral) of absolute values of all turns your road takes. However this may be misleading, too. Say you go straight from point X to Y, but you take a little loop (like the lowercase phi letter) at the halfway. The loop does not make a big change in your trip, however it adds from 2π up to about 3π radians to the 'total direction change'. Another counterexample are piecewise straight lines with a single right angle turn on the picture below:
Being more specific might help here - did you mean the straightness of relatively straight lines, or the straightness of obviously curved lines.(see radius of curvature)87.102.86.73 (talk) 19:58, 26 June 2008 (UTC)
- How about just dividing the length of the line by the distance of its endpoints to get a measure of straigtness? – b_jonas 12:05, 27 June 2008 (UTC)
- Yeah, that's a much clearer way of stating what I suggested above. Prestidigitator pointed out one shortcoming, but it seems to me like the closest to workable, pending any clarification from the OP. jeffjon (talk) 12:32, 27 June 2008 (UTC)
One might also consider the methods described in the article Tortuosity, although some of them have already been mentioned here. --Martynas Patasius (talk) 11:39, 28 June 2008 (UTC)
- How about calculating the aspect ratio of the smallest rectangle that contains the line ? Take the previously mentioned examples (A) (10 units north, 10 units east) and (B) (1 unit north, 1 unit east, repeated 10 times). The smallest rectangle containing A is by and has an aspect ratio of . The smallest rectangle containing B is by and has an aspect ratio of . B is thus 10 times straighter than A. Turiacus (talk) 22:33, 29 June 2008 (UTC)
Matrix definition
[edit]Hi, where does the term "matrix" come from? --88.104.167.212 (talk) 19:17, 26 June 2008 (UTC)
- Matrix_(mathematics)#History states that "The term "matrix" was coined in 1848 by J. J. Sylvester" - the word is much older, see http://www.etymonline.com/index.php?term=matrix
87.102.86.73 (talk) 20:04, 26 June 2008 (UTC)
Thank you - --88.104.167.212 (talk) 06:10, 27 June 2008 (UTC)
- And Sylvester may have had this type of matrix in mind when he coined the term (although I can't immediately find a source for this). Gandalf61 (talk) 08:41, 27 June 2008 (UTC)









