Jump to content

Capsid

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by A412 (talk | contribs) at 18:07, 21 January 2012 (Repairing links to disambiguation pages - You can help!). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Schematic of a Cytomegalovirus
3D model of Helical capsid structure
For the leaf bug, see Miridae.

A capsid is the protein shell of a virus. It consists of several oligomeric structural subunits made of protein called protomers. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomeres. The capsid encloses the genetic material of the virus.

Capsids are broadly classified according to their structure. The majority of viruses have capsids with either helical or icosahedral [1][2] structure. Some viruses, such as bacteriophages, have developed more complicated structures due to constraints of elasticity and electrostatics.[3] The icosahedral shape, which has 20 equilateral triangular faces, approximates a sphere, while the helical shape is cylindrical.[4] The capsid faces may consist of one or more proteins. For example, the foot-and-mouth disease virus capsid has faces consisting of three proteins named VP1–3.[5]

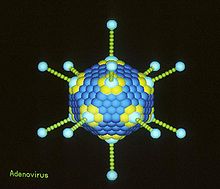
Icosahedral capsid of an Adenovirus

Some viruses are enveloped, meaning that the capsid is coated with a lipid membrane known as the viral envelope. The envelope is acquired by the capsid from an intracellular membrane in the virus' host; some examples would include the inner nuclear membrane, the golgi membrane, and the cell's outer membrane.[6]

Once the virus has infected the cell, it will start replicating itself, using the mechanisms of the infected host cell. During this process, new capsid subunits are synthesized according to the genetic material of the virus, using the protein biosynthesis mechanism of the cell. During the assembly process, a portal subunit is assembled at one vertex of the capsid. Through this portal, viral DNA or RNA is transported into the capsid.[7] The structure and assembly of the herpes virus capsid portal protein has been imaged via cryo-electron microscopy.[8]

It is this capsid or protein shell that makes protective vaccines a possibility. Structural analyses of major capsid protein (MCP) architectures have been used to categorise viruses into families. For example, the bacteriophage PRD1, Paramecium bursaria Chlorella algal virus, and mammalian adenovirus have been placed in the same family.[9]

T-number

Virus capsid T-numbers

Icosahedral virus capsids are typically assigned a T-number to describe the relation between the number of pentagons and hexagons i.e. their quasi-symmetry in the capsid shell. The T-number idea was originally developed to explain the quasi-symmetry by Caspar and Klug in 1962.[10]

For example, a purely icosahedral virus has a T-number of 1 (usually written, T=1) and a truncated icosahedron is assigned T=3. The T-number is calculated by (1) applying a grid to the surface of the virus with coordinates h and k, (2) counting the number of steps between successive pentagons on the virus surface, (3) applying the formula:

=

where and h and k are the distances between the successive pentagons on the virus surface for each axis (see figure on right). The larger the T-number the more hexagons are present relative to the pentagons.[11][12]

Representation of Viral Capsid T-numbers up to (6,6)
capsid parameters hexagon/pentagon system triangle system
(h,k) T # hex Conway notation image geometric name # tri Conway notation image geometric name
(1,0) 1 0 D Dodecahedron Dodecahedron 20 I Icosahedron Icosahedron
(1,1) 3 20 tI
dkD		 Truncated icosahedron Truncated icosahedron 60 kD Pentakis dodecahedron Pentakis dodecahedron
(2,0) 4 30 cD=t5daD Truncated rhombic triacontahedron Truncated rhombic triacontahedron 80 k5aD 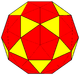Pentakis icosidodecahedron Pentakis icosidodecahedron
(2,1) 7 60 dk5sD 140 k5sD Pentakis snub dodecahedron
(3,0) 9 80 dktI 180 ktI Hexapentakis truncated icosahedron
(2,2) 12 110 dkt5daD 240 kt5daD Hexapentakis truncated rhombic triacontahedron
(3,1) 13 120 260
(4,0) 16 150 ccD 320 dccD
(3,2) 19 180 380
(4,1) 21 200 dk5k6stI
tk5sD		 420 k5k6stI
kdk5sD		 Hexapentakis snub truncated icosahedron
(5,0) 25 240 500
(3,3) 27 260 tktI 540 kdktI
(4,2) 28
(5,1) 31
(6,0) 36 350 tkt5daD 720 kdkt5daD
(4,3) 37
(5,2) 39
(6,1) 43
(4,4) 48 470 dadkt5daD 960 k5k6akdk5aD
(6,2) 48
(5,3) 49
(5,4) 61
(6,3) 64
(5,5) 75
(6,4) 76
(6,5) 91
(6,6) 108
...


T-numbers can be represented in different ways, for example T=1 can only be represented as a Icosahedron or a Dodecahedron and, depending on the type of quasi-symmetry, T=3 can be presented as a Truncated_dodecahedron, an Icosidodecahedron, or a Truncated icosahedron and their respective duals a Triakis icosahedron, a Rhombic triacontahedron, or a Pentakis dodecahedron. [13]

References

  1. ^ Lidmar J, Mirny L, Nelson, DR (2003). "Virus shapes and buckling transitions in spherical shells". Phys. Rev. E. 68 (5): 051910. doi:10.1103/PhysRevE.68.051910.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  2. ^ Vernizzi G, Olvera de la Cruz M (2007). "Faceting ionic shells into icosahedra via electrostatics". Proc. Natl. Acad. Sci. USA. 104 (47): 18382–18386. doi:10.1073/pnas.0703431104.
  3. ^ Vernizzi G, Sknepnek R, Olvera de la Cruz M (2011). "Platonic and Archimedean geometries in multicomponent elastic membranes". Proc. Natl. Acad. Sci. USA. 108 (11): 4292–4296. doi:10.1073/pnas.1012872108. PMC 3060260. PMID 21368184.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  4. ^ Branden, Carl and Tooze, John (1991). Introduction to Protein Structure. New York: Garland. pp. 161–162. ISBN 0-8153-0270-3.{{cite book}}: CS1 maint: multiple names: authors list (link)
  5. ^ "Virus Structure (web-books.com)".
  6. ^ Alberts, Bruce; Bray, Dennis; Lewis, Julian; Raff, Martin; Roberts, Keith; Watson, James D. (1994). Molecular Biology of the Cell (4 ed.). p. 280.{{cite book}}: CS1 maint: multiple names: authors list (link)
  7. ^ Newcomb WW, Homa FL, Brown JC (2005). "Involvement of the Portal at an Early Step in Herpes Simplex Virus Capsid Assembly". Journal of Virology. 79 (16): 10540–6. doi:10.1128/JVI.79.16.10540-10546.2005. PMC 1182615. PMID 16051846. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)
  8. ^ Cardone G, Winkler DC, Trus BL, Cheng N, Heuser JE, Newcomb WW, Brown JC, Steven AC (2007-05-10). "Visualization of the Herpes Simplex Virus Portal in situ by Cryo-electron Tomography". Virology. 361 (2): 426–34. doi:10.1016/j.virol.2006.10.047. PMC 1930166. PMID 17188319.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  9. ^ Khayat et al. classified Sulfolobus turreted icosahedral virus (STIV) and Laurinmäki et al. classified bacteriophage Bam35 – Proc. Natl. Acad. Sci. U.S.A. 103, 3669 (2006); 102, 18944 (2005); Structure 13, 1819 (2005)
  10. ^ Caspar, D. L. D. and Klug, A. (1962). "Physical Principles in the Construction of Regular Viruses". Cold Spring Harbor Symp. Quant. Biol. 27: 1–24. PMID 14019094.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  11. ^ Mannige RV, Brooks CL III (2010). "Periodic Table of Virus Capsids: Implications for Natural Selection and Design". PLoS ONE. 5 (3): e9423. doi:10.1371/journal.pone.0009423.{{cite journal}}: CS1 maint: unflagged free DOI (link)
  12. ^ "T-number index". VIPERdb. La Jolla, CA: The Scripps Research Institute. doi:10.1093/nar/gkn840. Retrieved March 17, 2011. {{cite web}}: External link in |work= (help)
  13. ^ K. V. Damodaran, Vijay S. Reddy, John E. Johnson and Charles L. Brooks III (2002). "A General Method to Quantify Quasi-equivalence in Icosahedral Viruses". J. Mol. Biol. 324 (4): 723–737. doi:10.1016/S0022-2836(02)01138-5. PMID 12460573.{{cite journal}}: CS1 maint: multiple names: authors list (link)

Template:Link GA

Retrieved from "https://en.wikipedia.org/w/index.php?title=Capsid&oldid=472465736"