Scale (music)

In music theory, a scale is "any consecutive series of notes that form a progression between one note and its octave", typically by order of pitch or fundamental frequency.[1][2]
The word "scale" originates from the Latin scala, which literally means "ladder". Therefore, any scale is distinguishable by its "step-pattern", or how its intervals interact with each other.[1][2]
Often, especially in the context of the common practice period, most or all of the melody and harmony of a musical work is built using the notes of a single scale, which can be conveniently represented on a staff with a standard key signature.[3]
Due to the principle of octave equivalence, scales are generally considered to span a single octave, with higher or lower octaves simply repeating the pattern. A musical scale represents a division of the octave space into a certain number of scale steps, a scale step being the recognizable distance (or interval) between two successive notes of the scale.[4] However, there is no need for scale steps to be equal within any scale and, particularly as demonstrated by microtonal music, there is no limit to how many notes can be injected within any given musical interval.
A measure of the width of each scale step provides a method to classify scales. For instance, in a chromatic scale each scale step represents a semitone interval, while a major scale is defined by the interval pattern W–W–H–W–W–W–H, where W stands for whole step (an interval spanning two semitones, e.g. from C to D), and H stands for half-step (e.g. from C to D♭). Based on their interval patterns, scales are put into categories including pentatonic, diatonic, chromatic, major, minor, and others.
A specific scale is defined by its characteristic interval pattern and by a special note, known as its first degree (or tonic). The tonic of a scale is the note selected as the beginning of the octave, and therefore as the beginning of the adopted interval pattern. Typically, the name of the scale specifies both its tonic and its interval pattern. For example, C major indicates a major scale with a C tonic.
Background
[edit]Scales, steps, and intervals
[edit]
Scales are typically listed from low to high pitch. Most scales are octave-repeating, meaning their pattern of notes is the same in every octave (the Bohlen–Pierce scale is one exception). An octave-repeating scale can be represented as a circular arrangement of pitch classes, ordered by increasing (or decreasing) pitch class. For instance, the increasing C major scale is C–D–E–F–G–A–B–[C], with the bracket indicating that the last note is an octave higher than the first note, and the decreasing C major scale is C–B–A–G–F–E–D–[C], with the bracket indicating an octave lower than the first note in the scale.
The distance between two successive notes in a scale is called a scale step.
The notes of a scale are numbered by their steps from the first degree of the scale. For example, in a C major scale the first note is C, the second D, the third E and so on. Two notes can also be numbered in relation to each other: C and E create an interval of a third (in this case a major third); D and F also create a third (in this case a minor third).
Pitch
[edit]A single scale can be manifested at many different pitch levels. For example, a C major scale can be started at C4 (middle C; see scientific pitch notation) and ascending an octave to C5; or it could be started at C6, ascending an octave to C7.
Types of scale
[edit]
Scales may be described according to the number of different pitch classes they contain:
- Chromatic, or dodecatonic (12 notes per octave)
- Nonatonic (9 notes per octave): a chromatic variation of the heptatonic blues scale
- Octatonic (8 notes per octave): used in jazz and modern classical music
- Heptatonic (7 notes per octave): the most common modern Western scale
- Hexatonic (6 notes per octave): common in Western folk music
- Pentatonic (5 notes per octave): the anhemitonic form (lacking semitones) is common in folk music, especially in Asian music; also known as the "black note" scale
- Tetratonic (4 notes), tritonic (3 notes), and ditonic (2 notes): generally limited to prehistoric ("primitive") music
Scales may also be described by their constituent intervals, such as being hemitonic, cohemitonic, or having imperfections.[5] Many music theorists concur that the constituent intervals of a scale have a large role in the cognitive perception of its sonority, or tonal character.
"The number of the notes that make up a scale as well as the quality of the intervals between successive notes of the scale help to give the music of a culture area its peculiar sound quality."[6] "The pitch distances or intervals among the notes of a scale tell us more about the sound of the music than does the mere number of tones."[7]
Scales may also be described by their symmetry, such as being palindromic, chiral, or having rotational symmetry as in Messiaen's modes of limited transposition.
Harmonic content
[edit]The notes of a scale form intervals with each of the other notes of the chord in combination. A 5-note scale has 10 of these harmonic intervals, a 6-note scale has 15, a 7-note scale has 21, an 8-note scale has 28.[8] Though the scale is not a chord, and might never be heard more than one note at a time, still the absence, presence, and placement of certain key intervals plays a large part in the sound of the scale, the natural movement of melody within the scale, and the selection of chords taken naturally from the scale.[8]
A musical scale that contains tritones is called tritonic (though the expression is also used for any scale with just three notes per octave, whether or not it includes a tritone), and one without tritones is atritonic. A scale or chord that contains semitones is called hemitonic, and without semitones is anhemitonic.
Scales in composition
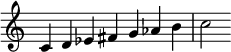
[edit]Scales can be abstracted from performance or composition. They are also often used precompositionally to guide or limit a composition. Explicit instruction in scales has been part of compositional training for many centuries. One or more scales may be used in a composition, such as in Claude Debussy's L'Isle Joyeuse.[9] To the right, the first scale is a whole-tone scale, while the second and third scales are diatonic scales. All three are used in the opening pages of Debussy's piece.
Western music
[edit]Scales in traditional Western music generally consist of seven notes and repeat at the octave. Notes in the commonly used scales (see just below) are separated by whole and half step intervals of tones and semitones. The harmonic minor scale includes a three-semitone step; the anhemitonic pentatonic includes two of those and no semitones.
Western music in the Medieval and Renaissance periods (1100–1600) tends to use the white-note diatonic scale C–D–E–F–G–A–B. Accidentals are rare, and somewhat unsystematically used, often to avoid the tritone.
Music of the common practice periods (1600–1900) uses three types of scale:
- The diatonic scale (seven notes)—this includes the major scale and the natural minor
- The melodic and harmonic minor scales (seven notes)
These scales are used in all of their transpositions. The music of this period introduces modulation, which involves systematic changes from one scale to another. Modulation occurs in relatively conventionalized ways. For example, major-mode pieces typically begin in a "tonic" diatonic scale and modulate to the "dominant" scale a fifth above.

In the 19th century (to a certain extent), but more in the 20th century, additional types of scales were explored:
- The chromatic scale (twelve notes)
- The whole-tone scale (six notes)
- The pentatonic scale (five notes)
- The octatonic or diminished scales (eight notes)
A large variety of other scales exists, some of the more common being:
- The Phrygian dominant scale (a mode of the harmonic minor scale)
- The Arabic scales
- The Hungarian minor scale
- The Byzantine music scales (called echoi)
- The Persian scale
Scales such as the pentatonic scale may be considered gapped relative to the diatonic scale. An auxiliary scale is a scale other than the primary or original scale. See: modulation (music) and Auxiliary diminished scale.
Note names
[edit]In many musical circumstances, a specific note of the scale is chosen as the tonic—the central and most stable note of the scale. In Western tonal music, simple songs or pieces typically start and end on the tonic note. Relative to a choice of a certain tonic, the notes of a scale are often labeled with numbers recording how many scale steps above the tonic they are. For example, the notes of the C major scale (C, D, E, F, G, A, B) can be labeled {1, 2, 3, 4, 5, 6, 7}, reflecting the choice of C as tonic. The expression scale degree refers to these numerical labels. Such labeling requires the choice of a "first" note; hence scale-degree labels are not intrinsic to the scale itself, but rather to its modes. For example, if we choose A as tonic, then we can label the notes of the C major scale using A = 1, B = 2, C = 3, and so on. When we do so, we create a new scale called the A minor scale. See the musical note article for how the notes are customarily named in different countries.
The scale degrees of a heptatonic (7-note) scale can also be named using the terms tonic, supertonic, mediant, subdominant, dominant, submediant, subtonic. If the subtonic is a semitone away from the tonic, then it is usually called the leading-tone (or leading-note); otherwise the leading-tone refers to the raised subtonic. Also commonly used is the (movable do) solfège naming convention in which each scale degree is denoted by a syllable. In the major scale, the solfège syllables are: do, re, mi, fa, so (or sol), la, ti (or si), do (or ut).
In naming the notes of a scale, it is customary that each scale degree be assigned its own letter name: for example, the A major scale is written A–B–C♯–D–E–F♯–G♯ rather than A–B–D♭–D–E–E![]() –G♯. However, it is impossible to do this in scales that contain more than seven notes, at least in the English-language nomenclature system.[10]
–G♯. However, it is impossible to do this in scales that contain more than seven notes, at least in the English-language nomenclature system.[10]
Scales may also be identified by using a binary system of twelve zeros or ones to represent each of the twelve notes of a chromatic scale. The most common binary numbering scheme defines lower pitches to have lower numeric value (as opposed to low pitches having a high numeric value). Thus a single pitch class n in the pitch class set is represented by 2^n. This maps the entire power set of all pitch class sets in 12-TET to the numbers 0 to 4095. The binary digits read as ascending pitches from right to left, which some find discombobulating because they are used to low to high reading left to right, as on a piano keyboard. In this scheme, the major scale is 101010110101 = 2741. This binary representation permits easy calculation of interval vectors and common tones, using logical binary operators. It also provides a perfect index for every possible combination of tones, as every scale has its own number.[11][12]
Scales may also be shown as semitones from the tonic. For instance, 0 2 4 5 7 9 11 denotes any major scale such as C–D–E–F–G–A–B, in which the first degree is, obviously, 0 semitones from the tonic (and therefore coincides with it), the second is 2 semitones from the tonic, the third is 4 semitones from the tonic, and so on. Again, this implies that the notes are drawn from a chromatic scale tuned with 12-tone equal temperament. For some fretted string instruments, such as the guitar and the bass guitar, scales can be notated in tabulature, an approach which indicates the fret number and string upon which each scale degree is played.
Transposition and modulation
[edit]This section may be confusing or unclear to readers. In particular, transposition and modulation are different;. (August 2018) |
Composers transform musical patterns by moving every note in the pattern by a constant number of scale steps: thus, in the C major scale, the pattern C–D–E might be shifted up, or transposed, a single scale step to become D–E–F. This process is called "scalar transposition" or "shifting to a new key" and can often be found in musical sequences and patterns. (It is D–E–F♯ in Chromatic transposition). Since the steps of a scale can have various sizes, this process introduces subtle melodic and harmonic variation into the music. In Western tonal music, the simplest and most common type of modulation (or changing keys) is to shift from one major key to another key built on the first key's fifth (or dominant) scale degree. In the key of C major, this would involve moving to the key of G major (which uses an F♯). Composers also often modulate to other related keys. In some Romantic music era pieces and contemporary music, composers modulate to "remote keys" that are not related to or close to the tonic. An example of a remote modulation would be taking a song that begins in C major and modulating (changing keys) to F♯ major.
Jazz and blues
[edit]
Through the introduction of blue notes, jazz and blues employ scale intervals smaller than a semitone. The blue note is an interval that is technically neither major nor minor but "in the middle", giving it a characteristic flavour. A regular piano cannot play blue notes, but with electric guitar, saxophone, trombone and trumpet, performers can "bend" notes a fraction of a tone sharp or flat to create blue notes. For instance, in the key of E, the blue note would be either a note between G and G♯ or a note moving between both.
In blues, a pentatonic scale is often used. In jazz, many different modes and scales are used, often within the same piece of music. Chromatic scales are common, especially in modern jazz.
Non-Western scales
[edit]Equal temperament
[edit]In Western music, scale notes are often separated by equally tempered tones or semitones, creating 12 intervals per octave. Each interval separates two tones; the higher tone has an oscillation frequency of a fixed ratio (by a factor equal to the twelfth root of two, or approximately 1.059463) higher than the frequency of the lower one. A scale uses a subset consisting typically of 7 of these 12 as scale steps.
Other
[edit]Many other musical traditions use scales that include other intervals. These scales originate within the derivation of the harmonic series. Musical intervals are complementary values of the harmonic overtones series.[13] Many musical scales in the world are based on this system, except most of the musical scales from Indonesia and the Indochina Peninsulae, which are based on inharmonic resonance of the dominant metalophone and xylophone instruments.
Intra-scale intervals
[edit]Some scales use a different number of pitches. A common scale in Eastern music is the pentatonic scale, which consists of five notes that span an octave. For example, in the Chinese culture, the pentatonic scale is usually used for folk music and consists of C, D, E, G and A, commonly known as gong, shang, jue, chi and yu.[14][15]
Some scales span part of an octave; several such short scales are typically combined to form a scale spanning a full octave or more, and usually called with a third name of its own. The Turkish and Middle Eastern music has around a dozen such basic short scales that are combined to form hundreds of full-octave spanning scales. Among these scales Hejaz scale has one scale step spanning 14 intervals (of the middle eastern type found 53 in an octave) roughly similar to 3 semitones (of the western type found 12 in an octave), while Saba scale, another of these middle eastern scales, has 3 consecutive scale steps within 14 commas, i.e. separated by roughly one western semitone either side of the middle tone.
Gamelan music uses a small variety of scales including Pélog and Sléndro, none including equally tempered nor harmonic intervals. Indian classical music uses a moveable seven-note scale. Indian Rāgas often use intervals smaller than a semitone.[16] Turkish music Turkish makams and Arabic music maqamat may use quarter tone intervals.[17][page needed] In both rāgas and maqamat, the distance between a note and an inflection (e.g., śruti) of that same note may be less than a semitone.
See also
[edit]References
[edit]- ^ a b Denyer, Ralph (30 November 1982). The Guitar Handbook. New York: Alfred A. Knopf. p. 104.
- ^ a b "Scale | Definition, Music Theory, & Types | Britannica". www.britannica.com. Retrieved 25 June 2024.
- ^ Benward, Bruce and Saker, Marilyn Nadine (2003). Music: In Theory and Practice, seventh edition: vol. 1, p. 25. Boston: McGraw-Hill. ISBN 978-0-07-294262-0.
- ^ Hewitt, Michael (2013). Musical Scales of the World, pp. 2–3. The Note Tree. ISBN 978-0-9575470-0-1.
- ^ "All The Scales". www.allthescales.org. Archived from the original on 15 October 2017. Retrieved 28 April 2018.
- ^ Nzewi, Meki, and Odyke Nzewi (2007), A Contemporary Study of Musical Arts. Pretoria: Centre for Indigenous Instrumental African Music and Dance. Volume 1 p. 34 ISBN 978-1-920051-62-4.
- ^ Nettl, Bruno, and Helen Myers (1976). Folk Music in the United States, p.39. ISBN 978-0-8143-1557-6.
- ^ a b Hanson, Howard. (1960) Harmonic Materials of Modern Music, pp.7ff. New York: Appleton-Century-Crofts. LOC 58-8138.
- ^ Tymoczko, Dmitri (2004). "Scale Networks and Debussy" (PDF). Journal of Music Theory. 48 (2): 219–294 (254–264). doi:10.1215/00222909-48-2-219. ISSN 0022-2909. Archived (PDF) from the original on 9 August 2017. Retrieved 18 July 2017..
- ^ "C Major Scale". All About Music Theory.com. Retrieved 12 September 2022.
- ^ Daniel Starr. ‘Sets, Invariance, and Partitions’. In: Journal of Music Theory 22.1 (1978), pp. 1–42
- ^ Alexander Brinkman. Pascal Programming for Music Research. University of Chicago Press, 1990.
- ^ Explanation of the origin of musical scales clarified by a string division method Archived 24 August 2012 at the Wayback Machine by Yuri Landman on furious.com
- ^ Wu, Dan; Li, Chao-Yi; Yao, De-Zhong (1 October 2013). "An ensemble with the chinese pentatonic scale using electroencephalogram from both hemispheres". Neuroscience Bulletin. 29 (5): 581–587. doi:10.1007/s12264-013-1334-y. ISSN 1995-8218. PMC 5561954. PMID 23604597.
- ^ Van Khê, Trân (1985). "Chinese Music and Musical Traditions of Eastern Asia". The World of Music. 27 (1): 78–90. ISSN 0043-8774. JSTOR 43562680.
- ^ Burns, Edwaard M. 1998. "Intervals, Scales, and Tuning.", p. 247. In The Psychology of Music, second edition, edited by Diana Deutsch, 215–264. New York: Academic Press. ISBN 0-12-213564-4.
- ^ Zonis [Mahler], Ella. 1973. Classical Persian Music: An Introduction. Cambridge, Massachusetts: Harvard University Press.
Further reading
[edit]- Barbieri, Patrizio (2008). Enharmonic Instruments and Music, 1470–1900. Latina, Italy: Il Levante Libreria Editrice. ISBN 978-88-95203-14-0.
- Yamaguchi, Masaya (2006). The Complete Thesaurus of Musical Scales (revised ed.). New York: Masaya Music Services. ISBN 978-0-9676353-0-9.
