Arithmetic

For the song by Brooke Fraser, see Arithmetic (song).

Arithmetic tables for children, Lausanne, 1835

Arithmetic (from Ancient Greek ἀριθμός (arithmós) 'number', and τική [τέχνη] (tikḗ [tékhnē]) 'art, craft') is an elementary part of mathematics that consists of the study and use of the traditional operations on numbers: addition, subtraction, multiplication, and division. It can also be regarded as including exponentiation, extraction of roots, and taking logarithms. Types of numbers manipulated in arithmetic include the natural numbers, which are used to count quantities; integers, which include the negative counterparts of the positive natural numbers 1, 2, 3, ...; fractions or rational numbers, which can fall in between the integers; and all of the other real numbers, which together form the complete number line. Arithmetic can be applied in even wider contexts, like the complex numbers.

The practice of arithmetic is at least thousands and possibly tens of thousands of years old. Ancient civilizations including the Egyptian and Sumerian used arithmetic to solve practical problems, and Euclid's Elements records early results in number theory, the exploration of numbers in the abstract. Much of the work on the logical foundation of arithmetic dates to the 19th century, and the implementation of arithmetic operations on electronic computers became a major concern during the 20th. There yet remain questions about arithmetic whose answers are unknown.

Definition, etymology, and related fields

Arithmetic is the fundamental branch of mathematics that studies numbers and their operations. In particular, it deals with numerical calculations using the arithmetic operations of addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and logarithm. The term "arithmetic" has its root in the Latin term "arithmetica" which derives from the Ancient Greek words ἀριθμός (arithmos), meaning "number", and ἀριθμητική τέχνη (arithmetike tekhne), meaning "the art of counting".

There are disagreements about its precise definition. According to a narrow characterization, arithmetic deals only with natural numbers. However, the more common view is to include operations on integers, rational numbers, real numbers, and sometimes also complex numbers in its scope. Some definitions restrict arithmetic to the field of numerical calculations. When understood in a wider sense, it also includes the study of how the concept of numbers developed, the analysis of properties of and relations between numbers, and the examination of the axiomatic structure of arithmetic operations.

Arithmetic is closely related to number theory and some authors use the terms as synonyms. However, in a more specific sense, number theory is restricted to the study of integers and focuses on their properties and relationships such as divisibility, factorization, and primality. Traditionally, it is known as higher arithmetic.

Arithmetic is intimately connected to many branches of mathematics that depend on numerical operations. Algebra relies on arithmetic principles to solve equations using variables. These principles also play a key role in calculus in its attempt to determine rates of change and areas under curves. Geometry uses arithmetic operations to measure the properties of shapes while statistics utilizes them to analyze numerical data.

Numbers

Numbers are mathematical objects used to count quantities and measure magnitudes. They are fundamental elements in arithmetic since all arithmetic operations are performed on numbers. There are different types of numbers and different numeral systems to represent them.

Types

Different types of numbers on a number line. Integers are black, rational numbers are blue, and irrational numbers are green.

The main types of numbers employed in arithmetic are natural numbers, whole numbers, integers, rational numbers, and real numbers. The natural numbers are whole numbers that start from 1 and go to infinity. They exclude 0 and negative numbers. They are also known as counting numbers and can be expressed as {1, 2, 3, 4, ...}. The symbol of the natural numbers is $\mathbb {N}$. The whole numbers are identical to the natural numbers with the only difference being that they include 0. They can be represented as {0, 1, 2, 3, 4, ...} and have the symbol $\mathbb {N} _{0}$. Some mathematicians do not draw the distinction between the natural and the whole numbers by including 0 in the set of natural numbers. The set of integers encompasses both positive and negative whole numbers. It has the symbol $\mathbb {Z}$ and can be expressed as {..., -2, -1, 0, 1, 2, ...}.

A number is rational if it can be represented as the ratio of two integers. For example, the rational number ${\tfrac {1}{2}}$ is formed by dividing the integer 1, called the numerator, by the integer 2, called the denominator. Other examples are ${\tfrac {3}{4}}$ and ${\tfrac {281}{3}}$. The set of rational numbers includes all integers, which are fractions with a denominator of 1. The symbol of the rational numbers is $\mathbb {Q}$. Decimal fractions like 0.3 and 25.12 are a special type of rational numbers since their denominator is a power of 10. For example, 0.3 is equal to ${\tfrac {3}{10}}$, and 25.12 is equal to ${\tfrac {2512}{100}}$. Every rational number corresponds to a finite or a repeating decimal.

Irrational numbers are numbers that cannot be expressed through the ratio of two integers. Examples are many square roots, such as ${\sqrt {2}}$, and numbers like π and e (Euler's number). The decimal representation of an irrational number is infinite without repeating decimals. The set of rational numbers together with the set of irrational numbers makes up the set of real numbers. The symbol of the real numbers is $\mathbb {R}$. Even wider classes of numbers include complex numbers and quaternions.

Based on how numbers are used, they can be distinguished into cardinal and ordinal numbers. Cardinal numbers, like one, two, and three, are numbers that express the quantity of objects. They answer the question "how many?". Ordinal numbers, such as first, second, and third, indicate order or placement in a series. They answer the question "what position?".

Numeral systems

A numeral is a symbol to represent a number and numeral systems are representational frameworks. They usually have a limited amount of basic numerals, which directly refer to certain numbers. The system governs how these basic numerals may be combined to express any number. Numeral systems are either positional or non-positional. All early numeral systems were non-positional. For non-positional numeral systems, the value of a digit does not depend on its position in the numeral.

Tally marks and some tally sticks use the non-positional unary numeral system.

The simplest non-positional system is the unary numeral system. It relies on one symbol for the number 1. All higher numbers are written by repeating this symbol. For example, the number 7 can be represented by repeating the symbol for 1 seven times. This system makes it cumbersome to write large numbers, which is why many non-positional systems include additional symbols to directly represent larger numbers. Variations of the unary numeral systems are employed in tally sticks using dents and in tally marks.

Table showing different ways to write the Egyptian numerals

Egyptian hieroglyphics had a more complex non-positional numeral system. They have additional symbols for numbers like 10, 100, 1000, and 10,000. These symbols can be combined into a sum to more conveniently express larger numbers. For example, the numeral for 10,405 uses one time the symbol for 10,000, four times the symbol for 100, and five times the symbol for 1. A similar well-known framework is the Roman numeral system. It has the symbols I, V, X, L, C, D, M as its basic numerals to represent the numbers 1, 5, 10, 50, 100, 500, and 1000.

A numeral system is positional if the position of a basic numeral in a compound expression determines its value. Positional numeral systems have a radix that acts as a multiplier of the different positions. For each subsequent position, the radix is raised to a higher power. In the common decimal system, also called the Hindu–Arabic numeral system, the radix is 10. This means that the first digit is multiplied by $10^{0}$, the next digit is multiplied by $10^{1}$, and so on. For example, the decimal numeral 532 stands for $5\cdot 10^{2}+3\cdot 10^{1}+2\cdot 10^{0}$. Because of the effect of the digits' positions, the numeral 532 differs from the numerals 325 and 253 even though they have the same digits.

Another positional numeral system used extensively in computer arithmetic is the binary system, which has a radix of 2. This means that the first digit is multiplied by $2^{0}$, the next digit by $2^{1}$, and so on. For example, the number 13 is written as 1101 in the binary notation, which stands for $1\cdot 2^{3}+1\cdot 2^{2}+0\cdot 2^{1}+1\cdot 2^{0}$. In computing, each digit in the binary notation is corresponds to one bit. The earliest positional system was developed by ancient Babylonians and had a radix of 60.

Arithmetic operations

Arithmetic operations are ways of combining, transforming, or manipulating numbers. They are functions that have numbers both as input and output. The most important operations in arithmetic are addition, subtraction, multiplication, and division. Further operations include exponentiation, extraction of roots, and logarithm. If these operations are performed on variables rather than numbers, they are sometimes referred to as algebraic operations.

Two important concepts in relation to arithmetic operations are identity elements and inverse elements. The identity element or neutral element of an operation does not cause any change if it is applied to another element. For example, the identity element of addition is 0 since any sum of a number and 0 results in the same number. The inverse element is the element that results in the identity element when combined with another element. For instance, the additive inverse of the number 6 is -6 since their sum is 0.

There are not only inverse elements but also inverse operations. In an informal sense, one operation is the inverse of another operation if it undoes the first operation. For example, subtraction is the inverse of addition since a number returns to its original value if a second number is first added and subsequently subtracted, as in $13+4-4=13$. Defined more formally, the operation "$\star$" is an inverse of the operation "$\circ$" if it fulfills the following condition: $t\star s=r$ if and only if $r\circ s=t$.

Commutativity and associativity are laws governing the order in which some arithmetic operations can be carried out. An operation is commutative if the order of the arguments can be changed without affecting the results. This is the case for addition, for example, $7+9$ is the same as $9+7$. Associativity is a rule that affects the order in which a series of operations can be carried out. An operation is associative if in a series of two operations, it does not matter which operation is carried out first. This is the case for multiplication, for example, since $(5\times 4)\times 2$ is the same as $5\times (4\times 2)$.

Addition and subtraction

Main articles: Addition and Subtraction

Addition and subtraction

Addition is an arithmetic operation in which two numbers, called the addends, are combined into a single number, called the sum. The symbol of addition is $+$. Examples are $2+2=4$ and $6.3+1.26=7.56$. The term summation is used if several additions are performed in a row. Counting is a type of repeated addition in which the number 1 is continuously added.

Subtraction is the inverse of addition. In it, one number, known as the subtrahend, is taken away from another, known as the minuend. The result of this operation is called the difference. The symbol of subtraction is $-$. Examples are $14-8=6$ and $45-1.7=43.3$. Subtraction is often treated as a special case of addition: instead of subtracting a positive number, it is also possible to add a negative number. For instance $14-8=14+(-8)$. This helps to simplify mathematical computations by reducing the number of basic arithmetic operations needed to perform calculations.

The additive identity element is 0 and the additive inverse of a number is the negative of that number. For example, $13+0=13$ and $13+(-13)=0$. Addition is both commutative and associative.

Multiplication and division

Main articles: Multiplication and Division (mathematics)

Multiplication and division

Multiplication is an arithmetic operation in which two numbers, called the multiplier and the multiplicant, are combined into a single number called the product. The symbols of multiplication are $\times$, $\cdot$, and *. Examples are $2\times 3=6$ and $0.3\cdot 5=1.5$. If the multiplicant is a natural number then multiplication is the same as repeated addition, as in $2\times 3=2+2+2$.

Division is the inverse of multiplication. In it, one number, known as the dividend, is split into several equal parts by another number, known as the divisor. The result of this operation is called the quotient. The symbols of division are $\div$ and $/$. Examples are $48\div 8=6$ and $29.4/1.4=21$. Division is often treated as a special case of multiplication: instead of dividing by a number, it is also possible to multiply by its reciprocal. The reciprocal of a number is 1 divided by that number. For instance, $48\div 8=48\times {\tfrac {1}{8}}$.

The multiplicative identity element is 1 and the multiplicative inverse of a number is the reciprocal of that number. For example, $13\times 1=13$ and $13\times {\tfrac {1}{13}}=1$. Multiplication is both commutative and associative.

Exponentiation and logarithm

Main articles: Exponentiation and Logarithm

Exponentiation and logarithm

Exponentiation is an arithmetic operation in which a number, known as the base, is raised to the power of another number, known as the exponent. The result of this operation is called the power. Exponentiation is sometimes expressed using the symbol ^ but the more common way is to write the exponent in superscript right after the base. Examples are $2^{4}=16$ and $3$^$3=27$. If the exponent is a natural number then exponentiation is the same as repeated multiplication, as in $2^{4}=2\times 2\times 2\times 2$.

Roots are a special type of exponentiation using a fractional exponent. For example, the square root of a number is the same as raising the number to the power of ${\tfrac {1}{2}}$ and the cube root of a number is the same as raising the number to the power of ${\tfrac {1}{3}}$. Examples are ${\sqrt {4}}=4^{\tfrac {1}{2}}=2$ and ${\sqrt[{3}]{27}}=27^{\tfrac {1}{3}}=3$.

Logarithm is the inverse of exponentiation. In it, the base and the argument of the logarithm are used to determine the power to which the base must be raised to produce the argument. The result of this operation is known as the anti-logarithm. For example, to determine the logarithm of 16 in relation to the base 2, it is necessary to find what exponent should be used on the base 2 for the result to be 16. The anti-logarithm of this operation is 4 since 2 raised by 4 results in 16.

Exponentiation and logarithm do not have general identity elements and inverse elements like addition and multiplication. The neutral element of exponentiation in relation to the exponent is 1, as in $14^{1}=14$. However, exponentiation does not have a general identity element since 1 is not the neutral element for the base. Exponentiation and logarithm are neither commutative nor associative.

Integer arithmetic

Integer arithmetic is the branch of arithmetic that deals with the manipulation of positive and negative whole numbers. Simple one-digit operations can be performed by following or memorizing a table that presents the results of all possible combinations, like an addition table or a multiplication table. Other common methods are verbal counting and finger-counting.

Addition table

+	0	1	2	3	4	...
0	0	1	2	3	4	...
1	1	2	3	4	5	...
2	2	3	4	5	6	...
3	3	4	5	6	7	...
4	4	5	6	7	8	...
...	...	...	...	...	...	...

Multiplication table

×	0	1	2	3	4	...
0	0	0	0	0	0	...
1	0	1	2	3	4	...
2	0	2	4	6	8	...
3	0	3	6	9	12	...
4	0	4	8	12	16	...
...	...	...	...	...	...	...

Example of addition with carry. The black numbers are the addends, the green number is the carry, and the blue number is the sum.

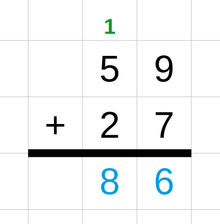
For operations on numbers with more than one digit, different techniques can be employed to calculate the result by using several one-digit operations in a row. For example, in the method addition with carries, the two numbers are written one above the other. Starting from the rightmost digit, each pair of digits is added together. The rightmost digit of the sum is written below them. If the sum is a two-digit number then the leftmost digit, called the "carry", is added to the next pair of digits to the left. This process is repeated until all digits have been added. Other methods used for integer additions are the number line method, the partial sum method, and the compensation method. A similar technique is used for subtraction: it also starts with the rightmost digit and uses a "borrow" or a negative carry for the column on the left if the result of the one-digit subtraction is negative.

Example of long multiplication. The black numbers are the multiplicand and the multiplier. The green numbers are intermediary products gained by multiplying the multiplicant with only one digit of the multiplier. The blue number is the total product calculated by adding the intermediary products.

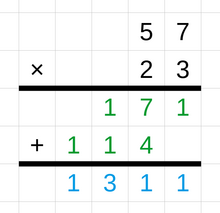
A basic technique of integer multiplication uses repeated addition. For example, the product of 3 × 4 can be calculated as 3 + 3 + 3 + 3. A common technique for multiplication with larger numbers is called long multiplication. This method starts by writing the multiplicand above the multiplier. The calculation begins by multiplying the multiplicand only with the rightmost digit of the multiplier and writing the result below, starting in the rightmost column. The same is done for each digit of the multiplier and the result in each case is shifted one position to the left. As a final step, all the individual products are added to arrive at the total product of the two multi-digit numbers. Other techniques used for multiplication are the grid method and the lattice method. Computer science is interested in multiplication algorithms with a low computational complexity to be able to efficiently multiply very large integers, such as the Karatsuba algorithm, the Schönhage-Strassen algorithm, and the Toom-Cook algorithm. A common technique used for division is called long division. Other methods include short division and chunking.

Integer arithmetic is not closed under division. This means that when dividing one integer by another integer, the result is not always an integer. For example, 7 divided by 2 is not a whole number but 3.5. One way to ensure that the result is an integer is to round the result to a whole number. However, this method leads to inaccuracies as the original value is altered. Another method is to perform the division only partially and retain the remainder. For example, 7 divided by 2 is 3 with a remainder of 1. These difficulties are avoided by rational arithmetic, which allows for the exact representation of fractions.

A simple method to calculate exponentiation is by repeated multiplication. For example, the exponentiation of 3⁴ can be calculated as 3 × 3 × 3 × 3. A more efficient technique used for large exponents is exponentiation by squaring. It breaks down the calculation into a number of squaring operations. For example, the exponentiation 3⁶⁵ can be written as (((((3²)²)²)²)²)² × 3. By taking advantage of repeated squaring operations, only 7 individual operations are needed rather than the 64 operations required for regular repeated multiplication. Methods to calculate logarithms include the Taylor series and continued fractions. Integer arithmetic is not closed under logarithm and under exponentiation with negative exponents, meaning that the result of these operations is not always an integer.

Rational arithmetic

Rational arithmetic is the branch of arithmetic that deals with the manipulation of numbers that can be expressed as a ratio of two integers. Most arithmetic operations on rational numbers can be calculated by performing a series of integer arithmetic operations on the numerators and the denominators of the involved numbers. If two rational numbers have the same denominator then they can be added by adding their numerators and keeping the common denominator. For example, ${\tfrac {2}{7}}+{\tfrac {3}{7}}={\tfrac {5}{7}}$. A similar procedure is used for subtraction. If the two numbers do not have the same denominator then they must be transformed to find a common denominator. This can be achieved by scaling the first number with the denominator of the second number while scaling the second number with the denominator of the first number. For example, ${\tfrac {1}{3}}+{\tfrac {1}{2}}={\tfrac {1\cdot 2}{3\cdot 2}}+{\tfrac {1\cdot 3}{2\cdot 3}}={\tfrac {2}{6}}+{\tfrac {3}{6}}={\tfrac {5}{6}}$.

Two rational numbers are multiplied by multiplying their numerators and their denominators respectively, as in ${\tfrac {2}{3}}\cdot {\tfrac {2}{5}}={\tfrac {2\cdot 2}{3\cdot 5}}={\tfrac {4}{15}}$. Dividing one rational number by another can be achieved by multiplying the first number with the reciprocal of the second number. This means that the numerator and the denominator of the second number change position. For example, ${\tfrac {3}{5}}:{\tfrac {2}{7}}={\tfrac {3}{5}}\cdot {\tfrac {7}{2}}={\tfrac {21}{10}}$. Unlike integer arithmetic, rational arithmetic is closed under division as long as the divisor is not 0.

Both integer arithmetic and rational arithmetic are not closed under exponentiation and logarithm. One way to calculate exponentiation with a fractional exponent is to perform two separate calculations: one exponentiation using the numerator of the exponent followed by drawing the nth root of the result based on the denominator of the exponent. For example, $5^{\tfrac {2}{3}}={\sqrt[{3}]{5^{2}}}$. The first operation can be completed using methods like repeated multiplication or exponentiation by squaring. One way to get an approximate result for the second operation is to employ Newton's method, which uses a series of steps to gradually refine an initial guess until it reaches the desired level of accuracy. The Taylor series or the continued fraction method can be used to calculate logarithms.

The decimal fraction notation is a special way of representing rational numbers whose denominator is a power of 10. For example, the rational numbers ${\tfrac {1}{10}}$, ${\tfrac {371}{100}}$, and ${\tfrac {44}{10000}}$ are written as 0.1, 3.71, and 0.0044 in the decimal fraction notation. Modified versions of integer calculation methods like addition with carry and long multiplication can be applied to calculations with decimal fractions. Not all rational numbers have an finite representation in the decimal notation. For example, the rational number ${\tfrac {1}{3}}$ corresponds 0.333... with an infinite number of 3s. The shortened notation for this type of repeating decimal is 0.3. Every repeating decimal expresses a rational number.

Real arithmetic

Real arithmetic is the branch of arithmetic that deals with the manipulation of both rational and irrational numbers. Irrational numbers are numbers that cannot be expressed through fractions or repeated decimals, like the root of 2 and π. Unlike rational arithmetic, real arithmetic is closed under exponentiation as long as it uses a positive number as its base. The same is true for the logarithm of positive real numbers as long as the logarithm base is positive and not 1.

Irrational numbers involve an infinite non-repeating series of decimal digits. Because of this, there is often no simple and accurate way to express the results of arithmetic operations like ${\sqrt {2}}+\pi$ or $e\cdot {\sqrt {3}}$. In cases where absolute precision is not required, the problem of calculating arithmetic operations on real numbers is usually addressed by truncation or rounding. For truncation, a certain number of significant digits to the left are kept and additional digits to the right of the last significant digit are removed. For example, the number π has an infinite number of digits starting with 3.14159... . If this number is truncated to 4 significant digits, the result is 3.141. Rounding is a similar process in which the last significant digit is increased by one if the next digit is 5 or greater. If the next digit is less than 5, the last digit remains the same. For example, if the number π is rounded to 4 significant digits, the result is 3.142 because the following digit is a 5. These methods are essential to allow computers to efficiently perform calculations on real numbers.

Very large and very small real numbers are often expressed using normalized scientific notation. In it, numbers are represented using a so-called significand multiplied by a power of 10. The significand is a digit followed by a decimal point and a series of digits. For example, the normalized scientific notation of the number 8276000 is $8.276\times 10^{6}$ and the number 0.00735 has the normalized scientific notation of $7.35\times 10^{-3}$.

A common method employed by computers to approximate real arithmetic is called floating-point arithmetic. It represents real numbers similar to the scientific notation through three numbers: a significand, a base, and an exponent. The precision of the significand is limited by the number of bits allocated to represent it. If an arithmetic operation results in a number that requires more bits than are available, the computer rounds the result to the closest representable number. This leads to rounding errors. A consequence of this behavior is that certain laws of arithmetic are violated by floating-point arithmetic. For example, floating-point addition is not associative since the rounding errors introduced can depend on the order of the additions. This means that the result of $(a+b)+c$ is sometimes different from the result of $a+(b+c)$. The most common technical standard used for floating-point arithmetic is called IEEE 754. Among other things, it determines how numbers are represented, how arithmetic operations and rounding are performed, and how errors and exceptions are handled.

Decimal arithmetic

Decimal representation refers exclusively, in common use, to the written numeral system employing arabic numerals as the digits for a radix 10 ("decimal") positional notation; however, any numeral system based on powers of 10, e.g., Greek, Cyrillic, Roman, or Chinese numerals may conceptually be described as "decimal notation" or "decimal representation".

Modern methods for four fundamental operations (addition, subtraction, multiplication and division) were first devised by Brahmagupta of India. This was known during medieval Europe as "Modus Indorum" or Method of the Indians. Positional notation (also known as "place-value notation") refers to the representation or encoding of numbers using the same symbol for the different orders of magnitude (e.g., the "ones place", "tens place", "hundreds place") and, with a radix point, using those same symbols to represent fractions (e.g., the "tenths place", "hundredths place"). For example, 507.36 denotes 5 hundreds (10²), plus 0 tens (10¹), plus 7 units (10⁰), plus 3 tenths (10⁻¹) plus 6 hundredths (10⁻²).

The concept of 0 as a number comparable to the other basic digits is essential to this notation, as is the concept of 0's use as a placeholder, and as is the definition of multiplication and addition with 0. The use of 0 as a placeholder and, therefore, the use of a positional notation is first attested to in the Jain text from India entitled the Lokavibhâga, dated 458 AD and it was only in the early 13th century that these concepts, transmitted via the scholarship of the Arabic world, were introduced into Europe by Fibonacci using the Hindu–Arabic numeral system.

Algorism comprises all of the rules for performing arithmetic computations using this type of written numeral. For example, addition produces the sum of two arbitrary numbers. The result is calculated by the repeated addition of single digits from each number that occupies the same position, proceeding from right to left. An addition table with ten rows and ten columns displays all possible values for each sum. If an individual sum exceeds the value 9, the result is represented with two digits. The rightmost digit is the value for the current position, and the result for the subsequent addition of the digits to the left increases by the value of the second (leftmost) digit, which is always one (if not zero). This adjustment is termed a carry of the value 1.

The process for multiplying two arbitrary numbers is similar to the process for addition. A multiplication table with ten rows and ten columns lists the results for each pair of digits. If an individual product of a pair of digits exceeds 9, the carry adjustment increases the result of any subsequent multiplication from digits to the left by a value equal to the second (leftmost) digit, which is any value from 1 to 8 (9 × 9 = 81). Additional steps define the final result.

Similar techniques exist for subtraction and division.

The creation of a correct process for multiplication relies on the relationship between values of adjacent digits. The value for any single digit in a numeral depends on its position. Also, each position to the left represents a value ten times larger than the position to the right. In mathematical terms, the exponent for the radix (base) of 10 increases by 1 (to the left) or decreases by 1 (to the right). Therefore, the value for any arbitrary digit is multiplied by a value of the form 10ⁿ with integer n. The list of values corresponding to all possible positions for a single digit is written as {..., 10², 10, 1, 10⁻¹, 10⁻², ...}.

Repeated multiplication of any value in this list by 10 produces another value in the list. In mathematical terminology, this characteristic is defined as closure, and the previous list is described as closed under multiplication. It is the basis for correctly finding the results of multiplication using the previous technique. This outcome is one example of the uses of number theory.

Compound unit arithmetic

Compound unit arithmetic is the application of arithmetic operations to mixed radix quantities such as feet and inches; gallons and pints; pounds, shillings and pence; and so on. Before decimal-based systems of money and units of measure, compound unit arithmetic was widely used in commerce and industry.

Basic arithmetic operations

The techniques used in compound unit arithmetic were developed over many centuries and are well documented in many textbooks in many different languages. In addition to the basic arithmetic functions encountered in decimal arithmetic, compound unit arithmetic employs three more functions:

• Reduction, in which a compound quantity is reduced to a single quantity—for example, conversion of a distance expressed in yards, feet and inches to one expressed in inches.
• Expansion, the inverse function to reduction, is the conversion of a quantity that is expressed as a single unit of measure to a compound unit, such as expanding 24 oz to 1 lb 8 oz.
• Normalization is the conversion of a set of compound units to a standard form—for example, rewriting "1 ft 13 in" as "2 ft 1 in".

Knowledge of the relationship between the various units of measure, their multiples and their submultiples forms an essential part of compound unit arithmetic.

Principles of compound unit arithmetic

There are two basic approaches to compound unit arithmetic:

• Reduction–expansion method where all the compound unit variables are reduced to single unit variables, the calculation performed and the result expanded back to compound units. This approach is suited for automated calculations. A typical example is the handling of time by Microsoft Excel where all time intervals are processed internally as days and decimal fractions of a day.
• On-going normalization method in which each unit is treated separately and the problem is continuously normalized as the solution develops. This approach, which is widely described in classical texts, is best suited for manual calculations. An example of the ongoing normalization method as applied to addition is shown below.

The addition operation is carried out from right to left; in this case, pence are processed first, then shillings followed by pounds. The numbers below the "answer line" are intermediate results.

The total in the pence column is 25. Since there are 12 pennies in a shilling, 25 is divided by 12 to give 2 with a remainder of 1. The value "1" is then written to the answer row and the value "2" carried forward to the shillings column. This operation is repeated using the values in the shillings column, with the additional step of adding the value that was carried forward from the pennies column. The intermediate total is divided by 20 as there are 20 shillings in a pound. The pound column is then processed, but as pounds are the largest unit that is being considered, no values are carried forward from the pounds column.

For the sake of simplicity, the example chosen did not have farthings.

Operations in practice

A scale calibrated in imperial units, with an associated cost display

During the 19th and 20th centuries various aids were developed to aid the manipulation of compound units, particularly in commercial applications. The most common aids were mechanical tills which were adapted in countries such as the United Kingdom to accommodate pounds, shillings, pence and farthings, and ready reckoners, which are books aimed at traders that catalogued the results of various routine calculations such as the percentages or multiples of various sums of money. One typical booklet that ran to 150 pages tabulated multiples "from one to ten thousand at the various prices from one farthing to one pound".

The cumbersome nature of compound unit arithmetic has been recognized for many years—in 1586, the Flemish mathematician Simon Stevin published a small pamphlet called De Thiende ("the tenth") in which he declared the universal introduction of decimal coinage, measures, and weights to be merely a question of time. In the modern era, many conversion programs, such as that included in the Microsoft Windows 7 operating system calculator, display compound units in a reduced decimal format rather than using an expanded format (e.g., "2.5 ft" is displayed rather than "2 ft 6 in").

Number theory

Main article: Number theory

Number theory studies the structure and properties of integers as well as the relations and laws between them. Some of the main branches of modern number theory include elementary number theory, analytic number theory, algebraic number theory, and geometric number theory. Elementary number theory studies aspects of integers that can be investigated using elementary methods. In this regard, it excludes the use of methodes found in analysis and calculus. Its topics include divisibility, factorization, and primality. Analytic number theory, by contrast, relies on techniques from analysis and calculus. It examines problems like how prime numbers are distributed and the claim that every even number is a sum of two prime numbers. Algebraic number theory employs algebraic structures to analyze the properties of and relations between numbers. Examples are the use of fields and rings, as in algebraic number fields like the ring of integers. Geometric number theory uses concepts from geometry to study numbers. For instance, it investigates how lattice points with integer coordinates behave in a plane. Further branches of number theory are probabilistic number theory, combinatorial number theory, computational number theory, and applied number theory.

Influential theorems in number theory include the fundamental theorem of arithmetic, Euclid's theorem, and Fermat's last theorem. According to the fundamental theorem of arithmetic, every integer greater than 1 is either a prime number or can be represented as a unique product of prime numbers. For example, the number 18 is not a prime number and can be represented as $2\times 3\times 3$, all of which are prime numbers. The number 19, by contrast, is a prime number that has no other prime factorization. Euclid's theorem states that there are infinitely many prime numbers. Fermat's last theorem is the statement that no integer values can be found for $a$, $b$, and $c$, to solve the equation $a^{n}+b^{n}=c^{n}$ if $n$ is greater than $2$.

Arithmetic in education

Primary education in mathematics often places a strong focus on algorithms for the arithmetic of natural numbers, integers, fractions, and decimals (using the decimal place-value system). This study is sometimes known as algorism.

The difficulty and unmotivated appearance of these algorithms has long led educators to question this curriculum, advocating the early teaching of more central and intuitive mathematical ideas. One notable movement in this direction was the New Math of the 1960s and 1970s, which attempted to teach arithmetic in the spirit of axiomatic development from set theory, an echo of the prevailing trend in higher mathematics.

Also, arithmetic was used by Islamic Scholars in order to teach application of the rulings related to Zakat and Irth. This was done in a book entitled The Best of Arithmetic by Abd-al-Fattah-al-Dumyati. The book begins with the foundations of mathematics and proceeds to its application in the later chapters.

History

Main article: History of arithmetic

Some historians interpret the Ishango bone as one of the earliest arithmetic artifacts.

The earliest forms of arithmetic are sometimes traced back to counting and tally marks used to keep track of quantities. Some historians suggest that the Lebombo bone (dated about 43,000 years ago) and the Ishango bone (dated about 22,000 to 30,000 years ago) are the oldest arithmetic artifacts but this interpretation is disputed. However, a basic sense of numbers may predate these findings and might even have existed before the development of language.

However, it was not until the emergence of ancient civilizations that a more complex and structured approach to arithmetic began to evolve, starting around 3000 BCE. This became necessary because of the increased need to keep track of stored items, manage land ownership, and arrange exchanges. All the major ancient civilizations developed non-positional numeral systems to facilitate the representation of numbers. They also included symbols for operations like addition and subtraction and were aware of fractions. Examples are Egyptian hieroglyphics as well as the numeral systems used in Sumeria, China, and India. The first positional numeral system was developed by the Babylonians starting around 1800 BCE. This was a significant improvement over earlier numeral systems since it made the representation of large numbers and calculations on them more efficient. Abacuses were used as hand-operated calculating tools since ancient times as efficient means for performing complex calculations.

Abacuses were used as manual calculation tools in ancient civilizations, such as the Suanpan in China.

Early civilizations primarily used numbers for concrete practical purposes and lacked an abstract concept of number itself. This changed with the ancient Greek mathematicians, who began to explore the abstract nature of numbers rather than studying how they are applied to specific problems. Another novel feature was their use of proofs to establish mathematical truths and validate theories. A further contribution was their distinction of various classes of numbers, such as even numbers, odd numbers, and prime numbers. This included the discovery that numbers for certain geometrical lengths are irrational and therefore cannot be expressed as a fraction. The works of Thales of Miletus and Pythagoras in the 7th and 6th centuries BCE are often regarded as the inception of Greek mathematics. Diophantus was an influential figure in Greek arithmetic in the 3rd century BCE because of his numerous contributions to number theory and his exploration of the application of arithmetic operations to algebraic equations.

The ancient Indians were the first to developed the concept of zero as a number to be used in calculations. The exact rules of its operation were written down by Brahmagupta in around 628 CE. The concept of zero as a general term existed long before but it was understood as an empty placeholder rather than an object of arithmetic operations. Brahmagupta further provided a detailed discussion of calculations with negative numbers and their application to problems like credit and debt. The concept of negative numbers itself is significantly older and was first explored in Chinese mathematics in the first millennium BCE.

Indian mathematicians developed the positional decimal numeral system common today. For example, a detailed treatment of its operations was provided by Aryabhata around the turn of the 6th century CE. The Indian decimal system was further refined and expanded during the Islamic Golden Age by Arab mathematicians such as Al-Khwarizmi. His work was influential in introducing the decimal numeral system to the Western world, which had previously relied on the non-positional Roman numeral system. There, it was popularized by mathematicians like Leonardo Fibonacci, who lived in the 12th and 13th centuries and also developed the Fibonacci sequence. During the Middle Ages and Renaissance, many popular textbooks were published to cover the practical calculations for commerce. The use of abacuses also became widespread in this period. In the 16th century, the mathematician Gerolamo Cardano conceived the concept of complex numbers as a way to solve cubic equations.

Leibniz's stepped reckoner was the first calculator that could perform all four arithmetic operations.

The first mechanical calculators were developed in the 17th century and greatly facilitated complex mathematical calculations, such as Blaise Pascal's calculator and Gottfried Wilhelm Leibniz's stepped reckoner. The 17th century also saw the discovery of the logarithm by John Napier.

In the 18th and 19th centuries, mathematicians such as Leonhard Euler and Carl Friedrich Gauss laid the foundations of modern number theory. Another development in this period concerned work on the formalization and foundations of arithmetic, such as Georg Cantor's set theory and the Dedekind–Peano axioms used as an axiomatization of natural-number arithmetic. Computers and electronic calculators were first developed in the 20th century. Their widespread use revolutionized both the accuracy and speed with which even complex arithmetic computations can be calculated.

See also

• Outline of arithmetic
• Arbitrary-precision arithmetic - the closest implementation of arithmetic using computers but still imperfect.
• Calculator - most calculators are limited and not suitable for arbitrary-precision arithmetic.

Related topics

• Addition of natural numbers
• Arithmetic properties
• Elementary arithmetic
• Finite field arithmetic
• Mental calculation
• Plant arithmetic

References

Sources

• Booker, George; Bond, Denise; Sparrow, Len; Swan, Paul (20 May 2015). Teaching Primary Mathematics. Pearson Higher Education AU. ISBN 978-1-4860-0488-1.
• Cafaro, Massimo; Epicoco, Italo; Pulimeno, Marco (21 August 2018). "Techniques for Designing Bioinformatics Algorithms". Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics. Elsevier. ISBN 978-0-12-811432-2.
• Cuyt, Annie A. M.; Petersen, Vigdis; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (12 April 2008). Handbook of Continued Fractions for Special Functions. Springer Science & Business Media. ISBN 978-1-4020-6949-9.
• Davis, Andrew; Goulding, Maria; Suggate, Jennifer (17 February 2017). Mathematical Knowledge for Primary Teachers. Taylor & Francis. ISBN 978-1-317-21901-9.
• Ebby, Caroline B.; Hulbert, Elizabeth T.; Broadhead, Rachel M. (23 November 2020). A Focus on Addition and Subtraction: Bringing Mathematics Education Research to the Classroom. Routledge. ISBN 978-1-000-22087-2.
• Geary, David C. (11 May 2006). "Development of Mathematical Understanding". In Damon, William; Lerner, Richard M.; Kuhn, Deanna; Siegler, Robert S. (eds.). Handbook of Child Psychology, Cognition, Perception, and Language. John Wiley & Sons. ISBN 978-0-470-05054-5.
• Gellert, W.; Hellwich, M.; Kästner, H.; Küstner, H. (6 December 2012). The VNR Concise Encyclopedia of Mathematics. Springer Science & Business Media. ISBN 978-94-011-6982-0.
• Goodstein, R. L. (14 July 2014). Fundamental Concepts of Mathematics. Elsevier. ISBN 978-1-4831-5405-3.
• Hafstrom, John Edward (10 June 2013). Basic Concepts in Modern Mathematics. Courier Corporation. ISBN 978-0-486-31627-7.
• Haylock, Derek; Cockburn, Anne D. (14 October 2008). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers. SAGE. ISBN 978-1-4462-0497-9.
• Hindry, Marc (2011). Arithmetics. London: Springer. ISBN 978-1-4471-2130-5.
• Hoffman, Joe D.; Frankel, Steven (3 October 2018). Numerical Methods for Engineers and Scientists. CRC Press. ISBN 978-1-4822-7060-0.
• Igarashi, Yoshihide; Altman, Tom; Funada, Mariko; Kamiyama, Barbara (27 May 2014). Computing: A Historical and Technical Perspective. CRC Press. ISBN 978-1-4822-2741-3.
• Kay, Anthony (14 September 2021). Number Systems: A Path into Rigorous Mathematics. CRC Press. ISBN 978-0-429-60776-9.
• Klein, Elise; Moeller, Korbinian; Dressel, Katharina; Domahs, Frank; Wood, Guilherme; Willmes, Klaus; Nuerk, Hans-Christoph (September 2010). "To carry or not to carry — Is this the question? Disentangling the carry effect in multi-digit addition". Acta Psychologica. 135 (1). doi:10.1016/j.actpsy.2010.06.002.
• Klein, Andreas (8 April 2013). Stream Ciphers. Springer Science & Business Media. ISBN 978-1-4471-5079-4.
• Klose, Orval M. (16 May 2014). The Number Systems and Operations of Arithmetic: An Explanation of the Fundamental Principles of Mathematics Which Underlie the Understanding and Use of Arithmetic, Designed for In-Service Training of Elementary School Teachers Candidates Service Training of Elementary School Teacher Candidates. Elsevier. ISBN 978-1-4831-3709-4.
• Koepf, Wolfram (11 July 2021). Computer Algebra: An Algorithm-Oriented Introduction. Springer Nature. ISBN 978-3-030-78017-3.
• Kupferman, Raz (29 October 2015). Elementary School Mathematics For Parents And Teachers - Volume 1. World Scientific Publishing Company. ISBN 978-981-4699-93-8.
• Lange, Kenneth (15 June 2010). Numerical Analysis for Statisticians. Springer Science & Business Media. ISBN 978-1-4419-5944-7.
• Ma, Liping (6 January 2020). Knowing and Teaching Elementary Mathematics: Teachers' Understanding of Fundamental Mathematics in China and the United States. Routledge. ISBN 978-1-000-02734-1.
• Mahajan, Sanjoy (5 March 2010). Street-Fighting Mathematics: The Art of Educated Guessing and Opportunistic Problem Solving. MIT Press. ISBN 978-0-262-26559-1.
• Mooney, Claire; Briggs, Mary; Hansen, Alice; McCullouch, Judith; Fletcher, Mike (10 June 2014). Primary Mathematics: Teaching Theory and Practice. Learning Matters. ISBN 978-1-4739-0707-2.
• Muller, Jean-Michel; Brunie, Nicolas; Dinechin, Florent de; Jeannerod, Claude-Pierre; Joldes, Mioara; Lefèvre, Vincent; Melquiond, Guillaume; Revol, Nathalie; Torres, Serge (2 May 2018). Handbook of Floating-Point Arithmetic. Birkhäuser. ISBN 978-3-319-76526-6.
• Musser, Gary L.; Peterson, Blake E.; Burger, William F. (16 September 2013). Mathematics for Elementary Teachers: A Contemporary Approach. John Wiley & Sons. ISBN 978-1-118-48700-6.
• Prata, Stephen (2002). C Primer Plus. Sams Publishing. ISBN 978-0-672-32222-8.
• Quintero, Ana Helvia; Rosario, Hector (2 March 2016). Math Makes Sense!: A Constructivist Approach To The Teaching And Learning Of Mathematics. World Scientific. ISBN 978-1-78326-866-5.
• Reilly, Norman R. (2 November 2009). Introduction to Applied Algebraic Systems. Oxford University Press. ISBN 978-0-19-970992-2.
• Resnick, L. B.; Ford, W. W. (12 November 2012). Psychology of Mathematics for Instruction. Routledge. ISBN 978-1-136-55759-0.
• Romanowski, Perry (2008). "Arithmetic". In Lerner, Brenda Wilmoth; Lerner, K. Lee (eds.). The Gale encyclopedia of science (4th ed.). Detroit: Thompson Gale. pp. 302–305. ISBN 978-1-4144-2877-2.
• Sperling, Abraham; Stuart, Monroe (1981). Mathematics. Elsevier Science. ISBN 978-0-7506-0405-5.
• Uspenskii, V. A.; Semenov, A. L. (2001). "Solvable and Unsolvable Algorithmic Problems". In Tabachnikov, Serge (ed.). Kvant Selecta: Combinatorics, I: Combinatorics, I. American Mathematical Soc. ISBN 978-0-8218-2171-8.
• Wallis, W. D. (14 March 2013). A Beginner’s Guide to Discrete Mathematics. Springer Science & Business Media. ISBN 978-1-4757-3826-1.
• Roe, John; deForest, Russ; Jamshidi, Sara (26 April 2018). Mathematics for Sustainability. Springer. ISBN 978-3-319-76660-7.
• Rossi, Richard J. (5 October 2011). Theorems, Corollaries, Lemmas, and Methods of Proof. John Wiley & Sons. ISBN 978-1-118-03057-8.
• Reitano, Robert R. (29 January 2010). Introduction to Quantitative Finance: A Math Tool Kit. MIT Press. ISBN 978-0-262-01369-7.
• Bronshtein, I. N.; Semendyayev, K. A.; Musiol, Gerhard; Mühlig, Heiner (19 March 2015). Handbook of Mathematics. Springer. ISBN 978-3-662-46221-8.
• EoM staff (2020). "Real number". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• Rooney, Anne (15 July 2021). Think Like a Mathematician. The Rosen Publishing Group. ISBN 978-1-4994-7092-5.
• Young, Cynthia Y. (19 January 2010). Precalculus. John Wiley & Sons. ISBN 978-0-471-75684-2.
• Young, Cynthia Y. (31 August 2021). Algebra and Trigonometry. John Wiley & Sons. ISBN 978-1-119-77830-1.
• Koren, Israel (8 October 2018). Computer Arithmetic Algorithms. CRC Press. ISBN 978-1-4398-6371-8.
• Muller, Jean-Michel; Brisebarre, Nicolas; Dinechin, Florent de; Jeannerod, Claude-Pierre; Lefèvre, Vincent; Melquiond, Guillaume; Revol, Nathalie; Stehlé, Damien; Torres, Serge (11 November 2009). Handbook of Floating-Point Arithmetic. Springer Science & Business Media. ISBN 978-0-8176-4705-6.
• Swartzlander, Earl E. (19 December 2017). "High-Speed Computer Arithmetic". In Oklobdzija, Vojin G. (ed.). Digital Design and Fabrication. CRC Press. ISBN 978-0-8493-8604-6.
• Stewart, David E. (1 December 2022). Numerical Analysis: A Graduate Course. Springer Nature. ISBN 978-3-031-08121-7.
• Meyer, Carl D. (18 May 2023). Matrix Analysis and Applied Linear Algebra: Second Edition. SIAM. ISBN 978-1-61197-744-8.
• Brent, Richard P.; Zimmermann, Paul (25 November 2010). Modern Computer Arithmetic. Cambridge University Press. ISBN 978-1-139-49228-7.
• Cryer, C. W. (4 March 2014). A Math Primer for Engineers. IOS Press. ISBN 978-1-61499-299-8.
• Smith, David E. (1 June 1958). History of Mathematics. Courier Corporation. ISBN 978-0-486-20430-7.
• Peirce, Charles S. (28 April 2015). Arithmetic. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-086970-5.
• EoM staff (2020a). "Arithmetic". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• EoM staff (2020b). "Number theory". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• Wilson, Robin (2020). Number Theory: A Very Short Introduction. Oxford University Press. ISBN 978-0-19-879809-5.
• HS staff (2022). "The American Heritage Dictionary entry: arithmetic". www.ahdictionary.com. HarperCollins. Retrieved 19 October 2023.
• MW staff (13 September 2023). "Definition of Arithmetic". www.merriam-webster.com. Retrieved 19 October 2023.
• Kleiner, Israel (2 February 2012). Excursions in the History of Mathematics. Springer Science & Business Media. ISBN 978-0-8176-8268-2.
• Marcus, Russell; McEvoy, Mark (11 February 2016). An Historical Introduction to the Philosophy of Mathematics: A Reader. Bloomsbury Publishing. ISBN 978-1-4725-3291-6.
• Monahan, John F. (6 July 2012). "2. Basic Computational Algorithms". In Gentle, James E.; Härdle, Wolfgang Karl; Mori, Yuichi (eds.). Handbook of Computational Statistics: Concepts and Methods. Springer Science & Business Media. ISBN 978-3-642-21551-3.
• Oliver, Alexander D. (2005). "arithmetic, foundations of". In Honderich, Ted (ed.). The Oxford Companion to Philosophy. Oxford University Press. ISBN 9780199264797.
• Hofweber, Thomas (2016). "The Philosophy of Arithmetic". Ontology and the Ambitions of Metaphysics. Oxford University Press. ISBN 978-0-19-876983-5.
• Stevenson, Angus; Waite, Maurice (18 August 2011). Concise Oxford English Dictionary: Luxury Edition. OUP Oxford. ISBN 978-0-19-960111-0.
• Sophian, Catherine (25 September 2017). The Origins of Mathematical Knowledge in Childhood. Routledge. ISBN 978-1-351-54175-6.
• Duverney, Daniel (2010). Number Theory: An Elementary Introduction Through Diophantine Problems. World Scientific. ISBN 978-981-4307-46-8.
• Lozano-Robledo, Álvaro (21 March 2019). Number Theory and Geometry: An Introduction to Arithmetic Geometry. American Mathematical Soc. ISBN 978-1-4704-5016-8.
• Campbell, Stephen R. (12 October 2012). "Understanding Elementary Number Theory in Relation to Arithmetic and Algebra". In Zazkis, Rina; Campbell, Stephen R. (eds.). Number Theory in Mathematics Education: Perspectives and Prospects. Routledge. ISBN 978-1-136-50143-2.
• Robbins, Neville (2006). Beginning Number Theory. Jones & Bartlett Learning. ISBN 978-0-7637-3768-9.
• Nagel, Ernest; Newman, James Roy (1 January 2008). Godel's Proof. NYU Press. ISBN 978-0-8147-5837-3.
• Waite, Maurice (9 May 2013). Pocket Oxford English Dictionary. OUP Oxford. ISBN 978-0-19-966615-7.
• Ore, Oystein (1948). Number Theory and Its History. McGraw-Hill. OCLC 1397541.
• Mazumder, Pinaki; Ebong, Idongesit E. (27 July 2023). Lectures on Digital Design Principles. CRC Press. ISBN 978-1-000-92194-6.
• HC staff (2022). "Numeral". www.ahdictionary.com. HarperCollins. Retrieved 11 November 2023.
• HC staff (2022a). "Number System". www.ahdictionary.com. HarperCollins. Retrieved 11 November 2023.
• Stakhov, Alexey (3 September 2020). Mathematics Of Harmony As A New Interdisciplinary Direction And "Golden" Paradigm Of Modern Science - Volume 2: Algorithmic Measurement Theory, Fibonacci And Golden Arithmetic's And Ternary Mirror-symmetrical Arithmetic. World Scientific. ISBN 978-981-12-1348-9.
• Nakov, Svetlin; Kolev, Veselin (1 September 2013). Fundamentals of Computer Programming with C#: The Bulgarian C# Book. Faber Publishing. ISBN 978-954-400-773-7.
• Jena, Sisir Kumar (28 December 2021). C Programming: Learn to Code. CRC Press. ISBN 978-1-000-46056-8.
• Moncayo, Raul (29 March 2018). Lalangue, Sinthome, Jouissance, and Nomination: A Reading Companion and Commentary on Lacan's Seminar XXIII on the Sinthome. Routledge. ISBN 978-0-429-91554-3.
• Null, Linda; Lobur, Julia (2006). The Essentials of Computer Organization and Architecture. Jones & Bartlett Learning. ISBN 978-0-7637-3769-6.
• Luderer, Bernd; Nollau, Volker; Vetters, Klaus (29 June 2013). Mathematical Formulas for Economists. Springer Science & Business Media. ISBN 978-3-662-12431-4.
• Khattar, Dinesh (September 2010). The Pearson Guide To Objective Arithmetic For Competitive Examinations, 3/E. Pearson Education India. ISBN 978-81-317-2673-0.
• Rajan, Hridesh (3 May 2022). An Experiential Introduction to Principles of Programming Languages. MIT Press. ISBN 978-0-262-36243-6.
• Ward, J. P. (6 December 2012). Quaternions and Cayley Numbers: Algebra and Applications. Springer Science & Business Media. ISBN 978-94-011-5768-1.
• Orr, David B. (1 April 1995). Fundamentals of Applied Statistics and Surveys. CRC Press. ISBN 978-0-412-98821-9.
• Nelson, Gerald (10 January 2019). English: An Essential Grammar. Routledge. ISBN 978-1-351-12273-3.
• Yan, Song Y. (9 March 2013). Number Theory for Computing. Springer Science & Business Media. ISBN 978-3-662-04053-9.
• Introduction to Computer Science. Pearson Education India. 2011. ISBN 978-81-317-6030-7.
• EoM staff (2016). "Natural number". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• Nagel, Rob (2002). U-X-L Encyclopedia of Science. U-X-L. ISBN 978-0-7876-5440-5.
• Hosch, William L. (2023). "Rational number". Encyclopædia Britannica. Retrieved 24 October 2023.
• Smyth, William (1864). Elementary Algebra: For Schools and Academies. Bailey and Noyes.
• Husserl, Edmund; Willard, Dallas (6 December 2012). "Translator's Introduction". Philosophy of Arithmetic: Psychological and Logical Investigations with Supplementary Texts from 1887–1901. Springer Science & Business Media. ISBN 978-94-010-0060-4.
• O'Leary, Michael L. (8 September 2015). A First Course in Mathematical Logic and Set Theory. John Wiley & Sons. ISBN 978-0-470-90588-3.
• Khan, Khalid; Graham, Tony Lee (12 June 2018). Engineering Mathematics with Applications to Fire Engineering. CRC Press. ISBN 978-1-351-59761-6.
• Rising, Gerald R.; Matthews, James R.; Schoaff, Eileen; Matthew, Judith (2021). About Mathematics. Linus Learning. ISBN 978-1-60797-892-3.
• Tarasov, Vasily (6 June 2008). Quantum Mechanics of Non-Hamiltonian and Dissipative Systems. Elsevier. ISBN 978-0-08-055971-1.
• Mazzola, Guerino; Milmeister, Gérard; Weissmann, Jody (2004). Comprehensive Mathematics For Computer Scientists 1: Sets And Numbers, Graphs And Algebra, Logic And Machines, Linear Geometry. Springer Science & Business Media. ISBN 978-3-540-20835-8.
• Krenn, Stephan; Lorünser, Thomas (28 March 2023). An Introduction to Secret Sharing: A Systematic Overview and Guide for Protocol Selection. Springer Nature. ISBN 978-3-031-28161-7.
• Sally, Judith D.; Sally (Jr.), Paul J. (2012). Integers, Fractions, and Arithmetic: A Guide for Teachers. American Mathematical Soc. ISBN 978-0-8218-8798-1.
• Burgin, Mark (22 April 2022). Trilogy Of Numbers And Arithmetic - Book 1: History Of Numbers And Arithmetic: An Information Perspective. World Scientific. ISBN 978-981-12-3685-3.
• Wheater, Carolyn (2 June 2015). Algebra I. Dorling Kindersley Limited. ISBN 978-0-241-88779-0.
• Wright, Robert J.; Ellemor-Collins, David; Tabor, Pamela D. (4 November 2011). Developing Number Knowledge: Assessment,Teaching and Intervention with 7-11 year olds. SAGE. ISBN 978-1-4462-8927-3.
• Achatz, Thomas; Anderson, John G. (2005). Technical Shop Mathematics. Industrial Press Inc. ISBN 978-0-8311-3086-2.
• Rodda, Harvey J. E.; Little, Max A. (2 November 2015). Understanding Mathematical and Statistical Techniques in Hydrology: An Examples-based Approach. John Wiley & Sons. ISBN 978-1-119-07659-9.
• Thiam, Thierno; Rochon, Gilbert (31 August 2019). Sustainability, Emerging Technologies, and Pan-Africanism. Springer Nature. ISBN 978-3-030-22180-5.
• Ponticorvo, Michela; Schmbri, Massimiliano; Miglino, Orazio (9 May 2019). "How to Improve Spatial and Numerical Cognition with a Game-Based and Technology-Enhanced Learning Approach". In Vicente, José Manuel Ferrández; Álvarez-Sánchez, José Ramón; López, Félix de la Paz; Moreo, Javier Toledo; Adeli, Hojjat (eds.). Understanding the Brain Function and Emotions: 8th International Work-Conference on the Interplay Between Natural and Artificial Computation, IWINAC 2019, Almería, Spain, June 3–7, 2019, Proceedings, Part I. Springer. ISBN 978-3-030-19591-5.
• Ang, Tian Se; Lam, Lay Yong (6 April 2004). Fleeting Footsteps: Tracing The Conception Of Arithmetic And Algebra In Ancient China (Revised Edition). World Scientific. ISBN 978-981-4483-60-5.
• Yadin, Aharon (19 August 2016). Computer Systems Architecture. CRC Press. ISBN 978-1-315-35592-4.
• Brown, David (26 April 2010). "The measurement of time and distance in the heavens above Mesopotamia, with brief reference made to other ancient astral science". In Morley, Iain; Renfrew, Colin (eds.). The Archaeology of Measurement: Comprehending Heaven, Earth and Time in Ancient Societies. Cambridge University Press. ISBN 978-0-521-11990-0.
• Madden, Daniel J.; Aubrey, Jason A. (12 September 2017). An Introduction to Proof through Real Analysis. John Wiley & Sons. ISBN 978-1-119-31472-1.
• Payne, Andrew (2017). The Teleology of Action in Plato's Republic. Oxford University Press. ISBN 978-0-19-879902-3.
• Bloch, Ethan D. (14 May 2011). The Real Numbers and Real Analysis. Springer Science & Business Media. ISBN 978-0-387-72177-4.
• Lützen, Jesper (2023). A History of Mathematical Impossibility. Oxford University Press. ISBN 978-0-19-286739-1.
• Klein, Jacob (22 April 2013a). Greek Mathematical Thought and the Origin of Algebra. Courier Corporation. ISBN 978-0-486-31981-0.
• Bradley, Michael J. (2006). The Birth of Mathematics: Ancient Times To 1300. Infobase Publishing. ISBN 978-0-7910-9723-6.
• Cai, Tianxin (25 July 2023). A Brief History of Mathematics: A Promenade through the Civilizations of Our World. Springer Nature. ISBN 978-3-031-26841-0.
• Conradie, Willem; Goranko, Valentin (28 April 2015). Logic and Discrete Mathematics: A Concise Introduction. John Wiley & Sons. ISBN 978-1-118-76109-0.
• Oakes, Elizabeth (1 July 2020). Encyclopedia of World Scientists, Updated Edition. Infobase Publishing. ISBN 978-1-4381-9545-2.
• Wedell, Moritz (31 August 2015). "Numbers". In Classen, Albrecht (ed.). Handbook of Medieval Culture. Volume 2. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-037763-7.
• Koetsier, Teun (20 November 2018). The Ascent of GIM, the Global Intelligent Machine: A History of Production and Information Machines. Springer. ISBN 978-3-319-96547-5.
• Cignoni, Gioanni A.; Cossu, Giovanni A. (30 November 2016). "The Global Virtual Museum of Information Science & Technology, a Project Idea". In Tatnall, Arthur; Leslie, Christopher (eds.). International Communities of Invention and Innovation: IFIP WG 9.7 International Conference on the History of Computing, HC 2016, Brooklyn, NY, USA, May 25-29, 2016, Revised Selected Papers. Springer. ISBN 978-3-319-49463-0.
• Eriksson, Kenneth; Estep, Donald; Johnson, Claes (9 March 2013). Applied Mathematics: Body and Soul: Volume 2: Integrals and Geometry in IRn. Springer Science & Business Media. ISBN 978-3-662-05798-8.
• Weil, André (21 May 2009). Number Theory: An approach through history From Hammurapi to Legendre. Springer Science & Business Media. ISBN 978-0-8176-4571-7.
• Karlsson, Anders (20 December 2011). "Applications of heat kernels on abelian groups". In Goldfeld, Dorian; Jorgenson, Jay; Jones, Peter; Ramakrishnan, Dinakar; Ribet, Kenneth; Tate, John (eds.). Number Theory, Analysis and Geometry: In Memory of Serge Lang. Springer Science & Business Media. ISBN 978-1-4614-1259-5.
• Wang, Hao (3 February 1997). A Logical Journey: From Gödel to Philosophy. MIT Press. ISBN 978-0-262-26125-8.
• Curley, Robert (1 November 2011). Computing: From the Abacus to the iPad. Britannica Educational Publishing. ISBN 978-1-61530-707-4.
• Hua, Jueming; Feng, Lisheng (14 December 2020). Thirty Great Inventions of China: From Millet Agriculture to Artemisinin. Springer Nature. ISBN 978-981-15-6525-0.
• Chemla, Karine; Keller, Agathe; Proust, Christine (1 January 2023). Cultures of Computation and Quantification in the Ancient World: Numbers, Measurements, and Operations in Documents from Mesopotamia, China and South Asia. Springer Nature. ISBN 978-3-030-98361-1.
• Vullo, Vincenzo (14 February 2020). Gears: Volume 3: A Concise History. Springer Nature. ISBN 978-3-030-40164-1.
• MacDuffee, C. C. "Arithmetic". Encyclopedia Britannica. Retrieved 18 November 2023.
• Adamowicz, Zofia (1994). "The Power of Exponentiation in Arithmetic". In Joseph, Anthony; Mignot, Fulbert; Murat, François; Prum, Bernard; Rentschler, Rudolf (eds.). First European Congress of Mathematics: Paris, July 6-10, 1992 Volume I Invited Lectures (Part 1). Birkhäuser. ISBN 978-3-0348-9110-3.
• Yan, Song Y. (9 March 2013). Number Theory for Computing. Springer Science & Business Media. ISBN 978-3-662-04053-9.
• Grigorieva, Ellina (6 July 2018). Methods of Solving Number Theory Problems. Birkhäuser. ISBN 978-3-319-90915-8.
• Page, Robert L. (1 January 2003). "Number Theory, Elementary". Encyclopedia of Physical Science and Technology (Third Edition). Academic Press. ISBN 978-0-12-227410-7.
• Křížek, Michal; Somer, Lawrence; Šolcová, Alena (21 September 2021). From Great Discoveries in Number Theory to Applications. Springer Nature. ISBN 978-3-030-83899-7.
• EoM staff (2014). "Analytic number theory". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• EoM staff (2019). "Algebraic number theory". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• EoM staff (2014a). "Elementary number theory". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• Riesel, Hans (6 December 2012). Prime Numbers and Computer Methods for Factorization. Springer Science & Business Media. ISBN 978-1-4612-0251-6.
• Yan, Song Y. (29 January 2013). Computational Number Theory and Modern Cryptography. John Wiley & Sons. ISBN 978-1-118-18858-3.

Further reading

• Cunnington, Susan, The Story of Arithmetic: A Short History of Its Origin and Development, Swan Sonnenschein, London, 1904
• Dickson, Leonard Eugene, History of the Theory of Numbers (3 volumes), reprints: Carnegie Institute of Washington, Washington, 1932; Chelsea, New York, 1952, 1966
• Euler, Leonhard, Elements of Algebra, Tarquin Press, 2007
• Fine, Henry Burchard (1858–1928), The Number System of Algebra Treated Theoretically and Historically, Leach, Shewell & Sanborn, Boston, 1891
• Karpinski, Louis Charles (1878–1956), The History of Arithmetic, Rand McNally, Chicago, 1925; reprint: Russell & Russell, New York, 1965
• Ore, Øystein, Number Theory and Its History, McGraw–Hill, New York, 1948
• Weil, André, Number Theory: An Approach through History, Birkhauser, Boston, 1984; reviewed: Mathematical Reviews 85c:01004

External links

• MathWorld article about arithmetic
• The New Student's Reference Work/Arithmetic (historical)
• The Great Calculation According to the Indians, of Maximus Planudes – an early Western work on arithmetic at Convergence
• Weyde, P. H. Vander (1879). "Arithmetic" . The American Cyclopædia.