Algebra

For the kind of algebraic structure, see Algebra over a field. For other uses, see Algebra (disambiguation).

The quadratic formula expresses the solution of the equation ax² + bx + c = 0, where a is not zero, in terms of its coefficients a, b and c.

Algebra (Arabic: الجبر Al-Jabr, transl. 'reunion of broken parts' or 'bone-setting'; [ʔldʒbr] listen^ⓘ) is the study of variables and the rules for manipulating these variables in formulas. Originating in ancient Babylonian techniques of calculation, it is now a way of thinking that appears throughout almost all areas of mathematics.

Elementary algebra deals with the manipulation of variables (commonly represented by Roman letters) as if they were numbers and is therefore essential in all applications of mathematics. "Higher" or "abstract" algebra, which professional mathematicians typically just call "algebra", is the study of algebraic structures that generalize the operations familiar from ordinary arithmetic. For example, a group is a set with a binary operation, a rule for combining two members of that set to produce a third, which satisfies some of the same basic properties as addition of integers. Other algebraic structures include rings and fields. Linear algebra, which deals with linear equations and linear mappings, is used for modern presentations of geometry, and has many practical applications (in weather forecasting, for example). There are many areas of mathematics that belong to algebra, some having "algebra" in their name, such as commutative algebra, and some not, such as Galois theory.

The word algebra is not only used for naming an area of mathematics and some subareas; it is also used for naming some sorts of algebraic structures, such as an algebra over a field, commonly called an algebra. Sometimes, the same phrase is used for a subarea and its main algebraic structures. For example, the subject known as Boolean algebra studies structures called Boolean algebras. A mathematician specialized in algebra is called an algebraist.

Etymology

The word algebra comes from the title of a book by Muhammad ibn Musa al-Khwarizmi.

The word algebra comes from the Arabic: الجبر, romanized: al-jabr, lit. 'reunion of broken parts, bonesetting' from the title of the early 9th century book ʿIlm al-jabr wa l-muqābala "The Science of Restoring and Balancing" by the Persian mathematician and astronomer al-Khwarizmi. In his work, the term al-jabr referred to the operation of moving a term from one side of an equation to the other, المقابلة al-muqābala "balancing" referred to adding equal terms to both sides. Shortened to just algeber or algebra in Latin, the word eventually entered the English language during the 15th century, from either Spanish, Italian, or Medieval Latin. It originally referred to the surgical procedure of setting broken or dislocated bones. The mathematical meaning was first recorded (in English) in the 16th century.

Definition

Algebra is the branch of mathematics that studies algebraic operations and algebraic structures. An algebraic structure is a non-empty set of mathematical objects, such as the real numbers, together algebraic operations defined on that set, such addition and multiplication. Algebra explores the laws, general characteristics, and types of algebraic structures. Within certain algebraic structures, it studies the use of variables in equations and how to manipulate these equations.

Algebra is often understood as a generalization of arithmetic. Arithmetic studies arithmetic operations, like addition, subtraction, multiplication, and division, in a specific domain of numbers, like the real numbers. Elementary algebra constitutes the first level of abstraction. Like arithmetic, it restricts itself to specific types of numbers and operations. It generalizes these operations by allowing indefinite quantities in the form of variables in addition to numbers. A higher level of abstraction is achieved in abstract algebra, which is not limited to a specific domain and studies different classes of algebraic structures, like groups and rings. These algebraic structures are not restricted to typical arithmetic operations and cover other binary operations besides them. Universal algebra is still more abstract in that it is not limited to binary operations and not interested in specific classes of algebraic structures but investigates the characteristics of algebraic structures in general.

The term "algebra" is sometimes used in a more narrow sense to refer only to elementary algebra or only to abstract algebra. When used as a countable noun, an algebra is a specific type of algebraic structure that involves a vector space equipped with a certain type of binary operation. Depending on the context, "algebra" can also refer to other algebraic structures, like a Lie algebra or an associative algebra.

Algebra as a branch of mathematics

Algebra began with computations similar to those of arithmetic, with letters standing for numbers. This allowed proofs of properties that are true no matter which numbers are involved. For example, in the quadratic equation

$ax^{2}+bx+c=0,$

$a,b,c$ can be any numbers whatsoever (except that $a$ cannot be $0$), and the quadratic formula can be used to quickly and easily find the values of the unknown quantity $x$ which satisfy the equation. That is to say, to find all the solutions of the equation.

Historically, and in current teaching, the study of algebra starts with the solving of equations, such as the quadratic equation above. Then more general questions, such as "does an equation have a solution?", "how many solutions does an equation have?", "what can be said about the nature of the solutions?" are considered. These questions led extending algebra to non-numerical objects, such as permutations, vectors, matrices, and polynomials. The structural properties of these non-numerical objects were then formalized into algebraic structures such as groups, rings, and fields.

Before the 16th century, mathematics was divided into only two subfields, arithmetic and geometry. Even though some methods, which had been developed much earlier, may be considered nowadays as algebra, the emergence of algebra and, soon thereafter, of infinitesimal calculus as subfields of mathematics only dates from the 16th or 17th century. From the second half of the 19th century on, many new fields of mathematics appeared, most of which made use of both arithmetic and geometry, and almost all of which used algebra.

Today, algebra has grown considerably and includes many branches of mathematics, as can be seen in the Mathematics Subject Classification where none of the first level areas (two digit entries) are called algebra. Today algebra includes section 08-General algebraic systems, 12-Field theory and polynomials, 13-Commutative algebra, 15-Linear and multilinear algebra; matrix theory, 16-Associative rings and algebras, 17-Nonassociative rings and algebras, 18-Category theory; homological algebra, 19-K-theory and 20-Group theory. Algebra is also used extensively in 11-Number theory and 14-Algebraic geometry.

History

Main articles: History of algebra, Abstract algebra § History, and Timeline of algebra

The use of the word "algebra" for denoting a part of mathematics dates probably from the 16th century. The word is derived from the Arabic word al-jabr that appears in the title of the treatise Al-Kitab al-muhtasar fi hisab al-gabr wa-l-muqabala (The Compendious Book on Calculation by Completion and Balancing), written in circa 820 by Al-Kwarizmi.

Al-jabr referred to a method for transforming equations by subtracting like terms from both sides, or passing one term from one side to the other, after changing its sign.

Therefore, algebra referred originally to the manipulation of equations, and, by extension, to the theory of equations. This is still what historians of mathematics generally mean by the term algebra.

In mathematics, the meaning of algebra has evolved after the introduction by François Viète of symbols (variables) for denoting unknown or incompletely specified numbers, and the resulting use of the mathematical notation for equations and formulas. So, algebra became essentially the study of the action of operations on expressions involving variables. This includes but is not limited to the theory of equations.

At the beginning of the 20th century, algebra evolved further by considering operations that act not only on numbers but also on elements of so-called mathematical structures such as groups, fields and vector spaces. This new algebra was called modern algebra by van der Waerden in his eponymous treatise, whose name has been changed to Algebra in later editions.

Early history

A page from Al-Khwārizmī's al-Kitāb al-muḫtaṣar fī ḥisāb al-ğabr wa-l-muqābala

The roots of algebra can be traced back to the ancient Babylonians, who developed an advanced arithmetical system with which they were able to do calculations in an algorithmic fashion. The Babylonians developed formulas to calculate solutions for problems typically solved today by using linear equations, quadratic equations, and indeterminate linear equations. By contrast, most Egyptians of this era, as well as Greek and Chinese mathematics in the 1st millennium BC, usually solved such equations by geometric methods, such as those described in the Rhind Mathematical Papyrus, Euclid's Elements, and The Nine Chapters on the Mathematical Art. The geometric work of the Greeks, typified in the Elements, provided the framework for generalizing formulae beyond the solution of particular problems into more general systems of stating and solving equations, although this would not be realized until mathematics developed in medieval Islam.

By the time of Plato, Greek mathematics had undergone a drastic change. The Greeks created a geometric algebra where terms were represented by sides of geometric objects, usually lines, that had letters associated with them. Diophantus (3rd century AD) was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, and have led, in number theory, to the modern notion of Diophantine equation.

Earlier traditions discussed above had a direct influence on the Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī (c. 780–850). He later wrote The Compendious Book on Calculation by Completion and Balancing, which established algebra as a mathematical discipline that is independent of geometry and arithmetic.

The Hellenistic mathematicians Hero of Alexandria and Diophantus as well as Indian mathematicians such as Brahmagupta, continued the traditions of Egypt and Babylon, though Diophantus' Arithmetica and Brahmagupta's Brāhmasphuṭasiddhānta are on a higher level. For example, the first complete arithmetic solution written in words instead of symbols, including zero and negative solutions, to quadratic equations was described by Brahmagupta in his book Brahmasphutasiddhanta, published in 628 AD. Later, Persian and Arab mathematicians developed algebraic methods to a much higher degree of sophistication. Although Diophantus and the Babylonians used mostly special ad hoc methods to solve equations, Al-Khwarizmi's contribution was fundamental. He solved linear and quadratic equations without algebraic symbolism, negative numbers or zero, thus he had to distinguish several types of equations.

In the context where algebra is identified with the theory of equations, the Greek mathematician Diophantus has traditionally been known as the "father of algebra" and in the context where it is identified with rules for manipulating and solving equations, Persian mathematician al-Khwarizmi is regarded as "the father of algebra". It is open to debate whether Diophantus or al-Khwarizmi is more entitled to be known, in the general sense, as "the father of algebra". Those who support Diophantus point to the fact that the algebra found in Al-Jabr is slightly more elementary than the algebra found in Arithmetica and that Arithmetica is syncopated while Al-Jabr is fully rhetorical. Those who support Al-Khwarizmi point to the fact that he introduced the methods of "reduction" and "balancing" (the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation) which the term al-jabr originally referred to, and that he gave an exhaustive explanation of solving quadratic equations, supported by geometric proofs while treating algebra as an independent discipline in its own right. His algebra was also no longer concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study". He also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems".

According to Jeffrey Oaks and Jean Christianidis neither Diophantus nor Al-Khwarizmi should be called "father of algebra". Pre-modern algebra was developed and used by merchants and surveyors as part of what Jens Høyrup called "subscientific" tradition. Diophantus used this method of algebra in his book, in particular for indeterminate problems, while Al-Khwarizmi wrote one of the first books in arabic about this method.

Another Persian mathematician Omar Khayyam is credited with identifying the foundations of algebraic geometry and found the general geometric solution of the cubic equation. His book Treatise on Demonstrations of Problems of Algebra (1070), which laid down the principles of algebra, is part of the body of Persian mathematics that was eventually transmitted to Europe. Yet another Persian mathematician, Sharaf al-Dīn al-Tūsī, found algebraic and numerical solutions to various cases of cubic equations. He also developed the concept of a function. The Indian mathematicians Mahavira and Bhaskara II, the Persian mathematician Al-Karaji, and the Chinese mathematician Zhu Shijie, solved various cases of cubic, quartic, quintic and higher-order polynomial equations using numerical methods. In the 13th century, the solution of a cubic equation by Fibonacci is representative of the beginning of a revival in European algebra. Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412–1486) took "the first steps toward the introduction of algebraic symbolism". He also computed Σn², Σn³ and used the method of successive approximation to determine square roots.

Modern history

Italian mathematician Girolamo Cardano published the solutions to the cubic and quartic equations in his 1545 book Ars magna.

François Viète's work on new algebra at the close of the 16th century was an important step towards modern algebra. In 1637, René Descartes published La Géométrie, inventing analytic geometry and introducing modern algebraic notation. Another key event in the further development of algebra was the general algebraic solution of the cubic and quartic equations, developed in the mid-16th century. The idea of a determinant was developed by Japanese mathematician Seki Kōwa in the 17th century, followed independently by Gottfried Leibniz ten years later, for the purpose of solving systems of simultaneous linear equations using matrices. Gabriel Cramer also did some work on matrices and determinants in the 18th century. Permutations were studied by Joseph-Louis Lagrange in his 1770 paper "Réflexions sur la résolution algébrique des équations" devoted to solutions of algebraic equations, in which he introduced Lagrange resolvents. Paolo Ruffini was the first person to develop the theory of permutation groups, and like his predecessors, also in the context of solving algebraic equations.

Abstract algebra was developed in the 19th century, deriving from the interest in solving equations, initially focusing on what is now called Galois theory, and on constructibility issues. George Peacock was the founder of axiomatic thinking in arithmetic and algebra. Augustus De Morgan discovered relation algebra in his Syllabus of a Proposed System of Logic. Josiah Willard Gibbs developed an algebra of vectors in three-dimensional space, and Arthur Cayley developed an algebra of matrices (this is a noncommutative algebra).

Areas of mathematics with the word algebra in their name

Linear algebra lecture at the Aalto University

Some subareas of algebra have the word algebra in their name; linear algebra is one example. Others do not: group theory, ring theory, and field theory are examples. In this section, we list some areas of mathematics with the word "algebra" in the name.

• Elementary algebra, the part of algebra that is usually taught in elementary courses of mathematics.
• Abstract algebra, in which algebraic structures such as groups, rings and fields are axiomatically defined and investigated.
• Linear algebra, in which the specific properties of linear equations, vector spaces and matrices are studied.
• Boolean algebra, a branch of algebra abstracting the computation with the truth values false and true.
• Commutative algebra, the study of commutative rings.
• Computer algebra, the implementation of algebraic methods as algorithms and computer programs.
• Homological algebra, the study of algebraic structures that are fundamental to study topological spaces.
• Universal algebra, in which properties common to all algebraic structures are studied.
• Algebraic number theory, in which the properties of numbers are studied from an algebraic point of view.
• Algebraic geometry, a branch of geometry, in its primitive form specifying curves and surfaces as solutions of polynomial equations.
• Algebraic combinatorics, in which algebraic methods are used to study combinatorial questions.
• Relational algebra: a set of finitary relations that is closed under certain operators.

Many mathematical structures are called algebras:

• Algebra over a field or more generally algebra over a ring.
  Many classes of algebras over a field or over a ring have a specific name:
  • Associative algebra
  • Non-associative algebra
  • Lie algebra
  • Composition algebra
  • Hopf algebra
  • C*-algebra
  • Symmetric algebra
  • Exterior algebra
  • Tensor algebra
• In measure theory,
  • Sigma-algebra
  • Algebra over a set
• In category theory
  • F-algebra and F-coalgebra
  • T-algebra
• In logic,
  • Relation algebra, a residuated Boolean algebra expanded with an involution called converse.
  • Boolean algebra, a complemented distributive lattice.
  • Heyting algebra

Elementary algebra

Main article: Elementary algebra

Algebraic expression notation:
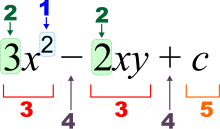
  1 – power (exponent)
  2 – coefficient
  3 – term
  4 – operator
  5 – constant term
  x y c – variables/constants

Elementary algebra, also referred to as school algebra, college algebra, and classical algebra, is the oldest and most basic form of algebra. It is a generalization of arithmetic that relies on the use of variables and examines how formulas may be transformed.

Arithmetic is the study of numerical operations and investigates how numbers are combined and transformed using arithmetic operations like addition, subtraction, multiplication, and division. For example, the operation of addition combines two numbers, called the addends, into a third number, called the sum, as in $2+5=7$.

Elementary algebra uses the same operations while allowing the use of variables in addition to regular numbers. Variables are symbols for unspecified or unknown quantities. They make it possible to state relationships for which one does not know the exact values and to express general laws that are true independent of which numbers are used. For example, the equation $2\times 3=3\times 2$ belongs to arithmetic and expresses an equality only for these specific numbers. By replacing the numbers with variables, it is possible to express a general law that applies to any possible combinations of numbers, as in the equation $a\times b=b\times a$.

Elementary algebra is interested in algebraic expressions, which are formed by using arithmetic operations to combine variables and numbers. For example, the expression $5x+3$ is an algebraic expression created by multiplying the number 5 with the variable x and adding the number 3 to the result. Other examples of algebraic equations are $32xyz$ and $64x^{2}+7y-13$.

Algebraic expressions are used to construct statements that relate two expressions to one another. An equation is a statement formed by comparing two expressions using an equals sign (=), as in $5x^{2}+6x=3y+4$. Inequations are formed using symbols like the less-than sign (<) and the greater-than sign (>). Unlike mere expressions, statements can be true or false and their truth value usually depends on the values of the variables. For example, the statement $x^{2}=4$ is true if x is either 2 or -2 and false otherwise.

The main objective of elementary algebra is to determine for which values a statement is true. To achieve this, it relies on different techniques used to transform and manipulate statements. A key principle guiding this process is that whatever is done to one side of an equation also needs to be done to the other side of the equation. For example, if one subtracts 5 from the left side of an equation one also needs to subtract 5 from the right side of the equation to balance both sides. The goal of these steps is usually to isolate the variable one is interested in on one side, a process known as solving the equation for that variable. For example, the equation $x-7=4$ can be solved for x by adding 7 to both sides, which isolates x on the left side and results in the equation $x=11$.

There are many other techniques used to solve equations. Simplification is used to replace a complicated expression with an equivalent simpler one. For example, the expression $7x-3x$ can be replaced with the expression $4x$. Factorization is used to rewrite an expression as a product of several factors. This technique is common for polynomials to determine for which values the expression is zero. For example, the polynomial $x^{2}-3x-10$ can be factorized as $(x+2)(x-5)$. The polynomial as a whole is zero if one of its factors is zero, i.e., if x is either -2 or 5. For statements using several variables, substitution is a common technique to replace one variable with an equivalent expression that does not use this variable. For example, if one knows that $y=3x$ then one can simplify the expression $7xy$ to arrive at $21x^{2}$. Other techniques include making use of the commutative, distributive, and associative properties.

Algebraic equations can be used to describe geometric figures. All values for x and y that solve the equation are interpreted as points and drawn as a red line.

Elementary algebra has applications in many branches of mathematics, the sciences, business, and everyday life. An important application in the field of geometry concerns the use of algebraic equations to describe geometric figures in the form of a graph. To do so, the different variables in the equation are interpreted as coordinates and the values that solve the equation are interpreted as points of the graph. For example, if x is set to zero in the equation $y=0.5x-1$ then y has to be −1 for the equation to be true. This means that the x-y-pair (0, −1) is part of the graph of the equation. The x-y-pair (0, 7), by contrast, does not solve the equation and is therefore not part of the graph. The graph encompasses the totality of all x-y-pairs that solve the equation.

Education

See also: Mathematics education

It has been suggested that elementary algebra should be taught to students as young as eleven years old, though in recent years it is more common for public lessons to begin at the eighth grade level (≈ 13 y.o. ±) in the United States. However, in some US schools, algebra instruction starts in ninth grade.

Linear algebra

Main article: Linear algebra

Linear algebra employs the methods of elementary algebra to study systems of linear equations. An equation is linear if no variable is multiplied with another variable and no operations like exponentiation, extraction of roots, and logarithm are applied to variables. For example, the equations $0.25x-4=y$ and $x_{1}-7x_{2}+3x_{3}=0$ are linear while the equations $x^{2}=y$ and $3x_{1}x_{2}+15=0$ are non-linear. Several equations form a system of equations if they all rely on the same set of variables.

Systems of linear equations are often expressed through matrices and vectors to represent the whole system in a single equation. This can be done by moving the variables to the left side of each equation and moving the constant terms to the right side. The system is then expressed by formulating a matrix that contains all the coefficients of the equations and multiplying it with the vector made up of the variables. For example, the system of equations

1. $9x_{1}+3x_{2}-13x_{3}=0$
2. $2.3x_{1}+7x_{3}=9$
3. $-5x_{1}-17x_{2}=-3$

can be written as

$${\begin{bmatrix}9&3&-13\\2.3&0&9\\-5&-17&0\end{bmatrix}}\cdot {\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}}={\begin{bmatrix}0\\9\\-3\end{bmatrix}}$$

Like elementary algebra, linear algebra is interested in manipulating and transforming equations to solve them. It goes beyond elementary algebra by dealing with several equations at once and looking for the values for which all equations are true at the same time. For example, if the system is made of the two equations $3x_{1}-x_{2}=0$ and $x_{1}+x_{2}=8$ then using the values 1 and 3 for $x_{1}$ and $x_{2}$ does not solve the system of equations because it only solves the first but not the second equation.

Two central questions in linear algebra are whether a system of equations has any solutions and, if so, whether it has a unique solution. A system of equations that has solutions is called consistent. This is the case if the equations do not contradict each other. If two or more equations contradict each other, the system of equations is inconsistent and has no solutions. For example, the equations $x_{1}-3x_{2}=0$ and $x_{1}-3x_{2}=7$ contradict each other since no values of $x_{1}$ and $x_{2}$ exist that solve both equations at the same time.

Whether a consistent system of equations has a unique solution depends on the number of variables and the number of independent equations. Several equations are independent of each other if they do not provide the same information and cannot be derived from each other. A unique solution exists if the number of variables is the same as the number of independent equations. Underdetermined systems, by contrast, have more variables than equations and have an infinite number of solutions if they are consistent.

Linear equations with two variables can be interpreted geometrically as lines. The solution of a system of linear equations is where the lines intersect.

Many of the techniques employed in elementary algebra to solve equations are also applied in linear algebra. The substitution method starts with one equation and isolates one variable in it. It proceeds to the next equation and replaces the isolated variable with the found expression, thereby reducing the number of unknown variables by one. It applies the same process again to this and the remaining equations until the values of all variables are determined. The elimination method creates a new equation by adding one equation to another equation. This way, it is possible to eliminate one variable that appears in both equations. For a system that contains the equations $-x+7y=3$ and $2x-7y=10$, it is possible to eliminate y by adding the first to the second equation, thereby revealing that x is 13. Many advanced techniques implement algorithms based on matrix calculations, such as Cramer's rule, the Gauss–Jordan elimination, and LU Decomposition.

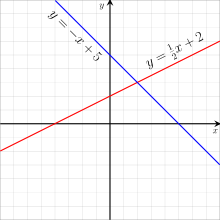
On a geometric level, systems of equations can be interpreted as geometric figures. For systems that have two variables, each equation represents a line in two-dimensional space. The point where the two lines intersect is the solution. For inconsistent systems, the two lines run parallel, meaning that there is no solution since they never intersect. If two equations are not independent then they describe the same line, meaning that every solution of one equation is also a solution of the other equation. These relations make it possible to graphically look for solutions by plotting the equations and determining where they intersect. The same principles also apply to systems of equations with more variables, with the difference being that the equations do not describe lines but higher dimensional figures. For instance, equations with three variables correspond to planes in three-dimensional space and the points where all planes intersect solve the system of equations.

Abstract algebra

Main article: Abstract algebra

Abstract algebra, also called modern algebra, studies different types of algebraic structures. An algebraic structure is a framework for understanding operations on mathematical objects, like the addition of numbers. While elementary algebra and linear algebra work within the confines of particular algebraic structures, abstract algebra takes a more general approach that compares how algebraic structures differ from each other and what types of algebraic structures there are, such as groups, rings, and fields.

Many algebraic structures rely on binary operations, which take two objects as input and combine them into a single object as output.

On a formal level, an algebraic structure is a set of mathematical objects, called the underlying set, together with one or several operations. Abstract algebra usually restricts itself to binary operations that take any two objects from the underlying set as inputs and map them to another object from this set as output. For example, the algebraic structure $\langle \mathbb {N} ,+\rangle$ has the natural numbers as the underlying set. Addition is its binary operation and takes two numbers as input to produce one number in the form of the sum as output. The underlying set can contain mathematical objects other than numbers and the operations are not restricted to regular arithmetic operations.

Abstract algebra classifies algebraic structures based on the laws or axioms that its operations obey and the number of operations it uses. One of the most basic types is a group, which has one operation and requires that this operation is associative and has an identity element and inverse elements. An operation is associative if the order of several applications does not matter, i.e., if $(a\circ b)\circ c$ is the same as $a\circ (b\circ c)$ for all elements. An operation has an identity element or a neutral element if one element e exists that does not change the value of any other element, i.e., if $a\circ e=e\circ a=a$. An operation admits inverse elements if for any element $a$ there exists a reciprocal element $a^{-1}$ that reverses its effects. If an element is linked to its inverse then the result is the neutral element e, expressed formally as $a\circ a^{-1}=a^{-1}\circ a=e$. Every algebraic structure that fulfills these requirements is a group. For example, $\langle \mathbb {Z} ,+\rangle$ is a group formed by the set of integers together with the operation of addition. The neutral element is 0 and the inverse element of any number $a$ is $-a$. The natural numbers, by contrast, do not form a group since they contain only positive numbers and therefore lack inverse elements. Group theory is the subdiscipline of abstract algebra studying groups.

Diagram of relations between some algebraic structures

A ring is an algebraic structure with two operations ($\circ$ and $\star$) that work similarly to addition and multiplication. All the requirements of groups also apply to the first operation: it is associative and has an identity element and inverse elements. Additionally, it is commutative, meaning that $a\circ b=b\circ a$ is true for all elements. The axiom of distributivity governs how the two operations interact with each other. It states that $a\star (b\circ c)=(a\star b)\circ (a\star c)$ and $(b\circ c)\star a=(b\star a)\circ (c\star a)$. The ring of integers is a ring of the form $\langle \mathbb {Z} ,+,\cdot \rangle$. A ring becomes a field if both operations follow the axioms of associativity, commutativity, and distributivity and if both operations have an identity element and inverse elements. The ring of integers does not form a field because it lacks multiplicative inverses. For example, the multiplicative inverse of $7$ is ${\tfrac {1}{7}}$, which is not part of the integers. The rational numbers, the real numbers, and the complex numbers each form a field.

Besides groups, rings, and fields, there are many other algebraic structures studied by abstract algebra. They include magmas, semigroups, monoids, abelian groups, commutative rings, modules, lattices, vector spaces, and algebras over a field. They differ from each other in regard to the types of objects they describe and the requirements that their operations fulfill. Many of them are related to each other in that a basic structure can be turned into a more advanced structure by adding additional requirements. For example, a magma becomes a semigroup if its operation is associative.

Universal algebra

Main article: Universal algebra

Universal algebra is the study of algebraic structures in general. It is a generalization of abstract algebra that is not limited to binary operations and allows operations with more inputs as well, such as ternary operations. Universal algebra is not interested in the specific elements that make up the underlying sets and instead investigates what structural features different algebraic structures have in common. One of those structural features concerns the identities that are true in different algebraic structures. In this context, an identity is a universal equation or an equation that is true for all elements of the underlying set. For example, commutativity is a universal equation that states that $a\circ b$ is identical to $b\circ a$ for all elements. Two algebraic structures that share all their identities are said to belong to the same variety. For instance, the ring of integers and the ring of polynomials form part of the same variety because they have the same identities, such as commutativity and associativity. The field of rational numbers, by contrast, does not belong to this variety since it has additional identities, such as the existence of multiplicative inverses.

Besides identities, universal algebra is also interested in structural features associated with quasi-identities. A quasi-identity, also referred to as Horn clause, is an identity that only needs to be present under certain conditions. It is a generalization of identity in the sense that every identity is a quasi-identity but not every quasi-identity is an identity. Algebraic structures that share all their quasi-identities have certain structural characteristics in common, which is expressed by stating that they belong to the same quasivariety.

Subalgebras restrict their operations to a subset of the underlying set of the original algebraic structure.

Homomorphisms are a tool in universal algebra to examine structural features by comparing two algebraic structures. A homomorphism is a function that takes the elements of the underlying set of one algebraic structure as input and has the elements of the underlying set of another algebraic structure as output. Its special feature is that it preserves certain structural characteristics of the algebraic structures. If the two algebraic structures use binary operations and have the form $\langle A,\circ \rangle$ and $\langle B,\star \rangle$ then the function $h:A\to B$ is a homomorphism if it fulfills the following requirement: $h(x\circ y)=h(x)\star h(y)$. The existence of a homomorphism reveals that the operation $\star$ in the second algebraic structure plays the same role as the operation $\circ$ does in the first algebraic structure.

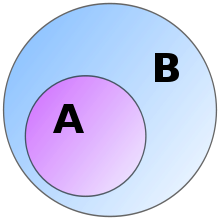
Another tool of comparison is the relation between an algebraic structure and its subalgebra. If $\langle A,\circ \rangle$ is a subalgebra of $\langle B,\circ \rangle$ then the set A is a subset of B. A subalgebra has to use the same operations as the algebraic structure and they have to follow the same axioms. This includes the requirement that all operations in the subalgebra are closed in A, meaning that they only produce elements that belong to A. For example, the set of even integers together with addition is a subalgebra of the full set of integers together with addition. This is the case because the sum of two even numbers is again an even number. But the set of odd integers together with addition is not a subalgebra since adding two odd numbers produces an even number, which is not part of the chosen subset.

See also

• Algebra tile
• Outline of algebra
• Outline of linear algebra

References

Sources

• Boyer, Carl B. (1991). A History of Mathematics (2nd ed.). John Wiley & Sons. ISBN 978-0-471-54397-8.
• Gandz, S. (January 1936). "The Sources of Al-Khowārizmī's Algebra". Osiris. 1: 263–277. doi:10.1086/368426. JSTOR 301610. S2CID 60770737.
• Herstein, I. N. (1964). Topics in Algebra. Ginn and Company. ISBN 0-471-02371-X.
• Golan, Jonathan S. (1995). "Algebras Over A Field". Foundations of Linear Algebra. Springer Netherlands. ISBN 978-94-015-8502-6.
• Walz, Guido (1 December 2016). "Algebra". Lexikon der Mathematik: Band 1: A bis Eif (in German). Springer-Verlag. ISBN 978-3-662-53498-4.
• Weisstein, Eric W. (2003). CRC Concise Encyclopedia of Mathematics (2nd ed.). Chapman & Hall/CRC. ISBN 1-58488-347-2.
• Renze, John; Weisstein, Eric W. "Algebra". Wolfram MathWorld. Wolfram. Retrieved 12 January 2024.
• Gilbert, William J.; Nicholson, W. Keith (30 January 2004). Modern Algebra with Applications. John Wiley & Sons. ISBN 978-0-471-46989-6.
• Grillet, Pierre Antoine (2007). "Universal Algebra". Abstract Algebra. Springer. ISBN 978-0-387-71568-1.
• EoM Staff (2020a). "Arithmetic". Encyclopedia of Mathematics. Springer. Retrieved 23 October 2023.
• MW Staff (2023). "Definition of Arithmetic". www.merriam-webster.com. Retrieved 19 October 2023.
• HC Staff (2022). "Arithmetic". www.ahdictionary.com. HarperCollins. Retrieved 19 October 2023.
• Romanowski, Perry (2008). "Arithmetic". In Lerner, Brenda Wilmoth; Lerner, K. Lee (eds.). The Gale Encyclopedia of Science (4th ed.). Thompson Gale. ISBN 978-1-4144-2877-2.
• Burgin, Mark (2022). Trilogy Of Numbers And Arithmetic - Book 1: History Of Numbers And Arithmetic: An Information Perspective. World Scientific. ISBN 978-981-12-3685-3.
• Wagner, Sigrid; Kieran, Carolyn (7 December 2018). Research Issues in the Learning and Teaching of Algebra: the Research Agenda for Mathematics Education, Volume 4. Routledge. ISBN 978-1-135-43421-2.
• Maddocks, J. R. (2008). "Algebra". In Lerner, Brenda Wilmoth; Lerner, K. Lee (eds.). The Gale Encyclopedia of Science (4th ed.). Thompson Gale. ISBN 978-1-4144-2877-2.
• Fiche, Georges; Hebuterne, Gerard (1 March 2013). Mathematics for Engineers. John Wiley & Sons. ISBN 978-1-118-62333-6.
• Pratt, Vaughan (2022). "Algebra". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 11 January 2024.
• EoM Staff (2017). "Algebra". Encyclopedia of Mathematics. Springer. Retrieved 11 January 2023.
• EoM Staff (2020). "Algebra(2)". Encyclopedia of Mathematics. Springer. Retrieved 11 January 2023.
• EoM Staff (2023). "Algebraic operation". Encyclopedia of Mathematics. Springer. Retrieved 11 January 2023.
• Benson, Donald C. (2003). A Smoother Pebble: Mathematical Explorations. Oxford University Press. ISBN 978-0-19-514436-9.
• Rohde, Ulrich L.; Jain, G. C.; Poddar, Ajay K.; Ghosh, A. K. (12 January 2012). Introduction to Differential Calculus: Systematic Studies with Engineering Applications for Beginners. John Wiley & Sons. ISBN 978-1-118-13014-8.
• Axler, Sheldon (8 March 2011). Algebra and Trigonometry. John Wiley & Sons. ISBN 978-0-470-58579-5.
• McKeague, Charles P. (10 May 2014). Intermediate Algebra: A Text/Workbook. Academic Press. ISBN 978-1-4832-1417-7.
• Zill, Dennis; Dewar, Jacqueline (19 January 2011). Algebra and Trigonometry. Jones & Bartlett Publishers. ISBN 978-0-7637-5461-7.
• Lamagna, Edmund A. (15 January 2019). Computer Algebra: Concepts and Techniques. CRC Press. ISBN 978-1-351-60583-0.
• Berggren, John L. (2015). "Elementary algebra". Encyclopædia Britannica. Retrieved 14 January 2024.
• Buthusiem, Gregory; Toth, Gabor (2020). Precalculus. Linus Learning. ISBN 978-1-60797-798-8.
• Young, Cynthia Y. (19 January 2010). Precalculus. John Wiley & Sons. ISBN 978-0-471-75684-2.
• Majewski, Miroslaw (2004). MuPAD Pro computing essentials (2 ed.). Berlin Heidelberg New York: Springer. ISBN 978-3-540-21943-9.
• Tan, Kiat Shi; Steeb, Willi-Hans; Hardy, Yorick (6 December 2012). SymbolicC++:An Introduction to Computer Algebra using Object-Oriented Programming: An Introduction to Computer Algebra using Object-Oriented Programming. Springer Science & Business Media. ISBN 978-1-4471-0405-6.
• Sullivan, Michael (29 March 2010). Finite Mathematics: An Applied Approach. John Wiley & Sons. ISBN 978-0-470-87639-8.
• Harrison, Michael; Waldron, Patrick (31 March 2011). Mathematics for Economics and Finance. Routledge. ISBN 978-1-136-81921-6.
• Young, Cynthia Y. (16 May 2023). Precalculus. John Wiley & Sons. ISBN 978-1-119-86940-5.
• Williams, Gareth (17 August 2007). Linear Algebra with Applications. Jones & Bartlett Learning. ISBN 978-0-7637-5753-3.
• Mortensen, C. E. (14 March 2013). Inconsistent Mathematics. Springer Science & Business Media. ISBN 978-94-015-8453-1.
• Andrilli, Stephen; Hecker, David (5 April 2022). Elementary Linear Algebra. Academic Press. ISBN 978-0-323-98426-3.
• Anton, Howard; Rorres, Chris (4 November 2013). Elementary Linear Algebra: Applications Version. John Wiley & Sons. ISBN 978-1-118-47422-8.
• Barrera-Mora, Fernando (8 May 2023). Linear Algebra: A Minimal Polynomial Approach to Eigen Theory. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-113591-5.
• EoM Staff (2011). "Linear equation". Encyclopedia of Mathematics. Springer. Retrieved 10 January 2024.
• Anton, Howard (4 November 2013). Elementary Linear Algebra. John Wiley & Sons. ISBN 978-1-118-67730-8.
• Cooper, Ellis D. (2011). Mathematical Mechanics: From Particle to Muscle. World Scientific. ISBN 978-981-4289-70-2.
• Tanton, James (2005). Encyclopedia of mathematics. Facts On File. ISBN 0-8160-5124-0.
• Dominich, Sándor (3 April 2008). The Modern Algebra of Information Retrieval. Springer Science & Business Media. ISBN 978-3-540-77659-8.
• Irving, Ronald S. (8 January 2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer Science & Business Media. ISBN 978-0-387-40397-7.
• Kramer, Jürg; Pippich, Anna-Maria von (15 November 2017). From Natural Numbers to Quaternions. Springer. ISBN 978-3-319-69429-0.
• McWeeny, R. (1 January 2002). Symmetry: An Introduction to Group Theory and Its Applications. Courier Corporation. ISBN 978-0-486-42182-7.
• Terr, David; Weisstein, Eric W. "Ring of Integers". Wolfram MathWorld. Wolfram. Retrieved 12 January 2024.
• Maxwell, E. A. (18 June 2009). Algebraic Structure and Matrices Book 2. Syracuse University Press. ISBN 978-0-521-10905-5.
• EoM Staff (2016a). "Ring". Encyclopedia of Mathematics. Springer. Retrieved 11 January 2023.
• Khattar, Dinesh; Agrawal, Neha (29 June 2023). Group Theory. Springer Nature. ISBN 978-3-031-21307-6.
• EoM Staff (2016). "Group". Encyclopedia of Mathematics. Springer. Retrieved 11 January 2023.
• Ovchinnikov, Sergei (26 February 2015). Number Systems. American Mathematical Society. ISBN 978-1-4704-2018-5.
• Rowland, Todd; Weisstein, Eric W. "Group". Wolfram MathWorld. Wolfram. Retrieved 12 January 2024.
• Weisstein, Eric W. "Ring". Wolfram MathWorld. Wolfram. Retrieved 12 January 2024.
• Weisstein, Eric W. "Field". Wolfram MathWorld. Wolfram. Retrieved 12 January 2024.
• Weisstein, Eric W. "Field Axioms". Wolfram MathWorld. Wolfram. Retrieved 12 January 2024.
• Negro, Luca Dal (19 May 2022). Waves in Complex Media. Cambridge University Press. ISBN 978-1-107-03750-2.
• Artamonov, V. A. (15 October 2003). "Quasivarieties". In Hazewinkel, M. (ed.). Handbook of Algebra. Elsevier. ISBN 978-0-08-053297-4.
• Cox, David A.; Little, John; O'Shea, Donal (30 April 2015). Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra. Springer. ISBN 978-3-319-16721-3.
• Silvia, M. T.; Robinson, E. A. (1 January 1979). Deconvolution of Geophysical Time Series in the Exploration for Oil and Natural Gas. Elsevier. ISBN 978-0-08-086864-6.
• Grätzer, George (2008). Universal Algebra (2 ed.). Springer. ISBN 978-0-387-77486-2.
• Insall, Matt; Sakharov, Alex. "Universal Algebra". Wolfram MathWorld. Wolfram. Retrieved 12 January 2024.
• Mal’cev, A. I. (1973). "Quasivarieties". Algebraic Systems. Springer. ISBN 978-3-642-65374-2.
• Indurkhya, Bipin (9 March 2013). "6.5 Algebras and Structures". Metaphor and Cognition: An Interactionist Approach. Springer Science & Business Media. ISBN 978-94-017-2252-0.
• Mal'cev, Anatolij Ivanovic (6 December 2012). Algebraic Systems. Springer Science & Business Media. ISBN 978-3-642-65374-2.

Further reading

• Allenby, R. B. J. T. (1991). Rings, Fields and Groups. ISBN 0-340-54440-6.
• Asimov, Isaac (1961). Realm of Algebra. Houghton Mifflin.
• Euler, Leonhard (2005). Elements of Algebra. ISBN 978-1-899618-73-6. Archived from the original on 2011-04-13.
• Herstein, I. N. (1975). Topics in Algebra. ISBN 0-471-02371-X.
• Hill, Donald R. (1994). Islamic Science and Engineering. Edinburgh University Press.
• Joseph, George Gheverghese (2000). The Crest of the Peacock: Non-European Roots of Mathematics. Penguin Books. ISBN 978-0140277784.
• O'Connor, John J.; Robertson, Edmund F. (2005). "History Topics: Algebra Index". MacTutor History of Mathematics archive. University of St Andrews. Archived from the original on 2016-03-03. Retrieved 2011-12-10.
• Sardar, Ziauddin; Ravetz, Jerry; Loon, Borin Van (1999). Introducing Mathematics. Totem Books.

External links

• Khan Academy: Conceptual videos and worked examples
• Khan Academy: Origins of Algebra, free online micro lectures
• Algebrarules.com: An open source resource for learning the fundamentals of Algebra
• 4000 Years of Algebra, lecture by Robin Wilson, at Gresham College, October 17, 2007 (available for MP3 and MP4 download, as well as a text file).
• Pratt, Vaughan. "Algebra". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.