Talk:Monty Hall problem: Difference between revisions
| Line 3,972: | Line 3,972: | ||
:::::Of course; I hope I didn't do anything that hinted otherwise. [[User:Dicklyon|Dicklyon]] ([[User talk:Dicklyon|talk]]) 19:22, 7 December 2009 (UTC) |
:::::Of course; I hope I didn't do anything that hinted otherwise. [[User:Dicklyon|Dicklyon]] ([[User talk:Dicklyon|talk]]) 19:22, 7 December 2009 (UTC) |
||
Well, that's quite a Wikipedia education I was administered today. And I want to give thanks to the man who taught me this lesson, Dicklyon. |
|||
Thank you Dicklyon for: |
|||
:Vandalizing my edit |
|||
:Accusing me of being the vandal (That was outstanding. Really. Not many can pull this one off successfully! Kudos!) |
|||
:Calling my personal opinion on a talk page 'obviously incorrect' |
|||
:Lecturing me on the proper 'tone' to use on Wikipedia talk pages |
|||
:Denying in carefully chosen words that you did any of the above |
|||
:Making it necessary for another Wikipedian to defend me. That does wonders for my self esteem. |
|||
:Teaching me who the baddest edit warrior on Wikipedia is. |
|||
:Giving me permission to return the section I created to it's original status. |
|||
:Assuring me that you won't further violate Wikipedia rules regarding my edits in talk pages |
|||
:I'm sure there is much more I'm overlooking. I'm only human. |
|||
But anyways, an apology is in order to all you Wikipedia editors who were forced to sit through this. |
|||
In the spirit of the guy who got shot in the face by VP Dick Cheney, I apologize to Dicklyon for being the recipient of your unprovoked savage violation of my good faith edits to a Wikipedia talk page. [[User:Glkanter|Glkanter]] ([[User talk:Glkanter|talk]]) 21:49, 7 December 2009 (UTC) |
|||
== What "the conditional problem" and "the unconditional problem" mean == |
== What "the conditional problem" and "the unconditional problem" mean == |
||
Revision as of 21:49, 7 December 2009
| This is the talk page for discussing changes to the Monty Hall problem article itself. Please place discussions on the underlying mathematical issues on the Arguments page. If you just have a question, try Wikipedia:Reference desk/Mathematics instead. |
| This article is of interest to the following WikiProjects: | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
 | Monty Hall problem is a featured article; it (or a previous version of it) has been identified as one of the best articles produced by the Wikipedia community. Even so, if you can update or improve it, please do so. | |||||||||||||||||||||
| This article appeared on Wikipedia's Main Page as Today's featured article on July 23, 2005. | ||||||||||||||||||||||
| ||||||||||||||||||||||
New archive
This page has been quiet for a few weeks, so I created a new archive at Talk:Monty Hall problem/Archive 9 for the discussions from mid Oct 2008 through Feb 2009 (indicated as "archived" above). Several of the issues aren't exactly resolved (they will perhaps never be resolved to everyone's satisfaction), but the period of relative calm seemed like an opportune time to create a new archive. I added a new section (post archiving) much like this one. user:Glkanter has reverted these changes, suggesting we talk about it first. OK. Since we're at a lull in the discussion here, and the talk page is huge, I suggest now is an appropriate time to archive. -- Rick Block (talk) 15:14, 15 March 2009 (UTC)
- Agree with archiving now. The talk page is monster-sized, and nobody is going to read through it all anyway. –Henning Makholm (talk) 15:29, 15 March 2009 (UTC)
- I don't agree there has been a 'lull'. It's just been re-directed to the arguments page. I assume most readers (not necessarily editors) do NOT read archives. If they're interested, maybe they get as far as a talk page. Anyway, I think that the existence and vehement nature of the MHP article disagreement would not be evident if the entire thing were archived. A reader might think that there was universal satisfaction with the construction of the article. That would be an inaccurate impression to give. Glkanter (talk) 15:55, 15 March 2009 (UTC)
- This thread will remain here, and it already says there are unresolved issues. If you'd like to enumerate them here that will remain here as well. Good enough? -- Rick Block (talk) 17:37, 15 March 2009 (UTC)
- I didn't know there was an "arguments" page, so I too thought it had settled down. It would be very useful to have a concise list here of what the ongoing issues about the article are, phrased as neutrally as possible, with links to where some discussion about them may be found. Dicklyon (talk) 21:38, 15 March 2009 (UTC)
- The main one continues to be around whether it's necessary for the problem to be approached as a problem in conditional probabilities (i.e. whether an "unconditional solution" is sufficient). I wrote a FAQ section on this (referenced from the top of this page, see Talk:Monty_Hall_problem/FAQ). -- Rick Block (talk) 21:53, 15 March 2009 (UTC)
- The issue is there's a faction here (Glkanter and Martin Hogbin, perhaps others) who think the conditional analysis is completely unnecessary and that the problem as generally stated is appropriately addressed by an unconditional solution. They strongly object to Morgan et al.'s characterization of unconditional solutions as "false" solutions. There are others (Nijdam, for one, and I believe most participants in WP:WikiProject Mathematics willing to comment) who object to presenting an unconditional solution as the solution, since (in their view) an unconditional solution isn't actually addressing the problem as stated (and think whether or not the problem is stated to force a 2/3 answer, the unconditional solution is basically wrong). I've been suggesting the folks in favor of presenting an unconditional solution offer up a reference for such a solution from a source that understands the difference between conditional and unconditional. So far, no source has been offered. Most popular sources (notably vos Savant) ignore this issue - one is tempted to conclude most popular sources do not understand it. -- Rick Block (talk) 22:47, 15 March 2009 (UTC)
- So, lacking such other sources, we should obviously present the "usual" unconditional solution, with sources, and also the "conditional" solution and the fact of who says it's necessary and that the other is inadequate. Or does someone argue for more than this, or less than this? Dicklyon (talk) 23:28, 15 March 2009 (UTC)
- The specific problem with the current article is that it offers a somewhat wordy unconditional solution as the first solution. But then immediately follows that by saying "Although the reasoning above is correct it doesn't answer the precise question posed by the problem,...". Then the lengthy remainder of the article addresses this so-called deficiency. So, if I'm trying to settle a bet (of course using the unconditional solution, just try using the other stuff in a bar), the other guy says to me, 'but Wikipedia says that's not the solution'. So, as long as any claims that the unconditional solution is inadequate remain in the article, I am not for a two-tier solution. Glkanter (talk) 03:29, 16 March 2009 (UTC)
- But aren't the "claims that the unconditional solution is inadequate" well sourced? Or are you suggesting that Morgan et al. 1991 should be treated as just an opinion? And are you saying that the "one tier" or unconditional solution is adequate? Based on a source that says so? Or based on the fact that it comes up with the same answer, in terms of player strategy and average probability of winning, even though it's not an air-tight proof? Or based on the "standard analysis" where the host must "open one of the remaining two doors randomly if the player initially picked the car (Barbeau 2000:87)"? In this "standard" interpretation, is the idea that the host's action offers no new information about the probability of the originally chosen door have a car, and therefore it's a non-event and you don't need a conditional analysis? Or what? Could we resolve this by having a section the "standard interpretation" and its standard simple solution, and another section on other interpretations that require the more elaborate analysis? Dicklyon (talk) 04:32, 16 March 2009 (UTC)
- As you know, I reject the argument that the unconditional solution is inadequate. Interestingly, you bring up the point that Monty's decision only happens when the contestant chooses the car. Rick mentioned the same thing tonight. I just can't get past the idea that Monty choosing between two losing doors has any affect on the probability of winning. Check out the last section of the Arguments page for the latest and greatest unconditional solution. It contains no goats and no Monty. And, it has been approved as an unconditional solution to the MHP by a Wikipedia guru.
- http://en.wikipedia.org/wiki/User_talk:Tsirel#Is_this_a_valid_unconditional_proof_of_the_Monty_Hall_Problem.3F It's the 3rd section from the bottom. Glkanter (talk) 05:43, 16 March 2009 (UTC)
- Well, I think we can all agree that "Monty choosing between two losing doors" doesn't have any affect on the probability of winning, normally; but your "proof" is just an assertion with no proof logic, so hardly helpful at convincing anyone that it can be made rigorous. If you add some condition, like that Monty reveals no extra information about the prob of the first door having a car behind it, then it could be made rigorous pretty easily. On the other hand, if you allow Monty to reveal extra info, either by being known to always choose the left-most goat, or by stopping to flip a coin when the contestant has chosen a car, then you've got a different problem, requiring a different solution (in this latter case, the contestant's probability of winning a car is 100% if he follows the optimal strategy of switching only if Monty doesn't flip a coin). Dicklyon (talk) 05:52, 16 March 2009 (UTC)
- If you agree that ""Monty choosing between two losing doors" doesn't have any affect on the probability of winning, normally;..." then we're done here. Maybe I don't speak such good probability, but I'm sure you agree that 1/3 of the time the contestant picks the car. And that the probability of 'car' or 'not car' = 1. And that 1 - 1/3 = 2/3. And you just agreed that ""Monty choosing between two losing doors" doesn't have any affect on the probability of winning, normally;...". What's the problem? Why is this unconditional solution inadequate? Please note, the solution makes no mention of a 'Monty' or any 'goats'. What do you make of the comment at the above link? And I agree, the contestant knowing of a left door Monty bias, or flipping a coin is a new constraint to a different problem than the MHP. Glkanter (talk) 06:22, 16 March 2009 (UTC)
- There's a problem here, which is that the "proof" is not showing what it purports to show. What it does show is that if the player decides to switch before the host opens a door she has a 2/3 chance of winning. However, the question is what is the chance of winning when deciding to switch after the host opens a door. The problem can be (but often isn't) sufficiently constrained to make these the same. The whole point of the Morgan et al. paper (and the Gillman paper, and this point is echoed in the Grinstead and Snell book and others) is that an unconditional approach is fundamentally the wrong way to approach this kind of problem and using one without qualification is unsound at best (Morgan considers these "false" solutions). My understanding is that Glkanter does not agree with this, and does not want anything like it in the article - no matter how many reliable sources say it. The bottom line is that Morgan et al., and Gillman, and others basically discredit the unconditional approach which means (to me) that Wikipedia should either not present an unconditional "solution" at all, or is obligated to follow it up with the very sorts of words Glkanter objects to. -- Rick Block (talk) 14:45, 16 March 2009 (UTC)
- I sort of agree; not because the "proof is not showing what it purports to show", but because we have reliable sources that say so. The simple proof can even be made "correct", based on those same sources I suspect, by showing that the "chance of winning when deciding to switch after the host opens a door" can not change from the "chance of winning when deciding to switch before the host opens a door" under some reasonable and normal set of assumptions. They can both be correct, and both rigorous, if the problem is appropriately formulated. Dicklyon (talk) 16:16, 16 March 2009 (UTC)
- The value of the unconditional solution is that it explains the underlying logic (why 2/3 instead of 1/2) in a nice, simple way. If it were offered as an entirely valid analysis of the basic veridical paradox, then followed up with a "however, the problem as stated requires a more complicated solution", we'd have a good article. We're not willing to do this: instead, we say "here's the unconditional solution, which is wrong". We need to say, with no neurosis, "the unconditional solution is right, albeit in a constrained manner". And furthermore we need to focus on offering the unconditional solution in the clearest possible way in order to make the article as useful as possible to the general reader: right now, it's statisticiancruft.
- Unfortunately, the "problem as stated" has the attention of this article's editors to a degree that harms our ability to offer a solid, simple explanation to our readers. During the time that I've been involved with this article, I've seen it constantly degrade in quality. There's a pedantry at work that forces every explanation of the unconditional solution we offer to mutate into something that straddles the unconditional and conditional solutions, compromising both accuracy and clarity. We've got to ditch this neurosis and be willing to offer both solutions robustly, while noting the limitations of each.
- Drop the textbooks for a second and think about how you would write this article to be useful to an audience of 10-year-olds. Then write that article, and add to it whatever is needed to make it useful to a statistician as well.--Father Goose (talk) 16:47, 16 March 2009 (UTC)
- What would the "solid, simple explanation" be an explanation of? If an explanation of the "problem as stated," then the editors' attention is correctly directed. If it is an explanation of something else, what is it? The problem as usually understood? Please clarify. Visualaudio (talk) 04:21, 28 March 2009 (UTC)
I agree with a lot that Father Goose said, but not 100%. I refuse to focus on anything but the original 1/3 car and 2/3 not car. And nobody has ever said how the 1/3 can possibly change, so the 2/3 can't change either. There's an old saying, 'Are you interested, or committed? The hen, who provided the eggs, is interested in your breakfast, the pig, who provided the bacon, is committed to your breakfast.' I'm committed to the unconditional solution as being valid, rigorous, complete, etc. My goal all along has been to eliminate any statements in the Article, let alone the Solutions section, that undercuts this. The heck with the 10 year old. Try getting paid off on a bet by explaining the 'equal goat door constraint'. Glkanter (talk) 19:51, 16 March 2009 (UTC)
- I more or less agree with that. That's not to say that we need to drop the conditional explanations, the Bayesian analysis, or anything else. It's just that we need to have an absolutely pristine explanation of the unconditional analysis (such as the one diagrammed here) that is wholly untouched by conditional gremlins.
- The fact that every unconditional explanation present in the article keeps getting butchered into a conditional explanation (or worse still, a pseudo-conditional one) is a source of anguish to me. I'm serious, it anguishes me. It results in us having an article that is of negative value to the overwhelming majority of our readers, as it fails to give them a nice, simple, accurate, easy-to-understand solution to the paradox in its most general form, and misleads them into thinking that that solution is for some reason an invalid way to analyze the paradox -- which it is not. It's an invalid way to analyze the question-as-usually-asked -- but the question-as-usually-asked is not the subject of the article -- the paradox is. The question-as-usually-asked is merely one of the "sources of confusion", which has led our explanation of the paradox to be a confused one as well.--Father Goose (talk) 22:06, 16 March 2009 (UTC)
- Rick, would you be willing to consider a rewrite, with my help if need be, that would allow both the "conditional" and "unconditional" explanations to be fully and clearly presented, without introducing any inaccuracies?--Father Goose (talk) 22:10, 16 March 2009 (UTC)
- Propose away. I think this version has the exact structure you're suggesting. I'll also note that even the current version doesn't say the unconditional solution is wrong, just that it doesn't answer the precise question that is asked (which is what the reliable sources actually say). I'd suggest anyone consider rewording the solution consider whether the wording holds for slight variants - like the "host forgets" variant (where the correct answer is probability of winning by switching is 1/2, not 2/3) or the "host opens leftmost door if possible" variant (where the correct answer is probability of winning by switching is 1/2 or 100% depending on which door the host opens). The point of thinking about such variants is to explore how "robust" the solution is. If your solution only works for one carefully constructed version of the problem, it probably doesn't explain anything at all about the underlying logic. -- Rick Block (talk) 01:43, 17 March 2009 (UTC)
- That version still contaminates the simple solution section with the statement "Although the reasoning above is correct it doesn't answer the precise question posed by the problem, which is whether a player should switch after being shown a particular open door." It might be better to present a problem that this is the exactly correct solution to, and then treat the other problem where's it's not separately. A simple way to do this is to introduce the condition that the host choose randomly when there are two goats left, in a way that reveals no additional information to the contestant (since, as I pointed out, if he chooses random by flipping a coin only when he has to, and the contestant can see that, then it's a completely different ball game), so that the contestant's strategy of always switching is clearly going to lead to 2/3 chance of winning, without any conditionalizing on which door the host opens. In the diagram that Father Goose linked, I think one can rigorously show that "The player has an equal chance of initially selecting the car, Goat A, or Goat B. Switching results in a win 2/3 of the time." as it says in the caption, and that no strategy of maybe not switching based on which door the host opens can beat that. Dicklyon (talk) 02:25, 17 March 2009 (UTC)
- Contaminates? That wording is sourced - the exact quote is "F1's [one unconditional solution's] beauty as a false solution is that is is a true statement! It just does not solve the problem at hand". If someone can come up with a reference for a version of the MHP for which this solution (or any unconditional solution) is the exactly correct solution that'd be great - although one of the points of the Morgan et al. and Gillman papers is that the problem is about conditional probabilities (so I'm kind of skeptical that anyone is going to find such a reference). Per the question I've added to Talk:Monty Hall problem/FAQ, Gillman suggests an unconditional solution would be appropriate for a version where "you need to announce before a door has been opened whether you plan to switch" (which is such an unusual wording I don't think anyone would claim it's still the MHP). Ultimately the only thing that matters here is references. Change the article to say anything you'd like. But base it on references, not WP:OR. -- Rick Block (talk) 04:08, 17 March 2009 (UTC)
- Yes, "contaminates" in the sense of the proposal above for a discussion that is "wholly untouched by conditional gremlins." We all agree that there are sources that say such an analysis in inadequate; but it would not be NPOV to rely only on that analaysis. Try this one: [1]. Do we have to all agree that it's mathematically "exactly correct" in order to report what it says? It does look pretty carefully done, as it lists a bunch of assumptions needed to conclude that the host's opening of a door "gives no additional information about the likhihood of the initially chosen door being correct. etc." Dicklyon (talk) 04:17, 17 March 2009 (UTC)
- "Do we all have to agree it's mathematically exactly correct"? No, however given that this is a featured article we should clearly do our best to use sources of the highest quality, particularly if we're talking about a source for what will be presented as the "main" solution (which is what I believe some folks are talking about here). This source says the probability of winning by switching is .67 - which (IMO) makes this source somewhat suspect (and if the point is to use this as a "gold standard" for the solution, I would say we can't interpret this "loosely" as 2/3). It's also published as an appendix to vos Savant's book, and listed on the copyright page of the book as a reprint - which brings up the question of where it was originally published. As best as I can tell this appendix is a revised version (not a reprint) of this paper originally published in Personality and Social Psychology Bulletin (I did a lot of the original sourcing for this article, so I have most of the sources - including vos Savant's book and this paper). Note that this is a psychology journal, not a math journal, which makes this an excellent source for psychological aspects of the Monty Hall problem, but a somewhat less excellent source for mathematical aspects (and, I'll note, Granberg is a professor of sociology at the University of Missouri, not a mathematician). Does this mean we can't use this source? No. In fact, it's already referenced in the article (both the original paper and the "reprint" from vos Savant's book). On the other hand, I would hesitate to use this paper as the source for what we intend to be a mathematically sound unconditional solution. -- Rick Block (talk) 14:09, 17 March 2009 (UTC)
- Let me ask you, Rick: does this diagram somehow not map perfectly onto a truly unconditional presentation of the problem? If not, could tweaks be made to it to make it a truly unconditional framing of the problem?--Father Goose (talk) 05:55, 17 March 2009 (UTC)
- The diagram has the same basic issue as vos Savant's solution published in the December 1990 Parade column, which is that the problem says to consider the case where the player has picked door 1 and the host has opened door 3 (using these as representative of the situation where the player is deciding to switch after picking one of the doors and the host has opened another one) but the solution considers other cases. In the diagram the player has picked door 1 only in case 1 (so cases 2 and 3 simply don't apply - at least not to the problem as stated) and the host opens door 2 sometimes in case 1 and all the time in case 3 (so even case 1 doesn't always apply and again case 3 never applies). We could presumably restate the problem somehow to make the diagram fit (putting us in WP:OR territory), perhaps:
- You'll pick one of these three doors and after you've made your choice I'll open a different door revealing a goat. You can choose now whether your "final" door will be your original pick or the other door that remains unopened after I've opened a door to show a goat. Now, what door would you like and would you like it to be your final door or would you prefer to switch to the other door that's left after I open a door?
- Let me ask you something: doesn't the diagram currently in the article clearly show the exact problem that's asked? The player's pick is always door 1 (but the car can be behind any door), and the two cases (host opens door 2 vs. host opens door 3) are clearly grouped. In the problem as asked, the host opens door 3 putting us in the right half of the picture where switching wins twice as often as staying. -- Rick Block (talk) 14:09, 17 March 2009 (UTC)
- The diagram has the same basic issue as vos Savant's solution published in the December 1990 Parade column, which is that the problem says to consider the case where the player has picked door 1 and the host has opened door 3 (using these as representative of the situation where the player is deciding to switch after picking one of the doors and the host has opened another one) but the solution considers other cases. In the diagram the player has picked door 1 only in case 1 (so cases 2 and 3 simply don't apply - at least not to the problem as stated) and the host opens door 2 sometimes in case 1 and all the time in case 3 (so even case 1 doesn't always apply and again case 3 never applies). We could presumably restate the problem somehow to make the diagram fit (putting us in WP:OR territory), perhaps:
- Let me ask you, Rick: does this diagram somehow not map perfectly onto a truly unconditional presentation of the problem? If not, could tweaks be made to it to make it a truly unconditional framing of the problem?--Father Goose (talk) 05:55, 17 March 2009 (UTC)
- Accept for a second that the unconditional diagram is not a depiction of the conditionally stated problem. Pretend for a second that you've never heard of the Parade version of the problem (or any other conditionally phrased version), and that you're trying to create a diagram that depicts a purely unconditional form of the problem. Does this diagram successfully do that? If not, what changes would be needed to make it represent an unconditional form of the problem?--Father Goose (talk) 21:10, 18 March 2009 (UTC)
Rick, checking back, I see you're been shepherding this article for many years, since before it made "featured" in 2005. But at that time, it didn't have any of the current problem, of overloading the commonly-published simple solution with all the conditional stuff, and all the strife, confusion, and bloat that has come from that. A solution to the problem was proposed above. Surely you have enough good sources, including the Granberg paper with its list of conditions to make the initial 1/3 probability not change when a goat is revealed, to fix the problem as suggested. If you don't want to use this source on its own, because some idiot editor converted 2/3 to .67, combine it with some others that don't make that mistake. But don't us this stuff about him not being a mathematician; it doesn't take a professional mathematician to analyze a problem in probability, does it? Dicklyon (talk) 15:14, 17 March 2009 (UTC)
- Yes, I originally nominated it as a featured article and responded to the criticisms from the FAC review, and the two FARs it's been through as well. My opinion is almost exactly the opposite of Father Goose's - specifically that it has dramatically improved over the last several years (it was originally woefully under-referenced and presented a very shaky unconditional argument as its main "solution"). The inclusion of a more mathematically rigorous solution was largely due to the efforts of an anonymous editor, shortly before the most recent FAR with highly voluminous discussions on the talk page (starting at Talk:Monty Hall problem/Archive 6#Rigorous solution). This editor was the first to mention the Morgan et al. reference - which I believe is the first mathematically rigorous treatment of the MHP published in a peer reviewed math journal. Since this rigorous treatment has already been published, there in all likelihood will never be another (Gillman is sort of an oddity - my assumption is Gillman's paper was already "in press" when the Morgan et al. paper actually appeared). There is certainly no shortage of popular sources about this problem, but the Morgan et al. paper is (more or less) the definitive reference.
- You ask whether it takes a professional mathematician to analyze a problem in probability. Of course, in general, no. On the other hand, this problem generates massive amounts of controversy, IMO (well, actually backed up by lots of psychology sources like Granberg) because it deals with conditional probabilities which are not very well understood by most people - but it is a very simple problem on the surface which leads many people to think they understand it when they actually don't. This problem generates so much controversy that "serious mathematicians" at this point pretty much refuse to talk about it since they understand the rat-hole it becomes. The "many people" who think they understand it but actually don't includes lots of people who write about it as well as lots of academics (as evidenced by the large numbers of academics who wrote to vos Savant telling her she was wrong). The point is not that it would take a professional mathematician to produce a sound unconditional solution for this problem, but that it is harder than it seems and just because something happens to be published about this problem does not mean it is mathematically sound.
- I definitely understand the request being made here - for an easily understandable (which probably means unconditional), convincing, and (I'll add) mathematically sound solution. Unfortunately, I am not aware of a published solution that meets this criteria. -- Rick Block (talk) 19:40, 17 March 2009 (UTC)
- Well, it's great that they got you to come around to the "rigorous" conditional solution. But I think think the Granberg reference is plenty adequate for the "usual" solution, irrespective of whether you think it's "rigorous". And you probably have others that present the usual solution along with some words to the effect that it's applicable when the host's action doesn't provide any extra information about the probability of the originally chosen door having a car. Just go with it. Leaving it the way it is is too higher-math POV. Dicklyon (talk) 22:06, 17 March 2009 (UTC)
- Here is another in which it is at least stated that the contestant "learns nothing new" to justify the usual solution; in this type of solution, the different between deciding ahead of time to switch and deciding after a door is opened is moot, based on the assumptions, so the actions you condition on are irrelevant and can be ignored. Oh, and by the way, it's the overwhelmingly most common analysis, and nobody disputes that it gives the right answer (that you should switch) and the right probability of winning (2/3), even if one did decimalize it poorly. Dicklyon (talk) 22:12, 17 March 2009 (UTC)
- It (or some other unconditional solution) is certainly the most common analysis and nobody disputes the "you should switch" answer, but plenty of folks note the actual probability of winning by switching (without the "equal goat constraint") is not 2/3 but something in the interval [0.5, 1]. vos Savant has even written about the "host forgets" variant [2] and says:
- Back in 1990, everyone was convinced that it didn’t help to switch, whether the host opened a losing door on purpose or not. Assuming a knowledgeable host who would always open a losing door, that was incorrect. (A knowledgeable host who opened a winning door on purpose wouldn’t have much of a show, would he?!)
- It (or some other unconditional solution) is certainly the most common analysis and nobody disputes the "you should switch" answer, but plenty of folks note the actual probability of winning by switching (without the "equal goat constraint") is not 2/3 but something in the interval [0.5, 1]. vos Savant has even written about the "host forgets" variant [2] and says:
- Now everyone is convinced that it always helps to switch, regardless of what the host knows. But this is just as incorrect!
- Here's some of my own WP:OR - the reason "everyone" now says it always helps to switch is because many sources (like, ahem, vos Savant - whose own book ironically enough is titled "The Power of Logical Thinking") have presented an unconditional solution for the original problem as the (or at least "a") correct solution. Whether it's the standard version or the host forgets version or the host always picks the leftmost door version, it's always a conditional probability problem. Using an unconditional solution without understanding exactly what you're doing is dangerous, and (more of my own WP:OR) most people who present an unconditional solution don't really know what they're talking about.
- We've tried to straddle this line before (e.g. this version). I have no objection to this in principle, so long as we're very clear about when and why an unconditional solution is valid. I don't like "Solution" and "Conditional solution" as equal level headers, perhaps Solution with subheaders for "Popular solution" and "Conditional solution". This has been discussed before, with no one on either the "unconditional" or "conditional" side willing to accept a section heading that implied anything other than "this is the solution" (which is why both have been in the same "Solution" section). -- Rick Block (talk) 02:02, 18 March 2009 (UTC)
- We should just ignore anyone who comes here to promote the idea that there is only one Right way to argue for the solution, whatever his or her preferred way is. That premise is contrary to the idea of an encyclopedia, and contrary to how things are solved in mathematics in general.
- Also, I don't think your headings are good -- "popular solution" appears to imply that there is something wrong with the solution (which the hoi polloi cannot appreciate); "conditional solution" sounds as if the solution itself is only valid on certain conditions.
- I suggest we drop the assumption that the headings should be noun phrases that describe the solution. Let them refer to a key idea used in the argument instead. Perhaps "Anticipated choice" and "Conditional probabilities" would do. –Henning Makholm (talk) 12:52, 18 March 2009 (UTC)
Slow down, guys!
This talk page is moving too fast for anybody but the most zealous editors to follow the debate. I suspect this in itself makes it difficult for a good consensus to form. How about we
- Archive the old stuff already.
- Put everybody on a "two talkpage comments per day" restriction.
That would give more people than the two or three protagonists a fighting chance to contribute, at the possible expense of arriving at a conclusion a little slower. But remember, there is no deadline! –Henning Makholm (talk) 13:04, 18 March 2009 (UTC)
- I'll slow down; thanks for your willingness to participate. Dicklyon (talk) 22:22, 18 March 2009 (UTC)
General criticisms of the article
At this time I have two criticisms of the article. One is that the diagram in the "popular solution" section depicts the "conditional solution" and thus is in the wrong section. Another is that if the "unconditional solution" is an invalid way to analyze the problem in general, then the simulation approach, as described, is invalid as well.--Father Goose (talk) 22:04, 18 March 2009 (UTC)
- Right, why don't you go back to that older version that did a better job on the usual solution, and substitute its image and change words as needed? I was just checking to see if the basic structure got any objections first. And on the simulation approach, it might be good to mention the conditions under which the simulation addresses the problem, hopefully from sources about the simulations. Dicklyon (talk) 22:21, 18 March 2009 (UTC)
- I strongly object to reverting to the earlier image since the current image has several advantages. In particular, the current image makes the conditional solution accessible, it matches the problem as described (player picks door 1 and host opens door 3) and its formatting is carefully arranged to convey additional meaning (the column widths reflect the relative probabilities of the items in the column and the "host opens door 3" vs. "host open door 2" cases are adjacent). Showing both images would be possible, but they're so close that this would be redundant. -- Rick Block (talk) 00:42, 19 March 2009 (UTC)
- Rick, I thought you had agreed in principle to represent the usual simple solution simply, without reference to complication by the conditional appproach. That figure does that, but it sounds like that's why you object now. I think you also need to reconsider your interpretation of what the problem says. It doesn't really say the host opens door 3, it merely uses that as an illustrative example, where it says "say No. 3", or at least that's the way many of us read it. So why complicate this section by trying to get it to anticipate the more complex interpretation? Dicklyon (talk) 03:55, 20 March 2009 (UTC)
- We can present an unconditional solution that doesn't conflict with a conditional solution - choosing to do otherwise seems perverse. Goose's original diagram (which, BTW, the current one descends from) keeps the arrangement of car and goats constant and varies the door the player selects. The current version flips this (consistent with the problem statement) making the placement of the car the dominant variable, rather than the player's pick. Either way works just fine for an unconditional solution and either way is a simplification (there are actually 9 possibilities of car placement and player pick). We want to show a simplification with 3 possibilities to resonate with the 1/3 chance of picking the car. The current diagram doesn't require the goats to be distinguishable and even works with empty doors rather than goats as well.
- I agree the "say No. 3" language is meant as an illustrative example and make no claim that the only case to be considered is when the host opens door 3. If you're interpreting anything I've said to mean this you're not understanding what I'm saying. What I am saying is that the question pertains to the probabilities involved after a player has picked a door (any door, not just door 1) and the host has opened some other door (not just door 3). llustratively, we call these "door 1" and "door 3", but we could just as well call them "the door the player initially picked" and "the door the host opened". Whatever we call these doors, "my interpretation" (this is really the interpretation of Morgan et al., and Gillman, and Grinstead and Snell - and pretty much any mathematician who reads the problem) is that we're talking about a conditional probability (not the "average" across all players, but the probabilities for a player initially selecting some specific door when the host has opened some other specific door in response). If we analyze the specific case of "door 1/door 3", we can generalize the answer for "door i/door j". If this answer is the same for all i and j, it must also be the same as the unconditional solution (but not vice versa). -- Rick Block (talk) 04:55, 20 March 2009 (UTC)
- No, I get what you mean, but I think the way the example was presented in the problem statement was also strongly suggestive of the situation wherein things are symmetric enough that you don't need to care which door is opened or how they're numbered or whether there might be any door-number-dependent aspect at all intended. Let's see what kind of diagrams are used in publications on the popular solution; maybe that will help guide us. Dicklyon (talk) 05:05, 20 March 2009 (UTC)
- If I may ask, what is your response to the two criticisms I made?--Father Goose (talk) 02:18, 19 March 2009 (UTC)
- Although I agree the current split into Popular and Conditional sections is kind of a mess (I don't mean this in a derogatory kind of way, it's pretty clearly simply a work in progress) I think the existing diagram can serve both purposes. Specifically, all but the very last line apply to both the conditional and unconditional analysis - and, ignoring the last line, you have switching wins with probability 1/3+1/3 and switching loses with probability 1/6+1/6.
- The simulation section explicitly says "a switching strategy really does win two out of three times on the average" (emphasis added). We could certainly make this more clear, and probably should. The "Combining doors" section has a similar issue, and a similar disclaimer. A long, long time ago, the "Combining doors" section was part of the main "Solution" section (it is another commonly presented "popular" solution). How about illustrating the popular solution section with the figure from this section? (this is my second edit to the talk page today, so I guess I'm done until tomorrow - I agree a rate limit here might help control the volume, and I think the /Arguments page is helping as well) -- Rick Block (talk) 03:08, 19 March 2009 (UTC)
- I would just like to point out that there are at least 2 separate discussions taking place regarding this article. And I understand there is a 3rd page as well. If our goal is to reach consensus on editing the Article, I think we would benefit from all editors being in 1 discussion. Yes? Glkanter (talk) 15:12, 19 March 2009 (UTC)
- Links to them please? If you mean the Arguments page, you'll have to get more specific, as I can't find much there about how to evolve the article. I don't need the math tutorial, as I understand the conditional solution just fine, unlike some people who don't seem to get it. But it's not the solution that most sources present, and it's not neutral to treat it is the only acceptable solution. These math arguments aren't going to help us get to a better article, I think. Dicklyon (talk) 04:04, 20 March 2009 (UTC)
- I'm not sure, but I think Glkanter means here, and at /Arguments, and at /Analysis (a page user:Martin Hogbin has created with his own WP:OR analysis). -- Rick Block (talk) 04:55, 20 March 2009 (UTC)
Criticism and a new approach
My general criticism of the article is that it is much too long. A specific criticism of the article is that the Bayesian analysis is cumbersome and restrictive. Why should the quiz-master use equal probabilities for the two doors to open, when he has a choice? I like to see the problem as a game in which the quiz-team (including the quiz-master) has various possible deterministic strategies, and in general will use one of the possible deterministic strategies at random, according to some probability distribution. At the same time, the player has various possible deterministic strategies, and in general will use one of these strategies at random, according to some probability distribution. Here is a complete list:
Quiz-team's 6 possible deterministic (non-random) strategies:
Car behind door 1 and QM will open door 2 when player chooses door 1
Car behind door 1 and QM will open door 3 when player chooses door 1
Car behind door 2 and QM will open door 1 when player chooses door 2
Car behind door 2 and QM will open door 3 when player chooses door 2
Car behind door 3 and QM will open door 1 when player chooses door 3
Car behind door 3 and QM will open door 2 when player chooses door 3
The player's 12 possible deterministic strategies:
Choose door 1 and switch if QM opens 2, switch if QM opens 3
Choose door 1 and switch if QM opens 2, don't switch if QM opens 3
Choose door 1 and don't switch if QM opens 2, switch if QM opens 3
Choose door 1 and don't switch if QM opens 2, don't switch if QM opens 3
Choose door 2 and switch if QM opens 1, switch if QM opens 3
Choose door 2 and switch if QM opens 1, don't switch if QM opens 3
Choose door 2 and don't switch if QM opens 1, switch if QM opens 3
Choose door 2 and don't switch if QM opens 1, don't switch if QM opens 3
Choose door 3 and switch if QM opens 1, switch if QM opens 2
Choose door 3 and switch if QM opens 1, don't switch if QM opens 2
Choose door 3 and don't switch if QM opens 1, switch if QM opens 2
Choose door 3 and don't switch if QM opens 1, don't switch if QM opens 2
This is a zero-sum game and it has a saddle-point, or equilibrium, when we allow randomized strategies, ie each of the two sides chooses from their respective lists at random, according to two lists of probabilities. The quiz-team's minimax strategy is to choose between each of their 6 fixed strategies with equal probabilities. Ie the location of the car is uniform at random (equal probabilities 1/3), and the quizmaster makes his choice of door to open by a fair coin toss, if he has a choice. Then the player cannot win with probability greater than 2/3. The player's minimax strategy is to choose his door initially uniformly at random and then to always switch. Thus he puts equal probabilities 1/3 on the 3 deterministic strategies in which he always switches, and never uses the other 9. This way the player is guaranteed to win the car with probability 2/3, whatever strategy is used by the quiz-team. Whether or not he wins the car with probability 2/3 given his own initial choice, and if you like, also given the choice of the quiz-master, depends on the quiz-team's strategy. For some conditions it can be above 2/3, for others below; the only guarantee we have is that it averages out at exactly 2/3.
I feel that the Bayesian analysis section therefore gives misleading information. The conditional probability, given your initial and given the quiz-master's choice, that the car lies behind "the other" closed door, is only 2/3 when the quiz-master's and indeed the whole quiz-team's behaviour has been unreasonably limited. In order for the player to win 2/3 of the time it is sufficient that the player makes a true random choice of door, and thereafter always switches. Whether or not the player is going to win with conditional probability 2/3 given his initial choice (and also given the quiz-master's choice, if you like), depends on the quiz-team's strategy. Which, we suppose, the player doesn't know.
See http://www.math.leidenuniv.nl/~gill/threedoors.pdf
I shall try to get this paper into a peer-reviewed journal.
Gill110951 (talk) 22:14, 22 March 2009 (UTC)
- @Gill: With your analysis as a zero-sum game, you're addressing a different problem than the stated MHP. You are analyzing the problem as if the player leaves home and after closing his front door decides what to do in all possible circumstances. But the MHP puts the player on stage, whith a door chosen (that's why it says: say No. 1) and seeing a goat behind another door (say No. 3). 82.75.140.46 (talk) 17:10, 23 March 2009 (UTC)
- You're right, in a sense. But what difference does it make? The player might just as well imagine what he will do if does first choose door 1 and then is shown a goat behind door 3. He can imagine in advance all possibilities. Or: we can imagine that he imagines in advance, all possibilities. What the game-theoretic analysis makes explicit is that there is no way he gets any guarantee by choosing a non-random strategy (ie deciding in advance certainly to choose door 1, etc). There is only a unique conditional solution to the problem, if we restrict the actions of the quizmaster. What we also learn is that the only way the quizmaster can guarantee that the player doesn't win with a probability larger than 2/3 (unconditional) is to put the car behind a uniform random door, and to open a uniform random door when he has a choice. At the same time, the only way the player can guarantee himself to win with probability at least 2/3 is to choose his door uniform at random and thereafter always to switch doors. In the situation that the quizmaster plays the minimax strategy it is true that the conditional probability of the car being behind the other door is 2/3. But how do we know he uses the minimax strategy? I don't see it stated in the problem. So strictly speaking there is no answer to the question "what is the probability the car is behind the other door, given the player chose door 1 [even if he chose it uniformly at random] and the quizmaster opened door 3".
- By the way, I am not editing the page itself at this stage, just throwing a new titbit into the arena, for anyone who is interested. Since it is original new research - of the day before yesterday - I am not even allowed to put it on the page. Gill110951 (talk) 10:45, 24 March 2009 (UTC)
- Thanks you for your contribution, I think it confirms what I and other have been saying for some time which is that the Morgan paper, although not exactly wrong, answers a question than nobody would ever ask. Martin Hogbin (talk) 22:31, 26 March 2009 (UTC)
- In the fully explicit version stated in the article, which seems to match most people's expectations for how the problem should be defined, the host is constrained to open a door randomly if given a choice. This behavior is not specified in the Parade version, leaving open the possibility for other host behaviors. The Morgan et al. paper analyzes the Parade version and expresses this host behavior as a variable q (where q=1/2 means the host is constrained to pick randomly) and shows the player's chance of winning is 1/(1+q). With q=1/2 (which is not stated, but is perhaps the "intended" interpretation) the answer is 2/3, but since q can range from 0-1, the chance of winning by switching without this constraint varies between 1/2 and 1. Rather than confirming they've answered a question nobody would ever ask, I think this thread is confirming the exact opposite. -- Rick Block (talk) 00:12, 27 March 2009 (UTC)
- Rick, I think most people agree that Morgan et al.'s interpretation is a bit far fetched, and also it's still the case that averaged over the possible configurations the prob of winning by switching remains 2/3. Since there's nothing in the problem statement to suggest that door 3 was anything but an example, or that the answer could depend on what door the host opened, it takes a bit of imagination to formalate a problem in which it matters and in which the example given is taken to define the question being asked. Sure, it's a perfectly fine precise mathematical interpretation, with the added caveat that the host's choice can be modeled as a stochastic event, and Morgan et al. give a great solution of that problem. But reasonable balance and NPOV would suggest that we put the most weight on the mainstream interpretation of the problem. Right? Dicklyon (talk) 02:00, 27 March 2009 (UTC)
- I don't understand your point here. Are you saying the "mainstream interpretation" is that it's an unconditional problem? If the point of the problem is to evaluate the probabilities when the player is in front of two closed doors and one open door (which I think is the standard interpretation), then it's a conditional problem. The natural symmetry of the situation makes the conditional probability of interest the same as the unconditional probability, but without an explicit constraint that the host pick randomly if the player initially picks the car the problem is not necessarily symmetric. This is the main point of the Morgan et al. paper (and Gillman's paper, and numerous other references). It's a quite reasonable assumption that the host has no preference if the player's initial selection is the car and this makes the answer 2/3, but even explicitly stating this constraint doesn't turn it into an unconditional problem. Is there a competing POV here? -- Rick Block (talk) 04:52, 27 March 2009 (UTC)
- I'm not saying the mainstream interpretation is that it's an unconditional problem; rather, that in the mainstream interpretation that distinction doesn't come up, and so what you're calling the unconditional solution is generally considered to be the solution. Furthermore, the mainstream interpretation includes the symmetry condition when people go further and try to make it more mathematically rigorous by saying that the host's choices doesn't affect the 1/3 probability of the original choice still being the car after a door is opened. I quite understand the Morgan solution, and that he teaches that all other solutions are inadequate, but that's certainly not the mainstream view. Is it? Dicklyon (talk) 05:07, 27 March 2009 (UTC)
- It depends on what you mean by "mainstream interpretation". I believe the mainstream interpretation in published probability theory articles (Morgan et al., Gillman - there are more) and books (Grinstead and Snell for one) is that the problem is a conditional probability problem and that the host's choice when the player initially picks the car therefore matters. Likely because of Morgan et al. and Gillman, the "standard analysis" now includes the condition that the host pick randomly in this case - forcing the answer to unambiguously be 2/3 chance of winning by switching. On the other hand, the popular sources (starting with vos Savant) generally treat the problem as if the question were "what is the chance of winning if the player's predetermined strategy is to switch" (which is an unconditional problem). I don't think this is a POV issue - it's simply a case of the popular sources (led by vos Savant) choosing to answer a simpler question (without saying so - leaving the question open of whether they understand what they're talking about or not). Many of the solutions that claim the host's choice doesn't affect the player's initial 1/3 probability (because the host must open a door and must show a goat - without saying anything about the host's choice if the player initially picks the car) confuse unconditional and conditional probabilities and are arguably simply wrong (Falk is a good reference for this).
- Rather than continuing to argue about this, how about following an approach similar to the one used in Grinstead and Snell? They start with the sticker (wins 1/3) vs. switcher (wins 2/3) player strategy, but then go on to explain that this doesn't actually address the conditional probability question that the problem asks and show a conditional solution. -- Rick Block (talk) 00:03, 28 March 2009 (UTC)
- That's exactly what I'd like to see as well. We could, in the process, tie it closely to the "simulation" proof, since the usual form of the simulation is multiple trials of the unconditional problem. Using the unconditional problem to prove the solution (via a simulation) apparently had cachet with the originator of the problem (Gardner), so that's got to lend it some weight.--Father Goose (talk) 08:44, 28 March 2009 (UTC)
- Ok to me, be it that I would call the "simple solution" a "simple way of understanding" rather than a solution. And as Father Goose already mentioned, the simulation approach is mainly (always) the unconditional one, and the article should mention this shortcoming. Nijdam (talk) 10:07, 28 March 2009 (UTC)
- If you don't call it a "solution", you're inflicting a POV about what the problem is, which conflicts with the usual interpretation. And as the simulation, simulating an "always switch" strategy versus and "always stick" strategy doesn't really embody a conditional or unconditional probability model, does it? How is it a shortcoming? Dicklyon (talk) 14:51, 28 March 2009 (UTC)
- The usual simulation does not address the conditional probability the problem seemingly asks for. A proper simulation would keep track of switch/stay success per combination of initial player pick and door the host opens (6 combinations). Lumping these all together means the simulation answers the question "what is the chance of winning by switching if deciding to switch before the host opens a door". How about saying something like "Most popular sources assume that the question intends the probability of winning by switching to be the same whether the player decides to switch before or after the host opens a door, and analyze the before case." I believe this is the truth - but finding a reliable source that puts it this way might be challenging. -- Rick Block (talk) 16:20, 28 March 2009 (UTC)
- If you don't call it a "solution", you're inflicting a POV about what the problem is, which conflicts with the usual interpretation. And as the simulation, simulating an "always switch" strategy versus and "always stick" strategy doesn't really embody a conditional or unconditional probability model, does it? How is it a shortcoming? Dicklyon (talk) 14:51, 28 March 2009 (UTC)
- Ok to me, be it that I would call the "simple solution" a "simple way of understanding" rather than a solution. And as Father Goose already mentioned, the simulation approach is mainly (always) the unconditional one, and the article should mention this shortcoming. Nijdam (talk) 10:07, 28 March 2009 (UTC)
- That's exactly what I'd like to see as well. We could, in the process, tie it closely to the "simulation" proof, since the usual form of the simulation is multiple trials of the unconditional problem. Using the unconditional problem to prove the solution (via a simulation) apparently had cachet with the originator of the problem (Gardner), so that's got to lend it some weight.--Father Goose (talk) 08:44, 28 March 2009 (UTC)
- See, for example, /Arguments#Excel simulation of difference between "random goat" and "leftmost goat" variants. Note the effect the host strategy can have on the probability of winning by switching when given knowledge of which door the host opens. -- Rick Block (talk) 16:27, 28 March 2009 (UTC)
(outindent) Dick - you say "we get that". What "we" are you talking about? The question asks about a conditional probability (you agree with this don't you?). Without making it clear what they're doing, most popular sources present a solution based on an analysis of unconditional probabilities. For the conditional and unconditional probabilities to be the same, the host must pick randomly between two goats in the case the player initially picks the car. One might say the popular sources know what they're doing and are simply assuming this to be the case - others might say the popular sources are misunderstanding the problem and are, without realizing it, solving a different problem (one where the player must decide whether to switch before the host opens a door). Morgan et al. and Gillman (and many others) say the latter. You're saying it's POV for Wikipedia to say the popular sources are misunderstanding the problem (right?). Given the number of reliable sources that say exactly this, isn't it also POV to avoid saying it? I think this may perhaps be a case involving a prevalent popular misconception about something where the "experts" say the truth is something different than what is popularly believed to be true. Off hand, I can't think of other examples (surely there must be some). If anyone can think of others it might be interesting to see how they're handled. -- Rick Block (talk) 02:48, 29 March 2009 (UTC)
- By "we" I mean myself and any other intelligent discussants here; if someone doesn't get it by now, why bother talking to them? I understand what you're saying, especially that "Without making it clear what they're doing, most popular sources present a solution based on an analysis of unconditional probabilities." I don't think it's necessary to agree with you on "The question asks about a conditional probability (you agree with this don't you?)" since that's not the interpretation of most popular sources, as you note. As to whether the popular sources are "misunderstanding" or not, I don't think we have to know the answer to that. Morgan et al. and Gillman take a position on that, which we can report, but which we don't need to endorse. You can report as much as you like that top statisticians say the popular solution is wrong. But first you need to present the popular solution; then, move on to those who say it's wrong. Don't pollute the presentation of popular solution with the modern revised solution; first the one, then the other with an explanation of why they say the one is inadequate. That's the NPOV way to go about it. Dicklyon (talk) 03:01, 29 March 2009 (UTC)
- Interesting idea. You could start with a listing of all the elements that make the conditional solution 'required':
- It only applies when the contestant chooses door 1, the host reveals door 3, and the car is behind door 1
- Without the 'equal goat door' constraint it has no numeric solution
- There is some sort of 'host behaviour', but no one's really sure what it might be, or whether the contestant knows about it
- Whatever else you guys consider important
- Interesting idea. You could start with a listing of all the elements that make the conditional solution 'required':
(Counter)example
Maybe the next example is helpful to understand the problems with the problem.
I throw a fair dice. What is the probability of my outcome?
- Some people may reason: the outcome is one of the numbers 1 ... 6, so the probability that "the outcome is one of the numbers 1 ... 6" is 1. And they are right in some sense.
- The common meaning of the question is of course: for each possible outcome the probability is 1/6.
- Imagine you are standing next to me and you see the outcome of my throw. You definitely will say: 1/6.
Nijdam (talk) 09:29, 27 March 2009 (UTC)
- It's not clear what this is an example of. Dicklyon (talk) 15:45, 27 March 2009 (UTC)
- Please explain yourself instead. What is this an example of? How does it relate to the article? –Henning Makholm (talk) 17:00, 29 March 2009 (UTC)
Replace the Popular Solution Section With the 'Combining Doors' Solution
I propose the article be changed in the following way:
Replace the Popular Solution Section with the 'Combining Doors' Solution. Further, I would remove any statements regarding how the host chooses between the two doors. (Only 1 of the four sources in this section mention any 'host behaviour'). I would also add some formal notation of the diagrams, that would convey this:
Once the contestant has selected a door: 1/3 + (1/3 + 1/3) = 1 where the 1/3 on the left of the '+' sign represents the chosen door, and the numbers inside the parenthesis represent the remaining doors.
After a goat is revealed, the formula appears as: 1/3 + (2/3 + 0) = 1 or 1/3 +(0 + 2/3) = 1
As the only two possible outcomes are equivalent, regardless of which door the host reveals, this can be stated as: 1/3 + 2/3 = 1
Therefore switching, once it is offered by the host, will win the car 2x as often as not switching.
Glkanter (talk) 16:50, 27 March 2009 (UTC)
- In the light of the ongoing discussion this seemes highly premature, not to say complete without any sense of reality.Nijdam (talk) 17:25, 27 March 2009 (UTC)
- Perhaps you could respond in the manner described below:
- Please treat this the same way you would an article nominated at WP:FAC. There, each objection must provide a specific rationale that can be addressed. Do you have any specific suggestions for how to improve the proposal above? -- Rick Block (talk) 18:19, 29 March 2009 (UTC)
A concrete proposal
Given the voluminous discussions above, and in the archives of this page and at the #Arguments page, how about the following? Please comment below. -- Rick Block (talk) 17:18, 29 March 2009 (UTC)
Solution
There are two main approaches to solving the Monty Hall problem.
Evaluating switching versus staying
The probability of winning for all players who switch or all players who don't switch can be determined by examining all possible outcomes in either case (Grinstead and Snell 2006:137). For example, the figure below shows the outcomes when switching if the car is randomly placed behind one of the doors and the player initially picks Door 1. Switching will win if the car is behind either Door 2 or Door 3 with probability 2/3 while switching will lose only if the car is behind Door 1 with probability 1/3. Not switching wins if the car is behind Door 1 with probability 1/3, and otherwise loses with probability 2/3. The situation is similar no matter which door the player initially picks, so players who switch win twice as often as players who don't.
Evaluating the conditional probability
The solution above shows that the probability of winning by switching for all players who switch is 2/3, but this does not necessarily mean the probability of winning by switching is 2/3 given which door the host opens. This probability is a conditional probability (Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137). The difference is whether the analysis, as above, considers all possible scenarios or only the scenarios where the host opens a specific door. Another way to express the difference is whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992). The conditional probability may differ from the overall probability depending on the exact formulation of the problem.
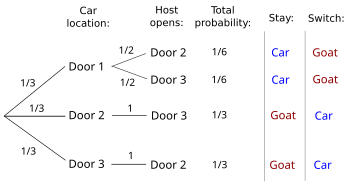
The conditional probability of winning by switching given which door the host opens can be determined referring to the expanded figure below or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138). For example, if the host opens Door 3 and the player switches, the player wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability 1/6 if the car is behind Door 1—the possibilities involving the host opening Door 2 do not apply. To convert these to conditional probabilities they are divided by their sum, so the conditional probability of winning by switching given the player picks Door 1 and the host opens Door 3 is (1/3)/(1/3 + 1/6), which is 2/3. This analysis depends on the constraint in the explicit problem statement that the host choose which door to open randomly if the player has initially selected the car.
Morgan et al. (1991) and Gillman (1992) both show a more general solution where the host is not constrained to pick randomly if the player has initially selected the car, which is how they both interpret the well known statement of the problem in Parade. They consider a scenario where the host chooses which door to open in this case with a preference expressed as a probability q, having a value between 0 and 1. If the host picks randomly q would be 1/2 and switching wins with probability 2/3 regardless of which door the host opens. If the player picks Door 1 and the host's preference for Door 3 is q, then in the case where the host opens Door 3 switching wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability (1/3)q if the car is behind Door 1. The conditional probability of winning by switching given the host opens Door 3 is therefore (1/3)/(1/3 + (1/3)q) which simplifies to 1/(1+q). Since q can vary between 0 and 1 this conditional probability can vary between 1/2 and 1. This means even without constraining the host to pick randomly if the player initially selects the car, the player is never worse off switching.
References
- Gillman, Leonard (1992). "The Car and the Goats," American Mathematical Monthly 99: 3–7.
- Grinstead, Charles M. and Snell, J. Laurie (2006-07-04). Grinstead and Snell’s Introduction to Probability (PDF). Online version of Introduction to Probability, 2nd edition, published by the American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell. Retrieved 2008-04-02.
{{cite book}}: Check date values in:|date=(help)CS1 maint: multiple names: authors list (link) - Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma," American Statistician 45: 284-287.
Comments on the above proposal
I think Nijdam said it best. "In the light of the ongoing discussion this seemes highly premature, not to say complete without any sense of reality." Glkanter (talk) 17:34, 29 March 2009 (UTC)
- Please treat this the same way you would an article nominated at WP:FAC. There, each objection must provide a specific rationale that can be addressed. Do you have any specific suggestions for how to improve the proposal above? -- Rick Block (talk) 18:19, 29 March 2009 (UTC)
What the article needs is a simpler, clearer, and more convincing explanation of the more general 'conditional' problem, which is equivalent to the unconditional problem. By this I mean that the Morgan argument applies only to the specific case where the host has opened door 3 as is made clear above. It is far from clear that this what what the original questioner intended to ask. In the more general case, where the host has opened either door 2 or door 3 the probability is 2/3. As I have said before, opening either door 2 or door 3 is essentially a null condition in that it has no effect whatsoever on the probability of winning by switching, thus the conditional and unconditional answers and solutions are both the same. The thing that makes this problem notable is that, even when unambiguously described in a form where the unconditional answer is valid, most people still get it wrong. Martin Hogbin (talk) 21:22, 29 March 2009 (UTC)
- Yep, this whole wild goose chase is about how the host decides, in the specific case of the contestant choosing the car, which LOSING door to show. However he decides, there's never been any indication that he shares this algorithm with the contestant. That would kind of violate the 'host vs contestant' roles, wouldn't it? The 'equal goat door' constraint is meaningless and therefore, worthless (as in 'it adds no value'). Glkanter (talk) 00:10, 30 March 2009 (UTC)
- In case it's not obvious, I'm suggesting three things here:
- Changing the outline a bit by introducing a level 2 "Solution" header and changing the existing level 2 headings "Popular solution" and "Conditional solution" to level 3 headings "Is always switching better?" and "Is switching always better?"
- Replacing the content currently in the "Popular solution" section with the content above under "Is always switching better?"
- Replacing the content currently in the "Conditional solution" section with the content above under "Is switching always better?"
- Martin and Glkanter - are you objecting to the proposed heading structure, or the proposed content under "Is always switching better?" or both? The intent of the "Is always switching better?" section is to convey the 1/3 + 2/3 = 1 style of solution, simply and convincingly. If you think this could be expressed better please suggest improvements. Neither of you apparently have any comprehension whatsoever of the "Is switching always better?" section, so other than suggesting some wording for prerequisites assumed for this section (per Wikipedia:Make technical articles accessible) perhaps it's best if you simply don't comment on this section. -- Rick Block (talk) 15:35, 30 March 2009 (UTC)
Your proposal is promising, Rick -- it does a good job of explaining the differences between the unconditional and conditional solutions, and why a number sources suggest that they are not both valid analyses of "the question as asked".
Somewhat off-topic, what I'd really like to see -- and this may be wishful thinking -- is an analysis of why both the unconditional and conditional scenarios (with the extra stipulation of "host's random pick) produce the same odds: 2/3ds when switching. Is it entirely coincidental?--Father Goose (talk) 22:21, 30 March 2009 (UTC)
- Assuming this wasn't just a rhetorical question (and this is probably more appropriate for the #Arguments page), of course it's not coincidental. The random host pick constraint forces the conditional probability to be the same regardless of which door the host opens. The unconditional probability is sort of like the "average" probability - if all conditional probabilities are the same the unconditional probability has to be the same as the conditional probabilities. This would (well, should) be covered in any undergraduate (perhaps even high school) level probability class. -- Rick Block (talk) 00:35, 31 March 2009 (UTC)
Rick, I see several problems with the first part; first, I think it complicates the issue and misrepresents the source when it says "for all players who switch or all players who don't switch;" there's nothing in Grinstead and Snell 2006:137 about "all players." The source says "if a contestant plays the “switch” strategy, then he will win whenever the door he originally picked does not have the car behind it, which happens 2/3 of the time." This applies to any individual player; saying "all players" makes it sound like you're averaging or requiring an emsemble, or somehow not answering the question for a player. It goes on to say "This very simple analysis, though correct, does not quite solve the problem that Craig posed. Craig asked for the conditional probability that you win if you switch, given that you have chosen door 1 and that Monty has chosen door 3." Yet, that is clearly just an interpretation, since Craig's problem statement doesn't say anything about conditional probabilities, and makes it clear that the door numbers are illustrative, not a special problem that needs an answer different from other illustrative numberings. It's fine to present this interpretation, but to present it as a part of the first solution, when it's really a criticism of that solution, is not a neutral approach. Your solution statement continues to focus on door numbers, which is not usual in sources that present this solution as the solution; again, not at all neutral, just a setup for saying why it's wrong. And the figure is similarly peculiar, being focused on the illustrative numbering of which door is originally picked. Look at the simpler figure that I used, which illustrates the simple solution as often presented. Also, you source says "Now suppose that a contestant decides in advance to play the “stay” strategy," but it does not rule out the possibility that the player will choose to use the "stay" or the "switch" strategy after the host reveals a goat. He thens goes on to show how the probabilities can be different from the 1/3 and 2/3 if the host isn't choosing equally between the doors. But that stretch, though valid, is still not the only possible viewpoint on the problem of deciding after the host opens a door. In the common usual reading of the problem, the player has no probabilistic model of the host behavior, so asking for probabilities conditioned on that behavior is just outside the universe of what the player is going to be able to consider in making their strategic choice. So choosing after a door is open is not a different problem from choosing before. This is a common interpretation, not the only one; we need not argue about which interpretation is better; just don't present the solution corresponding to one interpretation in the terms of the other, OK? Dicklyon (talk) 04:38, 5 April 2009 (UTC)
Diagram
I just created this. Does this help make it clearer at all? If so, we could add it to the article.
DavidSJ (talk) 02:20, 31 March 2009 (UTC)
New "Traditional solution" section
Given the complexity of the discussions, I thought it best to just be bold and rewrite the "traditional" solution as simply as possible, with no hint of the conditional approach, using the old figure where the only three relevant cases are what the contestant had behind their orignally picked door. Then, a separate section to say why some object to the that approach, before the other solution. I picked a ref that I think predated any mention of conditional solutions in the literature, yet which explicity says that the host's action doesn't change the probability of the car being behind the originally chosen door. I'm not claiming that it's rigorous or correct, just that it's traditional, which seems indisputable; we could add more such sources if anyone thinks that will help.
Comments? Dicklyon (talk) 03:09, 1 April 2009 (UTC)
- I'm not too happy about "It is assumed that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen, so the "proper Bayesian" still sees the probability of there being a car behind the chosen door as 1/3 ..." The fact that no information is revealed is exactly what those who get fooled have difficulty seeing -- their fallacy is exactly the assumption that revealing a goat will reveal information and somehow "compress" the total probability into the remaining doors. Just asserting the right conclusion it with nothing more than "it is assumed" to back it is not very convincing.
- The key step in the elementary argument is "suppose you make your decision to switch or not before Monty opens a door", followed by an argument that deciding later makes no difference (essentially, something like "you already knew you were going to be looking at a goat and an option to switch. Knowing which door that goat is behind is not going to help you decide better"). When this two-step argument is compressed into "it is assumed", the whole thing in my eyes collapses into handwaving. –Henning Makholm (talk) 15:03, 1 April 2009 (UTC)
Does anyone think Dick's version is any better than the version I suggested above? I'm somewhat perplexed why Dick has created a new version rather than discuss the version I suggested. I'm perhaps somewhat biased (as is Dick) but I'll offer the following observations:
- Dick's source is an analysis of DNA sequences, which seems like a distinctly odd source for a math problem. The source I reference is a probability and statistics textbook.
- Dick's version deletes the image showing the conditional solution - my version includes consistent images for both solutions.
I would suggest that if we're unhappy presenting the previous "confusing mess" it would be better to switch to the version I suggest. -- Rick Block (talk) 16:22, 1 April 2009 (UTC)
- Just to recap, point of my attempt at a new version is to present the traditional solution untainted by the more "modern" conditional solution. Rick's proposal recasts the traditional solution as a solution of a different problem, which he calls "probability of winning for all players who switch." Sure, it can be interpreted this way, but that's not the problem that was asked, nor the problem for which the tradtional solution is offered, but rather a recasting in light of the modern conditional way of looking at things. I think we need to avoid that, and just present the solution that was commonly accepted before the conditional one came along. Similarly, I picked the old figure because it better illustrates the traditional solution; I think this is better than picking a figure designed to set up the conditional solution; of course, putting that figure back in the next section would be fine. As for the source, this was just a concise one that I found that had the pretty much exact statement of the problem, as opposed to the sometimes different or over-simplified statements sometimes found with the traditional solution. It's in an article on Bayesian analysis, and it hardly matters that the field is DNA.
- As to me being biased, I'm not sure why you say that. I have no preconception or bias in this that I'm aware of. Rick, back on 18 March you said you had no objection in principle to presenting an unconditional solution first, making clear when it is valid, and then introducing a conditional solution afterward, and you invited me that try it. Your proposed version is not in that form at all, and that's why I'm trying again to get one that is. And with the traditional solution "uncontaminated" by the idea that maybe it doesn't solve the stated problem; that can come next. Dicklyon (talk) 04:43, 2 April 2009 (UTC)
- If a "popular solution" is presented first, it should be as short as possible, with no suggestive form or formulation giving it a status it doesn't deserve. It may read as: A popular way of understanding the problem is that by sticking to her original choice the player has a chance 1/3 of winning the car, hence switching will increase her chance to 2/3. With the additional remark: For a full understanding one needs to calculate the conditional probabilities, as is done in the next sections. Please improve the formulation and my English. Nijdam (talk) 12:35, 2 April 2009 (UTC)
- I think that adding For a full understanding one needs to calculate the conditional probabilities, as is done in the next sections would be over-representing that point of view. It's already represented as a criticism and as a subsequent section; the point of what I thought we had agreed to in principle was to present the typical, original, popular, traditional solution first, untainted by that alternate point of view, and then introduce that other POV next. Sounds like you guys aren't liking that, and are insisting in having the conditional-solution-needed POV intrude on the simple solution section. Do I understand correctly? Dicklyon (talk) 14:29, 2 April 2009 (UTC)
- You're (d) right, I don't like the "popular explanation" at all, because it is wrong. And more and more I notice, teachers and pupils in highschools, who like to "discuss" this for them so highly interesting problem, to be satisfied with the popular explanation, missing the point what it is all about. Namely: conditional probabilities! So let us make things clear, and not leaving any ambiguity. Nijdam (talk) 17:30, 2 April 2009 (UTC)
- I read Henning Makholm suggestion, and I like it very much. So let me expand my suggested text: A popular way of understanding the problem is that if the player makes the decision not to switch before Monty opens a door she has a chance 1/3 of winning the car. This chance is not affected by Marty opening a door, hence switching will increase her chance to 2/3. For a full understanding one needs to calculate the conditional probabilities, as is done in the next sections Nijdam (talk) 17:42, 2 April 2009 (UTC)
- Nijdam, I really do understand your suggestion and your position, and the reasoning for preferring a solution that treats the conditional probabilities. But your POV that "it is wrong" is not the only POV; NPOV suggests that we should present this common/popular/tradtional solution, even though from some points of view it is considered wrong, and then go to say what those alternative points of view are. You can't base the structure of the whole article around your one POV. Dicklyon (talk) 20:08, 2 April 2009 (UTC)
- Dick, it's always easy to judge one's opinion as POV, but it's not only my personal opinion, it is also found in the paper of Morgan et al. and others as you may well know. So let us present the right solution first, and then come with the popular explanation. Ok? BTW do you agree that the popular explanation is not complete? Nijdam (talk) 15:05, 3 April 2009 (UTC)
- Nijdam, I really do understand your suggestion and your position, and the reasoning for preferring a solution that treats the conditional probabilities. But your POV that "it is wrong" is not the only POV; NPOV suggests that we should present this common/popular/tradtional solution, even though from some points of view it is considered wrong, and then go to say what those alternative points of view are. You can't base the structure of the whole article around your one POV. Dicklyon (talk) 20:08, 2 April 2009 (UTC)
- Dick - The bias I alluded to above was that we each would naturally prefer our own writing. You've used the words "traditional" and "modern" a couple of times to refer to the unconditional and conditional approaches. These seem not very accurate to me. Perhaps "non-mathematical", or "intuitive", or something might be a better terminology for the unconditional approach - although I realize this runs into your view that this is a POV matter - but calling the conditional approach "modern" is simply absurd. In Gardner's 1959 version of the Three Prisoners problem he has the guard secretly flip a coin to decide in the case corresponding to the MHP host picking between two goats. The notion that an unconditional solution is sufficient was popularized by vos Savant more than 30 years later. The MHP has been known in mathematics, and known to be a conditional probability problem, since 1975. The two papers that are the best source for this view are the Morgan et al. and Gillman papers, published in late 1991 and early 1992 respectively (roughly a year after vos Savant's original column - pretty much directly in response to her columns). This is not a "traditional" vs. "modern" issue - it's an expert vs. non-expert issue.
- Rather than rewrite, can we work on revising the proposal I made above to address your concerns? I don't think this should be terribly difficult. For example, rather than say "There are two main approaches to solving the Monty Hall problem that answer slightly different questions." we could say "There are two main approaches to solving the Monty Hall problem." We have an issue with what to call the two approaches. If you're not willing to use the problems that the expert sources say they address to identify them, or any terms that convey some sort of value judgment between them (like "popular", or "expert", or "common", or "mathematically rigorous") I think we're left with a description of the solution itself. Perhaps "Examining outcomes of switching versus not switching" and "Examining conditional probabilities after the host opens a door". -- Rick Block (talk) 01:57, 3 April 2009 (UTC)
- I agree with Rick on the absurdity of calling this a "Traditional" vs "Modern" difference. In addition, this new "Traditional Solution" section is poorly written and confusing. It forces the reader to dance between a frequentist and a Bayesian view, as if he or she had already gone through this talk page and digested pages of conditiona/unconditional mumbo-jumbo even before reading the article. In fact, I am tempted to be bold and revert immediately, but will wait for the argument to settle a bit. Note, I don't have any problem with presenting a frequentist solution (a.k.a. unconditional) along with the bayesian (conditional) one, especially because the more mathematically naive readers will be more attuned to the former than the latter. But please let's not pretend that the frequentist interpretation is "The Correct One(tm)", when it rather obviously isn't (and I won't repeat Rick's excellent argument here for why it isn't).glopk (talk) 16:43, 3 April 2009 (UTC)
- I don't have a strong opinion about what to call them, except that the "conditional" idea shouldn't be used to frame the other solution by calling it unconditional. Perhaps "popular" was better in that it expresses the idea of both common and less rigorous and expert. What I object to is just letting the POV of the experts who want to treat it as a problem in conditional probabilities frame the whole structure of the article and the solution, when a perfectly good popular and traditional solution, agreed to by many other smart people, gives the right answer for the problem as usually understood. Each time I think we some agreement in principle, it does out the window with bickering by those who want everything to be framed relative to their "correct" conditional POV. This isn't right. Dicklyon (talk) 23:43, 3 April 2009 (UTC)
- The picture illustrates what the text describes: doors have no numbers and the player has chosen either the car, or goat A, or goat B, with equal probabilities. This is really the simple way to look at it that makes it clear that specifying door numbers is irrelevant. Dicklyon (talk) 23:45, 3 April 2009 (UTC)
- The "popular" solution is unconditional, why do you object to calling it what it is? Are you happier with this old version? It presents an unconditional solution, says it's correct and then says what the experts say about it as a transition to the conditional solution (and apparently doesn't make anyone happy - Martin Hogbin and Glkanter have been complaining about that version for months from the one side and Nijdam didn't like it either from the other side). I still don't understand what you don't like about my proposal above. Can we work out changes you think would be needed to address your concerns? -- Rick Block (talk) 02:14, 4 April 2009 (UTC)
- I object to calling it conditional because that's how it's framed by those who argue that it's incorrect. I think "unconditional" is not a useful characterization of the reasoning except when you're trying to contrast it with the more elaborate "conditional" approach. Neither of the sources present it as "unconditional". Are there sources that call it that, other than those that are presenting the conditional solution as better? Dicklyon (talk) 02:00, 5 April 2009 (UTC)
How complicated is it???
I might have missed something, but surely it's not a difficult problem. Two times out of three, the host indicates to the contestant what door the car is behind by having no choice but to open the other door, therefore it's always worthwhile to swap, because two times out of three he will have chosen the correct door for you. It's more of a psychological trick or an illusion than any great mathematical conundrum. —Preceding unsigned comment added by 88.97.18.12 (talk) 23:57, 2 April 2009 (UTC)
- I can't understand the fuss. You know that there are two goats and one car. You know that the host has to open one of the two remaining doors. You know that 2/3 times, he will be faced with one car and one goat, and have to open the door with the goat behind it, leaving the car behind the remaining door. Ergo, if you always switch, you win the car 2/3 of the time. What alternative explanations are there? The illusion is that all doors start out with a 1/3 chance, but after the host has opened one door, he has increased the chances of the remaining door having the car behind it to 2/3. Even if you happen to have chosen the car, over the long run you are bound to win. —Preceding unsigned comment added by 81.137.245.144 (talk) 09:10, 3 April 2009 (UTC)
- The fuss is that mathematicians say the problem clearly asks about a conditional probability, and that the answer "2/3" is correct only if the host is constrained to pick randomly between two goats (in the case the player picks the car). See the second question in this FAQ. -- Rick Block (talk) 13:47, 3 April 2009 (UTC)
- It's a conditional probability problem - you're standing in front of two closed doors and looking at a goat. Of course across all players who switch, 2/3 will win the car - but what about you, the player standing in front of two doors? Maybe the other guys (whoever they are) always win and you not so often. If the host has opened door 3 your chances of winning are the probability that the car is behind door 2 (i.e. 1/3). Your probability of losing by switching is the probability that the host has opened door 3 (let's say this is 1/2) times your probability of having picked the car - i.e. 1/3 * 1/2 = 1/6. Winning 1/3 versus losing 1/6 means winning 2/3. But why is the probability the host opens door 3 when you've picked the car exactly 1/2? Unless we specify the host has to flip a coin or something the host can open whatever door he'd like in this case. This means unless we say how the host decides in this case, the host opens door 3 with some probability between 0 and 1. Let's see what happens using these extremes:
- host opens door 3 with probability 0 means you win 1/3 (when the car is behind door 2) and lose (when the car is behind door 1) 0 * 1/3 = 0. Winning 1/3 versus losing 0 means winning with probability 1.
- host opens door 3 with probability 1 means you win 1/3 and lose 1 * 1/3 = 1/3. Winning 1/3 versus losing 1/3 means winning with probability 1/2.
- This means if the other guys always win you win 1/2 the time. If the host opens a door, no matter how he picks when you've picked the car you win at least 1/2 and maybe you're one of the lucky ones who win with probability 1. Not quite so simple, but yes you should switch every time. And, if you do, you'll not only win 2/3 of the time overall but your chances of winning every time you switch are between 1/2 and 1. -- Rick Block (talk) 02:51, 3 April 2009 (UTC)
- And, if the host picks randomly when you've picked the car, you'll win with probability 2/3 every time. But even if you don't know this, you'll win with probably 2/3 overall (and between 1/2 and 1 every time). -- Rick Block (talk) 03:02, 3 April 2009 (UTC)
- That's only one of the two prominent points of view on the problem, and we need to represent both, preferably with the traditional one first since it's older and simpler and widely known. By the other POV, if the player doesn't know anything about how the host is going to choose a door, and even if the host is doing something as biased as choosing the left door when he has a choice, the player can not base their estimate of the probability on that, since they don't know it, and so will still be correct -- or as correct as possible -- in using an unconditional model and estimating their probability of winning at 2/3. It's only when they have access to information about the host's behavior that they can use that information to estimate different probabilities, and even then the answer about what they should do, and why, doesn't change. So let's not let this more complex POV about rigorous conditional probabilities derail the discussion of the simple solution. Dicklyon (talk) 05:29, 3 April 2009 (UTC)
- Yes, Dick you are quite right. The simple unconditional problem is the one that is notable and interesting and is the one that should have the most prominence in this article. On the arguments page I explain how the paper that is central to the 'academic' approach (that by Morgan et al) conjures up a more complex explanation by imposing arbitrary and unjustified choices. Martin Hogbin (talk) 08:41, 3 April 2009 (UTC)
- Let us be precise in our phrasing: there is no such as an "unconditional problem" in the MHP. We're discussing the need for a "conditional solution", and the flaw in the so called "unconditional solution". Nijdam (talk) 19:22, 3 April 2009 (UTC)
- That is not what Morgan say. They give a statement of the unconditional problem. Perhaps we could agree on 'unconditional formulation'. Martin Hogbin (talk) 20:45, 3 April 2009 (UTC)
- Ok, it is possible to formulate an unconditional problem, that seems to be related with the MHP. It reads: From 3 doors only 1 hides a car, without you knowing which one. Pick a door. What is the probability you pick the car? It may be formulated with much more wording. Hardly an interesting problem. Morgan mentions this, because the "simple solution" is addressing this problem. Nijdam (talk) 11:35, 4 April 2009 (UTC)
- That is not what Morgan say. They give a statement of the unconditional problem. Perhaps we could agree on 'unconditional formulation'. Martin Hogbin (talk) 20:45, 3 April 2009 (UTC)
- Let us be precise in our phrasing: there is no such as an "unconditional problem" in the MHP. We're discussing the need for a "conditional solution", and the flaw in the so called "unconditional solution". Nijdam (talk) 19:22, 3 April 2009 (UTC)
- Yes, Dick you are quite right. The simple unconditional problem is the one that is notable and interesting and is the one that should have the most prominence in this article. On the arguments page I explain how the paper that is central to the 'academic' approach (that by Morgan et al) conjures up a more complex explanation by imposing arbitrary and unjustified choices. Martin Hogbin (talk) 08:41, 3 April 2009 (UTC)
- Actually, that is exactly the MHP as many people interpret it. As 88.97 wrote above "It's more of a psychological trick or an illusion than any great mathematical conundrum." Because many people insist that the odds become 1/2 & 1/2, not 1/3 & 2/3. That's why it's the world's most famous paradox. Not because people care 'which goat will Monty reveal?' Glkanter (talk) 13:40, 4 April 2009 (UTC)
- No, it's too bad for the innocent Wikipedia reader who is subjected to all that stuff you self-proclaimed experts have cluttered up the MHP article with. Can't you and Rick find a more appropriate forum to demonstrate your mastery of Probability? Because this article is not the place for it. Glkanter (talk) 15:11, 4 April 2009 (UTC)
- Morgan's 'mastery of probability' only exists because they set the problem up to specifically create it. It has now been agreed that it only applies to the case where the producer's possible preference for placing the car is ignored but the host's preference in opening a door is considered important. Martin Hogbin (talk) 20:52, 4 April 2009 (UTC)
- Dick - is there some reason you're not addressing my comments above (previous section)? There's no clear consensus for your version, so adding it still seems premature. -- Rick Block (talk) 14:18, 3 April 2009 (UTC)
- ??? As far as I can tell, you haven't responded to comments from Nijdam, Glopk, Henning, or myself. At this point, I'd say there's a better consensus for the version I've proposed than the one you've edited into the article (favorable comments from Father Goose and Nijdam and arguably Glopk vs. no one other than you apparently supporting your version). On the other hand, it's also clear to me there is not a general consensus for either of these versions. I think some slight variation on the version I've proposed is more likely to generate broader support than your version. What has to change in this version to address your concerns? If you'd rather simply edit the version above than discuss changes, please feel free (diffs will be in the history). I've made some changes already attempting to address what I think you've objected to. Better? -- Rick Block (talk) 00:49, 5 April 2009 (UTC)
- Exactly; there seem to be several people who support this general direction; I'd rather seem them work on fixing up the article to be better than more of this incessant bickering that is this talk page. The comments of Nijdam seem to be rather empty; just doesn't like it. And Henning's comments are more about why the other solution is better, rather than commenting on the article change I made; he did suggest we not pretend it is "the correct solution", which I agree with; we need to present all POVs without taking sides. And I already agree we don't need to call it "traditional"; waiting for constructive alternatives. And Rick, which comments have I missed that you want a response to? Dicklyon (talk) 02:03, 5 April 2009 (UTC)
- Clearly Glkanter believes that we need a straightforward presentation of the simple popular solution. Martin Hogbin says it "should have the most prominence," but I see no need to go that far; he says the Morgan et al. paper "conjures up a more complex explanation by imposing arbitrary and unjustified choices," which I don't think is an opinion that can be justified from sources. Nevertheless, it does help to clarify the sharp distinction between the different points of view on what the problem is and what the solutions are. As long as we continue to have people who side with these different POVs trying to get the article to go their way, we're not going to get unwedged. What we need is a fair representation of both points of view. That's exactly why the simple solution needs to be presented simply, without value judgement as to whether it correct or adequate or not, and without framing it in the terms of the POV that says it's wrong. After that, the alternative more complex POV should be introduced and discussed. Can I hear from all whether they agree with this general approach or not? Dicklyon (talk) 04:11, 5 April 2009 (UTC)
- Dick - Comments not addressed: the generally weak references (not up to par for a featured article - and adding more weak references doesn't help, what is needed is an authoritative reference from a math journal or math textbook), the image issues (doesn't match the problem description and you've deleted the conditional image), the prose issues Glopk pointed out, and my request that you say what you don't like about the alternative I've proposed (which is an attempt to simply present the solution Glkanter and Martin prefer, without any value judgment - have you even read the changed version above?). I'd rather we discuss changes here first, before changing the article but you seem to be completely unwilling to following this approach. Directly answering your question, I'm OK with the general approach, however I think we need to be very careful not to present something that experts would consider to be flat-out wrong. -- Rick Block (talk) 05:00, 5 April 2009 (UTC)
- No, I disagree on the refs; the math journals primarily represent the more complicated conditional POV on the problem, because they're mathematicians. The simpler POV isn't something that you could publish a math journal article on, but it's still a viable POV that needs to be represented. Don't take the ScienceApologist route and try trump NPOV with SPOV (scientific point of view). As for the images, the image used illustrates the solution as described; if a conditional image was removed, feel free to put it back in the conditional section. I worked on the prose a bit already, and am happy if Glopk can do more to improve it. And I commented on what's wrong with your version above. Dicklyon (talk) 05:59, 5 April 2009 (UTC)
Combining Doors Solution
I proposed about a week ago that the Combining Doors Solution receive priority in the article, without it being called 'inadequate'. Still waiting for any informed criticisms.
How long is it customary to wait before editing the article? Glkanter (talk) 03:27, 4 April 2009 (UTC)
- The Combining Doors Solution, in spite of its interesting and promising name, is essentially the same as the "simple solution". So, let us not give it much attention. Nijdam (talk) 11:38, 4 April 2009 (UTC)
- At this point we have 3 alternatives on the table. This one, the one I've suggested, and the one Dick has edited into the article. This one has generated much less commentary than the others, but none have any clear consensus so editing any of them into the article is premature. You should take two other proposals being offered up after this one as objections to this one. -- Rick Block (talk) 12:16, 4 April 2009 (UTC)
- I think both of your answers are non-answers.
- Please treat this the same way you would an article nominated at WP:FAC. There, each objection must provide a specific rationale that can be addressed. Do you have any specific suggestions for how to improve the proposal above? -- Rick Block (talk) 18:19, 29 March 2009 (UTC)
- From Morgan et al.:
- Solution F5. The probability that a player is shown a goat is 1. So conditioning on this event cannot change the probability of 1/3 that door 1 is a winner before a goat is shown, that is, the probability of winning by not switching is 1/3, and by switching is 2/3.
- The combining doors solution is simply a rephrasing of this solution. Rather than present this as the first solution (with the addition of unreferenced "equations"), I think it is more appropriate to present the switch vs. stay comparison (as I suggest above) from a math textbook which is a more authoritative source than any of the references for the combining door solution. -- Rick Block (talk) 15:40, 4 April 2009 (UTC)
- From Morgan et al.:
- Yes, but also keep in mind the Morgan's POV is but one way to frame the problem. Many do not consider it to be the solution to a different problem from the one stated, even if it's different from the other other one that Morgan analyzes, in which the host's choice of door can provide some extra information about the probability of the original door being the car. Dicklyon (talk) 04:02, 5 April 2009 (UTC)
- Thank you, Rick. Can you please expand your response so that I can understand where Morgan is finding fault with the Combining Doors solution? I'm sorry, but it's not clear. You're right, my equations are not referenced. They don't go in. Comparing the two proposals? I think the Combining Doors is more concise and the diagrams are more intuitive. And all they show is a goat behind a door, with no comment on where the car is. Which, imho is what the puzzle is really about. Glkanter (talk) 16:05, 4 April 2009 (UTC)
No more comments? I'll make this change later today. Glkanter (talk) 10:27, 10 April 2009 (UTC)
- Dick Lyon, except for removing the diagram, you made some nice enhancements. I always liked the way it flowed (sort of) from 1/3, 1/3, 1/3 (although the diagram did not specifically say this, I wish it had) before the goat is revealed, to the 1/3, 2/3, 0 after the goat is revealed.
- On a related note, what is with the diagram above it? Are the heads necessary? I could see where someone might find it offensive. Glkanter (talk) 06:23, 11 April 2009 (UTC)
More than three choices
I consider this an encyclopedic question, because it is just as much for my information as it is for my curiosity.
In the game show Deal or No Deal, you may have noticed that, when a contestant is down to two cases, the host offers them a chance to switch cases. Would switching cases increase your chances - even slightly - of getting the higher value case, due to this paradox, and if so, how would you compute that probability. I doubt your chances of getting the higher case would become 25/26. —Preceding unsigned comment added by Wikieditor1988 (talk • contribs) 03:44, 5 April 2009 (UTC)
- Each choice in Deal or No Deal is a random choice. With N cases left, the player's chances are 1/N of having the highest prize left. So, no advantage in switching. This is like the "random Monty" variant. -- Rick Block (talk) 03:56, 5 April 2009 (UTC)
Consider comparing the Monty hall problem to Deal or No Deal. If you want to win the top prize (£250,000), then your probability of picking it to start with is 1/22. If you then eliminate the other 20 boxes and are left with the £250,000, then an application of the Monty Halls problem would tell you to switch, because:
Imagine that there are 22 doors. You select one door, and are then shown the other twenty. This means that you have a 21/22 chance of winning the prize if you switch. Whether the host knows where the prises are doesn't matter, because the situation is the same. You have picked a box, and then been shown 20 that you don't want. Therefore switching is best.
Also, even though the box picked is random, at the end you still get left in a situation where you have seen what is behind 20 boxes, and then have the option to swap (see above). Therefore I think the probability of winning big if you swap is bigger than 1/2. If you think there is something wrong with my logic, then please make me aware of it.
(Another statistical quirk is that if you work out the probability of not taking out the quarter of a million by the sum 20/21 x 19/20 x 18/19... x 2/3 then the answer is 2/21. This means that on average 2 games out of 21 should occur where the £250,000 is left as one of the last two boxes.)Cricketmad5Wk (talk) 20:03, 24 April 2009 (UTC)
- If we start with 22 boxes, yours and all the rest each have a 1/22 chance of being the grand prize. If you pick one randomly and open it and it is not the grand prize there are 21 left. Each of these 21 (yours and all the rest) now have a 1/21 chance of being the grand prize. Why? Because this is a conditional probability problem. The only possibility you've eliminated is the one where the opened box had the prize. All other possibilities are still in play. The conditional chance for each box is now the unconditional chance (1/22) divided by the total probability that you're in this case (21/22), i.e. (1/22) / (21/22) which is 1/21. If you open another random box and it isn't the grand prize you have another conditional probability problem just like the first one. The remaining (now 20) boxes each have a probability of (1/21) / (20/21) or 1/20. This continues until there are two left and the chances are 1/2 for each box.
- This is entirely different from the host randomly opening boxes but avoiding your box and the grand prize (as in the Monty Hall problem). If this is what is going on, then after the first box has been opened you have a 1/21 chance of being in each situation where one specific box is opened. In each of these, you have a (1/22) * (1/21) chance of having the grand prize. There are 21 of these possibilities, so your overall chances of having the grand prize are 21 * (1/22) * (1/21) which is 1/22. The remaining 21/22 chance of the grand prize being somewhere is split evenly among the other 20 boxes, so each of them now has a (21/22) * (1/20) chance of having the grand prize. When the second box is opened, you have a 1/20 chance of being in any of these specific possibilities, so in each you have a (1/22) * (1/20) chance (and there are 20 of these, so you still have a 1/22 chance overall). The remaining 21/22 chance is now split among only 19 so they each have a (21/22) * (1/19) chance. This continues so with N boxes left you have a 1/22 chance and the remaining boxes each have a (21/22) * (1/(N-1)) chance. When we get to two boxes left, your box still (!) has a 1/22 chance and the other box has a 21/22 chance.
- Completely random versus random except for the grand prize and your box makes a huge difference. -- Rick Block (talk) 02:11, 25 April 2009 (UTC)
- Here is a little something that I came up with myself to prove you right(i.e. the probability is the same)
Let the boxes equal the letters A-V
Let the prize that you want to win be behind box A (It doesn't matter which box the prize you want to win is in, [also assume biggest prize])
Now if you pick box A, then the probability of getting through to the end of the game with the prize you want still in the game is 1(certain).
This occurs is (1/22) cases. (1)*(1/22)=(1/22)
If you don't pick box A then the probability of you getting to the end of the game without taking out the prize you want is:
(20/21)*(19/20)*(18/19)... *(1/2).
This can be re-written as:
((20!)*(1!))/(21!).
The sum works out with a value of (1/22) = 0.04545454545454545454545 This occurs is 21/22 cases so:
(21/22)*(1/22)= (1/22)
Therefore, you are correct, and the probabilities remain the same
N.B. I came up with this by accident when trying to prove mathematically that the opposite was true. Perhaps it should be posted as a proof for the probabilities remaining the same?? .Cricketmad5Wk (talk) 16:02, 25 April 2009 (UTC)
- Original proofs should not be posted in articles - see WP:OR. It's fine to discuss them on talk pages, but unless something is published in a reliable source it can't be used in an article. -- Rick Block (talk) 17:37, 25 April 2009 (UTC)
The stages in the decision
I'll try to find out where each of you stand. (Again I use X=choice, C=car, A=open and the rules)
1. Before the player made her choice
The probability she picks the car is: P(X=C)=1/3. This means that on the average 1 out of 3 players will choose the door with the car. One may reason from here that switching after the choice of door and the showing of a goat will on the average result in 2/3 winning the car.
2. After the player has chosen a door and before the quizmaster opens one
If the player chooses door x, we now have to condition on the event {X=x}. For every x the (conditional) probability she picks the car is: P(C=x|X=x)=P(C=x)=1/3 (because X an C are independent and the car is placed randomly). One may reason from here that for every choice x switching after the showing of a goat will on the average for players with this choice result in 2/3 winning the car.
3. After the player has chosen a door and the quizmaster has opened one
If the player chooses door x and the quizmaster has opened door a (≠x), we now have to condition on the event {X=x, A=a}. For every x and a (≠x) the (conditional) probability she picks the car is: P(C=x|X=x,A=a)=1/3. Why is this?
We can directly calculate it:
- P(C=x|X=x,A=a) = P(A=a|X=x,C=x)P(C=x|X=x)/P(A=a|X=x) = {1/2.1/3}/{1/2.1/3+1.1/3+0/1/3}=1/3
Or use the symmetry. For x,a,b all different:
- P(C=x|X=x,A=a)=P(C=x|X=x,A=b)=(let's say)t
Now is:
- P(C=x)=P(C=x|X=x)=P(C=x|X=x,A=a)P(A=a|X=x)+P(C=x|X=x,A=b)P(A=b|X=x)=
- =t{P(A=a|X=x)+P(A=b|X=x)} = t
hence:
- t=P(C=x)=1/3
For every choice x and opened door a switching will on the average for players with this choice and opened door, result in 2/3 winning the car.
Really unconditional is the reasoning in case 1. Although formally conditional on the choice, due to the independance of the choice and the place of the car, case 2 may also be considered as unconditional. Case 3. is definitely conditional, and only in this case has the player made her choice and the quizmaster opened a door. I cannot imagine someone to disagree with these considerations. The controversy just originates from the idea that case 1 or case 2 forms a solution to the stated MHP. Does anyone agree with this? Nijdam (talk) 12:52, 5 April 2009 (UTC)
- I don't see the point of this discussion. It doesn't really matter how we analyze the problem or solution. What matters is what analyses we find in reliable sources. Dicklyon (talk) 15:00, 5 April 2009 (UTC)
- Where I stand is simply that the different points of view on the solutions need to be fairly represented; your way of framing the problem is alinged with one of those POVs, I think, and going into it in more depth is sort of off-topic here, I think. Or if I misunderstood, what were trying to find out with this posting? Your statement "If the player chooses door x and the quizmaster has opened door a (≠x), we now have to condition on the event {X=x, A=a}" represents one POV clearly; we get that; let's just no lose sight of the other POV in which you don't have to do that. Dicklyon (talk) 22:29, 5 April 2009 (UTC)
- Yet you haven't said what you think about the problem, let us say: your POV. You often use the term POV. Is it because other opinions than yours are just POV's? All I have explained can be found in scientific articles (although I do not need them for such a simple problem). My concern is, what is demonstrated in the following reaction of Candy.Nijdam (talk) 14:36, 6 April 2009 (UTC)
- In the literature on this problem, there are two main points of view: one simple analysis, that you call unconditional; and one conditional analysis by people who say that the other is insufficient or solves the wrong problem. Editors here have polarized over these two points of view, and conduct lengthy arguments over the merits of them, rather than discussing how to fairly represent both in the article. My position is that both points of view are reasonable, and that the article has been firmly in the grip of the people who support the conditional point of view; that's why I'm pushing in the other direction, to get back to some balance and objectivity and proper weight. As far as I can tell, I'm the only one willing to not take sides, but maybe I'm missing someone. Reactions by people like Candy, who haven't yet come to understand the issue, are natural, need to be politely addressed and dismissed, but shouldn't confuse the main discussion. Dicklyon (talk) 15:05, 6 April 2009 (UTC)
- Yet you haven't said what you think about the problem, let us say: your POV. You often use the term POV. Is it because other opinions than yours are just POV's? All I have explained can be found in scientific articles (although I do not need them for such a simple problem). My concern is, what is demonstrated in the following reaction of Candy.Nijdam (talk) 14:36, 6 April 2009 (UTC)
- Where I stand is simply that the different points of view on the solutions need to be fairly represented; your way of framing the problem is alinged with one of those POVs, I think, and going into it in more depth is sort of off-topic here, I think. Or if I misunderstood, what were trying to find out with this posting? Your statement "If the player chooses door x and the quizmaster has opened door a (≠x), we now have to condition on the event {X=x, A=a}" represents one POV clearly; we get that; let's just no lose sight of the other POV in which you don't have to do that. Dicklyon (talk) 22:29, 5 April 2009 (UTC)
- I don't understand why you have gone to these lengths to explain what is extremely simple. Regardless of what happens, if the contestant sticks with their original choice the probability of getting the car is 1/3. You seem to have made a bit of a mountain out of a molehill? --Candy (talk) 04:35, 6 April 2009 (UTC)
- Are you agreeing or disagreeing with me Nijdam? --Candy (talk) 23:18, 6 April 2009 (UTC)
- Please see the "Conditional solution" section of the article, or the FAQ at the top of this page. If you'd like to discuss this, please use the /Arguments page. -- Rick Block (talk) 03:17, 7 April 2009 (UTC)
Outline changes
Can we have a focused discussion about the recent outline changes (and, after we agree on an outline we can discuss the individual sections)? It's not clear to me where folks stand overall on these. The article now has
- Problem
- Popular solution
- Criticisms of the traditional solution
- Conditional solution
all at the same heading level. I'd prefer
- Problem
- Solution
- Popular solution
- Conditional solution
with the bit in the "criticisms" section about experimental validation moved to the "Popular solution" section. I'd simply delete the other parts of this section (starting with "Nevertheless ...") since they are addressed in the "Conditional solution" section.
Related to this, I object to including the unconditional solution in the lead and think the paragraph starting with "Simple probability ..." should be deleted.
Other opinions? -- Rick Block (talk) 17:06, 5 April 2009 (UTC)
- The alternative is to leave the simple (popular/traditional) solution in the lead, and keep the criticisms from the conditional guys outside the presentation of the simple solution. I think the current structure works better, with the "criticism" section, what you want to call it, making the transition to the more complex analysis. I'm OK moving the "experimental validation" part into the popular solution section, as long as it's not phrased according to the conditional POV. The outline you proposed would also get complicated, as the "Problem" section would have to already go into the two different points of view about how to interpret the problem statement; it's probably best to leave those POVs, especially the more complicated one, to the corresponding solution section. Dicklyon (talk) 17:30, 5 April 2009 (UTC)
- As in the example above, the "Solution" section can simply say there are multiple approaches (surely you're not suggesting that saying there are multiple approaches is POV?). The point about deleting the unconditional solution from the lead is that including it but not the conditional solution is favoring this POV. -- Rick Block (talk) 18:04, 5 April 2009 (UTC)
- Yes, it would be fine to say there are multiple solutions, in the lead; but we should probably also say the result, that it is always advantageous to switch because the probably of winning will be double that way, under the usual interpretation of the problem (we don't need to say exactly how we arrive at it, or under what conditions it is the exactly answer, until the sections that follow); but to leave that out of the lead is probably not a good idea. Dicklyon (talk) 19:08, 5 April 2009 (UTC)
- We seem to be talking about two different leads here. In the article lead, not the section lead, I'm suggesting deleting the paragraph that says "Simple probability indicates ..." - this would leave the sentence from the previous paragraph that says "In fact, in the usual interpretation of the problem the player should switch — doing so doubles the probability of winning the car from 1/3 to 2/3.". Then, in the solution section, I'm suggesting under "Solution" we say "There are two main approaches to solving the Monty Hall problem." (as in the linked section above) and present both as subsections. -- Rick Block (talk) 19:40, 5 April 2009 (UTC)
I would prefer something along these lines:
- Problem
- Popular solution
- Sources of confusion
- Aids to understanding
- Criticisms of the popular solution
- Conditional solution
- Sources of confusion
- Aids to understanding
- Criticisms (or limitations) if the conditional solution
Where each solution has its own 'Sources of confusion' and 'Aids to understanding', and 'Criticism' section. At the moment these two sections merely add more confusion and less understanding to the popular solution. I accept that we may have a problem with reliable sources for the 'Criticisms (or limitations) if the conditional solution'. Martin Hogbin (talk) 18:55, 5 April 2009 (UTC)
Suggested wording for Popular solution section
- I would like to speak about "popular explanation" rather than solution. It's fine with me to start with it. But let us keep it simple and short, and without all kind of pictures, tables, decision trees etc., because the wording of the explanation may be right, be it incomplete, but the usual extra's are wrong. Nijdam (talk) 22:21, 5 April 2009 (UTC)
- Let me kick off for a formulation of the popular explanation:
- After the player has chosen a door, the probability it hides the car is 1/3. This probability is not influenced by the opening of a door with a goat by Monty. It may indeed be proven that after a door is opened the probability the original chosen door hides the car is also 1/3. Because clearly the open door does not show the car, the remaining closed door must hide the car with probability 2/3. Hence switching increases the probability of winning the car from 1/3 to 2/3.
- It is a first shot, but I think it contains all (Dicklyon: POV) it should. And I think (POV) anything more is superfluous. Modify the wording, improve the text, give me some comment. Nijdam (talk) 14:50, 6 April 2009 (UTC)
- Not bad, but I'd just leave out the weasel-worded "It may indeed be proven"; either state or reference a proof, or leave it as an informal observation. It's not clear to me what part of what I put in before you consider to be wrong, or why you think the picture is not helpful. Dicklyon (talk) 14:57, 6 April 2009 (UTC)
- Ok, I'll change it into:
- After the player has chosen a door, the probability it hides the car is 1/3. This probability is not influenced by the opening of a door with a goat by Monty, hence after Monty has opened a door with a goat, the probability the original chosen door hides the car is also 1/3. Because clearly the open door does not show the car, the remaining closed door must hide the car with probability 2/3. Hence switching increases the probability of winning the car from 1/3 to 2/3.
- Better? Nijdam (talk) —Preceding undated comment added 15:21, 6 April 2009 (UTC).
- I think it looks good. I haven't paid much attention to the "combining doors" solution, as I haven't encountered something called that in a source. It may be the same, in some sense, but it's not clear why we need to consider "combining doors" as a concept. Now that I check the description of that solution, I see that 4 sources are cited; all 4 are accessible online; so I check them all, and didn't find any language like "combining" in any of them. It would be OK to cite these sources to further describe the solution if we do it in terms that they do support, but it's not clear that "combining doors" is it. In some sense I agree that the "combining door" solution is "equivalent", but it still seems like a somewhat different approach at the analysis; let us know more about what the sources say, and we can decide whether to merge with the simple solution or not. Dicklyon (talk) 18:24, 6 April 2009 (UTC)
- Why no pictures or diagrams for the popular formulation? We should use this word as the difference is one of formulation of the problem rather than rigour of the solution. The popular formulation and its associated solution is the problem that most people get wrong most of the time, it is the notable problem, and it is the problem that should be addressed fully and convincingly in this article. Martin Hogbin (talk) 21:36, 6 April 2009 (UTC)
- I agree it should have an illustration. Dicklyon (talk) 03:27, 7 April 2009 (UTC)
- Why call it "popular formulation"? I always thought it served as an explanation to the stated problem. If not, please, let us not mix things up, and in that case formulate the different problems seperately. Why pictures or diagrams? In my opinion (POV) the words say anything needed. Nijdam (talk) 12:29, 7 April 2009 (UTC)
- I agree it should have an illustration. Dicklyon (talk) 03:27, 7 April 2009 (UTC)
- Why no pictures or diagrams for the popular formulation? We should use this word as the difference is one of formulation of the problem rather than rigour of the solution. The popular formulation and its associated solution is the problem that most people get wrong most of the time, it is the notable problem, and it is the problem that should be addressed fully and convincingly in this article. Martin Hogbin (talk) 21:36, 6 April 2009 (UTC)
- I think it looks good. I haven't paid much attention to the "combining doors" solution, as I haven't encountered something called that in a source. It may be the same, in some sense, but it's not clear why we need to consider "combining doors" as a concept. Now that I check the description of that solution, I see that 4 sources are cited; all 4 are accessible online; so I check them all, and didn't find any language like "combining" in any of them. It would be OK to cite these sources to further describe the solution if we do it in terms that they do support, but it's not clear that "combining doors" is it. In some sense I agree that the "combining door" solution is "equivalent", but it still seems like a somewhat different approach at the analysis; let us know more about what the sources say, and we can decide whether to merge with the simple solution or not. Dicklyon (talk) 18:24, 6 April 2009 (UTC)
Is it just me or does this appear to be illogical?
The paragraph, "Simple probability indicates that the player has a 2/3 chance of initially choosing a goat. Players who unconditionally stick to that choice therefore have only a 1/3 chance of winning the car. Players who unconditionally switch get the opposite of their original choice, so they have a 2/3 chance of winning a car.", appears to me to be illogical. If they unconditionally switch they still have a 1/3 chance. --Candy (talk) 04:41, 6 April 2009 (UTC)
- We're likely deleting this paragraph anyway (see just above), but why do say it's illogical? Unconditionally switching means deciding to switch before the host opens a door knowing that the host will open a door. If players who stay win 1/3 of the time, since there are only two closed doors at the end players who switch must win 2/3 of the time (right?). -- Rick Block (talk) 13:21, 6 April 2009 (UTC)
- Quite so Candy. When I added this bit it said "Players initially have a 1/3 chance of choosing the car and a 2/3 chance of choosing the goat. Players who stick to their original choice therefore have only a 1/3 chance of winning the car (and a 2/3 chance of getting a goat). Players who switch always get the opposite of their original choice so they have a 2/3 chance of getting a car (and 1/3 chance of getting a goat)", but this is Wikipedia. Martin Hogbin (talk) 21:31, 6 April 2009 (UTC)
- Let me go to the source perhaps of the problem with this 1/3 and 2/3. In the reference, [3], there is a statement:
- "Using the “stay” strategy, a contestant will win the car with probability 1/3, since 1/3 of the time the door he picks will have the car behind it. On the other hand, if a contestant plays the “switch” strategy, then he will win whenever the door he originally picked does not have the car behind it, which happens 2/3 of the time."
- The 2/3 is not the probability of winning after a goat is revealed. It is also not the probability of winning if the person simply decides to change their mind before any more information is revealed It is referring to the "switch strategy" defined in the article. Therefore, I continue to contend that the statement I quoted earlier in this Wikipedia article is incorrect and illogical. It appears, to me at least. to be taken out of context. --Candy (talk) 23:57, 6 April 2009 (UTC)
- I want to stipulate that in the referred textbook, the authors also put it straight, that the "unconditional" solution is, allthough logically a sound reasoning, not addressing the posed question. The question, they argue, needs conditional probabilities to be answered. BTW: the problem posed is our MHP!.Nijdam (talk) 16:26, 7 April 2009 (UTC)
- The 2/3 is not the probability of winning after a goat is revealed. It is also not the probability of winning if the person simply decides to change their mind before any more information is revealed It is referring to the "switch strategy" defined in the article. Therefore, I continue to contend that the statement I quoted earlier in this Wikipedia article is incorrect and illogical. It appears, to me at least. to be taken out of context. --Candy (talk) 23:57, 6 April 2009 (UTC)
- Of course you're right, but the statement is also right. The "unconditional" part means players who make the decision to switch or not BEFORE a goat is revealed and do not "simply decide to change their mind". If the decision to switch or not is made AFTER knowing which door was opened showing a goat then the problem must be solved conditionally. --67.193.128.233 (talk) 14:30, 7 April 2009 (UTC)
- Why are you saying Candy is right? Her statement "If they unconditionally switch they still have a 1/3 chance" clearly indicates that her misunderstanding is not as subtle as you're making it out to be. In the context of the statement, there's only one door that can be switched to – nobody is talking about "changing your mind" before the host opens a door; if that's not clear enough, it could be fixed, but it's not "illogical". Dicklyon (talk) 14:35, 7 April 2009 (UTC)
- It makes no difference why the players switch, when they decide to switch, what the host does (within the standard rules), or what new information they may or may not have received after they have chosen their door. Players who switch have a 2/3 chance of winning. That is all there is to it.
- This is not the same as the MH problem as it is formulated by Morgan. To make the distinction clear, consider the extreme case where, after the player has chosen their door, the host says where the car is situated. Regardless of this fact, players who switch still have a 2/3 chance of winning. This statement refers to players in general not one particular player.Martin Hogbin (talk) 22:08, 7 April 2009 (UTC)
Can we not squabble about pointless things? We agreed to delete the paragraph from the intro. I just deleted it. This issue is now moot. -- Rick Block (talk) 00:53, 8 April 2009 (UTC)
- We have all refrained from edit waring over the content, preferring to try to reach a consensus by discussion. I certainly did not agree to the deletion of that paragraph. Martin Hogbin (talk) 08:05, 9 April 2009 (UTC)
- Martin - The suggestion to delete this paragraph had not been opposed by anyone. For reference, the paragraph said this:
- Simple probability indicates that the player has a 2/3 chance of initially choosing a goat. Players who unconditionally stick to that choice therefore have only a 1/3 chance of winning the car. Players who unconditionally switch get the opposite of their original choice, so they have a 2/3 chance of winning a car.
- My reason for suggesting we delete it is because the lead already says the player should switch and that doing so doubles the probability of winning the car. Adding this solution but not the expert discussion about this solution violates NPOV. Rather than get into this in the lead, I think it's far better just to state what the result is rather than any particular solution method. We can certainly discuss this further if you'd like, however the point of the lead is to summarize the entire article so it clearly must not favor one POV over another. -- Rick Block (talk) 14:18, 9 April 2009 (UTC)
Weasels ahoy!
"Nevertheless, some statisticians cricitize the solution as being incorrect for the problem as stated..." needs both a citation for specification. --Candy (talk) 23:21, 6 April 2009 (UTC)
- No, they are answering a different question. Martin Hogbin (talk) 22:10, 7 April 2009 (UTC)
- Morgan certainly do criticize the simple solution and they are cited throughout the article. Martin Hogbin (talk) 09:32, 8 April 2009 (UTC)
- My suggestion above (see #Outline changes) is to delete this section and incorporate the experimental validation parts in the previous section. I believe the remainder is sufficiently covered in the current "Conditional solution" section. Dick said above the current structure works better, with the "criticism" section, what you want to call it, making the transition to the more complex analysis. Are there any other opinions on deleting the criticism section? -- Rick Block (talk) 00:47, 8 April 2009 (UTC)
- I do not mind the criticism leading to the academic solution but I object to the simple solution being presented as in any way inferior to or less rigorous than the academic solution, it simply answers a different question. I also believe that there should be something to indicate the limited circumstances (still being discussed on the arguments page) under which the academic solution applies. Even considering only the Parade statement, there are many ways the problem can be formulated. To some of these the academic solution applies, to others the simple solution, and to others yet more complex solutions.
- It is the simple formulation and solution that makes this problem notable and of interest to the general public, and that formulation should have a substantial, clear, and convincing section of its own. Martin Hogbin (talk) 09:32, 8 April 2009 (UTC)
- This is my point as well, sort of. The simple solution needs to be presented as a solution; if there are sources that comment on how "rigorous" it is, that can follow, but we can't say it's somehow less without saying who says so. Even saying it solves a different problem is the opinion of its critics, not of its adherents, typically, so needs to be presented as such. Dicklyon (talk) 15:24, 8 April 2009 (UTC)
- There we go again! Nijdam (talk) 16:03, 8 April 2009 (UTC)
- What is the meaning of ...Imagine that you chose Door 1 and the host opens Door 3, which has a goat. He then asks you "Do you want to switch to Door Number 2?' Any idea?Nijdam (talk) 16:14, 8 April 2009 (UTC)
- Firstly Nijdam let me point out that, like Morgan, you have misquoted the original question which, with my emphasis, actually says ,'You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No.3'. The door numbers are just given as examples, the questioner surely does not want an answer that applies only to the specific case that the host has opened door 3.
- This is my point as well, sort of. The simple solution needs to be presented as a solution; if there are sources that comment on how "rigorous" it is, that can follow, but we can't say it's somehow less without saying who says so. Even saying it solves a different problem is the opinion of its critics, not of its adherents, typically, so needs to be presented as such. Dicklyon (talk) 15:24, 8 April 2009 (UTC)
- Secondly let me quote from the commentary by Prof R G Seymann at the end of the Morgan paper. He says, 'Without a clear understanding of the precise intent of the questioner, there can be no single correct solution to any problem' (my emphasis again). Note that it is the intent of the questioner that we should consider. The original question was a comment from a reader of a general interest magazine not a question in a statistics exam. My guess is that what the questioner really wanted to know was whether it is generally better to swap doors on the show, in other words the unconditional problem That quotation from Seymann's commentry should be written in bold at the top of this article. Martin Hogbin (talk) 21:17, 8 April 2009 (UTC)
[Outindented]The above qouted wording come fom the (more exact) formulation of the problem in the article itself. It is on this formulation I gave - it seems ages ago to me - my reaction. And right I was, as it turns out. There is the original formulation of the question by Whitaker. It is also in the article. The reformulation was merely meant to get rid of the unknown strategy of the host, but it also made the doors (more) explicit. It is an interesting question why some people, who understand (in the mean time) the nature of probability and conditional probability, want to maintain the "simple solution". Maybe it is psychological. Once thought one understood the 2/3 chance instead of the 50/50, one is reluctant to admit it was on false grounds. And hence the problem has to be adapted, as to fit the simple solution. Let us face the practical situation: the player is on stage, she points to door and another is opened. The player knows her situation, and in this situation she has to decide. If we decide for her, we formulate for each possible situation, the decision. Only in our thoughts can we imagine a door is opened, without us knowing which one. In the practical situation it would mean, the player points to a door, Monty opens a door, but the player is blindfolded, so doesn't see which one. Why opening a door if she is not allowed to see it? Is she allowed to use the information, given by opening a door? If yes, she will give a conditional answer like: if door x is opened then ... If she is not allowed to use the information, then don't bother about opening a door. Even don't bring it up, it hasn't happened as far as the player is concerned. Let me finally repeat, that when this whole - in my opinion (POV) too lengthy - discussion started, it was about the more exact formulation in which the door numbers were given. And in my opinion (POV) the problem is only of interest when the player sees the opened door. Nijdam (talk) 06:38, 9 April 2009 (UTC)
- The question that you are interested in is the academic version as formulated by Krauss and Wang. That is fine, I have no objection to that but there is another much more notable question, that posed by Whitaker, which is what this article should about. Kraus and Wang have clearly formulated the question to make it unambiguously conditional, the academic question, but that is not the the question that will be of interest to most of our readers. This is what I have been saying all along, there are two distinct classes of ways to formulate the question, neither is any more correct or rigorous than the other, they each interpret the question differently. If the question is formulated as K an W do then it is necessarily conditional, if on the other hand, we take it that the questioner meant to ask an unconditional formulation of the question, or that he did not intend to identify the doors, or that he assumed that the host would act randomly, then the unconditional solution is correct. In the article we should give both solutions with an explanation of which class of formulation each is applicable to. You my be more interested in the academic solution, I am more interested in the popular solution. Let us work together to give excellent examples of each. Martin Hogbin (talk) 08:00, 9 April 2009 (UTC)
- Martin - From what I can tell, what you're suggesting is contrary to Dick's intent which is that the popular solution be presented without qualification. He's not arguing that the question is interpreted differently or that the popular solution is "correct", but that the popular solution is the popular solution. This perspective completely avoids any need to talk about exactly what problem those who publish the popular solution think it is solving. We frankly don't care. We don't need to justify its correctness. It is published in reliable sources, so we include it here clearly identified in some way (and attributed to one or more sources that have published it). The job of the article is not to convince anyone that this solution is correct, and whether any of us as individuals think it is or not is completely irrelevant (to the editing process). Discussions about the correctness of what reliable sources say or what the "truth" is generally have no particular place in Wikipedia - they continually come up with regard to this problem which is why there's now a Talk:Monty Hall problem/Arguments page.
- Nijdam - ditto the "expert" POV. I've suggested this before, but from an academic viewpoint you should view this article more like a summary of the literature than anything else. We can certainly say "popular sources say this" and "experts say the popular sources are not quite right, and say instead ...", but unlike a literature summary we can't really take a stance. If the article faithfully (neutrally) says what both the popular sources say and what the experts say (including what the experts say about the popular sources) anyone reading the article will be able to draw their own conclusions.
- Dick - does this roughly capture what you're trying to do here?
- -- Rick Block (talk) 14:04, 9 April 2009 (UTC)
- I do not think that Dick is against stating the assumptions under which the popular/unconditional solution is valid and there is no need not to do so. The concept of 'first decide the question' is made clear by the Seymann quote and a clearly unconditional formulation of the problem is given by Morgan (as we have now). I want the unconditional problem not to be seen as the poor relation of the conditional one, it is a problem in its own right and probably the question that Whitaker intended to ask. I think it is important for the unconditional problem to have its own 'aids to understanding' as bringing up the issue of conditionality only complicates the problem further for most people. Martin Hogbin (talk) 17:06, 9 April 2009 (UTC)
- I interpret what Martin is saying is that he wants to "clarify" the problem in such a way as to justify that the popularly presented solutions are correct. In my opinion this would be WP:OR. If we're not going to simply present the expert POV (which I think would be perfectly justifiable - it is a math problem after all, so saying anything other than what the most reliable math sources have to say about it seems kind of silly to me but I understand Dick's NPOV argument), then the popular solution needs to stand by what the popular sources say. They never (as far as I have seen) "clarify" the problem. They generally use a statement like the Parade statement and proceed to say "and the answer is ...". Any clarifications or justifications would need to be sourced. If we're going to go this "it's a POV issue" route, then we need to keep our opinions out of it and say what the sources say. This means no more in the case of the popular solution (specifically, no justifications or clarifications unless these can be sourced), and no less in the case of what the math sources say (specifically, no omitting what they say about the popular sources). -- Rick Block (talk) 18:43, 9 April 2009 (UTC)
Let's Eliminate the "Criticisms of the traditional solution" section
I'm once again returning from the arguments page.
On those pages, particularly the last couple of sections, you will see that the two main opponents to meaningful changes to the article are out of objections. They have no game. It would be almost comical, but I've invested dozens (hundreds?) of hours in this. But, read it and decide for yourself.
I propose we remove the "Criticisms of the traditional solution" section. I'm not going to repeat that section here. It says that in some cases the host revealing a door might provide the player more information...
Of course, that's ridiculous. The Contestant, and anyone else not associated with the program, do not know the original location of the car. Nor does anyone outside of the program know of any host behaviours. Of which none are described in the problem.
Then it says, "Under more general conditions, however, a more general solution is needed (Morgan et al. 1991).". Which, while published, may not have enough merit to discredit the previously provided solution.
I would also like to see the Combining Doors moved from 'Aids to Understanding' to the 'Solutions' section. I think this is far and away the best representation of why it's 1/3 vs 2/3 and not 1/2 vs 1/2. It's already in the article, and has passed muster for 2 or 3 FA reviews.
There may be other statements that negate the validity of the Solution now in place. I'd like to remove all of these as well. Glkanter (talk) 20:21, 8 April 2009 (UTC)
And I would take out the 'equal goat door constraint' from the existing Combining Doors solution. Only 1 of 4 sources mention it, and there is no other mention of host behaviour in the MHP. Glkanter (talk) 20:28, 8 April 2009 (UTC)
- Most of my students understood the complete problem and (conditional) solution in no more than 5 minutes. Of course some didn't: they failed the exam.Nijdam (talk) 06:44, 9 April 2009 (UTC)
Maybe a way forwards
Although the details are not yet agreed it is clear that there are two classes of formulation of the problem, to avoid further argument here let me call them the conditional and the unconditional formulations. It is perfectly reasonable to take Whitaker's original question to be asking the unconditional question. On the other most academic sources formulate it conditionally.
Why do we not have two sections, conditional and unconditional, where those interested in that particular formulation take the responsibility for deciding that section's format and structure? Each section should indicate precisely the assumptions on which their solution applies. The normal standards of WP quality should apply to both sections. Martin Hogbin (talk) 08:18, 9 April 2009 (UTC)
- We could do that. My suggestion was to segue from the unconditional to the conditional via a short statement that some mathematicians have found the former lacking; I did this with a criticisms section, but it could just as well be an introductory sentence in the conditional solution section. Furthermore, while I'm happy to refer here to the "unconditional" solution, I wouldn't call it that in the article, as the sources that present it as the solution don't generally call it that, and as the term frames it with respect to the other solution; it's really not at all clear what "unconditional" means until you specify what particular events you're not conditioning on, and those particular events don't come up until the conditional section; it's silly. Dicklyon (talk) 14:38, 9 April 2009 (UTC)
- As you might expect, I agree with Glkanter that the unconditional section should not be seen as the poor relation of the conditional section. The unconditional formulation is probably what Whitaker actually meant to ask and it certainly is the notable problem. Martin Hogbin (talk) 16:52, 9 April 2009 (UTC)
- As long as the formulation of the problem permits the simple solution as a solution it's fine to me. Otherwise it should be discredited as being incomplete or even wrong. Nijdam (talk) 19:04, 9 April 2009 (UTC)
- Yes, of course. Martin Hogbin (talk) 21:11, 9 April 2009 (UTC)
- As long as the formulation of the problem permits the simple solution as a solution it's fine to me. Otherwise it should be discredited as being incomplete or even wrong. Nijdam (talk) 19:04, 9 April 2009 (UTC)
- As you might expect, I agree with Glkanter that the unconditional section should not be seen as the poor relation of the conditional section. The unconditional formulation is probably what Whitaker actually meant to ask and it certainly is the notable problem. Martin Hogbin (talk) 16:52, 9 April 2009 (UTC)
The key to peaceful coexistence seems to be to find a way to segue into conditional probabilities without implying that the simple solution lacks something that it ought to have. Here are two suggestions for the transition:
- Remark that analysis via conditional probabilities allow generalization to related but different problems, such as if we have knowledge of Monty's bias towards different doors. Then show how the c.p. analysis gives the same result as the simple analysis, and afterwards briefly discuss other possibilities.
- Note that the first solution is simple and clever, but requires a creative insight (namely, that under appropriate assumptions it is irrelevant whether you decide before or after being given the choice). What follows is a less creative argument for the same answer that does things by the book without clever shortcuts: (bla bla bla)
The second one is the one I like best, but might not be acceptable to the conditional-probabilities camp. –Henning Makholm (talk) 22:56, 9 April 2009 (UTC)
- Sorry, I don't care for either. Maybe there is no segue. Rather, an intro that says here are two different techniques, both published. Then present them. Glkanter (talk) 23:12, 9 April 2009 (UTC)
- Your contribution would be more helpful if you explained what you think is wrong with the proposal rather than just rejecting them. –Henning Makholm (talk) 23:26, 9 April 2009 (UTC)
- For #1, I don't believe there is such a thing as knowledge of Monty's bias. Not outside the show's production team, anyways. (see the Arguments page). #2, I disagree with your characterization. Because the problem is simple, the solution is simple. And there's no shortcuts. There's just no extraneous bs. Glkanter (talk) 23:53, 9 April 2009 (UTC)
- G, while I sympathize with the POV that the simple solution is all that's needed, it's not all that's out there. We need to report the other interpretation and why people use the conditional approach; and do so in their terms, not ours. I agree that a contestant isn't likely to have a model of Monty's bias, and that it's peculiar to interpret the problem as if she has, nevertheless, it's what they do, and they publish in top journals, so it should get good coverage. It just shouldn't trump the simple POV. Dicklyon (talk) 00:30, 10 April 2009 (UTC)
- I agree that the Morgan pov is published and deserves some mention. To help determine how much, let's talk about the Contestant's knowledge of a host bias. First, there's no such item mentioned until Morgan. Second, the only reasonable presumption is that once the bias is created, the Contestant becomes aware of it. So, it becomes a new premise, making it a new puzzle. Check out Rick Block's 'forgetful host' bias on the Arguments page. It's really "Deal or No Deal". And, three out of the 5 premises change. How is that relevant to the MHP? Lastly, how did the Contestant become aware of any such bias? Does the production team tell him? For what purpose? Heck, in the US that would be against the law. So, yes, it's published. Does it make much sense? Not to me. Not at all. So, mention it if we must, but severely limit it's prominence. Glkanter (talk) 00:47, 10 April 2009 (UTC)
- Neither sounded great to me, either, but I'd have to see them done out. What matters most to me is that the statements be sourced. If Morgan or someone uses a statement like one or the other of these, and we can attribute it him, or someone else, it will be OK. But since they both sounded like something you made up, it's hard to say yet. Can we follow a source? Dicklyon (talk) 23:45, 9 April 2009 (UTC)
- I like the concept involved in Henning's option 2 in that it extends the applicability of the unconditional solution to special conditional cases. As the unconditional solution is the really notable one I think the more we make of it the better.
- To avoid confusion we should have two sub-sections in the 'unconditional' section. The first treats the problem strictly unconditionally and the second considers intuitive extensions of the treatment to cover the appropriate conditional cases. This then naturally leads to further discussion of the more general conditional case.
- On thing I would also like to clear up, probably on the arguments page, is the matter of problem style. I am not an expert on statistics but it seems to me that there are various styles in which a question can be posed. In the formal style we are given a problem, to be answered only on the information given in the question; what any of the characters in the problem may or may not know is irrelevant. The more traditional style is to pose the question from a particular point of view or state of knowledge of an individual involved in the problem itself. Common statements of the 'three prisoners' problem are good examples of this approach. Would somebody who is an expert on the subject like to comment on my understanding, either here or on the arguments page. I think much of the argument about this topic results from failing to adequately make the above distinction. Martin Hogbin (talk) 10:28, 10 April 2009 (UTC)
Is there anyone arguing we should keep the "Criticisms of the popular solution" section? Like I suggested above, if we move the first three sentences (up to but not including "Nevertheless ...") to the "Popular solution" section I think the rest is covered adequately in the current "Conditional solution" section. -- Rick Block (talk) 02:46, 10 April 2009 (UTC)
- I'm OK getting rid of the section and moving the content; however, the first sentence is really Morgan et al.'s criticism and narrowing of the solution, and doesn't belong as part of the solution; but it can be modified to work, I think. You want me to work on it? Dicklyon (talk) 04:11, 10 April 2009 (UTC)
- I'm mostly just checking to make sure no one is going to complain if the section is deleted. We'll need to talk about the specific content at some point (completing deleting the first sentence for now would be OK with me, but it's the lead-in to the second sentence so ...), but first things first. -- Rick Block (talk) 04:43, 10 April 2009 (UTC)
- I think it is best to leave the lead until last. As you have said, it should be a summary of the article as a whole. In that case it might as well be left as it is with the intention of rewriting it when the article changes have been completed, but I do not care much either way. Martin Hogbin (talk) 10:04, 10 April 2009 (UTC)
- I'm mostly just checking to make sure no one is going to complain if the section is deleted. We'll need to talk about the specific content at some point (completing deleting the first sentence for now would be OK with me, but it's the lead-in to the second sentence so ...), but first things first. -- Rick Block (talk) 04:43, 10 April 2009 (UTC)
I have changed the intro to the popular solution section to show it as a correct solution to a different formulation. Is everyone OK with this? Martin Hogbin (talk) 16:10, 10 April 2009 (UTC)
- Absolutely not. In my opinion, the problem statement you've included is not anyone's usual understanding of the Monty Hall problem. If you want to claim that it is, I respectfully request that you provide a reference to some published source that actually says it is common to interpret the problem this way. Without a source that says something like "this is how the problem is usually interpreted" (which, BTW, is the exact opposite of what Morgan et al. say - so using them to justify this problem statement is perverse) this claim is simply your own WP:OR. -- Rick Block (talk) 18:40, 10 April 2009 (UTC)
- Morgan refer to this statement as 'the unconditional problem' . They also say in their conclusions that 'The unconditional problem is of interest too...'. The statement that I quoted obviously is a possible interpretation of the problem and Morgan say that it is of interest, what more do I need? Martin Hogbin (talk) 19:25, 10 April 2009 (UTC)
- My suggestion, which seems to have some support, is for the unconditional solution to stand in its own right as a solution to the unconditional problem (and special conditional cases). In order to do this we need a statement of the unconditional problem and it would be best to use one from a reliable source. Morgan have just such a statement and I do not see why we cannot use it, purely as a published statement of the unconditional problem. We do not have to suggest that Morgan themselves interpret the problem unconditionally. Alternatively, does anyone know of another unconditional problem statement that we could use? Martin Hogbin (talk) 09:24, 11 April 2009 (UTC)
How about we delete the 4th paragraph of the Sources of Confusion section?
Here's what it says:
"Another source of confusion is that the usual wording of the problem statement asks about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open if the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3. In its usual form the problem statement does not specify this detail of the host's behavior, making the answer that switching wins the car with probability 2/3 mathematically unjustified. Many commonly presented solutions address the unconditional probability, ignoring which door the host opens; Morgan et al. call these "false solutions" (1991)."
This is just another Morgan pov. And it adds a non-existent premise, so it's not even addressing the MHP. Glkanter (talk) 10:16, 10 April 2009 (UTC)
- I have started to address the point you (we) make. I have added a quotation from the Seymann comment at the end of the Morgan paper. No one seems to have objected to this, which does not surprise me as it is a quote from a reliable source making a point that cannot really be contested. Martin Hogbin (talk) 10:45, 10 April 2009 (UTC)
- You might like to look at my above remark about question style. I believe that there are two styles of asking probability problems which must be approached in different ways. I am waiting for someone who knows about such things to confirm this as I believe this fact may be responsible for much of the argument here. Martin Hogbin (talk) 10:48, 10 April 2009 (UTC)
- Oh sure, I read it. This issue came up earlier this week. It immediately became muddled, so I started using the phrase "anyone not associated with the production of the show". That covers the Contestant and all of us 'observers'. I think it only arises with 'host behaviour', which is a euphemism for 'new premise' (and, therefore, a different problem). And 'host behaviour' doesn't exist in the MHP, beyond revealing a goat and always offering the switch. Please, don't get me started. BTW, do you agree with my suggested deletion? Glkanter (talk) 11:06, 10 April 2009 (UTC)
- I think the whole article needs to be restructured to give at least equal prominence to the 'unconditional' formulation. This would include splitting the 'Sources of confusion' section in two, one to deal exclusively with the 'unconditional' problem. AS it is now it only adds more confusion. How to start this process, if everyone agrees, I do not know.
- I think you should discuss the question style issue but probably on the arguments page. I believe that many of the arguments her come from mixing the two styles. Martin Hogbin (talk) 11:23, 10 April 2009 (UTC)
- I'm not much interested in beginning that discussion. I think it's just one of the various obfuscation techniques.
- Quite the reverse. I am trying to clarify things. Once you understand how formal probability problems are treated you can see how the trick is done. Martin Hogbin (talk) 14:55, 10 April 2009 (UTC)
- I just read your new section. Very interesting, very well written. I hope you're right, that this will help to properly define the problem, in order that it can be properly solved. You have much more patience than I do. I've been at this almost 6 months (although I took a two month break), and I dread the thought of this new discussion with the same cast of editors. I'll probably sit it out. But, if it codifies that new premises make new problems, that alleged 'host behaviours' are new premises, and that for this Wikipedia article we're only discussing the MHP, well, then maybe it's worth it. But it's still a shame that it's necessary. What about deleting the 4th paragraph of the Sources of Confusion section? Glkanter (talk) 15:58, 10 April 2009 (UTC)
- Thank you for your support, there have been no serious challenges to what I have said so far. Regarding sources of confusion, I believe that it is essential to have a separate section for the unconditional/traditional/simple solution before we can address this point and there seems to be something of a consensus to do this. There is plenty of confusion about the unconditional problem, that is why the problem is notable, and it does nothing to reduce this confusion to discuss the conditional problem. There is plenty to say about the conditional problem also but that should be said in a separate section. Martin Hogbin (talk) 09:17, 11 April 2009 (UTC)
- In light of the fact that there have already been 37 edits to the article in April, I think the process has already started. You've mentioned numerous times that neither of the competing approaches can claim sole bragging rights. In that vein, I'd like to remove all the statements that 'weaken' the unconditional solution. Glkanter (talk) 11:48, 10 April 2009 (UTC)
- I disagree with the suggestion to delete this paragraph. It's impeccably sourced and is one of the most significant points in the entire article. Would anyone prefer the "The distinction between the conditional and unconditional situations here seems to confound many" to the "false solutions" quote? You two have both amply demonstrated how profoundly confounded you are, so let's all just assume you violently disagree with this and let others weigh in with their opinions. -- Rick Block (talk) 13:31, 10 April 2009 (UTC)
- The accusation that I am profoundly confused is rude and unjustified. I have demonstrated on the arguments page that I fully understand the issue of conditional probability. Perhaps you should continue with discussion of the subject matter rather that try to make your point by attacking editors who disagree with you. Martin Hogbin (talk) 22:05, 11 April 2009 (UTC)
- I agree with Rick on this, too. However, it might make sense to make it very clear that this is Morgan et al's interpretation; if we state "the usual wording of the problem statement asks about the conditional probability" as a fact verifiable by Morgan, as opposed to an opinion thereof, that should be fixed, or made more clear. Dicklyon (talk) 05:15, 11 April 2009 (UTC)
- Now that I look at, though, it's really not clear what to report, or whether it belongs in the "sources of confusion" section. Rick, can you give us a quote or two? Does Morgan reall refer to this as a source of confusion? Or is it just his statement of the problem he's solving? Same with Gilman. Do they present it the same way? Can we rephrase it properly attributed as their interpretations and/or opinions, instead of as a statement that's verifiable in their papers? Dicklyon (talk) 05:25, 11 April 2009 (UTC)
- If Morgan is right, that the unconditional solution is a 'false solution', how does he explain the experts that have used it subsequent to his criticism? Like Devlin, for example. http://www.maa.org/devlin/devlin_07_03.html Devlin seems pretty aware of the MHP's history. I wonder why he didn't mention Morgan's 'equal goat door constraint'? It should be his duty, yes? My guess? To the professional community, Morgan is like the crazy old uncle hidden in your attic. Glkanter (talk) 22:54, 11 April 2009 (UTC)
- In this particular instance, I guess my only point is that as a 'Source of Confusion' the article includes Morgan's opinion that the unconditional solution is a 'false solution'. That would seem to be contradicted by Devlin's (and others') use of it as their sole method, subsequent to Morgan's paper.
- In the larger scheme of things, it's been stated repeatedly by the Morganians that absent any direct published criticism of Morgan, his is the final word. I'm just showing that there have been unconditional solutions published since Morgan, which, while not a full on smack-down, show disagreement with his conclusions. I presume it would be unseemly for these professionals to get into a public argument, so as you suggest, they ignore him. I wish we could do the same with the article. Glkanter (talk) 02:03, 12 April 2009 (UTC)
- It's no problem reporting different points of view, even if they're mutual contradictory, without deeming one final. We can report the "source of confusion" if Morgan called it that. What worries me here though is that Morgan didn't call it that, and that it's really an editor's interpretation to call it a source of confusion. Seems to me I had a copy of Morgan, but now I can't find it. Does anyone have one they can send me? Dicklyon (talk) 02:58, 12 April 2009 (UTC)
- I'm traveling and my participation will be somewhat limited over the next week or so. Between the archives of this page and the /Arguments page, I think most of the relevant passages from the Morgan et al. paper have already been quoted. The main points are:
- 1. The usual statement of the problem (such as the one from Parade) asks about the conditional probability of winning by switching given that the host has opened a particular door.
- 2. The popular solutions do not address this question but address a different question (e.g. the success of a pre-selected "switch strategy")
- 3. The answers to these questions can be different unless the host is constrained to open a randomly selected door in the case the player's initially selected door hides the car.
- A quote from the paper concerning what they label as "F1" ("false solution" #1) is at Talk:Monty_Hall_problem/Archive_9#Wrong explanation. Note in particular the phrase "The distinction between the conditional and unconditional situations here seems to confound many". So, yes, they're directly saying this is a source of confusion. Gillman's comments are similarly quoted in the same thread in the archive. The Grinstead and Snell book says something similar as well (it's freely available online). -- Rick Block (talk) 05:17, 12 April 2009 (UTC)
- Thanks, Rick, that's very helpful. I've added that brief quote from that quote into the relevant paragraph in the article, and rephrased it to more clearly attribute the interpretation to these authors. When you get a chance, let me know if that seems OK. I believe it is much better than the previous statement that a "source of confusion is that the usual wording of the problem statement asks about the conditional probability," which is not really verifiable as a fact. Dicklyon (talk) 06:08, 12 April 2009 (UTC)
- I think I agree and understand their main points that you summarize above, except that the "other question" doesn't really require the player to decide on a strategy before a door is revealed; it really only requires that the player's decision not be influenced by which door is opened, right? For example, a player new to the game may not know that she's going to be offered a chance to switch until after a door is opened and the offer is made; then all the rules and such having been explained, she can choose to switch or not; having no statistical model of which door the host might open when given a choice, she might sensibly ignore that bit of information and still solve the unconditional problem, yes? So why are still guys (or Gillman at least) so insistent on the bold before a door has been opened? Dicklyon (talk) 06:08, 12 April 2009 (UTC)
- From my standpoint, this hasn't gotten any better.
- "That is, they, and some others, interpret the usual wording of the problem statement as asking about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open when the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3."
- Just once, I'd like to see Morgan's POV made without giving a host behaviour. Because I believe the act of giving a host behaviour makes it a different problem, and no longer the MHP. Without a host behaviour, it 'averages 2/3'. Unconditionally, it is 2/3.
- And this is clearly Morgan's POV: "In its usual form the problem statement does not specify this detail of the host's behavior, making the answer that switching wins the car with probability 2/3 mathematically unjustified. Many commonly presented solutions address the unconditional probability, ignoring which door the host opens; Morgan et al. call these "false solutions" (1991)." For example, Devlin says it's unconditionally 2/3. Is Devlin guilty of providing a 'false solution'?
- I don't understand; how can Morgan's POV be explained without reference to a model of the host behavior? The host behavior is what he's talking about conditioning on and exploiting a probabilistic model of. Are you just saying it's in the wrong place in the article? That the "confounding" concept is relevant only to one problem interpretation? I think that's clear now, but maybe not. Dicklyon (talk) 15:11, 12 April 2009 (UTC)
- Imho, Morgan is OK to say "because no host behaviour has been described as a premise, using the conditional solution can only provide a result that in any one instance is between 1/2 and 1, and averages 2/3". But the moment he says, 'take, for instance, the following behaviour...', he is adding a premise regarding the hosts behaviour. And still undecided is whether the Contestant, or whoever's 'state of knowledge' we're talking about, knows of this. To me, that is a new problem. Did you see in the arguments page where 'the forgetful host' behaviour actually turned out to be "Deal or No Deal?" 3 out of 5 'agreed upon' premises changed. That makes it a different problem. This is what they taught in my college. I assumed that was a universal principal.
- This is not a 'Source of Confusion' for anyone who is using the unconditional interpretation and solution. It is the reason for having the two different interpretations and solutions, as proposed by Martin. I'm suggesting that a section explaining why there are two solutions is the only appropriate place for this criticism. Glkanter (talk) 19:00, 12 April 2009 (UTC)
Well, maybe it needs to go someplace else. Because it doesn't belong in the Sources of Confusion. Glkanter (talk) 22:06, 13 April 2009 (UTC)
- This gets back to what problem are we solving? In nearly all phrasings of the problem the player chooses a door, then the host opens a door, and then the player is asked whether she wants to switch and we're asked to think about the probability of winning by switching. This much makes it a conditional probability problem (and calling this a "POV" seems like kind of a stretch - it's more like a simple fact that most people are unaware of). The "unconditional" solutions ignore which door the host opens, which produces the correct answer for this question if and only if the host opens one of the remaining doors with equal probability in the case the player has initially selected the car. If we're asking about the probability of winning by switching after the host has opened a door, as a math problem the host's preference in this case (where the player has initially picked the car) always affects the answer. In the Parade version of the problem the host's preference was not specified - which makes it unknown, rather than 1/2. If it is, say q, then the chances of winning by switching are 1/(1+q), i.e. somewhere between 1/2 and 1 (not simply "2/3", as it is when q is 1/2). Morgan (and Gillman, and others) are so insistent about this because "solving" this problem unconditionally introduces an assumption that was not in the Parade version of the problem statement (which is the version they both discuss). Their POV is that anyone approaching the problem unconditionally is confused about the nature of the problem and (for the Parade version) is introducing an assumption that is not stated. -- Rick Block (talk) 14:05, 14 April 2009 (UTC)
Dicklyon, is it OK to delete the 4th paragraph now? Glkanter (talk) 11:06, 18 April 2009 (UTC)
- It is not OK with me. -- Rick Block (talk) 16:57, 18 April 2009 (UTC)
- I agree it's not OK to delete it. It represents, as Rick says, the POV that "that anyone approaching the problem unconditionally is confused". However, that's not a confusion about the solution, but about what the problem is, and it's probably a minority POV, so probably belongs more in the conditional section, or a transition to that section, rather than in a place were it appears to be trying to say something about why people are confused in their analysis of the more common interpretation of the problem. Dicklyon (talk) 17:36, 18 April 2009 (UTC)
Popular solution diagram
The popular solution diagram should be as simple as possible and should make a clear as possible the fact that the player has a 2/3 chance of winning by swapping. Although, in the case where the player has originally chosen the car, the host does have a choice of two goats, I do not believe that it is helpful to show this in the diagram, it would be better to simply state that the host opens one of the goat doors.
The problem with showing the option of the two goats is that it reinforces the view that there are four equal probability options, two of which win the car, thus leading the reader to believe that the chances of winning by switching should be 1/2. Also, the showing of two doors may give the impression that it matters which door the host opens, which in the unconditional case, it does not.
And please, can we drop the silly face! Martin Hogbin (talk) 10:44, 11 April 2009 (UTC)
- Do you have a simpler illustration? Or a source we can follow to make one? Dicklyon (talk) 01:32, 12 April 2009 (UTC)
- Sorry , I do not but I might try to Photoshop the existing one, if you agree. Martin Hogbin (talk) 23:14, 12 April 2009 (UTC)
Congrats
Congrats on the FA; I read it and this article is a very interesting read! However, I have one problem with it. Shouldn't the article use inline citations? ResMar 22:39, 12 April 2009 (UTC)
- It uses the alternative WP:HARVARD style. Dicklyon (talk) 23:41, 12 April 2009 (UTC)
Popular solution door numbers.
I have deleted this from the 'Popular solutions section, 'In the popular analysis, the probability of the originally chosen door hiding hiding the car or a goat is typically considered without respect to door numbering'.
Before it is reinserted it should be substantiated as a general statement about popular solutions. Many do in fact refer to door numbers. I would also be interested to know what point the statement is trying to make. The popular solution should be introduced as a solution in its own right, not as a failed attempt at the general conditional solution. Martin Hogbin (talk) 23:25, 12 April 2009 (UTC)
- The point it's trying to make is a distinction from those analyses that focus on the particular door numbers as is they matter; that posit that the host might have a different preference for opening door 2 as opposed to door 3, for example. The door numbers are irrelevant to the way the problem is sometimes stated and the analsys/solution explained, as illustrated by the Mack source I had cited, in which door numbers were never mentioned. The wording "In the popular analysis, the probability of the originally chosen door hiding hiding the car or a goat is typically considered without respect to door numbering" was meant to say that Mack is typical, not that all of the popular solutions don't mention door numbers, but it helps, I think the understand the explanation and the illustration if door numbers are said to be not part of it. It does sound a bit like an OR interpretation, though, so if you don't like it, that's fine. I don't see how you can take it as describing a "failed attempt at the general conditional solution". Dicklyon (talk) 23:40, 12 April 2009 (UTC)
- I do not like that wording because it implies that, although the door numbers are important, they have been ignored in popular solutions. Do you see what I mean? There is the implication that some important information has been ignored. Martin Hogbin (talk) 09:22, 13 April 2009 (UTC)
- That is the implication to me, but anyway I do not see what the statement adds to the discussion. What we need is a clear statement of the unconditional problem. Martin Hogbin (talk) 21:27, 13 April 2009 (UTC)
- Martin - as you know, Morgan et al., Gillman, and Grinstead and Snell all provide problem statements that the unconditional solutions solve. However, none of them are arguing that these problem statements are how the MHP "should" be interpreted. They all suggest these to illustrate how different the unconditional problem statement would be from the usual way the problem is worded.
- Dick - not numbering the doors doesn't make it an unconditional problem. Numbers are usually used just to make it easier to reference "the door the player initially picked", "the door the host opened", and "the unpicked, unopened one". The "POV" that we can or should treat the doors as indistinguishable, effectively making it an urn problem, is (IMO) absurd. The problem clearly describes a game show involving physical doors on a stage which means the doors are distinguishable.
- Both - since the "popular solutions" never seem to exactly clarify what they're talking about it seems like we shouldn't try to on their behalf. Most of them present something like the Parade version of the problem and then proceed to "solve" it using an unconditional approach (right?). If the sources themselves don't clarify what problem they're solving, then we shouldn't either. -- Rick Block (talk) 14:52, 14 April 2009 (UTC)
- I understand what you are saying but I think we can do a little better than you suggest. Morgan, for example, do not tell us what problem the popular solutions are trying to solve but they do say what problem they do in fact solve. For example they say 'F1 is a solution to the unconditional problem, which may be stated as follows...'.
- None of the popular solutions make clear what exact formulation they are solving but there is no reason for us to take Morgan or any of the academic papers as experts in what the question was meant to be. Morgan are ostensibly a reliable source for statistics but not for the interpretation of a reader's question in general interest magazine. As I have said before, if anyone is to be considered a reliable source on this subject it should be vos Savant. Alternatively we might take it that there are no reliable sources on what Whitaker meant (has anyone asked him, assuming he is a real person?). If we take that view, then we should present both the conditional and unconditional problems with their respective solutions without claiming to know which is the 'real' MHP. Martin Hogbin (talk) 17:17, 14 April 2009 (UTC)
- And can what I propose be any worse than the current, 'It is assumed that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door he has chosen'? Assumed by whom? Says who? For what problem formulation? This is just apologist fantasy. Martin Hogbin (talk) 18:21, 14 April 2009 (UTC)
(outindented) I don't know where we stand at the moment with the discussion. It is not our task to find a new formulation of the problem. The way it's presently presented: first Whitaker's question, comment on it, then the more precise formulation of Kraus & Wang, it is fine to me. The next step will be the solutions. In the right formulation the simple explanation may come first, with the additional remark of its shortcoming. Then the (conditional) solution, be it in plain wording, understandable for the average reader. And of course the solution in mathematical form, using Bayes' rule, but not calling it Bayesian analysis, because it has hardly anything to do with a Bayesian approach. Further ...?Nijdam (talk) —Preceding undated comment added 19:13, 14 April 2009 (UTC).
- I do much prefer K&W's paper. At least their problem statement makes clear that the car is initially randomly placed. It also specifies that the host chooses randomly. This leaves the way open for a less apologetic introduction to the simple solution. We could say something like, 'Because the host chooses randomly, no information is given to the player about the placement of the car, thus the unconditional solution applies'. Martin Hogbin (talk) 17:48, 15 April 2009 (UTC)
- Do others agree with this approach? K&W also state that most people make the assumptions that they make explicit, thus their statement has some verifiable claim to be the 'real' MHP. Martin Hogbin (talk) 00:42, 17 April 2009 (UTC)
- I have changed the quotation from K&W to the mathematically explicit version. We have the original vague statement from Whitaker, there is no point in having a second ambiguous version. K&W's exact words on the subject, following this formulation in their paper, are, 'participants still assume the intended rules, even if those rules are not stated explicitly'. This also gives us a much better place to start in considering the 'popular' solutions since the exact question that most people assume that they are answering is made clear.Martin Hogbin (talk) 21:49, 17 April 2009 (UTC)
Why does the Conditional Solution begin with the non-existent 'equal goat door constraint?
As I've been claiming, this, or any host behaviour is a new premise which makes it not the MHP. It seems to me that the Conditional Solution should demonstrate that the answer is between 1/2 and 1, and averages 2/3. Glkanter (talk) 23:36, 12 April 2009 (UTC)
In fact, the entire 2nd paragraph, the tree, and the concluding diagram all rely on the 'equal goat door constraint'. All this does is provide a contrivance where the result is forced to 2/3. Why choose this particular host behaviour? (Not that there should be ANY host behaviour.) Why not show the 'left most door constraint', or the 'host forgets constraint' (aka Deal or No Deal). And maybe this section should include an explanation of how any of these behaviours give the Contestant any knowledge of where the car is? Since they don't, despite what the opening paragraph says. Glkanter (talk) 23:47, 12 April 2009 (UTC)
- If the player has a probabilistic model of the host's behavior, the door opened can give the player some info about where the car might be, different from in the unconditional case if the probabilities are biased. I think they do the equal probs first to show that it gets the same solution to the what's effectively the same problem. Dicklyon (talk) 00:02, 13 April 2009 (UTC)
- But where did the Contestant get it from? It simply doesn't exist without adding a host behaviour premise of some type. (Plus a mechanism for transferring this model into the Contestant's brain. Is this collusion? ESP, perhaps?) Doesn't a new premise make it a different problem than the MHP? One that coincidentally (or not?) has the same result? Isn't this the Morganians entire point on why the unconditional is a 'false solution'? Can't the Morganians make their point without adding unsupported premises? Is it common to give a solution to one problem using a different problem? I'm not familiar with this technique. Glkanter (talk) 00:58, 13 April 2009 (UTC)
- Well, I agree with you that's it's far fetched as an interpretation of the intended problem, and not likely practical in reality, but that's not their point, is it? The Morganians point is that if you can model the probabilistic behavior of the host you can determine the probabilities in a given situation (a given door having been opened), and that if you can't model it then you can't really compute your probability of winning. As I read it, the original problem only asked if you should switch, so you can certainly interpret this as working a different problem; so is providing the 2/3 answer from the unconditional method; the only answer really called for is that you should always switch, and even that one needs more assumptions than are sometimes stated in the problem. Dicklyon (talk) 01:32, 13 April 2009 (UTC)
- Is it just me, or is this as tedious and irrelevent a nitpick as saying, "Since the problem does not explicitly specify which way up the host is, we must also consider the possibility that he is standing on his head for the entire game" ? Honestly, what kind of person, apart from a mathematician who has already studied the problem and knows to think about it, would hear the problem as (originally) stated and not assume the host will choose one of the two remaining doors with equal probability? For that matter, what kind of foolish assertion is "any similar problem in which the (inexplicably necessary, for some people) host behaviour is specified is a totally different problem distinct from the entire idea of the Monty Hall Problem" ? Come on. This is just silliness, right? Maelin (Talk | Contribs) 05:39, 19 April 2009 (UTC)
These discussions are very stimulating to a mathematician! Inspired by them, I have now written two short notes on the Monty Hall problem, plan to merge and rewrite and submit to a reputable journal. I hope that especially the second note might clarify some points. Links: Gill's first attempt, including novel game theoretic approach; Gill's second attempt, comparison of conditional and unconditional approaches. I try to see what can be derived with what assumptions, ideally a mathematician comes up with "necessary and sufficient conditions": "If you do assume X, then Y is true; if you don't assume X, then Y is not true". Nearly there, I think. Gill110951 (talk) 13:16, 21 April 2009 (UTC)
- @Gill: I read your second attempt. Lookes fine to me, and it describes in a plain mathematical way the problem and the analysis. What remains is the connection of the problem in words and the math. Will you try? BTW: your remark above about "necessary and sufficient conditions" puzzles me. Nijdam (talk) 16:16, 21 April 2009 (UTC)
- @Nijdam: I am glad you liked the second note. I was hoping that someone who understands my maths and likes the solution, would themselves build the word-bridge from the original problem formulation(s) to the mathematical analysis. I may do it myself one day, when I work those pdf's into a real paper and offer it for publication somewhere, but it is not going to be very soon.
- Concerning necessary and sufficient conditions, I mean the following. Let's agree that conditional and unconditional Monty-Hall problem can be formulated in terms of a sequence of three probability distributions: the quiz-team's choice of door, the player's choice of door, the quizmaster's choice of door given the preceding two. Let's agree that the quizmaster must open a door revealing a goat. Let's agree that the quizteam's and the player's choice are (statistically) independent of one another. Then everything depends on 1) three probabilities, adding to 1, of the original location of the car; 2) three probabilities, adding to 1, of the player's choice; and 3) for each of three possible locations of the car, two conditional probabilities, adding to 1, that the quizmaster will open each of the other two doors with goats behind them given that player and quiz-team have both chosen the same, particular, door. Taking account of the constraints that probabilities add to one, it follows that by specifying exactly (3-1)+(3-1)+(2-1)+(2-1)+(2-1)=7 input probabilities, everything else is determined, including the output probabilities of interest. Certain combinations of values of those 7 input probabilities imply that Prob(win|switch)=2/3. Other combinations imply that Prob(car is behind 3|player chose 1 and QM opens 2) is greater than or equal to 1/2. Yet other combinations imply that Prob(car is behind door x|player chose y, QM chose z) is at least 1/2 for all of the six possible values of the triple (x,y,z). So far, everyone talks about sufficient conditions: that is, (preferably nice/attractive/intuitively meaningful) conditions on the input probabilities, which imply a desired property of an output probability. Looking for necessary conditions is going the other way: suppose I tell you that it is never disadvantageous to switch, ie all six conditional probabilities of the other door being the good door are at least 0.5, what can we deduce about the 7 input probabilities? Can we say something nice/meaningful about them? I don't think anyone has every looked at the problem in this way before, just as it seems no-one ever asked themselves what game theory has to say about this game. Gill110951 (talk) 16:17, 26 April 2009 (UTC)
- Ok, if that's what you mean, I understand. One remark: to be complete, you should introduce conditional probabilities, not only depending on the position of the car, but also on the choice of the door by the player. BTW: I'm not an expert on game theory, so I have difficulty in understanding that part of your paper, although I would like to see the connection with the probabilistic approach. Yet I'm familiar with the basic concepts of game theory, that's why I think you might change the wording as to make it understandable for the lesser expert. Nijdam (talk) 20:02, 26 April 2009 (UTC)
Aids to Understanding
The "Aids to Understanding" section should be revised. The fourth sub-section includes no references. The first sub-section includes one reference, but the rest of what is written is not an illustration or explication of the referenced point. The second and third sub-sections are relevant, referenced descriptions of explanations that have been presented as aids in understanding why the best answer to the posed question is not "No." (The posed question is "Is it to your advantage to switch your choice?") The first and fourth sub-sections should be eliminated, and the section title or an introduction to the section should imply that the subject matter of each remaining sub-section is a suggested aid to understanding. This isn't a "how-to" magazine article. —Preceding unsigned comment added by 74.248.220.132 (talk) 03:30, 19 April 2009 (UTC)
- The first thing that needs to happen to this section is that it needs to be split into two parts, the first dealing with the simple, notable, 'real', Monty Hall problem, which is one of the most unintuitive and notorious probability problems known, and the academic complications to the problem which are less notable but many may find interesting. Martin Hogbin (talk) 09:50, 19 April 2009 (UTC)
- Perhaps many things about this puzzle should be split into two parts. Why not let's start by splitting the unreferenced parts that should be eliminated from the referenced parts that might (or might not) be worth keeping? And seriously, the "real" Monty Hall problem might be all kinds of things. GameSetPoint (talk) 02:57, 21 April 2009 (UTC)
Proposed new section - Problem formulations and approaches
I propose that we add a section on the above subject immediately after the 'Problem' section but before the various solutions. This should make clear some of the way the problem can be interpreted and formulated and the correct approach to a solution in each case.
Krauss and Wang (I strongly suggest that anyone interested in this article reads their paper) make the following points:
- Most people interpret the problem as their mathematically explicit version (this is already in the section above).
- 'No other statistical puzzle comes so close to fooling all the people all the time'. [Referring to vos Savant's formulation and solution]
- The conditional solution is only relevant in the case that the door opened by the host is identified in the problem formulation. They say:
- 'As demonstrated different assumptions about Monty Hall's strategy lead to different Bayesian solutions [referring to their version of Morgan's calculation].... The advantage of the no-door and the one-door scenarios, in which Monty hall's behaviour is not specified, is that participants do not need to consider the possible strategies that Monty Hall might use '. [The one-door scenario refers to the case where the door opened by Monty is not specified.]
This last point is one that I have been making all along. I have to admit that I deleted a section that may have been trying to make this point but it made it so badly that I did not understand the point bing made. We need to make clear that this distinction is based on a reasonable interpretation of the question not mathematical sloppiness. Martin Hogbin (talk) 10:41, 19 April 2009 (UTC)
- That sounds like a good idea. Contrasting the interpretations of the problem will make the presentation of solutions much more clear and simple, I think. But it has to be presented with a good neutral balanced presentation of the alternative views on what the problem is. Can you draft that? Dicklyon (talk) 16:09, 19 April 2009 (UTC)
TeaDrinker deleted my change following the "opening more doors" ilustration, as follows and asked for comment: "Marilyn’s illustration based on a million doors (where all doors are eliminated but two – Door 1 (which had one in a million chance of having a car) plus one of the other 999,999 doors (which either has the car, 999,999 out of a million times, or one time in a million has a goat) is powerful but misleading. This assumes that the original problem calls for Monty to reveal ALL remaining goats except (possibly) one. The problem could just as easily be looked at as Monty revealing just ONE goat from behind Doors 2 through 1,000,000. If only one of the 999,999 doors were revealed to have a goat, and you had to choose between keeping Door 1 or choosing any one of the 999,998 other remaining doors, your odds were still be better if you switched to one of the 999,998 doors, but only very slightly better." TeaDrinker admitted that my point was valid but suggested that this does not explain why my odds are still better even if I have to choose from 999,998 remaining doors. But the point was not that I disagree with Marilyn, rather that for her dramatic illustration of the correct answer she may have smuggled in an unwarranted assumption about Monty's task.83.5.134.48 (talk) 09:09, 20 April 2009 (UTC)
I agree with Hogbin & others (I think!) and believe that the current page could be reorganized to be more helpful. Specifically, the classic problem should be stated in isolated, simple terms, although spelling out some of the main assumptions that were not spelled out originally. Mainly these are (1) Monty knows where the car is, (2) Monty always offers the choice (he's not playing a head game, deciding to offer a choice based on private, perhaps spiteful reasons, e.g. mostly when someone has in fact chosen the car and he wants to 'cheat' them out of it - even if this would be more fun on a real show! (and necessary if people were familiar with the problem beforehand and therefore would always switch when given a choice)), and (3) if both remaining doors conceal goats, Monty's choice of which goat to show is random. Then the solution(s) to the classic problem should be stated. Only later should variations in the problem itself be presented. In my view the so-called "conditional solution" as presented here is not really a solution to the classic problem but rather a discussion of certain variations on the classic problem and thus muddies the waters. It should be moved to the variations section. (For example, if both doors have goats, does Monty have a rule that he must open a certain door and not the other one? That would give away the solution every time, etc. etc.) When the classic problem is properly presented, it is easier to concede that (telescoping the illusory motions), the player is effectively allowed from the outset to choose either just Door 1, or the better of Doors 2 and 3. That said, could there be feedback on this before (or a lack thereof) so one could safely make a change without some good soul like TeaDrinker (greetings) just deleting it? (There must be a game theory to that, too.)83.5.134.48 (talk) 13:12, 20 April 2009 (UTC)
- The question we keep running up against is what is the probability question that is being asked. I think there are two main interpretations:
- 1) What is the probability of winning by switching, averaged across all players?
- 2) What is the probability of winning by switching for a player deciding to switch after the host opens a door, this player looking at two closed doors and one open door showing a goat?
- The math sources ALL say the question is #2 and that this is a conditional probability question. Perhaps the popular sources understand that these are different questions, or perhaps not. Solving a conditional problem with an unconditional approach works, but only under certain assumptions. Rather than stand on our heads trying to force an unconditional solution to "work" I think what we should really do is present a conditional solution and then follow this up with a discussion of the "popular" (unconditional) solutions, specifically mentioning that they are valid only for a very constrained version of the problem or a version that asks about the probability averaged across all players.
- The issue with the unconditional approaches is that it leads the reader to think that these approaches are generally correct ("the host opening a door doesn't affect the player's initial 1/3 chance", or "the combined probabilities of the unchosen doors must always be 2/3", or even "dividing the cases by where the car is initially placed results in a 1/3:1/3:1/3 distribution that is unaffected by the host opening a door"). In a fairly recent column, vos Savant addresses the "host forgets" variant (exactly the same as the classic MHP, but the host forgot which door the car is behind and opens a door revealing a goat accidentally). In her analysis of this version she laments [4] "Back in 1990, everyone was convinced that it didn’t help to switch, whether the host opened a losing door on purpose or not. ... Now everyone is convinced that it always helps to switch, regardless of what the host knows. But this is just as incorrect!" This is absolutely true. And, IMO, it's precisely because the popular sources do NOT address the "classic" MHP as a conditional probability problem. As a featured article on Wikipedia, IMO this article must not make the same mistake. -- Rick Block (talk) 13:53, 20 April 2009 (UTC)
- I'm not saying the popular solutions address #1 (and since they don't say we can't really tell). On the other hand, we do know (and I don't think this is a POV issue) that the mathematically precise way to solve a conditional probability problem is to treat it as a conditional probability problem and that the popular solutions do not do this. What I'm suggesting is the main solution in the article be a conditional solution, presented as comprehensibly as we can. And then, perhaps in the "aids to understanding" section, present one or more of the popular solutions with some discussion about why they work only in the case where the host is constrained to pick randomly if the player has initially selected the car. I crafted a conditional solution in the same general style as vos Savant's wording for the "host forgets" variant in a thread on the Talk:Monty Hall problem/Arguments page. Here's a slightly different version:
- Here’s one way to look at it. Some of the time, the host will open door 2. In our puzzle, that didn’t occur. So we’re considering only the times when either: 1) You have chosen the door with the prize and the host has opened door 3 - and if the host opens door 2 and door 3 each half the time when you've initially chosen the car, your original 1/3 chance is divided in half and is now 1/6; or 2) The prize is behind the unopened door, which it is with probability 1/3 (in which case the host is forced to open door 3). The car is behind the unopened door one-third of the time but behind your door only 1/6 of the time, so your chances of getting the car double by switching.
- The "host forgets" variant is one example of very minor variants where the unconditional approaches result in the wrong answer for reasons which aren't exactly obvious - e.g. how does the host forgetting where the car is change the original 1/3 probability of having selected the car?. The answer is it doesn't, but that's not the same as the conditional probability after the host has opened a door. In explaining this version, vos Savant treats it as a conditional probability problem. -- Rick Block (talk) 19:08, 20 April 2009 (UTC)
- I'm not saying the popular solutions address #1 (and since they don't say we can't really tell). On the other hand, we do know (and I don't think this is a POV issue) that the mathematically precise way to solve a conditional probability problem is to treat it as a conditional probability problem and that the popular solutions do not do this. What I'm suggesting is the main solution in the article be a conditional solution, presented as comprehensibly as we can. And then, perhaps in the "aids to understanding" section, present one or more of the popular solutions with some discussion about why they work only in the case where the host is constrained to pick randomly if the player has initially selected the car. I crafted a conditional solution in the same general style as vos Savant's wording for the "host forgets" variant in a thread on the Talk:Monty Hall problem/Arguments page. Here's a slightly different version:
- The above paragraph grossly mis-states vos Savants's discussion. The 'host forgets' is actually 'the host chooses among the 2 remaining doors randomly'. Which means, sometimes he reveals the car, ending the game. And three of the five 'agreed' premises change. It's not a 'minor' change. Here's vos Savant's link, see for yourself: http://www.parade.com/articles/web_exclusives/2007/02-04-2007/Marilyn-Readers-Respond . Since it's a random choice, it could be the contestant revealing (the) subsequent door(s). Just like Deal or No Deal! Here's where this fiction was most recently brought up. http://en.wikipedia.org/wiki/Talk:Monty_Hall_problem/Arguments#Since_The_Contestant_Can.27t_Know_Of_Any_Host_Behaviour...
- G - you're missing the point. In the "host forgets" variant it's given that the host opened door 3 and did not reveal the car. It's a conditional probability question - just like the standard MHP where it's given that the host has opened door 3. The only difference is whether the host did this on purpose or whether it was a fortuitous accident. -- Rick Block (talk) 00:57, 21 April 2009 (UTC)
- Rick, sounds like you're missing the point, too. It's a totally different question when it's given that the host always opens a door with a goat than when the host opens a door at random. The probabilities depend on the game definition; when the usual definition is used, which door the host opens, and what's behind it, provides no new information, so the result of the conditional problem can be worked unconditionally before the game, or on the fly, without conditioning on which door was opened. Dicklyon (talk) 16:36, 21 April 2009 (UTC)
- Right - the question is how do you know that in the standard version no new information is provided by the host opening a door? I mean, in the host forgets version, the host is actually acting completely randomly - how can there be more information provided in this variant? Yes, the "normal" rules ensure the unconditional and conditional probabilities are the same, but asserting the host's actions do not change the player's initial chance of having selected the car is effectively assuming the solution. What Nijdam is saying is that this assertion should have some reasoning behind it. The generally published popular solutions omit this. Mathematically, it's like a geometry proof that uses as a "fact" that an angle in the accompanying diagram is a right angle without saying why this is so (in a case where the angle is indeed a right angle). The published mathematical criticisms of the popular solutions are that these solutions either 1) don't answer the conditional question that is apparently asked (they answer question #1 from above, not #2), or 2) (if they're actually attempting to answer question #1) assume something without explaining why it's true - making them (as Morgan et al. put it) "false solutions" . -- Rick Block (talk) 18:41, 21 April 2009 (UTC)
- Rick, you seem to the one be making assertions. For example what is your justification for saying, 'asserting the host's actions do not change the player's initial chance of having selected the car is effectively assuming the solution'? If the only information given is random information then it is no information, this is well accepted.
- You have also ignored the question of what Whitaker actually wanted to know. Do you think he actually wanted the answer to the specific question Morgan took him to be asking or is it more realistic to take it that what he actually wanted to know was simply, 'Is it generally better to swap?'. I know which my money is on. Taking his rather vague question as being intended to be a formal conditional probability problem is simply a way of adding pointless academic complexity. A simple problem that most people get wrong is interesting and notable, a complicated problem that most people do not understand is not. Martin Hogbin (talk) 22:14, 21 April 2009 (UTC)
- I have been arguing these points and others on the arguments page where you have not produced any evidence or arguments to the contrary. You now state your opinion as though it were fact. Martin Hogbin (talk) 22:14, 21 April 2009 (UTC)
- I do - of course - fully agree with Rick. And for the people who still do not understand the issue: look at it this way: the door chosen is No. 1; "the" probability of hiding the car is:
door 1 2 3 before action host 1/3 1/3 1/3 after opening door 3 ? ? 0
At least anyone agrees about the zero chance of door 3 (I hope). Therefore the second line is different from the former, and hence a different probability. The first line we call the unconditional probabilities (although the choice may also be considerd as a condition). The second line shows the conditional probabilities. On forehand we do not know much about the question marks, only they sum up to 1. Nijdam (talk) 09:27, 21 April 2009 (UTC)
- Where are the brave ones to tell me what the question marks are? And why? Nijdam (talk) 22:49, 22 April 2009 (UTC)
What reliable sources actually say is that given that usual rules and if the question is interpreted such that the player has picked a specific identified door and the host has opened a specific identified door, the problem is conditional, which I agree. If the question is interpreted in a way that the host opens one (unspecified) of the two unchosen doors the condition becomes non-existent.
In the specific conditional case where the producer (or whoever) places the car randomly but the host does not open a door randomly the host's door opening strategy is important. In the case where the host chooses randomly the conditional case is equivalent to the unconditional one.
On the other hand, reliable sources, referring to the simple unconditional solution, say that no other statistical puzzle comes so close to fooling all of the people all of the time. They also say that incomplete information is not the cause of the difficulty most people have in solving the problem and that even when the problem is made quite clear, with the host choosing randomly, most people still get it wrong. It is clear that a substantial and separate part of this article should be devoted to clearly and convincingly explaining the basic (unconditional, fully defined or whatever) problem and solution. Martin Hogbin (talk) 18:07, 21 April 2009 (UTC)
- Martin - Do you have a reference for your statement just above that the Massimo Piattelli-Palmarini quote ("no other statistical puzzle ...") refers to the unconditional solution? You keep saying the unconditional problem is the most notable one and the one that people get wrong. Do you have a reference for this claim as well? As far as I know, the problem is always stated in a conditional form, and (according to at least Falk, who is a psychologist who has studied it) it is the conditional nature of the problem that trips people up (Boy or Girl paradox being another classic example). Perhaps we can agree that people have trouble solving conditional probability problems using any method, but I think approaching MHP as a conditional problem is actually both more convincing and more useful than approaching it unconditionally. As I've said repeatedly, the problem I have with unconditional approaches is that the conditions under which they're valid are not at all obvious - the easiest example perhaps being the "host forgets" scenario for which the unconditional approach fails. -- Rick Block (talk) 14:08, 22 April 2009 (UTC)
- requested ref. Dicklyon (talk) 15:55, 22 April 2009 (UTC)
- This reference is where the quote comes from, but it doesn't say anything like "this is referring to the unconditional solution". It's clearly referring to the MHP - but Martin is claiming it's referring to his unconditional interpretation. -- Rick Block (talk) 16:21, 22 April 2009 (UTC)
- I doubt that there is a reliable source saying that the Massimo Piattelli-Palmarini quote specifically refers to the unconditional problem or for that matter that it refers to the conditional problem, however, we do have some evidence on the subject from reliable sources. Krauss and Wang quote Piattelli-Palmarini on the second page of their paper where the subject of conditionality has not yet been discussed and shortly after they have said, 'These discussions have verified vos Savant's conclusion that it is is mathematically correct to switch...'. I note that this only says 'correct to switch' but also that it refers specifically to vos Savant's conclusion.
- It is hard to see what other plausible meaning the quote could have. Are you suggesting that it only refers to conditional formulations of the problem and that otherwise people find it easy. Krauss and Wang discount this possibility.
- My position on the problem has hardened a little. I now see the conditional issue as little more than an academic complication and K&W seem to support this view. I have tried several times to discuss this with you on the arguments page but you have not always engaged. I would be happy to continue this discussion there.
- Your view is that reliable sources all say that the problem must be treated conditionally and that any solution that does not do so is false. That may be the view of Morgan et al for a specific formulation of the problem but such a rigid interpretation does not seem to be universal. So what I am essentially saying is that Morgan overstate the case for conditional treatment and you overstate the case that reliable sources only support this treatment of the problem. There is another side to the problemMartin Hogbin (talk) 17:22, 22 April 2009 (UTC)
One door to be selected - two doors will remain unselected (each regarded solely and regarded as a group of two doors)
For each single one of the two remaining unselected doors, each one of these two doors regarded solely for itself alone, the chance of winning amounts to 1/3 according to the rule (together thus 2/3). Risk to contain a goat for each of these two doors regarded solely for itself alone amounts to 2/3 (risk together thus 4/3).
- [Nijdam]Let C be the number of the door with the car: P(C=c)=1/3 for c=1,2,3. That's all there is to say. Risks of 2/3 and adding up to 4/3 are unknown to me.Nijdam (talk) 22:19, 22 April 2009 (UTC)
- @Nijdam: 4/3 unknown to you? What about training to count beyond 1, if possible to 2 at least. So: 3 doors, two goats. Risk for every single door=2/3. In case the player has chosen the winning door, there will remain two doors with two goats. Makes two goats for the two remaining two doors altogether. Repeat: 2 goats (or 6/3, if you like). But two goats are not granted every time. Only ONE goat is for sure, and for the second door a further risk of 1/3. So: 3/3 + 1/3 = 4/3 goats for two doors. Or in other words: one and 1/3 goat for two doors altogether. Kind regards, Gerhardvalentin (talk) 00:55, 23 April 2009 (UTC)
- [Nijdam]Let C be the number of the door with the car: P(C=c)=1/3 for c=1,2,3. That's all there is to say. Risks of 2/3 and adding up to 4/3 are unknown to me.Nijdam (talk) 22:19, 22 April 2009 (UTC)
But since a group of two doors must inevitably contain at least one goat however according to the rule (there is only one car), one of these two remaining doors obviously has the risk=1 to contain a goat and a chance=0 to contain the car, imperatively from the start. This is a fact in reference to the group of TWO unselected doors (The player does not know yet to which one of the two doors this applies). As accentuated, this applies anyway only to ONE of the two doors that are going to remain unselected. Thus the other one of these two doors inevitabely will have a chance of winning of 2/3 and a risk to contain a goat of 1/3, imperatively from the start. (The player does not know yet to which one of the two doors this applies).
The opening of one door by the host, showing a goat, changes neither the chance of winning of the door originally selected (1/3) nor the chance of winning of the two doors not selected (of together 2/3).
- [Nijdam]This is no more than just a statement, that needs to be proven. Right is that the sum of the two (conditional) probabilities is 1. So if one in not changed, so is not the other. Without this proof, no more can be said. And besides: after the opening of the door, the probabilities at stake are conditional probabilities. Nijdam (talk) 22:19, 22 April 2009 (UTC)
However: The opening of the door with one goat shows the aforementioned distribution of chance and risk within the group of the two doors not selected. The door opened will have a risk to contain a goat=1 and will have a chance to contain the car=0. The other one that will remain still closed thus is the one with a chance of winning=2/3 and it has the remaining risk to contain a goat=1/3. All of that as a compulsive implication of the rules, imperatively from the beginning.
Opening the door by the host, showing a goat, did in no way bring any additional information regarding the position of the car, however. -- Gerhardvalentin (talk) 21:27, 21 April 2009 (UTC)
- Comments? Say: What the article needs is a clear presentation of the given inevitable consequences that are valid right from the beginning, set by the original conditions of task. Of the clearly laid out intrinsic consequences that inevitably result right from the problem definition. A clearly represented definition of the initial position and its immanent consequences. -- Gerhardvalentin (talk) 10:47, 22 April 2009 (UTC)
- @Nijdam: Thank you for your recurring thoughts and would like to suggest some experimental training / proof. Regards, -- Gerhardvalentin (talk) 23:09, 22 April 2009 (UTC)
The flaw in the assertion that "switching wins 2 out of 3 times" is this that there is only ONE guesser who only can only make ONE guess. Therefore switching has no bearing on the probability of the result. —Preceding unsigned comment added by 194.202.122.223 (talk) 08:29, 22 April 2009 (UTC)
- If you are arguing that it is not better to switch then you are wrong. It is accepted by all that, in the simple case, you have a 2/3 chance of winning by switching. This page is for discussing ways to improve the article not the validity of the simple solution. If you want to discuss this probability further , I suggest that you do it on the arguments page. Martin Hogbin (talk) 09:33, 22 April 2009 (UTC)
The crux of the issue that dominates this page is the statement above:
- The opening of one door by the host, showing a goat, changes neither the chance of winning of the door originally selected (1/3) nor the chance of winning of the two doors not selected (of together 2/3).
This is a true, but confusing, statement. I think a better, less confusing, way to phrase the same thing would be:
- The opening of one door by the host, showing a goat, changes neither the overall chance of winning of the door originally selected (1/3) nor the overall chance of winning of the two doors not selected (each 1/3, so together 2/3).
The point is that the chances described in this statement are the overall chances, which are the chances in effect before the host opens a door. Nijdam puts it quite succinctly above
door 1 2 3 before host opens a door 1/3 1/3 1/3 after opening door 3 ? ? 0
The chances this statement refers to are the 1/3:1/3:1/3 chances from the first line. The host does not, and can not, change these. When the host opens a door (say door 3) the chances have clearly changed. If we want to talk about chances that never change, then we need to talk about what happens when the host opens either door, perhaps like this:
1/3 + 1/3 + 1/3 = 1
/\ /\ /\
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
host opens: door 2 door 3 door 2 door 3 door 2 door 3
/ \ / \ / \
/ \ / \ / \
? + ? + 0 + 1/3 1/3 + 0 = 1
What the statement above is actually saying is that for the player's chosen door ?+?=1/3 (not that each ? in this diagram is 1/3) and that the 1/3 for each of the unchosen doors don't change either (so, still, 1/3+1/3=2/3). The problem statement asks about the case where the host opens door 3, so (rearranging slightly) we have
door 1 2 3 1 2 3 before host opens a door 1/3 + 1/3 + 1/3 = 1 after opening door 3 ? + 1/3 + 0 + (host opens door 2) ? + 0 + 1/3 = 1
In the case the host opens door 3, we have ? + 1/3 + 0. The sum is not 1, but the overall probability the host opens door 3. To make these terms conditional probabilities that sum to 1 we have to divide by their sum, but since one of the terms is ? we don't exactly know how to do this. If we assume the two ? terms are the same, they're both 1/6 and then we have 1/6 + 1/3 + 0, so conditionally we have 1/3 + 2/3 + 0 = 1 - but note that the 1/3 here is not the "chance of winning of the door originally selected" unchanged, but half of this. -- Rick Block (talk) 15:32, 22 April 2009 (UTC)
Rick Block: Did you consider that 1/3 + 1/3 + 1/3 only applies BEFORE the player made his choice?
Only before he made his choice. For:
As soon as he has chosen one of the three doors the situation has changed completely:
- One door chosen: chance=1/3 and risk=2/3.
As to the two doors he denied (with an overall chance=2/3, overall risk=4/3):
- One door NOT chosen chance=0 and risk to contain a goat=1 (There's only 1 car! But the player still does not know yet to which one of those two unselected doors this applies)
- The other door NOT chosen: chance=2/3 and risk=only 1/3 (the player still doesn't know yet to which one of the two doors that have not been selected this will apply).
But after the host has opened one of the two doors not selected, showing a goat:
- One door not chosen showing a goat chance=0 and risk=1 (Now the player knows to which one of those two unselected doors this applies, i.e. to the open door showing a goat).
- The other door not chosen (still closed): chance=2/3 and risk is reduced to 1/3 (now the player knows to which of the two unselected doors this applies, i.e. to the still closed door)
Regards, -- Gerhardvalentin (talk) 20:16, 22 April 2009 (UTC)
- One of several flaws in Rick's explanation is this. For some unexplained reason it is assumed that the producer acts randomly when he has the car placed behind one of the doors. If this assumption is not made then the chance of initially picking the car is not 1/3 but indeterminate. When it comes to the host's choice of door the host is presumed to act non-randomly thus we cannot assume that the host may pick door 2 or 3 with equal probability.
- The above explanation therefore only applies in the somewhat contrived case that the producer (or his agent) is taken to act randomly but the host is not. If the both act non-randomly the question is indeterminate and if they both act randomly the chances of having picked the car, given that the host has picked a particular door are always 1/3. I would be interested to hear Rick's response to this. Martin Hogbin (talk) 07:00, 23 April 2009 (UTC)
- The explanation above relates to the problem statement from Krauss & Wang where both the car placement and host's choice of door in the case the player initially picked the car are explicitly random. It can be easily extended to the interpretation of the Parade version analyzed by Morgan et al. and Gillman where the host's preference is treated as an unknown variable, but in the above the host's preference is assumed to be 1/2 (i.e. random).
- It does indeed turn out that the chances of having picked the car remains numerically 1/3 if the producer acts randomly and the host acts as specified in the K&R statement of the problem, but this fact is the result of the analysis not the reason the analysis ends up the way it does. If we assume the doors (and goats) are indistinguishable, i.e. treat the problem as an urn problem (which forces the random choices Martin mentions), the marginally simpler approach of enumerating all possibilities assuming the player switches is valid and leads to the same result without using conditional probability (these conditions force all conditional outcomes to have the same probability as the unconditional outcome).
- On the other hand, if we're answering the conditional question that the problem statement apparently asks (flipping from win by switching to win by staying, the question is what is the probability of the player's door being the one with the car given the player has picked door 1 and the host has opened door 3), the "1/3" which is the probability of the player's initial chance of picking the car is not the same as the "1/3" corresponding to this conditional probability. For example, if we're talking about 3000 players who have picked door 1, we'd expect about 1000 to have selected the car and if all 3000 stay with their initial choice only these 1000 will win the car (and, if all 3000 switch, the other 2000 will win the car). The initial "1/3" is these 1000 players. After the host has opened door 3 we're no longer talking about all 3000 of these players but only a subset. If the host picks randomly between doors 2 and 3 if the player has initially selected the car, we're talking about roughly 1500 of the 3000. Of these, about 500 will have initially selected the car. These 500 is what the conditional probability of "1/3" is talking about. These two "1/3" are of course numerically the same, but they correspond to distinctly different sets of players. -- Rick Block (talk) 13:56, 23 April 2009 (UTC)
- Of course the conditional sample is a subset of the unconditional one but, in the case that the host acts randomly, it is a representative sample since it is taken randomly. So yes, the problem is conditional in the sense that we have applied a condition but it is a condition that makes no difference. If the host chooses randomly we can fill in the question marks in your diagram above with the value 1/6 (as is done in the article itself). As others have pointed out this is not a numerical coincidence but the result of an obvious symmetry. Now tell me why the case that the car is not initially non-randomly placed is never considered. Martin Hogbin (talk) 21:27, 23 April 2009 (UTC)
- The non-random initial placement certainly can be considered, and there are actually sources that examine a variant where the player knows the initial non-random placement. About such a variant, Morgan et al. say "Other variations appear to be of less interest. One possibility is to incorporate prior information on the part of the player as to the location of the car, or, related to this, to allow nonuniform probabilities of assignment of the car to the three doors, but these are unlikely to correspond to a real playing of this particular game show situation." My opinion (which I freely admit is WP:OR) is that the variant Morgan et al. (and Gillman, who you keep ignoring) analyze pretty much exactly matches an actual game show situation (of course, the actual rules of Let's Make a Deal were not the same as any version of the MHP, so this entire discussion is one of conjecture). In an actual game show the car would be hidden, and as Glkanter has observed, providing the player information about the location of the car would violate US laws, which means the initial location should be assumed to be random. The constraint that the host pick randomly if the player initially selects the car is NOT in most statements of the problem (and doesn't seem to me like something a game show would clarify), so when analyzing the conditional probabilities it seems entirely reasonable to consider the case where the host has a preference (and, to Glkanter - it doesn't matter whether the player knows this preference or not, it influences the probability in either case - and, to you Martin, this preference might be entirely momentary and might change player by player or day by day). Assigning this preference to a variable, and analyzing the extremes says the player is never worse off switching.
- If we are going to refer to the actual show then I see no greater reason to assume the car was initially placed randomly than to assume the host chooses randomly. In reality they were probably both roughly random. They probably put the car behind a door without thinking too much about it and the host probably made up his mind at the time, having no special preference. Martin Hogbin (talk) 17:03, 24 April 2009 (UTC)
- If where you're really going is that we should assume the host picks randomly in the case the player initially selects the car, please tell me where in the simple solution we say anything like "in the case that the host acts randomly, it is a representative sample since it is taken randomly" or the conditional cases are clearly the same because "of an obvious symmetry". As far as I recollect, I've never seen an unconditional solution that actually provides any kind of justification for ignoring the possibility that the host might have an unknown preference. To some extent, as Dicklyon would say, this entire discussion is moot since we should say what the sources say - not what we might wish they say. -- Rick Block (talk) 01:31, 24 April 2009 (UTC)
- Vos Savant later justified her solution by saying that she took the host to be acting purely as the agent of chance. All the sources make clear that the chances of winning by switching are in fact 2/3 if the host chooses randomly. So what we have is a solution that ignores something that makes no difference and gets the right answer, it probably shares these features with most mathematical solutions. Martin Hogbin (talk) 17:20, 24 April 2009 (UTC)
Explaining the solution
Before the player makes her choice, there are, in conformity with the rule: 1 car, 2 goats, and three closed doors, each one
with a chance of winning of 1/3 and a risk to contain a goat of 2/3. Chances= 1/3 + 1/3 + 1/3, risks= 2/3 + 2/3 + 2/3.
After the player has made her choice however to one of the three doors (with a chance=1/3 and a risk=2/3), the situation has changed dramatically:
The remaining residue of the two unselected doors, with an overall chance of winning amounting together to 2/3, and their overall risk of together 4/3, must – as to the rule – inevitably contain at least 1 goat with a chance=0 and a risk=1 (for, as to the rule, there’s only one car).
Solely from the terms of the rule, the compelling implications are:
- The selected door has a chance=1/3 and a risk=2/3 (no more info about this door).
- One of the two doors that have not been selected has inevitably a chance=0 and a risk=1 (Only 1 car. The player still doesn’t know to which one of those two doors this will apply).
- The other one of those two unselected doors – according to the rule – thus has inevitably a chance of 2/3 and a risk of only 1/3 (The player still does not know to which one of the two unselected doors this will apply).
But when the host opens one door from the rest of the two unselected doors, showing a goat, he shows to the player the position of the inevitable rivet, and by this the player also has knowledge of the position of the (still closed) door with the chance of 2/3 and the risk of 1/3.
Its chance of winning is twice as high (2/3) as the chance of winning of the door originally selected by the player (1/3), but in one third of all cases (i.e. whenever the player should coincidentally have selected the winning door with the car), it will contain a goat also.
So, the opening of the door containing a goat has definitely shown the distribution of chances within the group of the two unselected doors, but beyond that it has not given any further information regarding the chances of the door originally selected (1/3) nor regarding the chances of the group of the two unselected doors (overall by 2/3), nor any reference to the actual position of the car, whatsoever.
All these facts stated above do result exclusively from the regulations already specified in the rule, and from its inevitable consequences. And any mathematical calculations, if provided correctly, will lead to the same results:
In 1/3 of all cases, in which the player should coincidentally have selected the winning door, she would lose by a change and win by persisting. In the other 2/3 of all cases, in which she should have selected one of the two doors each containing a goat, she wins by changeing and loses when persisting.
Thus, by changing, the player doubles her chance from 1/3 on 2/3.
The persistent "WHY ?" should be considered, and should be responded. Who will put this info on top of the article? Kind regards, -- Gerhardvalentin (talk) 22:04, 22 April 2009 (UTC)
- @Gerhardvalentin. Your problem is partly your unfamiliarity with probability theory. You try to make computations, from which I understand the purpose, but the focus is on the wrong issue. You should focus on why the probability of the door initially chosen to hide the car is 1/3 before the opening of one of the other doors, and also 1/3 after. That is the whole and only issue. Nijdam (talk) 22:28, 22 April 2009 (UTC)
- @Nijdam: Probability theory is concerned with analysis of random phenomena. It's not fair to blame reality for resulting misjudgements of any calculations whatsoever, i.e. stochastics not to be neglected. Thank you for your efforts, hope you're going to find a correct theorem that corresponds to reality. Regards, -- Gerhardvalentin (talk) 23:34, 22 April 2009 (UTC)
- @Gerhardvalentin. Your problem is partly your unfamiliarity with probability theory. You try to make computations, from which I understand the purpose, but the focus is on the wrong issue. You should focus on why the probability of the door initially chosen to hide the car is 1/3 before the opening of one of the other doors, and also 1/3 after. That is the whole and only issue. Nijdam (talk) 22:28, 22 April 2009 (UTC)
@Gerhardvalentin. The problem is that Rick and Nijdam cannot decide which model of probability to apply. If you apply the 'probability is a state of knowledge' principle and take it that any information not given should be treated as random, then you are right. The player has no knowledge of the initial car placement or the host's door choice policy, we therefore should take both of these to be random, and the chances of winning by switching are consequently 2/3.
If, one the other hand, we take the more formal view that anything not specified in the problem statement must be taken as indeterminate it is possible to contrive a case where the probability of winning by switching is not 2/3. If you are interested I can show you how. Martin Hogbin (talk) 07:15, 23 April 2009 (UTC)
- I'm really amused about such statements. Rick and I do perfectly know what to do and what to apply. And whatever model we or you apply, the needed solution is with conditional probabilities, whether you like it or not. Nijdam (talk) 14:51, 23 April 2009 (UTC)
- Nijdam - the difference here is that Martin wants to treat the problem as an urn problem which might be stated as follows:
- There are one white ball and two (indistinguishable) black balls in an urn. The player withdraws one without looking at it. The host now looks in the urn and withdraws a black ball and shows it to the player. The host offers the player the opportunity to switch for the remaining ball in the urn. If the player wins a car by ending up with the white ball should she switch?
- This is the problem the "unconditional" solutions address. Martin's claim is that this is the "true", "notable" MHP. Unfortunately, in the MHP the doors have numbers and physical locations on a stage so the doors are clearly distinguishable which you and I are saying means it's NOT an urn problem, but a conditional probability problem. -- Rick Block (talk) 15:18, 23 April 2009 (UTC)
- Nijdam - the difference here is that Martin wants to treat the problem as an urn problem which might be stated as follows:
Let me answer the question of what I am trying to do. It is something quite separate from the conditional issue and from the distinguishability of the doors.
Consider this quotation from the Three Prisoners Problem (where the prisoners are all clearly distinguishable), 'Prisoner A, prior to hearing from the warden, estimates his chances of being pardoned as 1/3, the same as both B and C'. Note that A estimates his chances of being pardoned as 1/3. This is not strictly valid as nothing in the problem statement says that the choice of prisoner to be pardoned is random, however, it is taken that, as the prisoner has no information as to who will be pardoned, he will estimate his chances as 1/3. This is common, but less formal, way of looking at things. If some information is unknown it is taken to be random. In Morgan's interpretation of the MHP this approach is not taken. Although the player has no knowledge of the host's door opening policy we do not take this to be random. Martin Hogbin (talk) 22:48, 23 April 2009 (UTC)
Bayesian approach
I’ve added a link in “See also” to the discussion at Bayes' theorem. I see that Bayesian approaches (etc.) have occasioned controversy (in this talk page); my feeling is that:
- while the Monty Hall problem is a good illustration of Bayesian probability, and thus warrants discussion (under “Bayesian probability”),
- for readers just wanting to understand the Monty Hall problem, Bayesian analysis likely confuses matters, and shouldn’t be on the Monty Hall page itself – the simple analysis (1/3 right at first, switching reverses these) is plenty, and clearly is confusing enough as is.
For comparison, see this paper on variants – which essentially gives a Bayesian/Principle of Indifference approach:
- Monty Hall, Monty Fall, Monty Crawl, by Jeffrey Rosenthal
- I’ve linked Rosenthal’s paper from the variants he mentions, as it’s available online and the statements (why half the time?) may be confusing – which he elaborates and clarifies – but I’ve made no mention of Bayesian approaches vs. enumeration, leaving that to the references.
- —Nils von Barth (nbarth) (talk) 02:11, 23 April 2009 (UTC)
- I've just restored the formal Bayesian approach that had been in the article for a long time and deleted fairly recently by user:Nijdam. IMO, the article is incomplete without it. -- Rick Block (talk) 04:44, 23 April 2009 (UTC)
- I only deleted it, because I replaced it with a much shorter formulation, as part of the probabilistic approach. In my opinion it should not be called a Baysian approach, as it hardly has anything to do with Bayesian analysis. It is plain probability theory, using Bayes' law, that all. Nijdam (talk) 08:21, 23 April 2009 (UTC)
- I've just restored the formal Bayesian approach that had been in the article for a long time and deleted fairly recently by user:Nijdam. IMO, the article is incomplete without it. -- Rick Block (talk) 04:44, 23 April 2009 (UTC)
- Hi Rick – I agree that the Bayesian analysis is informative; thanks!
- One may argue that the section is a bit long, and may be technical for readers unfamiliar with probability, though putting it as the last section seems to address that.
- To Nijdam – it seems reasonable that some mention of Bayes' law should be made, whether it be framed as a Bayesian analysis or not, no?
- The distinction between a frequentist/probabilistic statement of applying Bayes' law vs. a Bayesian statement seems to me to turn on whether one should say “1/3 of the time the car will be behind each door” vs. “By the principle of indifference, one should assign a prior probability of 1/3 to each door,” – and similar framings for the inference/likelihood.
- The Bayesian interpretation of probability is widespread and valued, which argues for an explicitly Bayesian statement of this interpretation; in how much detail might be argued about though.
- So does it seem reasonable to both explicitly mention Bayes' law and to give a (brief or detailed) discussion from the Bayesian perspective?
- —Nils von Barth (nbarth) (talk) 11:15, 23 April 2009 (UTC)
- I have no objection of mentioning Bayes' law, on the contrary. But it has nothing to do with a Bayesian type of analysis, as some people seem to think as soos as they happen to hear the name Bayes. My problem is the naming of "Baysian approach" as one and further the quite heavy formulation. It is no more than the needed formulation for the solution, and it can be written down quite easy as I did in my formulation of the "probabilistic approach", which alas has been deleted recently. Nijdam (talk) 14:47, 23 April 2009 (UTC)
- Hi Nijdam,
- I’ve made some changes to your formulation (formatting and linking Bayes' law).
- Substantively, I’ve also mentioned that the Bayesian interpretation of P(Car behind door 1)=1/3 is as the principle of indifference (prior belief), as opposed to the frequentist “Model as a uniform distribution/In the long run 1/3 of the time it will be”, as this is an important philosophical point as I understand it.
- (I imagine there may be some more back-and-forth on how best to discussion Bayesian interpretations, as per Rick’s comments.)
- —Nils von Barth (nbarth) (talk) 15:51, 23 April 2009 (UTC)
- Well to be honest, I don't like it. According to the rules the car is placed randomly, so why complcate things in mentioning notions of Baysian approach. The interested reader has nothing to gain from it. Nijdam (talk) 20:41, 23 April 2009 (UTC)
- At least at first glance it seems to me, that it might be wise to keep the probability/statistic schools (frequentists vs bayesians) out of the problem at the elementary. Because to the average reader and probably even the average mathematician this might be rather confusing then helpful. If analyzing the problem from the 2 different philosophies provides some useful insight (I'm not knowlegdable there) it should be treated in a separate section with more detail and not mixed with the "elementary" Bayes solution section.--84.174.195.210 (talk) 11:35, 1 May 2009 (UTC)
- The point of the previous section was that it is a rigorous proof, referenced to a published source. To be rigorous it needs to be in the context of a specific formalism - yes, it is quite elementary and only uses Bayes' law, but it is a formal proof unlike the "replacement" section which is informal and unreferenced (making it effectively WP:OR). I'm not going to edit war about this, but I vastly prefer the more formal treatment. -- Rick Block (talk) 16:07, 23 April 2009 (UTC)
- Nijdam - your version is an entire section without a reference, which is pretty much a no-no for a featured article. And, why would you say the former version is "hardly Bayesian"? It's simple, but precisely follows the formalism - which has the advantage of being mathematically rigorous. I've asked user:Glopk (the primary author of the section you've replaced) to comment. -- Rick Block (talk) 14:12, 24 April 2009 (UTC)
- I just reformulated the formal derivation as can be found in Morgan etc. Bayesian statistics is typical concerned with parameter estimation, using prior distribution of the parameter in achieving specific estimators. Although Bayesian methods use Bayes' law, not every use of this law is a Bayesian method. Bayes' law is a simple rule in probability theory as you know. Nijdam (talk) 16:01, 24 April 2009 (UTC)
- I am reverting this edit. The derivation is much less clear than the original one, and the typesetting is an ugly mixture of ASCII and inline math images. We may argue on whether the section should be titled "Bayesian Analsys" or just "Formal Probabilistic Analysis", but the replacement of its content with the current one is just bad.glopk (talk) 19:48, 27 April 2009 (UTC)
- I'm strongly against reverting. If it is the ugliness, may be you may enhance the beauty of the section. But the former section was way to long and used a much to complicated notation. Not only should it not be named 'Bayesian approach', it also should not mention anything of this kind in the text. Nijdam (talk) 21:51, 27 April 2009 (UTC)
- I am reverting this edit. The derivation is much less clear than the original one, and the typesetting is an ugly mixture of ASCII and inline math images. We may argue on whether the section should be titled "Bayesian Analsys" or just "Formal Probabilistic Analysis", but the replacement of its content with the current one is just bad.glopk (talk) 19:48, 27 April 2009 (UTC)
[outindent]Nijdam, please re-check your priorities and onus assignment. The previous "Bayesian Analysis" section was well-referenced, complete as any elementary proof should be, and used a standard mathematical notation (the notation of most modern probability theory textbooks that I am aware of). Its graphical editing was well up to par with other articles of mathematical content. Because of the above, it has passed two FA reviews along with the rest of the article. Now you are replacing it with something concise to the point of being almost a link, unreadable for the non-mathematically initiated, and using an ugly mashup of ASCII and LaTeX notation. Now think again and answer: on whom does the onus of "enhancing the beauty" of the section fall, you or me? This new section is going away as soon as I have a few minutes to unravel the pile of **** you have larded upon it. Man, are you on a mission to ruin this article?glopk (talk) 22:35, 27 April 2009 (UTC)
- I don't know if I can helpfully moderate here, but before this gets more heated I just want to mention that (unlike many who choose to comment on this page) you are both math professors and should treat each other with due respect. Per my previous comments above I favor the original treatment. -- Rick Block (talk) 23:29, 27 April 2009 (UTC)
- And, to be clear, I'm definitely NOT saying that only folks who are self-identified math professors should be treated with respect. Since you really don't know who you might be interacting with here, it's best to treat everyone as a colleague (even though in reality they might be dogs). -- Rick Block (talk) 00:24, 28 April 2009 (UTC)
- Well, very glad to hear that, since I am not a math professor (where did you get the idea ? :-)
- Generally speaking, and to begin with, I have a hard time respecting the arguments of someone who starts with a strawman. A few paragraphs above Nijdam states: "Bayesian statistics is typically concerned with parameter estimation". This is inane in general, but particularly so when referring to a section that had absolutely nothing to do with statistics - its very first sentence stated: "An analysis of the problem using the formalism of Bayesian probability theory". If Nijdam does not understand the difference between Statistics and Probability Theory, I surmise that he has no business arguing about either. Further, it is really baffling to replace an FA-quality section with one so poorly edited, and then invite a critic to "enhance its beauty". Seriously? Are we talking about editing a reference resource that people have come to rely upon, or is it the faculty bocce-ball club newsletter? Surely prof. Nijdam would not ask the same of a reviewer of one of his academical papers, and I expect he should treat his WP reviewers with as much respect.
- More to the point of his criticism. Those who attended the last two FA-reviews will remember that both points - article length and formalism - were discussed at lenght, and the consensus was that the article in the then-current form, inclusive of the Bayesian Analysis section, were more than acceptable. Nijdam is not presenting any argument that hasn't been already rehashed and found wanting.glopk (talk) 03:38, 28 April 2009 (UTC)
- My problem with this section is that it is not of interest for the average interested reader of an encyclopedia. It is a very formal way of Bayesian terminology, which is not appropriate for this problem, at least not for the presentation in Wikipedia. The (common) solution of the MHP asks for the calculation of conditional probability that can be straightforward done. It involves using Bayes' law, that's all. This simple derivation, as found in many text books is now nowhere found in the article. Nijdam (talk) 07:42, 28 April 2009 (UTC)
outindented)See i.e. Behrends, Ehrhard (2008). I'll just use some other symbols.
The solution may be given in terms of the following events:
- , the car is placed behind door No. i,
and:
- , the host opens door No. i.
The car is placed randomly behind the doors, hence every door has the same probability of hiding the car:
Let us assume the player has initially chosen door No. 1. From the rules of the game it follows:
- (The chosen door is never opened)
- (If the car is behind the chosen door, the host chooses randomly to open one of the other doors.)
- (The host only reveals a goat)
If the host has opened door 3, the probability of the car being behind door 2 may be calculated using Bayes' law:
This is all there is to it. Plain, straightforward, found in many textbooks. Nothing my own research, simple, easy to understand for someone familiar with the basics of probability theory, nice lay out, etc. etc. What do we want more.Nijdam (talk) 13:08, 28 April 2009 (UTC)
- Let's see, I count at least 3 POV statements in your last (indented) paragraph above, which is OK since this is a discussion. What is not OK is your uncritical application of them to the article. Face it: you are not the mythical "average interested reader" - a non-existent construct of imagination until someone show the results of a controlled poll of readers on a well-defined set of questions. However, from our experience with students (BTW, yes, years ago I did teach elementary prob. theory at both undergrad and grad level), and from the history of editing a long-lived article such as this, it is possible to draw some suggestive conclusion. Feel free to call them my POV's, if you wish. One is that a reader that is curious and conversant with math, but not (yet) a student of particular math discipline, favors a proof in which as many steps as possible are clearly spelled out, from first principles and hypotheses to thesis. Call it "The average reader dislikes jumps" principle. This, of course, is possible only for elementary proofs that are only a few theorems removed from the axioms - but guess what, we are exactly in this situation here, and - ri-guess what, that's exactly why a good author like Gill puts the problem and this solution in the first chapter of his textbook. Of course the calculation can be done in a straightforward manner, but that is precisely NOT the point of this section.
- On your repetition of the formulation above. Yes, absolutely, it is plain, easy, quick. It is also un-readable unless you already know very well what the symbols mean, why you are allowed to combine them in this manner, and how they relate (if at all) to the MHP. I think you just proved my point, thanks. On the other hand, the Bayesian analysis section as it stands now (I put it back, as you can see) is self-contained, except for pointers to more general topics, and uses standard textbook notation as well. It just take several lines more in order to spell out all the logical steps, but not so many as to become a treatise unto itself.glopk (talk) 15:05, 28 April 2009 (UTC)
- Seemes you missed the words: with some extra text, which I added to indicate it's needed to make my suggestion readable to this mythical average reader. The formulation above, as a framework, is just for this discussion. Nijdam (talk) 16:35, 28 April 2009 (UTC)
- I'll complete the text. Nijdam (talk) 16:48, 28 April 2009 (UTC)
- Seems you have forgotten what your (now deleted) section in the article looked like - there wasn't any "extra text" in there either, yet you were "strongly against" reverting it. I'll be happy to see it - in a proposal page or section of this discussion page, rather than on the main article until it's ready (if ever). Please avoid defacing the article again. glopk (talk) 16:57, 28 April 2009 (UTC)
- Question: What more do you want? Nijdam (talk) 10:01, 29 April 2009 (UTC)
- Question: Why won't you leave this section alone? You have three users already (me included) telling you it's fine and informative as it is. Your arguments for changing it are either old and already refuted (length, symbols) or specious ("average reader", a foggy notion of what Bayesian probability theory is about). If not, propose changes that make sense AND keep this article at FA-level. And please use a fine brush and leave the jackhammer home, because - believe it or not - noone likes to drive a steamroller over your edits. glopk (talk) 15:13, 29 April 2009 (UTC)
- Simply because the explanation in words, may (even should) be followed by a formal mathematical dervation. And that's what the proposed part is. Special attention to Bayesian probability theory is not the purpose of this article. Nijdam (talk) 10:28, 30 April 2009 (UTC)
- Let's first dispose of this new variant of your "Bayesian, boooh!" strawman. Exactly how does Bayesian probability theory get special attention in this article? If you bothered to count words, you'd notice that the vast majority of the article's content reflects a frequentist view of probability. More, the lede is a frequentist "Popular solution". Recent edits (by you and others) even managed to beat into a small pulp of packed text and inline ASCII formulae Rick Block's elegant presentation of the "conditional" (i.e. Bayesian) interpretation of the problem. Besides, your whole point is bizantyne: BPT is simply used in this section as an explanatory tool, and in this sense no more "special attention" is given to it than the top figure gives to Cartoon Graphics. Are you going to argue next for removing the figures because the purpose of the article is not to give special attention to cartoons?
- Simply because the explanation in words, may (even should) be followed by a formal mathematical dervation. And that's what the proposed part is. Special attention to Bayesian probability theory is not the purpose of this article. Nijdam (talk) 10:28, 30 April 2009 (UTC)
- Question: Why won't you leave this section alone? You have three users already (me included) telling you it's fine and informative as it is. Your arguments for changing it are either old and already refuted (length, symbols) or specious ("average reader", a foggy notion of what Bayesian probability theory is about). If not, propose changes that make sense AND keep this article at FA-level. And please use a fine brush and leave the jackhammer home, because - believe it or not - noone likes to drive a steamroller over your edits. glopk (talk) 15:13, 29 April 2009 (UTC)
- Question: What more do you want? Nijdam (talk) 10:01, 29 April 2009 (UTC)
- Seems you have forgotten what your (now deleted) section in the article looked like - there wasn't any "extra text" in there either, yet you were "strongly against" reverting it. I'll be happy to see it - in a proposal page or section of this discussion page, rather than on the main article until it's ready (if ever). Please avoid defacing the article again. glopk (talk) 16:57, 28 April 2009 (UTC)
- Second, the position of the formal derivation in the article. This section was at one point higher up, above the "History", and part of a wider "Aids to understanding" section. It was moved to the bottom of the article when revised for a past FA review. The reasoning went, give or take, like this: only a quite small fraction of readers is conversant with mathematical symbolism and willing to read a formal proof (*any* formal proof), therefore let's do something akin to the way in which, in many journal articles, math proofs are placed in appendices. The interested readers will find and enjoy it, while those not interested won't be distracted. So no harm is done to anyone, and the "flow" of the article is enhanced. glopk (talk) 16:05, 30 April 2009 (UTC)
- Imho the current version fine and I agree that Nijdam's edit/revert was problematic for several reasons you've outlined above (independent of the question which version one personally consider as nicer). I do however have some questions/possible about the current title and the references to Bayesian statistics. My understanding so far is, that frequentists and Bayesians alike do use Bayes' formula on an elementary level and they would both model/explain the MHP problem as stated here. So assuming I'm not mistaken here, the terminology bayesian as well as the references, as they are used now, can create a misleading impression (in particular that this analysis would only be valid from bayesian viewpoint and frequentists may decline it). Hence overall I prefer the current solution and I agree with your criticism of Nijdam's actions. However I do think some of the wording/title should be revised nevertheless for the reason i just outlined.--Kmhkmh (talk) 12:11, 1 May 2009 (UTC)
- Second, the position of the formal derivation in the article. This section was at one point higher up, above the "History", and part of a wider "Aids to understanding" section. It was moved to the bottom of the article when revised for a past FA review. The reasoning went, give or take, like this: only a quite small fraction of readers is conversant with mathematical symbolism and willing to read a formal proof (*any* formal proof), therefore let's do something akin to the way in which, in many journal articles, math proofs are placed in appendices. The interested readers will find and enjoy it, while those not interested won't be distracted. So no harm is done to anyone, and the "flow" of the article is enhanced. glopk (talk) 16:05, 30 April 2009 (UTC)
- I partially agree with your points above. Indeed the solution of the "conditional" interpretation of the problem would be similarly written in any sane formulation of probability theory, but there are non-trivial differences in the conceptualization of both hypotheses and result. Yes, we could shove these differences under the "purely philosophical" carpet, and come up with a text neutral with respect to probability interpretation. However, I believe that doing so would be a disservice to the reader, for (at least) the following reasons: (1) What a waste of an excellent opportunity to offer the reader a complete and self-consistent treatment, rather than a bunch of pointers. (2) WP editing rules strongly discourage using "weasel expressions" in text, so why accept them in math?
Consider, for example, Nijdam's text above. It starts with the sentence "The solution may be given in terms of the following events", which of course begs the question of what is an "event" in the context of the MHP. And if we are going to make the terminology precise, why not do it the "right" way, that is, introducing the theoretical context of the formulation and proceeding within it?
So, if you stipulate (at least for the sake of argument) that a formal treatment of the MHP should be written with explicit (if abbreviated) reference to a specific interpretation of probability, well, then we have to choose one: frequentist, bayesian, measure-theory (Kolmogorov), ...? Well, the bayesian interpretation is particularly attractive for a puzzle of logic because it needs not introduce any extraneous concepts ("sample space", "ensembles of identically-prepared random experiments", etc.). Rather, probabilities are defined as numbers measuring a degree of belief in the truth of propositions - i.e. of assertions that are unequivocally true or false, and thus subject to the rules of boolean logic. Cox's genius was to show that such an assignment of numbers to propositions cannot be arbitrary and must follow the standard product and sum rules of probability, under penalty of logical inconsistency (see Dutch book). glopk (talk) 03:50, 4 May 2009 (UTC)- Well, this is an encyclopedia, not a higher level math textbook. Any student who just has learned something of probability theory, may (or even will) be confronted with the MHP. The formal solution is no more than an application of Bayes' law, which the student has just met in his course. No Bayesian approach for him. And if the formal solution is presented, in its simple form, the so called Bayesian approach is superfluous. Actually I don't see what it contributes to the article. Nijdam (talk) 22:07, 10 June 2009 (UTC)
- So you are not answering any of my points, but are saying that the level of the article should be as directed to someone who as "just has learned something of probability theory". I believe this sort of "soft bigotry of low expectations" is adequate for Conservapedia, not here. glopk (talk) 22:57, 14 June 2009 (UTC)
- Well, this is an encyclopedia, not a higher level math textbook. Any student who just has learned something of probability theory, may (or even will) be confronted with the MHP. The formal solution is no more than an application of Bayes' law, which the student has just met in his course. No Bayesian approach for him. And if the formal solution is presented, in its simple form, the so called Bayesian approach is superfluous. Actually I don't see what it contributes to the article. Nijdam (talk) 22:07, 10 June 2009 (UTC)
- I partially agree with your points above. Indeed the solution of the "conditional" interpretation of the problem would be similarly written in any sane formulation of probability theory, but there are non-trivial differences in the conceptualization of both hypotheses and result. Yes, we could shove these differences under the "purely philosophical" carpet, and come up with a text neutral with respect to probability interpretation. However, I believe that doing so would be a disservice to the reader, for (at least) the following reasons: (1) What a waste of an excellent opportunity to offer the reader a complete and self-consistent treatment, rather than a bunch of pointers. (2) WP editing rules strongly discourage using "weasel expressions" in text, so why accept them in math?
Ok forget about the math, let's tackle the english!
Why does it matter if the host knows or does not know which door the car is behind? If the host does not know and opens up a door the result is either a goat or a car. If it's the car well, he can't offer you a choice of switching, that's just dumb. So once the game has reached the stage of "Do you want to switch?" the math shows it's probably in your best interest to switch. 190.93.76.58 (talk) 05:31, 25 April 2009 (UTC)
- Evidently you haven't read or understood much of the stuff that's already been said about this. It does matter very much how you got to that game state. Having one door open and two doors to choose between can have all sorts of different probabilities on the two doors depending on the rules of the game, how you got there, and what your model of the host behavior is. Dicklyon (talk) 05:36, 25 April 2009 (UTC)
- And yet you [Dicklyon] have missed my point and completely overlooked the heading of my discussion. Math is math. You either get the right answer or the wrong answer. What is intriguing about the Monty Hall problem is common human misconception in deciding weather to switch or not switch and the tendency to choose the outcome not in your best interest. Consider a change up of the old question.
- Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and then the host, says would you like a chance to see what is behind one of the doors you didn’t choose. You say yes. He then asks you to choose another door. So you choose a door No. 3 and it’s a goat. [1]. He then says to you, "Do you want to switch to door No. 2?" Is it to your advantage to switch your choice?
- [1] And in case your wondering if you choose door No. 3 and it’s the car, no you don’t win it. He just says “Too bad, maybe you should have choose door No. 3 first.” You go home knowing you picked the car only at the wrong time.
- As I said math is math. Once your at "Do you want to switch to door No. 2?" the math is the same regardless of knowing/not knowing what is really behind door No. 3. and the rational solution is to always switch. Just remember the original problem states the host knows what's behind door No. 3, it never said he told you he knows.
- 190.93.76.58 (talk) 08:22, 25 April 2009 (UTC)
- Not so. You need to draw yourself a diagram to prove this but if the host opens any unchosen door randomly there are three possibilities each having equal probability. These are: you have chosen a goat and the host reveals another goat (you win by switching), you have chosen a goat and the host reveals a car (game is void), you have chosen the car and the host reveals a goat (you lose by switching). Considering only the non-void games, you have the same probability of winning by switching as you have of losing by switching. The fact that it matters whether the host always opens a door to reveal a goat (in which case he must know where the goat is) or opens either of the two doors not chosen by the player randomly, and we then disregard (or replay) the cases where he happens to reveal a car, is surprising and it is what the Monty Hall problem is all about. Martin Hogbin (talk) 14:04, 25 April 2009 (UTC)
- I think we should stop discussing novel interpretations bases on content-free nonsense like "math is math", and get back to discussing how best to improve the article based on sources. Interpretations and developments not based on sources are irrelevant to our deliberations. Dicklyon (talk) 14:40, 25 April 2009 (UTC)
- Anyone mind if we simply move this thread to the /Arguments page? -- Rick Block (talk) 17:33, 25 April 2009 (UTC)
I am sorry if anyone feels disagreeable to the discussion this topic is on. Just to reiterate this discussion is not about math. If you can’t handle this basic math take a refresher class or two.
My contribution is about the human aspect of the Monty Hall problem whereby enough data is presented to the contestant and he is asked to make a decision and inevitably chooses an answer not in his best interest.
Furthermore the Monty Hall problem is not a mid term math problem where you have 30 minutes to solve it, show all working. You don’t have 30 minutes, you are not required to use only mathematical algorithms, you are on TV and the host is expecting a response in 30 seconds. It is an entertaining puzzle that allows one to look into human psychology.
A “Monty Hall problem” has the following simple characteristics: - there are three doors - there is a prize behind each door - two of the prizes are undesirable one is desirable - you are asked initially to choose one door - subsequently one door which was not chosen is opened to reveled one of the undesirable prizes. - you are then asked “Do you want to switch to door …?” My solution is simply recognize the problem is of type Monty Hall and always accept the switch which is in your best interest.
As for you math purest. The acceptable answers to the Monty Hall problem are “Yes, I will like to switch.” or “No, I do not want to switch.” There is no “If I choose Yes to switch the probability of that is …” response required.
The actual structure of a Monty Hall problem (elegant or not) can change the working of the mathematical solution but it does not affect that in the general sense the option to always accept the switch is never mathematically not in your best interest.
The root of this discussion deals with whether the host knows or does not know what is behind each door and its effect on reveling a door with a goat. The information stated that the host knows what is behind the doors is for an observer to the problem. Remember you are the contestant and you have to arrive at your solution based on the information presented to you. The Wikipedia article does not discuss this in length. 190.93.76.58 (talk) 02:38, 26 April 2009 (UTC)
- What the article says is what reliable sources say about the problem. Are there reliable sources you can point to that are not represented by what the article says? Conversely, if what you're saying is not published in reliable sources it should not (must not) be in the article. -- Rick Block (talk) 03:36, 26 April 2009 (UTC)
- I thought you [Rick Block] might say that. My rebuttal is simply if someone made a comment on the Monty Hall problem based on mathematics which could be shown to be in error you would not include it as part of the article even if it were published. However, I disagree with the logic of some of your "reliable sources" in solving the Monty Hall problem using the assumption that the host knows what is behind the doors just because he was able to open one door and show a goat. Yet you have many citations to "reliable sources" that purport this idea. The Month Hall problem is a simple problem and I am not going to look for a published article that supports my comments. My contribution to the article is from the perspective of the reader, your article structure should not imply any one discussion on the logic aspect of solving the Monty Hall problem is right (or wrong) just by citing sources. Also, your article goes on and on about the different mathematical methods and the varying possible probability solutions, but does not clearly answer the fundamental question asked. Do I switch doors or not?
- 190.93.76.58 (talk) 04:19, 26 April 2009 (UTC)
- The article says (in the lead) "In fact, the player should switch—doing so doubles the probability of winning the car from 1/3 to 2/3.". Is this not clear enough? Regarding the "assumption" that the host knows what is behind the doors, the problem statement (the one from Parade) says "You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door" (emphasis added). This is not an inference based on the fact that the host was able to open a door showing a goat (which indeed some sources argue), but is explicitly given by the problem statement. It would seem you're thinking of some other statement of the problem. If you're not willing to offer published sources supporting your comments, you're on the wrong website. -- Rick Block (talk) 17:00, 26 April 2009 (UTC)
- I can see you have fallen into the Monty Hall trap. Not the trap that argues whether you have a 2/3 or 1/2 chance by accepting the switch but the trap that the Monty Hall problem is a math problem. Seeing just how many educated people are confused just by the implications of the different mathematical permutations to the Monty Hall problem analysis, I can see you "adamantly defending your stand in print."
- Just to be clear. "In fact, the player should switch—doing so doubles the probability of winning the car from 1/3 to 2/3." is not an answer, especially to a question with a riddle component; the answer is "Yes, I accept the switch." notice the full-stop after switch. If you want to support the answer using mathematics go ahead but that is not part of the answer.
- Regarding the "assumption" that the host knows what is behind the doors, the problem statement (the one from Parade) says "You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door" (emphasis added). Who exactly is this information for? If Monty himself was calculating the best odds he was giving his contestant he would arrive at 2/3 chance. How is the contestant to know that Monty knows what's behind the doors. If Monty had clearly said, "Now, before I open the door No. 1 you have chosen let me first open one of the doors with a goat" and then he offered the switch it is clear to the contestant (who is the one playing the game and the one the question is directed to) that Monty knows what is behind the doors.
- As there are rules w.r.t citing sources to support arguments which you keep reminding me this will me my last post since I am not as invested in your Monty Hall article as you are. Just note your article has to glue the citations together for readability, unfortunately it seems you have force fit some of the puzzle pieces together.
- 190.93.76.58 (talk) 18:33, 26 April 2009 (UTC)
Once more, How about we delete the 4th paragraph of the Sources of Confusion section?
Here's what it says:
"Another source of confusion is that the usual wording of the problem statement asks about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open if the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3. In its usual form the problem statement does not specify this detail of the host's behavior, making the answer that switching wins the car with probability 2/3 mathematically unjustified. Many commonly presented solutions address the unconditional probability, ignoring which door the host opens; Morgan et al. call these "false solutions" (1991)."
This is just another Morgan pov. And it adds a non-existent premise, so it's not even addressing the MHP. Please refer to the arguments page http://en.wikipedia.org/wiki/Talk:Monty_Hall_problem/Arguments#This_is_Morgan.27s_Entire_Argument_Against_the_.22Combining_Doors.22_Solution where the Morganians agree that this is not a source of mathematical confusion, but merely Morgan's opinion of what Whitaker is NOT asking. Glkanter (talk) 09:58, 28 April 2009 (UTC)
- I am not sure that I would want to delete this but it certainly should be in an 'academic solutions' section. It is of no relevance at all to the notable MHP. Martin Hogbin (talk) 17:43, 28 April 2009 (UTC)
- Has anything changed since the last time we discussed this 2 weeks ago? -- Rick Block (talk) 00:02, 29 April 2009 (UTC)
The key approach to comprehension of the MHP problem
As experience shows, the fact is not so intuitively and easily observable, that a group of 2 doors that – as per the rule – must inevitably contain one goat at least, one goat that even can be shown later on – can have a chance of winning=2/3. And, "even because" one door must contain a goat, the "other" door quasi automatically consolidates the whole chance of winning of the group, from the beginning, as soon as the player made his choice. That means that the chance of that "other" door is even twice as high as the chance of winning for the single door that the player has individually selected from 3 doors. Of course, actually the simple logic says so, but even mathematicians often have difficulties in recognizing this fact intuitively. And, instead, they look for some mathematical proof, and for this purpose they are making probabilistic evaluations, that always show the same result, however.
A group of 2 doors inevitably contains at least 1 door with a goat that is already guaranteed by the rule. It must contain a goat, as to the rule, thus, from the beginning, without any chance of winning. And this group of 2 gates nevertheless has a chance of winning of 2/3 (???) - There are two doors. Can the door that, as per the rule, contains a goat and no car, can this door have a chance of winning of 1/3? It hardly can. Even "because" of the fact that one door is to contain a goat, and does contain a goat, it has no chance of winning at all. And even "because" of this fact the "other" door has a consolidated chance of the whole group.
I made that edit in the article (unfortunately as IP 62.47.250.187) Gerhardvalentin (talk) 07:40, 30 April 2009 (UTC)
- Lacking references, this amounts to original research which is prohibited (see WP:OR). All Wikipedia content must be verifiable against reliable sources. -- Rick Block (talk) 13:46, 30 April 2009 (UTC)
- Sorry, Rick, everyone can add 1+1=2. Source? Yes, this explanation is the result of my endless discussion abt exactly this approach in German WP. The discussion wasn't successful at all, he refuses to get the point. But by and by, over the months, my perception zeroed in on the point, more and more. And this discussion already did last since February. This contribution in the article was created me alone, by me alone and by nobody but me alone. I did put it in the German WP last night. And I do not guess it is possible than anyone else has formulated this model of approach in similar words. Otherwise it would not be possible that nobody ever made reference to at least a similar view in similar words: "Because of an imperative goat" (in any group of any two doors) - all chance of the group "therefore" is consolidated by the other door that automatically imperatively must have the chance of the whole group. No "theory", but a matter of fact that everyone can see, if he just might glance at this end.
No WO:OR therefore, as it is the result of my very own research. Ask Nijdam, he knows more about the history of my phrasing, as I tried and tried to explain my point of view, initially in Februar, 2008 in German WP.
But I regret Nijdam deleted my contribution "The key approach to comprehension of the MHP" without any comment. I'm going to put it on the page, again. Please comment my point of view, am very interested in first comments. Thank you. Gerhardvalentin (talk) 14:19, 30 April 2009 (UTC)
- Sorry, Rick, everyone can add 1+1=2. Source? Yes, this explanation is the result of my endless discussion abt exactly this approach in German WP. The discussion wasn't successful at all, he refuses to get the point. But by and by, over the months, my perception zeroed in on the point, more and more. And this discussion already did last since February. This contribution in the article was created me alone, by me alone and by nobody but me alone. I did put it in the German WP last night. And I do not guess it is possible than anyone else has formulated this model of approach in similar words. Otherwise it would not be possible that nobody ever made reference to at least a similar view in similar words: "Because of an imperative goat" (in any group of any two doors) - all chance of the group "therefore" is consolidated by the other door that automatically imperatively must have the chance of the whole group. No "theory", but a matter of fact that everyone can see, if he just might glance at this end.
- Something that is the result of your very own research is the definition of WP:OR. I'm deleting this section again. If it is not your own research and you want to add it again, please find a reference. If it is your own research this is not the place for it. -- Rick Block (talk) 03:20, 1 May 2009 (UTC)
Broken figure position
Help, WP-fu black belt needed to please fix the position of the second "goat" figure. It now spans the boundary between two sections (see attached screenshot). This happens in both Firefox 2 and Chrome, with several window sizes. I have tried some obvious tricks, but can't seem to get it right. I think it should be entirely contained withing the "Popular solution" section. glopk (talk) 15:06, 4 May 2009 (UTC)
- I had placed the first figure on the left side of the text. That solved the problem. Someone didn't like it, so they put it back as you see it now. Glkanter (talk) 15:19, 4 May 2009 (UTC)
Mutually Exclusive Published Reliable Sources
Much (most) of our arguing revolves around the conditional/unconditional solutions of the problem. There are published reliable sources that claim any unconditional solution is false, and there are published reliable sources that solve the MHP using an unconditional solution.
So, we get into arguments about which source is more reliable, or who is asking the 'right' question.
Since the two viewpoints can't both be right, we should be able to find the error in one or the other party's logic. I would think in this case OR would have to be acceptable in order to pick the more appropriate alternative.
These are the five previously agreed upon premises:
car is randomly placed
initial pick is random
host must show a goat (and, hence, knows where the car is)
host must make the offer to switch
player decides after the host opens a door
To these I propose adding:
the puzzle is to be solved from the contestant's point of view
the hosts behaviour cannot provide information to the contestant as to the car's location
- As I have posted frequently in the last month or so, this is due to both the definition (nature) of game shows, and in the US, it is forbidden by law.
Of course, I will start with Morgan. Here is the first paragraph following the introduction:
- "1. TO SWITCH OR NOT TO SWITCH
- We begin by enumerating and discussing the most appealing of the false solutions. To avoid any confusion, here is the situation: The player has chosen door 1, the host has then revealed a goat behind door 3, and the player is now offered the option to switch. Thus is the player having been given additional information, faced with a conditional probability problem. The event of interest is "win by switching"; both "lose by switching" and "win by not switching" are complements of this event. For clarity and equality, we refer to the host as "he" and the player as "she.""
What is this 'additional information' they speak of? The only information of any value would be to be told where the car is. Is that what Morgan is saying? That because Monty has given me information as to the location of the car, this is now a conditional problem? I'll call this Case A.
Or is he saying that showing me a goat behind a numbered door in and of itself is 'additional information' that makes this a conditional problem? I'll call this Case B.
Case A: This violates one of the premises, and is eliminated
Case B: As Monty cannot divulge any information as to the whereabouts of the car when he opens the door, his actions can be considered 'random'. When Monty acts in a random manner, the probabilities are exactly equal for the conditional and the unconditional solutions.
Here's Morgan's description of the unconditional problem:
- Solution Fl. If, regardless of the host's action, the player's strategy is to never switch, she will obviously win the car 1/3 of the time. Hence the probability that she wins if she does switch is 2/3.
Here's Morgan's argument against the unconditional solution:
- Fl is immediately appealing, and we found its advocates quite reluctant to capitulate. Fl's beauty as a false solution is that it is a true statement! It just does not solve the problem at hand. Fl is a solution to the unconditional problem, which may be stated as follows: "You will be offered the choice of three doors, and after you choose the host will open a different door, revealing a goat. What is the probability that you win if your strategy is to switch?" The distinction between the conditional and unconditional situations here seems to confound many, from whence much of the pedagogic and entertainment value is derived.
Conclusion: Since Case: A is eliminated, that leaves only Case: B. For Case: B, since the conditional and unconditional probabilities will always be equal, we may use an unconditional solution to correctly determine the probabilities of the Monty Hall problem. This contradicts Morgans criticism of the unconditional solution. Therefore, Morgan's criticism of the unconditional solutions is invalid, and the article should be corrected accordingly. Glkanter (talk) 12:33, 3 June 2009 (UTC)
- I assume by "corrected" you mean deleting what Morgan et al. have to say from the article. Morgan et al. is a paper specifically about the Monty Hall problem published in a peer reviewed math journal that has not been discredited in any way in any published source. As such, it meets Wikipedia:Verifiability and Wikipedia:Reliable sources and whether you like what it has to say or not is irrelevant. It would be a violation of Wikipedia:Neutral point of view to omit what this paper says fom the article. -- Rick Block (talk) 13:19, 3 June 2009 (UTC)
- I would hope that a consensus would be reached whereby the following changes are affected:
- Unqualified recognition of the validity of the unconditional solutions would, of course, diminish Morgan's claim as the only 'true' solution. Noteworthy, perhaps, but not due the emphasis it currently enjoys. There are numerous citations in the article of the unconditional solutions being false, etc., and these would be removed. Extensive discussion of 'variants' would also be less important, as 'host behaviour' would no longer be a necessary component in understanding the solution. I believe these changes would result in a more concise article, leading the reader to a better comprehension of the Monty Hall problem.
- I would hope that a consensus would be reached whereby the following changes are affected:
- Do you agree that the continued publication of unconditional solutions from reliable sources indicates professional disagreement as to the validity of the unconditional solutions? Do you not see this as being a paradox? How can both be right? Who decided that Morgan was 'most' right? Or do you claim that Morgan is 'uniquely' right? Perhaps you could indicate where my analysis is flawed? Or do you believe it is correct? Glkanter (talk) 13:39, 3 June 2009 (UTC)
Don't bother about the US law. It has no jurisdiction in mathematical problems. These are the agreed upon premises:
- car is randomly placed
- initial pick is independent of the position of the car
- host never shows the car
- "random" strategy of the host
- initial pick is door 1
- host opens door 3
- host offers to switch
- player decides after the host opened a door
- what 'probability' does the player have winning the car?
Now what??Nijdam (talk) 22:42, 3 June 2009 (UTC)
- Your questions:
- Do you agree that the continued publication of unconditional solutions from reliable sources indicates professional disagreement as to the validity of the unconditional solutions?
- Not necessarily, and since there has been no "followup paper" anyone has offered that directly contradicts Morgan et al. (and Gillman, and Grinstead and Snell, and Falk) per WP:NPOV the best approach is to present what all "sides" have to say.
- Do you not see this as being a paradox?
- See what? That a peer reviewed paper in a math journal says one thing and then "reliable" popular sources and some (but by no means all) subsequent academic sources say something else? No, I don't see this as a paradox.
- How can both be right?
- As a matter of policy (WP:NPOV), as long as they're all published in reliable sources Wikipedia doesn't care. If you want to discuss this in a personal sense, feel free to do so at the Talk:Monty Hall problem/Arguments.
- Who decided that Morgan was 'most' right?
- No one. The article currently presents both views (right?). I don't see the emphasis you're objecting to.
- Or do you claim that Morgan is 'uniquely' right?
- If this is a personal opinion question, please take it to Talk:Monty Hall problem/Arguments.
- Perhaps you could indicate where my analysis is flawed? Or do you believe it is correct?
- This is another topic for the arguments page and has no relevance here (hint: there's a difference between presenting an unconditional solution as if it addresses the conditional question that is asked, and presenting an argument that the conditional and unconditional solutions must be equal and then presenting an unconditional solution). -- Rick Block (talk) 00:44, 4 June 2009 (UTC)
Just comment on the original dilemma posed at the beginning of this section. From WP's standpoint it should be clear that in doubt if there differing reputable sources, then WP has to mention them both. If we decide to peer review/validate/judge various publication on our own, we are performing OR, which is normally a big no no. Also note, that in such problem as Monty Hall the tricky part is coming up with an appropriate model and there might be more than one appropriate model. The only certain way to exclude a model is , when it yields false predictions, however all models yield correct predictions for the original goat problem.--Kmhkmh (talk) 01:20, 4 June 2009 (UTC)
- Rick, I have suggested removing the following from the 'Sources of Confusion' more than once:
- "According to Morgan et al. (1991) "The distinction between the conditional and unconditional situations here seems to confound many." That is, they, and some others, interpret the usual wording of the problem statement as asking about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open when the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3. In its usual form the problem statement does not specify this detail of the host's behavior, making the answer that switching wins the car with probability 2/3 mathematically unjustified. Many commonly presented solutions address the unconditional probability, ignoring which door the host opens; Morgan et al. call these "false solutions" (1991). Others, such as Behrends (2008), conclude that "One must consider the matter with care to see that both analyses are correct.""
- You have not been in favor of that change to the article. Despite the Behrends quote at the end of the paragraph, this strikes me as a POV that Morgan is right. This was already addressed in the Probabilistic solution section. Why repeat it here? I have advocated for the removal of the 3rd paragraph as well, for essentially the same reason.
- The first item in the 'Aids to understanding' section says:
- "This difference can be demonstrated by contrasting the original problem with a variation that appeared in vos Savant's column in November 2006. In this version, Monty Hall forgets which door hides the car. He opens one of the doors at random and is relieved when a goat is revealed. Asked whether the contestant should switch, vos Savant correctly replied, "If the host is clueless, it makes no difference whether you stay or switch. If he knows, switch" (vos Savant, 2006)."
- If, as I propose, there is agreement that the host must act randomly, then a valid 'editorial' decision could be made to remove this. Why discuss a problem with a different premises that couldn't happen? Why not include a 4 door variant as well? I don't see it as an aid to understanding at all. Besides, as we have discussed, Marilyn describes in this scenario that Monty could reveal the car. So that's a second changed premise. Of course, if Monty reveals a car, there can be no offer to switch, a third changed premise. Now it's Deal or No Deal, with the Host selecting randomly rather than the contestant. Glkanter (talk) 06:43, 4 June 2009 (UTC)
Take a look at the FAQ for this page. Would anyone agree with me that there is a pro-Morgan POV at work here? Glkanter (talk) 14:38, 4 June 2009 (UTC)
By the way, Morgan's entire objection to the unconditional solutions is that it answers the wrong question. I've read numerous comments from what I presume are knowledgeable people that if the host acts randomly, the conditional and unconditional solutions are equivalent. I think I proved he must act randomly, and as Nijdam included this as one of his premises in his response, I guess I'm right.
So it's not just "chocolate is better than vanilla". But I'm sure this "correct vs published" argument gets very old, very fast. Glkanter (talk) 16:01, 4 June 2009 (UTC)
- We've previously discussed deleting the paragraph you dislike from the "Sources of confusion section", twice in fact (see #How about we delete the 4th paragraph of the Sources of Confusion section? and #Once more, How about we delete the 4th paragraph of the Sources of Confusion section?). Is there anything different now that would warrant reconsidering this?
- The "Aids to understanding" section was butchered a while ago since the bulk of it was not referenced. It used to look like this. What remains is essentially an introduction to a section that no longer exists (it was vaguely based on [5], which is not a reliable enough source for a featured article). That this section needs some work does not seem like a reason to delete it.
- Do I understand correctly that you're complaining that the FAQ response explaining the issue you're complaining about is not NPOV? And you're not joking? -- Rick Block (talk) 19:01, 4 June 2009 (UTC)
- Yes, Rick, as you know, I believe your POV is not a NPOV as it relates to the MHP. And that this has a negative affect on the content and utility of the article and the FAQ. There's no point in you and I debating this further. I'm more interested in what other editors have to say. Glkanter (talk) 19:09, 4 June 2009 (UTC)
- Well, no point in debating with me then, because I totally agree with Rick (and Morgan, except for his minor miscalculation). My advice: study the analysis I gave on Talk:Monty Hall problem/Arguments#Analysis and feel challenged to react. Nijdam (talk) 22:04, 4 June 2009 (UTC)
- Yes, Rick, as you know, I believe your POV is not a NPOV as it relates to the MHP. And that this has a negative affect on the content and utility of the article and the FAQ. There's no point in you and I debating this further. I'm more interested in what other editors have to say. Glkanter (talk) 19:09, 4 June 2009 (UTC)
Remove the First Item In the 'Aids to understanding' Section
Here's What It Says:
- "Aids to understanding"
- ""Why the probability is not 1/2"
- "This difference can be demonstrated by contrasting the original problem with a variation that appeared in vos Savant's column in November 2006. In this version, Monty Hall forgets which door hides the car. He opens one of the doors at random and is relieved when a goat is revealed. Asked whether the contestant should switch, vos Savant correctly replied, "If the host is clueless, it makes no difference whether you stay or switch. If he knows, switch" (vos Savant, 2006)."
I'm not sure which readers will find this an 'Aide to Understand' of 'Why the probability is not 1/2'. There are three changed premises:
- Host does not always reveal a goat
- Host does not always offer a switch
- Contestant does not always decide after the door is open
So, while this new puzzle may indeed have a 1/2 probability, I don't see how it answers why the subject puzzle is not 1/2. Further, this puzzle is already included in the 'Variants' section. I suggest it be deleted. Glkanter (talk) 20:50, 5 June 2009 (UTC)
- No one has any comments? Would anyone revert my edit if I deleted the paragraph? Glkanter (talk) 11:24, 7 June 2009 (UTC)
- (repeating from immediately above) The "Aids to understanding" section was butchered a while ago since the bulk of it was not referenced. It used to look like this. What remains is essentially an introduction to a section that no longer exists (it was vaguely based on [6], which is not a reliable enough source for a featured article). That this section needs some work does not seem like a reason to delete it. (end of repeat)
- How about if you or someone else works on expanding this section to explain why in the "classic" MHP the probability is 2/3, but in this version the probability is 1/2? The only one of the three premises you claim are changed in this vos Savant "host forgets" version (relative to the version she originally discussed) is rather than the host must reveal a goat the host has revealed a goat. The situation is all the normal rules apply, except the host momentarily forgets which door the car is behind. Since the show must go on, he guesses and opens a door anyway. This door turns out not to reveal the car. Just like the regular version, the player has picked door 1, door 1 and door 2 are closed, and door 3 is open showing a goat - and we're asked what are the player's chances of winning by staying vs. switching. From the player's viewpoint, it's identical.
- Why the probability is 1/2 in this version but not 1/2 in the "regular" version seems to me to be exactly relevant and should be in this article. There are dozens of sources which contrast these two versions. -- Rick Block (talk) 14:57, 7 June 2009 (UTC)
- This is the link you referenced: http://www.parade.com/articles/web_exclusives/2007/02-04-2007/Marilyn-Readers-Respond
- This is a direct quote from MvS:
- "Here’s one way to look at it. A third of the time, the clueless host will choose the door with the prize, and the game will be over immediately. In our puzzle, that didn’t occur. So we’re considering the two-thirds of the time when either: 1) You have chosen the door with the prize; or 2) The prize is behind the unopened door. Each of these two events will occur one-third of the time, so you don’t gain by switching."
- I do not understand how you can disagree that 3 premises have been changed. This statement:
- "From the player's viewpoint, it's identical."
- is especially egregious. The way you look at it, why bother giving the contestant any rules (problem premises) at all?
- You wrote:
- "That this section needs some work does not seem like a reason to delete it."
- and
- "How about if you or someone else works on expanding this section to explain why in the "classic" MHP..."
- The way I read it, you agree it's not an 'Aid to understanding' in its current form. As I have demonstrated, with 3 premise changes, it is valueless in this section. That's why I have suggested removing it, rather than adding more diarrhea to the article. Glkanter (talk) 16:43, 7 June 2009 (UTC)
- You wrote:
Suggestion
While the discussion may continue forever, I would suggest to edit the article. I would like to start the "solutions" with a correct one, and made the following concept.
Solution
When the player is offered to switch, a new situation has arisen, in which Door 3 has been opened by the host. To make the right decision the player calculates the probability in this new situation of winning the car by switching to Door 2. This probability is a conditional probability (Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137).

The conditional probability of winning by switching given Door 3 has been opened by the host can be determined by referring either to the figure below or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138), or by the use of Bayes' theorem as in the Bayesian analysis section below. For example, if the host opens Door 3 and the player switches, the player wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability 1/6 if the car is behind Door 1 — the possibilities involving the host opening Door 2 do not apply. Hence, by switching to Door 2 the player will win the car twice as often as when sticking to the original choice of Door 1. The conditional probability of winning the car by switching, given the player picks Door 1 and the host opens Door 3, is therefore (1/3)/(1/3 + 1/6), which is 2/3.
Discussion
- So, 'host behaviour' is out? Calling the unconditional solution 'incomplete' or 'false' is out? This is a dramatic improvement over the current 'Probabilistic solution' section. Glkanter (talk) 17:19, 7 June 2009 (UTC)
- I would imagine at least Glkanter and Martin Hogbin will never agree to this, so unless there is overwhelming support from other editors constituting a consensus in spite of these two dissenting opinions this change should not be made. I don't know how many editors watch this page, but I think it might be helpful if everyone who does watch this page can make a brief comment here indicating whether they would support or oppose such a change. I would support such a change, but only if we can amicably resolve what to do with the "Popular solution" section. One possibility might be to simply switch the order of what is currently the "Probabilistic solution" and "Popular solution" sections. -- Rick Block (talk) 17:28, 7 June 2009 (UTC)
- I don't think I've ever exhibited a shyness towards expressing my own opinion, thank you. You need not 'imagine' anything, nor make presumptions as to what I may or may not do, on my behalf. I'll thank you, in advance, for not to setting me up as a straw man. Did you read my comment, above? Is "This is a dramatic improvement over the current 'Probabilistic solution' section." ambiguous in some way? Glkanter (talk) 17:48, 7 June 2009 (UTC)
- Just to be clear, Nijdam is suggesting this new text come before (or perhaps even instead of) the current "Popular solution" section. Are you saying you'd be OK with this? -- Rick Block (talk) 17:57, 7 June 2009 (UTC)
- Have I missed something here? What is the suggested change? Martin Hogbin (talk) 18:35, 7 June 2009 (UTC)
- Nijdam suggests starting a "Solution" section with the text above (see #Suggestion), presumably instead of following the "Problem" section with the current "Popular solution" section. -- Rick Block (talk) 19:54, 7 June 2009 (UTC)
- Thank you, that wasn't clear at all. Entirely remove the unconditional solution from the Solutions? I don't know if I'm on board with that so much. I mean, we wouldn't want the article not to have a NPOV would we? Wouldn't this ignore all the reliable published sources that use the unconditional solution? Glkanter (talk) 18:38, 7 June 2009 (UTC)
- Nijdam hasn't said what he'd propose doing with the "Popular solution" section. So far, he's suggesting only that there be a "Solution" section, and that it start with the above text. Perhaps Nijdam might flesh this proposal out in a little more detail. -- Rick Block (talk) 19:54, 7 June 2009 (UTC)
- Again, thanks Rick, for clarifying. I don't know how I could've interpreted this:
- "Just to be clear, Nijdam is suggesting this new text come before (or perhaps even instead of) the current "Popular solution" section."
- as at least one of you suggesting the removal of the unconditional solution from the article. Glkanter (talk) 20:40, 7 June 2009 (UTC)
- Again, thanks Rick, for clarifying. I don't know how I could've interpreted this:
- About the image: the image shows outcomes where the host has opened both Door 2 and Door 3. The problem statement only talks about the Door 3 outcome, so the entire left half of the image does not apply. That's what "As the host has opened Door 3, this didn't occur" means. This is what it means to be a conditional probability problem. We're not talking about all cases where the player has picked Door 1, only the subset of these cases where the player has picked Door 1 and the host has opened Door 3. It is in this subset of cases where the player is standing on a stage with Door 1 and Door 2 closed and Door 3 open showing a goat. The paradox is that the host has opened a door (say Door 3) leaving only two doors, but yet the probabilities of these two doors are not the same. These probabilities, the ones in effect after the host has opened the door, are conditional probabilities. -- Rick Block (talk) 19:54, 7 June 2009 (UTC)
(out) Indeed, my first suggestion is no more than to start the explanation of the problem with this (correct) solution. Feel free BTW to make suggestions to the text. Nijdam (talk) 09:05, 8 June 2009 (UTC)
- With Nijdam's newly proposed conditional solution, there is no further need for two separate solution sections. They no longer conflict one another. So, why not:
- Rename the 'Popular solution' section as 'Solution'
- Add Nijdam's new conditional solution to this renamed section
- Eliminate the existing 'Probabilistic solution' section
- Add Nijdam's text at the beginning of the renamed section? And what about the text (and figures) in the existing 'Popular solution' section? -- Rick Block (talk) 12:54, 8 June 2009 (UTC)
- As to your other vital concern, which solution comes first: Maybe we should throw you a bone here. I mean, after 4 years and 9 archives, the following aspects of your precious Morgan's paper have been discredited:
- The unconditional solutions are false
- The host may exhibit a behaviour which indicates to the contestant where the car is
- Misquotes Whitaker: "the host, who knows what's behind the doors, opens another door, say No. 3." becomes "the host, who knows what's behind the doors, opens No. 3," —Preceding unsigned comment added by Glkanter (talk • contribs) 22:55, 8 June 2009 (UTC)
- There's a mathematics error in the article
- His conclusion - "In general, we cannot answer the question "What is the probability of winning if I switch, given that I have been shown a goat behind door 3?" unless we either know the host's strategy or are Bayesians with a specified prior. Nevertheless, in the vos Savant scenario we can state that it is always better to switch. The fact that Pr(W | D3) - 1/2, regardless of the host's strategy, is the key to the solution."
- So, I guess from your point of view, Morgan merits top billing. Sorry, I don't see it that way. I would go with Marilyn vos Savant's solution first, which has been supported by countless reliable published sources subsequent to Morgan's article. Given that vos Savant single handedly popularized the MHP in contemporary American culture, I see no reason why her solution wouldn't go first. And please be certain to note: Morgan belongs in the article as it is a reliable, published source. That's in keeping with Wikipedia's NPOV policy. Glkanter (talk) 14:04, 8 June 2009 (UTC)
- It's okay with me if the "popular solution" stays first, as long as the text is a little improved: The player, having chosen a door, has a 1/3 chance of having the car behind the chosen door and a 2/3 chance that it's behind one of the other doors. It is assumed that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen, so, after a door has been opened, the probability of the car behind the chosen door will also be 1/3. And therefore the probability of the car behind the remaining door must be 2/3 (Wheeler 1991; Schwager 1994). Switching doors thus wins the car with a probability of 2/3, so the player should always switch (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8; Martin 2002). Like it?Nijdam (talk) 14:26, 8 June 2009 (UTC)
- Well, I actually are not very happy with the "assumed'. Let me change it into: From the symmetry in the problem it may be proven that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen. Nijdam (talk) 10:46, 9 June 2009 (UTC)
- It's okay with me if the "popular solution" stays first, as long as the text is a little improved: The player, having chosen a door, has a 1/3 chance of having the car behind the chosen door and a 2/3 chance that it's behind one of the other doors. It is assumed that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen, so, after a door has been opened, the probability of the car behind the chosen door will also be 1/3. And therefore the probability of the car behind the remaining door must be 2/3 (Wheeler 1991; Schwager 1994). Switching doors thus wins the car with a probability of 2/3, so the player should always switch (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8; Martin 2002). Like it?Nijdam (talk) 14:26, 8 June 2009 (UTC)
- I realize it's in the current article, but I don't think the 'assumed' in "It is assumed that when the host opens a door..." is necessary. You and I disagreed on the word 'also' in "...so, after a door has been opened, the probability of the car behind the chosen door will also be 1/3." on the arguments page. I think the word 'still' or 'remains' is more appropriate, for the reasons I put forth there. You didn't mention it, does the 'Combining Doors' solution remain in your proposed 'Solution' section? It does in mine. Glkanter (talk) 15:54, 8 June 2009 (UTC)
- I agree with Glkanter. Why 'assumed'. It is no more assumed than many other things in the problem. It is quite obvious that no information is given to the player about what is behind the door she has chosen when the host has opened a door. Anyone who disagrees please answer this question. You have chosen door 1, the host now opens door 3 to reveal a goat. What information does this give you about what is behind the door you have chosen? To be more specific, is the probability that you have chosen a car now more or less than 1/3? Martin Hogbin (talk) 19:32, 8 June 2009 (UTC)
- Actually there is information given to the player and whether or not that results in a modification of the probailities depends on certain assumptions. This is the scenario which was outlined by Morgan and Rosenthal (see under the section other host behaviour in the article). Also the phrasing of the question is no quite accurate. Since the question is not simply "What is the probability for the car being behind door 1?", but rather "What is the probability for the car being behind door 1 under the condition that the host has shown you a goat behind door 3?". At first glance that condition might not matter, however a more detailed modelling of the situation with a P-space constructed from a 3 step experiment (placing the car,select a door, showing a goat) reveals that the condition does matter and only under the assumption that the host select randomly the answer will be 1/3.--Kmhkmh (talk) 21:05, 8 June 2009 (UTC)
- I agree with Glkanter. Why 'assumed'. It is no more assumed than many other things in the problem. It is quite obvious that no information is given to the player about what is behind the door she has chosen when the host has opened a door. Anyone who disagrees please answer this question. You have chosen door 1, the host now opens door 3 to reveal a goat. What information does this give you about what is behind the door you have chosen? To be more specific, is the probability that you have chosen a car now more or less than 1/3? Martin Hogbin (talk) 19:32, 8 June 2009 (UTC)
- OK, I have chosen door 1. I think that we all agree that, if the car was intitially randomly placed, the probability that I have chosen the car is 1/3 before any door has been opened. The host then opens door 3 to reveal a goat. Is the probability that I have chosen a car now more or less than 1/3? Martin Hogbin (talk) 21:19, 8 June 2009 (UTC)
- The exact answer depends on the specified host behavior, but let's assume that if the host has the option to choose from 2 goats, he would always go for door 3. In that case the probability for the car behind door 1 under the condition of having being shown a goat at door 3 is 1/2, so greater than 1/3. --Kmhkmh (talk) 22:09, 8 June 2009 (UTC)
- OK, I have chosen door 1. I think that we all agree that, if the car was intitially randomly placed, the probability that I have chosen the car is 1/3 before any door has been opened. The host then opens door 3 to reveal a goat. Is the probability that I have chosen a car now more or less than 1/3? Martin Hogbin (talk) 21:19, 8 June 2009 (UTC)
- That is a ridiculous answer. You just claimed that information is given to the player that results in modification of the probabilities. I have just given you the exact same information that the player would have received, namely that door 3 has been opened. Kindly tell me what your revised probability is. Martin Hogbin (talk) 22:25, 8 June 2009 (UTC)
- I think you misunderstood my point or I misunderstood the intend of your question. The revised probability is 1/3 in the original problem, i.e. it stays the same. However my point was, that this is not something we can take for granted (hence the example with a revised host begaviour as an illustration, which might not have been helpful for you here). The important argument here is the following. It is a general feature of probility theory that additional information or conditions can change probabilities (basicly the concept of conditional probabilities). That is just a general fact completely independent from the problem at hand. Now being aware of this general fact, we need to assure that in our particular case (the MHP as posed by Vos Savant) the probabilities do not change. We can do that either by assuming it (as it seems reasonable in this oarticular case) or by proving it (doing the actual computation with conditional probabilities and getting as a result that they do indeed not change in this particular case). Since we are looking for an explanation without conditional probablities the proof option is not available and we need to use the assumption instead. That is why the "assumed" wording in the article is justified.--Kmhkmh (talk) 00:10, 9 June 2009 (UTC)
- I have not misunderstood anything, I asked a simple question which you cannot answer, you are just waffling. This page is really for discussion on how to improve the article. I will be happy to continue this discussion on the Arguments page. Martin Hogbin (talk) 09:29, 9 June 2009 (UTC)
- I think you misunderstood my point or I misunderstood the intend of your question. The revised probability is 1/3 in the original problem, i.e. it stays the same. However my point was, that this is not something we can take for granted (hence the example with a revised host begaviour as an illustration, which might not have been helpful for you here). The important argument here is the following. It is a general feature of probility theory that additional information or conditions can change probabilities (basicly the concept of conditional probabilities). That is just a general fact completely independent from the problem at hand. Now being aware of this general fact, we need to assure that in our particular case (the MHP as posed by Vos Savant) the probabilities do not change. We can do that either by assuming it (as it seems reasonable in this oarticular case) or by proving it (doing the actual computation with conditional probabilities and getting as a result that they do indeed not change in this particular case). Since we are looking for an explanation without conditional probablities the proof option is not available and we need to use the assumption instead. That is why the "assumed" wording in the article is justified.--Kmhkmh (talk) 00:10, 9 June 2009 (UTC)
- That is a ridiculous answer. You just claimed that information is given to the player that results in modification of the probabilities. I have just given you the exact same information that the player would have received, namely that door 3 has been opened. Kindly tell me what your revised probability is. Martin Hogbin (talk) 22:25, 8 June 2009 (UTC)
- It's not an 'assumption' at all. It's part of the definition of a 'game show'. So, the sentence would say, "Based on the rules of game shows...". But why would that qualification be necessary at all? Glkanter (talk) 23:48, 8 June 2009 (UTC)
- It is an assumption for the mathematical analysis (i.e. the game show regulation translates into an assumption for the simplified undontional math model). Also note however that original MHP afaik did not bother with game show regulations. Furthermore you cannot assume an average WP reader to be aware of specifics of US gameshow rules & regulations or legal issues even. In short such things cannot be taking for granted and should be stated explicitly. P.S. I somehat revised my posting to Martin to make the point more clear I hope, while you were posting your answer.--Kmhkmh (talk) 00:10, 9 June 2009 (UTC)
- It's not an 'assumption' at all. It's part of the definition of a 'game show'. So, the sentence would say, "Based on the rules of game shows...". But why would that qualification be necessary at all? Glkanter (talk) 23:48, 8 June 2009 (UTC)
- Yes, it's been debated ad nauseum on this talk page and on the arguments page whether the host is required to choose randomly when faced with two goats. This phrase from Whitaker, which comes very early in the Wikipedia article, brought that debate to a standstill:
- "Suppose you're on a game show..."
- Game show hosts don't reveal the whereabouts, or give clues as to the whereabouts, of the prize in a game like this. In the US, that would be illegal, as evidenced by the Quiz Show scandals of the 1950s. By virtue of this being a puzzle about a game show, from the contestant's point of view, it is therefore a premise that Monty acts randomly. At this point, based on his proposal, I believe Nijdam agrees. Maybe, Rick, too. I can't really be sure about either of them. Maybe they will volunteer what their views are. Glkanter (talk) 21:37, 8 June 2009 (UTC)
- The above response is only in regard to the word 'assumed' in the unconditional solution. I have stated earlier that I understand that Morgan should be included in the article as per Wikipedia NPOV, as for the time being anyway, it is regarded as a reliable published source. Glkanter (talk) 21:49, 8 June 2009 (UTC)
- Well it is a consequence of the conditional solution (or more precisely of a more detailed/accurate model in which you use conditional propabilities), that you need to use the word "assumed" in the unconditional solution. Anyhow in case the editors cannot agree on the exact wording here, then one obvious solution would be to ask the math portal for review/3rd opinion on the wording in question. It is in general a good idea, when doing (bigger) edits on a "difficult" article with the editors disagreeing, to make sure independent experts (best source for that in WP is the math portal) do review it.--Kmhkmh (talk) 22:09, 8 June 2009 (UTC)
- The above response is only in regard to the word 'assumed' in the unconditional solution. I have stated earlier that I understand that Morgan should be included in the article as per Wikipedia NPOV, as for the time being anyway, it is regarded as a reliable published source. Glkanter (talk) 21:49, 8 June 2009 (UTC)
- As for whether 'still' or 'remains' is preferable to 'also', I reference Nijdam's response on the arguments page http://en.wikipedia.org/w/index.php?title=Talk:Monty_Hall_problem/Arguments&diff=294935860&oldid=294935109. Glkanter (talk) 22:09, 8 June 2009 (UTC)
Can we please return to the original issue. Nijdam has proposed some major changes, I have further defined how I would like to see his proposed changes implemented. Glkanter (talk) 23:51, 8 June 2009 (UTC)
- I'm not sure I understand the proposal at this point. Is it essentially:
- replace the content currently under "Probabilistic solution" with the text above
- delete the heading "Probabilistic solution"
- change the heading "Popular solution" to "Solution"
- This basically deletes the first and third paragraphs in the "Probabilistic solution" section. Is this the substance of the proposal? -- Rick Block (talk) 01:53, 9 June 2009 (UTC)
- So close, Rick! You got 2 out of 3! Here's what I'm suggesting:
- Change the heading "Popular solution" to "Solution"
- Add Nijdam's new conditional solution to this renamed section
- Delete the "Probabilistic solution" section
- This will result in a a single 'Solution' section Glkanter (talk) 03:51, 9 June 2009 (UTC)
- So close, Rick! You got 2 out of 3! Here's what I'm suggesting:
- I don't see how this is different from what I said, but in any event I think the third paragraph in the existing "Probabilistic solution" section (the 1/1+q solution) should go somewhere and the bit in the first paragraph explaining the difference between conditional and unconditional should go somewhere as well. I'm not sure Nijdam was suggesting deleting these. To make this more concrete, I've created a version with the suggested changes at User:Rick Block/Monty Hall problem (draft). -- Rick Block (talk) 12:51, 9 June 2009 (UTC)
- I have formulated on User: Nijdam/conceptMHP my ideas about the beginning of the solution section. On second thoughts I left the simple solution as 'simple explanation' as I mentioned above at the start. Nijdam (talk) 15:02, 9 June 2009 (UTC)
You know, I only took an editor's interest in this problem because the way the solution was presented when I first looked at the article, I would not have been able to use the article to get paid off on a bar bet. Now, with Rick's version, I am certain I would get paid. With Nijdam's I think I would get paid. But it would be easier with either or both of the unconditional images and some related text. So, as long as 'host behaviour' is nowhere near the 'Solution' section, and the single obligatory mention of 'Morgan says the unconditional solution is false' is somewhere else in the article (not in the Solutions section) and is immediately followed by the statement, 'this viewpoint is not shared universally in the professional community' I'm good. Glkanter (talk) 15:50, 9 June 2009 (UTC)
Here's a direct question. Rick, will you be part of a consensus that de-emphasizes 'host behaviour' and 'the unconditional solution is false'? While staying true to the spirit of Wikipedia NPOV? Do you support Nijdam's proposed changes? Glkanter (talk) 19:58, 9 June 2009 (UTC)
- What I support is any version that meets Wikipedia:Featured article criteria (which explicitly includes all policy requirements, like WP:NPOV). Do you seriously think the version you're suggesting is better than, say, this version, which is how it looked after the last WP:FAR? The solution section in that version says the answer is 2/3, using both an unconditional and conditional approach (introducing the conditional solution as answering a "subtly different question"). The conditional solution in that version (which, as I recollect, you violently disliked) seems strikingly similar to Nijdam's version (which you seem to be OK with). Frankly, I'm puzzled. -- Rick Block (talk) 03:33, 10 June 2009 (UTC)
- Well, since that version starts with this incredible blunder:
- "The overall probability of winning by switching is determined by the location of the car.", I don't like it at all.
- But essentially, as I expected, this is just another of your stalling techniques. The only real comparison worth making is between the article as it is today, versus what Nijdam is proposing. But you know that. So, your stalling, and delaying, and obfuscating continues unabated. You put up pages so other editors will waste time on various drafts, with no honest intention of being part of a consensus to actually implement these changes. That shows a great disrespect for us other editors. Why not answer my direct questions above, instead? Glkanter (talk) 04:02, 10 June 2009 (UTC)
- Well, since that version starts with this incredible blunder:
- No, the only real comparison worth making is the state of the article now (or with any proposed change) to when it was last reviewed by the broader community. Are you trying to goad me into some incivility here? It won't work, so you might as well stop. My answer to your questions is what I said above. I'll support any version that meets WP:FACR. So, as long as de-emphasizing "host behavior" and the criticisms of the unconditional solution doesn't violate criteria 1b, and so long as the new version is WP:NPOV (this is a given), and so long as what's deleted from Nijdam's version ends up somewhere (that pesky 1b thing again), I'm good. This is what I meant. In comparison to the version I mention, I think the current and proposed versions don't measure up regarding 1a (and 3), either. -- Rick Block (talk) 04:42, 10 June 2009 (UTC)
- I didn't ask if it needed to be clearly stated as a premise, I asked approximately 'since this is a story problem about a game show, can it be interpreted any other way?' And I'm limiting this question to the MHP as presented by Marilyn vos Savant. I have little interest in different puzzles with different premises. But, no offense, I am primarily interested in Rick's point of view, as his concurrence is essential in reaching a consensus. Glkanter (talk) 09:31, 10 June 2009 (UTC)
- Yes it can, the original formulation by vos Savant made no statement regarding the host behaviour. Hence strictly speaking the question as posed by Vos Savant gives already rise to different variations and they are not simply different but related puzzles. From Vos Savants suggested solution however you can conclude, that it was to be understood that way, that the host picks randomly if he can. This is not just an issue regarding Rick but it has to do with factual correctness, meaning the answer to your posed question is yes (no matter Rick) whether personally sees it that way or not). In fact you just have to read the problem paragraph of current article to see that the answer is yes.--Kmhkmh (talk) 03:11, 11 June 2009 (UTC)
- I didn't ask if it needed to be clearly stated as a premise, I asked approximately 'since this is a story problem about a game show, can it be interpreted any other way?' And I'm limiting this question to the MHP as presented by Marilyn vos Savant. I have little interest in different puzzles with different premises. But, no offense, I am primarily interested in Rick's point of view, as his concurrence is essential in reaching a consensus. Glkanter (talk) 09:31, 10 June 2009 (UTC)
- Please address the salient point. The MHP is a story problem about an American game show. That the host cannot give out info on the car's location is already a premise in that it's a game show. It's counter-intuitive to think the host would give out this info. If he did, they would stop filming, and start over. The host giving out info on the location of the car is eliminated because its a game show. Glkanter (talk) 04:10, 11 June 2009 (UTC)
- I think there is a misunderstanding. There are variations of the host behaviour, where the host does not reveal the car, but can distort the probabilities nevertheless. This exactly what Morgan explained in his paper. In other words you can assume that the host never reveals the car (because it is a game show), but you cannot automatically assume that the host picks randomly when he can choose between 2 goats.--Kmhkmh (talk) 19:22, 11 June 2009 (UTC)
- Please address the salient point. The MHP is a story problem about an American game show. That the host cannot give out info on the car's location is already a premise in that it's a game show. It's counter-intuitive to think the host would give out this info. If he did, they would stop filming, and start over. The host giving out info on the location of the car is eliminated because its a game show. Glkanter (talk) 04:10, 11 June 2009 (UTC)
- Well, this guy http://en.wikipedia.org/wiki/Keith_Devlin would be part of it. He published this unconditional solution http://www.maa.org/devlin/devlin_07_03.html in 2003. There's plenty more. How many more than 1 reliable sources that are a Consulting Professor in the Department of Mathematics at Stanford University, do I need for the above statement to be true, correct, valid and, most importantly, be in the spirit of FACR 1b? Glkanter (talk) 09:39, 10 June 2009 (UTC)
- Ok, so i guess professional community then means scientists which would be ok by me. I took a look at Devlin's column and I agree that Devlin is a quotable source. However but imho it doesn't really prove your claim. To be more precise, what Devlins show that some mathematicians consider the simply unconditional as ok. However it doesn't really make statement regarding conditional solution and its potential superiority (or lack thereof), this means you cannot really tell from that column wether Devlin explicitly disagrees with Morgan or not.--Kmhkmh (talk) 03:11, 11 June 2009 (UTC)
- Well, this guy http://en.wikipedia.org/wiki/Keith_Devlin would be part of it. He published this unconditional solution http://www.maa.org/devlin/devlin_07_03.html in 2003. There's plenty more. How many more than 1 reliable sources that are a Consulting Professor in the Department of Mathematics at Stanford University, do I need for the above statement to be true, correct, valid and, most importantly, be in the spirit of FACR 1b? Glkanter (talk) 09:39, 10 June 2009 (UTC)
- Would Devlin, or any reliable source, publish an unconditional solution if they (without even knowing of Morgan) thought it was 'false'? Of course not. The statement 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.' is nothing more than a statement of fact. And I made no inference whatsoever to the relative merits of the different solutions. Neither should anyone else. Glkanter (talk) 04:10, 11 June 2009 (UTC)
- It is not that simple. Devlin (or similar resources) do allow to describe the simple solution as correct, however the article does that already in a proper fashion (Morgan et al. call these "false solutions" (1991). Others, such as Behrends (2008), conclude that "One must consider the matter with care to see that both analyses are correct."). In more general terms the assessment of "true" and "false" is question of the perspective under which the problem is analysed. Basically you have 2 models to explain/describe a real world problem: A (complex,conditional, Morgan et et al) and B (simple, unconditional, Devlin et al). Both models describe the problem nicely and predict the empiric result correctly. In that sense both solutions are correct and following Ockham's razor you can argue to prefer B. However A is the more powerful theory that allows you to treat problem generalizations and variations as well - in particular different host behaviours. From that perspective you can consider A as "better" or "more correct", because it provides a "deeper insights" and allows you to understand why B fails for other host behaviours. To pick a crude analogon from physics it is like arguing whether newtonian or einsteinian mechanics are correct or more precisely whether newton is "false" since we know Einstein. As far as the article is concerned it needs to contain both solutions and describe them both as correct. However it also should note Morgan's perspective that from a more a more general perspective B is "false" (or more friendly put inferior and providing less inside than A). Note that the quotes in "false" are absolutely essential, because false is to be understood as described in the brackets and not as plain false. This description in italic follows exactly from the sources and is already described in the current article as it is.--Kmhkmh (talk) 19:10, 11 June 2009 (UTC)
- Would Devlin, or any reliable source, publish an unconditional solution if they (without even knowing of Morgan) thought it was 'false'? Of course not. The statement 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.' is nothing more than a statement of fact. And I made no inference whatsoever to the relative merits of the different solutions. Neither should anyone else. Glkanter (talk) 04:10, 11 June 2009 (UTC)
- You wrote: "From that perspective you can consider A as "better" or "more correct", because it provides a "deeper insights" and allows you to understand why B fails for other host behaviours." Yes, I'm familiar with the opinion that this article should be treated as a primer in Logic and Probability, rather than solely addressing the MHP. I don't agree with that viewpoint. And NPOV says we should not judge which might be better. Glkanter (talk) 19:26, 11 June 2009 (UTC)
- We don't judge, but we paraphrase Morgan's publication (i.e. there is no NPOV issue here). And when addressing the MHP it is a fact, that the unconditional solution only models one interpretation of the MHP (as stated by vos Savant) correctly, while the conditional solution models other interpretations correctly as well. That is not a viewpoint but a fact. We don't have to use the term "better", but we can (and should) paraphrase Morgan (or similar sources) and we can (and should) state the fact given in italic the line before.--Kmhkmh (talk) 21:05, 11 June 2009 (UTC)
- You wrote: "From that perspective you can consider A as "better" or "more correct", because it provides a "deeper insights" and allows you to understand why B fails for other host behaviours." Yes, I'm familiar with the opinion that this article should be treated as a primer in Logic and Probability, rather than solely addressing the MHP. I don't agree with that viewpoint. And NPOV says we should not judge which might be better. Glkanter (talk) 19:26, 11 June 2009 (UTC)
- Kmhkmh, you wrote this above:
- "To be more precise, what Devlins show that some mathematicians consider the simply unconditional as ok."
- You agree Devlin is a reliable source, meeting your standard as a member of the professional community. Can Devlin say it is both "ok" and "false" at the same time?
- How can you still take issue with this simple, NPOV statement: 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.'? Glkanter (talk) 18:47, 11 June 2009 (UTC)
- yes he can because the answer is depending on context/perspective (see explnanation) above. Meaning Devlin argues from the context of giving the most simple explanation for most commonly assumed host behaviour and in that context the unconditional solution is correct. But Devlin makes no statement whatsoever regarding a advanced persptective from which you could consider the unconditional solution as false, in that sense he does not contradict Morgan at all. As far as the formulation goes false needs to be in quotes and I don't like the term professional community, since it is ambiguous to me. The current formulation (Morgan et al. call these "false solutions" (1991). Others, such as Behrends (2008), conclude that "One must consider the matter with care to see that both analyses are correct.") is imho better and more correct since after all wie just repeat the takes of a few mathematicians rather than the mathematical community at large. --Kmhkmh (talk) 19:10, 11 June 2009 (UTC)
- Alas it is not that simple. Morgan is absolute right when he states that the unconditional solution, of course not for the numerical answer, but for its way of reasoning, is false, wrong. And, as far as I know, none of the advocates of the unconditional solution has commented on Morgan's paper. The big problem is, it spreads illogical thinking, and as it sounds very attractive, it is adopted by many people, among them, as I mentioned before, pupils, teachers and students, who should being taught better. So it is my goal, within the rules of Wikipedia, to set this straight.Nijdam (talk) 19:33, 11 June 2009 (UTC)
(outindented)The quote from Behrends must not be considered out of its context. Here is the complete end of the chapter, of which the first part is completely concerned with the correct treatment in calculating the conditional probabilities (and especially the introduction of the concept for this purpose). Behrends made his last remark after being tipped by a German professor:
- Actually as far as WP is concerned it is rather simple - descriptions of reputable sources are repeated here, the rest stays out. Devlin is such reputable source, therefore considering unconditional solution in WP as correct is ok. And Devlin is by far not the only reputable mathematician stating it that way, Henze (statistics professor at the university of Karlsruhe) gives more or less the same treatmeant in his German probability textbook Stochastik für Einsteiger (Vieweg 1997), further examples are in the sources of the WP article). So to be rather clear : There is nothing to be set straight here. The unconditional solution is neither false nor illogic and students or teachers picking it up do correctly though. However it is true that the unconditional is inferior from a general perspective, that however is not really a question of true or false. --Kmhkmh (talk) 20:51, 11 June 2009 (UTC)
- So, Kmhkmh says "So to be rather clear : There is nothing to be set straight here. The unconditional solution is neither false nor illogic..." but continues to support Morgan's statement that 'The unconditional solution is false".
- No offense, but you need to make up your mind, whether you want to quote out of context to score rhetoric points or whether you want to argue content. Above i explained rather clearly that the notion of "false" and "true" depends on the perspective/context under which the problem is analyzed. And again Devlin is not contradicting Morgan (directly) since he is arguing from a different perspective and he is not making Morgan obsolete or superseeding him. Both Morgan and Devlin are correct from their given perspective, both are reputable sources and both can and should be quoted in the article.--Kmhkmh (talk) 15:32, 12 June 2009 (UTC)
- Nijdam says of Devlin (a Consulting Professor in the Department of Mathematics at Stanford University), who actually took the time and effort to publish an article on the MHP, "Well Devlin may be a source, as a source on the MHP he is not reputable." Somehow, however, Nijdam proclaims himself the ultimate arbiter of who is reliable, and finds he is he.
- Nijdam is wrong here regarding Devlin however that doesn't make you right. Imho you would both do the article a favour if you keep your respective condtional-probilities- are-just-an-academic-distraction and everything-must-be-explained-by-conditional-probabilities agendas out, since neither is appropriate nor backed up by all of the reputable sources.--Kmhkmh (talk) 15:32, 12 June 2009 (UTC)
- I have been recently been reminded that it is insanity to repeat the same steps over and over, expecting different results. I chose sanity. Glkanter (talk) 02:59, 12 June 2009 (UTC)
- It looks like Kmhkmh agrees with me, We have essentially two formulations and solutions. The simple (unconditional) and the academic(conditional). We currently have both of these in the article, which I support. The only change that I would like to see is greater separation of these two formulations, so that each has its own sources of confusion and aids to understanding sections. My suggestion is that those who favour the unconditional solution should contribute mainly to the unconditional section and vice versa. Martin Hogbin (talk) 19:59, 12 June 2009 (UTC)
- So, Kmhkmh says "So to be rather clear : There is nothing to be set straight here. The unconditional solution is neither false nor illogic..." but continues to support Morgan's statement that 'The unconditional solution is false".
- I don't know on what there might be agreement. Let me say I also agree with you, if that's what you mean, that one may formulate a problem, to be called 'unconditional problem', to which the simple explanation is the solution. It reads in short: 3 doors, random car, pick a door, what is the probability you pick the car, or if you prefer: what is the probability you did not pick the car. Interesting? The MHP deals with the extra of opening a door.
- You seem to be at odds with everyone else here. Rick, Glkanter, Kmhkmh, myself, and Morgan all agree that the full MHP (in which a door is opened by the host) can be formulated unconditionally. Morgan give an unconditional formulation of the problem in their paper. Martin Hogbin (talk) 21:57, 13 June 2009 (UTC)
- Speak for yourself. IMO, the MHP is a conditional problem. Period. Full stop. I'm going to start a new thread on this below since this thread is already too long. -- Rick Block (talk) 22:59, 13 June 2009 (UTC)
This argument can be refined a bit. Let p1, p2, p3 denote the probabilities that the auto is hidden behind door 1, door 2, door 3. Then if door 1 is chosen, the probability of "the car is won without switching doors" is equal to p1, and the probability of "the car is won in switching doors" is equal to p2 + p3.
It is possible that some readers might be puzzled by the fact that in the second analysis the actions of the quizmaster apparently play no role. One must consider the matter with care to see that both analyses are correct.
In the first analysis the initial situation was given thus: Door 1 is chosen, door 3 (with the goat) is opened. And from this one has to determine the relevant probabilities.
In the second analysis the situation was different. The action of the quizmaster was irrelevant, and one should switch in any case. Nevertheless, it is intuitively difficult to see that this different information is responsible for the different probabilities.
Note already the problem he gets: p3 = 1/3, but also p3 = 0?! Then see what he says about both the situations: the situations are different. Nijdam (talk) 21:41, 11 June 2009 (UTC)
- It is true that Behrens states that the 2 solutions strictly speaking adress slightly different problems. However despite the subtle differences both can be understood as valid solutions to the MHP with all its ambiguities. So in that sense current current description in the article is still ok imho. However if you feel the quote or description of Behrens argument is somewhat misleading, you could use Devlin or Henze instead. I don't think any of the referenced mathematicians for the unconditional solution can be understood as contradicting Morgan or the "superiority" of the conditional solution, they do however apparently consider the unconditional solution as a "good enough" explanation and so should we as far the description in WP goes.--Kmhkmh (talk) 00:18, 12 June 2009 (UTC)
- You're right in that it's a "good enough" explanation, and so it should be presented, but as a solution it's wrong. I hope the mathematicians, not always probabalists, are well aware of this fact. Although I have my doubts as turned out in discussions with some of them. Nijdam (talk) 10:49, 12 June 2009 (UTC)
- Let me ask you straight: are you able to formulate, in correct mathematics, an "unconditional solution" to the MHP (as stated above)? If so, I very much like to see it. If not, don't doubt your math skills, no-one can. That's my drive in the discussions here and elsewhere. Nijdam (talk) 21:25, 13 June 2009 (UTC)
- You're right in that it's a "good enough" explanation, and so it should be presented, but as a solution it's wrong. I hope the mathematicians, not always probabalists, are well aware of this fact. Although I have my doubts as turned out in discussions with some of them. Nijdam (talk) 10:49, 12 June 2009 (UTC)
(outindented)Well Devlin may be a source, as a source on the MHP he is not reputable. That is a problem for Wikipedia, not every source is reliable. And as we have to mention this type of so called solution as Devlin's, which BTW is definitely false and illogic, we may do it in confrontation with Morgan's, telling that in his paper such a solution is called false.Nijdam (talk) 21:49, 11 June 2009 (UTC)
- Let us not put too much emphasis on Devlin. He may be mentioned, but with a critical note referring to Morgan. Devlin just wrote about the problem in his popular column, and what he wrote was mainly a paraphrasing of Marylin's popular explanation. I emailed Devlin about it, but he prefers to stay low. The 'plenty more' is not an argument pro, it mainly shows how most people easily get confused and do not think for themselves. Nijdam (talk) 11:06, 10 June 2009 (UTC)
- Those are interesting opinions you have. Are you suggesting Devlin has retracted this work publicly? Would you also discount every other equally qualified source I provided for the same reasons? Is this consistent with FACR 1b? How is disregarding a reliable, published source like Professor Devlin's, because your opinion is "it mainly shows how most people easily get confused and do not think for themselves" remotely consistent with NPOV? Rick, you're pretty big on NPOV, what are your thoughts on this? Glkanter (talk) 11:12, 10 June 2009 (UTC)
Glkanter - you've asked several questions:
Given that Whitaker starts "Assume you're on a game show...", can the problem be interpreted any way other than 'Monty acts randomly when faced with two goats'? In the context of this page (talk page for the article), the only thing that matters is what reliable sources say. Plenty of reliable sources interpret it in other ways, so yes. If you're asking what I think the Truth is, this is a question for the Arguments page, not here, but I think the answer is yes.
Would something close to this satisfy FACR 1b in your mind: 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.'? This phrasing is problematic from several viewpoints. First, it's not NPOV, but stated in a way that casts doubt on Morgan's claim. Second, it says something the sources you're referring to don't actually say which is a WP:V issue. You could say "Subsequent sources present unconditional solutions", but that's not quite the same (you see the difference?). Third, this is not enough to explain the conditional vs. unconditional issue so if this is all the article says about it 1b is not satisfied either. There should be an explanation like the first paragraph in the current version of the "Probabilistic solution" section somewhere.
- Would Devlin, or any reliable source, publish an unconditional solution if they (without even knowing of Morgan) thought it was 'false'? Of course not. The statement as I presented it is nothing more than a statement of fact. Glkanter (talk) 02:11, 11 June 2009 (UTC)
(paraphrased) How do we treat Devlin and others who have presented unconditional solutions subsequent to Morgan et al. in an NPOV manner? Like anything else, we must say what they say, no more and no less. Many of them say things Morgan et al. discredits, but none of them (as far as I know) specifically say anything about the issue Morgan et al. brings up. We can't invent a response to Morgan et al. on their behalf. We can't assume they've seen Morgan et al. or are aware of the central issue raised unless they reference it in some way. The closest I've ever seen is vos Savant's letter to the editor (American Statistician, Nov 1991, pp 347-348) following the publication of Morgan et al., in which she says "Pure probability is the paradigm, and we published no significant reason to view the host as anything more than an agent of chance who always opens a losing door and offers the contestant the opportunity to switch". This can be taken to mean she considered the host to pick randomly when faced with two goats to pick from, but does not address the central criticism raised by Morgan et al. which is that the problem is inherently conditional and an unconditional solution is therefore a "false" solution. The NPOV approach is we say what Devlin says, and we say what Morgan et al. (and Gillman, and Grinstead and Snell, and others) say as well. Since Morgan et al. (and the rest) say the question is inherently conditional we say that. But since the unconditional "side" says nothing in response we can't put words in their mouths. -- Rick Block (talk) 01:20, 11 June 2009 (UTC)
- I don't like your paraphrasing. Please respond to the thread as posted. Do you support Nijdam's response? Is that consistent with your understanding of Wikipedia NPOV? Glkanter (talk) 02:11, 11 June 2009 (UTC)
Sources of confusion
The current section 'Sources of confusion' is, to say the least, confusing. It attempts to address at least three issues at once. These are:
1) People get the answer wrong even in the unconditional problem.
2) The rules of the game are uncertain.
3) The issue of conditional probability and the added confusion that this adds to an already difficult problem.
I suggest that 2 is dealt with earlier in the article so that here we are dealing only with the 'standard rules' version.
1 and 3 could either be dealt with in the same sections as their related solutions or should have sub-headings within this section.
Any comments? Martin Hogbin (talk) 21:32, 8 June 2009 (UTC)
- As I read it the section addresses the major reasons why so many people get the answer wrong. It says:
- people get the answer wrong
- people answer what they think the question says rather than what it actually says (this is quite different from the rules being uncertain)
- people think N unknowns each have probability 1/N whether this is the case or not
- people think revealing something that is already known cannot affect conditional probabilities whether this is the case or not
- people are unaccustomed to dealing with conditional probabilities (sort of a generalization of the previous two)
- All of these are meticulously sourced. Distributing them throughout the article rather than keeping them together in one section seems like a strange idea. -- Rick Block (talk) 01:41, 9 June 2009 (UTC)
I am trying to fine some kind of compromise between the views of Glkanter and myself that the notable Monty Hall problem is the simple (unconditional if you like) formulation and the conditional formulation is, at best, an academic diversion; and the views of yourself and Nijdam that the conditional formulation is the only correct one. Both sides are supported by reliable sources and I do not think that the conflict will be resolved by a 'battle of the sources'. My suggestion is that the article remains much as it is with the two solutions given, both properly sourced, but with their own sections on confusion and understanding. I suggest that it might be generally better to allow the supporters of each formulation to decide the wording in that section. Of course, this does not stop anybody from commenting or editing anywhere. Martin Hogbin (talk) 17:10, 9 June 2009 (UTC)
Concept
I mentioned this before: I have formulated on User: Nijdam/conceptMHP my ideas about the beginning of the solution section. On second thoughts I keep the simple solution as 'simple explanation'. What has to follow, like the different host strategy, may be dicussed later on. Please mention your comment or just your approval. Nijdam (talk) 11:17, 10 June 2009 (UTC)
- Perhaps you and Rick would first agree on whose document we should be working on. I prefer Rick's, in that it has the entire article, so that issues like 'where to discuss host strategy' can be fleshed out. Glkanter (talk) 11:22, 10 June 2009 (UTC)
- Can we draw a line in your version of the article up to the point were we agree on the text. As you may have seen in my concept, I don't want to change the introduction. I like to start the solutions with explicit naming the simple explanation. I changed the "assumed", to put more weight on the fact that some proof is omitted. Further I'm not happy with the accompanying picture, as it doesn't meet the conditions of the problem. In the problem formulation Door 1 is chosen, and the picture shows different chosen doors. Actually I would not put much emphasis on the simple explanation. Nijdam (talk) 22:26, 10 June 2009 (UTC)
- I forgot to say we may work on Rick's version, and consider my concept just as a proposal. Nijdam (talk) 22:29, 10 June 2009 (UTC)
- Nijdam, while I am enthusiastic to contribute, I have a concern. Will we be following the established protocols of Wikipedia, especially NPOV and FACR, or will be expected to operate according to your personal opinions regarding the reliable, published sources that use the unconditional solution? Here's an example:
- "Let us not put too much emphasis on Devlin. He may be mentioned, but with a critical note referring to Morgan. Devlin just wrote about the problem in his popular column, and what he wrote was mainly a paraphrasing of Marylin's popular explanation. I emailed Devlin about it, but he prefers to stay low. The 'plenty more' is not an argument pro, it mainly shows how most people easily get confused and do not think for themselves. Nijdam (talk) 11:06, 10 June 2009 (UTC)"
- Nijdam clearly has an opinion about what is "correct" (as do you, Glkanter). Similar to Wikipedia:Autobiography, it is sometimes difficult for experts to write in a way that is truly based on cited sources rather than what they know to be true. This is not at all to say that experts shouldn't write in their own field. Just that experts need to be particularly careful about injecting their own opinions into what they are writing. The way to tell whether this is going on is to look at each sentence and figure out specifically what reference it came from (and where). I haven't checked all the references, but I sort of doubt the second sentence in Nijdam's "Simple solution" came from one of them. BTW - this general structure looks promising to me and other than this one sentence seems very good. -- Rick Block (talk) 01:50, 11 June 2009 (UTC)
- I take the liberty to have my own opinion on this talk page. How far this will influence my suggestions about the article will depend on the sources that support my opinion. At least we have Morgan and as a other sources (the numbers doesn't matter in fact) are not in line with this, it seems to me not sufficient just mentioning them both, leaving the readers in uncertainty. BTW I changed the questionable second sentence. Nijdam (talk) 10:19, 11 June 2009 (UTC)
- Since there are reliable, published sources on both sides of the 'unconditional solution' question, of course the reader will be left with uncertainty. How could it be otherwise, without violating NPOV? The question is, how much time and text should be spent addressing it? And while your opinion may be interest, when you use it to 'win' arguments by violating Wikipedia standards, then not so much. To deny Devlin equal stature in this article as Morgan? Because you disagree with him, and think him lazy? Horse feathers! Glkanter (talk) 11:10, 11 June 2009 (UTC)
- In response to this question:
- "Will we be following the established protocols of Wikipedia, especially NPOV and FACR, or will be expected to operate according to your personal opinions regarding the reliable, published sources that use the unconditional solution?"
- You appear to have replied:
- "How far this will influence my suggestions about the article will depend on the sources that support my opinion."
- Should I interpret that as "We will only follow established protocols of Wikipedia, such as NPOV and FACR, when it is to my liking?" Glkanter (talk) 11:35, 11 June 2009 (UTC)
- In response to this question:
Variation where Monty doesn't know
Extract from reverted edit:
- "However, after a door opened and a goat revealed, the outcomes and the probabilities immediately shifted back to those of the classical Monty Hall problem. The correct decision, at this stage, would be switching doors."
Before anybody reinstates it, I shall explain why this is nonsense. It seems the editor has assumed that, just because the set of possible game states is the same, the relative probabilities of them are the same.
Let's compare them. WLOG suppose the contestant picks door A.
In the standard Monty Hall problem, there are four possible outcomes:
- Car is behind A, Monty opens B (prob 1/6)
- Car is behind A, Monty opens C (prob 1/6)
- Car is behind B, Monty opens C (prob 1/3)
- Car is behind C, Monty opens B (prob 1/3)
a probability of 1/3 that the car is behind A, i.e. the contestant has chosen the correct door in the first place, therefore it's advantageous to switch.
If Monty doesn't know which door conceals the car, then there are six possible outcomes:
- Car is behind A, Monty opens B (prob 1/6)
- Car is behind A, Monty opens C (prob 1/6)
- Car is behind B, Monty opens B (prob 1/6)
- Car is behind B, Monty opens C (prob 1/6)
- Car is behind C, Monty opens B (prob 1/6)
- Car is behind C, Monty opens C (prob 1/6)
If Monty reveals a goat, outcomes 3 and 6 are ruled out. This doesn't alter the probabilities of the remaining outcomes relative to each other, so it becomes
- Car is behind A, Monty opens B (prob 1/4)
- Car is behind A, Monty opens C (prob 1/4)
- Car is behind B, Monty opens C (prob 1/4)
- Car is behind C, Monty opens B (prob 1/4)
a probability of 1/2 that the car is behind A, so switching and sticking are equally favourable options.
There's an ambiguity in this variation, in that there's no comment on what the contestant is allowed to do if the car is revealed, but that's outside the case being considered. -- Smjg (talk) 13:05, 11 June 2009 (UTC)
- Yes, this is known as the game show 'Deal or No Deal'. The contestant reveals suitcases randomly, but it could be a host acting randomly as well. It's not all that relevant to the MHP problem, however, where the host knowingly always reveals a goat. Glkanter (talk) 13:16, 11 June 2009 (UTC)
Conditional vs. unconditional for the umpteenth time
(sort of continuing from the ridiculously long thread above) What the most reliable sources about the MHP say is that it is a conditional probability problem. Period. Full stop. There are related unconditional problems, but (IMO) the related problems are distinctly not what most people think of as the MHP or what most people "solving" the MHP using an unconditional solution mean to be solving. Rather than argue about this, we should focus on what the sources say. As far as I know, those sources presenting only an unconditional solution never rigorously say what problem they're solving but simply present a "solution" to "the MHP" (usually something very similar to the Parade version). There are numerous reliable sources that do this (including Devlin). Again as far as I know, every source examining what the problem actually means (including Morgan et al., Gillman, Falk, and Grinstead and Snell) says the problem is a conditional probability problem. It is certainly possible to invent a related problem for which the unconditional solution is the appropriate solution (Morgan et al., and Gillman, and Grinstead and Snell all do this). The question is what do we do with this?
The NPOV way to handle this is clear. We present the problem. We present one or more referenced unconditional solutions. We then present the published criticism of the unconditional solutions, and a conditional solution. All using reliable sources. This approach may seem to favor the POV of Morgan et al. (and Gillman, and Falk, and Grinstead and Snell), but it simply says what the sources say. Specifically, unless someone can find a source that defends the validity of an unconditional approach against the published criticisms, e.g. says specifically what unconditional problem some unconditional solution is addressing, or specifically how their unconditional solution addresses the commonly understood conditional problem, the article must not provide any such defense. Lacking any published response (and not just a subsequent regurgitation of an unconditional solution) from the "unconditional side" this is a completely NPOV approach.
It's well past time to stop with the WP:OR and personal opinions, and instead stick to what reliable sources actually say. Numerous reliable sources unequivocally say the MHP is a conditional probability problem and that unconditional solutions address a slightly different problem. Are there any sources that directly contradict this viewpoint? -- Rick Block (talk) 01:57, 14 June 2009 (UTC)
- I completely agree. However what the article still could do better, is to explicitly state the differences between "MHP related problem" ([1], where the unconditional solution is correct and complete) and the "MHP stated by Whitman" ([2], where unconditional solution is incomplete or requires assumption, that strictly speaking would have to proved via conditional probabilities). And we have a reputable source for this difference as well - Behrens, so instead instead of giving an abbreviated quote ("both solutions are correct"), he should be quoted in full, where he points out the differences. This is also important because [1] can be understood as correct and complete solution, if you phrase MHP somwhat differently.--Kmhkmh (talk) 14:30, 14 June 2009 (UTC)
Just my idea! Nijdam (talk) 06:16, 14 June 2009 (UTC)
- I am not against what you propose. The only thing I would like is for the simple solution to stand in it own right. By this I mean two things. Firstly, there should be no suggestion in the simple (unconditional) solution section that this approach is wrong. Suggestions that the problem must be treated conditionally should be reserved for the academic (conditional) section, where they can be appropriately referenced.
- Secondly, even when given a clearly unconditional formulation (or perhaps the issue of conditionality is not fully appreciated) most people still get the answer wrong. For this reason, I believe that the unconditional sections should have its own 'Aids to understanding' and 'Sources of confusion' section, which should come before the conditional section. This is not unlike the approach used by Krauss and Wang, who do not bring up the issue of conditional probability until some way through the paper.
- Finally, we need some neutral, balanced, and understandable names for the two sections. 'Popular' and 'Academic', for example, but disagreement on this detail need not prevent us from making progress on the content. Martin Hogbin (talk) 10:30, 14 June 2009 (UTC)
- You're basically suggesting that there are two problems both known at the "Monty Hall problem" and that we should treat them separately. What source is there that says there are two different problems? I would suggest there's only one problem, and we structure the article as follows:
- <lead as in the current article>
- Problem
- <as in the current article>
- Solutions
- <some short introduction that essentially says there are multiple approaches to solving the Monty Hall problem>
- 1/3 + 2/3 = 1
- <a description of the 1/3 + 2/3 = 1 solution, with File:Monty closed doors.svg and File:Monty open door chances.svg, sourced to Devlin, Wheeler, etc.>
- Analysis of the chances of winning by switching versus staying
- <a description of the switch/stay case analysis with vos Savant's table of outcomes, sourced to vos Savant, Grinstead and Snell, etc>
- Conditional probability analysis
- <a description of the conditional solution including the criticism of the unconditional approaches and both the 2/3 and 1/1+q answers with File:Monty tree door1.svg and the large image currently in User:Rick Block/Monty Hall problem (draft), sourced to Morgan et al., Gillman, etc.>
- Formal proof using Bayes' theorem
- <the proof currently in the "Bayesian analysis" section>
- I believe this structure follows the guidelines at Wikipedia:Make technical articles accessible. I'll work on a draft of this at User:Rick Block/Monty Hall problem (draft) so that it is very clear what I'm suggesting. -- Rick Block (talk) 14:56, 14 June 2009 (UTC)
- Well, Rick, no offense, but I'm not very happy with your draft and I can hardly imagine you are yourself. Month of discussion here seems to be wasted. The sole purpose of my intervening here was to edit the article in such a way that (within the possibilities of Wikipedia) no one would get the idea the simple explanations are complete. So what was wrong with my formulation of the simple solution? At least it made clear that some extra proof was needed, according to Morgan, Behrends, and definitely more. The I wouldn't call the solution "conditional prob, analysis". Just call it "probabilistic analysis", that's what it is. Also, as you may know, I don't much like the so called Bayesian approach. It is needless complicated where it should only be the formal proof in mathematical terms. Nijdam (talk) 21:40, 14 June 2009 (UTC)
- No offense taken. The point is to let the sources speak for themselves. I think the two unconditional solutions that are presented are faithful to the sources they're drawn from (and, on very careful reading, don't say anything that is actually incorrect). Whether the other section is called "conditional probability analysis" or "probabilistic analysis" is not that important but what are the others if not "probabilistic"? The fully formal nature of the Bayesian approach is possibly overkill, but I think there's value in precisely following a specific formalism. Would you be willing to live with something close to this if Glkanter and Martin would be OK with it? -- Rick Block (talk) 23:07, 14 June 2009 (UTC)
- Nijdam, you seem to be moving more to an extreme view here in insisting that simple explanations are always incomplete. There are, in principle, three ways the problem can be formulated. It can be formulated as an unconditional problem, as Morgan do when they give the question that they consider vos Savant to be answering. It can also be formulated in a way that must be treated conditionally if, for example the host is stated to open an identified door non-randomly. Finally there is a grey area in between, for example, where the host action is considered random or the door opened by the host is not identified. This is where most of the argument here has occurred. Martin Hogbin (talk) 12:16, 15 June 2009 (UTC)
- As you notice yourself, any solution belongs to the appropriate problem. That's why I'm reluctant to present fundamental different explanation to the "same" problem. So to be specific: the simple explanations are incomplete as an explanation to your second mentioned version of the MHP (which I consider the MHP, BTW). I can't imagine you may differ in opinion with me here. Nijdam (talk) 12:43, 15 June 2009 (UTC)
- In the context of this page (the talk page for the article) the focus should be on what the sources actually say. Martin - do any of the sources presenting an "unconditional solution" clarify how they're interpreting the problem, or do they simply quote or paraphrase the Parade version and proceed? If this is what they do we simply don't know what problem they think they're addressing and we certainly can't clarify this on their behalf. Unless they're rooted in what sources say, discussions about what the problem means do not belong here but on the Argument subpage. Nijdam - given there are reliable sources that do not share your POV about this, we must follow an WP:NPOV approach where the article says what the various sources say - no matter how "wrong" what they say might seem to you. The POV that the unconditional solutions are incomplete cannot be "Wikipedia's POV" but can certainly be a POV presented in the article attributed to one or more specific sources. -- Rick Block (talk) 14:39, 15 June 2009 (UTC)
- Well Devlin uses the Parade version (using letters for the doors instead of numbers), Behrens kinda states 2 versions a conditional and an unconditional and points out the difference (though somewhat compressed), Henze (a german book for introduction into probability from 1997, exact reference in the german interwiki) states the problem as in parade and suggest an conditional (like morgan) and an uncoditional solution (like devlin) without giving a clear preference.--Kmhkmh (talk) 00:58, 16 June 2009 (UTC)
- In the context of this page (the talk page for the article) the focus should be on what the sources actually say. Martin - do any of the sources presenting an "unconditional solution" clarify how they're interpreting the problem, or do they simply quote or paraphrase the Parade version and proceed? If this is what they do we simply don't know what problem they think they're addressing and we certainly can't clarify this on their behalf. Unless they're rooted in what sources say, discussions about what the problem means do not belong here but on the Argument subpage. Nijdam - given there are reliable sources that do not share your POV about this, we must follow an WP:NPOV approach where the article says what the various sources say - no matter how "wrong" what they say might seem to you. The POV that the unconditional solutions are incomplete cannot be "Wikipedia's POV" but can certainly be a POV presented in the article attributed to one or more specific sources. -- Rick Block (talk) 14:39, 15 June 2009 (UTC)
- I should also add that Krauss and Wang consider the reasons that people get the answer wrong without mention of conditional probability (which comes later). In fact they appear to consider the issue of door identification something of a distraction to clear thinking. Note that even Morgan refer to their approach as dealing with the problem, 'in one form'. I think we therefore have sufficient reason to deal with the unconditional case as a problem in its own right, with its own 'Sources of confusion' and 'Aids to understanding' sections. The reason that I want to do this is to help people who are struggling with the basic problem (that is to say most people) without confusing them further with potentially irrelevant subtleties of the problem formulation. Martin Hogbin (talk) 08:47, 16 June 2009 (UTC)
One more comment regarding the suggested new structure by Rick. The section history and problem variants seem to be missing. Does that mean they stay as they are or do you had in mind to delete them? In any case I'd consider them an important part of the article.--Kmhkmh (talk) 14:31, 16 June 2009 (UTC)
- The proposed outline above is only for sections through the solution. The remaining sections would remain the same. This draft has a complete version of the article (with two alternatives for the solution section).
- Martin - do you mean essentially splitting the article into two articles, one about the probabilities involved when always switching (or always staying with the original choice) and the other about the conditional probabilities in the situation where Door 1 is initially picked and Door 3 is opened? I still think there's only one problem, and most of the sources that mention both interpretations clearly state the "unconditional" one does not reflect a normal wording of the MHP. I would consider Morgan et al., Gillman, Grindstead and Snell, Falk, and even Behrends in this camp. I don't read German, so can't comment on the Henze book. -- Rick Block (talk) 15:34, 17 June 2009 (UTC)
- I'm with you, Nijdam, 110%. This Henze fellow is even lazier and stupider than that hack, Devlin. Glkanter (talk) 19:16, 17 June 2009 (UTC)
- Excuse me? Henze is a tenure professor for statistics at the university of Karlsruhe and the book is regular primer for probability theory. The source is "independent" as any standard textbook is. And of course he doesn't give a "formal" proof, since in the unconditional approach there isn't really much to prove formally. Also it clearly discusses the MHP in more detail then Grinstead/Snell do and is not giving "only" the combined door solution, but the complete conditional solution as well.
- Mea maxima culpa! You're right, I didn't read further after I had seen section with the problem in chapter 7. He does use the problem in ch. 15 as an example of the use of Bayes' law, but I have to add, without comparing it with the "solution" in ch.7. So he doesn't shed any new light. Nijdam (talk) 09:16, 18 June 2009 (UTC)
- Excuse me? Henze is a tenure professor for statistics at the university of Karlsruhe and the book is regular primer for probability theory. The source is "independent" as any standard textbook is. And of course he doesn't give a "formal" proof, since in the unconditional approach there isn't really much to prove formally. Also it clearly discusses the MHP in more detail then Grinstead/Snell do and is not giving "only" the combined door solution, but the complete conditional solution as well.
- I'm with you, Nijdam, 110%. This Henze fellow is even lazier and stupider than that hack, Devlin. Glkanter (talk) 19:16, 17 June 2009 (UTC)
- @rick Yes the unconditional approach is an "incomplete" solution for the normal wording of the MHP (which explicitly uses standing on door one and getting shown a goat at door 3 - that scenario is a conditional probability). But if you state it without explicit doors and moreover you simply ask, whether staying or switching is a better strategy, that you could answer with an unconditional argument, which can be considered as "complete". And again the source explaining that is Behrens.--Kmhkmh (talk) 23:57, 17 June 2009 (UTC)
- Let me get this straight: A German university-level textbook, written by Henze, used as a primer for probability theory includes prominently the 'combining doors' solution and a Bayesian solution for the MHP. But this 'combining doors' solution, which concludes with an open door #3 with a goat standing behind it, is not a sufficiently-reliable/good/complete/thorough/non-false/robust enough solution, on its own, for Wikipedia's readers? Glkanter (talk) 15:05, 18 June 2009 (UTC)
- This kinda hard to follow. First you dismiss Henze without any real argument and now you want to use him to back up your claim? In any case if you read Henze carefully, you will see that he essentially the same argument as Behrens. Meaning you can make a correct and complete unconditional argument, if you rephrase the MHP somewhat differently as Henze does in his unconditional solution. I've pointed out already earlier it might be useful to give a more thorough account of Behrens. However this is not really changing rick's general suggestion (which is ok), just an addon to it.--Kmhkmh (talk) 17:01, 18 June 2009 (UTC)
- Let me get this straight: A German university-level textbook, written by Henze, used as a primer for probability theory includes prominently the 'combining doors' solution and a Bayesian solution for the MHP. But this 'combining doors' solution, which concludes with an open door #3 with a goat standing behind it, is not a sufficiently-reliable/good/complete/thorough/non-false/robust enough solution, on its own, for Wikipedia's readers? Glkanter (talk) 15:05, 18 June 2009 (UTC)
- @rick Yes the unconditional approach is an "incomplete" solution for the normal wording of the MHP (which explicitly uses standing on door one and getting shown a goat at door 3 - that scenario is a conditional probability). But if you state it without explicit doors and moreover you simply ask, whether staying or switching is a better strategy, that you could answer with an unconditional argument, which can be considered as "complete". And again the source explaining that is Behrens.--Kmhkmh (talk) 23:57, 17 June 2009 (UTC)
- Excuse me? I "dismiss Henze without any real argument"? I agreed 110% with Nijdam's dismissal of Henze (and previously, Devlin) without any real argument. That's all the 'real argument' guys like me and Nijdam need. We're not so different, he and I. We get it. We're not brainiacs on the nerd patrol. We're not members of the factinista. We go straight from the gut, right Nijdam? That's where the truth lies, right down here in the gut.
- And you have the NERVE to say I "dismiss Henze without any real argument"? How DARE YOU, sir! Glkanter (talk) 04:01, 19 June 2009 (UTC)
Rick, no I do not suggest splitting the article into two articles. I suggest we deal with two interpretations of the same problem, as the article currently does. The first is the notable one, the one that made the problem famous and the one that was answered correctly by vos Savant. There are reliable sources for this interpretation thus we should include it. You can call this unconditional if you like, you could call it the interpretation in which the conditional aspect is considered unimportant or irrelevant. The second is the conditional interpretation.
The most reliable source for interpreting a question in a popular general interest magazine is vos Savant; that was her job. Academics have chosen to interpret the problem differently because that made it interesting for them. The normal hierarchy of reliability of sources does not apply here since the problem is one of interpreting the meaning of a question from a member of the public.
There are ample sources for an unconditional section (which we already have). These include vos Savant, Devlin, Krauss and Wang, and, some say, Behrends and Henze. So my point is this. If we stick to our current format of two interpretations, there is absolutely no point in having one 'Sources of confusion' and one 'Aids to understanding' section since some of the sources of confusion only apply if the problem is taken to be conditional. Martin Hogbin (talk) 21:32, 17 June 2009 (UTC)
- Well imho do Morgan and vos Savant answer the same problem, i.e. the normal wording for which the unconditional solution is "incomplete" (or more precisely requires the unspoken assumption that showing the goat does not change the original probability) and of course is Morgan and the "academic analysis" here the primary source and not vos Savant. This is not to devalue vos Savant's contributions, but it should be rather obvious that peer reviewed science journals are more reputable sources than (arbitrary) magazin columns. As far as i'm concerned (and i'm sure there a broad consensus among WP editors) there is no room for discussion ont that, i.e. that peer reviewed science journals overrule non science magazines can be considered a "WP-Axiom".--Kmhkmh (talk) 23:57, 17 June 2009 (UTC)
- How might this mythical "WP-Axiom" be applied in the following case: An allegedly peer-reviewed article with it's very own cautionary comment by Seymann versus a professionally-edited University-level textbook used as a primer for probability theory? One says unequivocally that the unconditional solutions are 'false', the other solely(?) and unrepentantly uses the 'combining doors' solution. Which brings up the question: Who decided that the 'combining doors' solution is unconditional? The 2nd image clearly shows door #3 open with a goat revealed. Glkanter (talk) 13:26, 18 June 2009 (UTC)
- Rick, I think it was you who originally (or most recently) said the 'combining doors' solution falls into the category of Morgan's 'F1', which Morgan says is "false due to being unconditional." Perhaps you would respond to the above question: "Who decided that the 'combining doors' solution is unconditional?." Glkanter (talk) 22:23, 19 June 2009 (UTC)
- Kmhkmh, you seem to adopting the strange position that the answer is the same regardless of the question. I agree that academic sources are more reliable within their area of expertise but this is not necessarily so otherwise. Would you take Morgan as a reliable source in the area of, say, veterinary medicine? Of course not. As experts giving an answer to a well-posed probability problem Morgan are to be considered reliable but as interpreters of what a member of the public actually wanted to know in a question in a popular general interest magazine they are no more reliable than anyone else, and less so than vos Savant, whose job it was to answer such questions. Martin Hogbin (talk) 16:41, 19 June 2009 (UTC)
- The area of expertise here is probability & statistics - period. And you cannot argue using vos Savant's columns as a source over a peer reviewed science journal for any well or ill posed math problem. If you want to focus non-mathematical aspects of reading/perceiving a problem then the authoritative resource would be an article in some psychology related journal (maybe something like Krauss- Wang) and again not vos Savant. If we were talking about veterinary medicine, then the authoritative source would be some academic journal for veterinary medicine.--Kmhkmh (talk) 21:16, 19 June 2009 (UTC)
- Kmhkmh, you seem to adopting the strange position that the answer is the same regardless of the question. I agree that academic sources are more reliable within their area of expertise but this is not necessarily so otherwise. Would you take Morgan as a reliable source in the area of, say, veterinary medicine? Of course not. As experts giving an answer to a well-posed probability problem Morgan are to be considered reliable but as interpreters of what a member of the public actually wanted to know in a question in a popular general interest magazine they are no more reliable than anyone else, and less so than vos Savant, whose job it was to answer such questions. Martin Hogbin (talk) 16:41, 19 June 2009 (UTC)
- "The area of expertise here is probability & statistics - period." Maybe not. Is the 'by switching, you always get the opposite' solution an example of Probability Theory? Or is it Logic and Symbolic Notation?
- So, since a Logic and Symbolic Notation solution is valid, is the very first sentence of the article incorrect: "The Monty Hall problem is a probability puzzle..."?
- I could argue that the only 'issues of probability' in the problem are the placement of the car, the contestant's selection, and the host's two-goat choice. All of which are random. What could possibly be less interesting, or less complex? Glkanter (talk) 22:07, 19 June 2009 (UTC)
To give a specific example, imagine a reader who is trying to understand why people are confused about the popular (unconditional) formulation. What sense can they make of, '..interpret the usual wording of the problem statement as asking about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability'? I am not saying that the quote from Morgan is wrong, just that it is completely unhelpful to someone who sees the problem as an unconditional one. Martin Hogbin (talk) 21:37, 17 June 2009 (UTC)
- Surely we should aim for both. There is no standard formulation of the MHP, nor even a standard wording. All you are referring to is Morgan's interpretation of the most common problem statement, that by Whitaker. However, it is possible to formulate the problem as a clearly unconditional one, just as it is possible to formulate the problem as one which must be treated conditionally. In the current article we give both solutions. It is possible to argue (wrongly in my opinion) that the unconditional solution should not be there, but it makes no sense at all to present the unconditional solution and then give aids to understanding for the conditional solution without any indication to the reader of what it is that you are trying to help them understand. If the unconditional solution had its own 'Aids to understanding' section, referring specifically to the unconditional formulation and solution, this would be easier for the reader to follow and be perfectly correct. Martin Hogbin (talk) 17:25, 19 June 2009 (UTC)
- Martin - we're talking about what sources say, not personal opinions. From Barbeau's Mathematical fallacies, flaws, and flimflam (in the references of the article): "The standard analysis of problem M [the Monty Hall problem] is based on the assumption that after the contestant makes the first choice, the host will always open an unselected door and reveal a goat (choosing the door randomly if both conceal goats) and then always offer the contestant the opportunity to switch." So, yes, there is a standard analysis and it includes the constraints present in the Krauss and Wang explicit version (which I believe you agree is conditional, right?). If you're going to keep arguing that the "unconditional problem" is the "notable" or popular one, I would really like you to provide a source that says something similar to this claim, or even a source that presents the problem using an unconditional phrasing (and by this I don't mean a source like Morgan et al. or Gillman that suggests an unconditional phrasing for purposes of contrast). Similarly, if you want any content in an "Aids to understanding the unconditional solution" section you'll need to find sources that clearly say that they're talking about the "unconditional" problem. -- Rick Block (talk) 19:06, 19 June 2009 (UTC)
- Rick, Henze wrote a university-level primer textbook on probability theory which includes the 'combining doors' solution. What more do you want? I get the feeling that since Henze did not specifically write: "Here's where I disagree with Morgan:", you consider him either 'uninformed' or perhaps 'agnostic' relative to Morgan. Why not just take him at his printed word, which he puts his entire professional reputation behind? He used the 'combining doors solution.' Glkanter (talk) 22:07, 19 June 2009 (UTC)
- Are you saying you read German and Henze presents "combining doors" as a correct solution to the MHP, or are you simply referring to Nijdam's and Kmhkmh's comments above? Looking at the Google books preview, the first appearance of the problem (first occurrence of "vos Savant") is in chapter 7 and the full solution is not given until chapter 15. Again, I don't read German, but my guess would be that the first mention in chapter 7 is before conditional probability has been introduced and uses only concepts introduced to that point - and is revisited in Chapter 15 after the necessary foundations have been established. I would be quite interested in an exact translation. On the other hand, since this is the English Wikipedia and there is no shortage of references in English I think we can safely ignore this particular reference.
- My request for Martin (and you if you'd like) is some source, any source, that says anything remotely like "the probability in question in the MHP is the overall probability of winning by switching". -- Rick Block (talk) 16:37, 20 June 2009 (UTC)
- Your quotation of what Barbeau call the standard analyis is simply a statement of the game rules, which we all agree. It does not include a question. Does Barbeau mention a standard question and, if so, on what basis does he describe it as such?
- We already have a section on the popular/unconditional problem and solution including some explanation of solution. This is well-sourced (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8; Martin 2002Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008)). All I am pointing out is that at present there is no way for the reader to tell which parts of, 'Aids to understanding' and 'Sources of confusion' apply to this section. This makes the situation even more confusing. So why not put the bits of these sections together with the solutions to which they apply rather than leaving it to the reader to work out by themselves which sources of confusion apply to which formulation Also, much of Krauss and Wang's explanation of why people get the problem wrong clearly applies to the unconditional case and could be added. Martin Hogbin (talk) 21:31, 19 June 2009 (UTC)
- We have a section on popular solutions, not a section on a separate "unconditional" problem. Are you suggesting that these solutions are intended to address a different problem than the one that is clearly conditional (e.g. Whitaker's phrasing, where the player picks Door 1 and the host opens Door 3 and the host then asks the player to decide whether to switch) and that people find this (other) problem confusing? What I'm saying is that unless there are sources that clearly say they are solving some theoretical "unconditional" version of the MHP there is really only one problem involving a first choice, the host opening a door, and then a second choice given the knowledge of the originally chosen door and the door the host opens. There are indeed plenty of published unconditional solutions, and they do indeed end up with the correct answer (given the "standard" interpretation of the problem), but if any of these solutions clarify the problem to be the "unconditional" problem please let me know which ones. If there's really only one problem then there's no need for separate sections as you suggest. -- Rick Block (talk) 16:37, 20 June 2009 (UTC)
Where do we stand?
I think we discussed almost anything there is to discuss on the MHP. I try to sum up the different positions we encounter here and ask the discussiants to take position.
A
MHP = K&W formulation, and the only solution is the one with conditional probabilities. Other explanations are incomplete for this MHP, but may address other formulations, which are of less interest.
- Nijdam
B
MHP = K&W formulation, which may be solved with conditional probabilities. Other explanations, like the simple explanation, also may solve the problem.
C
MHP has different formulations. One is the K&W formulation, another is the original Parade version. K&W needs conditional probabilities, Parade not.
D
MHP has different formulations. One is the K&W formulation, another is the original Parade version. Both may be solved with or without conditional probabilities.
E
??
This may help us in finding the necessary form of edits to the article. (I hope.) Nijdam (talk) 11:15, 20 June 2009 (UTC)
- I think it would be far more helpful to categorize what sources say, rather than identify what various editors think, since what editors think doesn't actually matter. It should be easier to agree as well. I think the sources fall into one of the following categories:
- The MHP is the Parade version with the additional assumptions that the car is uniformly distributed and the host always reveals a goat and always makes the offer to switch - with no explicit mention of how the host decides what door to open in the case the player initially selects the car. An unconditional solution showing the probability of winning by switching is 2/3 is presented without clarifying whether the problem is conditional or unconditional.
- vos Savant, Devlin, and most "popular" sources
- The MHP is as above but is clearly conditional, and since there is no constraint on the host in the case the player initially selects the car the host's preference in this case must be treated as an unknown variable q. Unconditional solutions (such as vos Savant) address a slightly different problem for which the answer is 2/3. The answer to the problem as stated is 1/(1+q), which is 2/3 only if q is 1/2.
- Morgan et al., Gillman, Rosenthal
- The MHP is as above but with the additional constraint that the host choose randomly if the player initially selects the car (e.g. the Krauss and Wang version, i.e. the same as immediately above with q=1/2). An unconditional (2/3) solution is presented without clarifying whether the problem is conditional or unconditional.
- Mueser and Granberg, Krauss and Wang
- The MHP is the Krauss and Wang version but is clearly conditional. Unconditional solutions say the answer is 2/3 (which is the correct numeric result) but answer a slightly different question.
- Grinstead and Snell
- The MHP is the Parade version with the additional assumptions that the car is uniformly distributed and the host always reveals a goat and always makes the offer to switch - with no explicit mention of how the host decides what door to open in the case the player initially selects the car. An unconditional solution showing the probability of winning by switching is 2/3 is presented without clarifying whether the problem is conditional or unconditional.
- I keep hearing Martin suggest another but I am not aware of any sources that present it this way:
- The MHP is the Parade version, but the probability of interest is explicitly the overall probability of winning by switching as opposed to the conditional probability faced by a player who has picked Door 1 and has seen the host open Door 3 (or, alternatively, a variant where the player must decide whether to switch before the host opens a door - "I'm going to open a door and show you a goat, decide now if you'd like to keep Door 1 or switch to the door I don't open").
- Can anyone provide a source for this specific interpretation?
- Behrens and Henze do that if you read them carefully. They do not state the MHP differently, but in their suggested unconditional solutions, they rephrase the problem somewhat in such way, i.e. they state explicitly that they compute the probabilities for staying versus switching regardless which door was chosen by the player and which was opened by the host.--Kmhkmh (talk) 03:10, 21 June 2009 (UTC)
- The MHP is the Parade version, but the probability of interest is explicitly the overall probability of winning by switching as opposed to the conditional probability faced by a player who has picked Door 1 and has seen the host open Door 3 (or, alternatively, a variant where the player must decide whether to switch before the host opens a door - "I'm going to open a door and show you a goat, decide now if you'd like to keep Door 1 or switch to the door I don't open").
- Again, what I think matters here is not what we each think about the problem but what sources actually say. If you'd like to add more sources in each of the categories above please feel free. If you'd like to suggest another interpretation that other sources use, also feel free. -- Rick Block (talk) 17:46, 20 June 2009 (UTC)
- There is a problem with a strict 'cut-and-paste' attitude to reliable sources, which is that people do not usually state all the things they do not do. In other words, sources that treat the problem as essentially unconditional may not specifically mention that they do not treat the problem as one requiring the use of conditional probability just as they do not mention other techniques that they do not use to solve the problem. It seems clear to me, however, that any sources that treat the problem unconditionally after the publication of Morgan do so because they consider this approach is valid. (I inserted this response before Glkanters as I think the two make more sense that way. I hope this is OK) Martin Hogbin (talk) 13:46, 21 June 2009 (UTC)
- Normally I would mind, but since my post is a hijack anyways, what difference does it make? And, you re-inforce, perhaps in a more erudite manner, this point: Absent this statement in any published source, "Here's where I disagree with Morgan:", I think Rick views all other author's viewpoints as either 'uninformed' or 'agnostic' regarding Morgan. Your statement "...(they) do so because they consider this approach is valid." is, of course, the most reasonable interpretation. Glkanter (talk) 14:38, 21 June 2009 (UTC)
- I'm sure nobody minds me re-hijacking this discussion...
- Why is the 'Combining Doors' solution considered 'unconditional'? It clearly shows an open door #3 with a goat behind it? Rick, I think you most recently labeled it as such, perhaps you could address this?
- Where does Devlin's reliable-sourced article stand in this discussion? What about similar articles from sources of equal reliability? Will Nijdam's casual blow-off become the defacto policy for this article? Is there a consensus that Morgan's article carries more weight than Zehne's textbook or Devlin's column? There are at least 5 errors in Morgan's paper. Other than not concurring with Morgan that 'the unconditional solutions are false', how many errors are in Devlin's paper, or Zehne's textbook?
- How much emphasis in the article will 'non-random host behaviour' continue to receive? Will it be part of the 'conditional' solution section, or will it appear elsewhere?
- Will something like this statement appear in the article: 'Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community.'? Glkanter (talk) 13:17, 21 June 2009 (UTC)
- I'm sure nobody minds me re-hijacking this discussion...
- @Martin - Most of the sources we're talking about are popular, not academic, and I think we have very little reason to expect them to be aware of Morgan et al. or Gillman. I've suggested this before, but if anyone wants to survey what academic sources say that cite Morgan et al. it's not that hard (although would probably require an afternoon in a university library). Here's a link from Google Scholar of (currently 52) sources that cite this paper [7]. Suggesting that any source published after Morgan et al., or Gillman, was likely to be aware of them, and by not saying anything about the conditional vs. unconditional issue they both bring up is saying they disagree seems like an absurd stance. My stance is if some later source doesn't actually reference either of these papers we simply don't know whether the later source was aware of them or not. It seems pretty obvious that we shouldn't invent an argument where there is none.
- @Glkanter - The combining doors solution is unconditional because it doesn't say anything about how the host decides what door to open in the case where the player initially picks the car. Another way you can tell is to apply the same solution to a variant where the conditional answer differs from the unconditional answer (for example, host always opens Door 3 if possible). Combining doors still says the answer is 2/3, when the actual answer (for this variant) is 1/2.
- Devlin's article is as reliable as Gillman's. They are both essentially columns written by math professors in general math sources, so they are both reliable sources by Wikipedia's standards. On the other hand, Morgan et al. is a paper in a peer reviewed statistics journal making it more reliable by Wikipedia's standards (which reflect normal academic standards as well). There are not 5 errors in Morgan et al. and although I'm not entirely sure I think continuing to repeat this could be considered to be libelous. I strongly suggest you (and Martin) stop saying this. Wikipedia's WP:libel policy applies to talk pages as well as articles. Saying you think there might be an error in a source is certainly fine. Incessantly repeating this as if it were an established fact is not.
- How much emphasis the article places on non-random host behaviors should reflect how much emphasis this aspect of the problem receives in the published literature. I wouldn't expect it to be mentioned in a section discussing an unconditional solution, but I think it is entirely relevant to sections discussing conditional solutions, variants of the problem, and sources of confusion.
- Your wording "Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community." is problematic for the reasons I already mentioned above (in the #Discussion thread), i.e. it's not NPOV and it's not verifiable to any specific source. In response you said it's simply a statement of fact, but it's not - it's a conjecture. What is a verifiable fact is that subsequent sources have published unconditional solutions. -- Rick Block (talk) 16:58, 21 June 2009 (UTC)
- Rick, it's not conjecture, at all. Watch how a logical argument works:
- Morgan published a paper that says 'the unconditional solution is false.'
- Devlin and Zehne, two members in good standing of the relevant professional community, published papers under their own names using an allegedly 'unconditional solution'.
- Devlin and Zehne would not put their names and reputations on a published paper they disagreed with.
- Therefore, Devlin and Zehne have reliably published that they believe the unconditional solution is not false.
- Therefore, the viewpoint that 'the unconditional solution is false' is not by shared Devlin and Zehne, two members of the relevant professional community.
- In conclusion, "Morgan says the unconditional solution is false. This viewpoint is not shared universally in the professional community." is a true AND valid statement, supported by the reliably published sources.
- But this has been instructive. The reason that these talk pages go on endlessly for 5 years is that you apparently do not understand how to parse a logical argument. Sue me. Glkanter (talk) 02:28, 22 June 2009 (UTC)
- Rick, it's not conjecture, at all. Watch how a logical argument works:
- Please read WP:SYNTHESIS. "This viewpoint is not shared universally in the professional community" is a statement of opinion (specifically your opinion). It is not based on what any particular source says, meaning from a Wikipedia policy standpoint it is original research. -- Rick Block (talk) 19:22, 22 June 2009 (UTC)
- No, Rick. It is a conclusion derived from the facts as enumerated in the logical argument presented above. What you would need to do is indicate which statement is not a fact, or how the conclusion doesn't follow from the factual statements. Then I would have a flawed argument, but still, not an opinion. Do you understand the difference? Glkanter (talk) 10:44, 23 June 2009 (UTC)
This is Morgan's argument against 'F1':
Here is the first paragraph following the introduction:
"1. TO SWITCH OR NOT TO SWITCH
We begin by enumerating and discussing the most appealing of the false solutions. To avoid any confusion, here is the situation: The player has chosen door 1, the host has then revealed a goat behind door 3, and the player is now offered the option to switch. Thus is the player having been given additional information, faced with a conditional probability problem. The event of interest is "win by switching"; both "lose by switching" and "win by not switching" are complements of this event. For clarity and equality, we refer to the host as "he" and the player as "she.""
Here's Morgan's description of the unconditional problem:
Solution Fl. If, regardless of the host's action, the player's strategy is to never switch, she will obviously win the car 1/3 of the time. Hence the probability that she wins if she does switch is 2/3.
Here's Morgan's argument against the unconditional solution:
Fl is immediately appealing, and we found its advocates quite reluctant to capitulate. Fl's beauty as a false solution is that it is a true statement! It just does not solve the problem at hand. Fl is a solution to the unconditional problem, which may be stated as follows: "You will be offered the choice of three doors, and after you choose the host will open a different door, revealing a goat. What is the probability that you win if your strategy is to switch?" The distinction between the conditional and unconditional situations here seems to confound many, from whence much of the pedagogic and entertainment value is derived.
But this does not describe the 'combining doors' solution, as the 'combining doors' solution clearly shows door #3 open with a goat revealed. I think Rick's personal interpretation (similar to OR) of Morgan's criticism is incorrect. There is no mention of any so-called 'host-behaviour'. Morgan does not specifically call the 'combining doors' solution 'false'. Glkanter (talk) 21:51, 21 June 2009 (UTC)
- Is this is a response to something I said above? I don't see how. Combining doors is unconditional because it does not say anything about the host's strategy in the case the player initially picks the car and because it gives the wrong answer for the conditional variant I suggest. Morgan's F1 is clearly equivalent. If you can't see this, I'm not sure I can help you. -- Rick Block (talk) 23:56, 21 June 2009 (UTC)
- We're discussing what the world's most reliable source says about the 'Combining Doors' solution, which in your opinion, based on Morgan's F1, is unconditional. Morgan, as shown above, says nothing of the sort. So, it is nothing more than your OR (or 'opinion') until you show a reliable published source that says the 'Combining Doors solution is unconditional'. And, please, no conjecture. 'Host's strategy' has nothing to do with 'conditional vs unconditional'. Why, Nijdam proposed a 'conditional' solution just last week which made no mention whatsoever of 'host's strategy'. Further, in another demonstration of your lack of understanding of how logical arguments work, 'because it gives the wrong answer for the conditional variant I suggest.' is not a valid method of dis-proving a solution. It is nothing more than something you invented out of whole cloth. Right, Nijdam? Glkanter (talk) 10:44, 23 June 2009 (UTC)
- I'm sorry Glkanter, the 'combined doors' is just a way of refrasing the 'simple solution'. You of all, with your continuing appeal on logic, should understand this. May be tomorrow someone will call it the 'restgroup solution'. There is of course no mention in Morgan's paper of it, but .... (guess what, use your logic). Nijdam (talk) 16:26, 23 June 2009 (UTC)
- Yes, continue to 'label' it rather than address the actual solution. It makes a proper and valid Logical Argument, and it addresses the 'after revealing door 3 issue.' In the form that Devlin and Zehne have published it, it is perfectly complete, valid, and instructive. And, you concur that Morgan does not even mention it. To claim that Morgan does, must be Rick's personal opinion. So, as a professor, what 'grade' would you give Rick's 'method of disproving the 'Combining Doors' solution. You know, where he posted "...and because it gives the wrong answer for the conditional variant I suggest."? I guess Zehne and Devlin didn't realize that (Of course they didn't. It's nonsensical drivel.). So, is it a failing grade? Or D- for 'creativity' and 'stick-to-it-ness'? Glkanter (talk) 19:52, 23 June 2009 (UTC) Glkanter (talk) 00:01, 25 June 2009 (UTC)
Yes, continue to 'label' it rather than address the actual solution.
- >>What the h... do you mean?
It makes a proper and valid Logical Argument, and it addresses the 'after revealing door 3 issue.'
- >>What does?
In the form that Devlin and Zehne have published it, it is perfectly complete, valid, and instructive.
- >>Definitely not!
And, you concur that Morgan does not even mention it.
- >>What do I?
To claim that Morgan does, must be Rick's personal opinion.
- >>There is no such.
So, as a professor, what 'grade' would you give Rick's 'method of disproving the 'Combining Doors' solution.
- >>A+
You know, where he posted "...and because it gives the wrong answer for the conditional variant I suggest."?
- >>Do I have to?
I guess Zehne and Devlin didn't realize that (Of course they didn't. It's nonsensical drivel.).
- >>I'm not sure whether they do realize anything.
So, is it a failing grade? Or D- for 'creativity' and 'stick-to-it-ness'?
Glkanter (talk) 19:52, 23 June 2009 (UTC)
- Rick, I will address the sensible content of your latest post later but please come back to Earth and stop being silly about libel. Martin Hogbin (talk) 22:45, 21 June 2009 (UTC)
- I'm absolutely serious about libel. If you or Glkanter persist in posting unsubstantiated claims about Morgan et al., I will ask an uninvolved admin to review your posts. From Defamation: [Libel is] the communication of a statement that makes a claim, expressly stated or implied to be factual, that may give an individual, business, product, group, government or nation a negative image. This seems to be your precise intent. You're saying Morgan et al., and Morgan in particular, published an article containing numerous factual errors. If I were to post at some newsgroup that you don't frequent that Martin Hogbin in his professional capacity as a physicist had published articles containing numerous factual errors would you not consider this to be libelous? I really am serious about this. You really do need to stop it. -- Rick Block (talk) 23:56, 21 June 2009 (UTC)
- No doubt we will also be burnt at the stake as heretics too. You make yourself look foolish by sticking to such an absurd line. In fact you have lost all credibility with me and, I would think, most other editors here.
- I'm absolutely serious about libel. If you or Glkanter persist in posting unsubstantiated claims about Morgan et al., I will ask an uninvolved admin to review your posts. From Defamation: [Libel is] the communication of a statement that makes a claim, expressly stated or implied to be factual, that may give an individual, business, product, group, government or nation a negative image. This seems to be your precise intent. You're saying Morgan et al., and Morgan in particular, published an article containing numerous factual errors. If I were to post at some newsgroup that you don't frequent that Martin Hogbin in his professional capacity as a physicist had published articles containing numerous factual errors would you not consider this to be libelous? I really am serious about this. You really do need to stop it. -- Rick Block (talk) 23:56, 21 June 2009 (UTC)
- Just to make my position on the subject absolutely clear. I believe that the paper by Morgan et al (which for brevity I often refer to as Morgan, although I have no idea which author contributed which bit) contains a number of errors. Firstly there is the error in the calculation of the probability of winning by switching given a uniform prior distribution of q. This is a basic and obvious error in which the authors fail to take account of the information revealed by the opening of a door by the host. A letter pointing out this error has been sent to the journal and is being given due consideration. Unsurprisingly, their response did not include threats of legal action for libel.
- I also believe that there are a a number of other serious mistakes in the paper of a somewhat more philosophical nature. Firstly the authors interpret Whitaker's question in a overly literal manner, considering its origin. This is alluded to in Seymann's comment at the end of the paper. Secondly the authors do not apply the principle of indifference consistently to the stated question, resulting is a spurious result in which a host choice parameter assumes undue significance. Finally the authors fail state explicitly in their paper the assumptions that they have actually made.
- I would welcome the opportunity to have the truth of the above claims examined in court but unfortunately I doubt that I will get the opportunity to do so. Martin Hogbin (talk) 09:12, 22 June 2009 (UTC)
- Are you really not understanding what I'm saying or are you just pretending to be stupid? You can certainly think whatever you'd like, and say what you think, but an assertion like Glkanter's above ("There are at least 5 errors in Morgan's paper.") is not OK. "Martin thinks there are at least 5 errors in Morgan's paper" would be fine. Criticize all you want, but don't malign. -- Rick Block (talk) 19:10, 22 June 2009 (UTC)
- I suggest we drop this ludicrous topic. I will not enter into any more discussion about it. Martin Hogbin (talk) 21:42, 22 June 2009 (UTC)
Refereed paper agreeing with Morgan et al.
Looking through some of the sources that reference Morgan et al. I ran into [8]. This is a paper apparently (I haven't actually seen it in the journal, but I trust that it is there) published in the Spring 2000 edition of Teaching Statistics, a refereed journal. From the "Controversy" section (referring to vos Savant's columns):
- Adding to the confusion, vos Savant then gave `a dubious analogy . . . [and] went on to defend her original claim with a false proof and also suggested a false simulation as a method of empirical verification' (Morgan et al. 1991, p. 284). Consequently, what could and should have been a correct and enlightening answer to the problem was made unconvincing and misleading. Subsequent work by Gillman (1992) and Falk (1992) applied the correct Bayesian mathematics to derive the general solution, but several other authors continued to perpetuate the `no news' argument, which at best relies on an unstated assumption.
This is a published article in a refereed journal, which completely agrees with Morgan et al.
To be completely fair, I also ran into [9] (as far as I can tell, a pre-publication draft of a chapter of The Remarkable Story of Math's Most Contentious Brain Teaser ), which has a largely critical account of the exchange between Morgan et al. and vos Savant (but, curiously, seemingly agrees with Morgan et al. "there was a subtle shift from the correspondent’s initial question, in which the host always opens door three, to the listing of the scenarios given by vos Savant, in which it was assumed only that the host always opens a goat-concealing door"). Unlike the source above, this one is not published in a refereed journal but it (or presumably something very much like it) is published by a reputable publisher (Oxford University Press).
I think the bottom line here is that Morgan et al. are clearly correct, but there is room for quibbling on the other side. -- Rick Block (talk) 23:07, 21 June 2009 (UTC)
- Your first source seems to agree with Morgan but the second (Rosenhouse)says this, 'But for all of that it seems clear that vos Savant successfully apprehended all of the major points of the problem, and explained them rather well considering the forum in which she was writing. Her intent was not to provide an argument of the sort a mathematician would regard as definitive, but rather to illuminate the main points at issue with arguments that would be persuasive and comprehensible. In this she was successful'. Of Morgan's comments on vos Savant he says, 'Rather strongly worded, wouldn't you say? And largely unfair...' and continues to defend her by saying, '... continuing with their lengthy essay makes clear that their primary issue with vos Savant is her shift from what they call the \conditional problem," as posed by her correspondent (in which it is stipulated that the contestant always chooses door one and the host always opens door three) to the \unconditional problem," in which we stipulate only that after the contestant chooses a door, the host opens one of the goatconcealing doors. She did, indeed, make this shift, but this was hardly the point at issue between vos Savant and her angry letter-writers'.
- In fact, as I read more, Rosenhouse is rapidly becoming one of my heroes as he (bravely risking legal action) refers the Morgan paper as, a 'bellicose and condescending essay'. Finally Rosenhouse provides a quote from vos Savant showing that the simple (unconditional) version is the one that everybody cares about, 'Nearly all of my critics understood the intended scenario, and few raised questions of ambiguity. I personally read nearly three thousand letters (out of many more thousands that ultimately arrived and found virtually every reader, from university lectern to kitchen table, insisting simply that because two options remained, the chances were even'. Martin Hogbin (talk) 22:03, 22 June 2009 (UTC)
- Sorry Martin, I don't like partial quotations. Let me add:
- Certainly vos Savant’s arguments are not mathematically rigorous, and we can surely point to places where her phrasing might have been somewhat more precise. Her initial argument based on the million door case is pedagogically effective, but mathematically incomplete (as we shall see). And there was a subtle shift from the correspondent’s initial question, in which the host always opens door three, to the listing of the scenarios given by vos Savant, in which it was assumed only that the host always opens a goat-concealing door.
- and about Morgan et al.:
- They, at least, were mathematically correct in their substantive points.
Nijdam (talk) 22:25, 22 June 2009 (UTC)
- Martin - how are you getting that the vos Savant quote shows "that the simple (unconditional) version is the one that everybody cares about"? I believe what she's saying people understood were the unstated assumptions about 1) the uniform distribution of the car, 2) the host always making the offer to switch, and 3) the host never revealing the car - these are points of ambiguity that some (not very many) folks raised and has nothing to do with whether the problem is conditional or not. I believe (notice the wording here - "I believe", not "it is a fact that") vos Savant meant to be answering the conditional question but completely overlooked that the unconditional and conditional answers might be different. While she is indeed very smart, she's not a mathematician. -- Rick Block (talk) 01:23, 23 June 2009 (UTC)
- There is no way of telling exactly question vos Savant intended to answer but she said this, 'virtually every reader...insisting simply that because two options remained, the chances were even'. In other words the issue that caused all the interest was the fact that people think the answer is 1/2 when it is in fact 2/3. This is the Monty Hall problem in a nutshell. There is no mention of conditional probability or host preference.
- To get back to improving the article, we already have a section describing the simple solution, followed by a section describing the conditional solution. All I am asking is that we have some way of indicating to the reader which sources of confusion and which aids to understanding apply to which section. I believe we have ample reliable sources to do this. Martin Hogbin (talk) 17:51, 23 June 2009 (UTC)
- Isn't it completely obvious that most people think the answer is 1/2 because they're thinking about the case the problem asks them to, where the player has picked a door, say Door 1, and the host has opened a door showing a goat, say Door 3, at which point there are only 2 closed doors - i.e. the conditional problem? Specifically, they're not thinking about the unconditional solution because the problem statement asks them not to. Doesn't this make the central source of confusion that people attempt to solve the problem conditionally, but do so incorrectly? Krauss and Wang's comments on this in the early section of their paper are interesting - they say that people who see the "correct" solution tend to have a 3 part mental model (following all possible locations of the car) and mostly simply ignore what they consider to be an extraneous fact that the host has opened Door 3. This means of course that these people are actually solving the unconditional problem, not the conditional problem. On the other hand if most people (those who end up with the 1/2 answer) actually see the problem in its conditional form shouldn't the primary focus of the article be on this interpretation? In any event, I think the sources of confusion about the unconditional and conditional interpretations are sufficiently intertwined that it makes little sense to try to specify which pertain to which interpretation. -- Rick Block (talk) 14:29, 24 June 2009 (UTC)
- We have reliable sources that treat the subject without making it conditional. We have sources that explain reasons for confusion and give aids to understanding based on the simple (unconditional or conditionality ignored) treatment of the problem. It seems to me that we are back where we started when I responded to the original RfC. Despite many editors taking a much less hard line on conditionality, a small number of editors are refusing to allow change to the page to make it more useful to the average reader. Martin Hogbin (talk) 17:46, 26 June 2009 (UTC)
- However that is imho somewhat of a mischaracterization of what we actually have. Almost all scientific sources (Devlin being the only exception) treat the problem with conditional probabilities, some of them explicitly criticizing the unconditional solution. 2 sources give an unconditional and conditional a solution without giving a clear pference but pointing out that the unconditional solution strictly speaking solves a slightly different problem (Henze, Behrens). Also there was never an argument of not offering the unconditional solution and making it less useful ro the average reader. However suppressing the criticism of the uncodintional solution is mischaracterization of the problem(and its treatment in reputable sources) and hence no service to the average reader at all.--Kmhkmh (talk) 22:28, 26 June 2009 (UTC)
- That is your opinion, but some sources, such as vos Savant, Devlin and to a large degree Krauss and Wang treat the problem non-conditionally, that is to say that the issue of which door the host opens is not considered important. Most 'scentific' treatments start by assuming a particular formulation of the problem, that the questioner wishes to know what the probability of winning by switching is after a specific sequence of events has occurred. This assumption is criticised in Seymann's commentary at the end of the Morgan paper. There is no reason that 'scientific' sources should be considered better at interpreting the precise intent of the question than popular sources are, If anybody is, vos Savant is the expert in this respect. It may be that 'non-scientific' sources take the question to be more general in nature, or that they consider the 'condition' that the host opens a random door to be self-evidently irrelevant.
- There nothing wrong with "non scientific" fources looking at a "more general" (or rather simpler) scenario und use that as an heuristic argument as well, but there is something wrong with suppressing the known and published caveats of that view. Frankly put such an attempt is a distortion of the facts we have.--Kmhkmh (talk) 11:21, 27 June 2009 (UTC)
- What is clear, however, is that we have reliable sources that treat the problem conditionally and reliable sources that treat the problem non-conditionally, including giving aids to understanding and causes of confusion. It is the non-conditional formulation and solution that makes this problem famous and a clear non-conditional treatment of the problem should be given in the article. Martin Hogbin (talk) 09:12, 27 June 2009 (UTC)
- Now you are trying to pull the same thing again simply equating all sources. That is a logical fallacy, which btw is related to MHP ittself or another fanous problem from statistics the Simpson Paradox. It is possible that from a more general/less detailed perspective you can draw a seemingly obvious solution, which however turns out to be false in some of the more detailed (sub)scenarios. Breaking that down regarding your argument we have variety of sources stating undconditional solution without stating any caveats, so from that that "general" perspective the unconditional solution might appear almost as good as conditional one. But if we examine the source in more detail and rank them by reputation/expertise then the picture looks rather different and we get a clear preference for the conditional solution, in particular having only 1 out of many scientific sources stating the unconditional solution without caveats.--Kmhkmh (talk) 11:21, 27 June 2009 (UTC)
- From where you get the idea that fame of the problem is based on the unconditinal solution is somewhat uncomprehensible to me. The fame of the problem is clearly based on the original 1/2 vs 2/3 controversy (and vos Savant being correct with 2/3) and later within the science domain as well known example for conditional probabilities and failing intuition.--Kmhkmh (talk) 11:21, 27 June 2009 (UTC)
- That is your opinion, but some sources, such as vos Savant, Devlin and to a large degree Krauss and Wang treat the problem non-conditionally, that is to say that the issue of which door the host opens is not considered important. Most 'scentific' treatments start by assuming a particular formulation of the problem, that the questioner wishes to know what the probability of winning by switching is after a specific sequence of events has occurred. This assumption is criticised in Seymann's commentary at the end of the Morgan paper. There is no reason that 'scientific' sources should be considered better at interpreting the precise intent of the question than popular sources are, If anybody is, vos Savant is the expert in this respect. It may be that 'non-scientific' sources take the question to be more general in nature, or that they consider the 'condition' that the host opens a random door to be self-evidently irrelevant.
- However that is imho somewhat of a mischaracterization of what we actually have. Almost all scientific sources (Devlin being the only exception) treat the problem with conditional probabilities, some of them explicitly criticizing the unconditional solution. 2 sources give an unconditional and conditional a solution without giving a clear pference but pointing out that the unconditional solution strictly speaking solves a slightly different problem (Henze, Behrens). Also there was never an argument of not offering the unconditional solution and making it less useful ro the average reader. However suppressing the criticism of the uncodintional solution is mischaracterization of the problem(and its treatment in reputable sources) and hence no service to the average reader at all.--Kmhkmh (talk) 22:28, 26 June 2009 (UTC)
- We have reliable sources that treat the subject without making it conditional. We have sources that explain reasons for confusion and give aids to understanding based on the simple (unconditional or conditionality ignored) treatment of the problem. It seems to me that we are back where we started when I responded to the original RfC. Despite many editors taking a much less hard line on conditionality, a small number of editors are refusing to allow change to the page to make it more useful to the average reader. Martin Hogbin (talk) 17:46, 26 June 2009 (UTC)
- There is no universally agreed formulation of the MHP. Before we can provide a definitive solution we must decide many things including the game rules (on which there is general agreement) which distributions are to be taken as random, whether the doors opened are specified and finally what question we are going to ask. Until all those (and probably other) points have been decided there can be no single correct solution. Perhaps you could tell be in what order you would rank the available sources for reputation/expertise in deciding what question is being asked. Martin Hogbin (talk) 15:10, 27 June 2009 (UTC)
- yes, but there is a original formulation of the MHP (the one in parade) and for none of its possible interpretations is Vos Savant's explanation "complete". Strictly speaking it "merely" provides a reasonable heuristic. Vos Savants explanation is only complete for answering the question: "Is switching in general better than staying", that however is strictly speaking not among the possible interpretations of the original MHP. As far as ranking of sources go, it should be something like this: 1.) peer reviewed science journals (Morgan, Gillman, ...) 2.) science publications (books, non peer reviewed journals or columns) by reputable science institutions, reputable science publishers, reputable science individuals (Devlin Henze, Snell/Grinstead, various other math books). 3.)reputable general publications (New York Times, Parade) 4.)reputable general individuals/"pundits" (on record outside their publication) (vos Savant, gero von randow,...)--Kmhkmh (talk) 17:12, 27 June 2009 (UTC)
- There is no universally agreed formulation of the MHP. Before we can provide a definitive solution we must decide many things including the game rules (on which there is general agreement) which distributions are to be taken as random, whether the doors opened are specified and finally what question we are going to ask. Until all those (and probably other) points have been decided there can be no single correct solution. Perhaps you could tell be in what order you would rank the available sources for reputation/expertise in deciding what question is being asked. Martin Hogbin (talk) 15:10, 27 June 2009 (UTC)
- I am not going to argue that Whitaker's was not the most notable statement of the problem but we need to understand what it was. It was a question from a member of the public in a popular general interest magazine about a TV show. It was not intended to be used as a question in a statistics exam. You say that vos Savant's answer is only complete for answering the question: "Is switching in general better than staying". That is almost certainly what Whitaker actually wanted to know. Do you really think he wanted to know the chances of winning by switching given that a particular door had been opened by the host? It was a TV show and Whitaker clearly wanted to know if was generally better to switch or stick, or to put it another way, what would be the players best strategy if they found themselves in the situation just described (bearing in mind that the player would have no idea of the host's strategy, if any) and how much better is this strategy. The conditional formulation and solution is clearly irrelevant to this situation.
- As far as the math goes, it is is not about intent, but about what was actually stated. As far as speculating or examining potential intent goes, the authoritative source would be a peer reviewed journal for psychology. Concerning your claims about Whitaker's intent, personally I believe he wanted to know what's best for the candidate in the stated situation and he probably was not looking for a "complicated" explanation involving conditional probabilities. From that point of view you can consider vos Savants answer as perfectly alright. However we are not writing a private explanation for Whitaker in particular nor a Parade article in general, we are writing an encyclopedic article on the problem. Hence we need to provide an explanation, that has to be correct rather than being only adequate for Whitaker (or Parade readers). Being slightly polemic and picking up you last line above: Conditional explanation might be irrelevant to Whitaker, however whether it is or not is rather irrelevant for us (=WP).--Kmhkmh (talk) 20:06, 27 June 2009 (UTC)
- I am not going to argue that Whitaker's was not the most notable statement of the problem but we need to understand what it was. It was a question from a member of the public in a popular general interest magazine about a TV show. It was not intended to be used as a question in a statistics exam. You say that vos Savant's answer is only complete for answering the question: "Is switching in general better than staying". That is almost certainly what Whitaker actually wanted to know. Do you really think he wanted to know the chances of winning by switching given that a particular door had been opened by the host? It was a TV show and Whitaker clearly wanted to know if was generally better to switch or stick, or to put it another way, what would be the players best strategy if they found themselves in the situation just described (bearing in mind that the player would have no idea of the host's strategy, if any) and how much better is this strategy. The conditional formulation and solution is clearly irrelevant to this situation.
- Why should peer reviewed journals be better at interpreting the precise intent of Whitaker's question that a very intelligent person whose job it was to answer such questions? Martin Hogbin (talk) 18:18, 27 June 2009 (UTC)
- The wikipedia is about the actual stated problem and what is known/publsihed about it in reputable sources. It is not about speculative or fictious "intent". Moreover even if we were to take a different intent for granted the result is kinda the same. The WP article still needs to point out the problems with vos Savant's explanation aplpied for the stated problem (no change there). Then it would need to state the "intended problem" (as far as resources for that exist) and explain how vos Savant argument correctly explains the "intended version". Also we would have to state the exact differences between the intended and the actually stated version and that most literature refers to the actually stated version and it variants.--Kmhkmh (talk) 19:39, 27 June 2009 (UTC)
- Why should peer reviewed journals be better at interpreting the precise intent of Whitaker's question that a very intelligent person whose job it was to answer such questions? Martin Hogbin (talk) 18:18, 27 June 2009 (UTC)
- There is no 'stated problem'. Whitaker's problem cannot be solved at all without many details being added. It is generally accepted principle in statistics that no problem can be solved until it is properly defined. For example I found this quote, 'Every statistic is the product of many human decisions about what the statistic is supposed to describe'. This is a fundamental principle of the science of statistics. Most arguments in statistics come from failing to define the question properly. To answer a statistics question properly it is necessary to consider what the questioner actually wants to know, but do not take my word for this, read the comment by Prof Seymann at the and of Morgan's paper, where this point is made abundantly clear.
- Adding the details that must be decided upon to get a well-defined problem is not 'speculative' or 'fictitious' it is an important part of statistics. The one thing that is essential, however, in any answer in which details have been filled in is to make absolutely clear the assumptions on which your answer is based. The most conspicuous failure to do this is in the paper by Morgan et al, where a form of solution is assumed at the start without most of the assumptions made being stated. Martin Hogbin (talk) 09:27, 28 June 2009 (UTC)
- Much (most?) of the problem's fame came from vos Savant. vos Savant did not discuss 'conditional' solutions or 'host behaviour'. It seems to be a logical fallacy then, that the 'confusion' would be based on either of these items. Why do you guys keep bringing up 'variants' and 'sub-scenarios'? They are not relevant to the vos Savant MHP. Of course, adding or changing assumptions/premises could change the solution. What's that got to do with anything? And your statement that there is 'only 1 out of many scientific sources stating the unconditional solution without caveats.' is false. Everyone, except Morgan, Gillman, and what, 2 or 3 others uses the 'unconditional' solution. So that's hundreds of reliable sources. And the 'combining doors' solution is not unconditional. It shows that Monty revealed a goat behind door #3. Glkanter (talk) 16:23, 27 June 2009 (UTC)
- Nobody disagrees with most of the publicity coming from Vos Savant (however Martin above referred to Vos Savants explanation not Vos Savant in general and that difference matters). Also you seem to misunderstand the argument above, the use of the "subscenario" above is not refering to MHP variants, the argument is about MHP itsself and a fallacy in Martin's argument. The basic idea here is that, some statistical property that holds for the overall population, does not have to be true for various subpopulations (="subscenarios"). For crude analogon, it is true that 50% of the population is male, however if i look at the subpopulation of people wearing skirts, it is not true that 50% of them are still male. Meaning additional information matters! While it is true, that in 2/3 of all cases switching wins, it does not necessarily mean that, when sitting on door X and knowing about a goat on door Z, that switching wins in 2/3 of the cases as well. --Kmhkmh (talk) 16:53, 27 June 2009 (UTC)
- As far as my statement regarding the scientific sources, strictly speaking it should have been, all scientific sources I'm aware of (>4 math papers, >7 math books). However your claim, that "hundreds of Scientific sources" (except devlin) do otherwise, seems to be rather unfounded to me. However please feel free to prove me wrong and share those sources with us.--Kmhkmh (talk) 16:53, 27 June 2009 (UTC)
- Much (most?) of the problem's fame came from vos Savant. vos Savant did not discuss 'conditional' solutions or 'host behaviour'. It seems to be a logical fallacy then, that the 'confusion' would be based on either of these items. Why do you guys keep bringing up 'variants' and 'sub-scenarios'? They are not relevant to the vos Savant MHP. Of course, adding or changing assumptions/premises could change the solution. What's that got to do with anything? And your statement that there is 'only 1 out of many scientific sources stating the unconditional solution without caveats.' is false. Everyone, except Morgan, Gillman, and what, 2 or 3 others uses the 'unconditional' solution. So that's hundreds of reliable sources. And the 'combining doors' solution is not unconditional. It shows that Monty revealed a goat behind door #3. Glkanter (talk) 16:23, 27 June 2009 (UTC)
- Are you saying that Monty revealing a goat provides useful information to the contestant? The contestant is indifferent as to which door may have the car. Glkanter (talk) 17:11, 27 June 2009 (UTC)
- I'm saying whether the goat info turns out to be useful or not in this particular, is something that to be proven/checked and not just to be assumed either way. --Kmhkmh (talk) 19:39, 27 June 2009 (UTC)
- There are simple, if not immediately obvious, arguments showing the revealing of a goat does not provide any useful information to the contestant. Even more so if the door opened by the host is defined to be random. Martin Hogbin (talk) 09:30, 28 June 2009 (UTC)
- And the point is without actually making one of these arguments the solution does not actually address the case where a player is deciding whether to switch while standing in front of two closed doors (which is presumably how most people interpret the problem). -- Rick Block (talk) 16:34, 28 June 2009 (UTC)
- There are simple, if not immediately obvious, arguments showing the revealing of a goat does not provide any useful information to the contestant. Even more so if the door opened by the host is defined to be random. Martin Hogbin (talk) 09:30, 28 June 2009 (UTC)
- I'm saying whether the goat info turns out to be useful or not in this particular, is something that to be proven/checked and not just to be assumed either way. --Kmhkmh (talk) 19:39, 27 June 2009 (UTC)
- Are you saying that Monty revealing a goat provides useful information to the contestant? The contestant is indifferent as to which door may have the car. Glkanter (talk) 17:11, 27 June 2009 (UTC)
What do the sources actually say
Can we get back to what the sources actually say. Two threads above, I listed 4 POVs and some sources that take each and conjectured a 5th (which I think matches Martin's) that Kmhkmh claims Behrens and Henze take. Sorry for repeating them but I think it's helpful not to have to dig them out of the thread above (which got rather violently sidetracked). In this thread I would like the discussion to be limited to what sources say as opposed to arguments about the problem. If anyone would like to suggest additional POVs that other sources take, please do so.
- "vos Savant": The MHP is the Parade version with the additional assumptions that the car is uniformly distributed and the host always reveals a goat and always makes the offer to switch - with no explicit mention of how the host decides what door to open in the case the player initially selects the car. An unconditional solution showing the probability of winning by switching is 2/3 is presented without clarifying whether the problem is conditional or unconditional.
- vos Savant, Devlin, and most "popular" sources
- "Morgan et al.": The MHP is as above but is clearly conditional, and since there is no constraint on the host in the case the player initially selects the car the host's preference in this case must be treated as an unknown variable q. Unconditional solutions (such as vos Savant) address a slightly different problem for which the answer is 2/3. The answer to the problem as stated is 1/(1+q), which is 2/3 only if q is 1/2.
- Morgan et al., Gillman, Rosenthal
- "Krauss and Wang": The MHP is as above but with the additional constraint that the host choose randomly if the player initially selects the car (e.g. the Krauss and Wang version, i.e. the same as immediately above with q=1/2). An unconditional (2/3) solution is presented without clarifying whether the problem is necessarily conditional or unconditional.
- Mueser and Granberg, Krauss and Wang
- "Grinstead and Snell": The MHP is the Krauss and Wang version but is clearly conditional. Unconditional solutions say the answer is 2/3 (which is the correct numeric result) but answer a slightly different question.
- Grinstead and Snell
- "Martin": The MHP is the Parade version, but the probability of interest is meant to be the overall probability of winning by switching as opposed to the conditional probability faced by a player who has picked Door 1 and has seen the host open Door 3 (or, alternatively, a variant where the player must decide whether to switch before the host opens a door - "I'm going to open a door and show you a goat, decide now if you'd like to keep Door 1 or switch to the door I don't open").
- Kmhkmh suggests Behrends, Henze
I'd consider Behrends actually to be closer to Grinstead and Snell since the conditional solution is presented first and the unconditional solution is described as addressing a different problem. Behrends doesn't exactly take a definitive stance, but immediately after saying both analyses are correct he says "In the second analysis the situation was different." (which sounds an awful like Grinstead and Snell's "This very simple analysis, though correct, does not quite solve the problem that Craig posed"). Like I've said I don't read German so can't really comment on Henze, but a conditional solution is presented so the POV is not "Martin" but perhaps
- "Henze": The MHP is the Parade version. An unconditional solution is presented as well as a conditional solution (one that assumes q=1/2) without taking a stance on whether the problem is necessarily conditional.
- Henze
The point of all of this is that I'm finding remarkably little support (possibly none at all) for what I'm calling the "Martin" POV. I believe Martin (the user, not the POV) considers vos Savant, and Devlin, and most popular sources to be taking the "Martin" POV above but I don't think this is actually supported by what they say. I think there's as much evidence (i.e. none) for the "Martin" POV as there is for the following "Block" POV
- "Block": The MHP is the Parade version with an unstated (and unacknowledged) assumption that q=1/2 (i.e. it is the Krauss and Wang version) and is clearly conditional. An unconditional solution is presented under the unstated (and unjustified) assumption that the conditional and unconditional solutions must be the same.
There is, of course, no published support for the "Block" POV either. Since they don't say, we simply don't know whether sources presenting unconditional solutions think they're solving an "unconditional" version of the MHP (per the "Martin" POV) or think their unconditional solution is addressing the conditional problem (per the "Block" POV). Rather than put words in their mouths, I think we have to consider these sources as taking the "vos Savant" POV - i.e. we don't know what exact problem they think they're addressing.
What we do have are sources that say the unconditional and conditional interpretations are different problems and (with the possible exceptions of Behrends and Henze) every single source that identifies these as different problems explicitly saying the MHP is the conditional one. Treating these as equally valid interpretations doesn't seem to be supported by the sources. -- Rick Block (talk) 17:17, 27 June 2009 (UTC)
- Henze (and Devlin) offers the 'Combining Doors' solution, which clearly shows a goat behind door #3. How is this unconditional? Is there a reliable published source you can provide who says it's 'unconditional'? Glkanter (talk) 17:43, 27 June 2009 (UTC)
In my reading Behrens and Henze do consider the conditional and unconditional solution as solutions to slightly different problems. But they consider the unconditional solution however as a good heuristic argument for switching in the original MHP (as long as no better analysis is vailable). The rationale behind this that, you usually assume statistical properties of the total population to be true for subpopulation as well as long as you have no clear indication to believe otherwise. So if switching wins overall in 2/3 of the cases, you take that as an indicator that switching will win in the candidate's specific situation as well. That of course is a heuristic argument and a such it might fail. In that sense you can see the unconditional solution as a valid heuristic argument for switching rather than a valid rigorous proof (using all infos/details being available). I agree with your comment regarding Martin POV vs Block's POV, in my eyes Martin's perception of the sources is somewhat distorted (see comments above) and it does not reflect the true source situation appropriately.--Kmhkmh (talk) 18:00, 27 June 2009 (UTC)
- Kmhkmh, From what you say above Behrens actually seems to support my argument for treating the non-conditional solution as a good one. Is there an English translation of it anywhere? Martin Hogbin (talk) 23:49, 27 June 2009 (UTC)
- Behrens is in English, the link is in the article. Or did you mean Henze? Henze is only available in German. You can find most of Henze online here: [10]. That pages also contains an extensive collection of scientific sources in english and german that are available online. As is said above in my view Behrens and Henze both give the unconditional solution, stating that the probabilities belong to a slightly different problem, but that they can be used as a heuristic argument for the original MHP. None of them can be understood as disagreeing with Morgan et al.--Kmhkmh (talk) 01:17, 28 June 2009 (UTC)
- Rick, Comments on the sources below.
- I would prefer to call the vos Savant solution non-conditional. We do not know whether she considered the question to be an unconditional one (what is the best strategy for the player), whether she considered the host to choose randomly and thus the condition that one particular door is opened to be irrelevant or whether she did neither of these. Her subsequent comments suggest she considered the door opened to be irrelevant. What we do know is that conditionality does not enter into her solution and that we have a section in the article that treats the problem the same way and that she gave aids to understanding and causes of confusion that specifically relate to her solution.
- What we do know is that her solution addresses the overall chance of winning by staying vs. switching (which other sources call unconditional, not "non-conditional"), and that her explanation includes cases where the car is behind Door 3 in apparent violation of the problem statement. We don't know whether she thought the same solution pertains to the specific (conditional) case mentioned in the problem statement (i.e. player picks Door 1 and host opens Door 3) or not. We might infer that she thought so, but then the criticism that her solution does not exactly address this case is completely valid. Are the aids to understanding you're referring to the million door variant and the experiment she suggested? I'm not aware of any causes of confusion she's discussed. My issue with providing aids to understanding and sources of confusion in a separate section including the "unconditional" solutions is that we don't exactly know what problem these solutions are talking about. I think you're assuming those offering these solutions interpret the problem statement to be about the overall chance of winning by switching vs. staying, but since the problem statement they use (e.g. the Parade version) doesn't clearly say this (IMO, it pretty clearly specifies the conditional probability is the one of interest, but in any event it certainly never mentions anything about the unconditional probability) I don't think we can change the problem statement on their behalf. Just out of curiosity, how would you introduce such a separate section? -- Rick Block (talk) 17:30, 28 June 2009 (UTC)
- I am using the term 'non-conditional' on this talk page to mean the any solution which does not treat the problem conditionally, for whatever reason, in other words the 'simple' solution. I accept that it is not a standard term and I am not necessarily advocating its use in the article.
- I would introduce the non-conditional section exactly as we do now but just move the relevant aids to understanding and causes of confusion to that section.
- Pretty well nobody, including Morgan, makes clear exactly what question they are answering. It is always possible to make maths problems more complicated by adding extra complexity and then treating the simple problem as a special case of a more complex one. In some cases this may be instructive but generally it is a good idea to make solutions as simple as possible. The MHP may be treated non-conditionally for a variety of formulations and many reliable sources do this. It may not always be clear exactly what problem they are addressing and why they are not treating the problem conditionally, but nevertheless they do treat the problem unconditionally and they do give the correct answer.
- When an expert answers a question from a non-expert member of the public they have a duty to try to determine what it is that the questioner actually wants to know rather than just answering the question as asked, not doing this is the kind of thing that gives statisticians a bad name For the question to be conditional we must take it that Whitaker considered that which door was opened by the host was relevant to the decision to be made. I very much doubt that this was the case. Martin Hogbin (talk) 09:50, 29 June 2009 (UTC)
- I will not repeat my views on the Morgan paper except to point out again that Seymann considered that they may have been answering the wrong question. I may put my many criticisms on the Morgan paper on a page in my user space so that I can link to them rather than repeating them. Now done, here is my comprehensive criticism of the Morgan paper
- I agree with you description of Krauss and Wang's paper and note that they also give causes of confusion for the non-conditional solution. In fact they suggest that too much information, such as the number of the door that the host opens, to be one of the reasons that people get the answer wrong. This again supports having a separate 'Causes of confusion' section fot the non-conditional solution that we already have.
- With the "Grinstead and Snell" (which I have not read) solution we are back to asking what 'the question' is and who is best qualified to judge this. Martin Hogbin (talk) 23:49, 27 June 2009 (UTC)
- Why haven't you read Grinstead and Snell yet? The PDF is linked from the article, all you have to do is click it and then search for "Monty Hall". Their discussion starts at the bottom of page 136, in the chapter on "Discrete Conditional Probability" (kind of hint about what kind of problem they think it is) - it's less than 3 pages. With regard to who is best qualified to judge what the question is, what exact question would you say vos Savant answers (and how do you know this)? -- Rick Block (talk) 17:30, 28 June 2009 (UTC)
- Actually, when I looked at it I had seen G & S before. Like many others their treatment seems to be based on the Morgan paper. Vos Savant answered the question where the player chooses after a door has been opened but the host chooses randomly. I know this because she says so. The condition in this case becomes a pointless complication since it clearly makes no difference to the answer as G & S say. Martin Hogbin (talk) 21:47, 29 June 2009 (UTC)
- "Seems to be based on the Morgan paper" is pure conjecture on your part (we're talking here about what the sources actually say, remember?). vos Savant says (in her response to Morgan's paper published in American Statistician, Nov 1991, p 347) "In the original column, no additional stated conditions appeared important to a general apprehension of the problem because circumstances in default are reasonably considered random." - but her explicit experimental procedure described in one of her followup Parade columns makes no mention of the host's choice in the case the player initially selects correctly (even though she explicitly randomizes both the initial car placement and the player's initial choice) and (as far as I know) she never exactly clarified if she was intending that her answer apply to the specific case mentioned in the problem statement (player picks Door 1 and host opens Door 3) or not. In Morgan et al.'s rejoinder to vos Savant they say "One of the ideas put forth in our article, and one of the few that directly concerns her responses, is that even if one accepts the restrictions that she places on the reader's question, it is still a conditional probability problem."
- Actually, when I looked at it I had seen G & S before. Like many others their treatment seems to be based on the Morgan paper. Vos Savant answered the question where the player chooses after a door has been opened but the host chooses randomly. I know this because she says so. The condition in this case becomes a pointless complication since it clearly makes no difference to the answer as G & S say. Martin Hogbin (talk) 21:47, 29 June 2009 (UTC)
- G&S certainly do not say the condition becomes a pointless complication or that it clearly makes no difference. What they do say (after clarifying the host's choice is random in the case the player initially picks the car and presenting both an unconditional and conditional solution) is "At this point, the reader may think that the two problems above are the same, since they have the same answers." and then proceed to show how they are indeed different problems that may have different solutions by assigning a probability other than 1/2 to the host's choice in the case the player initially picks the car. This seems to be the exact opposite of what you're saying, i.e. they're saying it is a necessary assumption and it clearly does make a difference. -- Rick Block (talk) 13:16, 2 July 2009 (UTC)
- We seem to be going over the same old ground again. We both read the same sources and come to different conclusions. I came here in response to an RfC in which it was said that a group of editors were claiming ownership of the article. I am not sure how to proceed now, I am convinced that the article currently does the average reader a massive disservice in that it fails to address what is commonly thought of as the MHP, but am not allowed to change this.
- I suggest that I ask some of the recent editors to come back and give their views again on how the problem should be presented. Martin Hogbin (talk) 15:58, 8 July 2009 (UTC)
Simple Solution
I don't understand why the solution in the article has to be so long? It's quite simple really.
According to the traditional description of the game the host cannot show you the car if you picked a goat. Therefore, if you picked a goat the host will always eliminate the other goat. Thus when you switch you are basically betting that you picked a goat. The only time switching loses is when you picked the car in the first place. Thus when you don't switch you are basically betting that you picked the car. It's trivial to say that there's a 2/3 probability you pick a goat and only a 1/3 chance you pick the car. Thus, betting you picked a goat, and therefore switching, will win more often since you will more often, randomly choose a goat. 167.6.247.204 (talk) 19:57, 10 July 2009 (UTC)
- I agree with you, but unfortunately some academics (Morgan et al) decided that the problem was too simple for them and that it need to be made more complicated. They managed to convince people that it somehow mattered which door the host opened when the player had initially chosen the car, thus making the problem one which required the use of conditional probability to solve. Martin Hogbin (talk) 20:16, 10 July 2009 (UTC)
- Isn't this what the "popular solution" section says? What Martin is referring to is the fact that this solution doesn't always work. What the "academics" say is the answer always depends on how the host chooses which door to open if you've initially picked the car. The simple solution works only if the host randomly picks which door to open in this case - a reasonable assumption but the fact the solution depends on this assumption is not readily apparent. The easiest way to see it does matter how the host decides in this case is to force the host to decide some other way (like always opening the rightmost door if the player initially picks the car). With this way of deciding, if you pick door 1 and the host opens door 3 you have a 50/50 chance of winning by switching. What the academics say is if the host opens the door with probability p (in the case the player's door hides the car) your probability of winning by switching is 1/(1+p). The only way this works out to 2/3, is if p is 1/2. -- Rick Block (talk) 23:54, 10 July 2009 (UTC)
- The complicated solution is only required if you make a number or arbitrary and unjustified assumptions. This has been argued many times on this page but if you are interested in my criticism of the 'academic' solution the look here. Martin Hogbin (talk) 09:31, 11 July 2009 (UTC)
- Also see the FAQ at the top of this page. -- Rick Block (talk) 13:15, 11 July 2009 (UTC)
new book
There is a new book out, The Monty Hall Problem: The Remarkable Story of Math's Most Contentious Brain Teaser by Jason Rosenhouse, Oxford University Press 2009, ISBN 9780195367898. I'm surprised the wikipedia article doesn't reference it. 67.117.147.249 (talk) 19:04, 1 August 2009 (UTC)
- There is discussion of this book's account of the exchange between Morgan et al. and vos Savant above (#Refereed paper agreeing with Morgan et al.). The book is not used as a reference so is not cited. Per WP:SOAP, Wikipedia is not to be used for advertising, so unless there is a legitimate reason to reference something from this book it should not be mentioned, just as http://www.amazon.com/Monty-Hall-Problem-Beyond-Closed/dp/1847530788 is not mentioned. One difference is that the Deaves book does not satisfy Wikipedia's criteria for WP:reliable sources since it is self-published. The Rosenhouse book is published by Oxford University Press, so could be used as a reference if it has anything to say that is not already covered in the article. -- Rick Block (talk) 15:11, 2 August 2009 (UTC)
My explanation (the average joe way)
This is how I understand it: Right off, everyone can say you have a 2/3 chance of picking the goat. Well, what most people are forgetting is the host *has to show you another goat* (at least in the "usual" way this problem is told). That means in the same 2/3 cases, the host will be *forced* to pick the other goat you didn't pick. Both you by choice and the host by force eliminate the goats 2/3 times without even realizing it. So 2/3 you should switch and get the car since it was the only thing not eliminated in this 2/3 world.
But, an astute person will feel cheated thinking there's only 3 possibilities. In reality, there's 12 moves you and the host could make, but in 8 of these switching is a winner. So 8/12 is just 2/3.
Trying to explain it with pictures or examples doesn't make much sense at least for me (And I'm in upper division college math). —Preceding unsigned comment added by 150.135.245.202 (talk) 09:13, 28 August 2009 (UTC)
"Monty Fall"
In two sections of the article-- Why the probability is not 1/2 (under Aids to understanding), and Other host behaviors (Monty Fall), it is stated that the probablity of winning by switching becomes 1/2 instead of 2/3 if Monty reveals a goat accidentally instead of intentionally. This is seemimgly wrong and absurd, since it asserts that probability can be dictated by intent. Perhaps the phrasing needs to be udpated to indicate whether the door opened can include the door the player initially picked, which would indeed drastically change the odds. Or maybe I'm wrong, and am missing some obscure mathematical subtlety of the Monty Fall problem. In either case, this example most certainly did NOT "aid my understanding", and rather served only to make an already-confusing problem even more confusing. Clayhalliwell (talk) 17:25, 6 September 2009 (UTC)
- As far as the quality of explanation goes, I agree with you to some degree, but that is another matter.
- Regarding your point, the host never picks the door chosen by the player but, if the host chooses randomly, the player's chances of winning by switching are indeed reduced to 1/2. How can this be? You first need to note that if the host chooses randomly he will sometimes choose the car. What happens to these games? We can only assume that they are declared void as there is no point in offering the player a swap as they know they will lose either way. Of the remaining games, the ones that have not been voided, the player has a 1/2 chance of winning by swapping. This has changed from the original 2/3 chance for the following reason. If the player has originally chosen the car the they will obviously lose by swapping, but in this case the host cannot reveal the car, because the player has it. If, on the other hand, the host has initially chosen a goat, and would therefore win by swapping, the host could possibly open a door to reveal the car thus voiding the game.
- So to sum up, some of the games (half of them) in which the player would have won the car by swapping will be voided if the host chooses randomly but none of the games in which the player would have lost by swapping car will be voided. This gives the payer only a 1/2 chance of winning by swapping overall. Martin Hogbin (talk) 17:56, 6 September 2009 (UTC)
- The "Why the probability is not 1/2" section was butchered a while ago since the bulk of it was not referenced. It used to look like this. What remains is essentially an introduction to a section that no longer exists (it was vaguely based on [11], which is not a reliable enough source for a featured article). There was a previous suggestion to delete this section, although the fact that it admittedly needs some work does not seem like a reason to delete it. -- Rick Block (talk) 00:09, 7 September 2009 (UTC)
- Another way to think about it is that we need to know why the host chooses to open his particular door if we are going to extract useful information from observing his choice. If the host chose a door randomly (and got lucky), we can't get the same information out as if the host chose a door because he knew it contained a goat. In the standard problem, the host is giving us a bit of information: of the two doors he can choose, he chose -this- one and not the other one. It's not perfect information, but it still helps (and it's how we improve our chances of winning in the swap from 1/2 to 2/3). However if Monty is forgetful and simply got lucky (by revealing a goat door, at random), he isn't imparting even partial information to us. He could just as easily have revealed the car. You might be able to think of other strategies that Monty could employ, and observe how they will give the player different probability estimates for winning by swapping. In summary, knowing why the host chooses his door is vital if we are to interpret his choice in our analysis. Maelin (Talk | Contribs) 02:55, 7 September 2009 (UTC)
- Well, honestly, the door-opening in both cases doesn't provide ANY information, since the problem functionally distills down to choosing one door, or two doors. Whether you get to see behind one of the two doors first should be statistically irrelevant. Clayhalliwell (talk) 17:00, 21 September 2009 (UTC)
- Perhaps you're confusing unconditional and conditional probabilities - which many explanations of this problem don't exactly explain very clearly. For example, one fairly popular solution says something like "your original chance of picking a door hiding a car is 1/3, so if you ignore what the host does and don't switch you'll win the car 1/3 of the time". Given that the host must open a door and won't ever reveal the car this is a true statement, but it doesn't really address the situation given in the problem statement which is that the player has picked a door and then the host has opened a door revealing a goat. The probability the car is behind the door the player initially picks, say door 1, is generally considered the unconditional probability. This probability is clearly 1/3 and stays 1/3 regardless of anything that later happens. The probability the car is behind the door the player picks given something has later happened, like say the host has opened some other door and has revealed a goat, is a conditional probability and may or may not be the same as the initial 1/3 probability. In the problem as usually presented no outcomes are excluded and all outcomes are equally likely so this conditional probability is the same as the initial unconditional probability. In the host forgets variant, all outcomes are equally likely but outcomes where the host opens a door and accidentally reveals the car are excluded. This allows the conditional probability to be different than the original (unconditional) 1/3. -- Rick Block (talk) 03:58, 22 September 2009 (UTC)
- Well, honestly, the door-opening in both cases doesn't provide ANY information, since the problem functionally distills down to choosing one door, or two doors. Whether you get to see behind one of the two doors first should be statistically irrelevant. Clayhalliwell (talk) 17:00, 21 September 2009 (UTC)
Simulations show 50%?
Unfortunately, every time I have I have attempted to simulate this problem, I have consistently achieved the 50% result. This makes it very difficult for me to believe the extensive rationales offered on this Wikipedia page. I'm willing to try again based on the deck-of-cards example, but I'm highly skeptical that the result will differ given my many past attempts. When experimentation agrees with intuition, it's time to suspect a math error. 173.48.171.191 (talk) 03:08, 1 October 2009 (UTC)
- How, exactly, are you simulating the problem? -- Rick Block (talk) 03:30, 1 October 2009 (UTC)
- What usually causes confusion in this type of a conditional probability problem, especially when you claim "proof by simulation," is the problem setup itself. Your simulation will get the correct answer to the wrong problem if you are not careful. Specifically, what other possibilities could have happened, but didn't in the specific instance of the experiment you simulate? For example, under "Monty Fall" above, Clayhalliwell observed: "It is stated that the probablity of winning by switching becomes 1/2 instead of 2/3 if Monty reveals a goat accidentally instead of intentionally. This is seemimgly wrong and absurd, since it asserts that probability can be dictated by intent." It isn't intent that changes the probability in that case, it is the fact that some possibilities are included in the case that leads to "2/3," while the same possibilities are excluded in the case that leads to "1/2." When the host intentionally reveals a goat, every single case must be included in your sample space. Because every time the host runs that game, he can reval a goat. If the host chooses randomly, then the host sometimes reveals the car, and those cases must be dismissed in your simulation because they do not match the problem description. If your simulation gets the answer 1/2, then you are dismissing some cases which you should not. That is why Rick Block asked how you are simulating the problem. --JeffJor (talk) 13:23, 1 October 2009 (UTC)
Simulation
How to correctly simulate the problem? If it is given that the player picks door 1 and the host opens door 3 (as described in the problem statement), then take for example 3 cards, ace of spades (car), 2 of hearts and 2 of diamonds (goats). Shuffle them and lay them out next to each other (face up!). Their position, left to right, represents the door number 1-3 (from left to right). Keep two tallies: win by switching (lose by staying) and win by staying (lose by switching). If the ace (car) is at the right, start again, because this event did not occur (this would mean the host must have opened door 2, but we're given the player picked door 1 and the host opened door 3!)- i.e. do not count this as a win either by staying or by switching. If the ace (car) is in the middle, add one to the tally of wins by switching. If the ace (car) is at the left, flip a coin representing the host's choice of which door to open in the case the car is behind the player's initially selected door (door 1). If the coin shows heads (host opens door 3), add one to the tally of wins by staying; if tails (host opens door 2, but since we're given the host opens door 3 this did not occur) nothing is done - i.e. do not count this as anything at all. Repeat as often as you like, but at least 20-30 times. You may already predict the outcome. Nijdam (talk) 21:50, 3 October 2009 (UTC) [edited by Rick Block (talk) 23:45, 3 October 2009 (UTC)]
- This procedure simulates the conditional problem as described, specifically the case where the player has selected door 1 and the host has opened door 3 (randomly choosing to open door 2 or door 3 if the player has initially selected the car). Simulations where all outcomes are counted, for example the one suggested by vos Savant [12] involving two people with one playing the "host" and the other taking the role of the "player", ignore the potential effect of the host's choice when the car is behind the player's initially selected door. In this unconditional problem (which might be described as what is the chance of winning for a player who decides to switch before seeing what door the host opens) there is a 2/3 chance of winning by switching regardless of how the host picks which door to open if the car is behind the player's initially selected door. The probability is the same in the conditional problem as described (where it is given the player picks door 1 and the host opens door 3) only if the host must choose between the two remaining doors equally often when the car is behind the player's initially selected door. -- Rick Block (talk) 23:45, 3 October 2009 (UTC)
What keeps the first choice from being entirely unrelated? The choice is being made by the player (who has no information as to what's behind the doors) on a set of three doors. Then, they are allowed to remake their choice (that is, theoretically a choice of the same weight) on a reduced set of two doors. Why is the probability of the second choice multiplied by the probability of the first, when the player makes the second choice between two options with no information? To put it another way, let's say we have N boxes and one contains a bunny. We are allowed two choices. Assuming that we don't find the bunny the first time and the known empty box is then removed, why is the chance of bunny not now 1/(N-1)? —Preceding unsigned comment added by 142.205.213.254 (talk) 20:51, 14 October 2009 (UTC)
- Do you mean "What keeps the second choice from being unrelated to the first? The fact that it isn't a new choice of a door at all. It is a choice to keep the first-chosen door, or change to the remaining closed door which represents the best prize of the two doors you didn't choose. To see what I mean, consider the "calling" of a simple flip of a coin instead of this game. Before the coin is revealed, you call "heads" or "tails." Then you are told what the coin did not land on, giving you some (actually, in this example, all) of the information in the event. Say you are then offered the chance to change your call, or keep your original call. If you choose "heads" or "tails" randomly (i.e., you make a second choice "unrelated" to the first), you will be right 50% of the time. But why would you do that? You know by elimination how the coin landed. The Game Show problem is different only in that you are given partial information rather than complete information. Before a door is open, you know that the two doors you didn't choose, between them, have a 2/3 chance of hiding the car. And that the host knows which one of them hides the goat. He can open that one without changing anything. Your choice to change isn't a new choice of a door, it is a choice to keep what you had first (a 1/3 chance) or change to a 2/3 chance. JeffJor (talk) 00:31, 15 October 2009 (UTC)
- The only thing that changed is that you stop using "unconditional probability," and start using "conditional probability." Anybody who insists there is no benefit to switching is refusing to recognize this. Before the host opens the door, there is no "conditional probability." There is only the "unconditional probability" that a car is behind a particular door. It is 1/3 for each. After he opens a door, you have to integrate the added information into your probabilities. But the added information only affects the two doors you didn't choose, never the one you did. This is because the host cannot choose that one, so it is unaffected by any action he take that does not eliminate all of the unchosen doors. Its (conditional) probability stays at 1/3, the door the host opens goes to 0 (because you know it doesn't have the car) and the "unconditional probability" it used to have is transfered to the remaining door, making its conditional probability 2/3.JeffJor (talk) 22:13, 25 October 2009 (UTC)
- The probability of the player's initially selected door happens to not change in the problem as generally understood, but this is not some immutable fact caused by the rule that the host cannot open this door. Frequent readers of this talk page may find this sort of example tiresome, however consider a host who never opens the door the player chooses (i.e. if the player chooses a goat the host opens the other goat door) but does not choose with equal probability if the player has initially chosen the car. For example, in this case let's say the host picks the leftmost door 1/3 of the time and the rightmost door 2/3 of the time. With this host, if the player picks door 1 and the host opens door 3, the conditional probabilities are NOT 1/3 for the player's initial door and 2/3 for door 2 but rather 2/5 and 3/5, respectively. The point of this example is not to say that the solution saying the player's chances of winning double by switching is wrong - but that the explanation that says "the added information only affects the two doors you didn't choose" is not quite right. The added information means the conditional probabilities must be calculated.
- The conditional chance of the door the player doesn't pick is 1/3 out of (1/3 + X), where X is 1/3 times the chance the host opens door 3 when the player picks door 1 and the car is behind door 1. Assuming the host picks equally when the player initially picks the car, this chance is 50% so X is 1/6 and the chance the car is behind door 2 is therefore (1/3) / (1/3 + 1/6), which is 2/3. Similarly, the chance the car is behind door 1 is X / (1/3 + X), which (still assuming the host picks equally) is (1/6) / (1/3 + 1/6) - i.e. 1/3.
- Saying "the player's initial chance doesn't change because the host cannot open the player's initially selected door" misses another critical condition - which is that the host also must choose equally if the player initially selects the car. Without this additional constraint, the statement is simply not true. BTW - I'm quite sure Professor Nijdam is not saying it doesn't matter if you switch but rather that the probabilities of the player's door and the remaining unopened door are always both affected by the host opening a door. -- Rick Block (talk) 23:43, 25 October 2009 (UTC)
- Rick? That action you described lets the host "eliminate all of the unchosen doors" 1/3 of the time, by revealing the car 1/3 of the time. Maybe I didn't phrase it as well as you would have liked, but I do understand this problem and I am on your "side" of the arguments. As long as the host CAN, BY ANY POSSIBLE OUTCOME OF HIS STRATEGY, ONLY REVEAL INFORMATION ABOUT WHERE THE CAR IS NOT, (a better choice of words), the a posteriori probability that the car is behind the chosen door remains 1/3 (or 1/N if you have N doors and one car), the same as the a priori probability. That condition happens if the host CAN reveal a car, or if he reveals all of the unchosen doors. You allowed him to reveal a car 1/3 of the time.
- Yes, the a posterioi of any unopened, unchoosen door changes from what its a priori probability was. My point was that the significant change is bewteen using a priori and a posteriori probabilities. Under the conditions I meant (Host can't reveal the car and can't reveal all unchosen doors), the a posteriori probability for the chosen door is always the same as its a priori porbability, while the a posteriori probability of any unopened, unchosen door is always greater than its a priori probability (assuming the host opens some number of a doors, that is).JeffJor (talk) 15:24, 26 October 2009 (UTC)
- The host action I'm suggesting never reveals the car. The change from the typical analysis is only in the case where the host has a choice (the case where the player's initially selected door hides the car). In this case, if the host's preference for the door that is opened is expressed as a probability p, the player's initially chosen door hides the car with probability p / (1+p) - and the other door's probability is 1 / (1+p). These are 1/3 and 2/3 only if p is 1/2, so the conditional probability of the player's initial selection changes from 1/3 to something else under all conditions except if the host makes an evenly random choice (when the host can choose). The Parade version of the problem doesn't specify how the host chooses if a choice is available. Many people (quite sensibly) take this to mean p should be assumed to be 1/2. However, in a mathematically pedantic sense, if it's not specified it should be left as a variable. Note you're never worse off switching, regardless of what p is. This is (more or less) the central point of both the Morgan et al. and Gillman papers. -- Rick Block (talk) 19:21, 26 October 2009 (UTC)
- I apologize; I didn't read it all - just enough to see that you said the probability changed, which it CAN NOT DO unless the contestant knows the host's strategy is biased as you said. It has to be an axiom that the contestant does not know it, if it is biased toward one door or the other. That represents additional information that is not in the problem statement. Think of it this way - the contestant can mentally name the doors Tom, Dick, and Harry. It is only if he can associate these names with the host's "left" and "right" that your biased strategy affects the conditional probability to contestant sees. Otherwise, when he choses Tom the chances are 1/2 that the host opens Harry or Dick. It isn't that P is assumed to be 1/2, it is that the contestant has a 1/2 chance of being right about which door is favored, and 1/2 chance of being wrong. So again, the a posteriori probability of the original choce DOES NOT CHANGE unless the host gives away information about where the car is, or how he is choosing, in a way that contradicts the problem statement. [Oops - I keep forgetting to log in before I sign with four tildas] JeffJor (talk) 22:31, 26 October 2009 (UTC)
- Is the question what the contestant knows, or is the question what the probability is? This gets into discussions that have been held at length on the /Arguments page. If the host chooses equally if given the choice and an alien lands at the point the player is deciding whether to switch and is told only that one door hides a car and the other hides a goat, what are the probabilities? From the player's perspective it's still 1/3 vs. 2/3 even though the alien has a 50/50 chance of picking the door hiding the car. Morgan et al. (1991) and Gillman (1992) solve for the probability, regardless of whether the contestant knows it. Perhaps the contestant isn't aware of the host's preference (like the alien isn't aware of the full problem set up), but not knowing the host's preference doesn't mean it has no effect on the actual probabilities. -- Rick Block (talk) 00:53, 27 October 2009 (UTC)
- The only possible question is what the contestant knows, since the question is about whether the contestant should switch. There in no such thing as an "absolute" probability for a particular instance of the game, as you insinuate here. Only probabilities based on the various perspectives. Since the actual problem is based on "What should the contestant do?," it has to be evaluated from his perspective. (The correct resolution to the arguments you refer to, which I have not read, is that "probability" does not apply to the specific instance of the game. Probability only applies to a process. The instance given to us merely demonstrates that process from the contestant's perspective.) But even if you consider the wrong perspective, since the problem does not say which door was opened, you need to consider all possibilities. And that still makes the answer P(switch to car)=2/3. Even the alien you refer to, when it switches doors, it wins 2/3 of the time; and when it keeps the original door, it wins 1/3 of the time. Since it actually switches half of the time, it wins (1/2*2/3+1/2*1/3)=1/2 of the time.
- For example, the car is behind one door that is known to the host. From the host's persepctive, the probability of switching to a car is either 0 or 1, because he knows where the car is. But those two cases don't happen in equal numbers. Regardless of his strategy, as long as he always opens one door with a goat, the probability that the original door had the car is 1/3 so that is the probability of getting a goat by switching. This answer does not depend on how the host choose what door to open.
- From the show's producer's standpoint (she doesn't know where the car is, but does know the host's strategy), which is what you attempted to calculate, there are four possibilities. Using a notation where CCOL means "contestant Choose Car, host Opened Leftmost door," they have probabilities P(CCOL)=1/9, P(CCOR)=2/9, P(CGOL)=1/3, and P(CGOR)=1/3. The conditional probability when when the host opened the leftmost door is P(switch to car|opened leftmost)=P(CGOL)/[P(CCOL)+P(CGOL)]=(1/3)/(1/9+1/3)=(1/3)/(4/9)=3/4. The conditional probability when when the host opened the rightmost door is P(switch to car|opened rightmost)=P(CGOR)/[P(CCOR)+P(CGOR)]=(1/3)/(2/9+1/3)=(1/3)/(5/9)=3/5. I presume the latter is what you calculated? More generally, these are 1/(1+P) and 1/(2-P), respectively, which does nto seem to be what you calculated. But, what you got is only part of what you needed to calculate, since it only represents the cases where the host opened the rightmost door. In actuality, P(swith to car)=P(CGOL)+P(CGOR)=1/3+1/3=2/3. Or you could use the Law of Total Probability to say P(switch to car)=P(swith to car|opened leftmost)*P(opened leftmost)+P(switch to car|opened rightmost)*P(opened rightmost)=(1/(1+p))*((1+p)/3)+(1/(2-P))*((2-P)/3)=2/3. Unless tyhe problem states "The host opened the rightmost door," that is the answer you need to use. The generality I made is correct.JeffJor (talk) 12:52, 27 October 2009 (UTC)
- In the typical problem statement, specifically the one from Parade, aren't we told to consider the case where the player picks door 1 and the host opens door 3? By computing the "total probability" you're actually computing the unconditional, a priori, probability not the conditional probability in a particular case. The point of introducing p is not to address a host with a specific rightmost or leftmost preference, but any preference for the door that has been opened. The conditional probability given the player picked door 1 and the host opened door 3 is P(CGO3) / [ P(CCO3)+P(CGO3) ]. Please show me how you would solve this without making an assumption about the probability of the host opening door 3 in the case the car is behind door 1. BTW - you might find the Morgan et al. paper interesting. And, since we're really not talking about changes to the article here should we move this thread to #Arguments? -- Rick Block (talk) 14:36, 27 October 2009 (UTC)
- No, we are not really told that the player opened a specific door. In the Parade quote (which is an ambiguous formulation), it is "You pick a door, say No. 1." The number is an example used to establish a way to distinguish the doors in the description, without saying which has a car or goat. The wording we are supposed to be using makes that even clearer by actually describing the process and naming the doors only at the end, in an example of the process. Neither gives a right-to-left ordering of doors, so your example is useless. And even if it was a specific door, it only matters (to the player) if the player knows how the host favors the specific doors, which most definitely is not in either problem statement. And the reason you can't use the calculation you asked for, is that it assumes the host's strategy is known to the player. [Added: But to avoid any confusion here, and when reading Morgan, just assume that the player and the host have each assigned their own sets of numbers, at random, to the three doors. The two sets are independent of each other. That is the problem intended. JeffJor (talk) 16:03, 27 October 2009 (UTC)]
- "A priori" and "a posteriori" are terms that apply relative to the gaining of some information. "Total" refers to the a set of probabilities that comprise the entire set of possibilities for the information you have (e.g., this is why you divide by the sum of all probabilities that meet the condition in Bayes' Theorem). So you can use "total probability" on both sides of gaining the information, as long as it uses the proper information. The set of a priori, total probabilities are 1/3 for each door, no matter what you use to designate them. If the information is "Player chooses one door, Host opens an unchosen door that he knows has a goat, chosing BY SOME MEANS UNKNOWN TO THE PLAYER if both have a goat," then the a posteriori, total probability is 1/3 for the door the player chose, 2/3 for the unopened door, and 0 for the opened door. There may be different information that goes into the host's assessment of a posteriori probabilities, and those use the contestant's a posteriori probabilities as their a priori probabilities, since the two sets are on opposite sides of the strategy information.
- I have read Morgan, but it was long ago. AFAIK, nothing I have said is contradicted there, and it should not be. But they may talking about these concepts in a different way. And yes, this should move - I just don't know how. JeffJor (talk) 15:57, 27 October 2009 (UTC)
- Ok, I went and perused Morgan. They misquoted the problem. They based everything on the assumption that the contestant always opens a door that is clearly labeled "Door #1" to both the player and the host. That not what the article they are referring to said (http://www.marilynvossavant.com/forum/viewtopic.php?t=64). Most of the solutions they said are "wrong" are still "wrong" for some very pedantic reasons, but most are trivial to correct. For example, F1 is "wrong" because it fails to equate P(win)=P(lose|switch to D2)*P(switch to D2)+P(lose|switch to D3)*P(switch to D3) and then set P(switch to D3) to 0, since the contestant will never do that. The point is that there can be differnet models set up to solve a probability problem, and theirs may not be the easiest. JeffJor (talk) 16:36, 27 October 2009 (UTC)
- Jeff, there is actually rather more than that wrong with the Morgan paper, including a rather surprising error. Have a look at User_talk:Martin_Hogbin/Morgan_Criticism Martin Hogbin (talk) 22:26, 27 October 2009 (UTC)
-- thread continues at /Arguments#JeffJor's comments to your redirection here from the MHP discussion page. -- Rick Block (talk) 20:19, 28 October 2009 (UTC)
Problem in opening should be changed
It doesn't mention you "win" by getting the car. Fafas (talk) 01:07, 22 October 2009 (UTC)
- The problem statement in the lead is a quote. I've added "[that is, booby prizes]" following the initial reference to "goats". Good enough? -- Rick Block (talk) 02:14, 22 October 2009 (UTC)
One more simulation question
If one was to write a program to simulate this problem would the same rules apply or would the ratio of win/losses be 50-50 because the programing would not be choosing to switch or not like a human would but simply randomly choosing one of the remaining two doors after one of the initial three non-win doors was dropped?
Granted I'm not a computer programmer but it seems to me the program would run something like this:
- Choose a random number between 1~3, set that number as WIN.
- Again choose a random number between 1~3 set that number as CHOICE.
- Discard one non-WIN non-CHOICE number (randomly chosen if there are two possibilities).
- Randomly choose one of the remaining two numbers (this represents staying or switching).
- Log and graph results.
Is this an accurate simulation?
If this has been addressed somewhere referenceable can someone point me to it? Thanks! Colincbn (talk) 12:31, 12 November 2009 (UTC)
- If a person or a program randomly chooses whether to switch, they'll win 50% of the time - but this is not what the problem is asking. In either case (person or program) you should keep track of how many times you switch and win, how many times you switch and lose, how many times you don't switch and win, and how many times you don't switch and lose. The ratio of (switch and win) to (switch and lose) is the chance of winning by switching and will be about 2:1 (2/3). The ratio of (don't switch and win) to (don't switch and lose) is the chance of winning by not switching and will be about 1:2 (1/3). These two ratios must add up to 1. If you randomly pick whether to switch or not the ratio of switch (win + lose) to don't switch (win + lose) will be about 1:1, and the ratio of (switch and win) to (don't switch and win) will be about 2:1. This doesn't mean the chance of winning by switching is 50%, but that the chance of winning by making a random choice between switching and not is 50%. Regardless of how you choose whether to switch or not, if you switch your chance of winning is 2/3 and if you don't your chance of winning is 1/3.
- Specific numbers might help. If you do this 600 times, and always switch you'll win about 400 times and lose about 200 times. Similarly, if you never switch you'll win about 200 times and lose about 400 times. However if you randomly pick whether to switch, you'll switch about 300 times and not switch about 300 times. Of the times you switch, you'll win about 200 and lose about 100. Of the times you don't switch, you'll win about 100 and lose about 200. Overall, because you're randomly picking whether to switch or not, you'll win about 300 times.
- There is source code for some simulations (in various languages) at http://en.wikibooks.org/wiki/Algorithm_Implementation/Simulation/Monty_Hall_problem. -- Rick Block (talk) 20:19, 12 November 2009 (UTC)
- BTW - the discussion above contrasts the probability of winning if you choose to switch randomly vs. the probability of winning by switching. There's another layer to the problem as usually stated which is that you're asked to imagine having chosen door 1 and the host having opened door 3. Opinions differ about whether this is significant, but most simulations, and many solutions to the problem, don't address this particular situation (or any other specific combination of player pick and door the host opens) but rather what might be called the overall probability of winning by switching assuming (usually without an explicit justification) that this overall probability must be the same as the conditional probability of winning by switching given the player picks door 1 and the host opens door 3. If you're actually interested in the conditional probability of winning by switching given that you've chosen some particular door (like door 1) and the host has then opened some other particular door (like door 3), the simulation should be more like the one suggested above by Nijdam where you only record cases where the player initially chooses door 1 and the host opens door 3.
- Again, specific numbers might help.
- If you run 600 simulations (initially picking door 1 each time) we'd expect the car to be behind each door about 200 times. So if you switch every time, you'll win about 400 times meaning the probability of winning by switching is 2/3. However, how many times will the host open door 3, and how many of those times will you win if you switch? The host has to open door 2 if the car is behind door 3. This should happen about 200 times. And the host has to open door 3 if the car is behind door 2 - which also should happen about 200 times. If the car is behind door 1 the host can open either door. If he picks which door to open randomly (in this case) he'll open each of doors 2 and 3 about 100 times. In total, the host opens door 3 about 300 times - all 200 times the car is behind door 2 but only 100 of the times the car is behind door 1. So if you switch given you've chosen door 1 and the host has then opened door 3 you'll win about 200 out of 300 times (i.e. 2/3 of the time).
- Keeping track of it this way also lets us figure out the probability of winning by switching if the host doesn't pick which door to open randomly (in the case the car is behind the door the player picks). For example, if the player picks door 1 and the host opens door 3 with probability p when the car is behind door 1 (the player may or may not know what p is), in the 200 times the car is behind door 1 the host opens door 3 200p times. These are all cases where switching loses, so switching wins about 200 times out of a total of 200+200p times. Expressed as a fraction this is 200/(200+200p) which simplifies to 1/(1+p). Since p can theoretically be anything between 0 and 1, this means the probability of winning by switching given the player picks door 1 and the host opens door 3 could be anything between 1/2 and 1, depending on p. Again, the player may not know what p is. Many folks (on this page) insist the player CANNOT know what p is and therefore p MUST be taken to be 1/2, which leads to the 2/3 answer. Note that if all you're interested in is the overall chance of winning by switching, p doesn't matter at all. Staying with the numbers we've been using all along, if you always switch you'll win about 400 out of 600 times no matter what p is. If you're interested in the chances given the player picks door 1 and the host opens door 3 (or given any other specific combination, where p refers to the probability that the host opens the door he's opened in the case the car is behind the player's chosen door), then p does matter. -- Rick Block (talk) 02:51, 13 November 2009 (UTC)
- Thanks for the link, that is exactly what I was looking for!
- As far as I understand the p problem (hehe, "p problem" hehe...) this only applies in real world situations where "Monty" has some kind of preference when choosing goats, and that in any "true" random pattern of choosing this never comes into play (I realize that there is a different problem with whether or not there is such a thing as "true" randomness but for our purposes computer generated "system clock randomness" is most likely sufficient). But where the conditional/unconditional argument comes into play is if someone spent everyday of their adult life watching Let's Make A Deal then got invited on the show; that person might have a better than 2/3 chance given that they have a better understanding of Monty's preference of goat choosing, is this an accurate simplification?
- On a side note I actually ran through this in a pub last night with my sister in-law. At first she was always staying but after I explained the math (using mainly the Cecil Adams approach) she started switching and winning much more (about twice as much as it were). We used a deck of cards (ie: red twos and the ace of spades), and my randomizer was shuffling under the table and me trying not to think about it if I had to choose between two "goats". It was an interesting way to spend twenty minutes while guzzling Guinness and I would recommend it to anyone. Colincbn (talk) 07:11, 13 November 2009 (UTC)
Even If it's not stated, the host MUST choose randomly between two goats contestant's assesment of the host's choice must be that it appears random to her.
- You do have to treat p as 1/2 unless you are told what its value is, and which doors it relates to. Many people, even those who should know better, forget that "probability" is not a property of the specific result, it is a property of the random process that led to the result. As Kreyszig said on page 714 of his famous book (mine is the 1972 edition), "For this reason we now postulate the existence of a number P(E) which is called the probability of the event E in that random experiment. Note that this number is not an absolute property if E but refers to a certain sample space S, that is, to a certain random experiment."
- Here's my favorite example of the difference: Suppose I draw a card at random. I look at it by myself and see that it is the Queen of Hearts. I tell Ann that it is red, Bob that it is a heart, Carl that it a face card (that means TJQKA), and Dee that its value is even. I ask each what the probability is, that it is the Queen of Hearts. Ann says 1/26, Bob says 1/13, Carl says 1/20, and Dee says 1/24. But I know that this "probability" is actually 1/1. Since all the answers are different, who is wrong?
- Answer: Nobody. The probability is not about the card, it is about the process. And each person sees a different process, one that leads to the specific piece of information I gave to them. Since each piece is different, the process each is evaluating is different. In the Monty Hall problem, the card represents one particular day's broadcast of this game show. The probability we are trying to evaluate is not a property of this broadcast, but of all possible broadcasts. Even ones where Monty might change how he picks.
- Those people who think you can use a p other than p=1/2 to get an answer are wrong, by their own arguments. Consider that Monty might vary how he chooses p. He might choose p=1/3 when he is wearing white underwear, and p=3/4 when he is wearing colored underwear. But only Monty knows what kind of underwwear he randomly selected that day, or what mix exists in his wardrobe. So even if you track many games, and think you know what p is, you will still be wrong every time you use that p. It is never the value Monty uses. The assumption that p can be something other than 1/2 in the solution to the problem, leads to the contradiction that you have to know every factor that goes into determining what p is before you can use it. JeffJor (talk) 17:41, 13 November 2009 (UTC)
- What those who say p is important (e.g. Morgan et al. 1991, and Gillman 1992) actually say is
- unless you're told the host picks randomly if given the chance then assuming p is 1/2 is an unwarranted assumption [note the randomization procedure Gardner included in his version of the Three Prisoners problem)
- in this case (not being told what p is) the probability given a specific initial player choice and door the host has opened does not have a single numerical answer and the best we can say is that it is in the range [1/2, 1]
- if you're saying the answer is 2/3, either you're not addressing the conditional probability in a specific case of initial player pick and door the host has opened or you've assumed p is 1/2
- What those who say p is important (e.g. Morgan et al. 1991, and Gillman 1992) actually say is
- I think you disagree with them, but do you at least agree that this is what these sources say? -- Rick Block (talk) 20:36, 13 November 2009 (UTC)
- Those who say p is important are addressing a different problem than the one this article is about. So what they say isn't appropriate here. But their problem is actually unsolvable by the methods they use, since nothing can be assumed about the value of p by those methods. Especially not a "uniform distribution" of p. Those references should be dropped from this article, regardless of what you think they say about p.
- There are references that say p=1/2 is the only valid option, even when addressing Morgan's problem. That includes Gardner's version of the Three Prisoners problem. Gardner's assumption that p=1/2 is not part of the problem statement, it is part of his solution. It comes after he says "Now assume, by renaming the prisoners if necessary, that A is the one questioning the warden, and B the one the warden names as executed" which actually necessitates that p=1-p since the solution's treatment toward B (assume a value of pB) and C (which has pC=1-pB) has to be the same. Or just look up the Principle of Indifference.
- If you think you need to solve "the case of not being told what p is, then you are addressing the probability of a particular instance of the random experiment (e.g., The show that aired on March 27, 1993), not the random experiment itself. You are essentially saying that there is one, and only one, correct answer to my card problem about the Queen of Hearts. Which person do you think gave the one correct answer? Why is that person's answer "better" than the others? Or, just see my reference about probability being about the samples space - the set of possibilities - not E itself.
- I am saying the one, and only, possible answer to the problem this article is about, is 2/3. Many more references support this solution than the fradulent Morgan, et al, treatment. The 2/3 solution applies if the player picks a specific door (which isn't part of the problem) and the host also picks a specific door (also not part of the problem), AS LONG AS THE PROBLEM STATEMENT DOES NOT SPECIFY ANY BIAS IN HOW THEY WERE CHOSEN. If you can find such information in the problem statement, the answer might not be 2/3. But you can't speculate about it - you need to be told a value for p to use it. See the Principle of Indifference, particularly the parts about names not being useable as identification. JeffJor (talk) 14:36, 14 November 2009 (UTC)
- The real problem, Jeff, is that Morgan et al managed to get their paper published in a respectable journal. You know their paper is wrong and I know it is wrong but unfortunately that counts for nothing here, we must rely on 'reliable' sources. Their most serious error was that pointed out by Professor Seymann in his comment, published in the same journal. This is that Morgan do not make clear exactly what question they are answering. In the circumstances this is inexcusable. Martin Hogbin (talk) 18:24, 14 November 2009 (UTC)
- My point was to try to shift this discussion from an argument about what you or I or anyone else thinks the Truth(tm) might be, to a discussion about what the sources say. The former topic is a fine topic for the /Arguments page, but really has no relevance to the content of this article.
- And that is fine. Morgan, et al, and Gillman, do not address the problem that this article is about. Regardless of anybody's POV, THOSE REFERENCES DO NOT BELONG HERE. You are wrong whan you say they are references about this problem. Now, secondary to that, it is POV (and quite provable, which is a property that can be used to ignore a reference), that their treatment is wrong even for the problem they address. That is not the reason to remove the references, although it is a good reason to ignore them.
- The Eisenhauer reference you give acknowledges that what Morgan and Gillman handle is a different problem. All it does is acknowledge that the contestant still does better by switching in that different problem; it does not attempt to say what the probability is. So it does, indeed, supercede both Morgans's and Gillman's conclusions about the problem the article addresses. JeffJor (talk) 15:20, 15 November 2009 (UTC)
- The claim that Morgan et al. 1991, and Gillman 1992 (and Grinstead and Snell 2006, and Falk 1992) are addressing a different problem than the one this article is about is directly contradicted by what these sources say. For example, they all reference the problem statement from Parade.
- Morgan misquoted the problem, and misinterpreted what they misquoted. And (to comment to what you said next) no, Gardner does not state p=1/2 explicitly. He states that you flip a coin, and in his solution implicitly through the Principle of Indifference assumes that the probability of the two outcomes are each 1/2. The same principle could be applied if he didn't say to flip a coin, so that part is irrelevant in the problem statement. It just makes it more apparent to the masses who do not realize the same Principle applies to "The warden chooses between B and C" and "The warden flips a coin to choose between B and C." Or that whan a problem says "flip a coin" it really means "Assume the Principle of Indifference applies." JeffJor (talk) 15:20, 15 November 2009 (UTC)
- Gardner's description of the Three Prisoners problem (as published in Scientific American, Oct 1959) includes the following:
- "Then tell me", said A, "the name of one of the others who will be executed. If B is to be pardoned, give me C's name. If C is to be pardoned, give me B's name. And if I'm to be pardoned, flip a coin to decide whether to name B or C."
- There's no appeal to the principle of indifference. His problem description unambiguously specifies p=1/2.
- I agree there are plenty of references that say the answer is 2/3. However, (as far as I know) nearly all of these are not in peer reviewed math journals. Without sources to back up it up, the opinion that the Morgan et al. treatment is "fradulent" is irrelevant to the content of this article. From wp:reliable sources: Academic and peer-reviewed publications are usually the most reliable sources when available. However, some scholarly material may be outdated, superseded by more recent research, in competition with alternate theories, or controversial within the relevant field. The Morgan et al. paper is specifically about this problem, and it appears in a peer reviewed math journal. Is it outdated or superseded by more recent research? On the contrary, it is directly supported by a subsequently published paper (also in a peer reviewed journal) (see #Refereed paper agreeing with Morgan et al., above). Is it controversial within the relevant field? Rosenhouse's recent book (The Monty Hall problem, Jason Rosenhouse) doesn't like the tone, but even he goes on to say They, at least, were mathematically correct in their substantive points. Is it in competition with alternate theories? There are plenty of popular sources that perpetuate vos Savant's solution, or other solutions directly criticized by Morgan et al. To consider this treatment to be in competition with alternate theories, I would expect there to be academic sources that reference Morgan et al. and directly dispute it. I think the academic response has been to clarify the problem description, consistent with the Krauss and Wang version presented in the article. In this version, the constraints on the host behavior explicitly force p to be 1/2 so that the answer is unambiguously 2/3 even if the problem is interpreted as Morgan et al. do.
- Anyone can personally have whatever POV he or she would like about this problem. On the other hand, the article needs to reflect what reliable sources say regardless of whether you or I or anyone else agrees with them. -- Rick Block (talk) 19:52, 14 November 2009 (UTC)
- Jeff - So, your claim is that Morgan et al., and Gillman (and presumably Grinstead and Snell, and Falk, and Eisenhauer) do not address the problem this article is about. Your opinion about this clearly reflects your POV, and is worth much less than a published opinion like (for example) Barbeau's - see either Barbeau 1993 or Barbeau 2000. Martin has previously suggested trying to split the article into sections about two different problems, what he considers the "notable" one (which I think is consistent with what you seem to consider to be the one, true, interpretation) and an explicitly conditional version. The issue with this approach is finding appropriate sources. Many sources treat the problem unconditionally even though the usual form of the problem statement is fairly clearly conditional. You're saying even though it's conditional the probability of the host's choice (in the case the host has a choice) must be treated as 1/2 because of the principle of indifference. Do you know of a source that explicitly (not implicitly) treats it this way? -- Rick Block (talk) 19:02, 15 November 2009 (UTC)
- Rick - have you noticed that this article explicitly says "If both remaining doors have goats behind them, he chooses one randomly?" All those references EXCEPT MORGAN (and I just found a copy of Gillman today) acknowledge that they are talking about a different problem when that allow p<>1/2, and solve for a probability based on the parameter p THAT THE CONTESTANT HAS ACCESS TO (example, from Gillman: "In the extreme case of q=1, the host's opening of door #3 'gives you no information [emphasis added]. It is not inforrmation ONLY IF YOU KNOW q=1.) They all - EXCEPT MORGAN - acknowledge that the probability they give is based on the contestant's knowledge of p. Those treatments are correct. Only Morgan takes the additional, and quite incorrect, step of saying you can solve for a probability when p is not known or implied, even parametrically. Essentially, Morgan is claiming lat ln(2) is an answer to the unconditional problem, and it is not. If you don't know pp, the probability is 2/3 if you switch AND NOTHING IS CONTRADICTED if somebody who does know p claims a different probability. The two peoepl are answering different problems.
- And no, regardless of how many people treat the original problem conditionally, it is not. Definitely not this article's problem, and not Parade's, either. The door numbers used were examples (for a similar case, look at Grinstead & Snell's problem #7 on page 13. Are you suggesting that Roulette only allows people to bet on a 17, or that the correct answer needs to include whether the roulette wheel is unbalanced toward a 17? Or does every book on probabiltiy need to be re-written to make their exampels into conditions?). Those people are just grabbing onto a more interesting problem, one that shows that "switch" is a good strategy even if you allow for biases. JeffJor (talk) 18:01, 16 November 2009 (UTC)
- On thing that is undoubtedly true about Morgan is that they do not make clear exactly what question they are attempting to answer. This is not just what I say on my Morgan criticism page but it is what Prof Seymann says in his comment in the same peer-reviewed journal that Morgan were published in. Martin Hogbin (talk) 23:11, 16 November 2009 (UTC)
- To start with, is there anyone who can tell me whether Morgan are answering the problem from:
- The point of view (state of knowledge) of the player.
- The point of view (state of knowledge) of the audience.
- Only on the information given in Whitaker's question.
- Only on the information given in Morgan's restatement of the question.
- Some other basis - please specify.
- This is not a minor detail but something that is universally accepted as an essential requirement in statistics - that the question being asked is clear. Martin Hogbin (talk) 11:32, 17 November 2009 (UTC)
- Reply added at the /Arguments page. JeffJor (talk) 19:17, 17 November 2009 (UTC)
- Martin - you know perfectly well what problem Morgan et al. are answering (we've been over this innumerable times before). To save any newcomer to this argument the trouble of looking back through this thread, Morgan et al. answer the question based on the information given in Whitaker's version of the question, as printed in Parade (which they trivially misquote) which is the same as the point of view of the player and the audience. They interpret the question to be about a game show (involving physically identifiable, distinguishable doors) and, in this game show, the probability of winning by switching given that the player has initially selected a door (an identified door) and then the host has opened another (identified) door. They work through the example situation suggested in the problem statement where the player has picked door 1 and the host has then opened door 3 as a straightforward application of conditional probability. Their analysis covers a variety of host protocols (what JeffJor is calling different problems), including the one vos Savant's published clarifications suggest she was attempting to solve where nothing is said about the host's choice if the player initially selects the car (which means the conditional probability equation contains an unspecified variable) as well as the Krauss & Wang version where the host is known to select equally randomly in this case. I'll reply to JeffJor's comments at the /Arguments page there. -- Rick Block (talk) 02:13, 19 November 2009 (UTC)
- Rick, you know perfectly well that Morgan did not use Whitiker's version of the problem. They edited it into a different form that more closely resembled the problem they misinterpreted it for - and were ambiguous about (more below) in their solution. In Whitiker's version, the contestant chose a door (not "door No. 1"), and "#1" was given as an example in an aside that in no way implied it was meant to be a condition of the problem. The host opens a door (not "door #3), and "#3" was given as an example. Do you know what "a" means in English? It is an indefinite article, "used before a singular noun not referring to any specific member of a class or group" according to my Random House dictionary. The literal meaning of Whitiker's problem is nonspecific doors. I know you don't agree, but those newcomers might. And that difference doesn't actually matter, and isn't what Martin was referring to. Newcomers should know that, too.
- If you would read Martin's comment, it is plainly obvious he wasn't talking about the difference between "the conditional problem" and "the unconditional problem" as you are. He is asking "From whose point of view is the probability calculated?" Yes, if the conditional problem is intended, both the audience and the contestant can include that information in their point of view. IT CHANGES NOTHING. It does not matter if the doors are phsycially identifiable (see the Principle of Indifference), because the contestant has no way to know how the host uses such distinctions on this particular day. ANY NAMES ATTACHED TO THE DOORS CANNOT MATTER. And if it could matter? Moragn's entire analysis is invalid because they must assign a similar set of parameters to the probabiltiy that the car is placed behind the specific door numbers. Neither Whitiker's problem, nor Morgan's, ever say the car is placed randomly. That fact is just as implicit (or not implied, as Morgan assumes) as any bias the host has about opening a specific (by name) door.
- There is no absolute-correct probability for the two remaining doors, in either the conditional or unconditional problem. Because all of the random elements of the problem have already been determined at the time the decision is to be made. The car 'is behind one of the two doors. Any probability that can be assigned is a only measure of the information you assume is avaliable to calculate it, not a measure of that door's worth. If the contestant has only the information available to Marilyn's Little Green Woman, that probability is 1/2 (yes, I know that is less information than the problem says the contestant has). If the contestant has only the information that the problem says she has, the probability is 2/3 EVEN IF THE CONDITIONAL PROBLEM IS CONSIDERED. And if you are going to assume the contestant has more information than the problem says - i.e., that she knows the host has a bias measured by a parameter q - you might as well assume the contestant also knows everything that the host knows. Because only the host really knows how his q was determined on this particular day. Even if he is consistent with past games, and we assume the contestant knows all that history (which the problem does not allow), there could be unseen factors that influence the actual q so that on that day, it is not what this omniscient contestant thinks it is. The only virtue in considering a possible q, is that whatever its value is, it is never detrimental to switch. JeffJor (talk) 13:16, 19 November 2009 (UTC)
- Yes, that is my main point. Rick, you say that the question is being answered from the point of view (state of knowledge) of the contestant (or the audience, which I agree is likely to be the same). What Morgan have done, in that case, is to arbitrarily dis-apply the principle of indifference to the host's choice of goat door. As Jeff says, the player has no more idea of the host's door opening policy than she does of the car's initial position, yet Morgan tacitly take the car's initial position to be random (which is quite reasonable as the player is presumed to have no information on its whereabouts) but they take the host's door choice to be non-random and described by the parameter q, even though the player has no information about the host's strategy. Thus, as I have said all along, Morgan add an artificial layer of complexity and obfuscation to what should be a simple (but very unintuitive) problem. Martin Hogbin (talk) 17:01, 19 November 2009 (UTC)
- I'll try one last time, but this is a tiresomely repetitive argument. I think everyone (more or less) agrees the problem should be answered from the state of knowledge of someone who knows what is given in the problem statement (which we could assume is the player's SoK). I also think everyone (more or less) agrees the principle of indifference applies to the player's initial selection since, even if the player suspects the initial distribution is not random, the player has no way to know what the distribution is and is therefore making a random initial choice. In her followup columns, vos Savant removes any doubt about this explicitly saying the car is meant to be randomly located. I think so far, everyone is on the same page.
- Now, the host comes into the picture.
- The Parade problem statement says only "the host, who knows what's behind the doors, opens another door" and shows a goat. To make a decision about whether she should switch, the player now needs a little more information about the host's intent not specified in the Parade problem statement. Does the host always open a door showing a goat and make the offer to switch, or is this perhaps a one-time attempted swindle being offered only because the player's initial choice hides the car or even is the host opening a random other door which (this time) happens to not reveal the car? In her followup columns, vos Savant makes it very clear (even though these conditions are not in the problem as originally stated in Parade) the problem is meant to be interpreted that the host always opens a door, never reveals the car, and always makes the offer to switch. Even to this point I think everyone (more or less) still agrees.
- So, back to the state of the knowledge of the player. The player knows
- The initial distribution is explicitly 1/3:1/3:1/3 (and, even if it isn't, can be assumed to be because of the principle of indifference)
- The host is compelled to open a door showing a goat and make the offer to swtich, and is not acting randomly because doing so would involve the chance of revealing the car
- Sounds like a simple conditional probability problem to me. If we take a specific case (like the one mentioned in the problem statement, where the player initially picks door 1 and the host opens door 3), the probability of winning by switching is
- P(car is behind door 2) / (P(car is behind door 1)*X + P(car is behind door 2))
- where X is the probability the host opens door 3 in the case the car is behind door 1. This equation is well within the SoK of the player to come up with (and, by renumbering the doors, applies to any specific player's case), and would now (I think) lead the player to wonder about X. What exactly does this X mean? Is there anything in the player's SoK (i.e. the problem statement) that constrains it? The player definitely knows the host is not acting completely randomly, but should she assume the host is acting randomly in this subcase? Note that it's not the player who's choosing between these doors, but the host. Does the principle of indifference apply here?
- This is the point where opinions differ. Morgan et al. have an opinion, that they published in a peer reviewed journal. Gillman published his opinion, which agrees with Morgan et al. Grinstead and Snell finesse the issue, by explicitly requiring the host to choose randomly in this case (while acknowledging the difference between the unconditional and conditional problems and the effect of X in the conditional case).
- We can, and seemingly may, argue about this forever, but the bottom line is that from the state of knowledge of a Wikipedia editor Morgan et al. is a wp:reliable source and any arguments about what it says that are not based on equally reliable sources are simply wp:original research that has absolutely no bearing on the article content (by Wikipedia policy). -- Rick Block (talk) 19:27, 21 November 2009 (UTC)
- Yes, Rick, it is quite tiresome. The reason is that you won't even consider the validity of arguments that disagree with the approach taken by Morgan, et al, or Gillman. The Principle of Indifference applies equally to the initial car placement and the host's choice of doors to open. It is inconsistent for "all to agree" it should be applied to one, and accept it for that choice, while insisting you can ignore it for the other. To paraphrase you, the player has no way to know what the distribution of the Host's bias is, and therefore it must be treated as a random choice. And before you try to deny this, apply the exact same argument you intend to use to the car placement.
- You used the argument that "vos Savant [in later columns] removes any doubt about [the randomness of the car placement by] explicitly saying the car is meant to be randomly located." She also makes it clear in later columns that the host's choice is random. You can't apply these arguments differently to the two sources of uncertainty. Again, apply the same arguments to both choices.
- And nobody is claiming the host's choice is random between the unchosen doors. It is well established that the host knows where the car is, and where the goats are. This provides a way, not based on names, for the host to distinguish all three doors in some cases. So the host's choice is random between the set of unchosen doors with goats, which are the ones the Principle of Indifference applies to from his SoK. A choice can still be considered random, by the Principle of Indifference, when n=1." Your point #2 above does not apply to any situation in the problem - if it did, the host would also open the contestant's chosen door 1/3 of the time. The implicit assumption vos Savant makes is that the host opens a random unchosen goat door.
- Morgan's analysis is not an "opinion." It is a solution to a problem that is never stated in any of the traditional forms. Never. It does not belong in the article. JeffJor (talk) 20:37, 21 November 2009 (UTC)
- I'm perfectly willing to consider the validity of arguments that disagree with the approach taken by Morgan et al., or Gillman. However, to be relevant to the article content it takes a published argument. I did a search on Google Scholar for "Monty Hall problem" and "principle of indifference". As far as I can tell, none of the hits say anything about applying this principle to the issue we're talking about. Including this argument in the article would require a published source - whether it's valid or not is a secondary issue and, unless there's a source making this argument, from Wikipedia's perspective it doesn't matter if it's a valid argument.
- Do I personally agree that it's a valid argument? If you're attempting to justify 2/3 as the answer, sure - but I definitely don't agree that this means the approach Morgan et al. take is invalid. What I actually believe is that the approach Morgan et al. take applies to a broader range of specific wordings of the problem, and is therefore more useful, than an approach targeted at one and only one interpretation of the problem statement. In particular, the Morgan et al. approach addresses (among others) what might be called the current "standard form" (e.g. the K&R version with explicit constraints on the host including random pick between two goats if it comes up), and the "Monty forgets" variant (that vos Savant has mentioned in the last year or so in her column), as well as the "host might have a preference" generalization of the standard form. As has been previously mentioned, they don't do it but their approach also easily extends to an analysis where the initial probabilities are not 1/3 for each door. I know opinions about this differ, but I think the explicit conditional approach is an extremely clear and utterly convincing way to present the solution (even the 2/3 solution!).
- Separately, your repeated assertion that Morgan's analysis does not belong in this article is (quite frankly) bizarre. It is I believe the first (and perhaps only) paper in a peer reviewed math journal specifically about the mathematical intricacies of the Monty Hall problem in its usual form. Google Scholar lists 60 citations. The article would not be complete without this reference. -- Rick Block (talk) 23:11, 21 November 2009 (UTC)
- Rick you seem to want to confuse the issue in question by bringing up things that we all agree about. We all agree that (in the standard rules) the host always offers the swap and we all agree that the host knows where the car is and never opens a door to reveal it. The point is that, where the host has a choice of which door to open in other words in the case that the player has initially chosen the car, the player has no information on which to decide how the host will make this choice and thus we must take it that, in this case, the choice is random. This is not what Morgan do, they take it that this choice is not random and assign it a host door choice parameter.
- I think that the article needs to concentrate much more on the simple problem. This is the notable problem. The simple fact is that the answer (chance of winning on swapping) is 2/3 but nearly everybody thinks otherwise. Th article should concentrate on explaining why this is so.
- Regarding reliable sources and scholarly discussion, there are many reliable sources on this subject and there is no reason that we must use Morgan as the guiding light in our article. Although the paper was published in a peer-reviewed journal it has been the subject of much criticism, starting with Seymann's comment in the same publication. I suggest that the article should be based more of the article on K & W, for example, who actually start to address the reason that so many people get the answer wrong. If we take it that The Monty Hall Problem is the fully defined problem as stated by K & W (as we seem to do in the article now) then the Morgan paper is irrelevant as it does not address this problem, where the host choice is defined to be random.
- Although the article should be based on reliable sources there is some latitude to decide which sources are most relevant to the problem being addressed. I have seen more of a consensus to use sources other than Morgan or those based on it. Martin Hogbin (talk) 12:16, 22 November 2009 (UTC)
- Martin - please read the "comprehensive" and "well-researched" criteria from WP:FACR. Omitting significant references because they don't address what you think is the "notable" problem is contrary to both of these. You and Jeff have both asserted your opinion that if the host preference is not constrained by the problem statement then it must be taken to be random, citing principle of indifference. Since there are reliable sources for this specific problem (including a peer reviewed paper co-authored by 4 members of the faculty of a university math and statistics department!) that don't do this, your opinion is apparently wrong. Moreover, your opinion doesn't matter here - what does matter is what reliable sources say. Find a reliable source that explicitly makes this argument about this problem, ideally directly referencing Morgan et al. or Gillman or some similar source, and then we'll talk. Until then, what you're saying is simply WP:OR.
- And, I think you're absolutely incorrect about what the consensus is. As far I as I remember, you, Jeff, and one or two others we haven't heard from in a while are the only ones in favor of dropping Morgan et al. and similar sources, while Nijdam, I, and at least as many others we haven't heard from in a while (I think it's actually far more than one or two) are not in favor of this. I think the discussion on this page is so tiresomely repetitive that many, many folks have simply checked out, so trying to gauge consensus based on current participation is not likely to be very accurate. -- Rick Block (talk) 20:09, 22 November 2009 (UTC)
Rick, I corrected your header for this section. The mistake you made in naming it points out the issues that you are misintpreting. Morgan does not take a broader view of the problem's various wordings, it is a narrower view in the sense of approaching a solution. It is narrower because the simpler wordings, that Morgan deny, allow some assumptions to be made. Assumptions that are traditioanlly made in word problems. I.e., if you can draw N balls out of a bag, the problem does not need to state that each has a probability 1/N. Morgan disallows such assumptions, but only where the "conditional" solution can still provide an answer to the question "should you switch?" They aren't calcualting a probability, they are showing that whatever the calculation could produce, switching is a good idea.
I agree that published work, and not our opinions, must be the basis for the article. But the theses of Morgan, et al, and Gillman, are not about the general problem this article is about. Morgan, et al, even say "In general, we cannot answer the question 'What is the probability of winning if I switch, given that I have been shown a goat behind door #3?' unless we ... know the host's strategy ..." So Morgan is not answering the "general" problem, they are answering one where p13 takes on a specific value that is unknown ot the contestant, p22=p33=0, and (the assumption they make but don't state) p11=p21=p31=0. So they explicitly state that their solution applies to just one variation of the unknown Host's Strategy. Essentially, they solved a variation of the general problem that is interesting because you can get an answer without making the usual assumptions for one part of that strategy, but do for others. And that is where they are inconsistent. The article is flawed because it suggests someone did calulate a probability.
If their approach belongs at all, it should be moved to below the discussion about alternate Host stratgeies. It applies - according to the authors - only if the contestant knows the host's stragtegy except for the exact value of p23. And they also say that if the contestant does not know the host's strategy, that the best appraoch gives "the popular answer" of 2/3. (Note: there is a typo in their article. They gave the wrong value for that part, 1/2 instead of 2/3. And I think that proves that any oversight of their article treated it more as a curiosity, than as a scholarly work to be checked for accuracy.)
About the Principle of Indifference. It is so basic a principle in probability, that it never is listed as the reason whan it is applied. Authors just go ahead and state that they are applying an even distribution to the indistinguishable items, and it is universally understood why. Morgan does it, for the car's palcement. The only reason I brought it up (by name) at all is because it says the door numbers don't distinguish the doors unless there is some other known reason to treat them differently based on the numbers. When there is not, the solution treats them equally even if they are not. And so gets a correct answer that reflects how any possible bias could favor either door.
Finally, and you seem to keep ignoring this, the Parade version of the problem, and the K & W one this article is based on, do not describe the so-called "conditional" problem. Morgan misinterpreted it, and I have shown you exactly how their problem statement is different. The vast majority of peopel who see teh word puzzle do not even consider the "conditional" problem. But even in Morgan, they admit the "conditional" answer only applies when the host's strategy is known to fit within certain boundaries, that include knowing p23. Several times, Gillman points out that not knowing it makes the answers to his Game I and Game II equivalent. This is why they deserve to be a sidebar, at best, in the article. It simply is not "about the mathematical intricacies of the Monty Hall problem in its usual form." Their problem is just an interesting fact about one possible variation of what everybody sees the the usual form of the puzzle to be. JeffJor (talk) 19:25, 23 November 2009 (UTC)
Do Morgan et al. address 'The Monty Hall Problem'
I have added a heading here for ease of editing.
Rick, I see nothing in WP:FACR that tells us that we must use an academic paper that does not address the problem as stated in the article. As Jeff has said above, the problem statement given in the article, namely that from K & W, clearly states that the host door choice is random (subject to the agreed rules) and the initial car placement is random. The Morgan paper clearly refers to the specific case where the initial car placement is random (even though this is not explicitly stated) but the host door choice is not random. Thus the paper by Morgan et al is not relevant to the article, except as a special, and rather unrealistic, variation of the basic problem. Martin Hogbin (talk) 22:42, 23 November 2009 (UTC)
- No, they don't. And just to make it clear, this article is about the variation where these are the defining points of the problem:
- The car is placed randomly.
- The contestant can choose any door.
- The host must open a door that is randomly selected from all unopened doors that hide goats (this could be a choice of one door only).
- This is the "K&W" problem. It is what the casual reader feels any version (unless explicitly contradicting some part of it, which Parade's version does not do) means. (Documentation: some of the scholarly references listed in the article are not as much about the Mathematics, as about the perception of the problem by readers. Falk and Fox & Levav, to name two.) It is teh problem Marilyn vos Savant (who is notorious for expressing problems in an amgiguous way, but assuming peoepl will only see one) assumed people would see, and so is what she answered. But the most general case, using Morgan's approach for what makes for a more "general" problem, has these defining ponts:
- The car can be placed with a bias.
- The contestant always chooses Door #1 (chosing other doors is a similar problem, but with different paramater values based on point #5 below).
- The host can open an unchosen door with the car. If he does, the game ends immediately.
- The host can open the contestant's door. If he does, the game ends immediately. (Note that revealing Door #3 has the car in the previous point is the same as revealing Door #1 has a goat here.)
- The host has a set of biases that depend on the car placement and the contestant's choice.
- The contesant knows this bias exists, but not what it is.
- In the case of interest, the host actually reveals a goat behind Door #3.
- Morgan and Gillman do not address this most general case, because the question "should the contestant switch" cannot be answered for it. Instead, they apply (whether they say so or not) the Principle of Indifference to the placement of the car, because to not apply it is "unlikely to correspond to a real playing of the game." I take that to mean either (A) that the car's placement cannot be observed to be biased in the past history of the game show, or (B) even if it could, the contestant's choice is uninformed about that history. Either criterion makes the Principle of Indifference apply.
- They ignore point #4 but not point #3 which is essentially the same thing. And finally, they ignore the Principle of Indifference for how the contestant evaluates the host's choice, even though that is just as "unlikely to correspond to a real playing of the game." The host would no more want to (A) exhibit a bias than the stagehands would in placing the car, and (B) the contestant is just as uninformed about whether he is biased. So Morgan's problem is:
- The car is placed randomly (Morgan assumes it, Gillman actually edited this into the problem he claimed "appeared in the Ask Marilyn column in Parade.)
- The contestant always chooses Door #1 (chosing other doors is a similar problem, but with different paramater values based on point #5 below).
- The host can open an unchosen door with the car. If he does, the game ends immediately.
- The host cannot open the contestant's door.
- The host has a set of biases that depend on the car placement and the contestant's choice.
- The contesant knows this bias exists, but not what it is.
- In the case of interest, the host actually reveals a goat behind Door #3.
- The interesty in this "conditional problem" is that it restricts (not eliminates) the host's ability to trick her into switching, thereby reducing the probability she will win the car. Specifically, he can trick her if his strategy included the option to end the game without offering the choice to switch. Otherwise, her probability after switching goes up to at least 1/2 (from the 1/3 it was before he applied his strategy), and possibly more. It goes to 2/3 if she does not have any idea how he is biased. It goes to somewhere in the range of 1/2 to 1 if she thinks she knows something of his bias, and is trying to out-guess him.
- These conclusions are not OR, they are contained in both Morgan's, and Gillman's, paper. They just are hard to read in the text because the authors were focused more on addressing the interesting issues, than on the problem from the contestant's point of view. The wiki article does a poor job (i.e., not at all currently) in separating out those issues. "The" answer to the probabiltiy after switching is 2/3 based on the K&W problem the article is about. JeffJor (talk) 17:08, 24 November 2009 (UTC)
- Jeff, I am puzzled by your point 3 above - The host can open an unchosen door with the car. If he does, the game ends immediately. This possibility is excluded in what they call the vos Savant scenario. Martin Hogbin (talk) 17:34, 24 November 2009 (UTC)
- Jeff is listing the range of problems the Morgan et al. paper addresses. Although it briefly mentions the possibility of the host opening a door and revealing the car, the majority of the paper addresses a problem (their interpretation of what vos Savant intended, based on her clarifications in Parade prior to the publication of their paper) which could perhaps be more simply expressed as having these defining characteristics:
- The car is placed randomly.
- The contestant has initially chosen a door (which we'll call door 1).
- The host has opened a different door (which we'll call door 3) revealing a goat and is not precluded from having a bias if given a choice between two "goat doors".
- The contestant, knowing which door was initially selected and now seeing two unopened doors and one open door showing a goat, can switch to the other unopened door.
- I believe this differs from the K&R version only in that the K&R version adds the explicit constraint that the host must choose randomly between two goats if this comes up.
- The main point of the Morgan et al. paper is that this is a conditional probability problem and should be approached as such. They use the unspecified host bias mostly to show that there is a difference between solving for the unconditional probability of winning by switching vs. the conditional probability of winning by switching given knowledge of which door was initially picked and which door the host opened. I believe most people understand the door 1/door 3 combination to be representative of the general solution, and (whether they realize it or not) erroneously evaluate the conditional probability in this case using the "equal probability" assumption (as described by Falk, and Fox and Levav). Whether the host has a bias or not, the probability of interest is the conditional probability. If you're an expert in probability theory, you can perhaps immediately see that unless the host has a bias the unconditional and conditional solutions must be the same - but (IMO) most people do not understand that these are different questions and consequently find an unconditional solution not very convincing since they're actually trying to solve the conditional problem.
- The root question the article needs to address is WHY the 1/3 probability of the car being behind door 1 remains the same AFTER the player sees the host open door 3. The first step to understanding this is to understand that the probability after the host opens door 3 is a conditional probability. The second step is either to understand that this conditional probability is the same regardless of which door the player initially picks and which door the host opens and that this means the conditional probability (whatever it is) must be the same as the unconditional probability (which is trivial to compute), or to understand how to actually compute the conditional probability.
- IMO, the article would be more clear if we explained the difference between the unconditional and conditional questions up front, and (perhaps) said the Monty Hall problem as generally interpreted intends for these two different questions to have the same answer. The problem is most published unconditional solutions make no mention of the unconditional and conditional questions, and only implicitly equate them (leaving open the question of what exact problem they are addressing).
- Jeff - do you agree given more or less any set of Monty Hall rules that asking what is the (unconditional) probability of winning by switching is a different question than asking what is the (conditional) probability of winning by switching given which door the player picks and which door the host opens? If so, which question do most people think the Monty Hall problem asks? -- Rick Block (talk) 20:36, 24 November 2009 (UTC)
- Martin, that point represents the parameter Morgan call p22. They never use it explicitly in their results, but they do use p23 and the identity 'p22+p23=1. So anytiem they discuss, p23, they are using that point.
- So, in Morgan's terminology, the scenarios are:
- Marilyn vos Savant's actually-intended scenario: p23=1 and p13=1/2. Marilyn clarified both parts of that.
- Their pedantic misinterpretation of Marilyn vos Savant's scenario: p23=1.
- Their general scenario: no restrictions of their stated paramaners.
- The actual general scenario, alluded to in their conclusion, incldues a non-zero p11.
- Rick, I don't know how many different ways I can try to say this, but it is not getting through to you. The "given knowledge of which door was initially picked and which door the host opened" is useless to the contestant unless she knows both the value of q and which door is favored. Morgan's conclusions DO NOT use any such knowledge as a given. They only use the fact that, whatever q is in what they call the "vos Savant scenario," that specific strategy can't make the probability less than 1/2 by switching. They only answer teh quesiton "shoudl she switch," not "what is the exact probability if she switches?"
- And the "door 1/door 3" combination IS REPRESENTATIVE OF the general solution, even if the the host is biased, because the contestant does not know which door is favored. Look at it this way: suppose the host says to the contestant "I am using Moragn's stratgey based on a q of..." and names a value. "But," he adds, "I won't tell you which of the two doors, #2 and #3, is favored this way." From the contestant's SoK, WHICH IS THE ONLY ONE RELEVANT TO THE PROBLEM, the exact probability of winning is 2/3. Fporm the host's SoK, it is either 1 or 0, since he knows where the car is. Nobody possesses the SoK where the probabiltiy is 1/(1+q). That wasn't Morgan's point.
- We all seem to have fairly entrenched positions here so let me suggest that we leave the issue of conditional/unconditional for the moment. I agree that even if the host goat door choice is taken to be random, the problem can be treated as one of conditional probability. Whether this is necessary or desirable is another matter, which I suggest we leave for the moment.
- This leaves the point that Jeff makes above, which is the same point that I made at the start of this conversation when I came here in response to the RfC. If we are answering the question from the state of knowledge of the player, and the player does not know the host door choice strategy (the value of the parameter q) then we must take host the choice of door (from those permitted by the rules) to be random. Rick, do you accept this? Martin Hogbin (talk) 23:11, 24 November 2009 (UTC)
- I'll accept that if your goal is to determine a single numerical answer for the probability it is most sensible to take the host's choice (from those otherwise permitted by the rules) to be random, and that most people who pose this problem intend this to be the case. On the other hand, must is too strong. It's perfectly legitimate to leave this as a variable and to express the probability as a function of this variable. It is, in fact, helpful since (as Jeff notes) it can be used to show a specific player's chances never decrease. Saying the answer is "2/3" and saying it is "1/(1+q) for some unknown value of q" do not contradict each other. Both answers are right.
- In Jeff's example above where the contestant knows q but not which door it pertains to, I'd say the exact probability is either 1/(1+q) or 1/(2-q). The total probability works out to 2/3 since the probability that it's 1/(1+q) is (1/3)(1+q) and the probability that it's 1/(2-q) is (1/3)(2-q), but saying you can simply ignore q in this case takes an argument of some form. If you're given conditions in the problem statement that you're ignoring, you really need to say why it's OK to ignore them. Ignoring them because you simply "know" they have no effect on the answer doesn't cut it.
- Similarly, expressing the probability in terms of something that it depends on but is not constrained by the problem statement is not wrong but (I'd say) is actually a better answer. From the formula you can derive what the numeric average should be for a random set of trials, but it also can lead you to other factors that you could observe that might be important. -- Rick Block (talk) 01:42, 25 November 2009 (UTC)
- No, Rick, "must" is not too strong. The ultimate question is "should the player switch," and that can only be evaluated in the player's SoK. And let me reiterate that there is no SoK where the probability is 1/(1+q), because the only SoK that includes any knowledge of a value for q - that is, the host's SoK - also includes the exact knowledge of where the car is. In that SoK, the probability is not a choice between 1/(1+q) and 1/(2-q), it is between 1/1 and 0/1.
- Let me try another example by tweaking the problem to get certain results that might re-focus you. Suppose before the initial choice, the host says "The car has 50% chance to be behind #1, and a 25% chance to be behind #2 or #3." The contestant, naturally enough, chooses #1. The host then says "I will now open one of the other doors that does not have a goat. If both have goats, I will choose with a 75%/25% bias - but I won't tell you which is favored. You can then either keep your initial choice, or switch to the other closed door." He then flips two coins behind his back, and opens #3. Should the contestant switch? If my math is right, by your approach the chances are either 40% that switching will win, or 66.7%. In one possibility, the chances of winning go down; in the other, they go up, but by more than the other case's chances went down. But still, the player should switch. The possible probabilities 40% and 66.7% are not what is important to the contestant when making this decision, only the combined probability of 53.3%. (And incidentally, I did not say whether the assignment of the bias by the host is itself biased - it doesn't matter.)
- The so-called "conditional solution" is only useful to answer the question "should the contestant switch" if every possible value that q could take (in my example, I made two possibilities) is weighted (as I did with the weights 25% and 75%), and the corresponding values for P(Ws|D3) are averaged. This is not possible to do, in general, as Morgan correctly points out. We can't know the weights. But since every P(Ws|D3) is at least 1/2 when the car is randomly placed, regardless of q, they can conclude that the weighted average is also at least 1/2, regardless of the weights. That means the player should switch regardless of any value q could take. Not because of a q, regardless of it. (And if you check my unbalanced scenario, it has the same property as long as neither door is associated with a q, even though some qs do make for a lower probability.)
- Rick, you asked, given a specific host strategy, (1) if I thought whether asking for the "conditional" answer was different that asking for the "unconditional" answer, and (2) which one most people see in the Monty Hall problem. The fact that you have to ask either question shows that you haven't understood anything I've said. First off, I had just explicitly said that K&W, Marilyn vos Savant, the cited researchers who did psychological studies, and most people all see the problem, all see the only the "unconditional" problem unless it is explicitly stated how the "conditional" scenario applies. It IS the Monty Hall Problem. Anything else is a variation.
- Second, there really is no difference between the two problems. The apparent difference is created by whatever boundaries are placed on what you want to call "one" specific host strategy. What you call "the unconditional solution" does allow for the host to have a bias, but it does not specify which door the host favors with that bias. So whatever q may be, the contestant sees two host strategies in your one: one with a split of q:(1-q) for the two unchosen doors, and one with a split of (1-q):q for the same doors. But the contestant sees them as equally likely, where you want to see only one as possible. Since these two strategies are indistinguishable to the contestant, the Principle of Indifference says they must have equal weights in the solution. So the contestant can replace those two host strategies with one, where she averages the two weights given to any specific door. The average of q and (1-q) is 1/2. So whether or not the host is biased, unless the contestant is told which door is favored, the contestant must treat the host as being unbiased.
- Morgan, et al, and Gillman, and any others who address what you call "the conditional problem," are all adding additional boundaries to the host's startegies. By doing so, they create a set of strategies that cannot be used directly when answering the question. Their entire thesis is that no matter which of the strategies that fit in their boundaries is actually the case, the answer is still "switching is best." And now my entire argument can be encapsulated in one statement, so I will set it apart:
- The formula that Morgan, et al, give for P(Ws|D3) is not an answer to the Monty Hall Problem. It is
- the complete set of possible answers based on certain assumptions. Any one of them could be
- the correct answer, keeping within their assumptions, if the contestant had more information.
- But every answer that is correct, within their assumptions, is in that set. And every answer is
- at least 1/2. So regardless of what additional information the contestant could gain, again keeping
- within their assumptions, it will always be advantageous to switch.
- They state, several times, that there is no need to assume the host is unbiased. They fail to recognize that, although that is one possible way to view the assumption being made, it isn't the actual assumption. The assumption, derived directly from the fact that the problem statement does not say which door could be favored, is that the contestant is unbiased in how she treats each door. Just like if you always choose "rock" in "rock, paper, scissors," but I don't know that and choose randomly, I have a 50% chance of winning. You are biased, by my assessment of your possible choices must be unbiased so I consider it a 1/3 chance that you will pick any of the three. The solution to the actual Monty Hall problem has to do the same. Even if the host is biased in opening doors, the contestant does not know how and so treats the host as unbiased. This isn't the same as saying he is unbiased.
- And they make similar assumptions, in order to get their set of possible soluitions. Just not about the host's choice. They assume the car is randomly placed, which vos Savant never said, and whcih is similarly unnecessary It must be treated as unbiased because the contestant will choose any one with equal likelihood.
JeffJor (talk) 16:38, 25 November 2009 (UTC)
- Rick, I agree with you that [my italics] "if your goal is to determine a single numerical answer for the probability it is most sensible to take the host's choice (from those otherwise permitted by the rules) to be random", but I am not sure what other goal one might have for a probability question. Of course it is possible to produce a general answer where we do not apply the principle of indifference to the choices about which we are given no information. If we represent all the unknown choices by parameters we simply find that the probability of winning by switching is from 0 to 1, depending on where the car was initially placed and which door the player chooses. Not a very interesting result. Martin Hogbin (talk) 17:04, 25 November 2009 (UTC)
- Jeff - I believe I understand what you're saying perfectly well. I am on the other hand less than certain that you're understanding what I'm saying. Your opinion (or Martin's, or mine) about what IS the Monty Hall problem, no matter how fervently you believe it, is (from Wikipedia's perspective) original research and is not relevant to the content of the article. What is relevant is what reliable sources say. We have (of course) already discussed this on this page, and it's not even archived yet (see above, #What do the sources actually say).
- Rick, I am not basing what I think the MHP "is" on OR. It is the expressed opinion of those who wrote it (MVS specifically), it is explicitly contained in the problem statement this article is based on, and it is what is used by many of the references. Do you disagree? With what? In all those versions, the car is placed randomly, the host's strategy is to always open a door, with a goat, and to pick randomly. They may not explain why they think "randomly" is included in there either once or twice; but they all do at least once, including Morgan and Gillman (who edited it into what he claimed was a quote). They never explain why. You may think my providing the reason for them is OR, but it is not. I'm just explaining what they assumed was so implicit they did not need to say it.
- The question is never "what is the probability of winning?", it is "should the contestant in the problem switch?" Morgan answers that question IN STRAWMAN FASHION under a set of assumptions that they (not quite clearly) state, which include "car is placed randomly" and "host's strategy is to always open a door, with a goat, and to pick with a parametric bias based on door numbers." All they concluded is that under those conditions, switching is either a neutral choice or it improves the odds. They did not address how the contestant should know what q, becasue their conclusion did not require knowing q. Or say that their answer is "correct" for the MHP in general. And look at the second paragraph of their conclusions. They imply they are solving "the unconditional problem," but if you compare it to Grinstead and Snell, you will see that they are not. They are taking the two possible "unconditional" solutions and combining them is a way that becomes transparent to the contestant not knowing which door is favored; which is to say, they are putting the conditional solution into the SoK of the contestant. The answer they give for that SoK is 2/3.
- And read that Grinstead and Snell. They state quite clearly that the probability for both the conditional and unconditional MHP, as stated, is 2/3. They just require different solution methods. To illustrate that, they apply a specific q=3/4 and so it is a different problem. It is a problem based on the MHP, but it not the MHP itself. The "before" and "after" bit you refer to is a red herring. The timing isn't what is important, it is the knowledge. If the contestant chooses to switch "before the host opens a door" = "without any knowledge of how the host may use door numbers to pick" then the probability is 2/3. That's what establishes the difference. Morgan implies this is the important difference when they talk about their anlysis only affecting "informed players." JeffJor (talk) 19:49, 25 November 2009 (UTC)
- Martin - Strawman arguments are not helpful. The sources that introduce q don't "represent all the unknown choices by parameters", but rather a specific interesting one that highlights the difference between variants of the problem where the player might as well choose to switch before the host opens a door from those where the player specifically chooses after. IMO (to be clear, this is my opinion - not something from a published source) the difficulty most people have with the MHP is precisely because the point of decision is after the host has opened a door meaning most people treat it as a conditional probability problem. I definitely agree with Morgan et al. that whether the host is explicitly constrained to pick randomly between two goats, or whether we treat this choice as random because we don't know q, or whether we know q and which door it applies to "it [the MHP] is still a conditional probability problem". -- Rick Block (talk) 18:16, 25 November 2009 (UTC)
- Rick, I thought we had agree to drop the conditional/unconditional argument for the moment. Yes. Morgan have, for reasons known only to themselves, chosen to address a specific interesting problem. But, as you have already agreed, there is only a difference between the case where the player chooses whether to swap or not before a door is opened and the case where they chose after it has been opened if the player knows the host door opening strategy. If the player does not know this, even though they may have seen which door was opened, '...it is most sensible to take the host's choice (from those otherwise permitted by the rules) to be random'. This gives exactly the same probability of winning by switching as in the case where the player chooses whether to switch or not before the door has been opened. Do you not agree?
- What you call my strawman argument was intended simply to show the natural result of dis-applying the principle of indifference consistently. Martin Hogbin (talk) 19:34, 25 November 2009 (UTC)
What the Morgan paper does do.
I have added this section to try to find find some common ground regarding the Morgan paper. Basically I can agree that the Morgan paper was a response to vos Savant and her solution. As I understand it, vos Savant, proposed the set of rules that were not stated in the Whitaker question, namely that the host always offers the choice and always opens a door to reveal a goat. These rules have become the standard rules for the problem and were not criticized by Morgan.
Vos Savant also states that she takes the initial car placement to be random, this assumption is tacitly accepted by Morgan. She does not state that she takes the players initial choice to be random, and from the player's perspective I guess it is not. As it happens, this turns out not to be important and Morgan do not criticize her for not stating her assumptions in this respect.
The only mistake that vos Savant makes is that she fails to state that she takes the host's legal door choice to be random, even though it is clear that she does in fact do this and later stated that this was what she assumed. What the Morgan paper does do is to point out this omission by vos Savant.
Thus we can agree that the Morgan paper is a valid criticism of the vos Savant solution.
From my personal point of view it is a grossly excessive response to a simple failure to point out one assumption and a response that attempts to make this simple omission into a major problem requiring an 'elegant solution'.
The Morgan paper is not, in my opinion, a well-written, detailed, and comprehensive analysis of the Monty Hall problem which makes clear the exact question that it is answering or all the assumptions that it is making in its calculations. Martin Hogbin (talk) 17:40, 25 November 2009 (UTC)
- The entire issue, as you propose it, boils down to whether the "Whitiker question" is about one specific instance of the game show, in which case every fact in it is to be taken literally and apply to that day only; or if it was supposed to be an illustrative example of the game in general, in which case such facts are circumstantial. They illustrtate a point of variability between different days if the game allows that variability, otherwise they describe the game itself. The problem is, that the question (as asked, not as misquoted by Morgan or Gillman) is unanswerable in the former case. We can't know if the host always offers a switch, among other things. We would only know that he did on that day.
- The only way to justify the assumptions needed to make it solvable, is to treat it as an illustrative example that defines the game itself. And you can't pick-and-choose which interpretation you want for different facets of the problem. There are always three doors, because nobody in the illustrative example choose a number of doors. A door is always opened, because nobody choose whether to do it in the example. A goat is alwasy revealed, because it didn't say Monty choose between a car and a goat. However, any specific circumstances about those choices vary with each show, and can only do so randomly. That includes car placement, contestant choices (it says "you choose a door," not "you always hoose Door #1"), and host choices. Most people who read the problem do not even consider that it is a specific instance. This is effectively admitted by Morgan, who say few even considered the "conditional" problem of Choose 1 Open 3. Then they fail to recognize that those whom they claim did, addressed the solution based on the host's choice being between indistinguishable doors. So theirs was not the same "conditional" problem Morgan addressed, where bias is important.
- Rick, I see little evidence that what you attribute to Marilyn vos Savant is correct. She explained no assumption in the original column, she just implied her assumptions by using them in her solution. Specifically, she never said the placement is random. In followups, she only explained one of the assumptions from that interpretation. She said "So let's look at it again, remembering that the original answer defines certain conditions, the most significant of which is that the host always opens a losing door on purpose. (There's no way he can always open a losing door by chance!) Anything else is a different question." She never even said "always opens a door." She never identified what the other conditions were, she just kept using "1/3" as the probability that the car was behind any door, and "1/2" for the probability when the host chooses between two goat doors. There was no discussion of why, contrary to what you think. But it is a clear implication of what she thought the other "certain conditions" were. All of the conditions were based on the illustrative example I described above.
- Thus, what we can see is that the Morgan critisism is about a question MVS never thought she asked. It is not valid. She did not "omit that the host's choice was random," she never considered it to be possible for the user to use such information even if it was true, which makes it random in the contestant's eyes. All the paper was, in my opinion, was an attempt to apply what tools could be applied to the problem in a real-worl setting. By scholars who were too familiar with applying their science to real-world cases, to see that they were requiring a specific game, and a specific host, in what can only be a hypothetical problem. The very suggestion that Bayesian Inference could be used to refine the host's strategy demonstrates how that could not separate the real-world from the hypothetical.
- But it does make its conclusions clearer than you allow for, once you read it with an educated mind. The primary conclusion is "The fact that P(Ws|D3)≥1/2, regardless of the host's strategy, is key to the solution." There is nothing unclear about that. They aren't saying what the probabiliy is, they are saying how its range affects the choice to switch. The fact that they never discuss the contestant using information about any of their parameters shows that they are keeping the two SoK's separate, even if they don't explain that to the reader. JeffJor (talk) 20:58, 25 November 2009 (UTC)
- Jeff - You do realize this section was started by Martin, not me (Rick) - right? I'll respond to both of you.
- Martin: the Morgan et al. criticism of MvS is not that she didn't specify that the host's choice between two goats is random, but that her solution is not the solution to the problem that is asked. We've been over this so many times I'm surprised you apparently continue to fail to understand this.
- I fail to understand this because there is no 'problem that is asked', but do not take my word for it, read the comment on the Morgan paper by Seymann. In order to get a clearly defined problem certain details must be added. Whitaker actually says, 'opens another door, say #3', Morgan take this to mean, 'opens door #3', which interpretation they support by misquoting the original question. Vos Savant takes the question to mean, 'opens another door (to reveal a goat)'. This is an equally valid interpretation of Whitaker's question, in fact it is much more likely to be what Whitaker actually wanted to know. Do you really believe that he was only interested in the case where the host opens door 3?
- Martin: the Morgan et al. criticism of MvS is not that she didn't specify that the host's choice between two goats is random, but that her solution is not the solution to the problem that is asked. We've been over this so many times I'm surprised you apparently continue to fail to understand this.
- Look at her enumeration of the cases that "exhaust all the possibilities" from her second column (reproduced here). In what she labels as games 1-3, the car location is placed behind door 1, door 2, and door 3 respectively. The listed result in these cases is the result of switching, assuming the player has initially picked door 1. Games 4-6 are the same but show the result of staying with the initial choice (of door 1). From the structure of this table we can clearly see she is assuming the doors are distinguishable (as implied by "Suppose you're on a game show"), she's assuming the car is uniformly placed initially, she's assuming the host must show a goat and make the offer to switch, and that she's following part, but not all, of the suggested case from the problem statement where the player picks door 1 and the host opens door 3. What this table literally addresses is:
- P(win by switching|player picked door 1)
- The probability is 2/3. She doesn't do it, but the same table can also be used to show the results given any other initial door choice, which is obviously also 2/3. No argument. But, this is not the probability that is asked about in the problem statement. What is asked about is
- P(win by switching|player picked door 1 and host opened door 3)
- This probability is not obvious from her table. In fact, if you casually try to infer it from her table you end up with 1/2 (the only excluded case is the one where the car is behind door 3). This is the error most people make when they initially think about this problem, i.e. they see three equally likely cases and one of them is made impossible by the problem statement leaving only two equally likely cases. And, to be clear, no one is claiming MvS is making this error, only that her approach is not addressing the problem that is asked. I suspect you've been following this page long enough to realize that there are people who "understand" the overall probability of winning by switching is 2/3 but who still think the conditional probability given the player has picked door 1 and the host has opened door 3 is 1/2.
- No not at all. I have never seen that particular misconception expressed here. Most people think the probability in both cases is 1/2, see K & W, for example. Martin Hogbin (talk) 18:39, 27 November 2009 (UTC)
- But you have missed my main point which is that the Morgan paper is criticism of vos Savant's explanation, it is not a well-written, detailed, and comprehensive analysis of the Monty Hall problem which makes clear the exact question that it is answering or all the assumptions that it is making in its calculations. It is thus not appropriate to base this article on the Morgan paper or its conclusions, despite its being published in a peer reviewed journal. Martin Hogbin (talk) 18:43, 27 November 2009 (UTC)
- Jeff: I agree with nearly everything you say here. I think the critical difference is whether you treat the doors as distinguishable or not. You treat them as indistinguishable. Morgan et al. don't. Assume for the moment the doors are distinguishable. Given this assumption, you must agree that
- P(win by switch|player picked door 1 and host opened door 2)
- P(win by switch|player picked door 1 and host opened door 3)
- P(win by switch|player picked door 2 and host opened door 1)
- P(win by switch|player picked door 2 and host opened door 3)
- P(win by switch|player picked door 3 and host opened door 1)
- P(win by switch|player picked door 3 and host opened door 2)
- are not all identically 2/3 unless q is 1/2 in each case, since if we're free to assign whatever q values we'd like in these cases we can make them each individually anything we want from 1/2 to 1. Getting back to where this thread started (two or three headings ago) I think what you're saying is that in a simulation of, say, 3000 iterations of the "problem" we can count ALL of them, if necessary renaming the door the player picks as door 1 and the door the host opens as door 3, and with this simulation the number of wins by switching will approach 2/3. I agree with this. However, if the doors ARE distinguishable, we can also keep track of the number of wins by switching separately, in each of the 6 combinations of initial player pick and host door, meaning we can ask about any of the following probabilities (which might be different):
- P(win by switching)
- P(win by switching|player picked door 1)
- P(win by switching|player picked door 1 and host opened door 3)
- Although it's a little harder to phrase unambiguously, I think the last of these probabilities is what most people understand as the question raised by the MHP, and is the one that most conflicts with people's intuition. -- Rick Block (talk) 18:05, 27 November 2009 (UTC)
- Rick - yes, I mistook who started it. I don't see that it matters much. Your statement, "The Morgan et al. criticism of MvS is not that she didn't specify that the host's choice between two goats is random" (emphasis added) is correct. Their criticism is that she didn't answer "the conditional problem," and they point out that it matters if the host's choice is not random. G&S are clearer when they say it only matters if the host's choice is not random. Morgan, et al, never say the contestant needs to know the host's bias to answer the question, they only say it isn't necessary to assume a uniform bias to answer the question. But no source suggests the contestant should consider that possibility, but the article suggests the contestant does.
- Morgan, et al, also says that MvS didn't consider a non-uniform placement of the cars. But they can't make the same conclusion here - that it isn't necessary to assume it is random - so they didn't placement bias at all. That is as much of an admission they give that it is a different problem. But it is such an admission, because they can't ignore it as they did if it is necessary. Had they provided their implied argument to justify ignoring car-placement bias, it would apply to host bias as well. I can't help it thay they omitted these arguments, but they did because even they consider host bias to be a different problem. And none of the sources you have quoted say it is necessary to consider in order to answer the MHP. They just say you don't need to assume it is uniform, either. But it is necessary to assume placement is.
- And in fact, I gave you the example (OR, I know, so I am not suggesting it go in the article - only that it be used to understand what Morgan is trying to say) where the car placement is non-random. If there is a 50% chance of being behind Door #1, and 25% for #2 and #3, then Morgan's approach does not work. The probability can be less than 1/2 that switching will increase the chances for a specific host stragegy favoring a specific door. But from the SoK of a contestant who does not know which door is favored and so must treat a bias either way with equal probility, it does always go up. Just not as much as with a random car placement. The point is that Morgan did not need to address why a contestant should assume a specific host bias, because it was not necessary. In their problem, it always went up.
- Yes, I will agree that those six probabilities you listed can be different, under one condition. That you agree that the contestant has no way to know which is different, and so must average the six probabilities before she can decide if switching is beneficial. That she cannot use any one of the those answers, which is EXCATLY' what Morgan means when they say the problem they are addessing can't be answered in general without knowing the host's strategy, but that she can use the non-informed combination of the three. And that if she does, the answer is 2/3m regardless of host strategy.
- The numbers MvS uses in her second column are only to distinguish the three doors "Chosen," "Opened," and "Unchosen, Unopened." She does it using the numbers in the example, rather than the more complicated names, because it is far more transparent to the reader. She assigns equal probability to them not because it is impossible for a bias to exist, but because the doors are truly interchangeable so they must appear that way to the contestant. If you read the text that goes with that table you refer to, she refers to the host openeinmg "a losing door," not "Door #3," and that she compares it to a shell game with indistinguishable shells. Then she uses face-down cards, which are also indistinguishable. She did not intend to ask, and in fact did not ask, "the conditional problem." Again, the numbers used in the original problem are examples only.
- And I disagree emphatically that "[P(win by switching|player picked door 1 and host opened door 3)] is what most people understand as the question raised by the MHP." Almost none do. Read the pages and pages of responses to that forum post you referenced. None see that problem, and I have only seen mathematicians who cannot see the forest for the trees do. When they do so, they never claim any typical readers to. So you need to stop inserting your own opinion, and OR, into the problem. JeffJor (talk) 18:55, 28 November 2009 (UTC)
- It's nice to see the conversation directed at the emphasis on Morgan, and not some of the old red herrings. Credible people were publishing solutions along the lines of the 'Combining Doors' solution before, during and after Morgan and the others. The idea that this problem can only be solved with 'conditional' or 'unconditional' probability formulas is bogus. Symbolic logic works perfectly well, and eliminates the 'hosts behaviour' canard. That the original door choice never changes from 1/3 based on Monty's actions is all that's required. Glkanter (talk) 00:43, 29 November 2009 (UTC)
- Jeff - again, I think we agree on many things. Morgan et al.'s criticism of MvS is that she didn't answer the conditional problem, and they say in this problem the host's protocol for choosing between two goats matters (to the extent that if it is not specified the we cannot answer what the probability is of winning by switching, only that it certainly doesn't go down).
- They don't exactly say why they assume uniform car placement, although they do say that non-uniform car placement could be considered. I'm not sure what your point is about this. The car placement can either be uniform or not. If you assume non-uniform the problem is really not very interesting (unless, perhaps, the player knows the distribution). Whether this distribution is uniform or not, it's still a conditional probability problem. If the distribution is as in your example Morgan's approach DOES work, they just didn't bother showing this generalization. Treating the doors as distinguishable, and the problem as a conditional probability problem, allows any variant to be easily analyzed.
- Regarding the six probabilities - I'll agree the contestant has no way to know which is different, but only if the doors are treated as indistinguishable. If "Door 1" means the door with the number 1 written on it (which I think it does - I understand you think it doesn't), then the contestant could know which is different. I think this boils down to what we take the introductory "Suppose you're on a game show" to mean. I (some WP:OR here) take it to mean the setting is a game show meaning real doors, on a stage, with identifying markings (numbers 1,2, and 3) so the player and host (and audience) can know which door is which. I think you're taking it to mean far less than this, perhaps only to help explain what we mean by "host" and "player" - but not "door". The assumption that the doors are distinguishable seems to me to be just as much implied as the roles of the host and player. They don't exactly say this either, but Morgan et al. are clearly treating the doors as distinguishable.
- The fact that MvS uses unconditional analogies, and addresses the MHP as an unconditional problem, is precisely the criticism Morgan et al. make. In their view, the problem is conditional (almost certainly because they view the doors to be distinguishable). It might have been nice if the problem used something that really is indistinguishable or explicitly said the doors are to be treated as indistinguishable, actually making it an urn problem, but that's not how the MHP is stated. On a game show, doors are distinguishable - the player knows which one she chose and can see which one the host opens. Modeling this as a math problem where the doors are indistinguishable addresses a different problem (which is what I understand you think IS the Monty Hall problem). This is exactly the point. Perhaps the MHP is BOTH of these problems. Certainly many solutions treat it as an urn problem, but this interpretation is what Morgan et al. criticize. I don't think I've seen anything published that explicitly makes the claim that in the MHP the doors should be treated as indistinguishable. From your POV they're simply solving the problem. What Morgan is saying is that they've oversimplified their model of the problem. -- Rick Block (talk) 16:19, 29 November 2009 (UTC)
- Rick, once again, nobody except the people who "solve" the "conditional" problem think that the MHP is about the "conditional problem." MvS did not. None of the lay people who read it thought it was. Very few of the mathematicians who read it though it was. Gardner did not. The literal interpretation of the MvS problem is not. The EXPLICIT statement of the MHP that defines what this article is about does not. I don't know how to more clear on this point, yet you refuse to acknowledge that it means the MHP is not "the conditional problem." Regardless of whether Morgan thinks so.
- Yes, the host's strategy in the "conditional problem" matters. But whether or not it matters is completely irrelevant, since the "conditional problem" is not the MHP. No matter how many times you ignore this, it still has to define how the article is written. The "conditional problem" is a different problem than the MHP, whether or not Morgan and Gillman think it is due to their misquoting it.
- And I can also repeat why the "car placement" distribution is important, but you will call it OR. It isn't. It is a trivial argument used universally in probability that is being applied inconsistently by Morgan as you read it. Where no explicit reason is given in the problem statement for why one option is more probable than the others, all equivalent options have to be treated equally in the solution of that problem. It is so trivial, that few people reference the reason when they use it. It is the Principle of Indifferece, it is well known, it is not OR, and it applies to both the host's choice and the car placement. Even if they are named, and so lok different. It is a principle that is NECESSARY for the solution to apply to both the host's strategy and the car placement. And that does not mean that anybody thinks thoses chocies are, in fact, uniform, which is where you keep making your mistake. It means that even if there is a bias, the contestant does not know what it is. So from the contestant's point of view, it LOOKS uniform. This is part of the trivial point of probability. It is part of the Principle of Indifference. It is not OR.
- When Morgan and Gillman take their TWO liberties, (1) addressing the conditional problem instead of the unconditional one that is intended and explict, and (2) letting the host have an undefined bias, they are addressing a different problem, and addressing it in a special way. They are saying that that one particular choice is unimportant EVEN IF IT IS CONSIDERED TO BE NONUNIFORM. The "interest" it has is not that it defines "the solution" as you seem to think, it is that it removes a question some might have about the correct solution. No refernce ever says it should be considered for the general MHP, they are just applying an interesting twist that says it is unimportant to that question. Morgan, et al, ignore the fact that there could be similar questions about car placement until the end, where they leave it as an exersize to the reader to apply it and find that there is no similar "interesting twist" there.
- About the "six probabilities." How do you suggest the contestant in this problem treat them differently? If you can suggest a way the contestant can do it, that is supported by the problem statement, I will withdraw everything I have said. But if you can't, you have to admit that the contestant has no way to do it and therefore can't. That means the contestant can't apply "the conditional solution," becasue teh contestant must treat the chocie as unbiased. And I will (again) reiterate that Morgan and Gillman never suggest a way, either. They don't say that the "conditional solution" is a solution to the MHP in general. They never say the doors can be treated as distinguishable. They only say that IF THEY ARE so treaed, it doesn't affect the answer to "should you switch?" You are confusing their hypothetical "if they are distinguishable" from a statement that "they are distinguishable." JeffJor (talk) 18:08, 29 November 2009 (UTC)
- Jeff - I'm sorry, but Morgan et al., Gillman, and Grinstead and Snell are very, very clear. All the following are quotes:
- Morgan et al.: Ms. vos Savant went on to defend her original claim with a false proof and also suggested a false simulation ...
- Morgan et al.: Solution F1: If, regardless of the host's action, the player's strategy is to never switch, she will obviously will the car 1/3 of the time. Hence, the probability that she wins if she does switch is 2/3. ... F1's beauty as a false solution is that it is a true statement! It just does not solve the problem at hand.
- Morgan et al.: Solution F2: The sample space is {AGG, GAG, GGA}, each point having probability 1/3, where the triple AGG, for instance, means the auto behind door 1, goat behind door 2, and goat behind door 3. The player choosing door 1 will win in two of these cases if she switches, hence the probability that she wins by switching is 2/3. ... That it [F2] is not a solution to the stated conditional problem is apparent in that the outcome GGA is not in the conditional sample space, since door 3 has been revealed as hiding a goat.
- Gillman: Marilyn's solution goes like this. The chance is 1/3 that the car is actually at #1, and in that case you lose when you switch. The chance is 2/3 that the car is either at #2 (in which case the host perforce opens #3) or at #3 (in which case he perforce opens #2)-and in these cases, the host's revelation of a goat shows you how to switch and win. This is an elegant proof, but it does not address the problem posed, in which the host has shown you a goat at #3.
- Grinstead and Snell: This very simple analysis [as a preselected strategy, staying wins with probability 1/3 while switching wins with probability 2/3], though correct, does not quite solve the problem that Craig posed. Craig asked for the conditional probability that you win if you switch, given that you have chosen door 1 and that Monty has chosen door 3. To solve this problem, we set up the problem before getting this information and then compute the conditional probability given this information.
- Your argument about what what people think the problem is would be much more convincing with references. I've been here before with Martin. The problem is, as far as I can tell, no one who treats the problem unconditionally bothers to make it clear exactly what they're talking about, but those who treat it conditionally do make it clear and go on to say that the unconditional interpretation is not what the problem says. So, who are we to believe - reliable sources that implicitly say X, or other reliable sources who explicitly say both not X and that the sources that say X are incorrect? As a matter of Wikipedia policy (WP:NPOV), the article needs to neutrally present both POVs here (which is what I think the current version of the article attempts to do). Whether you or I personally agree with any particular POV is irrelevant.
- Rather than continue this seemingly unproductive argument, can I ask what specific changes you think should be made to the article? It might be helpful to start a new section for this. -- Rick Block (talk) 01:11, 30 November 2009 (UTC)
- Rick, about your quotes: Morgan, et al, misquoted MvS. They thought she was trying to solve a problem where specific doors were included, and rewrote the problem so that it looked like she did. With her wording, to quote K&W, "semantically, Door 3 in the standard version is named merely as an example." That invalidates your quotes about it. Semantically, the actual MvS problem is not about Door #3. Semantically, the MHP is the so-called unconditional problem, not the conditional problem. Any reference that addresses the conditional problem has semantically changed the problem into a different one than was intended by MvS; whether they do it explicitly by changing the wording, like Morgan and Gillman did, or implicitly by allowing that the interpretation might be different, like G&S did.
- K&W also say that the solution to the conditional problem "focuses on the behavior of the host rather than on that of the contestant. Consequently, the change from the contestant’s perspective to Monty Hall’s perspective corresponds to a change from non-Bayesian to Bayesian thinking." Not one reference you have quoted ever justifies how a specific host perspective can be used BY THE CONTESTANT to answer the question "should I switch?" Or how a specific Bayesian prior could be chosen. They only establish the set of results that could exist, never a specific result that the contestant can use. They only establish that it is unnecessary to assume a specific host strategy w.r.t. opening a door, when the car is behind the chosen door, in order to answer that question. They all continue to make the standard assumptions for every other aspect - car placement, always opening a door, always revealing a goat - because those assumptions are necessary to answer the question. K&W tried to write those into the problem, to avoid having to assume them.
- The quote you gave from G&S is the one that is most (I would claim it is the only one that is) useful. You just skipped the parts that you don't want to include. "[The conditional problem] means only two paths [of the twelve in the unconditional problem) through the tree are possible (see Figure 4.4). For one of these paths, the car is behind door 1 and for the other it is behind door 2. The path with the car behind door 2 is twice as likely as the one with the car behind door 1. Thus the conditional probability is 2/3 that the car is behind door 2 and 1/3 that it is behind door 1, so if you switch you have a 2/3 chance of winning the car, as Marilyn claimed." In other words, under the standard assmptions, the two approaches to the solution give the same answer through different combinations of possibilities. G&S then go on to say "Now suppose instead that in the case that he has a choice, he chooses the door with the larger number with probability 3/4. In the 'switch' vs. 'stay' problem, the probability of winning with the 'switch' strategy is still 2/3. However, in the original problem, if the contestant switches, he wins with probability 4/7." All this does is demonstrate how the different solution methods give different answers under specific assumptions. It does not justify what specific assumptions should be made, and the difference in the answers is moot without such a justification.
- And while incorrect in several ways, Morgan takes the correct approach for how the conditional solution applies to the contestant when they say "The unconditional problem is of interest too, for it evaluates the proportion of winners out of all games with the player following the switch strategy. It is instructive to express this as a mixture of the two conditional cases: [derivation omitted] Pr(WS)=(p23+p32." This is incorrect because it is a still the conditional problem, it just uses four of G&S's twelve paths instead of two. Where they say "unconditional," they mean "not conditioned on knowing the host's strategy when Door 1 is chosen and has the car." They leave it in terms of two parameters that are a part of the host's strategy, but the usual assumption (explicit in the K&W statement) is that both are equal to one. In this conclusion, Morgan says the answer from the contestant's point of view is 2/3.
- I've given you references for people who treat it unconditionally. MvS. Gardner. Add Tierney. Mlodinow. I haven't read the others to find more such references, but I'm sure they are there. But all you need for proof is Morgan themselves, in their list of so-called false solutions. They all are employing the unconditional problem in one way or another. Your problem with seeing that, is that you only recognize one of the two ways of employing it. You can do it as G&S do, by making twelve paths through the set of possibilities; or you can do it by employing either two or four paths, and recognizing that the numbered doors are interchangable. THAT IS A CONCLUSION THAT CAN BE DRAWN DIRECTLY FROM THE UNCONDITIONAL INTERPRETATION, BUT ALLOWS USING DOOR NUMBERS IN THE SOLUTION. That is, assume the doors are lettered A, B, and C, and so are distinguishable in your approach (as opposed to your assumption, and it is an assumption, that the doors are numbered). Where the problem says "Door #1," that represents a uniform distribution of Doors A, B, and C. The twelve paths represented by G&S using A, B, and C reduce to four using 1, 2, and 3. Where the problem says "Door #3," that represents a uniform distribution of the two possible remaining doors (a different set in each case fo Door #1). That reduces four paths to two. The two-path solution does indeed represent the case where Door #1 is chosen, and Door #3 is opened. It is just form the contestant's SoK, which is the only SoK that is useful in answering the question.
- There is a good reason you have not seen more scholarly work on the unconditional problem. It is a simple problem that from a mathematical standpoint was completely understood and presented in citable works before MvS asked it. Nothing in any of the references you cite invalidates anything about it, and much supports it. The answer (for the probability) is 2/3, quite simply, with nothing to be learned about it.
- To "neutrally present" the conditional problem is what Martin and I are trying to accomplish. That isn't what is currently done. The current article's approach to it does not address the question in the MHP, "Should the contestant switch?" It addresses "given additional information, what can be said by a third party about the choice?" If you disagree, please show me a reference that specifically mentions how the contestant can use the conditional solution to decide. Not what some mathematician thinks the answer would be if additional information were available. This is about the third time I've asked, and you haven't done it. The conditional solution isn't an alternate POV, which Wikipedia policy says must be neutrally presented, it is a different problem that assumes there is a way to apply it that is unstated. A variant, to be sure, but a different problem. And I don't just mean conditional vs. unconditional. To use it requires additional information that is not in the problem statement, and so is not assumable.
- As we have said before, if that section is kept at all, it should be moved below the discussion of "Other Host behaviors" in the "Variants" section. It is not a "Probabilistic solution" to the general MHP, it is a solution to an alternate problem called "the conditional problem." It should say that some readers think specific doors are meant, but that the original fomulator did not (because she never said she did, and in every word she wrote she clearly thought the specific door numbers did not matter). As Seymann points out in the response to Morgan, she can't be held to rigorous standards in a sunday supplement. To prove that she emant the conditioanl problem, you need to provide positive proof that she intended those doors to be different. And there is none.
- The article should make clear that the Moragn's conclusions require two assumptions: (1) the conditional problem is considered, AND (2) the game-show strategy includes certain biases (but not others). Only then you can still conclude that switching is better. But this applies only to those specific biases, not to the general case. You can even cite Morgan for that last statement. The "Bayseian analysis" section can't be included as is without a discussion of the two different meanings of "Baysian." People too often forget that "Bayesian" can mean "Using conditional probabilities," or "Starting with a specific prior, using conditional probabilities to get answsers that apply in just that specific case." The latter meaning cannot be used in a hypothetical problem, since there is no basis for assuming a informed prior (a noninformative prior is not really assuming a prior, it is assuming that nothing can be distinguished even if there is nonuniformity). As such, it is really just the solution to the conditional problem, not a separate analysis that repeats the same conclusions. Regardless, it needs to be more closely associated with the conditioanl problem, since all it is, is that variant's solution.
- Finally, it is not a FAQ that people ask about the conditional problem. It is only mentioned by people who solve the conditional problem, or are reading an article about it so their quesiotn can be asnwered there. It needs to be de-emphasized anywhere it is mentioned. Oh, and most of this discussion needs to be archived. [Signature added later - I never get it right :)] JeffJor (talk) 19:11, 30 November 2009 (UTC)
- I can get on board with the changes to the article described here. Glkanter (talk) 16:27, 30 November 2009 (UTC)
- Claiming that Morgan is solving a "different" problem instead of the "real" one is at least as misguided as Morgan claiming, vos Savant was solving not the "real" problem. This is an ambiguous problem that can be modelled in several ways depending on which specifics you chose to replace the ambiguity and from which perspective you argue. Moreover it is not up to us to pick between vos Savant, Morgan or others, but we simply report their published approaches and criticism.--Kmhkmh (talk) 17:46, 5 December 2009 (UTC)
Is The Contestant Aware?
Has it been agreed by the editors of this article that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method?
It seems to me that this is a (unstated) premise of the problem, as both vos Savant (Whitaker) and Krauss and Wang begin the problem statement with: 'Suppose you're on a game show'. I read this as clearly stating it is only the contestant's point of view we are concerned about. And, being a game show, the host is prohibited from divulging to the contestant either where the car is, or where the car is not.
Is there agreement on this, or is this in dispute? Glkanter (talk) 11:28, 29 November 2009 (UTC)
- As far as I know, this is the only known instance where a contestant at home was able to determine a game show's strategy. It was an aberration, an unexpected outcome, and steps were immediately taken to prevent it from happening again.
- In my humble opinion, a particular contestant gaining usable information from the hosts actions, which would make that contestant's SoK something different than the 'average' contestant's SoK of '2/3 likelihood of a car if I switch' is inconsistent with the published problem statement: 'Suppose you're on a game show'. The problem statement would become: 'Suppose you are not on a game show'. This is not merely a 'variant', or a new or changed premise. It is a completely different problem. And why this completely different problem should be referenced as often and prominently as it is in the Wikipedia article does not make sense to me.
- There are countless reliable published sources which use the combining doors solution to derive the '2/3 likelihood of a car if I switch'. The contestant uses this method to determine the 2/3, then properly says to himself, 'Monty's actions haven't given me any new information, so I'll go with the 2/3 for the average contestant'. Glkanter (talk) 14:49, 29 November 2009 (UTC)
- Is there a specific change you're suggesting? If not, I'd suggest moving this thread to the /Arguments page. -- Rick Block (talk) 01:15, 30 November 2009 (UTC)
- Rick, this is the central element in my criticism of the over-reliance on Morgan's paper in the article. In order to develop a consensus that includes you, I need to know your position on it, so I would greatly appreciate your response to the original question:
- "Has it been agreed by the editors of this article that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method?."
- I see this as an 'editing' question more than a 'mathematics' question, so I'd prefer to leave it here. Thank you. Glkanter (talk) 13:51, 30 November 2009 (UTC)
- Rick, this is the central element in my criticism of the over-reliance on Morgan's paper in the article. In order to develop a consensus that includes you, I need to know your position on it, so I would greatly appreciate your response to the original question:
- Is there a published source that takes the stance that "Suppose you're on a game show" means what you're suggesting? If not, then what you're talking about is WP:OR which makes it a moot point as far as editing is concerned. I'm not saying it's a bad or invalid argument, just that if it's not published it's worthless for editing purposes. -- Rick Block (talk) 14:52, 30 November 2009 (UTC)
- Yes, I have previously linked to the Wikipedia articles showing the only 2 instances where individual contestants had a different State of Knowledge than would the average contestant. The 1950s Quiz Show Scandal and Whammy/Press Your Luck. Both were considered as extraordinary events.
- It wouldn't matter, even if it was OR. I'm not going to put this critical mistake of Morgan's in the article (unless other editors want to build a consensus for it). I'm only using it to decide, using facts rather than my personal opinion, how much emphasis Morgan should get in the article.
Rick, I have directly asked you this question many times, and have never seen a direct 'yes or no' answer from you. As this is a crucial element of the consensus that has been built, it is essential that we understand your reasons if you do not agree with the paragraph above:
- "It seems to me that this is a (unstated) premise of the problem, as both vos Savant (Whitaker) and Krauss and Wang begin the problem statement with: 'Suppose you're on a game show'. I read this as clearly stating it is only the contestant's point of view we are concerned about. And, being a game show, the host is prohibited from divulging to the contestant either where the car is, or where the car is not."
I look forward to your response. Glkanter (talk) 23:02, 1 December 2009 (UTC)
- Rick has responded under his comments section. For clarity and closure, I'll copy them into this discussion.
- "Glkanter asks why I haven't responded about his "Is The Contestant Aware?" question. Why should I? Glkanter has repeatedly demonstrated a complete lack of comprehension of nearly everything I've ever said. It's like trying to explain something to a cat. At some point you just have to give up. However, I'll give it another go. Meow, meeeow, meow, meowww. I'm not sure I have that quite right since I don't speak cat, but it's probably about as comprehensible to him as anything else I could say."
- Nijdam, your response to the question at the beginning of this section is also of great interest to the other editors. In the MHP that begins with "Suppose you are on a game show", is the contestant aware of Monty's door choice behaviour when there are 2 goats remaining? Thank you. Glkanter (talk) 15:14, 4 December 2009 (UTC)
- Has it been agreed by the editors of this article that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method? Yes, but that doesn't mean the contestant is prevented from wondering what affect this might have on her chances of winning by switching.
- Rick, how am I to parse 'yes, but' in the above paragraph? Is that "yes, I agree that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method?" Or, "but..." Let the contestant wonder, it's a free country. But that doesn't affect the game play. Glkanter (talk) 18:51, 5 December 2009 (UTC)
- And, being a game show, the host is prohibited from divulging to the contestant either where the car is, or where the car is not. Is there agreement on this, or is this in dispute? The problem specifies that a game show is the setting. How much information the host divulges to the contestant depends on how the problem is specifically phrased, not on what "must" be true of game shows.
- These are both questions that are more appropriate for the /Arguments page than here, since as editors what we believe to be the TRUTH is ultimately of no importance. What is important is what reliable sources say. Our task as editors is to accurately represent what these sources say regardless of whether we individually agree. This one of the three fundamental policies of Wikipedia, see WP:NPOV. -- Rick Block (talk) 17:44, 5 December 2009 (UTC)
Variants - Other Host Behaviours
http://en.wikipedia.org/wiki/Monty_Hall_problem#Other_host_behaviors
The term 'Host Behaviour' is used earlier in the article to dis-prove the Popular solutions. And the concept of a host's bias, without the word 'behaviour' is used numerous times to dis-prove the Popular solution. In this section, the same issue is used for some unstated (fun?) purpose. That's probably confusing to readers.
This section is inconsistent with the Monty Hall Problem in that the results shown are not from the contestant's SoK. It seems to me that except for the 'forgetful host variant' which vos Savant described as 'random' (aka Deal or No Deal) the contestant must still rely on the 2/3 average. This table is likely to confuse people, rather than enlighten them.
Does the contestant get a do-over if Monty reveals the car in the 'forgetful host (random, aka Deal or No Deal) variant'? If so, then I guess the contestant could infer that Monty is acting randomly, and determine the odds are 50/50. **Wait a minute, if it's a do-over, and he shows a goat this time, wouldn't it be 2/3 if I switch?** Still no harm in switching, though.
The paragraph under the table relating to 'game theory' also uses the term 'host's behaviour' differently than the earlier occurrence in the article. And the conclusion may not be correct. With no knowledge of the hosts behaviour (motivations?), it's understood that it's best to switch with a 2/3 probability. Glkanter (talk) 17:25, 29 November 2009 (UTC)
- I'm not seeing the term used in any way other than to mean constraints on the host. In particular, it is not used at all in the section titled "Probabilistic Solution". The first three variants in the "Other host behaviors" section are all referenced, and are all notable. Sources should be added for the ones that are not sourced. In the paragraph below the table, "host behavior" also means constraints on the host's actions included in the problem statement. The "for example" sentence means if the problem does not constrain the host to always make the offer to switch, the host could be offering the switch only in the case the player has initially picked the car (per the NY Times interview with Monty Hall - see the Tierney 1991 reference). With no constraints on the host's behavior, it's understood that the probability of winning by switching can be anything. That is sort of the point of this section. -- Rick Block (talk) 05:18, 30 November 2009 (UTC)
- The most meaningful point is that the contestant, whose State of Knowledge the problem uses, never knows about these biases. When shown a goat, he always sees himself as the 'average contestant' with a 2/3 likelihood of winning by switching. As I mention elsewhere, once a host behaviour is introduced, the problem statement becomes the opposite of the Monty Hall problem statement mentioned twice in the article. I mentioned a few reasons I think a reader, who knows how game shows must work, would be confused by the irrelevant tables, narrative and the illogical change in whose State of Knowledge is being discussed. Glkanter (talk) 05:59, 30 November 2009 (UTC)
- The "host behaviors" we're talking about here are constraints that are either taken to be implied by the problem statement or explicitly given as part of the problem statement. The Parade version of the problem statement is widely regarded as ambiguous since these constraints are not explicitly listed, in particular whether the host must make the offer to switch and exactly how the host chooses what door to open. There are countless references that consider the impact of slightly different constraints on the host, that would presumably be the well known rules (i.e. explicit and within the SoK of the contestant). This is a subsection of a major section called "Variants". You're perhaps arguing to delete this section, but can you instead suggest a way to make this more clear? -- Rick Block (talk) 15:18, 30 November 2009 (UTC)
- However you describe these things, they all rely on the contestant having knowledge of the host's behaviour. At that point it's no longer the Monty Hall problem about a game show, which is the subject of the article. They're confusing, and do not further the reader's understanding of the Monty Hall problem paradox. Glkanter (talk) 15:33, 30 November 2009 (UTC)
- Again, what is being called the "host's behavior" are the rules under which the game show would be run, which would be known to the contestant. It could still be a game show if the host is not required to make the offer to switch (in fact, that might be an interpretation that would be more consistent with the actual Let's Make a Deal show on which the problem is obviously based). The fact that the Parade version doesn't fully specify the host's behavior is in all likelihood one of the reasons the "Monty Hall problem" is so very contentious. Different people read it as different problems, and then insist their interpretation is the "right" one. Discussing variants leads most people (perhaps not you) to a better understanding of the issues that are involved in the problem description. Many, many sources do this. If the article didn't do this, it would not be complete. -- Rick Block (talk) 19:42, 30 November 2009 (UTC)
- (1) And again, we must assume that any knowledge that is available to the contestant is also avaiable to the person who is trying to determine what the contestant should do - the puzzle solver. The fact that it is not mentioned, especially in a non-rigorous forum like a sunday supplement (see Seymann), means that it isn't necessary to answer the puzzle. For the elements of policy, like if a switch is always offered, that means what is implied in the one example is the full policy. MvS EXPLICITLY says this is her intent in one of the sources you like to cite when it suits your purpose, but apparently not when it contradicts it. For the elements of random choice, like car placement and host choice, it means it is uniform, something even your sources assume when to do otherwise would not make an "interesting" (see Morgan, and Gilman's intentional misquote of MvS) problem.
- (2) Read K&W, and don't give us your unsupported (and unsupportable) opinion. They conclude that the reason for contention has nothing to do with any ambiguity, it is an inability to assess how information based on part of the random nature affects the results. It isn't "different problems," it is not understanding what is essentially the Principle of restricted choice. The two "unconditional camps" - the 1/2'ers and the 2/3'ers are conceptualizing the same problem. And it isn;t the conditioanl problem.
- (3) The only thing that discussing variants helps is understanding the variants. Again, not one of your references applies their results to the contestant. Morgan even reduces it to what they call the unconditional problem (but really isn't, it just has the same answers under the assumptions they do make that are equivalent to what they try not to make) when they try to apply it to the contestant. And there is a good reason: they were addressing a variant, not the MHP itself, and they did it only because it was interesting. Not topical. JeffJor (talk) 22:27, 30 November 2009 (UTC)
Wikipedia Editing Works Best With A Consensus
I probably know the least about this topic. But it looks like there is a lot of agreement amongst active editors. Not unanimous, of course, but that's not a requirement, is it? Glkanter (talk) 21:07, 29 November 2009 (UTC)
- What specific changes are you thinking there's consensus for? -- Rick Block (talk) 01:23, 30 November 2009 (UTC)
- Hi Rick. Thank you for your response. As you see, I've started 4 new sections. I'm especially interested in your responses to the various questions I ask and thought-provoking statements I made, as you appear to not be part of the consensus. We may have differing opinions, but we can work together within the parameters of Wikipedia. I'm laying all my cards out. That's what collaboration's all about, right? So, what's the Wikipedia definition of a 'proper' consensus? Glkanter (talk) 01:38, 30 November 2009 (UTC)
- Again, consensus for what? Assuming you're talking about major changes to the article, I would think any reasonable definition of consensus would have to include at least most of the folks who commented at the last featured article review, archived here. There were a flurry of changes since then - running any major changes by the folks involved in those would be a good idea as well (e.g. Dicklyon, Nijdam, Henning Makholm, Glopk). -- Rick Block (talk) 04:54, 30 November 2009 (UTC)
- Yes, of course, major changes, de-emphasisng the reliance on Morgan. I think that's consistent with the published views of JeffJor, Martin and myself. With all the documented problems with Morgan, it's time to get to work. I mean, the filibustering has to end sometime, right? I'm sure all those other guys you mentioned are anxious to join the discussion. Because, as I read on the subject of Wikipedia Consensus:
- Not hypothetical
- While everyone on Wikipedia has the right to be heard, this does not mean that discussions remain open indefinitely until we hear from them. Nor does it mean that a consensus should be overridden by an appeal to "Wikipedians out there" who silently disagree. In essence, silence implies consent. If you believe that the current discussion does not represent real opinion, either prove it by referring to an existing discussion, or suggest starting a new discussion with a wider audience.
- You are misinterpreting what you've quoted from Wikipedia:What is consensus?. We're talking here about things that have already been discussed, not a new topic. We know a specific set of users who have previously expressed opinions on these topics. It's a simple matter to ask them. Do you want to, or should I? -- Rick Block (talk) 15:35, 30 November 2009 (UTC)
- Which buddy would that be? -- Rick Block (talk) 16:16, 30 November 2009 (UTC)
Morgan's Paper Doesn't Specifically Mention The Combined Doors Solution
Is it meaningful for our purposes then, to assume, infer, or offer opinions on why or why not?
Can we infer anything about Morgan's thoughts on The Combined Door Solution if it's not specifically mentioned?
I think any such discussion would be out of order. Glkanter (talk) 22:08, 29 November 2009 (UTC)
- Are you specifically talking about the sentence that says "Morgan et al. (1991) state that the popular solutions are incomplete, because they all make assumptions about the probabilities after the host has opened a door, without proof"? How about:
- Morgan et al. (1991) state that many popular solutions are incomplete, because they do not explicitly address the specific case of a player who has picked Door 1 and has then seen the host open Door 3.
- If this is the sentence you're talking about, would you find this wording more acceptable? -- Rick Block (talk) 15:53, 30 November 2009 (UTC)
- No, a bigger picture than that. The article is edited as if Morgan's claim trumps all others. I'm pointing out that Morgan didn't state that 'The Combined Doors solution' is false/incomplete/etc'. That's an interpretation of Morgan's paper that you've made, but it's not supported by anything that's been published. So, it's wrong for the article to say, or have a POV, that the Combining Doors solution is in any way inferior/incomplete/etc., because that has not been explicitly published. Glkanter (talk) 16:05, 30 November 2009 (UTC)
- Well, then, where in the article are you seeing this criticism of the Combining Doors solution? The only occurrence of the letters "combin" in the entire article is in the paragraph describing this solution. If you're not talking about the sentence I've suggested, what are you talking about? The fourth paragraph in "Sources of confusion"? We can work on that paragraph, too, but if you're not going to say specifically what you don't like it's rather hard to fix it. -- Rick Block (talk) 01:29, 1 December 2009 (UTC)
- BTW, if nobody objects in the next day or so, I'll make the change I suggested above. -- Rick Block (talk) 01:32, 1 December 2009 (UTC)
Excessive Reliance On Morgan
Each instance in the article of a host behaviour, or host bias, or host prejudice is indicative of a reliance on Morgan's paper. Regardless of what is being illustrated, this topic only exists among Morgan and a few others.
Since the problem statement of both vos Savant (Whitaker) and Krauss & Wang begin with: "Suppose you are on a game show", we know that this host behaviour will not be shared with the contestant, whose State of Knowledge is the only one asked for in The Monty Hall problem.
So, while Morgan is published, his argument is flawed. It reminds me of what Nijdam once said about Devlin, 'His name is Morgan, not God'. The moment the problem is restated to rely on a host behaviour, it's no longer the Monty Hall problem. The problem statement becomes: 'Suppose you are not on a game show'. Which is the exact opposite of how both Monty Hall problem statements in the article begin.
Yes, Morgan should be referenced, but with such an obviously erroneous argument, it hardly deserves the great emphasis it currently enjoys. Glkanter (talk) 05:50, 30 November 2009 (UTC)
- You are completely and utterly wrong about any mention of "host behavior" being indicative of a reliance on Morgan. The Parade description of the problem is nearly universally agreed to be under qualified. What most people intend by the problem is consistent with the Krauss and Wang version, but the difference between this version and the Parade version is precisely the topic of "host behavior". As Seymann says (the quote Martin keeps bringing up): "Without a clear understanding of the precise intent of the questioner, there can be no single correct solution to any problem." It is by specifying the "host behavior" that the precise problem can be understood. If aspects of the host's behavior are not specified you may be able to make reasonable assumptions about them, but your assumptions may not match what whoever is posing the question meant. -- Rick Block (talk) 16:14, 30 November 2009 (UTC)
- Rick, I am not sure what you mean when you say that the difference between the K & W version and the parade version is host behaviour. In the K & W statement quoted in this article the host is stated to choose randomly, just like the car is stated to be placed randomly. Martin Hogbin (talk) 10:02, 3 December 2009 (UTC)
- "Host behaviour" means several things. Just because you can model all the different aspects with probabilities, that does not make them all fall under one umbrella. When "most people" (and I will supply as much support for that as you just did, Rick: none) use "host behavior," they interpret it to mean "does he always open a door," "can he reveal the car," and even "can he open the chosen door" which Morgan and Gillman ignore. Not "is the host biased toward one functionally equivalent choice over another, based on door numbers?" These are diffferent issues, and only Morgan (plus those that follow using the conditional problem) consider that possibility. But it is not something that can be used to directly address the question "should the contestant switch?" It can only be used by a third party who knows every factor that determines what p13 is on that particular day, to address the question "given this additional information, can we second-guess the contestant?" The answer is "no, given all of these other assumptions about behaviour that are as unfounded as the one about the choice of doors." That answer is useless to the contestant herself unless the problem statement says she has knowledge of p13. And nobody - not Morgan, not Gilman, not G&S, not K&W - says she does, or contradicts what I am saying here. JeffJor (talk) 19:35, 30 November 2009 (UTC)
Changes suggested by JeffJor, Martin Hogbin, and Glkanter
If you're here because you've been invited to comment, there are ,two,. three (related) suggestions.
- #Glkanter's suggestion: Eliminate all 'host behaviour, etc' influenced discussion, save for the Wikipedia minimum necessary references to Morgan and his ilk, as the 'conditional' problem is the converse of "Suppose you are on a game show."
- #JeffJor's suggestion: The so-called conditional problem needs to be a separate article, with "conditional" in its title.
- #Martin Hogbin's suggestion: This article should concentrate on the unconditional solution with the Morgan's conditional solution in a variations section.
Please indicate in subsections below whether you favor or oppose each of these suggested changes.
The intent is to try to determine whether there is community consensus for any of these changes. I would suggest one subsection per user who is commenting, and to avoid endless arguments, restricting your comments to your own section (this is modeled after the process used at Wikipedia:Arbitration Committee). I've precreated sections for everyone I've explicitly invited to comment. -- Rick Block (talk) 15:31, 2 December 2009 (UTC)
Discussion about setting up this section and inviting folks to comment
In this section please summarize the changes you're suggesting. I'll be asking the set of folks I mentioned to Glkanter above to come here and offer their opinions, so please keep it as brief as possible. Please let me know when you think this section is ready for others to comment on. -- Rick Block (talk) 01:07, 1 December 2009 (UTC)
- Rick, have you invited Boris Tsirel, William Connolley, or C S to contribute their opinions? What sort of time frame do you have in mind before 'In essence, silence implies consent' as per Wikipedia policy? Glkanter (talk) 15:47, 2 December 2009 (UTC)
- I haven't invited anyone yet. The list of folks is the set of users I added below, plus I'll post something at Wikipedia:WikiProject Mathematics. I can specifically invite Boris, William, and C S if you'd like. As far as the timeframe, I was thinking maybe something like a week or two. -- Rick Block (talk) 15:53, 2 December 2009 (UTC)
- I was going to, but had an edit conflict with Martin as he added his new section below. We need to straighten this out first. -- Rick Block (talk) 16:06, 2 December 2009 (UTC)
- I've notified all (including Wikipedia:WikiProject Mathematics) using template:please see referring them to this section. -- Rick Block (talk) 04:20, 3 December 2009 (UTC)
Glkanter's suggestion
- This is from the section above.
- Each instance in the article (and the various FAQs) of a host behaviour, or host bias, or host prejudice is indicative of a reliance on Morgan's paper. Regardless of what is being illustrated, this topic only exists among Morgan and a few others.
- Since the problem statement of both vos Savant (Whitaker) and Krauss & Wang begins with: "Suppose you are on a game show", we know that this host behaviour will not be shared with the contestant, whose State of Knowledge is the only one asked for in The Monty Hall problem.
- So, while Morgan is published, his argument is irretrievably flawed. The moment the problem is restated to rely on a host behaviour, it's no longer the Monty Hall problem. The problem statement becomes: 'Suppose you are not on a game show'. Which is the exact opposite of how both Monty Hall problem statements in the article begin: "Suppose you are on a game show". Morgan's criticism and his solutions are not relevant to the Monty Hall game show problem, which is the subject of this article.
- Only because it's been published, Morgan should be referenced, but with such an obviously erroneous argument, it hardly deserves the great emphasis it currently enjoys. All other references to host behavior, etc., 'conditional vs unconditional', 'variants', and the Popular solutions being in any way inadequate should be removed from the article.
JeffJor's suggestion
- Rick, I've changed my mind on one thing. The so-called conditional problem needs to be a separate article, with "conditional" in its title. It can be linked to the MHP, but it is not the MHP. For justification, see (and cite in the article) [url=http://www.jstor.org/stable/187880] Maya Bar-Hillel's article "How to Solve Probability Teasers," Philosophy of Science, Vol. 56, No. 2 (Jun., 1989), pp. 348-358. That addresses several points critical to the problem, that are quite specific to all of the arguments we have had here, incuding documented evidence. Specifically: (1) It's just a puzzle. It isn't supposed to present a rigorously-defined mathematical problem, (2) The simple assumptions implied by the informal problem statement are intended, and almost universally accepted by anyone who isn't expecting such a rigorously-defined mathematical problem, (3) Even when presented with alternate wordings that explicitly include elements of host strategy, the general audience does not take that strategy into account in their solutions, and (4) the clear majority of respondents get the wrong answer (1/2) that is based on naive intuition rather than a formal solution.
- By separating the articles this way, Wikipedia can clearly present both problems in a fair and uncluttered manner, allowing any reader who wants to depend on the more formal approach to do so, and allowing those who do not see that formalism as necessary to limit themselves to the information that is of interest to them. JeffJor (talk) 15:03, 1 December 2009 (UTC)
Martin Hogbin's suggestion
We should take the current K & W statement as our starting definition of the MHP.
- I suggest that we give the Whitaker statement first then say that the K & W statement is how this is generally interpreted. The K & W paper itself supports this view.
The primary solution and explanation should not use conditional probability
- Although it can be argued that, even in the case where the host is defined to choose a legal door randomly, conditional probability should still be used because the action of choosing a particular door reduces the sample set and thus the opening of a specific door represents a conditioning of the sample set, it is clear that this is a trivial condition that it is not necessary to consider. This is quite evident either from the symmetry of the problem or from the fact that the revealing of random information tells us nothing. I am sure that we can find reliable sources to support this view.
The Morgan paper clearly does not answer the question as stated in the article and thus should not be regarded as our ultimate reliable source.
- The Morgan paper introduces a parameter q for something that is defined by the article problem statement to have only the value of 1/2. The Morgan paper thus answers a different problem (I suggest that we call it the Morgan scenario) from that posed in the article. In the Morgan scenario it is known that the host might have some preference for one of the legal goat doors.
The Morgan solution should be introduced in a later section of the article that deals with variations of the problem.
- There are many variations of this problem and the Morgan Scenario is just one of many.
Colincbn's comments
(referring to JeffJor's suggestion)
- Hear, hear!! Colincbn (talk) 15:09, 1 December 2009 (UTC)
(referring to Glkanter's suggestion)
I really don't know jack about probability and whatnot, but I still tend to agree with Glkanter's points. I came to this article through looking up various paradoxes and this was a really neat one that I got to try out in the real world (see simulation question above). As I understand it the "Monty Hall problem" states that the host chooses randomly, so any other discussion about host behavior should be limited to the "Variants" section under "Other host behaviors". Just my 2 cents, Colincbn (talk) 02:41, 1 December 2009 (UTC)
- Just to clarify, I think a mention of the Host behaviour/Conditional problem should be made in a subsection of this article, such as the Variants section, with a "main article" link (ie: {{main|MHP Conditional solution}} ) to a separate article that goes into Morgan's conditional problem in detail. I figure this will give the casual reader all the info he/she is looking for with an easy way to delve into the mathematics more deeply if they want. (also thanks to Rick for maintaining this section!) Colincbn (talk) 01:07, 3 December 2009 (UTC)
Martin Hogbin's comments
- I agree that this article should concentrate on the simple and notable interpretation of the MHP, namely the version in which a conditional solution is an unnecessary complication. Morgan's academic problem could be a section of this article or could form a new one. Martin Hogbin (talk) 22:02, 1 December 2009 (UTC)
Glkanter's comments
By my count, that's 4 in favor of the proposed changes, and 0 against. I've been championing these changes since October, 2008, Martin prior to that, and countless other editors for about 5 years. When can we declare an end to the pointless filibustering, acknowledge a consensus, and move on? Rick, will you be offering your comments? Have you contacted the others? Glkanter (talk) 22:29, 1 December 2009 (UTC)
About Martin Hogbin's suggestion - :I agree 100% with your proposed changes. I would like to add my 2 cents to the rationale, however. Morgan is criticizing and solving something other than the Monty Hall game show problem in the article. The introduction of the contestant being aware of any 'host behaviour' when selecting from 2 remaining goats changes the Problem Statement of both vos Savant/Whitaker and Karauss & Wang from "Suppose you are on a game show" to the converse, "Suppose you are not on a game show". Individual contestants on game shows are never provided more information than the 'average' contestant will have. There can be no 'condition'. It's illogical. Glkanter (talk) 15:33, 2 December 2009 (UTC)
JeffJor's comments
[Repeated in part from comments below]
The point of separating the articles is not to eliminate any POVs. It is to emphasize them. To not let one facet of the MHP (simple solution w nonintuitive result) become overpowered by the other (good teaching tool for conditional probabilites). If we don't physically separate them, we need to more clearly divide the article. The first part should be about the classic (unconditional) MHP, as stated by MvS (not K&W), and listing the set of assumptions she has said (and 99.9% of readers agree) are implied: interchangable doors, and any kind bias becomes irrelevant because of interchangeable doors. Then a section about game protocals (part of what some call host stratgies) such as always opening a door or revealing a goat, WITHOUT mention of bias or conditional problems. This mostly exists. Finally, you can cite Gillman (not Morgan) as a reference that introduces the possibility that the conditional problem is intended, but matters only if there is a bias. Use the K&W statement here, not Gillman's misquote. Gillman is better than Morgan because it is clearer, includes placement bias, and does not launch into possibilities that we are never told how to use. I think this is pretty consistent with Martin's suggestion. JeffJor (talk) 17:44, 4 December 2009 (UTC)
- Rick, no paper that uses q<>1/2 is addressing the K&W problem. They allow for it as a very specific variant of what they are addressing. But make no mistake: they are treating the problem statement we are supposed to be working with as the variant. That is wrong. There is nothing wrong with addressing their solutions as the variant, because it is a (more general) variation of what the article is supposed to be about. It isn't even a variant that is supposed to be used: no references use it, they just present it and say you don't need to use it. And I feel you have been just as much as stone wall on points relating to this as you accuse others of being. Meow. JeffJor (talk) 17:56, 4 December 2009 (UTC)
- Rick, you keep treating the Morgan POV as though it is involiate. It is not. Morgan misquotes the MvS problem statement, and so their claim that "the conditional problem is intended" cannot be taken as a reliable interpretation of the MHP. It is just a possible interpretation. Any reference that derives from Morgan is similarly suspect. Gillman misquotes, too, but in different ways. Bar-Hillel's survey proves that few (she found none) readers think of the conditional problem. More references exist that ignore it completely, than that address it. Krauss and Wang admit what the mis-quoters do not - I'll repeat it since when I said it before, it was apparently in cat language before - "Semantically, Door 3 in the standard version is named merely as an example." Grinstead and Snell separate the problem in the exact same two ways I suggested (and in fact, were a model for the suggestion). In short, it is a very minor POV that the conditional problem is meant, and it is based on citable misquotation and misinterpretation. JeffJor (talk) 18:24, 4 December 2009 (UTC)
Rick Block's comments
As a matter of fundamental Wikipedia policy, articles MUST be written from a neutral point of view. What the proponents of these changes are essentially suggesting is that this article take the POV that the interpretation of the problem described by a significant number of reliable sources (the Morgan et al. reference and others) is invalid. Even if this were a stance taken by reliable sources (which, as far as I know, is not the case), by relegating the "Morgan" interpretation to a "variant" subsection or splitting it into a POV fork this article would then be taking the "anti-Morgan" POV. I've made this point to these editors numerous times before, but yet they keep tendentiously arguing that the "Morgan" POV is wrong, or the Morgan et al. reference has errors, or (most recently) that the Morgan POV is NOT about the "real" Monty Hall problem (as if by convincing me that their POV is "correct" I would then agree with the changes they're suggesting).
I sincerely hope the "consensus" from this process is against making these changes, because even if there is a consensus for these changes they cannot be implemented - doing so would violate Wikipedia policy. -- Rick Block (talk) 04:01, 3 December 2009 (UTC)
You all realize Martin's proposal implies the article will not even mention conditional probability except in a "variant" section, don't you? How anyone can think this is not a blatant POV issue escapes me. -- Rick Block (talk) 20:19, 3 December 2009 (UTC)
- Yes Rick, all three proposals are consistent that way. It's based on this very recent and brief section of this talk page (following long and lengthy discussions on various 'talk' and 'argument' pages), 'Is The Contestant Aware?':
- I started this section at 11:28, 29 November 2009 (UTC). You responded with 2 vague, filibuster-style questions, and at 23:02, 1 December 2009 (UTC) I wrote this:
- "Rick, I have directly asked you this question many times, and have never seen a direct 'yes or no' answer from you. As this is a crucial element of the consensus that has been built, it is essential that we understand your reasons if you do not agree with the paragraph above:
- "Has it been agreed by the editors of this article that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method?". [This question was ommitted when I asked Rick the 3rd time. I include it here for clarity]
- ""It seems to me that this is a (unstated) premise of the problem, as both vos Savant (Whitaker) and Krauss and Wang begin the problem statement with: 'Suppose you're on a game show'. I read this as clearly stating it is only the contestant's point of view we are concerned about. And, being a game show, the host is prohibited from divulging to the contestant either where the car is, or where the car is not.""
- To date, at 20:36, 3 December 2009 (UTC), you have still not responded directly to this question. Glkanter (talk) 20:36, 3 December 2009 (UTC)
I have to state the opposite view, which is that you have taken a ridiculously pro-Morgan POV. There are many reliable sources that relate to the MHP and not all of them have a host door choice parameter. Those that do generally quote Morgan as the source for this.
The article already takes a problem statement from a reliable source (K & W) and that same source confirms that this is how most people view the problem. In that statement, the host is defined to choose a legal goat door randomly. It is thus a simple matter of fact that the Morgan paper does not address that problem in so far as it allows a door choice parameter where none is permitted by the problem statement.
The Morgan paper clearly addresses a scenario where where the player is somehow aware of the host's policy for choosing a legal goat door. This rather bizarre scenario is not the one described by our problem statement and thus it should be viewed as a variant of the MHP as it is most commonly understood. Martin Hogbin (talk) 21:30, 3 December 2009 (UTC)
I thought I made it clear we were to use arbcom style rules here, which are that you only comment in your own section (it really does help keep the threads from getting absurdly long). However, since you've been rude enough to post here I'll respond to each of you, BUT please do not continue this as a thread here.
Glkanter asks why so dramatic? The argument has shifted from "present an unconditional analysis first (and don't criticize it)" to "exclude the conditional analysis completely (except as a variant)". This is a huge difference.
Glkanter asks why I haven't responded about his "Is The Contestant Aware?" question. Why should I? Glkanter has repeatedly demonstrated a complete lack of comprehension of nearly everything I've ever said. It's like trying to explain something to a cat. At some point you just have to give up. However, I'll give it another go. Meow, meeeow, meow, meowww. I'm not sure I have that quite right since I don't speak cat, but it's probably about as comprehensible to him as anything else I could say.
Martin (incorrectly) claims again that the Morgan et al. paper does not address the K&W version of the problem. Quote from the paper: "Incidentally, Pr(Ws | D3) = 2/3 iff p = q = 1/2". This is the solution to the K&R version of the problem statement. The Morgan et al. paper (and the Gillman paper and many, many others who approach the problem conditionally) absolutely address the K&R version. Because they also address other versions doesn't mean they don't address the K&R version.
- In the K & W statement q=1/2 by definition thus any problem in which q might not be equal to 1/2 must be a different problem. It is that simple. Martin Hogbin (talk) 19:04, 4 December 2009 (UTC)
Martin and Glkanter are both apparently completely incapable of understanding the main point of the Morgan et al. paper (and the Gillman paper, and what Grinstead and Snell have to say) which is that the MHP is fundamentally a conditional probability problem and that there's a difference between an unconditional and conditional solution. What these sources are saying is that a conditional solution clearly addresses the MHP (as they view the problem), but an unconditional solution doesn't unless it's accompanied by some argument for why it applies to the conditional case as well (and there are many valid arguments, but no argument at all which is what is generally provided with most unconditional solutions is not one of them). The fact that the problem can be (and typically is meant to be) defined in such a way that unconditional and conditional solutions have the same numeric answer in no way invalidates what these sources say. To have the article take the stance that the conditional solution is invalid (which would be truly absurd), or that the criticism these sources make of unconditional solutions is incorrect, or that a conditional solution applies only to a "variant" is making the article take a POV. This would be a direct violation of a FUNDAMENTAL Wikipedia policy. -- Rick Block (talk) 01:53, 4 December 2009 (UTC)
Antaeus Feldspar's comments
Glopk's comments
Father Goose's comments
Chardish's comments
Thanks for the invitation to comment. In my opinion, Martin Hogbin's suggestion seems the post prudent. The Monty Hall problem as popularly explained doesn't rely on conditional probability, and the Whitman explanation seems sufficient for anyone who is not a mathematician. Wikipedia is a general-purpose encyclopedia, and as such main articles should focus on explaining topics as they are popularly understood, with specific scientific analysis relegated to separate articles.
And, to be honest, the article as it stands is much harder to read and understand (as a layperson) than it was several years ago. NPOV isn't "pleasing everyone equally"; don't let efforts towards neutrality wind up hurting the article. - Chardish (talk) 02:53, 6 December 2009 (UTC)
Michael Hardy's comments
PMAnderson's comments
Melchoir's comments
Just from reading the present Wikipedia article, I agree with Martin Hogbin's suggestion, because I don't see why allowing the host to prefer one goat over the other is a more relevant generalization than allowing the host other behaviors. Melchoir (talk) 06:47, 3 December 2009 (UTC)
jbmurray's comments
Nijdam's comments
I fully support Rick's view. Nijdam (talk) 10:34, 3 December 2009 (UTC)
To make my position crystal clear: there is no such as an unconditional solution. There are different problems: an unconditional problem and a conditional one. The latter generally being called the MHP. Nijdam (talk) 22:24, 3 December 2009 (UTC)
- Please read my proposal. I do not claim that the MHP is an unconditional problem. What I say is that in the problem definition given in the article the host is taken to choose a legal goat door randomly. Morgan address the case where this choice is non-random,thus they do not address the problem as defined in this article. Martin Hogbin (talk) 22:39, 3 December 2009 (UTC)
- I'm in the audience looking at the stage. I see three doors and a player pointing to one of them. From the two remaining doors one is opened and shows a goat. That's what I call the MHP. (And I know of the random placement of the car and the random choice of the host.) Nijdam (talk) 22:50, 3 December 2009 (UTC)
- Quite, and that is not the problem that the Morgan paper addresses. The Morgan paper addresses the case where the host door choice is not random. Thus the Morgan paper addresses a variation on what we all agree is the MHP. Martin Hogbin (talk) 23:28, 3 December 2009 (UTC)
- The problem that you and K & W describe, which is the problem addressed by this article, is one in which q=1/2 by definition. Therefore, any problem in which there is a possibility that q might not equal 1/2 must be a different problem. Morgan clearly consider a problem in which it is possible for q to have a value other than 1/2. The problem they consider therefore must be different from that in which q is defined to be 1/2. Morgan do indeed address a (bizarrely) more general problem than the one we are considering but it is, for sure, a different problem. Martin Hogbin (talk) 19:35, 4 December 2009 (UTC)
Dicklyon's comments
I haven't been watching this article for a while; glad to see the K&W treatment up front; that looks like the most sensible article I've seen on it. As for the Morgan conditional approach, I think it's an unnecessary distraction, but it's out there in mainstream reliable sources about the topic, so we ought to cover it in the article. I think Martin Hogbin's proposal sounds best. Dicklyon (talk) 05:01, 3 December 2009 (UTC)
I agree with Rick Block that the other two proposals essentially violate WP:NPOV; but I disagree that moving the conditional stuff to a more minor position is a problem; his heavy promotion of the conditional approach violates WP:UNDUE in my opinion. Dicklyon (talk) 16:29, 3 December 2009 (UTC)
Henning Makholm's comments
I have long since given up on following these discussions, and am not even a very active editor these days. However, since somebody went to the length of creating a heading for me, here are my general recommendations -- for whatever they are worth:
- The article absolutely should discuss assumptions about the host's behavior. It is impossible to derive a valid answer without making some assumptions, and differences in which assumptions are implicit are one of the main reasons why smart people can disagree on the solution when the problem is stated sloppily. It would be a sorry encyclopedia that purported to treat the Monty Hall problem without explicitly pointing out this kind of confusion.
- The analysis that involves conditional probabilities and the one that considers whole-game expectations under different player strategies are both valid ways of approaching the problem, each with its own advantages and disadvantages. The article should present both, and must not suggest that one of them is inherently better or more correct than the other. (For this reason I would oppose splitting one of the analyses into a separate article, suggesting that it solves a fundamentally different problem, rather than being an alternative way of approaching the same problem).
- There has been far too much microlinguistic analysis about precise wordings of the problem in this source or that one, trying to argue that this analysis or that one is the one that most directly addresses the question being asked (implying that the other is a detour via a different but non-canonical presentation of the problem). Which analysis one chooses depends depends far more on which properties (besides being valid) one wants of it. For example, raw convincing power for a lay audience would favor the whole-game analysis, whereas a more in-depth discussion of the effect of different assumptions of the host's behavior is most easily done using conditional probabilities.
- Editors should keep in mind that Wikipedia is an encyclopedia, not a textbook, an question-and-answer database, or a Court of Public Opinion. The goal of an encyclopedia article is not to answer one particular question but to present a body of knowledge. Therefore the amount of energy spent on negotiating "the" question that this article should be about answering is fundamentally misspent. The body of knowledge the article ought to present encompasses several different but related questions (some of which are sometimes mistaken for each other), and several different way of approaching some of them. An approach that restricts ourselves to discussing just one of them would fail to cover the topic encyclopedically.
- I have no strong opinion about which analysis should be first in the article, as long as it is not being touted as inherently superior or inferior by virtue of its position. However, the general principle of progressing from the "quick and easily understood" to the "more complex but also more general and (possibly) enlightening" would seem to suggest starting with the whole-game analysis.
–Henning Makholm (talk) 07:13, 3 December 2009 (UTC)
- Most people, including Rick, think that the problems should be addresses from the player's point of view (state of knowledge). As has been pointed out by many people, it is extremely unlikely that the player would have any knowledge of the host's door opening policy, thus from the player's point of view the host policy must be taken as random (within the rules).
- I have no objection to the Morgan scenario (in which the payer is assumed to know the host's policy) as well as the more simple case being presented here provided that it is made clear exactly what case this applies to.
- What you call, 'microlinguistic analysis about precise wordings of the problem' was started by Morgan et al. who added a pointless layer of obfuscation to a simple puzzle that most people get wrong.
- The point is that the simple/symmetrical/non-conditional problem is the notable one and therefore it should come first. More complex versions should come later for the few that are interested in such complications. Martin Hogbin (talk) 22:36, 4 December 2009 (UTC)
Boris Tsirelson's comments
Being invited by Glkanter, I quote here some paragraphs of a discussion that happened on my talk page on February 2009. As far as I understand, my position is close to that of JeffJor. Boris Tsirelson (talk) 17:20, 2 December 2009 (UTC)
Why split? Because of different importance. The "conditional" article will be, say, of middle importance, while the "unconditional" article – of high importance. We surely have our point of view about importance (rather than content). Boris Tsirelson (talk) 05:54, 4 December 2009 (UTC)
The quotes follow.
Each time giving the course "Introduction to probability" for our first-year students (math+stat+cs) I spend 20-30 min on the Monty Hall paradox. I compare two cases: (a) the given case: the host knows what's behind the doors, and (b) the alternative case: he does not know, and it is his good luck that he opens a door which has a goat. Im addition I treat the case of 100 (rather than 3) doors (just like Monty Hall problem#Increasing the number of doors). And, I believe, students understand it.
I have no idea, why some people spend much more time on the Monty Hall paradox (and even publish papers). (Boris Tsirelson)
This simple little problem is deeper than it might appear, and likely well worth more than 20-30 mins of lecture time. Perhaps even worth revisiting once or twice during a term to explore its more subtle aspects. (Rick Block)
Deeper than it might appear? OK, why not; but still, for now I am not enthusiastic to deep into it. Tastes differ. I find it more instructive, to restrict myself to the simpler, symmetric case, and compare the two cases mentioned above.
If an article leaves many readers puzzled, why it is unnecessarily complicated, it is a drawback. (Boris Tsirelson)
If a problem that appears so simple to me, like the Monty Hall problem, is not sufficiently solved using my unconditional proof, in what circumstances is the unconditional proof appropriate? Thank you. (Glkanter)
The unconditional argument shows that "always switch" is better than "never switch". This is what it can do. Let me add: if you (that is, the player) are not informed about possible asymmetry then you cannot do better than these two strategies, either "always switch" or "never switch". (Boris Tsirelson)
William Connolley's comments
C S's comments
kmhkmh's comments
I'll start with a clear statement and give some more detailed information afterwards:
- I strongly disagree with any of the 3 suggestions (JeffJor, Glkanter, Martin Hogbin) and aside from minor difference fully support Rick Block's approach
If one surveys the available literature literature/publications on the topic, you pretty much get an relatively obvious outline for the article: original problem (in vos savant's column), unconditional solution (basically vos savant and/or various math sources), conditional solution (Morgan and almost in any math source), various problem variation and caveats, history of the problem, application of the problem outside the math domain. Which is essentially for the most part, what we already had and what Rick managed to maintain. In that context I fully agree with Henning Makholm's comments above, who puts it fairly well. The article wouldn't have such problems if all participants would follow that rationale.
The fuzz over quality or minor mistakes in Morgan's paper is a somewhat ridiculous distraction, since Morgan's paper is not needed to argue the conditional solution or caveats to the unconditional solution at all. There is plenty of other math literature dealing with the problem in more or less the same manner.
My personal advice would be to pass the article for final thorough review and modification to the math or a science portal. During that review neither of the 4 disagreeing authors (JeffJor, Glkanter, Martin Hogbin, Rick Block) are allowed to participate/edit. After that review the article should be fully protected for good.
I've seen what happened to the German version, that had similar problems (without a Rick Block around to constantly remain some standard). So we had a lot of people with a somewhat fanatic approach constantly pushing for their favoured explanation and constantly ignoring wiki standards, common sense and more important the available literature on the subject. As result mathematicians and scientists basically dumped the article and gave up on improving it.An effect this article has partially seen as well.--Kmhkmh (talk) 16:45, 4 December 2009 (UTC)
- Kmhkmh, no one is proposing a reduction in the quality of this article but you miss some essential points out in your outline. We should have: 'original problem (in vos savant's column), unambiguous problem definition (K&W), solution to the unambiguous problem (which is trivially conditional but need not be treated so, basically vos savant and/or various math sources), the Morgan scenario (in which the player knows host door choice policy) the conditional solution (Morgan). Martin Hogbin (talk) 19:46, 4 December 2009 (UTC)
- I don't quite see how that is "missing" in my outline above nor do I see any particular reason to give (K&W) a preferred treatment, such an approach does not reflect the publications on the topic.--Kmhkmh (talk) 20:11, 4 December 2009 (UTC)
- I am not proposing that we give K&W and preference but must have a clear and unambiguous problem statement before we (or anyone else) can attempt to answer the problem. Morgan do not have such a statement in their paper so we must use one from another reliable source, in this case another published paper. Note that the lack of clear problem statement in the Morgan paper is not just my opinion, that same point is made clear in the comment by Prof Seymann published in the same journal immediately after the Morgan paper. Martin Hogbin (talk) 20:20, 4 December 2009 (UTC)
- I'm really not interested in repeating now here the discussion that you're pushing for almost over a year now and which frankly from my perspective is entirely pointless and misguided. The original problem in vos Savant's column was ambiguous and hence various articles on the topic and its variations provide their own specifications. As pointed out above already Morgan doesn't really matter in that regard. What the Wikipedia article has to do, is to describe the all various specification and not arbitrarily picking one like K&W as the "right" one. I'd recommend you to reread Henning Makholm's comments carefully. Or to put it rather bluntly - you asked for my comment here it is: Leave the article alone.--Kmhkmh (talk) 21:46, 4 December 2009 (UTC)
- Actually I did not ask for your comment here and I certainly did not ask for, and do not need, your permission to edit Wikipedia. Neither did I pick K&W as the 'right one' as you put it, somebody else put it in the article as a clear and unambiguous description of the problem. As it happens I agree with whoever did this as K & W is the only published paper to seriously address the question of how most people interpret the MHP. It is therefore an excellent place to start the article. Martin Hogbin (talk) 22:25, 4 December 2009 (UTC)
- I'm really not interested in repeating now here the discussion that you're pushing for almost over a year now and which frankly from my perspective is entirely pointless and misguided. The original problem in vos Savant's column was ambiguous and hence various articles on the topic and its variations provide their own specifications. As pointed out above already Morgan doesn't really matter in that regard. What the Wikipedia article has to do, is to describe the all various specification and not arbitrarily picking one like K&W as the "right" one. I'd recommend you to reread Henning Makholm's comments carefully. Or to put it rather bluntly - you asked for my comment here it is: Leave the article alone.--Kmhkmh (talk) 21:46, 4 December 2009 (UTC)
- I am not proposing that we give K&W and preference but must have a clear and unambiguous problem statement before we (or anyone else) can attempt to answer the problem. Morgan do not have such a statement in their paper so we must use one from another reliable source, in this case another published paper. Note that the lack of clear problem statement in the Morgan paper is not just my opinion, that same point is made clear in the comment by Prof Seymann published in the same journal immediately after the Morgan paper. Martin Hogbin (talk) 20:20, 4 December 2009 (UTC)
- I don't quite see how that is "missing" in my outline above nor do I see any particular reason to give (K&W) a preferred treatment, such an approach does not reflect the publications on the topic.--Kmhkmh (talk) 20:11, 4 December 2009 (UTC)
Gill110951's comments
Friday's comments
Summary of opinions
I have added names to the sections below based on comments above. If I have got it wrong please move yourself.
Please do not make comments in this section.
Editors are invited to sign against their names to confirm that they are in the right section. Martin Hogbin (talk) 11:29, 5 December 2009 (UTC)
- Martin, What exactly do you mean by "for change" and "against change"? Dicklyon and JeffJor's opinions (for example) seem very different to me. By categorizing them both as "for change" I think you may be misrepresenting the situation. It would be better to be more specific about what change you're talking about, i.e. Glkanter's suggestion (
remove any mention of conditional probability and any host behavior variants)Eliminate all 'host behaviour, etc' influenced discussion, save for the Wikipedia minimum necessary references to Morgan and his ilk, JeffJor's suggestion (separate articles - basically Glkanter's suggestion plus create a new article for the "conditional" treatment), your suggestion (I'm not exactly sure precisely how to summarize yours). In addition, rather than "against change" the other alternative should probably be described in terms of what it is for, which I think could be described as "present both unconditional and conditional solutions without taking a POV about the validity of either one". And, I'll note that for the article to say that Morgan et al. criticize the unconditional solutions is not the same as taking that POV. You do understand this difference, don't you? -- Rick Block (talk) 16:52, 5
- Although there may be some discussion over the details it is fairly clear that several people would like to see the simple/unconditional solution/problem given more prominence here. This is the change that I am referring to. 'Against change' is fairly self explanatory Martin Hogbin (talk) 16:58, 5 December 2009 (UTC)
For change
Colincbn
Martin Hogbin Martin Hogbin (talk) 11:29, 5 December 2009 (UTC)
Glkanter Glkanter (talk) 12:16, 5 December 2009 (UTC)
JeffJor
Melchoir
Chardish
Dicklyon
Boris Tsirelson Boris Tsirelson (talk) 15:27, 5 December 2009 (UTC)
Against change
Rick Block
Nijdam
kmhkmh
Unable to classify
Please move your name to the correct section if appropriate. Martin Hogbin (talk) 11:24, 5 December 2009 (UTC)
Henning Makholm
Deal or No Deal
Asked whether the contestant should switch, vos Savant correctly replied, "If the host is clueless, it makes no difference whether you stay or switch. If he knows, switch" (vos Savant, 2006).
I read this, and then the following section on "increasing the number of doors" and had the instant comparisson in my mind to "Deal or No Deal". I came back here to see the debate over that game show, but to me it's quite obvious. If there are 22 cases, and you select one, your initial probability is 1/22 of having the mil.
The two situations are clearly fundamentally different as demonstrable:
- We've all see contestants painfully open a case that has the Mil$. This is because the contestant does NOT know the contents and is randomly selecting. The probabilities say that if there are 22 cases, this should happen 20/22 times with only 2/22 probability of getting down to your case and one other (the "switch" situation). This is why it is so uncommon for the Mil to still be in play at the switch point of that show [In reality it's even less common than two in every 22 contestants getting to the switch with a Mil$ due to the irrelevant fact that those who still have a Mil$ in play often take a deal rather than risk eliminating the Mil$ with three or four cases left]. But assuming the true math problem, If you happen to get down to the switch for a Mil$, your odds are equal. God knows which case you picked. You got lucky enough to leave the Mil in play. Now you're down to 50/50 odds.
- The Monty Hall situation would be if you select your case (1/22 odds) and then the HOST, KNOWING which case has the mil randomly selects 20 other cases to eliminate that DO NOT have the mil. It doesn't matter if he eliminates them one at a time or all at once because it's random and he can't eliminate the Mil$. He ends up with case 13 up there, and you have your case. What do you think the odds are that you picked right in the first place and he HAD to leave 13 because it has the Mil$, vs the odds that you picked right and he randomly left 13 up there? Well it's clearly 1/22 odds that you picked right. If you picked ANY of the 21 of the 22 cases that didn't have the Mil, he would have left the same case up there: The one with the mil. Only in that 1/22 case where you have the Mil does he need to be random. So the odds when the revealer KNOWS and AVOIDS revealing the million are the odds of your original choice being wrong.
The point I was going for here in this lengthly analysis is, perhaps the now-common format of Deal or No Deal would make for a good example of the contrast between Monty Hall Problem (revealer knows and avoids opening the prize door) and Deal or No Deal (revealer doesn't know and got lucky to leave two random cases). It's a very good everyday life scenario that many readers will understand and relate to in terms of getting the idea across. I guess the problem is it needs citation, but there must certainly be published works out there analysing the math of Deal or No Deal that can be cited... TheHYPO (talk) 06:29, 4 December 2009 (UTC)
- Yes, I also consider this aspect as the most instructive part of MHP. See above, in my comments: "I compare two cases: (a) the given case: the host knows what's behind the doors, and (b) the alternative case: he does not know, and it is his good luck that he opens a door which has a goat." Boris Tsirelson (talk) 06:41, 4 December 2009 (UTC)
- I agree, that is an interesting, and indeed surprising for most people, case to consider. Most people are amazed to discover that whether the host chooses a goat door by chance or because they know which door is which makes a difference. Of course, you need to decide what happens if the host chooses randomly and happens to choose the car.
- My explanation would be along the lines that when the host knows what is behind the doors you consider all games but when the host chooses randomly you consider a non-random sample of games.
- This is the kind of thing that this article should be concentrating on rather than the rather bizarre scenario where the player knows the hosts door opening strategy. Martin Hogbin (talk) 09:57, 4 December 2009 (UTC)
- Yes. And here is an analogy. The (elementary) geometry of a circle is a special case of the (differential) geometry of an arbitrary curve. However it would be terrible to treat the circle (in an encyclopedia) only inside an article on curves in general. The symmetric case is more notable, more important, this is the point. And let me repeat: we surely have our POV about importance (rather than content). Boris Tsirelson (talk) 12:19, 4 December 2009 (UTC)
- Exactly. The whole point about the symmetric MHP is that is is a very simple problem that nearly everybody gets wrong. The Morgan scenario (player knows the host door opening policy) obfuscates the central problem and leaves us with a more complicated and rather boring problem that most people are not interested in. Martin Hogbin (talk) 12:51, 4 December 2009 (UTC)
- Yes. And let me add: I have nothing against conditional probabilities. I only note that in the symmetric case there is no difference between conditional and unconditional probabilities. And it is not a coincidence. Not at all. An unconditional probability is an average of conditional probabilities (the total probability formula); these conditional probabilities are mutually equal (by symmetry); the equality follows. Boris Tsirelson (talk) 14:16, 4 December 2009 (UTC)
- (back from the weekend) Of course, different measures. Of course, for certain event. But Martin Hogbin understands what I mean, see below "Words, words, words". And again, I do not object to conditioning. I only say that the symmetric case is more important for an encyclopedia.
- Boris, when you teach this problem, do you or do you not introduce conditional probabilities? If not, how to you distinguish the "host forgets" case from the "host knows" case? Martin is still misinterpreting what Morgan et al. says, which is not that the player necessarily knows the host's door opening policy (in the "host knows" case), but that to solve for a specific conditional probability, e.g. P(car is behind Door 2|player picks Door 1 and host opens Door 3), you have to be given or make an assumption about how often the host opens Door 3 if the car is behind Door 1. Symmetry says this is 1/2 is a perfectly valid way to make this assumption. The player has no knowledge of a potential host preference between Door 2 or Door 3 so must treat these doors as indistinguishable is another perfectly valid way to make this assumption. If your solution says nothing about this, your 2/3 answer is not the answer to P(car is behind Door 2|player picks Door 1 and host opens Door 3) but something different, like perhaps P(win|player switches). Which of these conditional probabilities more accurately represents the conditions described by the MHP which specifically allows the player to choose whether to switch after seeing the host open a door?
- (back from the weekend) It seems, everything is already answered in the "Words, words, words" section below. Except for the "personal" question... Yes, I do introduce conditional probabilities. Indeed, I do not teach MHP; I just illustrate conditional probabilities by MHP. So what? First, Wikipedia is not a textbook. Second, I do not object to conditioning. I only say that the symmetric case is more important for an encyclopedia.Boris Tsirelson (talk) 15:18, 5 December 2009 (UTC)
- BTW - the paragraph just added to the article has no references. Citation standards for feature articles are quite demanding. Essentially every independent thought should be referenced (this ensures that what is said is verifiable). Unless a reference can be provided that uses the 100,000 door example to contrast MHP with Deal or No Deal, this paragraph should be deleted. -- Rick Block (talk) 15:20, 4 December 2009 (UTC)
- Rick, you said "Morgan et al. says ... that to solve for a specific conditional probability ... you have to be given or make an assumption about how often the host opens Door 3 if the car is behind Door 1." That isn't really what they say. They say that it is an interesting generalization of the MHP to consider one specific host strategy that avoids such an assumption. They also say that the fully gerneralized host strategy is not interesting in this way. They never say that the assumption q=1/2 is an invalid assumption, that it is not implied by the problem statement, or offer any way for a contestant to obtain information about q. They only say it isn't necessary to make it the assumption in order to answer the question. They do say that for other generalizations, such as placement bias, you are required to assume something to answer the question (because to not do so is "unlikely to correspond to a real playing" of the game). Their only point is to treat that one option as a vehicle for teaching conditional probability, not to say that any formula gives "the probability" for the MHP. So you are injecting your own POV into the article. The POV that a contestant can obtain this information and use it, even if how is unstated. That is an uncited, and uncitable, original thought that should not be included in the article by the very standards you insist others must adhere to. Why do you think you can avoid it?
- So it isn't Martin that is misinterpreting Morgan, it is you. Martin understands that not only are "symmetric assumptions" valid, but they are required for the very reason that no bias values are given. Martin undersatnd that mot published treatmens of the problem make that assumption, and yes I have told you some of them. He understands that what you call the "symmertic assumptions" can be implemented in two ways: either by assuming q=1/2, or by assuming the doors are symmetric and therefore not distinguished. And that the two are isomorphic problems that have different solution methods, but the same answer (of course). That the former symmetric assumption requires Morgan's analysis, but the latter can be solved with most of the methods Moragn calls "incomplete." And that the point of the MHP is to show that that simpler soluiton produces an unintuitive result, not to get an actual probability.
- How can you argue, that the doors cannot be distinguished? When obviously anybody can distinguish them (comletely independent on which solution approach you pursue)? Even more the original problem formulation itsself distinguishes them explicitly? You may argue a "symmetry assumption" for solving (or simplifying) the problem, but you cannot argue indistinguishable doors, unless you blindfold the candidate and rob him of any orientation.--Kmhkmh (talk) 12:48, 5 December 2009 (UTC)
- I don't argue that the doors cannot be distinguished somehow, each one from the others. (But please note, since you are trying to argue for a very strict reading of the Whitiker statement: it does not say the doors have numbers, or are distinguishable. That is an assumption you make. It does mention numbers, but it doesn't say whether the numbers are a manifestation you created in your mind, or are seen by everybody. And don't, as others have, tell me there were numbers on the Let's Make a Deal show - they never played a game remotely like this and it was also not mentioned in the Whitiker statement.) I argue that no factors relating to the uncertainty in the outcome can be applied to the doors, as they are distinguished that way, when solving the puzzle. Suppose I were to roll a pair of dice, one red and one green. If I ask you for the probability one die will roll higher than the other, would you give different answers based on color? How? JeffJor (talk) 13:55, 7 December 2009 (UTC)
- The doors are there to keep the contestant from seeing behind them. Which they accomplish 100% effectively. What if the contestant was sequestered away, and couldn't see the front of the doors or the relative locations of the doors? He relies on Monty's description, as verified by the studio audience. The contestant still has no more knowledge than that switching 2/3 of the time will win the car, before or after Monty has opened a goat door. How has this extra level of 'identicalness of doors', that you claim is required for the unconditional solution, helped or hurt the contestant in any way? How does it apply to the Combined Doors solution, in which Monty reveals 'which' door has a goat, but that has no effect on his offer to switch, or the response by the contestant?Glkanter (talk) 13:28, 5 December 2009 (UTC)
- All of what you've stated here does not affect the distinguishability of the doors, I was talking above. I was making no statement regading the solution and I'm definitely not going to rehash the seemingly endless (and imho rather boring) discussion on that. I just pointed out, that claiming the doors he doors are indistuingishable, is factually false as far as reality or the perception of the contestant concerned. The contestant always see a left, middle and right door, i.e. he can distinguish them. Whether it might make sense to declare the doors indistinguishable in a model to solve the problem is another matter I did not address.--Kmhkmh (talk) 13:50, 5 December 2009 (UTC)
- How can you argue, that the doors cannot be distinguished? When obviously anybody can distinguish them (comletely independent on which solution approach you pursue)? Even more the original problem formulation itsself distinguishes them explicitly? You may argue a "symmetry assumption" for solving (or simplifying) the problem, but you cannot argue indistinguishable doors, unless you blindfold the candidate and rob him of any orientation.--Kmhkmh (talk) 12:48, 5 December 2009 (UTC)
- So it isn't Martin that is misinterpreting Morgan, it is you. Martin understands that not only are "symmetric assumptions" valid, but they are required for the very reason that no bias values are given. Martin undersatnd that mot published treatmens of the problem make that assumption, and yes I have told you some of them. He understands that what you call the "symmertic assumptions" can be implemented in two ways: either by assuming q=1/2, or by assuming the doors are symmetric and therefore not distinguished. And that the two are isomorphic problems that have different solution methods, but the same answer (of course). That the former symmetric assumption requires Morgan's analysis, but the latter can be solved with most of the methods Moragn calls "incomplete." And that the point of the MHP is to show that that simpler soluiton produces an unintuitive result, not to get an actual probability.
- The point of separating the articles is not to eliminate any POVs. It is to emphasize them. To not let one facet of the MHP (simple solution w nonintuitive result) become overpowered by the other (good teaching tool for conditional probabilites). If we don't physically separate them, we need to more clearluy divide the article. The first half should be about the classic (unconditional) MHP, as stated by MvS (not K&W), and listing the set of assumptions she has said (and 99.9% of readers agree) are implied: interchangable doors, and any kind bias becoems irrelevant because of interchangeable doors. Then a section about game protocals (part of what you call host stratgies) such as always opening a door or revealing a goat, WITHOUT mention of bias or conditional problems. Finally, you can cite Gillman (not Morgan) as a reference that introduces the possibility that the conditional problem is intended, but matters only if there is a bias. Use the K&W sattemetn here, not Gillman's misquote. Gillman is better than Morgan because it is clearer, includes placement bias, and does not launch into possibilities that we are never told how to use. I think this is pretty consistent with Martin's suggestion. JeffJor (talk) 17:41, 4 December 2009 (UTC)
- Rick you keep saying that I am misinterpreting what Morgan says without proof or justification. Every mathematician here agrees that, if the player does not know the host door opening policy and we are to address the problem from the player's state of knowledge, we can only take it that the host is equally likely to open either goat door when he has a choice. No parameter q is required, it is fixed in value at 1/2.
- Whether the problem has to be considered from the players ("contestant") perspective or from an informed 3rd person's perspective ("problem solver") is entirely unclear and depends on the perspective you take. Meaning the original question could stand "How would you decide as a player?" or "what would you recomend the player?" Various publications on the topic have examined those different perspectives. Also if the player doesn't know the host's policy, he still has 2 options for his decision making. Simply pick the most reasonable assumption (fix q at 1/2) and base his conclusion on that. Or instead analyze a large variety of possible host policies to see whether all (or at least most) yield to the same conclusion anyway (q varies).--Kmhkmh (talk) 13:31, 5 December 2009 (UTC)
- Both problem statements begin: "Suppose you are on a game show..." I see no ambiguity in that we are taking only the contestant's perspective (State of Knowledge) into our analysis. Glkanter (talk) 13:37, 5 December 2009 (UTC)
- That is correct if you just look at those statements in a literal sense. However it is not so clear if look at some "interpretations" or variation of the problem in literature (see Mark Steinbach in German article as a source). But no matter how you regard that, it does not change the second part, where even from the player's perspective the bayesian analysis (variation of q) is still an option for his reasoning.--Kmhkmh (talk) 13:59, 5 December 2009 (UTC)
- Both problem statements begin: "Suppose you are on a game show..." I see no ambiguity in that we are taking only the contestant's perspective (State of Knowledge) into our analysis. Glkanter (talk) 13:37, 5 December 2009 (UTC)
- Whether the problem has to be considered from the players ("contestant") perspective or from an informed 3rd person's perspective ("problem solver") is entirely unclear and depends on the perspective you take. Meaning the original question could stand "How would you decide as a player?" or "what would you recomend the player?" Various publications on the topic have examined those different perspectives. Also if the player doesn't know the host's policy, he still has 2 options for his decision making. Simply pick the most reasonable assumption (fix q at 1/2) and base his conclusion on that. Or instead analyze a large variety of possible host policies to see whether all (or at least most) yield to the same conclusion anyway (q varies).--Kmhkmh (talk) 13:31, 5 December 2009 (UTC)
- Regarding Morgan's attempt to answer a more general problem, they make a very poor job of this. For the most part is is hard to determine exactly what problem they are trying to answer. But that is irrelevant here, we know the problem that we are trying to deal with and it is not the same one that Morgan address.Martin Hogbin (talk) 20:06, 4 December 2009 (UTC)
Words, words, words
Because in words one often doesn't distinquish between probability and conditional probability, a lot of the misunderstanding arises. As I tried before, I ask anyone of the discussiant to formulate the problem and the solution in rigorous mathematical notation. I'll do the kick-off:
- Three doors with numbers 1,2 and 3
- C is the random variable indicating the number of the door with the car
- X is the random variable indicating the number of the door chosen by the player
- C and X are independent
- H is the random variable indicating the number of the door opened by the host
As C and X are independent we may without loss of generality consider the case "X=1" and without explicit mentioning condition on this event. Probabilities are:
Did I leave something out? Is something wrong? Please comment! In my opinion the whole point of the MHP is the calculation of P(C=2|H=3). I'm looking forward to other opinions. Nijdam (talk) 12:40, 5 December 2009 (UTC)
- No, your calculation is fine and as I have made clear before I accept that the MHP problem (as defined by the K & W statement in which specific doors are mentioned) is a problem of conditional probability. The opening of a door by the host reduces the sample set (clearly the player can no longer change to that door the host has opened) thus the sample set has been conditioned and the problem is one of conditional probability.
But, even with this problem formulation we can ask the question as to whether we need to use conditional probability to answer the question. We can immediately note that there is an obvious symmetry in the question. Namely that:
and therefore that: P(C=2|H=3)=P(C=3|H=2) Thus, as Boris has ,said the conditional solution, whichever door the host chooses, must equal the unconditional solution. There is nothing wrong with this approach, many intractable mathematical problems have been solved by noticing some symmetry in the problem.
>>>Even so, as you say, we have to calculate the conditional probability. Nijdam (talk) 15:57, 5 December 2009 (UTC)
Alternatively we might say that, because the hosts choice is random (when he has a choice) it gives no information about the initial placement of the car and thus the original
must hold good after the host has opened a door.
>>>??It doesn't:
- You are right, of course. I should have just said that P(C=1)=1/3; Martin Hogbin (talk) 16:39, 5 December 2009 (UTC)
So to sum up, with the K & W formulation, the problem may be strictly conditional but it is clear that a simple unconditional solution will give the correct answer.
However there is more to the issue than this. The MHP is essentially a mathematical paradox and thus it is logical to formulate the problem so that the solution is as simple as possible. This is what was done before the Morgan paper was published. The door numbers were considered irrelevant. I have answered your question, now perhaps you will answer mine. Do you really believe that what Whitaker wanted to know was what the probability of winning was given only that specific doors had been chosen and opened? I would very much like to hear your answer to that question.
>>>Whitaker definitely wanted to know what for a chosen door and an opened one the (conditional) probability was for the car to be behind the remaining unopened door. Nijdam (talk) 15:57, 5 December 2009 (UTC)
I would say that the question that he actually wanted the answer to is: 'Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, and the host, who knows what's behind the doors, opens another door, which has a goat. He then says to you, "Do you want to pick the remaining door?" Is it generally to your advantage to switch your choice?'
He obviously wants to know what is the best strategy in playing the game: to switch or not. This a simple question with a simple answer that most people get wrong.
>>>Always given the situation the player is in. Nijdam (talk) 15:57, 5 December 2009 (UTC)
I can only repeat, yet again, the words of the wise Prof Seymann (with my emphasis) in the hopes that you will heed them: ' Without a clear understanding of the precise intent of the questioner, there can be no single correct solution to any problem. Thus, with respect to the three door problem, the answer is dependent on the assumptions one makes about the intent of the one who initially posed the question '. In my opinion Morgan et al. have completely misrepresented the original point of the question, resulting in all this conditional nonsense which only serves to obfuscate an interesting problem. Martin Hogbin (talk) 14:02, 5 December 2009 (UTC)
>>>There you have a point. The original problem may be interpreted in different ways. Also in the way of Morgan et al. BTW. But my main concern is that even in the precise definition (like the K&W formulation) many people, seemingly also mathematicians, probabalists and statisticians, give the wrong analysis. Nijdam (talk) 15:57, 5 December 2009 (UTC)
- I don't completely disagree with your description. However making claims about Whittaker's intentions is clearly WP:OR. Either his intentions are published somewhere, then they are known and we can incorporate them or they are not. In the latter case personal speculations of WP editors do not belong in the article. As far possible or real misinterpretation are concerned, WP has to describe or summarize how Whitaker was interpreted in various publication - period.--Kmhkmh (talk) 14:12, 5 December 2009 (UTC)
- I understand your point about sources; that is why I have not edited the article but continued to argue here. On the other hand may editors feel passionately that the current format of the article is wrong. There are many sources on this problem and it is, to some degree, up to us which ones we use and how we use them. See my suggestion below on mediation. Martin Hogbin (talk) 14:33, 5 December 2009 (UTC)
- I agree completely with the analysis done above by Nijdam and Martin Hogbin. Of course, the symmetry assumption should be formulated more accurately in the "official" text; not only C and X are independent, but also C is uniform on the 3-point set, and H is conditionally uniform on the rest (be it 1-point or 2-point set). Boris Tsirelson (talk) 15:04, 5 December 2009 (UTC)
- Actually Martin's description leaves me a bit confused since in my perception it is not quite in line with what he was pushing for earlier. However if we all essentially agree now, I don't quite get what the actual dissent is now. Are we just arguing about the order of various sections but agree about the general content (see also the outline under my comment)? I can live with more or less any order in the article as long as the (sourced) content stays (in whatever section). Or to be specific regarding the much debated Morgan, his approach (or that in similar publications) hast to be mentioned and his caveat to the vos savant's approach/simple solution as well, in which section of the article this happens however doesn't really matter.--Kmhkmh (talk) 15:22, 5 December 2009 (UTC)
- As for me, I only say that the symmetric case is more important for an encyclopedia than the general case. (Likewise, a circle is more important for an encyclopedia than an arbitrary curve.) Boris Tsirelson (talk) 15:32, 5 December 2009 (UTC)
- Actually Martin's description leaves me a bit confused since in my perception it is not quite in line with what he was pushing for earlier. However if we all essentially agree now, I don't quite get what the actual dissent is now. Are we just arguing about the order of various sections but agree about the general content (see also the outline under my comment)? I can live with more or less any order in the article as long as the (sourced) content stays (in whatever section). Or to be specific regarding the much debated Morgan, his approach (or that in similar publications) hast to be mentioned and his caveat to the vos savant's approach/simple solution as well, in which section of the article this happens however doesn't really matter.--Kmhkmh (talk) 15:22, 5 December 2009 (UTC)
- I agree completely with the analysis done above by Nijdam and Martin Hogbin. Of course, the symmetry assumption should be formulated more accurately in the "official" text; not only C and X are independent, but also C is uniform on the 3-point set, and H is conditionally uniform on the rest (be it 1-point or 2-point set). Boris Tsirelson (talk) 15:04, 5 December 2009 (UTC)
- Indeed; but I'm afraid, Rick Block will say that a featured article must be perfectly sourced... Boris Tsirelson (talk) 16:15, 5 December 2009 (UTC)
- I meant, please respond to my call. Formulate here your ideas about the symmetric case and its solution in the above terminology!! Nijdam (talk) 16:21, 5 December 2009 (UTC)
- OK, wait a bit. Boris Tsirelson (talk) 16:25, 5 December 2009 (UTC)
- I meant, please respond to my call. Formulate here your ideas about the symmetric case and its solution in the above terminology!! Nijdam (talk) 16:21, 5 December 2009 (UTC)
- Indeed; but I'm afraid, Rick Block will say that a featured article must be perfectly sourced... Boris Tsirelson (talk) 16:15, 5 December 2009 (UTC)
Not just words
Notation:
- Three doors with numbers 1,2 and 3
- C is the random variable indicating the number of the door with the car
- X is the random variable indicating the number of the door chosen by the player
- H is the random variable indicating the number of the door opened by the host
Assumptions:
- C is uniform on the set {1,2,3}
- C and X are independent
- H is conditionally uniform on the complement of the set {C,X} in the set {1,2,3} (be the complement a 1-point or 2-point set)
The "unconditional" solution:
A pure strategy of the player is a function that maps every possible pair (X,H) to either X or the "third" element of {1,2,3} (different from X and H).
A mixed strategy of the player is a function that maps every possible pair (X,H) to a probability measure on {1,2,3} that vanishes on {H}.
The winning probability is a function of a strategy. It is invariant under the rearrangement group of {1,2,3} (by the symmetry, of course). Therefore it is sufficient to consider only invariant mixed strategies. Such a strategy is nothing but a probability of switching. It is sufficient to consider only extremal values (0 and 1) of the probability. Thus, the question boils down to: to switch or not to switch. The simple unconditional calculation completes the analysis.
The "semi-conditional" solution:
The conditional winning probability without switching, P(X=C|X,H), is a function of X and H. It is invariant under the rearrangement group of {1,2,3} (by the symmetry, of course). Therefore it is the constant function. Taking into account that its expectation is equal to the unconditional probability (the total probability formula) we see that P(X=C|X,H) = P(X=C); that is, the conditional probability is equal to the unconditional probability. The simple unconditional calculation (the same as above) completes the analysis.
(You see, the conditional probability is used; but is reduced to the unconditional probability.)
There is also the "all-conditional" solution, not mentioning the unconditional probability; but probably I do not need to write it here.
What do you think about it? Boris Tsirelson (talk) 17:08, 5 December 2009 (UTC)
Maybe some words here sound a frightening math for some people; but they are just a formalization of the symmetry argument intuitively clear to most people. So much clear that they probably do not feel any need in formalization... Boris Tsirelson (talk) 17:27, 5 December 2009 (UTC)
- As I said; words, words, words and more words. Give me the correct formulation of this decision theoretical approach in formulas. BTW: I hope you don't tell this story to your first grade students in your introductory course. What I am actually interested in is what you tell in this course and then in the above formalism, with no more words than needed. Think you can manage? Nijdam (talk) 10:03, 6 December 2009 (UTC)
- Sorry, now I do not understand what do you mean by "words". Every mathematical paper consists of words (and formulas inside). The formulation above is correct. Yes, this is not what I teach. The reason is that I do not teach MHP; I teach probability, especially conditioning, and at that moment I use MHP as an instructive example. The goal of Wikipedia article is probably quite different. Boris Tsirelson (talk) 13:26, 6 December 2009 (UTC)
- I am not used to explain math in a sarcastic environment. If someone will ask me a reasonably specific question in a reasonably polite manner, I'll be reasonably helpful.
- I claim that the above texts are correct proofs (well, somewhat sketchy). I am not an anon; I am a professional mathematician.
- If you want to say that this is anyway too complicated for the article, just say so. In fact, I never proposed these solutions for the article. And I did not object against conditional probability. I only object against the general case treated as no less important (for Wikipedia, not for science) than the symmetric case. Boris Tsirelson (talk) 14:48, 6 December 2009 (UTC)
- I think the argument for this extensive treatment of the general case is, that is somewhat reflects the academic publications/treatment of that topic. I have hardly any objection against Martin's reaction to Nijdam's comment. Featuring the special case or unconditional solution and its benefits prominently in the first part of the article is perfectly fine. However if you review some of Martin's other or earlier comments and even more so some comments of JeffJor or Glkanter, then you can see they are pushing for things which partially factually false or unsourced and definitely not in line with bulk of reputable literature on the subject. Among these are glkanter "legal arguments", JeffJor's attempt to define the conditional approach as a "non MHP"-problem. There also seems to be an attempt to remove reputable sources from the article (via badmouthing) and ignoring that other sources more or less state same conclusions anyway. In particular there is one thing the WP-article cannot do, that is treating the MHP as a unconditional problem only, while the bulk of the literature treats it at least as a conditional problem as well. Another thing is, that the WP article cannot redefine the MHP to remove its ambiguity, since the original problem is ambiguous and much of the literature explicitly deals with the ambiguity. WP needs to report the definitions of others and not set its own.--Kmhkmh (talk) 15:38, 6 December 2009 (UTC)
- I agree. Boris Tsirelson (talk) 16:02, 6 December 2009 (UTC)
- I think the argument for this extensive treatment of the general case is, that is somewhat reflects the academic publications/treatment of that topic. I have hardly any objection against Martin's reaction to Nijdam's comment. Featuring the special case or unconditional solution and its benefits prominently in the first part of the article is perfectly fine. However if you review some of Martin's other or earlier comments and even more so some comments of JeffJor or Glkanter, then you can see they are pushing for things which partially factually false or unsourced and definitely not in line with bulk of reputable literature on the subject. Among these are glkanter "legal arguments", JeffJor's attempt to define the conditional approach as a "non MHP"-problem. There also seems to be an attempt to remove reputable sources from the article (via badmouthing) and ignoring that other sources more or less state same conclusions anyway. In particular there is one thing the WP-article cannot do, that is treating the MHP as a unconditional problem only, while the bulk of the literature treats it at least as a conditional problem as well. Another thing is, that the WP article cannot redefine the MHP to remove its ambiguity, since the original problem is ambiguous and much of the literature explicitly deals with the ambiguity. WP needs to report the definitions of others and not set its own.--Kmhkmh (talk) 15:38, 6 December 2009 (UTC)
- If you want to say that this is anyway too complicated for the article, just say so. In fact, I never proposed these solutions for the article. And I did not object against conditional probability. I only object against the general case treated as no less important (for Wikipedia, not for science) than the symmetric case. Boris Tsirelson (talk) 14:48, 6 December 2009 (UTC)
- I'm confused. If you agree then why are you listed here as supporting changing the article (to attempt to redefine the MHP to remove its ambiguity and to remove, badmouth, and ignore reputable sources). I suspect we don't have a common understanding of what changes are suggested. -- Rick Block (talk) 17:19, 6 December 2009 (UTC)
- Here is my position (once again): I only say that the symmetric case is more important for an encyclopedia than the general case. (Likewise, a circle is more important for an encyclopedia than an arbitrary curve.) Boris Tsirelson (talk) 18:43, 6 December 2009 (UTC)
- Then, I would suggest you change where your name appears in Martin's "summary" of opinions. I believe what Martin, and Glkanter, and JeffJor are actually arguing for is to banish any mention of conditional probability to a "variant" section. And they think you agree with this. -- Rick Block (talk) 20:20, 6 December 2009 (UTC)
- But I do support some change. First, prepare a list with a different formulation. Boris Tsirelson (talk) 20:42, 6 December 2009 (UTC)
- Rick, you are overstating my request. I do not want to banish any mention of conditional probability to a variant section but I do want to state that it is only really important if the host chooses non-randomly - the Morgan scenario. Martin Hogbin (talk) 21:55, 6 December 2009 (UTC)
Formulas, not words
Here is the "semi-conditional" solution rewritten for these that hate words and like formulas:
P(X=C|X=1,H=2) = P(X=C|X=1,H=3) = P(X=C|X=2,H=1) = P(X=C|X=2,H=3) = P(X=C|X=3,H=1) = P(X=C|X=3,H=2);
P(X=C) = P(X=C|X=1,H=2) P(X=1,H=2) + P(X=C|X=1,H=3) P(X=1,H=3) + P(X=C|X=2,H=1) P(X=2,H=1) + P(X=C|X=2,H=3) P(X=2,H=3) + P(X=C|X=3,H=1) P(X=3,H=1) + P(X=C|X=3,H=2) P(X=3,H=2);
P(X=1,H=2) + P(X=1,H=3) + P(X=2,H=1) + P(X=2,H=3) + P(X=3,H=1) + P(X=3,H=2) = 1;
therefore
P(X=C|X=1,H=2) = P(X=C|X=1,H=3) = P(X=C|X=2,H=1) = P(X=C|X=2,H=3) = P(X=C|X=3,H=1) = P(X=C|X=3,H=2) = P(X=C).
That is, the conditional probability is equal to the unconditional probability (in the symmetric case, of course). Boris Tsirelson (talk) 20:21, 7 December 2009 (UTC)
Observation and suggestion
- I noticed that request for comments and recent posting related to it already follow the same pattern as the old discussion. The same old points get reiterated by the mostly by same people over and over (right now including me I'm afraid). Also there is tendency of explaining each's (personal) understanding of the problem rather than sticking to the sources and there is a rather endless arguing about relatively minor points ("which goes first"). This "game" is now played by the same actors (partially including me) for over a year without any productive result.
- Due to the observation above I'd like to repeat my recommendation above. The article is best served, if it gets a review by a group of knowledgeable, competent and "neutral" editors. All former editors and constant participants of this endless discussion should state their point in a single comment and other than that (voluntarily) stay out of the way. They should only give further comments if they are explicitly requested by the reviewers. The former editors that should stay out of the way explicitly include Martin Hogbin, Glkanter, JeffJor, Rick Block, Nijdam and Kmhkmh.
--Kmhkmh (talk) 13:13, 5 December 2009 (UTC)
- The MHP has been described as the world's most intractable brain teaser. It contains elements of both mathematics and philosophy. I think a suitable body of knowledgeable and neutral editors who will be able to understand to issues involved will be hard to find.
- As an alternative I would suggest some form of mediation, possible by someone who makes no attempt to address the problem itself but who mediates on general content principles and policies might help. Martin Hogbin (talk) 14:15, 5 December 2009 (UTC)
- Finding a group of people being better or at least as qualified as he current long members of the discussion is not that hard. The reviewers don't have to be the perfect mix but just good enough for the job. There real issue here is, if people are willing to step back and accept the sound judgement of others, even if it does not support their favoured solution. As far as mediation i have no objection if the other editors are fine with it, but i'm quite skeptical regarding the success.--Kmhkmh (talk) 15:06, 5 December 2009 (UTC)
- Where are they now then? Are you thinking of a bunch of mathematicians? Most of them will probably not be that interested, the maths is pretty simple, all the problems lie elsewhere. Martin Hogbin (talk) 16:42, 5 December 2009 (UTC)
- I think most third part expert (mathematicians or otherwise) are put off by the endless (and often pointless) discussion and they are definitely not interested in participating in such a thing over months or even years (neither am I). They might however be willing to help out with a review/3rd opinion provided this can be handled in timely fashion and that the results will be heeded. This means the first step would be that the "warring parties" explicitly agree beforehand to accept the result and refrain from further edits.--Kmhkmh (talk) 16:59, 5 December 2009 (UTC)
- Whichever side lost in that case would feel that they had not had their case taken seriously. I think mediation, where the current proponents can present their cases to a mediator, is a better bet. Martin Hogbin (talk) 17:02, 5 December 2009 (UTC)
- I think most third part expert (mathematicians or otherwise) are put off by the endless (and often pointless) discussion and they are definitely not interested in participating in such a thing over months or even years (neither am I). They might however be willing to help out with a review/3rd opinion provided this can be handled in timely fashion and that the results will be heeded. This means the first step would be that the "warring parties" explicitly agree beforehand to accept the result and refrain from further edits.--Kmhkmh (talk) 16:59, 5 December 2009 (UTC)
- Where are they now then? Are you thinking of a bunch of mathematicians? Most of them will probably not be that interested, the maths is pretty simple, all the problems lie elsewhere. Martin Hogbin (talk) 16:42, 5 December 2009 (UTC)
- Finding a group of people being better or at least as qualified as he current long members of the discussion is not that hard. The reviewers don't have to be the perfect mix but just good enough for the job. There real issue here is, if people are willing to step back and accept the sound judgement of others, even if it does not support their favoured solution. As far as mediation i have no objection if the other editors are fine with it, but i'm quite skeptical regarding the success.--Kmhkmh (talk) 15:06, 5 December 2009 (UTC)
This whole discussion could have reached an amicable end long ago
If the Morgan supporters would please read and respond to the existing section "Is The Contestant Aware?", and it's question:
- "Has it been agreed by the editors of this article that regardless of how Monty handles the 'two goats remaining' situation, the contestant has no knowledge of the method?
- "It seems to me that this is a (unstated) premise of the problem, as both vos Savant (Whitaker) and Krauss and Wang begin the problem statement with: 'Suppose you're on a game show'. I read this as clearly stating it is only the contestant's point of view we are concerned about. And, being a game show, the host is prohibited from divulging to the contestant either where the car is, or where the car is not.
- "Is there agreement on this, or is this in dispute? Glkanter (talk) 11:28, 29 November 2009 (UTC)"
- http://en.wikipedia.org/wiki/Talk:Monty_Hall_problem#Is_The_Contestant_Aware.3F —Preceding unsigned comment added by Glkanter (talk • contribs) 16:15, 5 December 2009 (UTC)
- Yes this is in dispute. The view(s) that have to be described in the article, are the views taken in publication on the Monty Hall problem and there treatmeants which assume different perspectives. What we probably can be agreed on, that those different perspectives should be handled in a variations or generalization section and that they don't belong into the article lead. Also it is probably not appropriate to assume (specific und possibly) legal gameshow regulations. Since most of our readers, much of the original audience, potentially even whitaker himself and some of the people that have published on it, are possibly not aware of specific regulation and legal restrictions and definitely do not mention them. This means while the article can and should discuss how actual regulations (or the real monty's behaviour) might influence the analysis of the problem, but that definitely doesn't belong in the lead section nor can any such regulation simply be considered as an obvious "given" for analysing the problem.--Kmhkmh (talk) 17:01, 5 December 2009 (UTC)
- But it is indisputable. I don't care whether the problem starts with "Suppose you are on a game show," or what you think that implies. In every version of the MHP I have ever seen, the question is "Should the contestant switch?" It is not "What is the probability of winning the car if the contestant switches?" Or "Describe a parametric formula that allows the contestant, once given the proper data, to decide whether or not to switch." It is a yes/no question in the purest sense: only two answers address the question. "Yes, she should switch" and "No, she should not switch." If you are required to make assumptions to reduce your answer completely to one of those, there are acceptable means to do so. The point about the contestant being aware is indistutable because we have to make whatever assumptions are necessary to reduce the answer to "'yes' in all possibilities considered" or "'no' in all possibilities considered," which means that we have to apply the same knowledge we assume the contestant will use. When they address the actual MHP question, the sources that address the conditional problem make such assumptions; just not that specific assumption about how the host chooses between two goats. They do make the neutral contestant-knowledge assumptions for what I call "game protocol" (e.g., always revealing a goat) and placement bias.
- Morgan's point is NEVER that the answer to the MHP is 1/(1+q), or whatever. It is that one specific assumption is not really necessary when the problem is taken literally in conditional form (which itself is disputable: the sources that claim it is conditioanl misquote their sources in such a way that makes it conditional). You don't need to make the assumption that reduces 1/(1+q) to 2/3, since 1/(1+q) is always greater than 1/2. But that conditional form loses the real beauty of the MHP, that the seemingly paradoxical answer is correct. Far more sources discuss this aspect of the problem than address the "conditional solution," which is where some people's POV is interfering with their ability to approach the article objectively. Yes, the conditional problem is addressed by some sources. It is a minority, and neutrality means it should be treated as a variant. JeffJor (talk) 13:31, 7 December 2009 (UTC)
- These are the only 2 known English language Game Show situations (Whammy and the 1950s Scandal) in which the particular contestant had more 'information' than an 'average' contestant would have. Both situations were considered highly unexpected aberrations, and many steps were taken to prevent either from being repeated.
- So, yes, there is a commonly understood expectation of all game show watchers that each contestant has no information otherwise not available to other contestants, certainly not coming from the host (or the shows producers). And there's tons of laws and lawyers watching for this in the US.
- This is not ambiguous: 'Suppose you're on a game show' Glkanter (talk) 17:33, 5 December 2009 (UTC)
- You miss the point you are making assumptions based on your knowledge and perception of game shows. There is no evidence whatsoever that most of the readers have the same legal background as you have nor do most publications on subject deal with legal restrictions or "gameshow regulations". Basically this boils down to stick to the sources and no speculations by WP-Editors.--Kmhkmh (talk) 17:52, 5 December 2009 (UTC)
- Please see my response above. -- Rick Block (talk) 17:50, 5 December 2009 (UTC)
It is so pervasive, nobody bothered to mention it explicitly as an assumption. Everyone in the US understands this rule of game shows. The idea that one of the contestants on the screen has 'inside' knowledge? Folly. It's in the fine print that runs at the end of each and every episode. And I documented the only known times it improperly happened. This is not my opinion or interpretation. It's a defining characteristic of a game show, without which, it is no longer a game show. Your twisted interpretation more resembles a street hustler with a card table and a deck of cards. Or three shells and a pea, perhaps. Glkanter (talk) 18:11, 5 December 2009 (UTC)
- You make a bold claim (It is so pervasive, nobody bothered to mention it explicitly as an assumption.) without providing any evidence and moreover you miss the point again. The question was not posed to actual game show contestants (being most likely aware of all regulations) but to readers of weekly column and later through various (international) publications to a broader audience. Even if your most likely false claim was true for all readers of Marylin's column, it is certainly not true for the international audiences reading the various publications. I've sampled quite a lot of material on the subject in English and in German and on top of my head i cannot recall any of them mentioning legal restrictions and national game show regulations. In particular the German articles on the subject with a readership definitely being unaware of any such regulations do not mention any legal conditions whatsoever. The 2 cases you've posted above are not in question, however they do not prove your claim. What's in question here is your (false) line of reasoning.--Kmhkmh (talk) 18:35, 5 December 2009 (UTC)
Mediation?
Mathematics is the one area where there will be general agreement amongst those who understand the problem. The arguments are all about questions like: What is the MHP? What is the most notable aspect of the MHP? How should an encyclopedia article be presented? How should we use reliable sources? Which sources are the most reliable?
This list is not intended in any way to be exhaustive it just gives examples of the kind of thing that we are arguing over and both sides claim to have WP policies on their side. Does anyone think that we might benefit from mediation on the policies and principles involved here? Martin Hogbin (talk) 16:53, 5 December 2009 (UTC)
- Yes, I think a good mediator could be helpful in getting this long-festering discussion to converge sensibly. Dicklyon (talk) 17:23, 5 December 2009 (UTC)
- Sounds like a reasonable idea to me. -- Rick Block (talk) 18:23, 5 December 2009 (UTC)
- As a professional mathematician (indeed, a probabilist and statistician) I am excited there is a new serious discussion about what the MHP is all about. The problem with problems which appear mathematical problems, posed by non-mathematicians, is that the mathematician may well discover there are several ways to interpret what the original problem-poser meant. Mathematicians often work backwards. Someone asks a problem. The problem is in fact ambiguous. One discovers a way to disambiguate, which allows a pretty solution. Often, the disambiguation involves making some of the "hints" of the original poser much harder, and ignoring others. I was delighted to discover their are two ways to disambiguate the problem: one is the conditional version, one is the unconditional version. I was also delighted to discover that in order to get "the good solution" to the conditional problem, one needs to demand different conditions, than to get "the good solution" to the unconditional problem. I also discovered a game-theoretic resolution of the problem, and I discovered some more interesting literature, I'll add citations later. Since my own work (on my web page) is not yet converted into a regular mathematical paper, and not yet submitted to, let alone passed by, peer review, I don't suppose wikipedia can or should use my insights, for the time being! But I continue to follow the discussion with great interest and I'll certainly let you all know my five cents worth if I think I have few cents to chuck in. Gill110951 (talk) 15:40, 6 December 2009 (UTC)
- Just looked at the Morgan et al paper. It is published work in a well-known journal (but not a very high status one) and it is 20 years old, and there have been plenty more insights since then. Mathematics is never finished. Mathematicians will go on finding new variants of the problem and hopefully getting new insights about it. Also discussions between mathematicians and non-mathematicians about this particular problem will continue to expose new variants. Great!!! As a mathematician I am not particularly interested in what vos Savant really mean, what she thought was the solution, and whether or not it was correct. There are many nice problems here and many nice solutions. A mathematician's job is to simplify and unify and understand. Often, as I said, working backwards: to which questions is the answer "change doors" the (a) right answer? What I am saying is that the mathematician has somewhat different interests to the encyclopedia compiler. Also since mathematics is in principle more or less verifiable independent of knowing all kinds of facts about the real world, the idea that an encyclopeadia may not contain new results, is crazy. Finding new mathematics results is a creative process, but checking that they are correct is an exercise in logic, not a matter of citing authorities. Especially in this case, since understanding most versions of the MHP will presumably only involve elementary mathematics. I don't care too much about what "authorities" have written about this problem in the past. A mathematician is more convinced by a beautiful and transparent proof, with some new twists, of an a priori surprising result, than by a citation to some dusty printed matter. Gill110951 (talk) 16:27, 6 December 2009 (UTC)
- Finally for today, I actually edited the MHP page including the insights from my own researches from last March. Of course a wikipedia editor is not supposed to write about his or her own research. So you can all edit it all out again, but please think about what I am trying to say first. Maybe you can be convinced by the logic. If so you can decide whether notes for his students and for the many journalists who keep asking again about this problem, on the home page of a well known authority on mathematical statistics, who has been telling his students about MHP for years, is an authoritative enough source for wikipedia. If you like I can post the notes on arXiv.org so they will still be there after I'm retired... And maybe Boris Tsirelson can say if he agrees with my maths. I'll send him an email. Gill110951 (talk) 17:21, 6 December 2009 (UTC)
How about this as a start
Those in favour of change start a separate development article, no doubt based on the current one, that concentrates on the 'simple' problem and convincing explanations. Much of this is already in the current article. This would make clear exactly what changes are being sought. If the pro-changers cannot agree on what changes are wanted then the article stays as it is by default. On the other hand once we have an agreed alternative version, we can seek mediation on how to proceed from there. This will involve questions like: should we have one or two articles? What should they be called? How could the two versions be combined? What order should the sections be in? etc. The advantage of this approach is that it lets the mediator understand what the two sides are after. Martin Hogbin (talk) 12:41, 6 December 2009 (UTC)
- I'm sorry Martin, I think this suggestion just continues the horrid legacy of the 6 years and 9 archives (plus countless other argument and talk pages scattered throughout Wikipedia's servers, plus this HUGE talk page) filibuster engineered by Rick. You can spend all the time and effort you want, then in my opinion, Rick and Nijdam will ultimately exercise some sort of veto power, despite any majority opinion (including respected Mathematics professors) that would otherwise, by Wikipedia standards, be indicative of a clear consensus.
- For example, here's Rick's comment, before he decided to "reword to avoid potential misinterpretation as ownership".
- "(as if by convincing me that their POV is "correct" I would then agree to change the article as they wish)."
- Nijdam seems to think it's his way or the highway. So far, anyways, he's been right.
- No, you've got the attention of the whole Wikipedia Mathematics group. Follow through with gaining the consensus before wasting any more time on sandbox-style editing. Heck, if I recall correctly, there's already a 'new' page prototype somewhere under your own user name. I've contributed to it. And the only issue of contention is 'Is the contestant aware?'. Most everything else looks resolved, to me. Glkanter (talk) 13:10, 6 December 2009 (UTC)
- If not a development version the how about some kind of outline for the proposed article? I am trying to check that we are all after the same thing. Martin Hogbin (talk) 13:36, 6 December 2009 (UTC)
Martin, there's nothing ambiguous here:
Changes suggested by JeffJor, Martin Hogbin, and Glkanter
If you're here because you've been invited to comment, there are ,two,. three (related) suggestions.
- Glkanter's suggestion: Eliminate all 'host behaviour, etc' influenced discussion, save for the Wikipedia minimum necessary references to Morgan and his ilk, as the 'conditional' problem is the converse of "Suppose you are on a game show."
- JeffJor's suggestion: The so-called conditional problem needs to be a separate article, with "conditional" in its title.
- Martin Hogbin's suggestion: This article should concentrate on the unconditional solution with the Morgan's conditional solution in a variations section.
We've been clear and consistent throughout. And the consensus is really already here, save for whatever veto powers exist within Rick and Nijdam. Glkanter (talk) 13:46, 6 December 2009 (UTC)
- 8 to 4 (Henning Makholm's comments clearly indicate he's opposed to this change) with one side arguing a fundamental Wikipedia policy and the other arguing mostly WP:OR is not a consensus, and even if it were it cannot be used as a blank check to violate NPOV. -- Rick Block (talk) 15:30, 6 December 2009 (UTC)
- I wholeheartedly disagree with your characterization of this good faith discussion by many editors. Essentially, you're describing it as 'Good vs Evil', and 8 of us, so far are on the side of Evil. I'm not buying it. I reject your argument prima facie. Just more filibustering on your part. Glkanter (talk) 15:36, 6 December 2009 (UTC)
- Rick, perhaps you could ask Henning to put his name in the appropriate section and sign it.
Outline for an alternative article
This is where I would start, the current contents are given for reference. Martin Hogbin (talk) 16:12, 6 December 2009 (UTC)
Current
- Problem
- Popular solution
- Probabilistic solution
- Sources of confusion
- Aids to understanding
- Why the probability is not 1/2
- Increasing the number of doors
- Simulation
- Variants
- Other host behaviors
- N doors
- Quantum version
- History of the problem
- Bayesian analysis
- See also
- Similar problems
- References
- External links
Proposed
- Problem - Whitaker statement - Sourced unconditional restatement
- Solution - The unconditional solution, from one of many sources - clear diagrams.
- Sources of confusion - Much as it is now
- Aids to understanding
- Why the probability is not 1/2
- Increasing the number of doors
- Simulation
- Conditional Problem - Reasons the problem is strictly conditional.
- Variants
- Morgan Scenario
- N doors
- Quantum version
- History of the problem
- Bayesian analysis
- See also
- Similar problems
- References
- External links
I'd disagree with that. Morgan is not just variant but he explicitly deals with the original problem as well, so do other sources with a conditional problem. The conditional approach is not a different problem as the TOC seems to suggest now(?) but a different perspective or approach to the same (ambiguous) problem. The way you attempt to reframe, that in your table of content is clearly in contradiction to the treatment in various reputable sources and hence in this form nonnegationable. Not to mention it also contracts your own comments on Nijdam's recent posting ("No, your calculation is fine and as I have made clear before I accept that the MHP problem (as defined by the K & W statement in which specific doors are mentioned) is a problem of conditional probability."). If it this is just a case of ambiguous wording (i.e. I'm simply misreading you ) then please correct that before further discussion.--Kmhkmh (talk) 16:28, 6 December 2009 (UTC)
- I did not really expect you to agree as you are one of those who are against change here. This section was for those who want to change the article to check that they are all on the same wavelength. I will respond to your point about Morgan in a new section. Martin Hogbin (talk) 17:03, 6 December 2009 (UTC)
One time, in English please...
Would one of the Morgan supporters, using whichever published source you prefer, please finish this sentence:
Solving the unconditional K & W Monty Hall problem statement is not sufficient, and a conditional problem approach must be utilized due to the instance where the host chooses between 2 goats. Because...[Please continue here].
This is essentially your argument against the three similar proposals, right? Thank you. Glkanter (talk) 19:05, 5 December 2009 (UTC)
- Are you asking why this view should be in the article, or are you asking for an explanation of this view? If the former, see WP:NPOV. If the latter, see Talk:Monty Hall problem/FAQ or the Morgan et al., or Gillman, or Grinstead and Snell references. -- Rick Block (talk) 22:15, 5 December 2009 (UTC)
6 Years and 9 Archives Comes Down To The Definition of a Game Show.
"Suppose you are on a game show..."
That's how both Monty Hall problem statements begin in the article.
Call it whatever you want in Probability Speak, symmetry, indifference, random, unknown, or equal.
In game shows, it is understood that nothing will be communicated about this to the contestant. So he remains blissfully unaware of anything but symmetry, indifference, random, unknown, or equal.
This is not trivial, to be argued or interpreted away, it is the 5th and 6th words of the problem statement. GAME SHOW. Literate people the world over are expected to know and understand what they are watching on TV. It is not this article's responsibility to consider otherwise.
As part of the definition of Game Show, it was unnecessary to state outright as a premise: 'Host will not share location of car with contestant'. Because that's what you claim he 'could', bizarrely, illogically, somehow do.
So, go ahead and argue. Tell me, as always, that I am mis-interpreting, or simply wrong, or whatever. Do me one favor, though. Just tell the truth. Glkanter (talk) 22:27, 5 December 2009 (UTC)
- The explanation is given further up and btw i explained you that already almost half a year ago for the first time.--Kmhkmh (talk) 22:50, 5 December 2009 (UTC)
Why Is Mediation Even Being Considered?
I think a consensus already exists for the proposed changes. Or, it will exist soon enough, when everyone has had the opportunity to comment. Using the 80/20 rule, I figure we've already heard from most everybody that's going to weigh in.
I count:
- 3 editors for maintaining the status quo
- 8 editors who are in agreement with one of the 3 similar suggestions
- 1 editor who's preference is undetermined
- 10 'comments requested' editors who have not commented to date. I understand from my Wikipedia readings that ultimately 'silence implies consent'.
We know unanimity isn't required, or Wikipedia would call it 'Gaining Unanimity' instead of 'Gaining Consensus'. So unanimity isn't our goal. And certainly not going to happen.
And, while voting is improper, *counting* is necessary.
So, which is it:
- 'All editors are equal'
or
- 'All editors are equal, but some editors are more equal than others'?
Glkanter (talk) 14:34, 6 December 2009 (UTC)
- From WP:NPOV: "Neutral point of view" is one of Wikipedia's three core content policies, along with "Verifiability" and "No original research." Jointly, these policies determine the type and quality of material that is acceptable in Wikipedia articles. They should not be interpreted in isolation from one another, and editors should therefore familiarize themselves with all three. The principles upon which these policies are based cannot be superseded by other policies or guidelines, or by editors' consensus. [emphasis added]
- All 4 editors in the minority (Kmhkmh, Nijdam, Henning Makholm, and myself) have directly or indirectly cited this policy as the reason against the changes that have been suggested. I have made this point clear in my comments above and over and over and over and over again in response to your tendentious attempts to introduce this change. Although you know I am an administrator on this site (which means not that my opinion on content issues matters more than any other editor's, but that I am VERY familiar with Wikipedia policies), you apparently do not believe me. The point of mediation would be to bring in an outsider, also familiar with Wikipedia policy, who might help see some middle ground between what we 4 see as a direct violation of Wikipedia policy and the change that you're seeking to make.
- Is that clear? -- Rick Block (talk) 15:19, 6 December 2009 (UTC)
- I would point out first, that you, of all people, invoking Wikipedia's NPOV as a reason to maintain the MHP article is ironic and comedic. There's a consensus that doesn't agree with your interpretation of how to apply WP:NPOV. I see it as just more filibustering by you.
- Are you agreeing the article must be NPOV? If so, please explain how the changes you're seeking comply with this policy. I'm hearing what you're suggesting as "make the article take the POV that Morgan is wrong, or is addressing a different problem". If this is NOT what you mean, please explain what you DO mean. -- Rick Block (talk) 17:52, 6 December 2009 (UTC)
- Of course, NPOV is a requirement. I strongly and vocally for 14 months now have disagree with your assessment that the article currently satisfies WP:NPOV, especially for a Featured Article. I think it's drastically skewed to the conditional solutions, in emphasis, textual amounts, FAQs, additional optional narratives, etc. Doing the reader no good whatsoever. All I've said is give Morgan and his ilk the Wikipedia required reference for having been published. Not elimination, as you've mis-quoted me more than once. How much emphasis they receive remains to be determined by consensus. Glkanter (talk) 20:56, 6 December 2009 (UTC)
Why the Morgan scenario is a variant.
The problem statement in the current article is the unambiguous K&W version. In this, the host is stated to choose randomly when he has a choice of goat doors.
In the Morgan paper the authors assign a parameter q to the probability that the host will choose a specific door if the player has initially chosen the car. It is clearly envisaged that this parameter might have a value other than 1/2, thus Moragn are clearly considering a different scenario from that addressed by this article.
To be specific, Morgan are addressing the case that the car is initially placed randomly but the host is known to choose a goat door non-randomly when the player has initially chosen the car. They do not say this, in fact they say nothing about the initial car placement or the host's policy at the start of the paper. We are left to deduce the problem that they are addressing from the mathematics that they use to solve the problem. The fact that Morgan take the probability of the car initially being behind any given door as 1/3 tells us that they take the car to have been randomly placed at the start. This agrees with the K&W problem statement. The fact that Morgan take the probability that the host will open a specific door when the host has initially chosen a car tells us that the host is assumed to choose non-randomly in this case. This is not in agreement with our K&W problem statement.
The Morgan scenario is therefor a rather bizarre and unrealistic one in which we know that the car was placed randomly by the producer (or his agent) but we know that the host will choose a legal goat door non-randomly. Martin Hogbin (talk) 17:19, 6 December 2009 (UTC)
- Obviously Morgan paper (and other similar treatments) are a generalization of the non ambiguous case and as such can be seen as variant as well. However that does by no means change, that they use their generalization to deal with the non ambiguous case (K&W) too and explicitly state so themselves.
- That aside the attempt to frame the (K&W) formulation as "the" MHP problem is not appropriate either and not in line with sources. (K&W) is the most common approach to remove the ambiguity - not more, not less.--Kmhkmh (talk) 17:35, 6 December 2009 (UTC)
- As I have said before, I am not attempting to frame the K&W formulation as the MHP, others have done this for me, it is the formulation that a consensus of editors decided should represent the problem in this article. I do, in fact, support the K&W statement because it is based on their published and verified view of how most people interpret the problem.
- Morgan's problem statement, on the other hand, is criticised in the very journal in which it is published. Read Seymann's comment. It is about as critical as one can get whilst conforming to the strict protocol required for publication in peer reviewed journal. Why do you think it is there? It is quite unusual to have such a commentary immediately following a published paper
- K&W clearly state the problem that they are addressing, the only way to determine the problem that Morgan address is to work backwards from their calculations.
- Finally, to address a generalisation of a problem is to address a different problem. In Morgan's case it is an incomplete and unrealistic generalisation. Martin Hogbin (talk) 17:59, 6 December 2009 (UTC)
- I don't think the Morgan scenario is bizarre and unrealistic. I don't think the K&W version is a good version. There are different ways to disambiguate the original problem as posed by vos Savant; some are interesting in that they have interesting solutions. Why must we assume that the host chooses his door at uniformly at random, and so on? I think it is interesting that the unconditional problem has got the "paradoxical" (good) solution "always change" under rather weak assumptions: namely that the *player* chooses his initial door at random. He doesn't need to assume anything about the behaviour of the quiz team (where the car is located) nor of the quiz-master. Whatever probabilities are used for the quiz-teams and the hosts choices, the player will definitely win on 2/3 of the time. This is called an equalizer strategy in game-theory - the minimax solution is actually such that it doesn't matter a damn what the other player does, as long as you choose your equalizer strategy. The minimax solution or Nash equilibrium is the solution (which exists if you allow all choices of all parties at all stages to be random) such that for each player, if they use that strategy, they cannot do worse than the "value" of the game. ie if the player uses the solution "initial choice uniformly random, thereafter always switch" he is guaranteed at least a 2/3 (unconditional) chance of winning the car. If the team always locates the car uniformly at random and if the host always uniformly randomly opens a door revealing a goat and not chosen initially by the player, then the TV show is guaranteed at least a 1/3 (unconditional) chance of keeping the car. If either moves away from the minimax strategy, the other could in principle do better (by guessing the strategy of their opponent). So one might suppose that "reasonable" opponents will settle at Nash equilibrium. But why should anyone be reasonable? In practice, the players certainly weren't reasonable. Gill110951 (talk) 17:37, 6 December 2009 (UTC)
- Whether the K&W is a 'good' version is a matter of opinion but it is, according to the most reliable published source on this matter (K&W), the way most people actually interpret the problem.
- The MHP is notable because it is a very simple mathematical puzzle that most people get wrong. That is why there was such a furore about vos Savant's original and correct answer, most people did not believe it. It is the simple non-conditional problem that is notable and it is this that this article should initially address.
- Beyond this there are many ways to complicate the problem and I have no objections to these being discussed after the essential paradox has been dealt with. We can assume that the car is placed non-randomly, the player chooses non-randomly and that the host chooses non-randomly. With no further information, this makes the problem very uninteresting. There is no logical reason to take the host action to be non-random any more than there is to take the producer's initial car placement to be non-random, in reality they were probably both approximately random. We could envisage that the player has studied the history of the show. This would give information equally about the initial car placement and the host policy. There is no special reason to assume the car is placed randomly but host acts non-randomly except that it produces and 'elegant solution'. Martin Hogbin (talk) 18:18, 6 December 2009 (UTC)
- From the rejoinder to vos Savant's reply to the Morgan et al. article: "One of the ideas put forth in our article, and one of the few that directly concerns her responses, is that even if one accepts the restrictions she places on the reader's question, it is still a conditional probability problem. One may argue that the information necessary to use the conditional solution is not available to the player, or that given natural symmetry conditions, the unconditional approach necessarily leads to the same result, but this does not change the aforementioned fact."
- What I'm hearing you suggest is that the article exclude this POV, i.e. that the article should explicitly say (or implicitly imply, by omission) the "basic" MHP is NOT a conditional probability problem. Is that what you mean? -- Rick Block (talk) 19:54, 6 December 2009 (UTC)
- I accept that even with the K&W formulation, the problem is strictly one that requires conditional probability but that is not what makes the problem notable. Despite that fact, there are plenty of sources that treat the problem unconditionally and there are many reasons and justifications for us to do that here which we have been through many times.
- By the Morgan scenario, I mean the (rather unrealistic and somewhat contrived) formulation in which q can be other than 1/2. This clearly is not the K&W formulation that is stated at the start of this article. Thus Morgan address a different and (bizarrely) more general problem. This is what I call the Morgan scenario. Regrettable Morgan do not make clear the problem that they are addressing in their paper. Martin Hogbin (talk) 20:05, 6 December 2009 (UTC)
- Yes, there are plenty of sources that treat the problem unconditionally. But you're ALSO suggesting removing the conditional solution section and treating this as a variant (aren't you?). The article ALREADY leads with an unconditional solution. Excluding the conditional solution, or suggesting it applies only to a "variant" is what I'm objecting to. -- Rick Block (talk) 20:35, 6 December 2009 (UTC)
- Not quite. I suggest that after the unconditional solution we have 'Aids to understanding' and 'Sources of confusion' for the unconditional solution, then a bit to explain that in some formulations even the symmetric version should, strictly speaking, be treated conditionally but this makes no difference to the answer and there are good reasons not to do this. After that I would mention the Morgan scenario in which the host chooses non-randomly making a conditional approach essential. Martin Hogbin (talk) 21:48, 6 December 2009 (UTC)
- And, by doing this, aren't you making the article take the POV that the unconditional solution is complete and correct? YOU think that this is simply the truth, which is your prerogative. However, multiple sources (it's not just Morgan et al.) dispute this and say that the MHP is fundamentally a conditional probability problem, and that the unconditional solutions address a slightly different problem (that being the problem you think IS the MHP, but again this is your view). You want to elevate the unconditional approach to be the primary one, making the article NOT neutral on this issue. -- Rick Block (talk) 22:11, 6 December 2009 (UTC)
- I am making the point that the unconditional approach is the the notable one. If have accepted many times, even today, that for some problem formulations (such as the current K&W) the problem is, strictly speaking, conditional. The article is not currently neutral, it places far too much emphasis on the Morgan paper.
- 'Sources of confusion' and Aids to understanding' clearly belong to the unconditional section. Generally when people get to the stage that they realise that some problem formulations are conditional they are not confused and already understand the problem. Little of the the text in these sections relates to the conditional nature of some problem formulations. Martin Hogbin (talk) 22:36, 6 December 2009 (UTC)
- You say above that K&W is the "most reliable published source" on the matter of how people interpret the problem. From p.5 of the PDF version: "Although, semantically, Door 3 in the standard version is named merely as an example ("Monty Hall opens another door, say, number 3"), most participants take the opening of Door 3 for granted and base their reasoning on this fact. In a pretest we gave participants (N = 40) the standard version [the original Parade version], asking them to illustrate their view of the situation described by drawing a sketch. After excluding four uninterpretable drawings, we saw that 35 out of the remaining 36 (97%) indeed drew an open Door 3, and only a single participant (3%) indicated other constellations also remain possible according to the wording of the standard version. The assumption that only Door 3 will open is further reinforced by the question that follows: "Do you want to switch to Door Number 2?" Note that once formed, this assumption prevents the problem solver from gaining access to the intuitive solution illustrated in Figure 1."
- 97% drew an open Door 3. Are they thinking of the unconditional problem, or the conditional one? What, exactly, is confusing them?
- The unconditional solution is what is generally presented as the answer. But 35 out of 36 of K&W's test subjects try to solve the conditional problem. -- Rick Block (talk) 23:00, 6 December 2009 (UTC)
- What the unconditional solution says is something like: ha ha, the problem tricked you into looking at the problem wrong - what is really being asked isn't the conditional case you're trying to solve but the general chance of winning by switching which any idiot can see is 2/3. What the conditional solution says is: your approach was fine, you just didn't execute it quite right because you forgot that the host opens Door 2 sometimes when the car is behind Door 1. Both approaches are equally valid. That's what it means to be NPOV. -- Rick Block (talk) 00:31, 7 December 2009 (UTC)
- No, you are absolutely wrong about one thing, which is that any idiot can see that the chance of winning by switching for the unconditional case is 2/3. I have never seen that view expressed anywhere else, either here of in the literature. The average punter does not know what conditional and unconditional mean. I agree that the problem that they in fact address, when presented with the Whitaker question, is the problem that is strictly speaking conditional but there is no evidence that they see and understand and attempt to solve it this way. As you say above the unconditional solution is the most common.
- What the unconditional solution says is something like: ha ha, the problem tricked you into looking at the problem wrong - what is really being asked isn't the conditional case you're trying to solve but the general chance of winning by switching which any idiot can see is 2/3. What the conditional solution says is: your approach was fine, you just didn't execute it quite right because you forgot that the host opens Door 2 sometimes when the car is behind Door 1. Both approaches are equally valid. That's what it means to be NPOV. -- Rick Block (talk) 00:31, 7 December 2009 (UTC)
- What we agree on is that the unconditional solution is the most common and notable one. I also agree that, if the problem is presented in a conditional form, the solutions should strictly speaking be conditional, we agree that this is one of the valid points made by the Morgan paper, however the unconditional solution is by far the most notable one and it must be thoroughly addressed and explained in this article, including 'Aids to understanding' and 'Sources of confusion'. That is all that I am asking for. This may not be easy, whilst basing our article on reliable sources, but it is worth a try.Martin Hogbin (talk) 12:29, 7 December 2009 (UTC)
- Sorry - I was specifically talking about popular sources being the ones that are generally presented. The "any idiot" bit was meant to be part of what they say, not something I'm saying (they say any idiot can see that your initial chance of selecting the car is 1/3 so if you don't switch that must be your overall chance of winning). IMO, why people resist this solution is precisely because it violates their (conditional) mental model of what the problem is asking. To thoroughly address and explain this solution, you HAVE to talk about this.
- And, again, by presenting a more or less complete article (many sections) about the "unconditional" solution - in particular presenting a "solution" section that does not include a conditional solution - would make the article take the POV that the unconditional solution is the preferred (or most correct) solution. If you survey the breadth of the literature (not just the popular literature), this is a highly distorted view. -- Rick Block (talk) 14:24, 7 December 2009 (UTC)
Informal mediation requested
I have filed a request with the mediation cabal, see Wikipedia:Mediation Cabal/Cases/2009-12-06/Monty Hall problem. -- Rick Block (talk) 18:20, 6 December 2009 (UTC)
- What is the procedure now? Should we prepare a statement of what we definitely all do agree on? Martin Hogbin (talk) 18:56, 6 December 2009 (UTC)
- This mediation is completely informal and there's no guarantee anyone will accept this case (trying this first is generally a requirement before proceeding to formal mediation handled by the Mediation Committee). For now, I think we continue as best we can. -- Rick Block (talk) 19:17, 6 December 2009 (UTC)
The Mathematics Rule I Am Properly Applying
Way back in junior high, we did some proofs or problems or something to do with absolute values. That's all I can remember.
But the thing I do remember is that after you 'solved' the problem, you had to go back and check each of the results to make sure it didn't violate the original problem statement in some way.
That's all I'm saying about Morgan and the rest. When you check your work with some 'host behaviour' variant, it no longer meets the original problem statement, "Suppose you're on a game show..." Go ahead and argue. Better you should save your breath. Hosts don't tell contestants where the car is.
So, as an encyclopedia, Wikipedia will properly refer to reliably published sources like Morgan. And Devlin. No problem.
But, as a self-appointed 'explainer' of all things MHP, I think the article improperly gives the conditional solutions way too much emphasis. Because it doesn't match the original problem statement any longer. Glkanter (talk) 21:47, 6 December 2009 (UTC)
The Uber Reliably Published Source
Rick, you've used this argument before, and are likely to use it, again, soon.
So, to save us all a lot of time and typing, would you mind explaining why it's Morgan? Glkanter (talk) 00:39, 7 December 2009 (UTC)
Another five cents worth by a mathematician
Right now I agree that the conditional version of the problem is a "minor variant" and that the article should focus on the unconditional version. Here's some explanation for this opinion.
I think that the "nicest problem" is the unconditional problem which is solved by always changing doors, and in order to justify that, all you need is that the initial chance of choosing the good door is 1/3. This could be the case because the player chose a door uniformly at random, or because the quiz-team hid the door uniformly at random. A wise player will not allow the quizteam to fool him so he will choose his door uniformly at random. It's the minimax strategy (guarantees a win probability of 2/3) and even an equalizer strategy (win probability is 2/3 independently of strategy of the quiz team. [all probability statements here are unconditional ones]. I guess that Marilyn meant us to think about the unconditional problem because it is so beautiful, clean, paradoxical. But I haven't looked at all her writings (the obvious thing is to look at her answers, and see what problem she actually solves). This is a question of historical research and proper documentation, nothing wrong with that.
When the [unconditional] problem was first posed to me by my mathematician friend Adrian Baddeley I gave the wrong answer but afterwards could easily be convinced what was the right answer. My mother who is not a mathematician, indeed hardly had any schooling at all, instantly got the right answer by imagining the situation with 100 doors; you have chosen one, the quizmaster opens 98; do you switch? I think only a fool wouldn't.
But people (even Marilyn) feel it necessary to add to the question, "eg if you chose door 1 and the quizmaster opened door 2". This suggests to people who have heard about conditional probability that you ought to look at the conditional problem. Of course, nothing forbids you to study whatever problem you like. Then there is not a unique answer. I can tell you that if the player uses his minimax strategy (choose door at random, always switch) then there are strategies of the quizteam such that for some outcome of the first three moves (quizteam's car location, player's choice, host's choice) the car is certainly behind the player's initial door, for other outcomes of the first three moves the car is certainly behind the other closed door. So the conditional win chances, if your strategy is "switch, irrespective" vary from 0 through to 1. But on average you'll win 2/3 of the time. It's necessary to assume that the quizteam does not hide the car with uniform random chances for this situation to arise. EG the car is always behind door 1. You choose door 1. Quizmaster opens door 2. You switch. You don't get the car.
Things are not quite so bad if we insist that the car is hidden uniformly at random. Then, however you choose your door, and however the host makes his choice, your conditional probability of finding the car behind the other closed door is somewhere between 1/2 and 1. Again (of necessity) it averages out at 2/3.
At least we can say, in this situation it is never (ie, condionally) to your disadvantage to change.
But I repeat that in my opinion a wikipedia article on MHP ought to concentrate on a succinct expose of the unconditional problem, written in terms which will convince the man in the street (by its logic!) as well as satisfy the trained mathematician (who will know how to translate the english sentences into logical statements and mathematical expressions). Make some space for discussing variants.
The beauty of that is that one does not have to look at conditional probabilities, which as I mentioned could be anything, and in order to somehow force them to the nice answer you have to make assumptions about the host's behaviour. Why should you? All we know is that he always asks this question, every show, again and again. Such an article can be short and sweet and no maths elaboration is needed at all.
A section on variants of the problem could discuss the conditional formulation, and various answers to that under various assumptions.
The beauty of the simple unconditional pure MHP is that it is a true good mathematical paradox in the sense that everyone is first fooled but afterwards easily agrees what is the good answer (unless you are lawyers: in a survey at Nijmegen university, it was not possible to convince a lawyer that their initial answer was wrong). A paradox for talking about in the pub or at a party is not good if it requires tables of calculations and mathematical notation. The unconditional version is the version which you can solve by simulation, repeating over and over again (a splendid exercise, which forces one to fix each of the stages of the game). Gill110951 (talk) 04:43, 7 December 2009 (UTC)
- Yes; but also the conditional version can be "solved" by simulation. I always emphasize to students: you cannot enforce a condition to hold, but you can form a sub-sample by postselection! Boris Tsirelson (talk) 06:54, 7 December 2009 (UTC)
- There seems to be a bit of misconception though, if i read Gill's comment correctly. So to be sure here, vos Savant did not pose an (unconditional) problem, but she offered an (correct/reasonable) unconditional solution to a (conditional) problem posed by Whitaker. Moreover the original question goes back to Selvin, who suggested it for a statistical magazine and afaik as a conditional problem or with a conditional solution in mind. So while we can feature the unconditional solution first for its beauty/simplicity/accessibility and given the ambiguity as a perfectly correct solution, we cannot simply declare the problem itself unconditionally per se, since this mathematically speaking not quite true and grossly misrepresenting the bulk of publications/literature on the subject. So while you can argue that conditional perspective is not required, you cannot argue the conditional approach does not address the original problem (i.e. is mere variant). My 2 cents as a Wikipedian and fellow mathematician.--Kmhkmh (talk) 13:10, 7 December 2009 (UTC)
- You have been swayed in your opinion here by Morgan, who tried to take a question from an amateur in a popular general interest magazine to be a formal probability problem statement. What vos Savant did was to use her judgment to answer the question based on her interpretation of the intent of the questioner (as later suggested by Seymann). This is surely the better approach Martin Hogbin (talk) 13:41, 7 December 2009 (UTC)
- No i have not and i have told you so repeatedly in the past. In fact I haven't even read Morgan's paper. However I have read many other publications on the subject in German and English and as I've pointed out several times already almost all of them treat it at least as a conditional problem as well and sometimes as a conditional problem only.--Kmhkmh (talk) 15:00, 7 December 2009 (UTC)
- Or perhaps, Martin has been swayed in his opinion here by vos Savant. The relevant question here is not one of opinions, but about what the literature says. I hear Kmhkmh saying the literature as a whole does not give any preference to the unconditional solution. NPOV says then the article shouldn't either. -- Rick Block (talk) 14:39, 7 December 2009 (UTC)
- I guess his is where the mediation will come in. My opinion, stated many time before, is that Morgan et al. are experts on statistics, thus a paper published by them should be treated as a reliable source in matters of statistical calculation (after all they get most of this right). They have no more right to pontificate as to what 'The Monty Hall Problem' is than the average man in the street and considerably less credibility in this respect than vos Savant, whose job it was to regularly interpret vague questions from the general public. We say at the start of this article that the Monty Hall problem is a probability puzzle, and that is how it should be primarily treated here - as a simple puzzle that most people get wrong. Martin Hogbin (talk) 17:21, 7 December 2009 (UTC)
- You have been swayed in your opinion here by Morgan, who tried to take a question from an amateur in a popular general interest magazine to be a formal probability problem statement. What vos Savant did was to use her judgment to answer the question based on her interpretation of the intent of the questioner (as later suggested by Seymann). This is surely the better approach Martin Hogbin (talk) 13:41, 7 December 2009 (UTC)
Article removed from my watchlist.
This article keeps disappearing from my watchlist. Is anyone else having this problem? Martin Hogbin (talk) 12:48, 7 December 2009 (UTC)
Is This Chronology Correct?
Selvin poses the problem.
- It is solved unconditionally. It is hailed as a great Paradox.
Whitaker poses the problem to vos Savant.
- It is solved unconditionally. It is hailed as a great Paradox.
Morgan 'restates and formalizes' the problem.
- It is solved conditionally, but only if the 'two remaining goat doors' constraint is fixed at 1/2. Otherwise, Morgan offers no solution.
Devlin and others write articles and text books using only the unconditional solution. They make no mention of Morgan or conditionality.
Wikipedia editors decide that the conditional problem is why the MHP is a great paradox.
- The Wikipedia article is written to emphasize the lack of understanding of Probability by those we are satisfied with the unconditional solution.
We argue. Glkanter points out that the universal understanding of a TV game show denies any possibility of the conditional problem statement.
Is this roughly how we got here, today? Glkanter (talk) 14:05, 7 December 2009 (UTC)
- Roughly. But if you try to keep it more accurate, you will do better making your point. Dicklyon (talk) 16:37, 7 December 2009 (UTC)
I see Dick Lyon discusses his numerous edit wars on his user page. I cannot compete with that. What is my best approach to take to return my interpretation of how events happened, which I want to share on this talk page, to it's original form? Thank you. Glkanter (talk) 17:24, 7 December 2009 (UTC)
- Look at this edit summary from Dicklyon:
- (cur) (prev) 11:34, 7 December 2009 Dicklyon (talk | contribs) (792,974 bytes) (Reverted 1 edit by Glkanter; Obviously incorrect, pointy addition, bordering on vandalism. (TW)) (undo)
- I don't deserve that. What, I vandalized a section I just created? Why would someone write that? Glkanter (talk) 17:30, 7 December 2009 (UTC)
Dicklyon, I don't want any trouble. I just want my interpretation of the chronology to be on this talk page. Unedited, but certainly commented on below. So, do you want this section, and I'll start a new one? You want to start a new one, for your interpretation, and I'll fix this one back to my vision? Just let me know. Thanks. Glkanter (talk) 17:47, 7 December 2009 (UTC)
- You can just write a sensible summary instead of interspersing repeated stuff as a roundabout way to make a point. And my user pages doesn't discuss most of my edit wars, just the "dramatic" ones. Dicklyon (talk) 17:50, 7 December 2009 (UTC)
- Dick, deleting material from a talk page is rarely justified and not so in this case. Maybe glkanter could have formatted his contribution better but that is no reason to delete it. It certainly was not vandalism. Martin Hogbin (talk) 18:44, 7 December 2009 (UTC)
- Thanks for that. Despite very strong opinions this discussion has remained completely civil, let us keep it that way. Martin Hogbin (talk) 19:18, 7 December 2009 (UTC)
Well, that's quite a Wikipedia education I was administered today. And I want to give thanks to the man who taught me this lesson, Dicklyon.
Thank you Dicklyon for:
- Vandalizing my edit
- Accusing me of being the vandal (That was outstanding. Really. Not many can pull this one off successfully! Kudos!)
- Calling my personal opinion on a talk page 'obviously incorrect'
- Lecturing me on the proper 'tone' to use on Wikipedia talk pages
- Denying in carefully chosen words that you did any of the above
- Making it necessary for another Wikipedian to defend me. That does wonders for my self esteem.
- Teaching me who the baddest edit warrior on Wikipedia is.
- Giving me permission to return the section I created to it's original status.
- Assuring me that you won't further violate Wikipedia rules regarding my edits in talk pages
- I'm sure there is much more I'm overlooking. I'm only human.
But anyways, an apology is in order to all you Wikipedia editors who were forced to sit through this.
In the spirit of the guy who got shot in the face by VP Dick Cheney, I apologize to Dicklyon for being the recipient of your unprovoked savage violation of my good faith edits to a Wikipedia talk page. Glkanter (talk) 21:49, 7 December 2009 (UTC)
What "the conditional problem" and "the unconditional problem" mean
I wasn't quite sure where to respond, so a started a section.
- There are multiple ways to address any probability problem. If I ask "What is the probability a die rolled a 3, if we know it rolled odd?" we can solve it conditionally or unconditionally. We can say there are six equiprobable outcomes, and the conditional probability is found by P(3|odd)=P(3 and odd)/(P(1)+P(3)+P(5)) = (1/6)/(1/6+1/6+1/6)=1/3, or that there are three equiprobable outcomes that are odd, so P(3)=1/3. The unconditional problem is isomorphic with the conditional one.
- The MHP IS a conditional problem, but depending on how you address it, you can solve an isomorphic unconditional problem in its place. Just like my trivial example. That is not what we want for the so-called "unconditional problem" that the main part of the article should address.
- What we want, is for the contestant to base her decision on P(switch to car|she choose a door and host opened another door) as opposed to P(switch to car|she choose door #1 and host opened door #3). And I worded that carefully, because the first option is EXACTLY what the Whitiker problem statement says, and what K&W admit is the sematic meaning of the statement. We call it "the unconditional problem" because it is not conditioned on knowing how the host treats the doors differently. The doors cannot distinguished from each other in terms how probability applies. That does not mean that they can't be distinguished, it just means it can't be used.
- The question in the classic MHP is "should the contestant switch." We want "the unconditional problem" because we are not told how the host treats the different doors in any statement of the problem that I am aware of. So there is no known source that uses the unique aspects of "the conditional problem" to DIRECTLY answer the MHP. None.
- The two sources that seem to be recognized as starting the "game show" variation of this problem (as opposed to the related and much older "Three Prisoners" problem and Bertrand's Box Paradox), that is to say Steve Selvin's 1975 The American Statistician article and Marilyn vos Savant's Parade article, both used names for the boxes/doors as examples. But neither used those names to treat them differently in the solution. So they are both addressing the unconditional problem. Marilyn vos Savant, at least, has clarified that she intended the the "unconditional" problem.
- There are only two aspects to "the conditional problem." (There are more that are what I call "game protocol," like whether the host always offers a switch. I disregard those, because we have to assume the game protocol is well represented in the problem statement.) There are two random chioces, not one, that are part of the uncertainty in the game and that require assumptions. Not all of the "conditional problem" sources use both (Morgan does not), but those that do universally make the assumptions about the car placement that they eschew for the host's choice. Tat is, they treat it like "the unconditional problem." No conclusions can be drawn, nor HAVE been drawn, about the answer to the full "unconditioanl problem."
- There are, in general, three types of sources for the MHP: (A) Those that address problem from a common-knowledge standpoint, and that universally use "the unconditional problem" WHETHER OR NOT THEY USE CONDITIONAL PROBABILITY in their solution method. (B) Those that address the cognitive issues that cause confusion in people when first presented with the problem, and that emphasize in non-intuitive aaspect of switching to improve probability. This has nothing to do with the "condititional problem." (C) Those that explore it from a more rigorous mathematical viewpoint. Some emphasize either the unconditional, or the conditional. Call them CU and CC. Now, I haven't read all the references, but I did a quick run-down of the ones listed in the article. Of those that I could find quickly, 14 were in category A, 5 in category B, 4 in category CU, and 3 in CC. That shows that most people view the MHP as unconditional problem.
- Nobody is saying to disregard "the conditional problem." It is just a variation. JeffJor (talk) 20:22, 7 December 2009 (UTC)
Well said! Are you a new editor or did you forget to log in? I removed the linefeeds to fix your numbering. Martin Hogbin (talk) 18:40, 7 December 2009 (UTC)
No, I do log in - but somehow in switching windows I keep ending up in a non-logged-in window, and I don't notice that when the edit comes up. JeffJor (talk) 20:22, 7 December 2009 (UTC)
- See also #Formulas, not words above. Boris Tsirelson (talk) 20:29, 7 December 2009 (UTC)
@128.244.9.7:
- I completely agree
- I agree for the most part, however the bold line is a bit iffy. Who is exactly is "we"?
- This is bit iffy. K&W don't admit but assess what the real meaning is according to them, other publications differ on that. Your reading of Whitakers intent is fine, but alas it is only valid option to read the problem. You can also see it as P(switch to car|she choose a door and host opened a particalur door). If you use particular instead of another you end up exactly where Morgan & bulk of mathematical treatments go and you do use the particular door, i.e. doors can be distinguished and used. Note that both version treat door 1 and door 3 as examples.
- Not knowing the host behaviour per se does not mean we can't model it nor that we cannot draw conclusion from it. In fact Morgan & Co argue that no matter what the host behaviour is, you are never worse off by switching.
- Your descripion is not quite correct here. Selvin the mathematician/statistician who coined the problem 15 years before the parade buzz provides a unconditional and conditional solution to it (see Rosenhouse). This btw also defeats a point Martin keeps rising for more than half a year now, i.e. that the problem is essential not a math problem, but the mathematical perspective is just a minor sideshow. If the original problem was posed, solved and named by mathematician in math journal and this is not supposed to to be a math problem, then frankly i don't what is. That vos Savant solved the problem as an unconditional one is fine, however since she did not pose the problem, this tells us nothing of the "real" intent/perspective of the question.
- Here i admit, i'm not quite sure what point you're trying to make. What exactly is the "full unconditional" and to what literature/publications areyou refering for having drawn no conclusion. I assume you are aware that by now almost any recent primer into probability (in various language) contains a conditional treatment of MHP.
- I disagree with your assessment of (B). One thing about conditional probilities is that they are considered "unintuitive", i.e. unintuitive aspects and in particular the handling a posteriori/additional knowledge for reasoning are all about conditional probabilities. As far as (C) goes I don't quite buy your category count at first glance but even if that turns out to be accurate it does match for overall treatment in literature to my experience. As i pointed out already almost any modern probability primer has a conditional approach to the problem.
- yes and no, that depends on reading between the lines and carefully reviewing all the statement made here over time. Also see the recent suggestion by Jeffor and Glkanter, which to some degree you can consider as an attempt to remove the conditional approach from this article. Another thing is here.how you read/use the term variation. In light what else has been said here recently, I'd rather argue if you consider 2 problems to be isomorphic they are the "same".
- One additional reminder: In our attempts to understand/explain to "what was really meant", we easily overlook that as far as WP is concerned (in particular for contentious issues), we are supposed to describe what various reputable sources say and not what we think is right.
- FA-Class Statistics articles
- Mid-importance Statistics articles
- WikiProject Statistics articles
- FA-Class mathematics articles
- Mid-priority mathematics articles
- Wikipedia featured articles
- Featured articles that have appeared on the main page
- Featured articles that have appeared on the main page once
- Old requests for peer review