Equilateral triangle

Equilateral triangle
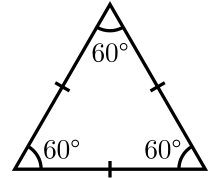Type	Regular polygon
Edges and vertices	3
Schläfli symbol	{3}
Coxeter–Dynkin diagrams
Symmetry group	D3
Area	${\tfrac {\sqrt {3}}{4}}a^{2}$
Internal angle (degrees)	60°

In geometry, an equilateral triangle is a triangle in which all three sides are equal. In traditional or Euclidean geometry, equilateral triangles are also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. They are regular polygons, and can therefore also be referred to as regular triangles.

Principal properties

Assuming the lengths of the sides of the equilateral triangle are a, we can determine using the Pythagorean theorem that:

• The area is $A={\frac {\sqrt {3}}{4}}a^{2}$
• The perimeter is $p=3a\,\!$
• The radius of the circumscribed circle is $R={\frac {\sqrt {3}}{3}}a$
• The radius of the inscribed circle is $r={\frac {\sqrt {3}}{6}}a$
• The geometric center of the triangle is the center of the circumscribed and inscribed circles
• And the altitude (height) from any side is $h={\frac {\sqrt {3}}{2}}a$.

In an equilateral triangle, the altitudes, the angle bisectors, the perpendicular bisectors and the medians to each side coincide.

Characterizations

A triangle ABC that has the sides a, b, c, semiperimeter s, area T, exradii r_a, r_b, r_c (tangent to a, b, c respectively), and where R and r are the radii of the circumcircle and incircle respectively, is equilateral if and only if any one of the statements in the following seven categories is true. These are also properties of an equilateral triangle.

Sides

• $\displaystyle a^{2}+b^{2}+c^{2}=ab+bc+ca.$
• $\displaystyle abc=(a+b-c)(a-b+c)(-a+b+c)\quad {\text{(Lehmus)}}$
• $\displaystyle {\frac {1}{a}}+{\frac {1}{b}}+{\frac {1}{c}}={\frac {\sqrt {25Rr-2r^{2}}}{4Rr}}.$

Semiperimeter

• $\displaystyle s=2R+(3{\sqrt {3}}-4)r\quad {\text{(Blundon)}}$
• $\displaystyle s^{2}=3r^{2}+12Rr.$
• $\displaystyle s^{2}=3{\sqrt {3}}T.$
• $\displaystyle s=3{\sqrt {3}}r$
• $\displaystyle s={\frac {3{\sqrt {3}}}{2}}R$

Angles

• $\displaystyle A=B=C$
• $\displaystyle \cos {A}+\cos {B}+\cos {C}={\frac {3}{2}}$
• $\displaystyle \sin {\frac {A}{2}}\sin {\frac {B}{2}}\sin {\frac {C}{2}}={\frac {1}{8}}.$

Area

• $\displaystyle T={\frac {a^{2}+b^{2}+c^{2}}{4{\sqrt {3}}}}\quad {\text{(Weizenbock)}}$
• $\displaystyle T={\frac {\sqrt {3}}{4}}(abc)^{^{\frac {2}{3}}}.$

Circumradius, inradius and exradii

• $\displaystyle R=2r\quad {\text{(Chapple-Euler)}}$
• $\displaystyle 9R^{2}=a^{2}+b^{2}+c^{2}.$
• $\displaystyle r={\frac {r_{a}+r_{b}+r_{c}}{9}}.$
• $\displaystyle r_{a}=r_{b}=r_{c}.$

Equal cevians

• the three altitudes have equal lengths.
• the three medians have equal lengths.
• the three angle bisectors have equal lengths.

Coincident triangle centers

Every triangle center of an equilateral triangle coincides with its centroid, and for some pairs of triangle centers, the fact that they coincide is enough to ensure that the triangle is equilateral. In particular, a triangle is equilateral if any two of the circumcenter, incenter, centroid, or orthocenter coincide. It is also equilateral if its circumcenter coincides with the Nagel point, or if its incenter coincides with its nine-point center.

Famous theorems

Morley's trisector theorem states that, in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle.

Napoleon's theorem states that, if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, the centers of those equilateral triangles themselves form an equilateral triangle.

A version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral.

Viviani's theorem states that, for any interior point P in an equilateral triangle, with distances d, e, and f from the sides, d + e + f = the altitude of the triangle, independent of the location of P.

Pompeiu's theorem states that, if P is an arbitrary point in an equilateral triangle ABC, then there exists a triangle with sides of length PA, PB, and PC.

Other properties

By Euler's inequality, the equilateral triangle has the smallest ratio R/r of the circumradius to the inradius of any triangle: specifically, R/r = 2.

The triangle of largest area of all those inscribed in a given circle is equilateral; and the triangle of smallest area of all those circumscribed around a given circle is equilateral.

The ratio of the area of the incircle to the area of an equilateral triangle, ${\frac {\pi }{3{\sqrt {3}}}}$, is larger than that of any non-equilateral triangle.

The ratio of the area to the square of the perimeter of an equilateral triangle, ${\frac {1}{12{\sqrt {3}}}},$ is larger than that for any other triangle.

For any point P in the plane, with distances p, q, and t from the vertices A, B, and C respectively,

$\displaystyle 3(p^{4}+q^{4}+t^{4}+a^{4})=(p^{2}+q^{2}+t^{2}+a^{2})^{2}.$

For any point P on the inscribed circle of an equilateral triangle, with distances p, q, and t from the vertices,

$\displaystyle 4(p^{2}+q^{2}+t^{2})=5a^{2}$

and

$\displaystyle 16(p^{4}+q^{4}+t^{4})=11a^{4}.$

For any point P on the minor arc BC of the circumcircle, with distances p, q, and t from A, B, and C respectively,

$\displaystyle p=q+t$

and

$\displaystyle q^{2}+qt+t^{2}=a^{2};$

moreover, if point D on side BC divides PA into segments PD and DA with DA having length z and PD having length y, then

$z={\frac {t^{2}+tq+q^{2}}{t+q}},$

which also equals ${\tfrac {t^{3}-q^{3}}{t^{2}-q^{2}}}$ if t ≠ q; and

${\frac {1}{q}}+{\frac {1}{t}}={\frac {1}{y}}.$

An equilateral triangle is the most symmetrical triangle, having 3 lines of reflection and rotational symmetry of order 3 about its center. Its symmetry group is the dihedral group of order 6 D₃.

Equilateral triangles are the only triangles whose Steiner inellipse is a circle (specifically, it is the incircle).

A regular tetrahedron is made of four equilateral triangles.

Equilateral triangles are found in many other geometric constructs. The intersection of circles whose centers are a radius width apart is a pair of equilateral arches, each of which can be inscribed with an equilateral triangle. They form faces of regular and uniform polyhedra. Three of the five Platonic solids are composed of equilateral triangles. In particular, the regular tetrahedron has four equilateral triangles for faces and can be considered the three dimensional analogue of the shape. The plane can be tiled using equilateral triangles giving the triangular tiling.

Geometric construction

Construction of equilateral triangle with compass and straightedge

An equilateral triangle is easily constructed using a compass. Draw a straight line, and place the point of the compass on one end of the line, and swing an arc from that point to the other point of the line segment. Repeat with the other side of the line. Finally, connect the point where the two arcs intersect with each end of the line segment

Alternate method:

Draw a circle with radius r, place the point of the compass on the circle and draw another circle with the same radius. The two circles will intersect in two points. An equilateral triangle can be constructed by taking the two centers of the circles and either of the points of intersection.

The proof that the resulting figure is an equilateral triangle is the first proposition in Book I of Euclid's Elements.

In culture and society

Equilateral triangles have frequently appeared in man made constructions:

• Some archaeological sites have equilateral triangles as part of their construction, for example Lepenski Vir in Serbia.
• The shape also occurs in modern architecture such as Randhurst Mall and the Jefferson National Expansion Memorial.
• The Flag of the Philippines, the Seal of the President of the Philippines and the Flag of Junqueirópolis contain equilateral triangles.
• It is a shape of a variety of road signs, including the Yield sign.
• Tau Kappa Epsilon a NIC Fraternity uses the equilateral triangle as its primary symbol.

See also

• Almost-equilateral Heronian triangle
• Dragon's Eye (symbol)
• Isoperimetric inequality
• Right triangle
• Trigonometry

External links

• Weisstein, Eric W. "Equilateral Triangle". MathWorld.