Majority judgment: Difference between revisions

Content deleted Content added

Inline

Revision as of 03:08, 5 January 2017

Majority judgment is a single-winner voting system proposed by Michel Balinski and Rida Laraki. Voters freely grade each candidate in one of several named ranks, for instance from "excellent" to "bad", and the candidate with the highest median grade is the winner. If more than one candidate has the same median grade, a tiebreaker is used which sees the "closest to median" grade. Majority judgment can be considered as a form of Bucklin voting which allows equal ranks.

Voting process

Voters are allowed rated ballots, on which they may assign a grade or judgment to each candidate. Balinski and Laraki suggest six grading levels, from "Excellent" to "Reject", as used in some French schools. Multiple candidates may be given the same grade if the voter wants to.

The median grade for each candidate is found, for instance by sorting their list of grades and finding the middle one. If the middle falls between two different grades, the lower of the two is used. The candidate with the highest median grade wins.

If several candidates share the highest median grade, all other candidates are eliminated. Then, one copy of that grade is removed from each remaining candidate's list of grades, and the new median is found, until there is an unambiguous winner. For instance, if candidate X's sorted ratings were ("Good", "Good", "Fair", "Poor"), while candidate Y had ("Excellent", "Fair", "Fair", "Fair"), the rounded medians would both be "Fair". After removing one "Fair" from each list, the new lists are, respectively, ("Good", "Good", "Poor") and ("Excellent", "Fair", "Fair"), so X would win with a recalculated median of "Good". To help communicate how this tiebreaker works, a plus sign or minus sign can be added to the median of each candidate, depending on whether the median would eventually rise or fall if the tiebreaker were applied to them.

Satisfied and failed criteria

Majority judgment voting satisfies the majority criterion for rated ballots, the mutual majority criterion, the monotonicity criterion, and later-no-help. By assuming that ratings are given independently of other candidates, it satisfies the independence of clones criterion and the independence of irrelevant alternatives criterion,^[1] but the latter criterion is incompatible with the majority criterion if voters shift their judgments in order to express their preferences between the available candidates.

Majority judgment fails reversal symmetry, but this is only because of the rounding used. That is, a candidate whose ratings are {fair, fair} will beat a candidate whose ratings are {good, poor} in both directions, because the more variable rating will be rounded down. However, this failure only happens when a candidate's median is perfectly balanced between two scores, which is unlikely in proportion to the number of voters. The probability of this is negligible; it is only a constant factor higher than that of a perfect tie in a two way race, a situation in which any neutral system can fail to have reversal symmetry.

Majority judgment voting fails the Condorcet criterion,^{[note 1]} later-no-harm,^{[note 2]} consistency,^{[note 3]} the Condorcet loser criterion,^{[note 4]} and the participation criterion.^{[note 5]} It also fails the ranked or preferential majority criterion, which is incompatible with the passed criterion independence of irrelevant alternatives.

Claimed resistance to tactical voting

In arguing for majority judgment, Balinski and Laraki (the system's inventors) mathematically proved that this system was the most "strategy-resistant" of any system that satisfies certain criteria considered desirable by the authors. While the definition of "strategy-resistant" used for the proof is not generally shared, their overall case is bolstered by a study they did on simulated elections in which, of the systems that they studied, majority judgment was the system that had its results swayed by strategic voters the least often.

Example application

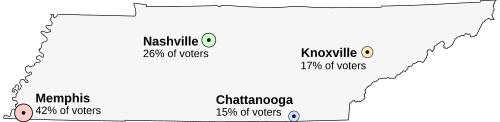
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:

Memphis, the largest city, but far from the others (42% of voters)
Nashville, near the center of the state (26% of voters)
Chattanooga, somewhat east (15% of voters)
Knoxville, far to the northeast (17% of voters)

The preferences of each region's voters are:

42% of voters Far-West	26% of voters Center	15% of voters Center-East	17% of voters Far-East
Memphis Nashville Chattanooga Knoxville	Nashville Chattanooga Knoxville Memphis	Chattanooga Knoxville Nashville Memphis	Knoxville Chattanooga Nashville Memphis

Suppose there were four ratings named "Excellent", "Good", "Fair", and "Poor", and voters assigned their ratings to the four cities by giving their own city the rating "Excellent", the farthest city the rating "Poor" and the other cities "Good", "Fair", or "Poor" depending on whether they are less than a hundred, less than two hundred, or over two hundred miles away:

City Choice	Memphis voters	Nashville voters	Chattanooga voters	Knoxville voters	Median rating^{[note 6]}
Memphis	excellent	poor	poor	poor	poor+
Nashville	fair	excellent	fair	fair	fair+
Chattanooga	poor	fair	excellent	good	fair-
Knoxville	poor	fair	good	excellent	fair-

Then the sorted scores would be as follows:

City

↓

Median point

Nashville

Knoxville

Chattanooga

Memphis

Excellent

Good

Fair

Poor

The median ratings for Nashville, Chattanooga, and Knoxville are all "Fair"; and for Memphis, "Poor". Since there is a tie between Nashville, Chattanooga, and Knoxville, "Fair" ratings are removed from all three, until their medians become different. After removing 16% "Fair" ratings from the votes of each, the sorted ratings are now:

City

↓

Median point

Nashville

Knoxville

Chattanooga

Chattanooga and Knoxville now have the same number of "Poor" ratings as "Fair", "Good" and "Excellent" combined, so their medians are rounded down to "Poor", while Nashville's median remains at "Fair". So Nashville, the capital in real life, wins.

If voters were more strategic, those from Knoxville and Chattanooga might rate Nashville as "Poor" and Chattanooga as "Excellent", in an attempt to make their preferred candidate Chattanooga win. Also, Nashville voters might rate Knoxville as "poor" to distinguish it from Chattanooga. In spite of these attempts at strategy, the winner would still be Nashville.

History

This system has several salient features, none of which is original in itself. First, it is a rated system. Since such systems include approval voting, which has been independently reinvented many times, this aspect is probably the least original. However, voting theory has tended to focus more on ranked systems, so this still distinguishes it from most voting system proposals. Second, it uses words, not numbers, to assign a commonly understood meaning to each rating. Balinski and Laraki insist on the importance of the fact that ratings have a commonly understood absolute meaning, and are not purely relative or strategic. Again, this aspect is unusual but not unheard-of throughout the history of voting. Finally, it uses the median to aggregate ratings. This method was explicitly proposed to assign budgets by Francis Galton in 1907^[2] and was implicitly used in Bucklin voting, a ranked or mixed ranked/rated system used soon thereafter in Progressive era reforms in the United States. Also, hybrid mean/median systems, which throw away a certain predefined number of outliers on each side and then average the remaining scores, have long been used to judge contests such as Olympic figure skating; such systems, like majority judgment, are intended to limit the impact of biased or strategic judges.

The full system of Majority judgment was first proposed by Balinski and Laraki in 2007.^[3] That same year, they used it in an exit poll of French voters in the presidential election. Although this regional poll was not intended to be representative of the national result, it agreed with other local or national experiments in showing that François Bayrou, rather than the eventual runoff winner, Nicolas Sarkozy, or two other candidates (Ségolène Royal or Jean-Marie Le Pen) would have won under most alternative rules, including majority judgment. They also note:

Everyone with some knowledge of French politics who was shown the results with the names of Sarkozy, Royal, Bayrou and Le Pen hidden invariably identiﬁed them: the grades contain meaningful information.^[4]

It has since been used in judging wine competitions and in other political research polling in France and in the US.^[5]

Notes

^ Strategically in the strong Nash equilibrium, MJ passes the Condorcet criterion.
^ MJ provides a weaker guarantee similar to LNH: rating another candidate at or below your preferred winner's median rating (as opposed to one's own rating for the winner) cannot harm the winner.
^ Majority judgment's inventors argue that meaning should be assigned to the absolute rating that the system assigns to a candidate; that if one electorate rates candidate X as "excellent" and Y as "good", while another one ranks X as "fair" and Y as "poor", these two electorates do not in fact agree. Therefore, they define a criterion they call "rating consistency", which majority judgment passes. Balinski and Laraki, "Judge, don't Vote", November 2010
^ Nevertheless, it passes a slightly weakened version, the majority condorcet loser criterion, in which all defeats are by an absolute majority (for instance, if there are not equal rankings).
^ It can fail the participation criterion only when, among other conditions, the new ballot rates both of the candidates in question on the same side of the winning median, and the prior distribution of ratings is more sharply peaked or irregular for one of the candidates.
^ A "+" or "-" is added depending on whether the median would rise or fall if median ratings were removed, as in the tiebreaking procedure.

References

^ Balinski and Laraki, Majority Judgment, p. 217
^ Francis Galton, “One vote, one value,” Letter to the editor, Nature vol. 75, Feb. 28, 1907, p. 414.
^ Balinski M. and R. Laraki (2007) «A theory of measuring, electing and ranking». Proceedings of the National Academy of Sciences USA, vol. 104, no. 21, 8720-8725.
^ Balinski M. and R. Laraki (2007) «Election by Majority Judgment: Experimental Evidence». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2007-28. Chapter in the book: «In Situ and Laboratory Experiments on Electoral Law Reform: French Presidential Elections», Edited by Bernard Dolez, Bernard Grofman and Annie Laurent. Springer, to appear in 2011.
^ Balinski M. and R. Laraki (2010) «Judge: Don't vote». Cahier du Laboratoire d’Econométrie de l’Ecole Polytechnique 2010-27.

@@ Line 168: / Line 168: @@
 == History ==
-This system has several salient features, none of which is original in itself. First, it is a rated system. Since such systems include [[approval voting]], which has been independently reinvented many times, this aspect is probably the least original. However, voting theory has tended to focus more on [[Ranked voting systems|ranked systems]], so this still distinguishes it from most voting system proposals. Second, it uses words, not numbers, to assign a commonly understood meaning to each rating. Balinski and Laraki insist on the importance of the fact that ratings have a commonly understood absolute meaning, and are not purely relative or strategic. Again, this aspect is unusual but not unheard-of throughout the history of voting. Finally, it uses the median to aggregate ratings. This method was explicitly proposed to assign budgets by [[Francis Galton]] in 1907<ref>Francis Galton, “One vote, one value,” Letter to the editor, Nature vol. 75, Feb. 28, 1907, p. 414.</ref> and was implicitly used in [[Bucklin voting]], a ranked or mixed ranked/rated system used soon thereafter in [[Progressive era]] reforms in the United States. Also, hybrid mean/median systems, which throw away a certain predefined number of outliers on each side and then average the remaining scores, have long been used to judge contests such as [[Olympic figure skating]]; such systems, like majority judgment, are intended to limit the impact of biased or strategic judges.
+This system has several salient features, none of which is original in itself. First, it is a [[Cardinal voting systems|rated system]]. Since such systems include [[approval voting]], which has been independently reinvented many times, this aspect is probably the least original. However, voting theory has tended to focus more on [[Ranked voting systems|ranked systems]], so this still distinguishes it from most voting system proposals. Second, it uses words, not numbers, to assign a commonly understood meaning to each rating. Balinski and Laraki insist on the importance of the fact that ratings have a commonly understood absolute meaning, and are not purely relative or strategic. Again, this aspect is unusual but not unheard-of throughout the history of voting. Finally, it uses the median to aggregate ratings. This method was explicitly proposed to assign budgets by [[Francis Galton]] in 1907<ref>Francis Galton, “One vote, one value,” Letter to the editor, Nature vol. 75, Feb. 28, 1907, p. 414.</ref> and was implicitly used in [[Bucklin voting]], a ranked or mixed ranked/rated system used soon thereafter in [[Progressive era]] reforms in the United States. Also, hybrid mean/median systems, which throw away a certain predefined number of outliers on each side and then average the remaining scores, have long been used to judge contests such as [[Olympic figure skating]]; such systems, like majority judgment, are intended to limit the impact of biased or strategic judges.
 The full system of Majority judgment was first proposed by Balinski and Laraki in 2007.<ref>Balinski M. and R. Laraki (2007) «A theory of measuring, electing and ranking». Proceedings of the National Academy of Sciences USA, vol. 104, no. 21, 8720-8725.</ref> That same year, they used it in an exit poll of French voters in the presidential election. Although this regional poll was not intended to be representative of the national result, it agreed with other local or national experiments in showing that [[François Bayrou]], rather than the eventual runoff winner, [[Nicolas Sarkozy]], or two other candidates ([[Ségolène Royal]] or [[Jean-Marie Le Pen]]) would have won under most alternative rules, including majority judgment. They also note: