Ranked pairs: Difference between revisions

Content deleted Content added

Inline

Revision as of 03:21, 5 January 2019

Ranked pairs (RP) or the Tideman method is an electoral system developed in 1987 by Nicolaus Tideman that selects a single winner using votes that express preferences. RP can also be used to create a sorted list of winners.

If there is a candidate who is preferred over the other candidates, when compared in turn with each of the others, RP guarantees that candidate will win. Because of this property, RP is, by definition, a Condorcet method.

Procedure

The RP (Ranked Pair) procedure is as follows:

Tally the vote count comparing each pair of candidates, and determine the winner of each pair (provided there is not a tie)
Sort (rank) each pair, by the largest strength of victory first to smallest last.^{[vs 1]}
"Lock in" each pair, starting with the one with the largest number of winning votes, and add one in turn to a graph as long as they do not create a cycle (which would create an ambiguity). The completed graph shows the winner.

RP can also be used to create a sorted list of preferred candidates. To create a sorted list, repeatedly use RP to select a winner, remove that winner from the list of candidates, and repeat (to find the next runner up, and so forth).

Tally

To tally the votes, consider each voter's preferences. For example, if a voter states "A > B > C" (A is better than B, and B is better than C), the tally should add one for A in A vs. B, one for A in A vs. C, and one for B in B vs. C. Voters may also express indifference (e.g., A = B), and unstated candidates are assumed to be equal to the stated candidates.

Once tallied the majorities can be determined. If "Vxy" is the number of Votes that rank x over y, then "x" wins if Vxy > Vyx, and "y" wins if Vyx > Vxy.

Sort

The pairs of winners, called the "majorities", are then sorted from the largest majority to the smallest majority. A majority for x over y precedes a majority for z over w if and only if one of the following conditions holds:

Vxy > Vzw. In other words, the majority having more support for its alternative is ranked first.
Vxy = Vzw and Vwz > Vyx. Where the majorities are equal, the majority with the smaller minority opposition is ranked first.^{[vs 1]}

Lock

The next step is to examine each pair in turn to determine the pairs to "lock in". This can be visualized by drawing an arrow from the pair's winner to the pair's loser in a directed graph. Using the sorted list above, lock in each pair in turn unless the pair will create a circularity in the graph (for example, where A is more than B, B is more than C, but C is more than A).

Winner

In the resulting graph, the source corresponds to the winner. A source is bound to exist because the graph is a directed acyclic graph by construction, and such graphs always have sources. In the absence of pairwise ties, the source is also unique (because whenever two nodes appear as sources, there would be no valid reason not to connect them, leaving only one of them as a source).

An example

The situation

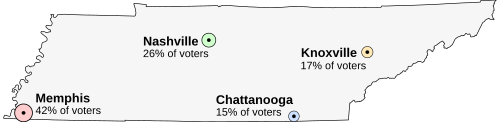
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:

Memphis, the largest city, but far from the others (42% of voters)
Nashville, near the center of the state (26% of voters)
Chattanooga, somewhat east (15% of voters)
Knoxville, far to the northeast (17% of voters)

The preferences of each region's voters are:

42% of voters Far-West	26% of voters Center	15% of voters Center-East	17% of voters Far-East
Memphis Nashville Chattanooga Knoxville	Nashville Chattanooga Knoxville Memphis	Chattanooga Knoxville Nashville Memphis	Knoxville Chattanooga Nashville Memphis

The results would be tabulated as follows:

Pairwise election results
		A
		Memphis	Nashville	Chattanooga	Knoxville
B	Memphis		[A] 58% [B] 42%	[A] 58% [B] 42%	[A] 58% [B] 42%
	Nashville	[A] 42% [B] 58%		[A] 32% [B] 68%	[A] 32% [B] 68%
	Chattanooga	[A] 42% [B] 58%	[A] 68% [B] 32%		[A] 17% [B] 83%
	Knoxville	[A] 42% [B] 58%	[A] 68% [B] 32%	[A] 83% [B] 17%
Pairwise election results (won-lost-tied):		0-3-0	3-0-0	2-1-0	1-2-0
Votes against in worst pairwise defeat:		58%	N/A	68%	83%

[A] indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
[B] indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption

Tally

First, list every pair, and determine the winner:

Pair	Winner
Memphis (42%) vs. Nashville (58%)	Nashville 58%
Memphis (42%) vs. Chattanooga (58%)	Chattanooga 58%
Memphis (42%) vs. Knoxville (58%)	Knoxville 58%
Nashville (68%) vs. Chattanooga (32%)	Nashville 68%
Nashville (68%) vs. Knoxville (32%)	Nashville 68%
Chattanooga (83%) vs. Knoxville (17%)	Chattanooga: 83%

Note that absolute counts of votes can be used, or percentages of the total number of votes; it makes no difference since it is the ratio of votes between two candidates that matters.

Sort

The votes are then sorted. The largest majority is "Chattanooga over Knoxville"; 83% of the voters prefer Chattanooga. Nashville (68%) beats both Chattanooga and Knoxville by a score of 68% over 32% (a tie, unlikely in real life for this many voters). Since Chattanooga > Knoxville, and they are the losers, Nashville vs. Knoxville will be added first, followed by Nashville vs. Chattanooga.

Thus, the pairs from above would be sorted this way:

Pair	Winner
Chattanooga (83%) vs. Knoxville (17%)	Chattanooga 83%
Nashville (68%) vs. Knoxville (32%)	Nashville 68%
Nashville (68%) vs. Chattanooga (32%)	Nashville 68%
Memphis (42%) vs. Nashville (58%)	Nashville 58%
Memphis (42%) vs. Chattanooga (58%)	Chattanooga 58%
Memphis (42%) vs. Knoxville (58%)	Knoxville 58%

Lock

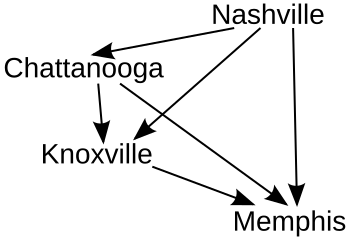
The pairs are then locked in order, skipping any pairs that would create a cycle:

Lock Chattanooga over Knoxville.
Lock Nashville over Knoxville.
Lock Nashville over Chattanooga.
Lock Nashville over Memphis.
Lock Chattanooga over Memphis.
Lock Knoxville over Memphis.

In this case, no cycles are created by any of the pairs, so every single one is locked in.

Every "lock in" would add another arrow to the graph showing the relationship between the candidates. Here is the final graph (where arrows point away from the winner).

In this example, Nashville is the winner using RP, followed by Chattanooga, Knoxville, and Memphis in second, third, and fourth places respectively.

Ambiguity resolution example

For a simple situation involving candidates A, B, and C.

A > B: 68%
B > C: 72%
C > A: 52%

In this situation we "lock in" the majorities starting with the greatest one first.

Lock B > C
Lock A > B
C > A is ignored as it creates an ambiguity or cycle.

Therefore, A is the winner.

Summary

In the example election, the winner is Nashville. This would be true for any Condorcet method.

Using the First-past-the-post voting and some other systems, Memphis would have won the election by having the most people, even though Nashville won every simulated pairwise election outright. Using Instant-runoff voting in this example would result in Knoxville winning even though more people preferred Nashville over Knoxville.

Criteria

Of the formal voting criteria, the ranked pairs method passes the majority criterion, the monotonicity criterion, the Smith criterion (which implies the Condorcet criterion), the Condorcet loser criterion, and the independence of clones criterion. Ranked pairs fails the consistency criterion and the participation criterion. While ranked pairs is not fully independent of irrelevant alternatives, it still satisfies local independence of irrelevant alternatives.

Independence of irrelevant alternatives

Ranked pairs fails independence of irrelevant alternatives. However, the method adheres to a less strict property, sometimes called independence of Smith-dominated alternatives (ISDA). It says that if one candidate (X) wins an election, and a new alternative (Y) is added, X will win the election if Y is not in the Smith set. ISDA implies the Condorcet criterion.

Comparison table

The following table compares Ranked Pairs with other preferential single-winner election methods:

Comparison of single-winner voting systems
Criterion Method	Majority	Majority loser	Mutual majority	Condorcet winner^{[Tn 1]}	Condorcet loser	Smith^{[Tn 1]}	Smith-IIA^{[Tn 1]}	IIA/LIIA^{[Tn 1]}	Cloneproof	Monotone	Participation	Later-no-harm^{[Tn 1]}	Later-no-help^{[Tn 1]}	No favorite betrayal^{[Tn 1]}	Ballot type
Anti-plurality	No	Yes	No	No	No	No	No	No	No	Yes	Yes	No	No	Yes	Single mark
Approval	Yes	No	No	No	No	No	No	Yes^{[Tn 2]}	Yes	Yes	Yes	No	Yes	Yes	Approvals
Baldwin	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	No	No	No	No	No	Ranking
Black	Yes	Yes	No	Yes	Yes	No	No	No	No	Yes	No	No	No	No	Ranking
Borda	No	Yes	No	No	Yes	No	No	No	No	Yes	Yes	No	Yes	No	Ranking
Bucklin	Yes	Yes	Yes	No	No	No	No	No	No	Yes	No	No	Yes	No	Ranking
Coombs	Yes	Yes	Yes	No	Yes	No	No	No	No	No	No	No	No	Yes	Ranking
Copeland	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	No	Yes	No	No	No	No	Ranking
Dodgson	Yes	No	No	Yes	No	No	No	No	No	No	No	No	No	No	Ranking
Highest median	Yes	Yes^{[Tn 3]}	No^{[Tn 4]}	No	No	No	No	Yes^{[Tn 2]}	Yes	Yes	No^{[Tn 5]}	No	Yes	Yes	Scores
Instant-runoff	Yes	Yes	Yes	No	Yes	No	No	No	Yes	No	No	Yes	Yes	No	Ranking
Kemeny–Young	Yes	Yes	Yes	Yes	Yes	Yes	Yes	LIIA Only	No	Yes	No	No	No	No	Ranking
Minimax	Yes	No	No	Yes^{[Tn 6]}	No	No	No	No	No	Yes	No	No^{[Tn 6]}	No	No	Ranking
Nanson	Yes	Yes	Yes	Yes	Yes	Yes	No	No	No	No	No	No	No	No	Ranking
Plurality	Yes	No	No	No	No	No	No	No	No	Yes	Yes	Yes	Yes	No	Single mark
Random ballot^{[Tn 7]}	No	No	No	No	No	No	No	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Single mark
Ranked pairs	Yes	Yes	Yes	Yes	Yes	Yes	Yes	LIIA Only	Yes	Yes	No^{[Tn 5]}	No	No	No	Ranking
Runoff	Yes	Yes	No	No	Yes	No	No	No	No	No	No	Yes	Yes	No	Single mark
Schulze	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	Yes	Yes	No^{[Tn 5]}	No	No	No	Ranking
Score	No	No	No	No	No	No	No	Yes^{[Tn 2]}	Yes	Yes	Yes	No	Yes	Yes	Scores
Sortition^{[Tn 8]}	No	No	No	No	No	No	No	Yes	No	Yes	Yes	Yes	Yes	Yes	None
STAR	No	Yes	No	No	Yes	No	No	No	No	Yes	No	No	No	No	Scores
Tideman alternative	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No	Yes	No	No	No	No	No	Ranking
Table Notes	^ ^a ^b ^c ^d ^e ^f ^g Condorcet's criterion is incompatible with the consistency, participation, later-no-harm, later-no-help, and sincere favorite criteria. ^ ^a ^b ^c Approval voting, score voting, and majority judgment satisfy IIA if it is assumed that voters rate candidates independently using their own absolute scale. For this to hold, in some elections, some voters must use less than their full voting power despite having meaningful preferences among viable candidates. ^ Majority Judgment may elect a candidate uniquely least-preferred by over half of voters, but it never elects the candidate uniquely bottom-rated by over half of voters. ^ Majority Judgment fails the mutual majority criterion, but satisfies the criterion if the majority ranks the mutually favored set above a given absolute grade and all others below that grade. ^ ^a ^b ^c In Highest median, Ranked Pairs, and Schulze voting, there is always a regret-free, semi-honest ballot for any voter, holding all other ballots constant and assuming they know enough about how others will vote. Under such circumstances, there is always at least one way for a voter to participate without grading any less-preferred candidate above any more-preferred one. ^ ^a ^b A variant of Minimax that counts only pairwise opposition, not opposition minus support, fails the Condorcet criterion and meets later-no-harm. ^ A randomly chosen ballot determines winner. This and closely related methods are of mathematical interest and included here to demonstrate that even unreasonable methods can pass voting method criteria. ^ Where a winner is randomly chosen from the candidates, sortition is included to demonstrate that even non-voting methods can pass some criteria.

References

^ ^a ^b In fact, there are different ways how the strength of a victory is measured. The approach used in this article is called winning votes. Another common approach also used by Tideman defining the ranked pairs method in 1987 is the variant using margins of a victory. The margin of victory, also called "defeat strength", is the difference of the number of votes of the two compared candidates.

Tideman, T.N. (1987) Independence of clones as a criterion for voting rules. Social Choice and Welfare 4: 185-206.

External links

Descriptions of ranked-ballot voting methods by Rob LeGrand
Example JS implementation by Asaf Haddad
Pair Ranking Ruby Gem by Bala Paranj
A margin-based PHP Implementation of Tideman's Ranked Pairs

[condorcet-iia-incompatibility-2] ^ ^a ^b ^c ^d ^e ^f ^g Condorcet's criterion is incompatible with the consistency, participation, later-no-harm, later-no-help, and sincere favorite criteria.

[IIA_rating_methods-3] Approval voting, score voting, and majority judgment satisfy IIA if it is assumed that voters rate candidates independently using their own absolute scale. For this to hold, in some elections, some voters must use less than their full voting power despite having meaningful preferences among viable candidates.

[4] Majority Judgment may elect a candidate uniquely least-preferred by over half of voters, but it never elects the candidate uniquely bottom-rated by over half of voters.

[mjmmc-5] Majority Judgment fails the mutual majority criterion, but satisfies the criterion if the majority ranks the mutually favored set above a given absolute grade and all others below that grade.

[semipc-6] In Highest median, Ranked Pairs, and Schulze voting, there is always a regret-free, semi-honest ballot for any voter, holding all other ballots constant and assuming they know enough about how others will vote. Under such circumstances, there is always at least one way for a voter to participate without grading any less-preferred candidate above any more-preferred one.

[MinimaxVarient-7] A variant of Minimax that counts only pairwise opposition, not opposition minus support, fails the Condorcet criterion and meets later-no-harm.

[8] A randomly chosen ballot determines winner. This and closely related methods are of mathematical interest and included here to demonstrate that even unreasonable methods can pass voting method criteria.

[9] Where a winner is randomly chosen from the candidates, sortition is included to demonstrate that even non-voting methods can pass some criteria.

[victorystrength-1] In fact, there are different ways how the strength of a victory is measured. The approach used in this article is called winning votes. Another common approach also used by Tideman defining the ranked pairs method in 1987 is the variant using margins of a victory. The margin of victory, also called "defeat strength", is the difference of the number of votes of the two compared candidates.

[vs 1]

[Tn 1]

[Tn 2]

[Tn 3]

[Tn 4]

[Tn 5]

[Tn 6]

[Tn 7]

[Tn 8]

@@ Line 12: / Line 12: @@
 The RP (Ranked Pair) procedure is as follows:
 # Tally the vote count comparing each pair of candidates, and determine the winner of each pair (provided there is not a tie)
+# Sort (rank) each pair, by the largest strength of victory first to smallest last.<ref group=vs name=victorystrength>In fact, there are different ways how the [[Minimax Condorcet#Variants of the pairwise score|''strength of a victory'']] is measured. The approach used in this article is called '''winning votes'''. Another common approach also used by Tideman defining the ranked pairs method in 1987 is the variant using '''margins''' of a victory. The margin of victory, also called "defeat strength", is the difference of the number of votes of the two compared candidates.</ref>
-# Sort (rank) each pair, by the largest strength of victory first to smallest last.
 # "Lock in" each pair, starting with the one with the largest number of winning votes, and add one in turn to a graph as long as they do not create a [[Cycle (graph theory)|cycle]] (which would create an ambiguity). The completed graph shows the winner.
@@ Line 40: / Line 40: @@
 #Vxy &gt; Vzw. In other words, the majority having more support for its alternative is ranked first.
-#Vxy = Vzw and Vwz &gt; Vyx. Where the majorities are equal, the majority with the smaller minority opposition is ranked first.<ref group=vs name=victorystrength>In fact, there are different ways how the [[Minimax Condorcet#Variants of the pairwise score|''strength of a victory'']] is measured. The approach used in this article is called ''winning votes''. Another common approach also used by Tideman defining the ranked pairs method in 1987 is the variant using ''margins'' of a victory.</ref>
+#Vxy = Vzw and Vwz &gt; Vyx. Where the majorities are equal, the majority with the smaller minority opposition is ranked first.<ref group=vs name=victorystrength></ref>
 === Lock ===