AC power

This article is about power in AC systems. For information on utility-supplied AC power, see Mains electricity. For pulsating current in negative and positive, see Alternating current.

The blinking of non-incandescent city lights is shown in this motion-blurred long exposure. The AC nature of the mains power is revealed by the dashed appearance of the traces of moving lights.

Instantaneous power in an electric circuit is the rate of flow of energy past a given point of the circuit. In alternating current circuits, energy storage elements such as inductors and capacitors may result in periodic reversals of the direction of energy flow.

The portion of instantaneous power that, averaged over a complete cycle of the AC waveform, results in net transfer of energy in one direction is known as active power (more commonly called real power to avoid ambiguity especially in discussions of loads with non-sinusoidal currents). The portion of instantaneous power that results in no net transfer of energy but instead oscillates between the source and load in each cycle due to stored energy, is known as instantaneous reactive power, and its amplitude is the absolute value of reactive power.

Active, reactive, and apparent power in sinusoidal steady-state

In a simple alternating current (AC) circuit consisting of a sinusoidal source and a linear time-invariant load, both the current and voltage are sinusoidal. If the load is purely resistive, the two quantities reverse their polarity at the same time. At every instant the product of voltage and current is positive or zero, the result being that the direction of energy flow does not reverse. In this case, only active power is transferred.

If the load is purely reactive, then the voltage and current are 90 degrees out of phase. For two quarters of each cycle, the product of voltage and current is positive, but for the other two quarters, the product is negative, indicating that on average, exactly as much energy flows into the load as flows back out. There is no net energy flow over each half cycle. In this case, only reactive power flows: There is no net transfer of energy to the load; however, electrical power does flow along the wires and returns by flowing in reverse along the same wires. The current required for this reactive power flow dissipates energy in the line resistance, even if the ideal load device consumes no energy itself. Practical loads have resistance as well as inductance, or capacitance, so both active and reactive powers will flow to normal loads.

Apparent power is the product of the RMS values of voltage and current. Apparent power is taken into account when designing and operating power systems, because although the current associated with reactive power does no work at the load, it still must be supplied by the power source. Conductors, transformers and generators must be sized to carry the total current, not just the current that does useful work. Failure to provide for the supply of sufficient reactive power in electrical grids can lead to lowered voltage levels and, under certain operating conditions, to the complete collapse of the network or blackout. Another consequence is that adding the apparent power for two loads will not accurately give the total power unless they have the same phase difference between current and voltage (the same power factor).

Conventionally, capacitors are treated as if they generate reactive power, and inductors are treated as if they consume it. If a capacitor and an inductor are placed in parallel, then the currents flowing through the capacitor and the inductor tend to cancel rather than add. This is the fundamental mechanism for controlling the power factor in electric power transmission; capacitors (or inductors) are inserted in a circuit to partially compensate for reactive power 'consumed' ('generated') by the load. Purely capacitive circuits supply reactive power with the current waveform leading the voltage waveform by 90 degrees, while purely inductive circuits absorb reactive power with the current waveform lagging the voltage waveform by 90 degrees. The result of this is that capacitive and inductive circuit elements tend to cancel each other out.

The Power Triangle
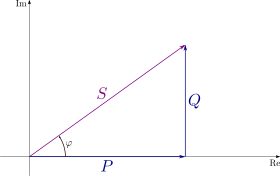
The complex power is the vector sum of active and reactive power. The apparent power is the magnitude of the complex power.
  Active power, $P$
  Reactive power, $Q$
  Complex power, $S$
  Apparent power, $|S|$
  Phase of voltage relative to current, $\varphi$

Engineers use the following terms to describe energy flow in a system (and assign each of them a different unit to differentiate between them):

• Active power, $P$, or real power: watt (W);
• Reactive power, $Q$: volt-ampere reactive (var);
• Complex power, $S$: volt-ampere (VA);
• Apparent power, $|S|$: the magnitude of complex power S: volt-ampere (VA);
• Phase of voltage relative to current, $\varphi$: the angle of difference (in degrees) between current and voltage; $\varphi =\arg(V)-\arg(I)$. Current lagging voltage (quadrant I vector), current leading voltage (quadrant IV vector).

These are all denoted in the adjacent diagram (called a Power Triangle).

In the diagram, $P$ is the active power, $Q$ is the reactive power (in this case positive), $S$ is the complex power and the length of $S$ is the apparent power. Reactive power does not do any net work, so it is represented as the imaginary axis of the vector diagram. Active power does do net work, so it is the real axis.

The unit for power is the watt (symbol: W). Apparent power is often expressed in volt-amperes (VA) since it is the product of RMS voltage and RMS current. The unit for reactive power is var, which stands for volt-ampere reactive. Since reactive power transfers no net energy to the load, it is sometimes called "wattless" power. It does, however, serve an important function in electrical grids and its lack has been cited as a significant factor in the Northeast Blackout of 2003. Understanding the relationship among these three quantities lies at the heart of understanding power engineering. The mathematical relationship among them can be represented by vectors or expressed using complex numbers, $S=P+j\,Q$ (where $j$ is the imaginary unit).

Being pedantic, the phrases flow of current and current flow are redundant because (instantaneous) current is already defined as a flow (of charges). Similarly, the phrases flow of power and power flow are also redundant, since (instantaneous) power is already defined as a flow (of energy).

Calculations and equations

In this section the following terminology is used.

• AC steady-state, as opposed to DC steady-state (constant instantaneous voltages and currents), means the instantaneous voltages and currents are periodic, whether sinusoidal (without harmonics) or non-sinusoidal (with harmonics).
  • Sinusoidal steady-state means the instantaneous voltages and currents are sinusoidal with the same fundamental frequency and without DC offset. In this case, the instantaneous voltage across the two-terminal device or network is $v(t)=|V_{\text{rms}}|{\sqrt {2}}\cos {(\omega t+\varphi _{v})}$ and the instantaneous conventional current through the two-terminal device or network is $i(t)=|I_{\text{rms}}|{\sqrt {2}}\cos {(\omega t+\varphi _{i})}$.
  • Non-sinusoidal steady-state means the rest of cases, e.g. the instantaneous voltages and current aren't both sinusoidal, or are both sinusoidal but with different fundamental frequencies. In non-sinusoidal steady-state at the same fundamental frequency, from Fourier series, the instantaneous voltage is $v(t)=V_{0}+{\sqrt {2}}\displaystyle \sum _{n=1}^{\infty }|V_{n,{\text{rms}}}|\cos {(n\omega _{0}t-\varphi _{v,n})}$, and the instantaneous current is $i(t)=I_{0}+{\sqrt {2}}\displaystyle \sum _{m=1}^{\infty }|I_{m,{\text{rms}}}|\cos {(m\omega _{0}t-\varphi _{i,m})}$.

An example in which sinusoidal steady-state occurs is when a linear time-invariant (LTI) two-terminal network is driven by a sinusoidal voltage and we wait until steady-state is reached. An example in which non-sinusoidal steady-state at the same fundamental frequencies occurs is when a linear time-invariant two-terminal network is driven by a periodic non-sinusoidal voltage and we wait until steady-state is reached. An example in which non-sinusoidal steady-state at different fundamental frequencies occurs is when a non-LTI two-terminal network (i.e. a network that isn't both linear and time-invariant, either because it is non-linear and/or because it is time-variant) is driven by a sinusoidal voltage and we wait until steady-state is reached.

• From the point of view of electric circuit analysis/theory, device, component, element and load are synonyms, since all of them may be conceived as black boxed whose voltage-current characteristics is only relevant.
• An electric network is a device itself or an interconnection of two or more devices. An electric circuit is a network with at least one closed path. All circuits are networks, but not all networks are also circuits.

The equations for different quantities (instantaneous power, average power, active or real power, apparent power, power factor, reactive or quadrature power, complex power, etc.) may be classified depending on the network under consideration and the conditions in which it is operating, similar to the IEEE standard 1459-2010:

• Single-phase power systems:
  • Single-phase (two-terminal) device or network operating in sinusoidal steady-state.
  • Single-phase (two-terminal) device or network operating in non-sinusoidal steady-state.
• Three-phase power systems:
  • Three-phase (three- or four-terminal) device or network operating in sinusoidal steady-state in balanced conditions.
  • Three-phase (three- or four-terminal) device or network operating in sinusoidal steady-state in unbalanced conditions.
  • Three-phase (three- or four-terminal) device or network operating in non-sinusoidal steady-state in balanced conditions.
  • Three-phase (three- or four-terminal) device or network operating in non-sinusoidal steady-state in unbalanced conditions.

Instantaneous power

The instantaneous power (in units of watts or joules per second, W = J/s) of a two-terminal device or network is defined as the time rate at which energy is being transferred or flowing or at which work is being done:

$p(t)={\frac {\mathrm {d} w(t)}{\mathrm {d} t}}$.

From the chain rule, the instantaneous power can be computed also as the product of the instantaneous voltage $v(t)$ across the device or network and the instantaneous conventional current $i(t)$ through it (i.e. the time-varying voltage and current waveforms):

$p(t)=v(t)\,i(t)$.

If the reference polarity of the voltage and the reference direction of the current satisfy the passive sign convention (i.e. if the arrowhead of the currents points towards the device into the positive reference terminal), then the previous expression yields the instantaneous power delivered to (or consumed or absorbed by) the two-terminal device or network under discussion from an external network connected to its terminals. This expression is useful because it applies to all waveforms, whether they are sinusoidal or not, even if they are not periodic. This is particularly useful in power electronics, where non-sinusoidal waveforms are common.

More generally, it can be proven the (total) instantaneous power consumed by an isolated (without energy coupling with any other physical system) $n$-terminal device or network is:

$p(t)=\sum _{k=1}^{n-1}v_{k}(t)\,i_{k}(t)$,

where the instantaneous voltages $v_{k}(t)$ are measured at each terminal of the device or network with respect to one common terminal, and the reference direction of the instantaneous conventional currents $i_{k}(t)$ point towards the device or network under consideration; the current of the common terminal is not used in the previous equation.

For example, if at some instant in time the instantaneous power of a two-terminal device or network (linear or non-linear, time-invariant or time-variant, passive or active, in transient or steady-state without or with harmonics) is +10 W and the passive sign convention is satisfied, it means that, at that instant, (the total) energy is being transferred from the external network (or source) to the device (or load) under consideration at a rate of 10 J each second. If at some other moment the instantaneous power of the same device is -15 W, it means that, at that moment, the total energy is being transferred from the device (or load) under consideration to the external network (or source) at a rate of 15 J/s.

Instantaneous power, instantaneous active power and instantaneous reactive power in sinusoidal steady-state

In the particular case where the instantaneous voltage and current are both sinusoidal of same frequency with no DC offset (e.g. in sinusoidal steady-state), the instantaneous power of a two-terminal device or network simplifies to:

${\begin{aligned}p(t)&=\underbrace {[|V_{\text{RMS}}|\,|I_{\text{RMS}}|\cos {(\varphi _{v}-\varphi _{i})}]} _{\text{DC component}}+\underbrace {[|V_{\text{RMS}}|\,|I_{\text{RMS}}|\cos {(2\omega t+\varphi _{v}+\varphi _{i})}]} _{\text{AC component}}\\&=\underbrace {[|V_{\text{RMS}}|\,|I_{\text{RMS}}|\cos {(\varphi _{v}-\varphi _{i})}]} _{\text{unidirectional}}+\underbrace {[|V_{\text{RMS}}|\,|I_{\text{RMS}}|\cos {(\varphi _{v}+\varphi _{i})}\cos {(2\omega t)}]-[|V_{\text{RMS}}|\,|I_{\text{RMS}}|\sin {(\varphi _{v}+\varphi _{i})}\sin {(2\omega t)}]} _{\text{bidirectional}}\end{aligned}}$

where $\varphi _{v}$ and $\varphi _{i}$ are respectively the phase angle of the instantaneous (or phasor) voltage and current (in units of degrees or radians) using the cosine function, $\omega$ is the fundamental angular frequency (in units of radians per second, rad/s) of the instantaneous voltage and current, and $\varphi =\varphi _{v}-\varphi _{i}$ is the power factor angle of the device or network. The first line of the previous equation shows the instantaneous power has a fundamental frequency (both angular and cyclic) that is twice that of the instantaneous voltage and current, and so its fundamental period is half that of the instantaneous voltage and current. If the voltage is chosen as angular reference ($\varphi _{v}=0^{\circ }$), the previous equation simplifies to:

$p(t)=\underbrace {[P(1+\cos {(2\omega t)})]} _{\text{unidirectional}}+\underbrace {[Q\sin {(2\omega t)}]} _{\text{bidirectional}}$

whilst if the current is chosen as angular reference ($\varphi _{i}=0^{\circ }$), the second previous equation simplifies to:

$p(t)=\underbrace {[P(1+\cos {(2\omega t)})]} _{\text{unidirectional}}-\underbrace {[Q\sin {(2\omega t)}]} _{\text{bidirectional}}$

From any of the two previous equations, it is noted the instantaneous power has three terms. The first term is a constant and equal to $P$ (the active power), while second and third terms have a zero time average. Thus the first term only is the average value (in time) of the (total) instantaneous power. The first and second terms, considered together, oscillate between $0$ and $2P$ with a pulsation of $2\omega$ and a time average of $P$; these two terms together are called instantaneous active power or instantaneous real power, and its peak value (or amplitude) is $2|P|$. The third term oscillates between $-Q$ and $+Q$ with a pulsation of $2\omega$ and a time average of $0$; this term is called the instantaneous reactive power, which leads or lags the instantaneous active power by 90° (since $\sin {(2\omega t)}=\cos {(2\omega t-90^{\circ })}$), and its peak value (amplitude) is the absolute value of reactive power, $|Q|$. It can be proven the peak value (amplitude) of the (total) instantaneous power is $|P|+S$.

Since instantaneous active power never changes sign, it corresponds to a unidirectional flow of energy (i.e. at all instants flowing either into or out of the two-terminal device or network under consideration). Since instantaneous reactive power changes sign, it corresponds to a bidirectional flow of energy (i.e. for half a cycle of it, it flows into the two-terminal device or network, and for the next half cycle it flows out of it).

Instantaneous active current, instantaneous reactive current, phasor active current and phasor reactive current in sinusoidal steady-state

In sinusoidal steady-state, since the instantaneous voltage and current of a two-terminal device or network are sinusoidal of same fundamental frequency without DC offset, they can be represented as phasors, and the phasor current can be decomposed into a phasor component $I_{\text{a,RMS}}$ that is in phase with (or parallel to) the phasor voltage $V_{\text{RMS}}$ or it's 180° out of phase with (or antiparallel to) it, and another phasor component $I_{\text{r,RMS}}$ that is in quadrature with (or perpendicular to) the phasor voltage. The former is called the active component of the phasor current and the latter is called the reactive component of the phasor current. From vector analysis:

$I_{\text{a,RMS}}={\frac {\Re [I_{\text{RMS}}]\,\Re [V_{\text{RMS}}]+\Im [I_{\text{RMS}}]\,\Im [V_{\text{RMS}}]}{\Re ^{2}[V_{\text{RMS}}]+\Im ^{2}[V_{\text{RMS}}]}}V_{\text{RMS}}=|I_{\text{RMS}}|\cos {(\alpha )}\,e^{j\varphi _{v}}$,

$I_{\text{r,RMS}}=I_{\text{RMS}}-I_{\text{a,RMS}}$,

where $\alpha$ is the smallest angle between the phasor voltage and phasor current, and can be obtained in terms of the power factor angle as follows:

$\alpha ={\begin{cases}\varphi =\varphi _{v}-\varphi _{i}&{\text{if }}0^{\circ }\leq \varphi \leq 180^{\circ }\\-\varphi =\varphi _{i}-\varphi _{v}&{\text{if }}-180^{\circ }\leq \varphi \leq 0^{\circ }\end{cases}}$.

Although the two previous equations for the phasor active and reactive currents give a correct phase angle for each, their phase angles can also be determined as follows:

$\varphi _{i,{\text{a}}}={\begin{cases}\varphi _{v}&{\text{if }}-90^{\circ }<\varphi <90^{\circ }\\\varphi _{v}+180^{\circ }&{\text{if }}-180^{\circ }<\varphi <-90^{\circ }{\text{ or }}90^{\circ }<\varphi <180^{\circ }\end{cases}}$,

$\varphi _{i,{\text{r}}}={\begin{cases}\varphi _{v}+90^{\circ }&{\text{if }}-180^{\circ }<\varphi <0^{\circ }\\\varphi _{v}-90^{\circ }&{\text{if }}0^{\circ }<\varphi <180^{\circ }\end{cases}}$.

Similar to the power triangle and the impedance triangle, a triangle can be formed using the phasor current and its active and reactive components. From it, the following equation is easily derived:

$|I_{\text{RMS}}|={\sqrt {|I_{\text{a,RMS}}|^{2}+|I_{\text{r,RMS}}|^{2}}}$.

In the time domain, the instantaneous values are:

$I_{\text{a}}(t)=\Re [{\sqrt {2}}\,I_{\text{a,RMS}}\,e^{j\omega t}]$,

$I_{\text{r}}(t)=\Re [{\sqrt {2}}\,I_{\text{r,RMS}}\,e^{j\omega t}]$.

In this way:

$i(t)=i_{\text{a}}(t)+i_{\text{r}}(t)$,

and the decomposition of instantaneous power into its active and reactive components is back-derived:

$p(t)=v(t)\,i_{\text{a}}(t)+v(t)\,i_{\text{r}}(t)=p_{\text{a}}(t)+p_{\text{r}}(t)$.

Average power

In general, engineers are interested in the instantaneous power averaged over a period of time, whether it is a low frequency line cycle or a high frequency power converter switching period. The simplest way to get that result is to take the integral of the instantaneous calculation over the desired period:

$P_{\text{avg}}={\frac {1}{t_{2}-t_{1}}}\int _{t_{1}}^{t_{2}}v(t)\,i(t)\,\mathrm {d} t$.

The previous expression apples to all waveforms, whether they are sinusoidal or not (i.e. regardless of harmonic content of the waveform), even if they are not periodic. In practical applications, this would be done in the digital domain, where the calculation becomes trivial when compared to the use of rms and phase to determine active power:

$P_{\text{avg}}={\frac {1}{n}}\sum _{k=1}^{n}v[k]\,i[k]$.

Active power in AC steady-state

In the particular case where the instantaneous power is periodic of fundamental period $T'$ (e.g. in AC steady-state, whether sinusoidal [without harmonics] or non-sinusoidal [with harmonics]), the instantaneous power of a two-terminal device or network can be time-averaged over one cycle of it. Using integrals, the mean is:

$P={\frac {1}{n\,T'}}\int _{t_{0}}^{t_{0}+n\,T'}v(t)\,i(t)\,\mathrm {d} t$,

where $t_{0}$ is any instant of time (for example, $t_{0}=0{\text{ s}}$ or $t_{0}=T'/2$ to simplify the equation), and $n$ is any positive integer number (for example, $n=1$ to simplify the equation). This is known as active power or real power (in units of watts, W).

If the voltage reference polarity and current reference direction are chosen such that the passive sign convention is satisfied, the previous expressions is the active power delivered to (or consumed or absorbed by) the device or network under discussion.

Active power is unfortunately also called average power. Although active power is certainly a mean of instantaneous power, just like average power, it can cause confusion between both terms, when in fact both are in general different. For average power, instantaneous power is time-averaged over any arbitrary time interval, even if the instantaneous power is not periodic, while in active power it is assumed the instantaneous power is periodic and it is time-averaged over an integer number of cycles of it. When the instantaneous power is periodic and it is time-averaged over an integer number of cycles of it, the average power and active power are the same.

From the definition of power factor, the active power of a two-terminal device or network can be computed also as:

$P=|S|\cdot {\text{pf}}$.

If the device or network is passive, the following is also true:

$P=|I_{\mathrm {RMS} }|^{2}R={\frac {|V_{\mathrm {RMS} }|^{2}}{|Z|^{2}}}\cdot R$,

where $|Z|={\sqrt {R^{2}+X^{2}}}$ is the magnitude of the complex impedance of the device or network (assuming such network is passive). A perfect resistor (i.e. ideal resistor with constant resistance) or purely resistive device or network stores no energy, so current and voltage are in phase. Therefore, there is no reactive power ($Q=0$) and $P=S$ (using the passive sign convention). Thus, for a perfect resistor or purely resistive device or network, active or real power can be simplified to:

$P=S=|V_{\mathrm {RMS} }|\,|I_{\mathrm {RMS} }|={\frac {|V_{\mathrm {RMS} }|^{2}}{R}}$,

where $R$ denotes the equivalent resistance (units in ohms, Ω) of the device or network. In a perfect capacitor or inductor, or in a purely reactive device or network, $P=0$.

For example, if the active power of a two-terminal device or network (linear or non-linear, time-invariant or time-variant, passive or active, in steady-state without or with harmonics) is +20 W and the passive sign convention is satisfied, it means that, on average, there’s a flow of 20 joules of energy per second in each cycle of the instantaneous power, from the external network (or source) to the device (or load) under consideration.

Active power in sinusoidal steady-state

In the particular case where the instantaneous voltage and current are both sinusoidal of same frequency with no DC offset (e.g. in sinusoidal steady-state), the active power of a two-terminal device or network simplifies to:

$P=|V_{\text{RMS}}||I_{\text{RMS}}|\cos {(\varphi _{v}-\varphi _{i})}=|S|\cdot {\text{pf}}=\Re {[S]}$,

and:

$|P|=|V_{\text{RMS}}||I_{\text{a,RMS}}|$.

where $|V_{\text{RMS}}|$ and $|I_{\text{RMS}}|$ are respectively the magnitude of the RMS phasor voltage and RMS phasor current, or simply the RMS value of the instantaneous voltage and instantaneous current; $\varphi _{v}$ and $\varphi _{i}$ are respectively the phase angle of the instantaneous or phasor voltage and current.

In a three-phase (either three-terminal or four-terminal, in wye or in delta) device operating in balanced sinusoidal steady-state, the phasors in the previous equation are phase quantities (as opposed to line quantities), and the active power is the single-phase or per-phase active power, that is:

$P_{1\phi }=|V_{\phi ,{\text{RMS}}}||I_{\phi ,{\text{RMS}}}|\cos {(\varphi _{v,\phi }-\varphi _{i,\phi })}$,

and the three-phase or total active power is:

$P_{3\phi }=3\,P_{1\phi }={\sqrt {3}}\,|V_{\text{L,RMS}}||I_{\text{L,RMS}}|\cos {(\varphi _{v,\phi }-\varphi _{i,\phi })}$.

Active power in non-sinusoidal steady-state at the same fundamental frequency

In the particular case where the instantaneous voltage and current are both periodic non-sinusoidal of same fundamental frequency (e.g. in non-sinusoidal AC steady-state at the same fundamental frequency), the active power of a two-terminal device or network simplifies to:

$P=\displaystyle \sum _{n=0}^{\infty }|V_{n,{\text{RMS}}}||I_{n,{\text{RMS}}}|\cos {(\varphi _{v,n}-\varphi _{i,n})}$.

Apparent power in AC steady-state

In the particular case where the instantaneous power is periodic of fundamental period $T'$ (e.g. in AC steady-state, whether sinusoidal [without harmonics] or non-sinusoidal [with harmonics]), the apparent power (in units of volt-amperes, VA) of a two-terminal device or network is defined as the product of the RMS value of the instantaneous voltage and the RMS value of the instantaneous current:

$|S|=|V_{\text{RMS}}|\,|I_{\text{RMS}}|$.

The apparent power of a two-terminal device or network, carried by a periodic instantaneous voltage of effective value $|V_{\text{RMS}}|$ and a periodic instantaneous current of effective value $|I_{\text{RMS}}|$, is the active power that would be carried by a DC voltage of same effective value than the periodic voltage and a DC current of same effective value than the periodic current.

For example, if a voltage of 120 V RMS is applied to a two-terminal passive device or network (linear or non-linear, time-invariant or time-variant, in steady-state without or with harmonics) and it draws a current of 2 A RMS, then its apparent power is 240 VA. This can be interpreted as follows: the apparent power of the device (or load) under consideration, 240 VA, is the same power that an ideal constant-resistance resistor consumes when a voltage of 120 V DC is applied and it results in a current of 2 A DC.

Apparent power in sinusoidal steady-state

In the particular case where the instantaneous voltage and current are both sinusoidal of same frequency with no DC offset (e.g. in sinusoidal steady-state), the apparent power of a two-terminal device or network simplifies to:

$|S|={\sqrt {P^{2}+Q^{2}}}$.

If the device or network is passive, the following is also true:

$|S|=|I_{\text{RMS}}|^{2}|Z|={\frac {|V_{\text{RMS}}|^{2}}{|Z|}}$.

In a three-phase (either three-terminal or four-terminal, in wye or in delta) device operating in balanced sinusoidal steady-state, the phasors in the previous equations are phase quantities (as opposed to line quantities), and the apparent power is the single-phase or per-phase apparent power, that is:

$|S_{1\phi }|=|V_{\phi ,{\text{RMS}}}||I_{\phi ,{\text{RMS}}}|=|I_{\phi ,{\text{RMS}}}|^{2}|Z|={\frac {|V_{\phi ,{\text{RMS}}}|^{2}}{|Z|}}$,

and the three-phase or total apparent power is:

$|S_{3\phi }|=3\,|S_{1\phi }|={\sqrt {3}}\,|V_{\text{L,RMS}}||I_{\text{L,RMS}}|$.

Power factor in AC steady-state

Main article: Power factor

In the particular case where the instantaneous power is periodic of fundamental period $T'$ (e.g. in AC steady-state, whether sinusoidal [without harmonics] or non-sinusoidal [with harmonics]), the power factor (dimensionless) of a two-terminal device or network is defined as the ratio of the active power to the apparent power:

${\text{pf}}={\frac {P}{|S|}}$.

The power factor of a two-terminal passive device or network is a measure of the effectiveness (not to be confused with the efficiency) of such device (or load), compared to an ideal constant-resistance resistor in a DC circuit operating in steady-state.

For example, if voltage and current of a two-terminal passive device or network (linear or non-linear, time-invariant or time-variant, in steady-state without or with harmonics) is respectively 120 V RMS and 2 A RMS, then its apparent power is 240 VA, and if the device (or load) absorbs an active power of 200 W, then its power factor is 0.95. This means the active power absorbed by the device (or load) in the actual AC circuit is only 0.95 times smaller than the (active) power absorbed by an ideal constant-resistance resistor with a voltage of 120 V DC and current of 2 A DC.

Power factor and reactive factor in sinusoidal steady-state

In the particular case where the instantaneous voltage and current are both sinusoidal of same frequency with no DC offset (e.g. in sinusoidal steady-state), the power factor of a two-terminal device or network simplifies to:

${\text{pf}}=\cos {(\varphi _{v}-\varphi _{i})}$,

and:

$|{\text{pf}}|={\frac {|I_{\text{a,RMS}}|}{|I_{\text{RMS}}|}}$,

where $\varphi _{v}$ and $\varphi _{i}$ are respectively the phase angle of the instantaneous or phasor voltage and current; the difference $\varphi _{v}-\varphi _{i}$ is called the power factor angle because it's the angle whose cosine is the power factor and it's usually denoted as $\varphi$. For a passive two-terminal device or network, the power factor angle is equal to the phase angle of the complex impedance.

Under the same assumptions, the following quantity is called the reactive factor (also dimensionless):

${\text{rf}}=\sin {(\varphi _{v}-\varphi _{i})}={\frac {Q}{|S|}}$,

and:

$|{\text{rf}}|={\frac {|I_{\text{r,RMS}}|}{|I_{\text{RMS}}|}}$.

If the device or network is passive, the following is also true, which can be easily proven from the impedance triangle:

${\text{pf}}={\frac {R}{|Z|}}$,

${\text{rf}}={\frac {X}{|Z|}}$.

Dependence of the power factor angle with the two-terminal network or type of load in sinusoidal steady-state.

In a series RL network (using the passive sign convention):

$0^{\circ }<\varphi <90^{\circ };\quad {\text{pf}}>0;\quad Q>0;\quad X>0;\quad P>0$.

In a series RC network (using the passive sign convention):

$-90^{\circ }<\varphi <0^{\circ };\quad {\text{pf}}>0;\quad Q<0;\quad X<0;\quad P>0$,

In a series RL or RC network, the power factor is said to be lagging or leading because the current respectively (instantaneous/waveform or phasor) lags or leads the voltage (instantaneous/waveform or phasor) by a positive angle between 0° and 90°. As the figure to the right shows, given only the power factor of a two-terminal network (for example 0.5), it's not possible to uniquely determine the power factor angle, since the cosine function is not an injective function and there can be two possible values (for example −60° and 60°); the type of power factor (lagging or leading) must also be known.

In a three-phase (either three-terminal or four-terminal, in wye or in delta) device operating in balanced sinusoidal steady-state, the previous equations are valid, and $\varphi =\varphi _{v}-\varphi _{i}$ would be the difference of the phase angle of the phase voltage (as opposed to line, line-to-line or phase-to-phase voltage) and the phase angle of the phase current (as opposed to line current) of the same phase (a, b or c). Furthermore, the following is also true:

${\text{pf}}=\cos {(\varphi _{v,\phi }-\varphi _{i,\phi })}={\frac {P_{1\phi }}{|S_{1\phi }|}}={\frac {P_{3\phi }}{|S_{3\phi }|}}$,

${\text{rf}}=\sin {(\varphi _{v,\phi }-\varphi _{i,\phi })}={\frac {Q_{1\phi }}{|S_{1\phi }|}}={\frac {Q_{3\phi }}{|S_{3\phi }|}}$.

Reactive power in AC steady-state

Reactive power in sinusoidal steady-state

In the particular case where the instantaneous voltage and current are both sinusoidal of same frequency with no DC offset (e.g. in sinusoidal steady-state), the reactive factor or quadrature power (in units of volt-amperes-reactive, var) of a two-terminal device or network is defined as:

$Q=|V_{\text{RMS}}||I_{\text{RMS}}|\sin({\varphi _{v}-\varphi _{i}})=|S|\cdot {\text{rf}}=\Im {[S]}$,

and:

$|Q|=|V_{\text{RMS}}||I_{\text{r,RMS}}|$.

If the device or network is passive, the following is also true:

$Q=|I_{\mathrm {RMS} }|^{2}X={\frac {|V_{\mathrm {RMS} }|^{2}}{|Z|^{2}}}\cdot X$.

In a perfect capacitor or inductor (i.e. ideal capacitor or inductor with constant capacitance or inductance) or purely reactive device or network, there is no net energy transfer and so $P=0$; thus all apparent power is reactive. Therefore, for a perfect capacitor or inductor or purely reactive device or network, reactive power simplifies to:

$Q=S=\pm |V_{\mathrm {RMS} }|\,|I_{\mathrm {RMS} }|={\frac {|V_{\mathrm {RMS} }|^{2}}{X}}$,

where $X$ denotes reactance (units in ohms, Ω) of the device or network, defined as positive for an inductor and negative for a capacitor; the positive or negative sign of the plus-minus sign ($\pm$) is used respectively if the reactance is positive (inductive load) or negative (capacitive load).

In a three-phase (either three-terminal or four-terminal, in wye or in delta) device operating in balanced sinusoidal steady-state, the phasors in the previous equation are phase quantities (as opposed to line quantities), and the reactive power is the single-phase or per-phase reactive power, that is:

$Q_{1\phi }=|V_{\phi ,{\text{RMS}}}||I_{\phi ,{\text{RMS}}}|\sin {(\varphi _{v,\phi }-\varphi _{i,\phi })}$,

and the three-phase or total reactive power is:

$Q_{3\phi }=3\,Q_{1\phi }={\sqrt {3}}\,|V_{\text{L,RMS}}||I_{\text{L,RMS}}|\sin {(\varphi _{v,\phi }-\varphi _{i,\phi })}$.

Since the absolute value of reactive power is the amplitude of the instantaneous reactive power, reactive power has a physical meaning in sinusoidal steady-state for a two-terminal device or network: it is the amplitude (peak value or maximum value) of the rate of flow of the energy oscillating between the device (or load) under consideration and the external network (or source). This interpretation is consistent with IEEE standard 1459-2010: “The magnitude of the reactive power $Q$ equals the amplitude of the oscillating instantaneous reactive power $p_{q}$”

For example, if a two-terminal device or network has a reactive power of ±15 VAR, it means that the maximum rate of transfer of the energy oscillating between the device (or load) under consideration and external network (or source) is 15 joules per second. Notice this is not “wasted energy”, but perhaps “unused energy”.

Reactive power in non-sinusoidal steady-state

In non-sinusoidal steady-state conditions, the definition of reactive power is controversial. Two popular definitions are those by Budeanu and Fryze, separetely, which are usually denoted respectively as $Q_{B}$ and $Q_{F}$ to distinguish each other. However, the Budeanu reactive power is not recommended by the Institute of Electrical and Electronics Engineers, as stated in the standard IEEE 1459-2010.

Complex power in sinusoidal steady-state

In the particular case where the instantaneous voltage and current are both sinusoidal of same frequency with no DC offset (e.g. in sinusoidal steady-state), the complex power (in units of volt-amperes, VA) of a two-terminal device or network is defined as the product of the RMS phasor voltage $V_{\text{RMS}}$ (i.e. the phasor voltage, with the amplitude as RMS value) times the complex conjugate of the RMS phasor current $I_{\text{RMS}}^{*}$ (i.e.the phasor current, with the amplitude as RMS value):

$S=V_{\text{RMS}}\,I_{\text{RMS}}^{*}$.

Also by convention, the complex conjugate of $I_{\text{RMS}}$ is used, which is denoted $I_{\text{RMS}}^{*}$ (or ${\overline {I}}_{\text{RMS}}$), rather than $I_{\text{RMS}}$ itself. There are at least two good reasons for doing so:

• Using the product $V_{\text{RMS}}\,I_{\text{RMS}}$ to define $S$ would result in a quantity that depends on the reference angle chosen for $V_{\text{RMS}}$ or $I_{\text{RMS}}$, while defining $S$ as $V_{\text{RMS}}\,I_{\text{RMS}}^{*}$ results in a quantity that doesn't depend on the reference angle.
• Using $V_{\text{RMS}}\,I_{\text{RMS}}^{*}$ as the definition of complex powers allows the complex power to contain all of the power information of a two-terminal device or network: its real part is the active power, its imaginary part (which is a real number) is the reactive power, its magnitude or modulus is the apparent power, and its phase angle or argument is the power factor angle. These geometrical relations are illustrated diagrammatically by the power triangle, and can be mathematically described as follows:

$S=\underbrace {P+jQ} _{\text{rectangular form}}=\underbrace {|S|\angle \varphi } _{\text{polar form}}=\underbrace {|S|e^{j\varphi }} _{\text{exponential form}}$.

If the two-terminal device or network is passive, meaning it has a complex impedance $Z$ (units in ohms, Ω), other forms of complex power are derived as:

$S=|I_{\text{RMS}}|^{2}Z={\frac {|V_{\text{RMS}}|^{2}}{Z^{*}}}$.

In a three-phase (either three-terminal or four-terminal, in wye or in delta) device operating in balanced sinusoidal steady-state, the phasors in the previous equation are phase quantities (as opposed to line quantities), and the complex power is the single-phase or per-phase complex power, that is:

$S_{1\phi }=P_{1\phi }+jQ_{1\phi }=|I_{\phi ,{\text{RMS}}}|^{2}Z={\frac {|V_{\phi ,{\text{RMS}}}|^{2}}{Z^{*}}}$,

and the three-phase or total complex power is:

$S_{3\phi }=3\,S_{1\phi }=P_{3\phi }+jQ_{3\phi }$.

Net energy and instantaneous energy

The total (instantaneous) energy $w(t)$ (in units of joules, J) delivered to a two-terminal device or network from the past ($-\infty$) up to the present ($t$) is given by the definite integral of the instantaneous power (i.e. the time rate at which energy is being transferred or work is being done):

$w(t)=\displaystyle \int _{-\infty }^{t}p(\tau )\,\mathrm {d} \tau$.

The net energy $W$ transferred across the two-terminal device or network between the instants $t_{1}$ and $t_{2}$ (where $t_{2}>t_{1}$) in terms of the instantaneous power is:

$W=\displaystyle \int _{t_{1}}^{t_{2}}p(t)\,\mathrm {d} t$

or also in terms of the average power (i.e. the time average/mean of the instantaneous power over the whole time interval) and the time interval under consideration as^[1]:

$W=P_{\text{avg}}\cdot (t_{2}-t_{1})$.

The three previous expressions apply to all waveforms, whether they are sinusoidal or not, even if they are not periodic.

Net energy in AC steady-state

In the particular case where the instantaneous power is periodic (e.g. in AC steady-state, whether sinusoidal [without harmonics] or non-sinusoidal [with harmonics]), the net energy can also be computed in terms of the active power (i.e. the time average/mean of the instantaneous power over one cycle of it)^[2]:

$W=P\cdot T'\cdot \left\lfloor {\frac {t_{2}-t_{1}}{T'}}\right\rfloor +\displaystyle \int _{t_{1}+T'\cdot \left\lfloor {\frac {t_{2}-t_{1}}{T'}}\right\rfloor }^{t_{2}}p(t)\,\mathrm {d} t\approx P\cdot (t_{2}-t_{1})$

where $T'$ is the fundamental period of the instantaneous power, and $\lfloor \cdot \rfloor$ is the floor function. This shows that, in general, the net energy cannot be computed as the product of the active power and the time interval; though that may be done to get an approximation.

In the particular case where the instantaneous power is periodic and the time interval under consideration is an integer multiple of the fundamental period of the instantaneous power, the net energy can also be computed in terms of the active power^[3]:

$W=P\cdot (t_{2}-t_{1})$.

Conservation of power

Conservation of instantaneous power

An isolated network (or circuit) is a circuit that has no energy coupling of any kind with the surroundings. A circuit can get coupled to the surroundings by electrostatic/electromagnetic coupling with other physically separate circuits in the vicinity or by mechanical, thermal or optical interaction with the environment. Also, ideal independent sources can deliver an infinite amount of energy for an infinite amount of time, being able to create it out of nowhere. Thus, the total energy of any isolated lumped network is constant, and so the total instantaneous power delivered to (or received or consumed by or absorbed by) all devices (including the supplied or generated instantaneous power as negative) is zero (since instantaneous power is the derivative of energy, and the derivative of a constant is zero):

$\sum p(t)=0{\text{ W}}$.

Said another way, the total instantaneous power received equals the negative of the total instantaneous power supplied, using the passive sign convention for each power term of both sides of the equation:

$\sum p_{\text{received}}(t)=-\sum p_{\text{supplied}}(t)$.

where the instantaneous power received is numerically positive and the instantaneous power supplied is numerically negative.

Conservation of complex power in sinusoidal steady-state

In the particular of an isolated lumped network operating in sinusoidal steady-state, the total complex power of the network is also conserved (defined using the passive sign convention):

$\sum S=0{\text{ VA}}\implies \sum S_{\text{received}}=-\sum S_{\text{supplied}}$,

and so the active power and reactive power also have a corresponding conservation equation:

$\sum P=0{\text{ W}}\implies \sum P_{\text{received}}=-\sum P_{\text{supplied}}$;

$\sum Q=0{\text{ var}}\implies \sum Q_{\text{received}}=-\sum Q_{\text{supplied}}$.

However, apparent power is not a conserved quantity. These equations are fundamental in the power flow problem of a power system.

Measurement

Instantaneous power measurement

The instantaneous power of a device or network can be measured using power analyzers.

In this section, the instantaneous power reading of the $k$-th power analyzer ${\text{PA}}_{k}$ will be denoted as $p_{k}(t)$; "A" and "V" stand respectively for the current probe (measuring amperes) and voltage probe (measuring volts). The (total) instantaneous power of the network will be denoted as $p(t)$.

One-power analyzer method (for two-wire networks)

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated two-wire (e.g. single-phase) networks operating in sinusoidal or non-sinusoidal steady-state or in DC steady-state or in transient state. With reference to the following figure, the instantaneous power consumed (since the passive sign convention is satisfied) by the network on the right is^[4]:

$p(t)=p_{1}(t)$.

Circuit diagram of one-power analyzer method for two-wire single-phase networks, taking the neutral as common. Click on image to expand it

Two-power analyzer method for two-wire networks

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated two-wire (e.g. single-phase) networks operating in sinusoidal or non-sinusoidal steady-state or in DC steady-state or in transient state. With reference to the following figure, the instantaneous power consumed by the network on the right is^[5]:

$p(t)=p_{1}(t)+p_{2}(t)$.

Circuit diagram of two-power analyzer method for two-wire single-phase networks, taking an external node as common. Click on image to expand it

Two-power analyzer method for three-wire networks

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated three-wire (e.g. split-phase or three-phase) networks operating in sinusoidal or non-sinusoidal steady-state or in DC steady-state or in transient state, and in balanced or unbalanced conditions. With reference to the following figures, the instantaneous power consumed by the network on the right is^[6]:

$p(t)=p_{1}(t)+p_{2}(t)$.

Circuit diagram of two-power analyzer method for three-wire three-phase networks, taking phase a as common. Click on image to expand it

Circuit diagram of two-power analyzer method for three-wire three-phase networks, taking phase b as common. Click on image to expand it

Circuit diagram of two-power analyzer method for three-wire three-phase networks, taking phase c as common. Click on image to expand it

Circuit diagram of two-power analyzer method for three-wire split-phase networks, taking the neutral as common. Click on image to expand it

Three-power analyzer method for three-wire networks

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated three-wire (e.g. split-phase or three-phase) networks operating in sinusoidal or non-sinusoidal steady-state or in DC steady-state or in transient state, and in balanced or unbalanced conditions. With reference to the following figures, the active power consumed by the network on the right is^[7]:

$p(t)=p_{1}(t)+p_{2}(t)+p_{3}(t)$.

Circuit diagram of three-power analyzer method for three-wire three-phase networks, taking an external node as common. Click on image to expand it

Circuit diagram of three-power analyzer method for three-wire split-phase networks, taking an external node as common. Click on image to expand it

Three-power analyzer method for four-wire networks

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated four-wire (e.g. three-phase) networks operating in sinusoidal or non-sinusoidal steady-state or in DC steady-state or in transient state, and in balanced or unbalanced conditions. With reference to the following figure, the instantaneous power consumed by the network on the right is^[8]:

$p(t)=p_{1}(t)+p_{2}(t)+p_{3}(t)$.

Circuit diagram of three-power analyzer method for four-wire three-phase networks, taking the neutral as common. Click on image to expand it

Four-power analyzer method (for four-wire networks)

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated four-wire (e.g. three-phase) networks operating in sinusoidal or non-sinusoidal steady-state or in DC steady-state or in transient state, and in balanced or unbalanced conditions. With reference to the following figure, the active power consumed by the network on the right is^[9]:

$p(t)=p_{1}(t)+p_{2}(t)+p_{3}(t)+p_{4}(t)$.

Circuit diagram of four-power analyzer method for four-wire three-phase networks, taking an external node as common. Click on image to expand it

Active power measurement

Since the (total) instantaneous power of any arbitrary isolated $n$-terminal (or $n$-wire) network can be computed using $(n-1)$ current-voltage pairs, it's evident that, when such network is operating in AC steady-state (sinusoidal or not, balanced or not), the (total) active power of it can be measured using $(n-1)$ wattmeters. This is known as Blondel's theorem. It's also possible, without any benefits, to use $n$ wattmeters.

In this section, the active power reading of the $k$-th wattmeter ${\text{W}}_{k}$ will be denoted as $P_{k}$; "CC" and "VC" stand respectively for the current coil and voltage coil. The (total) active power of the network will be denoted as $P$.

One-wattmeter method (for two-wire networks in AC steady-state)

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated two-wire (e.g. single-phase) networks operating in sinusoidal or non-sinusoidal steady-state. With reference to the following figure, the active power consumed by the network on the right is^[10]:

$P=P_{1}$.

Circuit diagram of one-wattmeter method for two-wire single-phase networks, taking the neutral as common. Click on image to expand it

Two-wattmeter method for two-wire networks in AC steady-state

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated two-wire (e.g. single-phase) networks operating in sinusoidal or non-sinusoidal steady-state. With reference to the following figure, the active power consumed by the network on the right is^[11]:

$P=P_{1}+P_{2}$.

Circuit diagram of the two-wattmeter method for two-wire single-phase networks, taking an external node as common. Click on image to expand it

Two-wattmeter method for three-wire networks in AC steady-state

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated three-wire (e.g. split-phase or three-phase) networks operating in sinusoidal or non-sinusoidal steady-state in balanced or unbalanced conditions. With reference to the following figures, the active power consumed by the network on the right is^[12]:

$P=P_{1}+P_{2}$.

Circuit diagram of two-wattmeter method for three-wire three-phase networks, taking phase a as common. Click on image to expand it

Circuit diagram of the two-wattmeter method for three-wire three-phase networks, taking phase b as common. Click on image to expand it

Circuit diagram of the two-wattmeter method for three-wire three-phase networks, taking phase c as common. Click on image to expand it

Circuit diagram of the two-wattmeter method for three-wire split-phase networks, taking the neutral as common. Click on image to expand it

Three-wattmeter method for three-wire networks in AC steady-state

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated three-wire (e.g. split-phase or three-phase) networks operating in sinusoidal or non-sinusoidal steady-state in balanced or unbalanced conditions. With reference to the following figures, the active power consumed by the network on the right is^[13]:

$P=P_{1}+P_{2}+P_{3}$.

Circuit diagram of the three-wattmeter method for three-wire three-phase networks, taking an external node as common. Click on image to expand it

Circuit diagram of the three-wattmeter method for three-wire split-phase networks, taking an external node as common. Click on image to expand it

Three-wattmeter method for four-wire networks in AC steady-state

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated four-wire (e.g. three-phase) networks operating in sinusoidal or non-sinusoidal steady-state in balanced or unbalanced conditions. With reference to the following figure, the active power consumed by the network on the right is^[14]:

$P=P_{1}+P_{2}+P_{3}$.

Circuit diagram of the three-wattmeter method for four-wire three-phase networks, taking the neutral as common. Click on image to expand it

Four-wattmeter method (for four-wire networks in AC steady-state)

This method is applicable to linear or non-linear, time-invariant or time-variant, bilateral or non-bilateral, passive or active, isolated four-wire (e.g. three-phase) networks operating in sinusoidal or non-sinusoidal steady-state in balanced or unbalanced conditions. With reference to the following figure, the active power consumed by the network on the right is^[15]:

$P=P_{1}+P_{2}+P_{3}+P_{4}$.

Circuit diagram of the four-wattmeter method for four-wire three-phase networks, taking an external node as common. Click on image to expand it

Reactive power measurement

Varmeters are instruments that measure reactive power (at least in sinusoidal steady-state), which are similar to wattmeters in the sense that they possess a current coil and a voltage coil, but the latter has a high inductance to obtain an additional phase shift of 90° in time between the voltage and current. In certain cases, reactive power can be measured using wattmeters.

Quadrature wattmeter method (for three-wire or four-wire networks in sinusoidal steady-state in balanced conditions)

This method is applicable to passive or active, isolated three-wire or four-wire three-phase networks operating in sinusoidal steady-state in balanced conditions. With reference to the following figure, the reactive power "consumed" by the network on the right is:

$Q={\sqrt {3}}\,P_{1}$.

Circuit diagram of quadrature wattmeter method for three-wire or four-wire three-phase networks, measuring the current of phase a. Click on image to expand it

Power factor

Main article: Power factor

The ratio of active power to apparent power in a circuit is called the power factor. For two systems transmitting the same amount of active power, the system with the lower power factor will have higher circulating currents due to energy that returns to the source from energy storage in the load. These higher currents produce higher losses and reduce overall transmission efficiency. A lower power factor circuit will have a higher apparent power and higher losses for the same amount of active power. The power factor is 1.0 when the voltage and current are in phase. It is zero when the current leads or lags the voltage by 90 degrees. When the voltage and current are 180 degrees out of phase, the power factor is negative one, and the load is feeding energy into the source (an example would be a home with solar cells on the roof that feed power into the power grid when the sun is shining). Power factors are usually stated as "leading" or "lagging" to show the sign of the phase angle of current with respect to voltage. Voltage is designated as the base to which current angle is compared, meaning that current is thought of as either "leading" or "lagging" voltage. Where the waveforms are purely sinusoidal, the power factor is the cosine of the phase angle ($\varphi$) between the current and voltage sinusoidal waveforms. Equipment data sheets and nameplates will often abbreviate power factor as "$\cos \phi$" for this reason.

Example: The active power is 700 W and the phase angle between voltage and current is 45.6° (assuming sinusoidal steady-state). The power factor is cos(45.6°) = 0.700. The apparent power is then: 700 W / cos(45.6°) = 1000 VA. The concept of power dissipation in AC circuit is explained and illustrated with the example.

For instance, in sinusoidal steady-state a power factor of 0.68 means that the RMS value of the active component of the total current (the one corresponding to the active power or net energy transfer) is just 68% of the RMS value of the total current, while the RMS value of the reactive component of the total current (the one corresponding to the reactive power or no net energy transfer) is sin(arccos(0.68)) ≈ 0.73 = 73% of the RMS value of the total current, where √(0.68^2 + 0.73^2) ≈ 1. Usually, utilities do not charge consumers for the reactive power losses, as they do no real work for the consumer. However, if there are inefficiencies at the customer's load source that cause the power factor to fall below a certain level, utilities may charge customers in order to cover an increase in their power plant fuel use and their worse line and plant capacities.

Reactive power

In a direct current circuit, the power flowing to the load is proportional to the product of the current through the load and the potential drop across the load. Energy flows in one direction from the source to the load. In AC power, the voltage and current both vary approximately sinusoidally. When there is inductance or capacitance in the circuit, the voltage and current waveforms do not line up perfectly. The power flow has two components – one component flows from source to load and can perform work at the load; the other portion, known as "reactive power", is due to the delay between voltage and current, known as phase angle, and cannot do useful work at the load. It can be thought of as current that is arriving at the wrong time (too late or too early). To distinguish reactive power from active power, it is measured in units of "volt-amperes reactive", or var. These units can simplify to watts but are left as var to denote that they represent no actual work output.

Energy stored in capacitive or inductive elements of the network gives rise to reactive power flow. Reactive power flow strongly influences the voltage levels across the network. Voltage levels and reactive power flow must be carefully controlled to allow a power system to be operated within acceptable limits. A technique is known as reactive compensation is used to reduce apparent power flow to a load by reducing reactive power supplied from transmission lines and providing it locally. For example, to compensate an inductive load, a shunt capacitor is installed close to the load itself. This allows all reactive power needed by the load to be supplied by the capacitor and not have to be transferred over the transmission lines. This practice saves energy because it reduces the amount of energy that is required to be produced by the utility to do the same amount of work. Additionally, it allows for more efficient transmission line designs using smaller conductors or fewer bundled conductors and optimizing the design of transmission towers.

Capacitive vs. inductive loads

Stored energy in the magnetic or electric field of a load device, such as a motor or capacitor, causes an offset between the current and the voltage waveforms. A capacitor is an AC device that stores energy in the form of an electric field. As current is driven through the capacitor, charge build-up causes an opposing voltage to develop across the capacitor. This voltage increases until some maximum dictated by the capacitor structure. In an AC network, the voltage across a capacitor is constantly changing. The capacitor opposes this change, causing the current to lead the voltage in phase. Capacitors are said to "source" reactive power, and thus to cause a leading power factor.

Induction machines are some of the most common types of loads in the electric power system today. These machines use inductors, or large coils of wire to store energy in the form of a magnetic field. When a voltage is initially placed across the coil, the inductor strongly resists this change in a current and magnetic field, which causes a time delay for the current to reach its maximum value. This causes the current to lag behind the voltage in phase. Inductors are said to "sink" reactive power, and thus to cause a lagging power factor. Induction generators can source or sink reactive power, and provide a measure of control to system operators over reactive power flow and thus voltage. Because these devices have opposite effects on the phase angle between voltage and current, they can be used to "cancel out" each other's effects. This usually takes the form of capacitor banks being used to counteract the lagging power factor caused by induction motors.

Reactive power control

Transmission connected generators are generally required to support reactive power flow. For example, on the United Kingdom transmission system, generators are required by the Grid Code Requirements to supply their rated power between the limits of 0.85 power factor lagging and 0.90 power factor leading at the designated terminals. The system operator will perform switching actions to maintain a secure and economical voltage profile while maintaining a reactive power balance equation:

$\mathrm {Generator\ MVARs+System\ gain+Shunt\ capacitors=MVAR\ Demand+Reactive\ losses+Shunt\ reactors}$

The ‘system gain’ is an important source of reactive power in the above power balance equation, which is generated by the capacitative nature of the transmission network itself. By making decisive switching actions in the early morning before the demand increases, the system gain can be maximized early on, helping to secure the system for the whole day. To balance the equation some pre-fault reactive generator use will be required. Other sources of reactive power that will also be used include shunt capacitors, shunt reactors, static VAR compensators and voltage control circuits.

Unbalanced sinusoidal polyphase systems

While active power and reactive power are well defined in any system, the definition of apparent power for unbalanced polyphase systems is considered to be one of the most controversial topics in power engineering. Originally, apparent power arose merely as a figure of merit. Major delineations of the concept are attributed to Stanley's Phenomena of Retardation in the Induction Coil (1888) and Steinmetz's Theoretical Elements of Engineering (1915). However, with the development of three phase power distribution, it became clear that the definition of apparent power and the power factor could not be applied to unbalanced polyphase systems. In 1920, a "Special Joint Committee of the AIEE and the National Electric Light Association" met to resolve the issue. They considered two definitions:

$S_{A}=|S_{\mathrm {a} }|+|S_{\mathrm {b} }|+|S_{\mathrm {c} }|$

$\mathrm {pf} _{A}={P_{\mathrm {a} }+P_{\mathrm {b} }+P_{\mathrm {c} } \over S_{A}}$,

that is, the arithmetic sum of the phase apparent powers; and

$S_{V}=|P_{\mathrm {a} }+P_{\mathrm {b} }+P_{\mathrm {c} }+j(Q_{\mathrm {a} }+Q_{\mathrm {b} }+Q_{\mathrm {c} })|$

$\mathrm {pf} _{V}={P_{\mathrm {a} }+P_{\mathrm {b} }+P_{\mathrm {c} } \over S_{V}}$,

that is, the magnitude of total three-phase complex power.

The 1920 committee found no consensus and the topic continued to dominate discussions. In 1930, another committee formed and once again failed to resolve the question. The transcripts of their discussions are the lengthiest and most controversial ever published by the AIEE. Further resolution of this debate did not come until the late 1990s.

A new definition based on symmetrical components theory was proposed in 1993 by Alexander Emanuel for unbalanced linear load supplied with asymmetrical sinusoidal voltages:

$S={\sqrt {\left(|V_{\mathrm {a} }^{2}|+|V_{\mathrm {b} }^{2}|+|V_{\mathrm {c} }^{2}|\right)\left(|I_{\mathrm {a} }^{2}|+|I_{\mathrm {b} }^{2}|+|I_{\mathrm {c} }^{2}|\right)}}$

$\mathrm {pf} ={P^{+} \over S}$,

that is, the root of squared sums of line voltages multiplied by the root of squared sums of line currents. $P^{+}$ denotes the positive sequence power:

$P^{+}=3|V^{+}||I^{+}|\cos {(\arg {(V^{+})}-\arg {(I^{+})})}$

where $V^{+}$ denotes the positive sequence voltage phasor, and $I^{+}$ denotes the positive sequence current phasor.

Multiple frequency systems

Since an RMS value can be calculated for any waveform, apparent power can be calculated from this. For active power it would at first appear that it would be necessary to calculate many product terms and average all of them. However, looking at one of these product terms in more detail produces a very interesting result.

${\begin{aligned}&A\cos(\omega _{1}t+k_{1})\cos(\omega _{2}t+k_{2})\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)+\left(\omega _{2}t+k_{2}\right)\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}t+k_{1}\right)-\left(\omega _{2}t+k_{2}\right)\right]\\={}&{\frac {A}{2}}\cos \left[\left(\omega _{1}+\omega _{2}\right)t+k_{1}+k_{2}\right]+{\frac {A}{2}}\cos \left[\left(\omega _{1}-\omega _{2}\right)t+k_{1}-k_{2}\right]\end{aligned}}$

However, the time average of a function of the form cos(ωt + k) is zero provided that ω is nonzero. Therefore, the only product terms that have a nonzero average are those where the frequency of voltage and current match. In other words, it is possible to calculate active (average) power by simply treating each frequency separately and adding up the answers. Furthermore, if voltage of the mains supply is assumed to be a single frequency (which it usually is), this shows that harmonic currents are a bad thing. They will increase the RMS current (since there will be non-zero terms added) and therefore apparent power, but they will have no effect on the active power transferred. Hence, harmonic currents will reduce the power factor. Harmonic currents can be reduced by a filter placed at the input of the device. Typically this will consist of either just a capacitor (relying on parasitic resistance and inductance in the supply) or a capacitor-inductor network. An active power factor correction circuit at the input would generally reduce the harmonic currents further and maintain the power factor closer to unity.

See also

• War of the currents
• Electric power transmission
• Transformer
• Mains electricity
• Deformed power

Notes

1.^ For a demonstration, read the Talk page.

2.^ For a demonstration, read the Talk page.

External links

• "AC Power Java Applet"