Histogram

For the histograms used in digital image processing, see Image histogram and Color histogram.

Histogram
One of the Seven Basic Tools of Quality
First described by	Karl Pearson
Purpose	To roughly assess the probability distribution of a given variable by depicting the frequencies of observations occurring in certain ranges of values

In statistics, a histogram is a graphical representation, showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson. A histogram consists of tabular frequencies, shown as adjacent rectangles, erected over discrete intervals (bins), with an area equal to the frequency of the observations in the interval. The height of a rectangle is also equal to the frequency density of the interval, i.e., the frequency divided by the width of the interval. The total area of the histogram is equal to the number of data. A histogram may also be normalized displaying relative frequencies. It then shows the proportion of cases that fall into each of several categories, with the total area equaling 1. The categories are usually specified as consecutive, non-overlapping intervals of a variable. The categories (intervals) must be adjacent, and often are chosen to be of the same size.

Histograms are used to plot density of data, and often for density estimation: estimating the probability density function of the underlying variable. The total area of a histogram used for probability density is always normalized to 1. If the length of the intervals on the x-axis are all 1, then a histogram is identical to a relative frequency plot.

An alternative to the histogram is kernel density estimation, which uses a kernel to smooth samples. This will construct a smooth probability density function, which will in general more accurately reflect the underlying variable.

The histogram is one of the seven basic tools of quality control.

Etymology

An example histogram of the heights of 31 Black Cherry trees.

The etymology of the word histogram is uncertain. Sometimes it is said to be derived from the Greek histos 'anything set upright' (as the masts of a ship, the bar of a loom, or the vertical bars of a histogram); and gramma 'drawing, record, writing'. It is also said that Karl Pearson, who introduced the term in 1895, derived the name from "historical diagram".

Examples

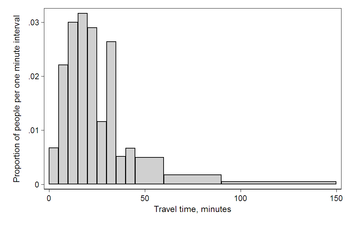
As an example we consider data collected by the U.S. Census Bureau on time to travel to work (2000 census, [1], Table 2). The census found that there were 124 million people who work outside of their homes. An interesting feature of this graph is that the number recorded for "at least 15 but less than 20 minutes" is higher than for the bands on either side. This is likely to have arisen from people rounding their reported journey time. This rounding is a common phenomenon when collecting data from people.

Histogram of travel time, US 2000 census. Area under the curve equals the total number of cases. This diagram uses Q/width from the table.

Data by absolute numbers

Interval	Width	Quantity	Quantity/width
0	5	4180	836
5	5	13687	2737
10	5	18618	3723
15	5	19634	3926
20	5	17981	3596
25	5	7190	1438
30	5	16369	3273
35	5	3212	642
40	5	4122	824
45	15	9200	613
60	30	6461	215
90	60	3435	57

This histogram shows the number of cases per unit interval so that the height of each bar is equal to the proportion of total people in the survey who fall into that category. The area under the curve represents the total number of cases (124 million). This type of histogram shows absolute numbers, with Q in thousands.

Histogram of travel time, US 2000 census. Area under the curve equals 1. This diagram uses Q/total/width from the table.

Data by proportion

Interval	Width	Quantity (Q)	Q/total/width
0	5	4180	0.0067
5	5	13687	0.0221
10	5	18618	0.0300
15	5	19634	0.0316
20	5	17981	0.0290
25	5	7190	0.0116
30	5	16369	0.0264
35	5	3212	0.0052
40	5	4122	0.0066
45	15	9200	0.0049
60	30	6461	0.0017
90	60	3435	0.0005

This histogram differs from the first only in the vertical scale. The height of each bar is the decimal percentage of the total that each category represents, and the total area of all the bars is equal to 1, the decimal equivalent of 100%. The curve displayed is a simple density estimate. This version shows proportions, and is also known as a unit area histogram.

In other words, a histogram represents a frequency distribution by means of rectangles whose widths represent class intervals and whose areas are proportional to the corresponding frequencies. The intervals are placed together in order to show that the data represented by the histogram, while exclusive, is also continuous. (E.g., in a histogram it is possible to have two connecting intervals of 10.5–20.5 and 20.5–33.5, but not two connecting intervals of 10.5–20.5 and 22.5–32.5. Empty intervals are represented as empty and not skipped.)

Shape or form of a distribution

The histogram provides important informations about the shape of a distribution. According to the values presented, the histogram is either highly or moderately skewed to the left or right. A symmetrical shape is also possible, although a histogram is never perfectly symmetrical. If the histogram is skewed to the left, or negatively skewed, the tail extends further to the left. An example for a distribution skewed to the left might be the relative frequency of exam scores. Most of the scores are above 70 percent and only a few low scores occure. An example for a distribution skewed to the right or positively skewed is a histogram showing the relative frequency of housing values. A relatively small number of expensive homes create the skeweness to the right. The tail extends further to the right. The shape of a symmetrical distribution mirrors the skeweness of the left or right tail. For example the histogram of data for IQ scores. Histograms can be unimodal, bi-modal or multi-modal, depending on the dataset.

Activities and demonstrations

The SOCR resource pages contain a number of hands-on interactive activities demonstrating the concept of a histogram, histogram construction and manipulation using Java applets and charts.

Mathematical definition

An ordinary and a cumulative histogram of the same data. The data shown is a random sample of 10,000 points from a normal distribution with a mean of 0 and a standard deviation of 1.

In a more general mathematical sense, a histogram is a function m_i that counts the number of observations that fall into each of the disjoint categories (known as bins), whereas the graph of a histogram is merely one way to represent a histogram. Thus, if we let n be the total number of observations and k be the total number of bins, the histogram m_i meets the following conditions:

$n=\sum _{i=1}^{k}{m_{i}}.$

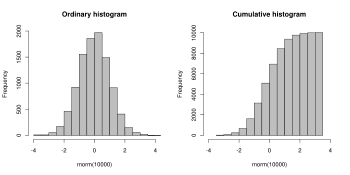
Cumulative histogram

A cumulative histogram is a mapping that counts the cumulative number of observations in all of the bins up to the specified bin. That is, the cumulative histogram M_i of a histogram m_j is defined as:

$M_{i}=\sum _{j=1}^{i}{m_{j}}.$

Number of bins and width

There is no "best" number of bins, and different bin sizes can reveal different features of the data. Some theoreticians have attempted to determine an optimal number of bins, but these methods generally make strong assumptions about the shape of the distribution. Depending on the actual data distribution and the goals of the analysis, different bin widths may be appropriate, so experimentation is usually needed to determine an appropriate width. There are, however, various useful guidelines and rules of thumb.

The number of bins k can be assigned directly or can be calculated from a suggested bin width h as:

$k=\left\lceil {\frac {\max x-\min x}{h}}\right\rceil .$

The braces indicate the ceiling function.

Sturges' formula

$h=\lceil \log _{2}n+1\rceil ,\,$

which implicitly bases the bin sizes on the range of the data, and can perform poorly if n < 30.

Scott's choice

$h={\frac {3.5\sigma }{n^{1/3}}},$

where $\sigma$ is the sample standard deviation.

Square-root choice

$h={\sqrt {n}},\,$

which takes the square root of the number of data points in the sample (used by Excel histograms and many others).

Freedman–Diaconis' choice

$h=2{\frac {\operatorname {IQR} (x)}{n^{1/3}}},$

which is based on the interquartile range.

Choice based on minimization of an estimated L² risk function

${\underset {h}{\operatorname {arg\,min} }}{\frac {2{\bar {m}}-v}{h^{2}}}$

where $\textstyle {\bar {m}}$ and $\textstyle v$ are mean and biased variance of a histogram with bin-width $\textstyle h$, $\textstyle {\bar {m}}={\frac {1}{k}}\sum _{i=1}^{k}m_{i}$ and $\textstyle v={\frac {1}{k}}\sum _{i=1}^{k}(m_{i}-{\bar {m}})^{2}$.

See also

• Data binning
• Freedman–Diaconis rule
• Image histogram
• Density estimation
• Kernel density estimation, a smoother but more complex method of density estimation
• Pareto chart
• Seven Basic Tools of Quality

Further reading

• Lancaster, H.O. An Introduction to Medical Statistics. John Wiley and Sons. 1974. ISBN 0 471 51250-8

External links

• Journey To Work and Place Of Work (location of census document cited in example)
• Understanding histograms in digital photography
• Smooth histogram for signals and images from a few samples
• Histograms: Construction, Analysis and Understanding with external links and an application to particle Physics.
• A Method for Selecting the Bin Size of a Histogram
• Interactive histogram generator
• Matlab function to plot nice histograms
• Digital Photography For Beginners-Histograms