Heptadecagon

Template:Odd polygon db In geometry, a heptadecagon (or 17-gon) is a seventeen-sided polygon.

Regular heptadecagon construction

The regular heptadecagon is a constructible polygon (that is, one that can be constructed using a compass and unmarked straightedge), as was shown by Carl Friedrich Gauss in 1796 at the age of 1. This proof represented the first progress in regular polygon construction in over 2000 years. Gauss's proof relies firstly on the fact that constructibility is equivalent to expressibility of the trigonometric functions of the common angle in terms of arithmetic operations and square root extractions, and secondly on his proof that this can be done if the odd prime factors of n are distinct Fermat primes, which are of the form $\scriptstyle F_{n}=2^{2^{\overset {n}{}}}+1$. Constructing a regular heptadecagon thus involves finding the cosine of $2\pi /17$ in terms of square roots, which involves an equation of degree 17—a Fermat prime. Gauss' book Disquisitiones Arithmeticae gives this as (in modern notation):

${\begin{aligned}16\,\operatorname {cos} {2\pi \over 17}=&-1+{\sqrt {17}}+{\sqrt {34-2{\sqrt {17}}}}+\\&2{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}.\end{aligned}}$

Constructions for a regular triangle and polygons with 2^h times as many sides had been given by Euclid, but constructions based on the Fermat primes other than 3 and 5 were unknown to the ancients. (The only known Fermat primes are F_n for n = 0, 1, 2, 3, 4. They are 3, 5, 17, 257, and 65537.)

The first explicit construction of a heptadecagon was given by Johannes Erchinger in 1825. Another method of construction uses Carlyle circles, as shown below. Based on the construction of the regular 17-gon, one can readily construct n-gons with n being the product of 17 with 3 or 5 (or both) and any power of 2: a regular 51-gon, 85-gon or 255-gon and any regular n-gon with 2^h times as many sides.

Petrie polygons

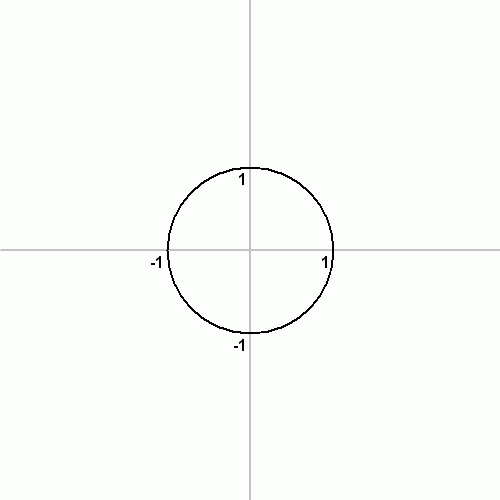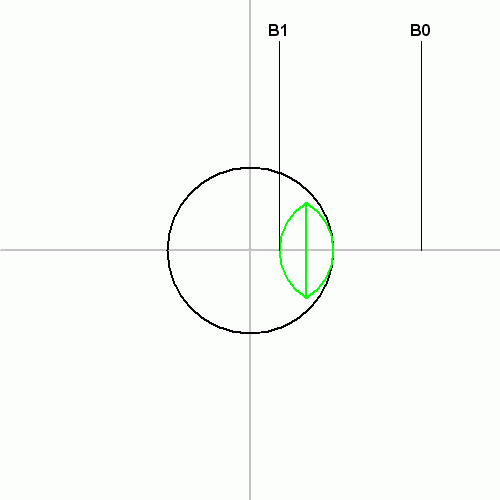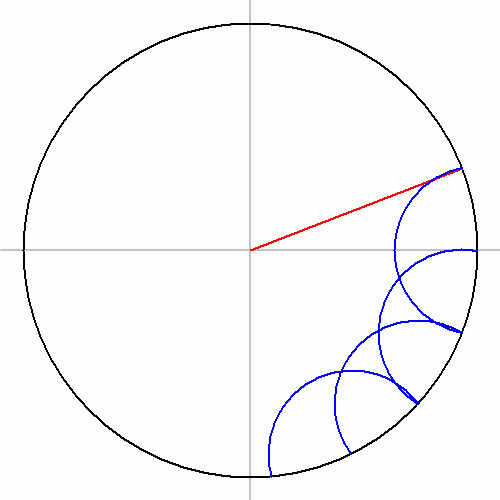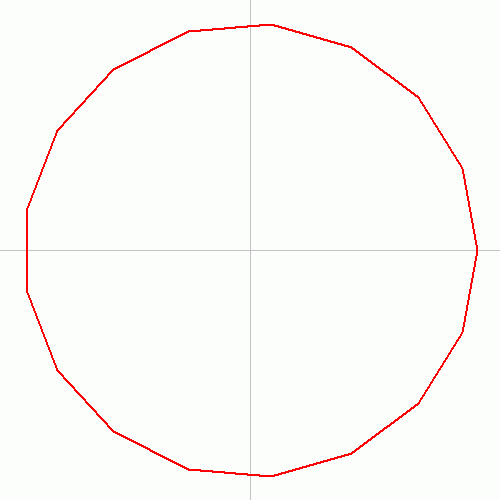
The regular heptadecagon is the Petrie polygon for one higher-dimensional polytope, projected in a skew orthogonal projection:

16-simplex (16D)

See also

• Compass and straightedge
• Constructible polygon

Further reading

• Dunham, William (September 1996). "1996—a triple anniversary". Math Horizons: 8–13. Retrieved 2009-12-06.
• Klein, Felix et al. Famous Problems and Other Monographs. – Describes the algebraic aspect, by Gauss.

External links

• Weisstein, Eric W. "Heptadecagon". MathWorld. Contains a description of the construction.
• "Constructing the Heptadecagon". MathPages.com.
• Heptadecagon trigonometric functions
• heptadecagon building New R&D center for SolarUK
• BBC video of New R&D center for SolarUK