Octatonic scale


An octatonic scale is any eight-note musical scale. However, the term most often refers to the ancohemitonic symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory (in contrast to jazz theory), this symmetrical scale is commonly called the octatonic scale (or the octatonic collection), although there are a total of 43 enharmonically inequivalent, transpositionally inequivalent eight-note sets.
The earliest systematic treatment of the octatonic scale was in Edmond de Polignac's unpublished treatise "Étude sur les successions alternantes de tons et demi-tons (Et sur la gamme dite majeure-mineure)" (Study of the Succession of Alternating Whole Tones and Semitones (and of the so-called Major-Minor Scale)) from c. 1879,[1] which preceded Vito Frazzi's Scale alternate per pianoforte of 1930[2] by 50 years.[3]
Nomenclature
[edit]In Saint Petersburg at the turn of the 20th century, this scale had become so familiar in the circle of composers around Nikolai Rimsky-Korsakov that it was referred to as the Korsakovian scale (Корсаковская гамма).[4] As early as 1911, the Russian theorist Boleslav Yavorsky described this collection of pitches as the diminished mode (уменьшённый лад), because of the stable way the diminished fifth functions in it.[5] In more recent Russian theory, the term octatonic is not used. Instead, this scale is placed among other symmetrical modes (total 11) under its historical name Rimsky-Korsakov scale, or Rimsky-Korsakov mode.[6][7])
In jazz theory, it is called the diminished scale[8] or symmetric diminished scale[9] because it can be conceived as a combination of two interlocking diminished seventh chords, just as the augmented scale can be conceived as a combination of two interlocking augmented triads. The two modes are sometimes referred to as the half-step/whole step diminished scale and the whole step/half-step diminished scale.[10]
Because it was associated in the early 20th century with the Dutch composer Willem Pijper, in the Netherlands it is called the Pijper scale.[11]
Construction
[edit]


The twelve tones of the chromatic scale are covered by three disjoint diminished seventh chords. The notes from two such seventh-chords combination form an octatonic collection. Because there are three ways to select two from three, there are three octatonic scales in the twelve-tone system.
Each octatonic scale has exactly two modes: the first begins its ascent with a whole step, while the second begins its ascent with a half step (semitone). These modes are sometimes referred to as the whole step/half-step diminished scale and the half-step/whole step diminished scale, respectively.[10]
Each of the three distinct scales can form differently named scales with the same sequence of tones by starting at a different point in the scale. With alternative starting points listed below in square brackets, and return to tonic in parentheses, the three are, ascending by semitones:
- C♯ D♯ [E] F♯ [G] A [A♯] B♯ (C♯)
- D E [F] G [G♯] A♯ [B] C♯ (D)
- E♭ F [G♭] A♭ [A♮] B [C] D (E♭)
It may also be represented as semitones, either starting with a whole tone (as above): 0 2 3 5 6 8 9 11 (12), or starting with a semitone: 0 1 3 4 6 7 9 10 (12), or labeled as set class 8‑28.[12]
With one more scale tone than described by the western diatonic scale, it is not possible to perfectly notate music of the octatonic scale using any conventional key signature without the use of accidentals. Across all conventional key signatures, at least two of the octatonic notes must share similar horizontal alignment on the staves, although the precise combination of accidentals and naturals varies. There are usually several equally succinct combinations of key signature and accidentals, and different composers have chosen to notate their music differently, sometimes ignoring the niceties of notation conventions designed to facilitate diatonic tonality.
Properties
[edit]Symmetry
[edit]The three octatonic collections are transpositionally and inversionally symmetric—that is, they are related by a variety of transposition and inversion operations:
They are each closed under transpositions by 3, 6, or 9 semitones. A transposition by 1, 4, 7, or 10 semitones will transform the E♭ scale into the D♭ scale, the C♯ scale into the D scale, and the D scale into the E♭ scale. Conversely, transpositions by 2, 5, 8, or 11 semitones acts in the reverse way; the E♭ scale goes to the D scale, D to C♯ and C♯ to E♭. Thus, the set of transpositions acts on the set of diminished collections as the integers modulo 3. If the transposition is congruent to 0 mod 3 the pitch collection is unchanged and the transpositions by 1 semitone or by 2 semitones are inverse to one another.[original research?]
The E♭ and C♯ collections can be swapped by inversions around E♭, F♯, A or C (the tones common to both scales). Similarly, the C♯ and D collections can be swapped by inversions around E, G, B♭/A♯, D♭/C♯ and the D and E♭ collections by inversions around D, F, A♭, or B. All other transformations do not change the classes (e.g. reflecting the E♭ collection around E gives the E♭ collection once again). This unfortunately means that the inversions do not act as a simple cyclic group on the set of diminished scales.[original research?]
Subsets
[edit]Among the collection's remarkable features is that it is the only collection that can be disassembled into four transpositionally related pitch pairs in six different ways, each of which features a different interval class.[13] For example:
- semitone: (C, C♯), (D♯, E) (F♯, G), (A, B♭)
- whole step: (C♯, D♯), (E, F♯), (G, A), (B♭, C)
- minor third: (C, E♭), (F♯, A), (C♯, E), (G, B♭)
- major third: (C, E), (F♯, B♭), (E♭, G), (A, C♯)
- perfect fourth: (C♯, F♯), (B♭, E♭), (G, C), (E, A)
- tritone: (C, F♯), (E♭, A), (C♯, G), (E, B♭)
Another remarkable feature of the diminished scale is that it contains the first four notes of four different minor scales separated by minor thirds. For example: C, D, E♭, F and (enharmonically) F♯, G♯, A, B. Also E♭, F, G♭, A♭, and A, B, C, D.
The scale "allows familiar harmonic and linear configurations such as triads and modal tetrachords to be juxtaposed unusually but within a rational framework" though the relation of the diatonic scale to the melodic and harmonic surface is thus generally oblique.[14]
History
[edit]Early examples
[edit]Joseph Schillinger suggests that the scale was formulated already by Persian traditional music in the 7th century AD, where it was called "Zar ef Kend", meaning "string of pearls", the idea being that the two different sizes of intervals were like two different sizes of pearls.[15]
Octatonic scales first occurred in Western music as byproducts of a series of minor-third transpositions. While Nikolai Rimsky-Korsakov claimed he was conscious of the octatonic collection "as a cohesive frame of reference" in his autobiography My Musical Life,[16][17] instances can be found in music of previous centuries. Eytan Agmon[18] locates one in Domenico Scarlatti's Sonata K. 319. In the following passage, according to Richard Taruskin,[19] "its descending whole-step/half-step bass progression is complete and continuous".

Taruskin[20] also cites the following bars from J. S. Bach's English Suite No. 3 as octatonic:

Honoré Langlé's 1797 harmony treatise contains a sequential progression with a descending octatonic bass, supporting harmonies that use all and only the notes of an octatonic scale.[21]
19th century
[edit]In 1800, Beethoven composed his Piano Sonata No. 11 in B♭, Op. 22. The slow movement of this work contains a passage of what was, for its time, highly dissonant harmony. In a lecture (2005),[22] pianist András Schiff describes the harmony of this passage as "really extraordinary". The chord progressions at the beginning of the second and third bars of this passage are octatonic:

Octatonic scales can be found in Chopin's Mazurka, Op. 50, No. 3 and in several Liszt piano works: the closing measures of the third Étude de Concert, "Un Sospiro," for example, where (mm. 66–70) the bass contains a complete falling octatonic scale from D-flat to D-flat, in the opening piano cadenzas of Totentanz, in the lower notes between the alternating hands, and in the First Mephisto Waltz, in which a short cadenza (m. 525) makes use of it by harmonizing it with a B-flat Diminished Seventh chord. Later in the 19th century, the notes in the chords of the coronation bells from the opening scene of Modest Mussorgsky's opera Boris Godunov, which consist of "two dominant seventh chords with roots a tritone apart" according to Taruskin,[23] are entirely derived from an octatonic scale.

Taruskin continues: "Thanks to the reinforcement the lesson has received in some equally famous pieces like Scheherazade, the progression is often thought of as being peculiarly Russian."[23]
Tchaikovsky was also influenced by the harmonic and coloristic potential of octatonicism. As Mark DeVoto[24] points out, the cascading arpeggios played on the celesta in the "Sugar Plum Fairy" from The Nutcracker ballet are made up of dominant seventh chords a minor third apart.

"Hagens Watch", one of the darkest and most sinister scenes in Richard Wagner's opera Götterdämmerung features chromatic harmonies using eleven of the twelve chromatic notes, within which the eight notes of the octatonic scale may be found in bars 9–10 below:

Late 19th and 20th century
[edit]

The scale is also found in the music of Claude Debussy and Maurice Ravel. Melodic phrases that move by alternating tones and semitones frequently appear in the works of both these composers. Allen Forte[27] identifies a five-note segment in the cor anglais melody heard near the start of Debussy's "Nuages" from his orchestral suite Nocturnes as octatonic. Mark DeVoto[28] describes "Nuages" as "arguably [Debussy's] boldest single leap into the musical unknown. 'Nuages' defines a kind of tonality never heard before, based on the centricity of a diminished tonic triad (B-D-F natural)." According to Stephen Walsh, the cor anglais theme "hangs in the texture like some motionless object, always the same and always at the same pitch".[29] There is a particularly striking and effective use of the octatonic scale in the opening bars of Liszt's late piece Bagatelle sans tonalité from 1885.[citation needed]
The scale was extensively used by Rimsky-Korsakov's student Igor Stravinsky, particularly in his Russian-period works such as Petrushka (1911), The Rite of Spring (1913), up to the Symphonies of Wind Instruments (1920). Passages using this scale are unmistakable as early as the Scherzo fantastique, Fireworks (both from 1908), and The Firebird (1910). It also appears in later works by Stravinsky, such as the Symphony of Psalms (1930), the Symphony in Three Movements (1945), most of the neoclassical works from the Octet (1923) to Agon (1957), and even in some of the later serial compositions such as the Canticum Sacrum (1955) and Threni (1958). In fact, "few if any composers have been known to employ relations available to the collection as extensively or in as varied a manner as Stravinsky".[30]
The second movement of Stravinsky's Octet[31] for wind instruments opens with what Stephen Walsh[32] calls "a broad melody completely in the octatonic scale". Jonathan Cross[33] describes a highly rhythmic passage[34] in the first movement of the Symphony in Three Movements as "gloriously octatonic, not an unfamiliar situation in jazz, where this mode is known as the 'diminished scale', but Stravinsky of course knew it from Rimsky. The 'rumba' passage... alternates chords of E-flat7 and C7, over and over, distantly recalling the coronation scene from Mussorgsky's Boris Godunov. In celebrating America, the émigré looked back once again to Russia." Van den Toorn[35] catalogues many other octatonic moments in Stravinsky's music.
The scale also may be found in music of Alexander Scriabin and Béla Bartók. In Bartók's Bagatelles, Fourth Quartet, Cantata Profana, and Improvisations, the octatonic is used with the diatonic, whole tone, and other "abstract pitch formations" all "entwined... in a very complex mixture".[36] Mikrokosmos Nos. 99, 101, and 109 are octatonic pieces, as is No. 33 of the 44 Duos for Two Violins. "In each piece, changes of motive and phrase correspond to changes from one of the three octatonic scales to another, and one can easily select a single central and referential form of 8–28 in the context of each complete piece." However, even his larger pieces also feature "sections that are intelligible as 'octatonic music'".[37]
Olivier Messiaen made frequent use of the octatonic scale throughout his career as a composer, and indeed in his seven modes of limited transposition, the octatonic scale is Mode 2. Peter Hill[38] writes in detail about "La Colombe" (The Dove),[39] the first of a set of Preludes for piano that Messiaen completed in 1929, at the age of 20. Hill speaks of a characteristic "merging of tonality (E major) with the octatonic mode" in this short piece.
Other twentieth-century composers who used octatonic collections include Samuel Barber, Ernest Bloch, Benjamin Britten, Julian Cochran, George Crumb, Irving Fine, Ross Lee Finney, Alberto Ginastera, John Harbison, Jacques Hétu, Aram Khachaturian, Witold Lutosławski, Darius Milhaud, Henri Dutilleux, Robert Morris, Carl Orff, Jean Papineau-Couture, Krzysztof Penderecki, Francis Poulenc, Sergei Prokofiev, Alexander Scriabin, Dmitri Shostakovich, Toru Takemitsu, Joan Tower,[40] Robert Xavier Rodriguez, John Williams[41] and Frank Zappa.[42] Other composers include Willem Pijper,[43] who may have inferred the collection from Stravinsky's The Rite of Spring, which he greatly admired, and composed at least one piece—his Piano Sonatina No. 2—entirely in the octatonic system.[44]
In the 1920s, Heinrich Schenker criticized the use of the octatonic scale, specifically Stravinsky's Concerto for Piano and Wind Instruments, for the oblique relation between the diatonic scale and the harmonic and melodic surface.[14]
Jazz
[edit]Both the half-whole diminished and its partner mode, the whole-half diminished (with a tone rather than a semitone beginning the pattern) are commonly used in jazz improvisation, frequently under different names. The whole-half diminished scale is commonly used in conjunction with diminished harmony (e.g., the Edim7 chord) while the half-whole scale is used in dominant harmony (e.g., with an F![]() ♭9 chord).
♭9 chord).
Examples of octatonic jazz include Jaco Pastorius' composition "Opus Pocus"[45] from the album Pastorius[46][failed verification] and Herbie Hancock's piano solo on "Freedom Jazz Dance"[47][48] from the album Miles Smiles (1967).
Rock and pop
[edit]Jonny Greenwood of the English rock group Radiohead uses the octatonic scale extensively, such as in the song "Just" and his soundtrack for the film The Power of the Dog.[49][50] He said "It's a slightly more grownup version of the pentatonic scales that we're all taught to do with xylophones and glockenspiels when you're a kid. It's not a major scale or a minor scale; it's something else. But all the notes work together and make a certain color that is its own thing."[49]
The scale is used in progressive heavy metal music such as that by Dream Theater and Opeth, both of which strive for a dissonant and tonally ambiguous sound in their music. Examples include the instrumental break in Dream Theater's Octavarium and Opeth's Deliverance. Earlier examples of the scale's use in progressive rock include King Crimson's Red and Emerson Lake & Palmer's The Barbarian.
Progressive keyboardist Derek Sherinian is also closely associated with the octatonic scale, which can be found in most of his works, both solo and as part of a band. Examples include Planet X's Desert Girl and Sons of Apollo's King of Delusion. The dissonances associated with the scale when used in conjunction with conventional tonality form an integral part of his signature sound which has influenced hundreds of keyboardists of the 21st century.
Harmonic implications
[edit]Petrushka chord
[edit]
The Petrushka chord is a recurring polytonal device used in Igor Stravinsky's ballet Petrushka and in later music. In the Petrushka chord, two major triads, C major and F♯ major – a tritone apart – clash, "horribly with each other", when sounded together and create a dissonant chord.[52] The six-note chord is contained within an octatonic scale.
French sixth and Mystic chord
[edit]While used functionally as a pre-dominant chord in the classical period, late romantic composers saw the French sixth used as a dissonant and unstable chord. The chord can be built from the first, fourth, sixth and eighth degrees of the half-step/whole-step octatonic scale, and is transpositionally invariant about a tritone, a property somewhat contributing to its popularity. The octatonic collection contains two distinct French sixth chords a minor third apart, and since they share no notes, the scale can be thought of as the union of those two chords. For example, two French sixths based on G and E contain all the notes of an octatonic scale between them.
The octatonic scale is used very frequently for melodic material above a French sixth chord throughout the 19th and 20th centuries, particularly in Russia, in the music of Rimsky-Korsakov, Mussorgsky, Scriabin and Stravinsky, but also outside Russia in the works of Debussy and Ravel. Examples include Rimsky's Scheherezade,[53] Scriabin's Five Preludes, Op. 74,[54] Debussy's Nuages and Ravel's Scarbo.[55] All works are full of non-functional French sixths, and the octatonic scale is almost always the mode of choice.
By adding a major sixth above the root, from within the scale, and a major second, from outside the scale, the new chord is the Mystic chord found in some of Scriabin's late works. While no longer transpositionally invariant, Scriabin teases the tritone symmetry of the French sixth in his music by alternating transpositions of the Mystic chord a tritone apart, implying the notes of an octatonic scale.
Bitonality
[edit]In Béla Bartók's piano piece, "Diminished Fifth" from Mikrokosmos, octatonic collections form the basis of the pitch content. In mm. 1–11, all eight pitch classes from the E♭ diminished scale appear. In mm. 1–4, the pitch classes A, B, C, and D appear in the right hand, and the pitch classes E♭, F, G♭, and A♭ are in the left hand. The collection in the right hand outlines the first four notes of an A minor scale, and the collection in the left hand outlines the first four notes of an E♭ minor scale. In mm. 5–11, the left and right hand switch—the A minor tetrachord appears in the left hand, and the E♭ minor tetrachord appears in the right hand.[original research?]
From this, one can see that Bartók has partitioned the octatonic collection into two (symmetrical) four-note segments of the natural minor scales a tritone apart. Paul Wilson argues against viewing this as bitonality since "the larger octatonic collection embraces and supports both supposed tonalities".[56]
Bartók also utilizes the two other octatonic collections so that all three possible octatonic collections are found throughout this piece (D♭, D, and E♭). In mm. 12–18, all eight pitch classes from the D♭ octatonic collection are present. The E♭ octatonic collection from mm. 1–11 is related to this D♭ octatonic collection by the transposition operations, T, T4, T7, T10. In mm. 26–29, all eight pitch classes from the D octatonic collection appear. This collection is related to the E♭ octatonic collection from mm. 1–11 by the following transposition operations: T2, T5, T8, T11.[original research?]
Other relevant features of the piece include the groups of three notes taken from the whole-half diminished scale in mm. 12–18. In these measures, the right hand features D♭, E♭, and G♭, the tetrachord without the 3rd (F). The left hand has the same tetrachord transposed down a tritone (G, A, C). In mm. 16, both hands transpose down three semitones to B♭, C, E♭ and E, G♭, A respectively. Later on, in mm. 20, the right hand moves on to A− and the left back to E♭−. After repeating the structure of mm. 12–19 in mm. 29–34 the piece ends with the treble part returning to A− and the bass part returning to E♭.[original research?]
Alpha chord
[edit]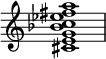

The alpha chord (α chord) collection is, "a vertically organized statement of the octatonic scale as two diminished seventh chords", such as: C♯–E–G–B♭–C–E♭–F♯–A.[57]
One of the most important subsets of the alpha collection, the alpha chord (Forte number: 4-17, pitch class prime form (0347)), such as E–G–C–E♭; using the theorist Ernő Lendvai's terminology,[58] the C alpha chord may be considered a mistuned major chord or major/minor in first inversion (in this case, C major/minor).[59][clarification needed] The number of semitones in the interval array of the alpha chord corresponds to the Fibonacci sequence.[60][further explanation needed]
Beta chord
[edit]
The beta chord (β chord) is a five-note chord, formed from the first five notes of the alpha chord (integers: 0,3,6,9,11;[61] notes: C♯, E, G, B♭, C♮). The beta chord can also occur in its reduced form, that is, limited to the characteristic tones (C♯, E, G, C♮ and C♯, G, C♮). Forte number: 5-31B.
The beta chord may be created from a diminished seventh chord by adding a diminished octave. It may be created from a major chord by adding the sharpened root (solfege: in C, di is C♯: C♯, E, G, C♮),[62] or from a diminished triad by adding the root's major 7th (called a diminished major 7th, or C#oMaj7. The diminished octave is inverted creates a minor ninth,[clarification needed] creating a C(♭9) chord, a sound commonly heard in the V chord during an authentic cadence in a minor key.[citation needed]
Gamma chord
[edit]The gamma chord (γ chord) is 0,3,6,8,11 (Forte number 5-32A)[61] It is the beta chord with one interval diminished: C♯, E, G, A, C♮. It may be considered a major-minor minor seventh chord on A: A, C♮, C♯, E, G. See also: Elektra chord. This is also commonly known as the Hendrix chord,[citation needed] or in jazz music as a Dominant 7♯9 chord; the notes in this case creating an A7♯9.
Hungarian major and Romanian major
[edit]The Hungarian major scale and Romanian major scale are both heptatonic subsets of the octatonic scale with one scale degree removed. The Hungarian major scale has the ♭2 degree removed, while the Romanian major scale has the ♭3 degree removed.
See also
[edit]- 15 equal temperament has a ten-note analogue
- Complexe sonore
- Alpha scale
- Beta scale
- Delta scale
- Gamma scale
- List of pieces which use the octatonic scale
References
[edit]- ^ Kahan 2009, [page needed].
- ^ Frazzi 1930.
- ^ Sanguinetti 1993, [page needed].
- ^ Taruskin 1985, 132.
- ^ Taruskin 1985, 111–113, citing Yavorsky 1911
- ^ Kholopov 1982, 30.
- ^ Kholopov 2003, 227.
- ^ Campbell 2001, 126.
- ^ Hatfield 2005, 125.
- ^ a b Levine 1995, 78.
- ^ Taruskin 1985, 73.
- ^ Schuijer 2008, 109.
- ^ Cohn 1991, 271.
- ^ a b Pople 1991, 2.
- ^ Schillinger 1946, [page needed].
- ^ Rimsky-Korsakov 1935.
- ^ Van den Toorn 1983, 329, 493n5.
- ^ Agmon 1990, 1–8.
- ^ Taruskin 1996, 266.
- ^ Taruskin 1996, 269.
- ^ Langlé 1797, 72, ex. 25.2.
- ^ Schiff 2005.
- ^ a b Taruskin 1996, 283.
- ^ DeVoto 2007, 144.
- ^ "Hagen's Watch"
- ^ van der Merwe 2005, 228.
- ^ Forte 1991, 144–145.
- ^ DeVoto 2003, 183.
- ^ Walsh 2018, 137.
- ^ Van den Toorn 1983, 42.
- ^ Stravinsky's Octet
- ^ Walsh 1988, 127.
- ^ Cross 2015, 144.
- ^ Archived at Ghostarchive and the Wayback Machine: "Igor Stravinsky - Symphony in Three Movements". YouTube. 15 March 2014.
- ^ Van den Toorn 1983.
- ^ Antokoletz 1984, [page needed].
- ^ Wilson 1992, 26–27.
- ^ Hill 1995, 73.
- ^ "La Colombe" (The Dove)
- ^ Alegant 2010, 109.
- ^ Durrand 2020, p. [page needed].
- ^ Clement 2009, 214.
- ^ Chan 2005, 52.
- ^ Van den Toorn 1983, 464n11.
- ^ "Opus Pocus"
- ^ Pastorius 1976.
- ^ Piano solo on "Freedom Jazz Dance"
- ^ Tymoczko, D. (2017, bars 18-21, right hand part) Transcription of Piano solo from “Freedom Jazz dance” https://dmitri.mycpanel.princeton.edu/transcriptions.html accessed 24/11/2021.
- ^ a b Ross, Alex (2021-12-19). "How Jonny Greenwood wrote the year's best film score". The New Yorker. Retrieved 2021-12-19.
- ^ Ross, Alex (August 12, 2001). "The Searchers". The New Yorker. Archived from the original on 14 February 2008. Retrieved 2021-07-11.
- ^ Taruskin 1987, 269.
- ^ Pogue 1997, 80.
- ^ Ears Wide Open Online | Deconstructing Rimsky-Korsakov's Scheherazade, 15 June 2020, retrieved 2023-08-19
- ^ Scriabin's Use Of The Octotonic Scale, 20 March 2022, retrieved 2023-08-19
- ^ Ravel, Maurice (1908). "Gaspard de la nuit: III. Scarbo, piano score" (PDF).
- ^ Wilson 1992, 27.
- ^ Wilson 1992, 7.
- ^ Lendvai 1971.
- ^ Wilson 1992, 9.
- ^ Slayton 2010, 15.
- ^ a b Honti 2007, 305.
- ^ Anon. 1977, 12.
Sources
- Anon. (1977). [Untitled article]. Soundings, 6–9, p. 12. University College.
- Agmon, Eytan (1990). "Equal Divisions of the Octave in a Scarlatti Sonata." In Theory Only 11, no. 5:1–8.
- Alegant, Brian (2010). The Twelve-Tone Music of Luigi Dallapiccola. [full citation needed] ISBN 978-1-58046-325-6.
- Antokoletz, Elliott (1984). The Music of Béla Bartók: A Study of Tonality and Progression in Twentieth-Century Music. Berkeley and Los Angeles: University of California Press. Cited in Wilson directly above.[where?] ISBN 0-520-06747-9.
- Campbell, Gary (2001). Triad Pairs for Jazz: Practice and Application for the Jazz Improvisor. [full citation needed] ISBN 0-7579-0357-6.
- Chan, Hing-yan (2005). New Music in China and the C.C. Liu Collection at the University of Hong Kong. [full citation needed] ISBN 978-962-209-772-8.
- Clement, Brett (2009). A Study of the Instrumental Music of Frank Zappa (PhD dissertation). University of Cincinnati.
- Cohn, Richard (1991). "Bartók's Octatonic Strategies: A Motivic Approach." Journal of the American Musicological Society 44, no. 2 (Summer): 262–300.
- Cross, Jonathan (2015). Igor Stravinsky. London: Reaction Books.
- DeVoto, Mark (2003). "The Debussy Sound: Colouyr, Texture, Gesture". In The Cambridge Companion to Debussy, edited by Simon Tresize, 179–196. Cambridge Companions to Music. Cambridge and New York: Cambridge University Press. ISBN 0-521-65243-X (cloth); ISBN 0-521-65478-5 (pbk).
- DeVoto, Mark (2007) "Boris's Bells, by Way of Schubert and Others". Current Musicology, no. 83 (Spring): [page needed]..
- Durrand, M. (2020). Music in Action Film. Taylor & Francis. ISBN 9781351204255.
- Forte, Allen (1991). "Debussy and the Octatonic". Music Analysis 10, nos. 1–2 (March–July): 125–169.
- Frazzi, Vito (1930). Scale alternate per pianoforte con diteggiature di Ernesto Consolo. Florence: A. Forlivesi.
- Hatfield, Ken (2005). Mel Bay Jazz and the Classical Guitar Theory and Applications.[full citation needed] ISBN 0-7866-7236-6.
- Hill, Peter (1995). The Messiaen Companion. London: Faber and Faber.
- Honti, Rita (2007). Principles of pitch organization in Bartók's Duke Bluebeard's Castle. University of Helsinki. ISBN 978-952-10-3837-2.
- Kahan, Sylvia (2009). In Search of New Scales: Prince Edmond de Polignac, Octatonic Explorer. Rochester, NY: University of Rochester Press. ISBN 978-1-58046-305-8.
- Kholopov, Yuri (2003). Harmony. Theoretical Course. Orig. title: Гармония. Теоретический курс. Moscow: Lan'.[full citation needed]
- Kholopov, Yuri (1982). "Modal harmony. Modality as a type of harmonic structure". Art of Music. General Questions of Music Theory and Aesthetics: 16–31; Orig. title: Модальная гармония: Модальность как тип гармонической структуры // Музыкальное искусство. Общие вопросы теории и эстетики музыки. Ташкент: Издательство литературы и искусства им. Г. Гуляма[full citation needed]
- Langlé, Honoré François Marie (1797). Traité d'harmonie et de modulation. Paris: Boyer.
- Lendvai, Ernő (1971). Béla Bartók: An Analysis of his Music. introd. by Alan Bush. London: Kahn & Averill. ISBN 0-900707-04-6. OCLC 240301. Cited in Wilson (1992).
- Levine, Mark (1995). The Jazz Theory Book. Sher Music. ISBN 1-883217-04-0.
- Pastorius, Jaco (1976). "Opus Pocus". Spotify.com (accessed 1 October 2015).
- Pogue, David (1997). Classical Music for Dummies. [full citation needed] ISBN 0-7645-5009-8.
- Pople, Anthony (1991). Berg: Violin Concerto. Cambridge and New York: Cambridge University Press. ISBN 0-521-39976-9.
- Rimsky-Korsakov, Nicholas (1935). My Musical Life, translated by Judah A. Joffee. New York: Tudor.
- Sanguinetti, Giorgio (1993). "Il primo studio teorico sulle scale octatoniche: Le 'scale alternate' di Vito Frazzi." Studi Musicali 22, no. 2:[page needed]
- Schiff, András (2005). "Untitled lecture". The Guardian TV (16 November; accessed 1 October 2015).
- Schillinger, Joseph (1946). The Schillinger System of Musical Composition, Vol. 1: Books I–VII, edited by Lyle Dowling and Arnold Shaw. New York: Carl Fischer.
- Schuijer, Michiel (2008). Analyzing Atonal Music: Pitch-Class Set Theory and Its Contexts. [full citation needed] ISBN 978-1-58046-270-9.
- Slayton, Michael K. (2010). Women of Influence in Contemporary Music: Nine American Composers. [full citation needed]ISBN 978-0-8108-7748-1.
- Taruskin, Richard (1985). "Chernomor to Kashchei: Harmonic Sorcery; or, Stravinsky's 'Angle'". Journal of the American Musicological Society 38, no. 1 (Spring): 72–142.
- Taruskin, Richard (1987). "Chez Pétrouchka- Harmony and Tonality "chez" Stravinsky". 19th-Century Music 10, no. 3 (Spring, Special Issue: Resolutions I): 265–286.
- Taruskin, Richard (1996) Stravinsky and the Russian Traditions. Oxford and New York: Oxford University Press.
- Van den Toorn, Pieter (1983). The Music of Igor Stravinsky. New Haven and London: Yale University Press. ISBN.
- Van der Merwe, Peter (2005). Roots of the Classical. Oxford and New York: Oxford University Press. ISBN 978-0-19-816647-4.
- Walsh, Stephen (1988). The Music of Stravinsky. London: Routledge.
- Walsh, Stephen (2018). Debussy, a Painter in Sound. London: Faber and Faber.[ISBN missing]
- Wilson, Paul (1992). The Music of Béla Bartók. [full citation needed] ISBN 0-300-05111-5.
- Yavorsky, Boleslav Leopoldovich (1911). "Neskol'ko myslei v sviazi s iubileem Frantsa Lista". Muzyka no. 45 (8 October): 961. Cited in Taruskin (1985, 113).
Further reading
[edit]- Baur, Steven (1999). "Ravel's 'Russian' Period: Octatonicism in His Early Works, 1893–1908." Journal of the American Musicological Society 52, no. 1:[page needed].
- Berger, Arthur (1963). "Problems of Pitch Organization in Stravinsky". Perspectives of New Music 2, no. 1 (Fall–Winter): 11–42.
- Gillespie, Robert (2015). "Herbie Hancock: Freedom Jazz Dance Transcription". (Accessed 1 October 2015).
- Keeling, Andrew (2013). "Red". The Concise Musical Guide to King Crimson and Robert Fripp (1969–1984). Cambridge: Spaceward. pp. 53–58. ISBN 978-0-9570489-3-5.
- Tymoczko, Dmitri (2002). "Stravinsky and the Octatonic: A Reconsideration". Music Theory Spectrum 24, no. 1 (Spring): 68–102.
- Wollner, Fritz (1924) "7 mysteries of Stravinsky in Progression" 1924 German international school of music study.[full citation needed]
