Chemostat
| Chemostat | |
|---|---|
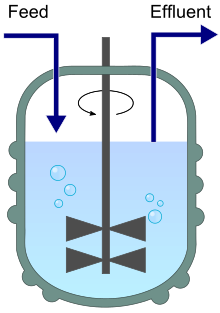 A chemostat diagram featuring inflow (feed) and outflow (effluent). | |
| Industry | Biological engineering |
| Application | Research and Industry |

A chemostat (from chemical environment is static) is a bioreactor to which fresh medium is continuously added, while culture liquid containing left over nutrients, metabolic end products and microorganisms is continuously removed at the same rate to keep the culture volume constant.[2][3] By changing the rate with which medium is added to the bioreactor the specific growth rate of the microorganism can be easily controlled within limits.
Operation[edit]
Steady state[edit]
One of the most important features of chemostats is that microorganisms can be grown in a physiological steady state under constant environmental conditions. In this steady state, growth occurs at a constant specific growth rate and all culture parameters remain constant (culture volume, dissolved oxygen concentration, nutrient and product concentrations, pH, cell density, etc.). In addition, environmental conditions can be controlled by the experimenter.[4] Microorganisms growing in chemostats usually reach a steady state because of a negative feedback between growth rate and nutrient consumption: if a low number of cells are present in the bioreactor, the cells can grow at growth rates higher than the dilution rate as they consume little nutrient so growth is less limited by the addition of limiting nutrient with the inflowing fresh medium. The limiting nutrient is a nutrient essential for growth, present in the medium at a limiting concentration (all other nutrients are usually supplied in surplus). However, the higher the number of cells becomes, the more nutrient is consumed, lowering the concentration of the limiting nutrient. In turn, this will reduce the specific growth rate of the cells, which will lead to a decline in the number of cells as they keep being removed from the system with the outflow. This results in a steady state. Due to self-regulation, the steady state is stable. This enables the experimenter to control the specific growth rate of the microorganisms by changing the speed of the pump feeding fresh medium into the vessel.
Well-mixed[edit]
Another important feature of chemostats and other continuous culture systems is that they are well-mixed so that environmental conditions are homogenous or uniform and microorganisms are randomly dispersed and encounter each other randomly. Therefore, competition and other interactions in the chemostat are global, in contrast to biofilms.
Dilution rate[edit]
The rate of nutrient exchange is expressed as the dilution rate D. At steady state, the specific growth rate μ of the micro-organism is equal to the dilution rate D. The dilution rate is defined as the flow of medium per unit of time, F, over the volume V of culture in the bioreactor
Maximal growth rate and critical dilution rate[edit]
Specific growth rate μ is inversely related to the time it takes the biomass to double, called doubling time td, by:
Therefore, the doubling time td becomes a function of dilution rate D in steady state:
Each microorganism growing on a particular substrate has a maximal specific growth rate μmax (the rate of growth observed if growth is limited by internal constraints rather than external nutrients). If a dilution rate is chosen that is higher than μmax, the cells cannot grow at a rate as fast as the rate with which they are being removed so the culture will not be able to sustain itself in the bioreactor, and will wash out.
However, since the concentration of the limiting nutrient in the chemostat cannot exceed the concentration in the feed, the specific growth rate that the cells can reach in the chemostat is usually slightly lower than the maximal specific growth rate because specific growth rate usually increases with nutrient concentration as described by the kinetics of the Monod equation. [citation needed] The highest specific growth' rates (μmax) cells can attain is equal to the critical dilution rate (D'c):
where S is the substrate or nutrient concentration in the chemostat and KS is the half-saturation constant (this equation assumes Monod kinetics).
Applications[edit]
Research[edit]
Chemostats in research are used for investigations in cell biology, as a source for large volumes of uniform cells or protein. The chemostat is often used to gather steady state data about an organism in order to generate a mathematical model relating to its metabolic processes. Chemostats are also used as microcosms in ecology[5][6] and evolutionary biology.[7][8][9][10] In the one case, mutation/selection is a nuisance, in the other case, it is the desired process under study. Chemostats can also be used to enrich for specific types of bacterial mutants in culture such as auxotrophs or those that are resistant to antibiotics or bacteriophages for further scientific study.[11] Variations in the dilution rate permit the study of the metabolic strategies pursued by the organisms at different growth rates.[12][13]
Competition for single and multiple resources, the evolution of resource acquisition and utilization pathways, cross-feeding/symbiosis,[14][15] antagonism, predation, and competition among predators have all been studied in ecology and evolutionary biology using chemostats.[16][17][18]
Industry[edit]
Chemostats are frequently used in the industrial manufacturing of ethanol. In this case, several chemostats are used in series, each maintained at decreasing sugar concentrations.[citation needed] The chemostat also serves as an experimental model of continuous cell cultures in the biotechnological industry.[13]
Technical concerns[edit]
- Foaming results in overflow with the volume of liquid not exactly constant.
- Some very fragile cells are ruptured during agitation and aeration.
- Cells may grow on the walls or adhere to other surfaces,[19] which may be overcome by treating the glass walls of the vessel with a silane to render them hydrophobic. However, cells will be selected for attachment to the walls since those that do will not be removed from the system. Those bacteria that stick firmly to the walls forming a biofilm are difficult to study under chemostat conditions.
- Mixing may not truly be uniform, upsetting the "static" property of the chemostat.
- Dripping the media into the chamber actually results in small pulses of nutrients and thus oscillations in concentrations, again upsetting the "static" property of the chemostat.
- Bacteria travel upstream quite easily. They will reach the reservoir of sterile medium quickly unless the liquid path is interrupted by an air break in which the medium falls in drops through air.
Continuous efforts to remedy each defect lead to variations on the basic chemostat quite regularly. Examples in the literature are numerous.
- Antifoaming agents are used to suppress foaming.
- Agitation and aeration can be done gently.
- Many approaches have been taken to reduce wall growth[20][21]
- Various applications use paddles, bubbling, or other mechanisms for mixing[22]
- Dripping can be made less drastic with smaller droplets and larger vessel volumes
- Many improvements target the threat of contamination
Experimental design considerations[edit]
This section relies largely or entirely on a single source. (December 2019) |
Parameter choice and setup[edit]
- The steady state concentration of the limiting substrate in the chemostat is independent of the influx concentration. The influx concentration will affect the cell concentration and thus the steady state OD.
- Even though the limiting substrate concentration in the chemostat is usually very low, and is maintained by discrete highly concentrated influx pulses, in practice the temporal variation in the concentration within the chemostat is small (a few percent or less) and can thus be viewed as quasi-steady state.
- The time it takes for the cell density (OD) to converge to a steady-state value (overshoot/undershoot) will often be long (multiple chemostat turnovers), especially when the initial inoculum is large. But, the time can be minimized with proper parameter choice.
Steady state growth[edit]
- A chemostat might appear to be in steady state, but mutant strain takeovers can occur continuously, even though they are not detectable by monitoring macro scale parameters like OD or product concentrations.
- The limiting substrate is usually at such low concentrations that it is undetectable. As a result, the concentration of the limiting substrate can vary greatly over time (percentage-wise) as different strains takeover the population, even if resulting changes in OD are too small to detect.
- A “pulsed” chemostat (with very large influx pulses) has a substantially lower selective capacity than a standard quasi-continuous chemostat, for a mutant strain with increased fitness in limiting conditions.
- By abruptly lowering the influx limiting substrate concentration it is possible to temporarily subject the cells to relatively harsher conditions, until the chemostat stabilizes back to the steady state (on the time order of the dilution rate D).
Mutation[edit]
- Some types of mutant strains will appear rapidly:
- If there is a SNP that can increase fitness it should appear in the population after only few chemostat doublings, for characteristically large chemostats (e.g. 10^11 E. coli cells).
- A strain that requires two specific SNPs where only their combination gives a fitness advantage (whereas each one separately is neutral), is likely to appear only if the target size (the number of different SNP locations that give rise to an advantageous mutation) for each SNP is very large.
- Other types of mutant strains (e.g. two SNPs with a small target size, more SNPs or in smaller chemostats) are highly unlikely to appear.
- These other mutations are expected only through successive sweeps of mutants with a fitness advantage. One can only expect multiple mutants to arise if each mutation is independently beneficial, and not in cases where the mutations are individually neutral but together advantageous. Successive takeovers are the only reliable way for evolution to proceed in a chemostat.
- The seemingly extreme scenario where we require every possible single SNP to co-exist at least once in the chemostat is actually quite likely. A large chemostat is very likely to reach this state.
- For a large chemostat the expected time until an advantageous mutation occurs to be on the order of the chemostat turnover time. Note, this is usually substantially shorter than the time for an advantageous strain to take over the chemostat population. This is not necessarily so in a small chemostat.
- The above points are expected to be the same across different asexually reproductive species (E. coli, S. cerevisiae, etc.).
- Furthermore, the time until mutation appearance is independent of genome size, but dependent on per-BP mutation rate.
- For characteristically large chemostats, a hyper-mutating strain does not give enough of an advantage to warrant use. Also, it does not have enough of a selective advantage to be expected to always appear through random mutation and take over the chemostat.
Single takeover[edit]
- The takeover time is predictable given the relevant strain parameters.
- Different dilution rates selectively favor different mutant strains to take over the chemostat population, if such a strain exists. For example:
- A fast dilution rate creates a selection pressure for a mutant strain with a raised maximal growth rate;
- A mid-range dilution rate creates a selection pressure for a mutant strain with a higher affinity to the limiting substrate;
- A slow dilution rate creates a selection pressure for a mutant strain which can grow in media with no limiting substrate (presumably by consuming a different substrate present in the media);
- The time for takeover of a superior mutant will be quite constant across a range of operation parameters. For characteristic operation values the take over time is on the order of days to weeks.
Successive takeovers[edit]
- When the conditions are right (a large enough population, and multiple targets in the genome for simple advantageous mutations) multiple strains are expected to successively takeover the population, and to do so in a relatively timed and paced manner. The timing depends on the type of mutations.
- In a takeover succession, even if the selective improvement of each of the strains stays constant (e.g. each new strain is better than the previous strain by a constant factor) – the takeover rate does not stay constant, but rather diminishes from strain to strain.
- There are cases where successive takeovers occur so rapidly that it is very difficult to differentiate between strains, even when examining allele frequency. Thus, a lineage of multiple takeovers of consecutive strains might appear as the takeover of a single strain with a cohort of mutations.
Variations[edit]
Fermentation setups closely related to the chemostats are the turbidostat, the auxostat and the retentostat. In retentostats, culture liquid is also removed from the bioreactor, but a filter retains the biomass. In this case, the biomass concentration increases until the nutrient requirement for biomass maintenance has become equal to the amount of limiting nutrient that can be consumed.
See also[edit]
- Bacterial growth
- Biochemical engineering
- Continuous stirred-tank reactor (CSTR)
- E. coli long-term evolution experiment
- Fed-batch
References[edit]
- ^ Madigan, Michael (2015). Brock Biology of Microorganisms. Pearson. pp. 152–153. ISBN 978-0-321-89739-8.
- ^ Novick A, Szilard L (1950). "Description of the Chemostat". Science. 112 (2920): 715–6. Bibcode:1950Sci...112..715N. doi:10.1126/science.112.2920.715. PMID 14787503.
- ^ James TW (1961). "Continuous Culture of Microorganisms". Annual Review of Microbiology. 15: 27–46. doi:10.1146/annurev.mi.15.100161.000331.
- ^ D Herbert; R Elsworth; RC Telling (1956). "The continuous culture of bacteria; a theoretical and experimental study". J. Gen. Microbiol. 14 (3): 601–622. doi:10.1099/00221287-14-3-601. PMID 13346021.
- ^ Becks L, Hilker FM, Malchow H, Jürgens K, Arndt H (2005). "Experimental demonstration of chaos in a microbial food web". Nature. 435 (7046): 1226–9. Bibcode:2005Natur.435.1226B. doi:10.1038/nature03627. PMID 15988524. S2CID 4380653.
- ^ Pavlou S, Kevrekidis IG (1992). "Microbial predation in a periodically operated chemostat: a global study of the interaction between natural and externally imposed frequencies". Math Biosci. 108 (1): 1–55. doi:10.1016/0025-5564(92)90002-E. PMID 1550993.
- ^ Wichman HA, Millstein J, Bull JJ (2005). "Adaptive Molecular Evolution for 13,000 Phage Generations: A Possible Arms Race". Genetics. 170 (1): 19–31. doi:10.1534/genetics.104.034488. PMC 1449705. PMID 15687276.
- ^ Dykhuizen DE, Dean AM (2004). "Evolution of specialists in an experimental microcosm". Genetics. 167 (4): 2015–26. doi:10.1534/genetics.103.025205. PMC 1470984. PMID 15342537.
- ^ Wick LM, Weilenmann H, Egli T (2002). "The apparent clock-like evolution of Escherichia coli in glucose-limited chemostats is reproducible at large but not at small population sizes and can be explained with Monod kinetics". Microbiology. 148 (Pt 9): 2889–902. doi:10.1099/00221287-148-9-2889. PMID 12213934.
- ^ Jones LE, Ellner SP (2007). "Effects of rapid prey evolution on predator-prey cycles". J Math Biol. 55 (4): 541–73. arXiv:q-bio/0609032. doi:10.1007/s00285-007-0094-6. PMID 17483952. S2CID 16927689.
- ^ Schlegel HG, Jannasch HW (1967). "Enrichment cultures". Annu. Rev. Microbiol. 21: 49–70. doi:10.1146/annurev.mi.21.100167.000405. PMID 4860267.
- ^ Varma, A.; Palsson, B. O. (1994-10-01). "Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli W3110". Applied and Environmental Microbiology. 60 (10): 3724–3731. Bibcode:1994ApEnM..60.3724V. doi:10.1128/aem.60.10.3724-3731.1994. ISSN 0099-2240. PMC 201879. PMID 7986045.
- ^ a b Fernandez-de-Cossio-Diaz, Jorge; Leon, Kalet; Mulet, Roberto (2017-11-13). "Characterizing steady states of genome-scale metabolic networks in continuous cell cultures". PLOS Computational Biology. 13 (11): e1005835. arXiv:1705.09708. Bibcode:2017PLSCB..13E5835F. doi:10.1371/journal.pcbi.1005835. ISSN 1553-7358. PMC 5703580. PMID 29131817.
- ^ Daughton CG, Hsieh DP (1977). "Parathion utilization by bacterial symbionts in a chemostat". Appl. Environ. Microbiol. 34 (2): 175–84. Bibcode:1977ApEnM..34..175D. doi:10.1128/aem.34.2.175-184.1977. PMC 242618. PMID 410368.
- ^ Pfeiffer T, Bonhoeffer S (2004). "Evolution of cross-feeding in microbial populations". Am. Nat. 163 (6): E126–35. doi:10.1086/383593. PMID 15266392. S2CID 31110741.
- ^ G. J. Butler; G. S. K. Wolkowicz (July 1986). "Predator-mediated competition in the chemostat". J Math Biol. 24 (2): 67–191. doi:10.1007/BF00275997. S2CID 120858390.
- ^ Dykhuizen DE, Hartl DL (June 1983). "Selection in chemostats". Microbiol. Rev. 47 (2): 150–68. doi:10.1128/mr.47.2.150-168.1983. PMC 281569. PMID 6308409.
- ^ Dykhuizen DE, Hartl DL (May 1981). "Evolution of Competitive Ability in Escherichia coli". Evolution. 35 (3): 581–94. doi:10.2307/2408204. JSTOR 2408204. PMID 28563589.
- ^ Bonomi A, Fredrickson AG (1976). "Protozoan feeding and bacterial wall growth". Biotechnol. Bioeng. 18 (2): 239–52. doi:10.1002/bit.260180209. PMID 1267931. S2CID 41343643.
- ^ de Crécy E, Metzgar D, Allen C, Pénicaud M, Lyons B, Hansen CJ, de Crécy-Lagard V (2007). "Development of a novel continuous culture device for experimental evolution of bacterial populations". Appl. Microbiol. Biotechnol. 77 (2): 489–96. doi:10.1007/s00253-007-1168-5. PMID 17896105. S2CID 25787277.
- ^ Zhang Z, Boccazzi P, Choi HG, Perozziello G, Sinskey AJ, Jensen KF (2006). "Microchemostat-microbial continuous culture in a polymer-based, instrumented microbioreactor". Lab Chip. 6 (7): 906–13. doi:10.1039/b518396k. PMID 16804595.
- ^ Van Hulle SW, Van Den Broeck S, Maertens J, Villez K, Schelstraete G, Volcke EI, Vanrolleghem PA (2003). "Practical experiences with start-up and operation of a continuously aerated lab-scale SHARON reactor". Commun. Agric. Appl. Biol. Sci. 68 (2 Pt A): 77–84. PMID 15296140.
- ^ a b c d e Wides A, Milo R (2018). "Understanding the Dynamics and Optimizing the Performance of Chemostat Selection Experiments". arXiv:1806.00272 [q-bio.PE].
External links[edit]
- http://www.pererikstrandberg.se/examensarbete/chemostat.pdf
- https://web.archive.org/web/20060504172359/http://www.rpi.edu/dept/chem-eng/Biotech-Environ/Contin/chemosta.htm
- A final thesis including mathematical models of the chemostat and other bioreactors
- A page about one laboratory chemostat design
- Comprehensive chemostat manual (Dunham lab). Procedures and principles are general.




