Coulomb's law

| Articles about |
| Electromagnetism |
|---|
 |
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law[1] of physics that calculates the amount of force between two electrically charged particles at rest. This electric force is conventionally called the electrostatic force or Coulomb force.[2] Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb. Coulomb's law was essential to the development of the theory of electromagnetism and maybe even its starting point,[1] as it allowed meaningful discussions of the amount of electric charge in a particle.[3]
The law states that the magnitude, or absolute value, of the attractive or repulsive electrostatic force between two point charges is directly proportional to the product of the magnitudes of their charges and inversely proportional to the squared distance between them.[4] Coulomb discovered that bodies with like electrical charges repel:
It follows therefore from these three tests, that the repulsive force that the two balls – [that were] electrified with the same kind of electricity – exert on each other, follows the inverse proportion of the square of the distance.[5]
Coulomb also showed that oppositely charged bodies attract according to an inverse-square law:
Here, ke is a constant, q1 and q2 are the quantities of each charge, and the scalar r is the distance between the charges.
The force is along the straight line joining the two charges. If the charges have the same sign, the electrostatic force between them makes them repel; if they have different signs, the force between them makes them attract.
Being an inverse-square law, the law is similar to Isaac Newton's inverse-square law of universal gravitation, but gravitational forces always make things attract, while electrostatic forces make charges attract or repel. Also, gravitational forces are much weaker than electrostatic forces.[2] Coulomb's law can be used to derive Gauss's law, and vice versa. In the case of a single point charge at rest, the two laws are equivalent, expressing the same physical law in different ways.[6] The law has been tested extensively, and observations have upheld the law on the scale from 10−16 m to 108 m.[6]
History[edit]

Ancient cultures around the Mediterranean knew that certain objects, such as rods of amber, could be rubbed with cat's fur to attract light objects like feathers and pieces of paper. Thales of Miletus made the first recorded description of static electricity around 600 BC,[7] when he noticed that friction could make a piece of amber attract small objects.[8][9]
In 1600, English scientist William Gilbert made a careful study of electricity and magnetism, distinguishing the lodestone effect from static electricity produced by rubbing amber.[8] He coined the Neo-Latin word electricus ("of amber" or "like amber", from ἤλεκτρον [elektron], the Greek word for "amber") to refer to the property of attracting small objects after being rubbed.[10] This association gave rise to the English words "electric" and "electricity", which made their first appearance in print in Thomas Browne's Pseudodoxia Epidemica of 1646.[11]
Early investigators of the 18th century who suspected that the electrical force diminished with distance as the force of gravity did (i.e., as the inverse square of the distance) included Daniel Bernoulli[12] and Alessandro Volta, both of whom measured the force between plates of a capacitor, and Franz Aepinus who supposed the inverse-square law in 1758.[13]
Based on experiments with electrically charged spheres, Joseph Priestley of England was among the first to propose that electrical force followed an inverse-square law, similar to Newton's law of universal gravitation. However, he did not generalize or elaborate on this.[14] In 1767, he conjectured that the force between charges varied as the inverse square of the distance.[15][16]

In 1769, Scottish physicist John Robison announced that, according to his measurements, the force of repulsion between two spheres with charges of the same sign varied as x−2.06.[17]
In the early 1770s, the dependence of the force between charged bodies upon both distance and charge had already been discovered, but not published, by Henry Cavendish of England.[18] In his notes, Cavendish wrote, "We may therefore conclude that the electric attraction and repulsion must be inversely as some power of the distance between that of the 2 + 1/50th and that of the 2 − 1/50th, and there is no reason to think that it differs at all from the inverse duplicate ratio".
Finally, in 1785, the French physicist Charles-Augustin de Coulomb published his first three reports of electricity and magnetism where he stated his law. This publication was essential to the development of the theory of electromagnetism.[4] He used a torsion balance to study the repulsion and attraction forces of charged particles, and determined that the magnitude of the electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
The torsion balance consists of a bar suspended from its middle by a thin fiber. The fiber acts as a very weak torsion spring. In Coulomb's experiment, the torsion balance was an insulating rod with a metal-coated ball attached to one end, suspended by a silk thread. The ball was charged with a known charge of static electricity, and a second charged ball of the same polarity was brought near it. The two charged balls repelled one another, twisting the fiber through a certain angle, which could be read from a scale on the instrument. By knowing how much force it took to twist the fiber through a given angle, Coulomb was able to calculate the force between the balls and derive his inverse-square proportionality law.
Scalar form[edit]
Coulomb's law can be stated as a simple mathematical expression. The scalar form gives the magnitude of the vector of the electrostatic force F between two point charges q1 and q2, but not its direction. If r is the distance between the charges, the magnitude of the force is where ε0 is the electric constant. If the product q1q2 is positive, the force between the two charges is repulsive; if the product is negative, the force between them is attractive.[19]
Vector form[edit]

Coulomb's law in vector form states that the electrostatic force experienced by a charge, at position , in the vicinity of another charge, at position , in a vacuum is equal to[20]
where is the displacement vector between the charges, a unit vector pointing from to , and the electric constant. Here, is used for the vector notation.
The vector form of Coulomb's law is simply the scalar definition of the law with the direction given by the unit vector, , parallel with the line from charge to charge .[21] If both charges have the same sign (like charges) then the product is positive and the direction of the force on is given by ; the charges repel each other. If the charges have opposite signs then the product is negative and the direction of the force on is ; the charges attract each other.
The electrostatic force experienced by , according to Newton's third law, is .
System of discrete charges[edit]
The law of superposition allows Coulomb's law to be extended to include any number of point charges. The force acting on a point charge due to a system of point charges is simply the vector addition of the individual forces acting alone on that point charge due to each one of the charges. The resulting force vector is parallel to the electric field vector at that point, with that point charge removed.
Force on a small charge at position , due to a system of discrete charges in vacuum is[20]
where is the magnitude of the ith charge, is the vector from its position to and is a unit vector in the direction of .
Continuous charge distribution[edit]
In this case, the principle of linear superposition is also used. For a continuous charge distribution, an integral over the region containing the charge is equivalent to an infinite summation, treating each infinitesimal element of space as a point charge . The distribution of charge is usually linear, surface or volumetric.
For a linear charge distribution (a good approximation for charge in a wire) where gives the charge per unit length at position , and is an infinitesimal element of length,[22]
For a surface charge distribution (a good approximation for charge on a plate in a parallel plate capacitor) where gives the charge per unit area at position , and is an infinitesimal element of area,
For a volume charge distribution (such as charge within a bulk metal) where gives the charge per unit volume at position , and is an infinitesimal element of volume,[21]
The force on a small test charge at position in vacuum is given by the integral over the distribution of charge
The "continuous charge" version of Coulomb's law is never supposed to be applied to locations for which because that location would directly overlap with the location of a charged particle (e.g. electron or proton) which is not a valid location to analyze the electric field or potential classically. Charge is always discrete in reality, and the "continuous charge" assumption is just an approximation that is not supposed to allow to be analyzed.
Coulomb constant[edit]
The Coulomb constant is a proportionality factor that appears in Coulomb's law and related formulas. Denoted , it is also called the electric force constant or electrostatic constant[23] hence the subscript 'e'. The Coulomb constant is given by . The constant is the vacuum electric permittivity (also known as the electric constant).[24] It should not be confused with , which is the dimensionless relative permittivity of the material in which the charges are immersed, or with their product , which is called "absolute permittivity of the material" and is still used in electrical engineering.
Since the 2019 redefinition of the SI base units,[25][26] the Coulomb constant, as calculated from CODATA 2018 recommended values, is[27]
Limitations[edit]
There are three conditions to be fulfilled for the validity of Coulomb's inverse square law:[28]
- The charges must have a spherically symmetric distribution (e.g. be point charges, or a charged metal sphere).
- The charges must not overlap (e.g. they must be distinct point charges).
- The charges must be stationary with respect to a nonaccelerating frame of reference.
The last of these is known as the electrostatic approximation. When movement takes place, Einstein's theory of relativity must be taken into consideration, and a result, an extra factor is introduced, which alters the force produced on the two objects. This extra part of the force is called the magnetic force, and is described by magnetic fields. For slow movement, the magnetic force is minimal and Coulomb's law can still be considered approximately correct, but when the charges are moving more quickly in relation to each other, the full electrodynamics rules (incorporating the magnetic force) must be considered.
Electric field[edit]
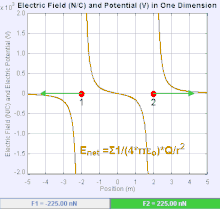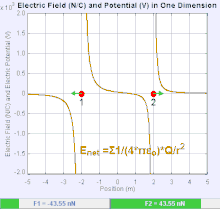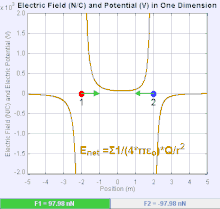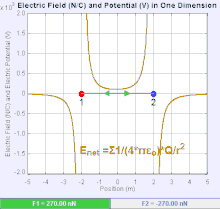
An electric field is a vector field that associates to each point in space the Coulomb force experienced by a unit test charge.[20] The strength and direction of the Coulomb force on a charge depends on the electric field established by other charges that it finds itself in, such that . In the simplest case, the field is considered to be generated solely by a single source point charge. More generally, the field can be generated by a distribution of charges who contribute to the overall by the principle of superposition.
If the field is generated by a positive source point charge , the direction of the electric field points along lines directed radially outwards from it, i.e. in the direction that a positive point test charge would move if placed in the field. For a negative point source charge, the direction is radially inwards.
The magnitude of the electric field E can be derived from Coulomb's law. By choosing one of the point charges to be the source, and the other to be the test charge, it follows from Coulomb's law that the magnitude of the electric field E created by a single source point charge Q at a certain distance from it r in vacuum is given by
A system of n discrete charges stationed at produces an electric field whose magnitude and direction is, by superposition
Atomic forces[edit]
Coulomb's law holds even within atoms, correctly describing the force between the positively charged atomic nucleus and each of the negatively charged electrons. This simple law also correctly accounts for the forces that bind atoms together to form molecules and for the forces that bind atoms and molecules together to form solids and liquids. Generally, as the distance between ions increases, the force of attraction, and binding energy, approach zero and ionic bonding is less favorable. As the magnitude of opposing charges increases, energy increases and ionic bonding is more favorable.
Relation to Gauss's law[edit]
This article duplicates the scope of other articles, specifically Gauss's_law#Relation_to_Coulomb's_law. |
Deriving Gauss's law from Coulomb's law[edit]
Gauss's law can be derived from Coulomb's law and the assumption that electric field obeys the superposition principle, which says that the resulting field is the vector sum of fields generated by each particle (or the integral, if the charges are distributed in a region of space).
Coulomb's law states that the electric field due to a stationary point charge is: where
- er is the radial unit vector,
- r is the radius, |r|,
- ε0 is the electric constant,
- q is the charge of the particle, which is assumed to be located at the origin.
Using the expression from Coulomb's law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give where ρ is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem[29]
where δ(r) is the Dirac delta function, the result is
Using the "shifting property" of the Dirac delta function, we arrive at which is the differential form of Gauss's law, as desired.
Note that since Coulomb's law only applies to stationary charges, there is no reason to expect Gauss's law to hold for moving charges based on this derivation alone. In fact, Gauss's law does hold for moving charges, and in this respect Gauss's law is more general than Coulomb's law.
Deriving Coulomb's law from Gauss's law[edit]
Strictly speaking, Coulomb's law cannot be derived from Gauss's law alone, since Gauss's law does not give any information regarding the curl of E (see Helmholtz decomposition and Faraday's law). However, Coulomb's law can be proven from Gauss's law if it is assumed, in addition, that the electric field from a point charge is spherically symmetric (this assumption, like Coulomb's law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).
Taking S in the integral form of Gauss's law to be a spherical surface of radius r, centered at the point charge Q, we have
By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is where r̂ is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get which is essentially equivalent to Coulomb's law. Thus the inverse-square law dependence of the electric field in Coulomb's law follows from Gauss's law.
In relativity[edit]
Coulomb's law can be used to gain insight into the form of the magnetic field generated by moving charges since by special relativity, in certain cases the magnetic field can be shown to be a transformation of forces caused by the electric field. When no acceleration is involved in a particle's history, Coulomb's law can be assumed on any test particle in its own inertial frame, supported by symmetry arguments in solving Maxwell's equation, shown above. Coulomb's law can be expanded to moving test particles to be of the same form. This assumption is supported by Lorentz force law which, unlike Coulomb's law is not limited to stationary test charges. Considering the charge to be invariant of observer, the electric and magnetic fields of a uniformly moving point charge can hence be derived by the Lorentz transformation of the four force on the test charge in the charge's frame of reference given by Coulomb's law and attributing magnetic and electric fields by their definitions given by the form of Lorentz force.[30] The fields hence found for uniformly moving point charges are given by:[31]where is the charge of the point source, is the position vector from the point source to the point in space, is the velocity vector of the charged particle, is the ratio of speed of the charged particle divided by the speed of light and is the angle between and .
This form of solutions need not obey Newton's third law as is the case in the framework of special relativity (yet without violating relativistic-energy momentum conservation).[32] Note that the expression for electric field reduces to Coulomb's law for non-relativistic speeds of the point charge and that the magnetic field in non-relativistic limit (approximating ) can be applied to electric currents to get the Biot–Savart law. These solutions, when expressed in retarded time also correspond to the general solution of Maxwell's equations given by solutions of Liénard–Wiechert potential, due to the validity of Coulomb's law within its specific range of application. Also note that the spherical symmetry for gauss law on stationary charges is not valid for moving charges owing to the breaking of symmetry by the specification of direction of velocity in the problem. Agreement with Maxwell's equations can also be manually verified for the above two equations.[33]
Coulomb potential[edit]
Quantum field theory[edit]
This article may be too technical for most readers to understand. (October 2020) |

The Coulomb potential admits continuum states (with E > 0), describing electron-proton scattering, as well as discrete bound states, representing the hydrogen atom.[34] It can also be derived within the non-relativistic limit between two charged particles, as follows:
Under Born approximation, in non-relativistic quantum mechanics, the scattering amplitude is: This is to be compared to the: where we look at the (connected) S-matrix entry for two electrons scattering off each other, treating one with "fixed" momentum as the source of the potential, and the other scattering off that potential.
Using the Feynman rules to compute the S-matrix element, we obtain in the non-relativistic limit with
Comparing with the QM scattering, we have to discard the as they arise due to differing normalizations of momentum eigenstate in QFT compared to QM and obtain: where Fourier transforming both sides, solving the integral and taking at the end will yield as the Coulomb potential.[35]
However, the equivalent results of the classical Born derivations for the Coulomb problem are thought to be strictly accidental.[36][37]
The Coulomb potential, and its derivation, can be seen as a special case of the Yukawa potential, which is the case where the exchanged boson – the photon – has no rest mass.[34]
Verification[edit]
This section may contain an excessive amount of intricate detail that may interest only a particular audience. (October 2020) |

It is possible to verify Coulomb's law with a simple experiment. Consider two small spheres of mass and same-sign charge , hanging from two ropes of negligible mass of length . The forces acting on each sphere are three: the weight , the rope tension and the electric force . In the equilibrium state:
| (1) |
and
| (2) |
| (3) |
Let be the distance between the charged spheres; the repulsion force between them , assuming Coulomb's law is correct, is equal to
| (Coulomb's law) |
so:
| (4) |
If we now discharge one of the spheres, and we put it in contact with the charged sphere, each one of them acquires a charge . In the equilibrium state, the distance between the charges will be and the repulsion force between them will be:
| (5) |
We know that and: Dividing (4) by (5), we get:
| (6) |
Measuring the angles and and the distance between the charges and is sufficient to verify that the equality is true taking into account the experimental error. In practice, angles can be difficult to measure, so if the length of the ropes is sufficiently great, the angles will be small enough to make the following approximation:
| (7) |
Using this approximation, the relationship (6) becomes the much simpler expression:
| (8) |
In this way, the verification is limited to measuring the distance between the charges and checking that the division approximates the theoretical value.
See also[edit]
- Biot–Savart law
- Darwin Lagrangian
- Electromagnetic force
- Gauss's law
- Method of image charges
- Molecular modelling
- Newton's law of universal gravitation, which uses a similar structure, but for mass instead of charge
- Static forces and virtual-particle exchange
- Casimir effect
References[edit]
- ^ a b Huray, Paul G. (2010). Maxwell's equations. Hoboken, New Jersey: Wiley. pp. 8, 57. ISBN 978-0-470-54991-9. OCLC 739118459.
- ^ a b Halliday, David; Resnick, Robert; Walker, Jearl (2013). Fundamentals of Physics. John Wiley & Sons. pp. 609, 611. ISBN 9781118230718.
- ^ Roller, Duane; Roller, D. H. D. (1954). The development of the concept of electric charge: Electricity from the Greeks to Coulomb. Cambridge, Massachusetts: Harvard University Press. p. 79.
- ^ a b Coulomb (1785). "Premier mémoire sur l'électricité et le magnétisme" [First dissertation on electricity and magnetism]. Histoire de l'Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 569–577.
- ^ Coulomb (1785). "Second mémoire sur l'électricité et le magnétisme" [Second dissertation on electricity and magnetism]. Histoire de l'Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 578–611.
Il résulte donc de ces trois essais, que l'action répulsive que les deux balles électrifées de la même nature d'électricité exercent l'une sur l'autre, suit la raison inverse du carré des distances.
- ^ a b Purcell, Edward M. (21 January 2013). Electricity and magnetism (3rd ed.). Cambridge. ISBN 9781107014022.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Cork, C.R. (2015). "Conductive fibres for electronic textiles". Electronic Textiles: 3–20. doi:10.1016/B978-0-08-100201-8.00002-3. ISBN 9780081002018.
- ^ a b Stewart, Joseph (2001). Intermediate Electromagnetic Theory. World Scientific. p. 50. ISBN 978-981-02-4471-2.
- ^ Simpson, Brian (2003). Electrical Stimulation and the Relief of Pain. Elsevier Health Sciences. pp. 6–7. ISBN 978-0-444-51258-1.
- ^ Baigrie, Brian (2007). Electricity and Magnetism: A Historical Perspective. Greenwood Press. pp. 7–8. ISBN 978-0-313-33358-3.
- ^ Chalmers, Gordon (1937). "The Lodestone and the Understanding of Matter in Seventeenth Century England". Philosophy of Science. 4 (1): 75–95. doi:10.1086/286445. S2CID 121067746.
- ^ Socin, Abel (1760). Acta Helvetica Physico-Mathematico-Anatomico-Botanico-Medica (in Latin). Vol. 4. Basileae. pp. 224–25.
- ^ Heilbron, J.L. (1979). Electricity in the 17th and 18th Centuries: A Study of Early Modern Physics. Los Angeles, California: University of California Press. pp. 460–462 and 464 (including footnote 44). ISBN 978-0486406886.
- ^ Schofield, Robert E. (1997). The Enlightenment of Joseph Priestley: A Study of his Life and Work from 1733 to 1773. University Park: Pennsylvania State University Press. pp. 144–56. ISBN 978-0-271-01662-7.
- ^ Priestley, Joseph (1767). The History and Present State of Electricity, with Original Experiments. London, England. p. 732.
- ^ Elliott, Robert S. (1999). Electromagnetics: History, Theory, and Applications. Wiley. ISBN 978-0-7803-5384-8. Archived from the original on 2014-03-10. Retrieved 2009-10-17.
- ^ Robison, John (1822). Murray, John (ed.). A System of Mechanical Philosophy. Vol. 4. London, England: Printed for J. Murray.
- ^ Maxwell, James Clerk, ed. (1967) [1879]. "Experiments on Electricity: Experimental determination of the law of electric force.". The Electrical Researches of the Honourable Henry Cavendish... (1st ed.). Cambridge, England: Cambridge University Press. pp. 104–113.
- ^ "Coulomb's law". Hyperphysics. Archived from the original on 2019-04-13. Retrieved 2007-11-30.
- ^ a b c Feynman, Richard P. (1970). The Feynman Lectures on Physics Vol II. Addison-Wesley. ISBN 9780201021158.
- ^ a b Fitzpatrick, Richard (2006-02-02). "Coulomb's law". University of Texas. Archived from the original on 2015-07-09. Retrieved 2007-11-30.
- ^ "Charged rods". PhysicsLab.org. Archived from the original on 2014-10-10. Retrieved 2007-11-06.
- ^ Walker, Jearl; Halliday, David; Resnick, Robert (2014). Fundamentals of physics (10th ed.). Hoboken, NJ: Wiley. p. 614. ISBN 9781118230732. OCLC 950235056.
- ^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, p. 15, ISBN 978-92-822-2272-0
- ^ BIPM statement: Information for users about the proposed revision of the SI (PDF), archived from the original (PDF) on 2018-01-21, retrieved 2020-04-15
- ^ "Decision CIPM/105-13 (October 2016)". Archived from the original on 2017-08-24. Retrieved 2020-04-15. The day is the 144th anniversary of the Metre Convention.
- ^ Derived from k\text{e} = 1 / (4πε0) – "2018 CODATA Value: vacuum electric permittivity". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Archived from the original on 2016-06-03. Retrieved 2019-05-20.
- ^ Discussion on physics teaching innovation: Taking Coulomb's law as an example. CRC Press. 2015-07-28. pp. 465–468. doi:10.1201/b18636-105. ISBN 978-0-429-22704-2.
{{cite book}}:|work=ignored (help) - ^ Griffiths, David J. (2013). Introduction to Electrodynamics (4th ed.). Prentice Hall. p. 50.
- ^ Rosser, W. G. V. (1968). Classical Electromagnetism via Relativity. pp. 29–42. doi:10.1007/978-1-4899-6559-2. ISBN 978-1-4899-6258-4. Archived from the original on 2022-10-09. Retrieved 2022-10-09.
- ^ Heaviside, Oliver (1894). Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge. Archived from the original on 2022-10-09. Retrieved 2022-10-09.
- ^ Griffiths, David J. (1999). Introduction to electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. p. 517. ISBN 0-13-805326-X. OCLC 40251748.
- ^ Purcell, Edward (2011-09-22). Electricity and Magnetism. Cambridge University Press. doi:10.1017/cbo9781139005043. ISBN 978-1-107-01360-5. Archived from the original on 2023-12-30. Retrieved 2022-10-09.
- ^ a b Griffiths, David J. (16 August 2018). Introduction to quantum mechanics (Third ed.). Cambridge, United Kingdom. ISBN 978-1-107-18963-8.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ "Quantum Field Theory I + II" (PDF). Institute for Theoretical Physics, Heidelberg University. Archived (PDF) from the original on 2021-05-04. Retrieved 2020-09-24.
- ^ Baym, Gordon (2018). Lectures on quantum mechanics. Boca Raton. ISBN 978-0-429-49926-5. OCLC 1028553174.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Gould, Robert J. (21 July 2020). Electromagnetic processes. Princeton, N.J. ISBN 978-0-691-21584-6. OCLC 1176566442.
{{cite book}}: CS1 maint: location missing publisher (link)
Spavieri, G., Gillies, G. T., & Rodriguez, M. (2004). Physical implications of Coulomb’s Law. Metrologia, 41(5), S159–S170. doi:10.1088/0026-1394/41/5/s06
Related reading[edit]
- Coulomb, Charles Augustin (1788) [1785]. "Premier mémoire sur l'électricité et le magnétisme". Histoire de l'Académie Royale des Sciences. Imprimerie Royale. pp. 569–577.
- Coulomb, Charles Augustin (1788) [1785]. "Second mémoire sur l'électricité et le magnétisme". Histoire de l'Académie Royale des Sciences. Imprimerie Royale. pp. 578–611.
- Coulomb, Charles Augustin (1788) [1785]. "Troisième mémoire sur l'électricité et le magnétisme". Histoire de l'Académie Royale des Sciences. Imprimerie Royale. pp. 612–638.
- Griffiths, David J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 978-0-13-805326-0.
- Tamm, Igor E. (1979) [1976]. Fundamentals of the Theory of Electricity (9th ed.). Moscow: Mir. pp. 23–27.
- Tipler, Paul A.; Mosca, Gene (2008). Physics for Scientists and Engineers (6th ed.). New York: W. H. Freeman and Company. ISBN 978-0-7167-8964-2. LCCN 2007010418.
- Young, Hugh D.; Freedman, Roger A. (2010). Sears and Zemansky's University Physics: With Modern Physics (13th ed.). Addison-Wesley (Pearson). ISBN 978-0-321-69686-1.
External links[edit]
- Coulomb's Law on Project PHYSNET
- Electricity and the Atom Archived 2009-02-21 at the Wayback Machine—a chapter from an online textbook
- A maze game for teaching Coulomb's law—a game created by the Molecular Workbench software
- Electric Charges, Polarization, Electric Force, Coulomb's Law Walter Lewin, 8.02 Electricity and Magnetism, Spring 2002: Lecture 1 (video). MIT OpenCourseWare. License: Creative Commons Attribution-Noncommercial-Share Alike.




































































































![{\displaystyle {\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62ed1b16522d9823535ec4bef15b8def28943175)