Henagon
| Henagon | |
|---|---|
 On a circle, a henagon is a tessellation with a single vertex, and one 360-degree arc. |
|
| Type | Regular polygon |
| Edges and vertices | 1 |
| Schläfli symbol | {1} |
| Coxeter–Dynkin diagram |  |
| Internal angle (degrees) | 360° |
In geometry a henagon (or monogon) is a polygon with one edge and one vertex. It has Schläfli symbol {1}. Since a henagon has only one side and only one interior angle, every henagon is regular by definition.
Contents |
[edit] In Euclidean geometry
In Euclidean geometry a henagon is usually considered to be an impossible object, because its endpoints must coincide, unlike any Euclidean line segment. For this reason, most authorities do not consider the henagon as a proper polygon in Euclidean geometry.
[edit] In spherical geometry
In spherical geometry, on the other hand, a finite henagon can be drawn by placing a single vertex anywhere on a great circle. Two henagons can be used to construct a dihedron on a sphere, with Schläfli symbol, {1,2}.
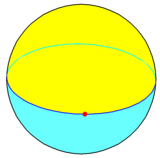The henagon can be used in spherical polyhedra, for example the henagonal dihedron {1,2}, the digonal hosohedron {2,1} and the henagonal henahedron {1,1}. The henagonal henahedron consists of a single vertex, no edges and a single face (the whole sphere minus the vertex.)
[edit] See also
[edit] References
- Olshevsky, George, Monogon at Glossary for Hyperspace.
- Herbert Busemann, The geometry of geodesics. New York, Academic Press, 1955
|
|||||||||||||||||
 |
This Elementary geometry related article is a stub. You can help Wikipedia by expanding it. |
