Square number

In mathematics, a square number, sometimes also called a perfect square, is an integer that can be written as the square of some other integer; in other words, it is the product of some integer with itself. So, for example, 9 is a square number, since it can be written as 3 × 3. Square numbers are non-negative. Another way of saying that a (non-negative) number is a square number, is that its square root is again an integer. For example, √9 = 3, so 9 is a square number.

A positive integer that has no perfect square divisors except 1 is called square-free.

The usual notation for the formula for the square of a number n is not the product n × n, but the equivalent exponentiation n², usually pronounced as "n squared". For a non-negative integer n, the nth square number is n², with 0² = 0 being the zeroth square. The concept of square can be extended to some other number systems. If rational numbers are included, then a square is the ratio of two square integers, and, conversely, the ratio of two square integers is a square (e.g., 4/9 = (2/3)²).

Starting with 1, there are $\lfloor {\sqrt {m}}\rfloor$ square numbers up to and including m.

Examples

The first 50 squares of natural numbers (sequence A000290 in the OEIS) are:

1² = 1

2² = 4

3² = 9

4² = 16

5² = 25

6² = 36

7² = 49

8² = 64

9² = 81

10² = 100

11² = 121

12² = 144

13² = 169

14² = 196

15² = 225

16² = 256

17² = 289

18² = 324

19² = 361

20² = 400

21² = 441

22² = 484

23² = 529

24² = 576

25² = 625

26² = 676

27² = 729

28² = 784

29² = 841

30² = 900

31² = 961

32² = 1024

33² = 1089

34² = 1156

35² = 1225

36² = 1296

37² = 1369

38² = 1444

39² = 1521

40² = 1600

41² = 1681

42² = 1764

43² = 1849

44² = 1936

45² = 2025

46² = 2116

47² = 2209

48² = 2304

49² = 2401

50² = 2500

The pattern between any perfect square from negative infinity to positive infinity is as follows,

$n^{2}=(n-1)^{2}+(2n-1).\$

Properties

The number m is a square number if and only if one can arrange m points in a square:

12 = 1
22 = 4
32 = 9
42 = 16
52 = 25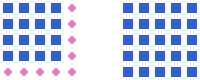

The formula for the nth square number is n². This is also equal to the sum of the first n odd numbers

$n^{2}=\sum _{k=1}^{n}(2k-1)$

as can be seen in the above pictures, where a square results from the previous one by adding an odd number of points (marked as '+'). So for example, 5² = 25 = 1 + 3 + 5 + 7 + 9.

The nth square number can be calculated from the previous two by doubling the (n − 1)-th square, subtracting the (n − 2)-th square number, and adding 2, because n² = 2(n − 1)² − (n − 2)² + 2. For example, 2 × 5² − 4² + 2 = 2 × 25 − 16 + 2 = 50 − 16 + 2 = 36 = 6².

A square number is also the sum of two consecutive triangular numbers. The sum of two consecutive square numbers is a centered square number. Every odd square is also a centered octagonal number.

Lagrange's four-square theorem states that any positive integer can be written as the sum of 4 or fewer perfect squares. Three squares are not sufficient for numbers of the form 4^k(8m + 7). A positive integer can be represented as a sum of two squares precisely if its prime factorization contains no odd powers of primes of the form 4k + 3. This is generalized by Waring's problem.

A square number can only end with digits 00,1,4,6,9, or 25 in base 10, as follows:

1. If the last digit of a number is 0, its square ends in 00 and the preceding digits must also form a square.
2. If the last digit of a number is 1 or 9, its square ends in 1 and the number formed by its preceding digits must be divisible by four.
3. If the last digit of a number is 2 or 8, its square ends in 4 and the preceding digit must be even.
4. If the last digit of a number is 3 or 7, its square ends in 9 and the number formed by its preceding digits must be divisible by four.
5. If the last digit of a number is 4 or 6, its square ends in 6 and the preceding digit must be odd.
6. If the last digit of a number is 5, its square ends in 25 and the preceding digits must be 0, 2, 06, or 56.

A square number cannot be a perfect number.

Easy ways to calculate square numbers

The formula to calculate any square number is: (n₁)² + (dn₁) + (dn₂)
An easy way to find square numbers is to find two numbers which have a mean of it, 21²:20 and 22, and then multiply the two numbers together and add the square of the distance from the mean: 22 × 20 = 440 and 440 + 1² = 441. This works because of the identity

$(x-y)(x+y)=x^{2}-y^{2}\$

known as the difference of two squares. Thus (21 − 1)(21 + 1) = 21² − 1² = 440, if you work backwards.

Special cases

• If the number is of the form m5 where m represents the preceding digits, its square is n25 where n = m × (m + 1) and represents digits before 25. For example the square of 65 can be calculated by n = 6 × (6 + 1) = 42 which makes the square equal to 4225.
• If the number is of the form m0 where m represents the preceding digits, its square is n00 where n = m². For example the square of 70 is 4900.

Odd and even square numbers

Squares of even numbers are even, since (2n)² = 4n².

Squares of odd numbers are odd, since (2n + 1)² = 4(n² + n) + 1.

It follows that square roots of even square numbers are even, and square roots of odd square numbers are odd.

Chen's theorem

Main article: Chen's theorem

Chen Jingrun showed in 1975 that there always exists a number P which is either a prime or product of two primes between n² and (n + 1)². See also Legendre's conjecture.

See also

• Integer square root
• Methods of computing square roots
• Quadratic residue
• Polygonal number
• Triangular square number
• Euler's four-square identity
• Automorphic number
• Gnomon
• Sum of odd numbers

References

• Weisstein, Eric W. "Square Number". MathWorld.

Further reading

• Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30-32, 1996. ISBN 0-387-97993-X

External links

• Learn Square Numbers. Practice square numbers up to 144 with this children's multiplication game
• Dario Alpern, Sum of squares. A Java applet to decompose a natural number into a sum of up to four squares.
• Fibonacci and Square Numbers at Convergence
• The first 1,000,000 perfect squares Includes a program for generating perfect squares up to 10^15.
• Knitted wall-hanging showing square numbers as the sum of odd numbers