Talk:Adequality
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
Vote for deletion
[edit]This article is completely non-noteworthy. What Fermat supposedly did, is exactly what you still do today in calculus.
0 ~ {b(x+e)-(x+e)^2-(bx-x^2)}/e
0 ~ b - 2x - e {same as f'(x)=0~b-2x-dx}
b ~ 2x + e {same as b = 2x }
166.249.130.7 (talk) 00:01, 15 June 2012 (UTC)
- This issue has been resolved. A majority of the editors are not in favor of article deletion. The material on a possible new version of the article has been moved to the subsection Talk:Adequality#New version below. Tkuvho (talk) 13:17, 20 February 2013 (UTC)
february thread
[edit]This seems dubious to me. Adequality has been interpreted by some scholars to mean "approximate equality". is a red flag: in maths, things mean something or they don't William M. Connolley (talk) 19:11, 7 February 2011 (UTC)
- A controversy exists concerning the meaning of Fermat's adequality. Weil is probably the most famous author to have written about it, and his views are reflected in this article. I hope to add additional references eventually. You can do it, as well :) Tkuvho (talk) 19:16, 7 February 2011 (UTC)
- Unfortunately, I don't know what it means. Would it be better if expressed as "In the history of mathematics..."? William M. Connolley (talk) 19:18, 7 February 2011 (UTC)
- One view is that it represents "approximate equality" in the sense of "equality up to an infinitesimal". Thus, 2x+dx adequals 2x, which allows us to compute the derivative of x2. Tkuvho (talk) 19:20, 7 February 2011 (UTC)
I just found this article and find in mystifying. What is 'd' in '2x+dx'? it is not explained. Algr (talk) 19:08, 14 April 2011 (UTC)
- Fermat uses two different latin words in place of the the equals sign = , namely: aequabitur and adaequabitur. Aequabitur is used when the equals sign stands between two constants or when the equation is universally valid. And he uses adaequabitur when the equation describes a relation between two variables which is not universally valid. Typical examples are (x+e)(b-x-e) aequabitur bx-x²-2ex+be-e², and bx-x² adaequabitur bx-x²-2ex+be-e²; or x³+y³ aequabitur (x+y)(x²-xy+y²) and x³+y³ adaequabitur 3xy. I have shown this in my paper Barner, Klaus: Fermats <<adaequare>> - und kein Ende?, Mathematische Semesterberichte 58 (2011), 13-45, which is unfortunately written in German. Fermat's works about maxima and minima and about tangents were written when he was very young (ca. 21 years old) and neither Descartes' nor Fermat's own work on analytic geometry was already created at that time. In Viete's work all equations between different terms (of one or more variables) are universally valid. They never describe curves or other relations where the variables are not independent. The young Pierre Fermat (1607-1665) broke new ground when he started his mathematical career in Bordeaux in 1628. There are only equations and nothing else (like pseudo-equations or counterfactual equations) in his work on maxima and minima or tangents. Klaus Barner (talk) 11:41, 4 February 2013 (UTC)
- Here "dx" should not be thought of as a product but rather as a single notation. This notation was developed by Leibniz, see Leibniz notation. It denotes an infinitesimal change in the x-variable. For example, if position s depends on time t, one would calculate the velocity by using a tiny change dt in time, calculate the corresponding change ds in position, and form the quotient ds/dt to get the velocity. In each case, the "d" alludes to the change in the corresponding variable. Tkuvho (talk) 04:50, 15 April 2011 (UTC)
- It is mentioned above that there is a controversy about what adequality means, and perhaps we should do a bit better to cover both sides and discuss the controversy itself. I have added some references that take a different point of view from Stillwell and Katz&Katz, but probably they are not worked in as well as could be. Thenub314 (talk) 07:06, 30 May 2011 (UTC)
- You should read the article from 1968 by Stromholm, where he preventively demolishes I. Kleiner and N. Movshovitz-Hadar. Kleiner is no historian. You have not yet answered my query at the bottom of the page. Tkuvho (talk) 13:22, 30 May 2011 (UTC)
- I will take a look at it, but even if he does, it is not a reason not to report on what they say. Also, more recent papers have continued to agree and disagree with what Stromholm said. Overall we should not say that Fermat did or didn't did anticipate the work of Robinson, we should say that the experts disagree on this point, and summarize the various positions. I thought the question below was rhetorical, but I will give you my opinion as soon as I have a bit of time to. Thenub314 (talk) 13:56, 30 May 2011 (UTC)
Copyright violation
[edit]I just removed part of a section which was a copyright violation, being copied directly from the source with maybe one word changed.--JohnBlackburnewordsdeeds 19:30, 16 April 2011 (UTC)
- Brief quotations are fine. Is this going to be a redux of A. H. Lightstone? Tkuvho (talk) 19:43, 16 April 2011 (UTC)
- To make it clear, quotations are allowed but they should be brief relative to the size of the articel, should be clearly marked as quotes (with attribution and source), should quoted verbatim and should only be used where encyclopaedic content won't do: where they express a particular POV, for example. They should not be used in place of proper encyclopaedic content.--JohnBlackburnewordsdeeds 19:49, 16 April 2011 (UTC)
- It is true that the article is currently short. Why don't you add to it instead of artificially creating problems? Tkuvho (talk) 04:27, 17 April 2011 (UTC)
- I am simply removing a clear copyright violation, and restoring and ISBN I added which you keep removing for no good reason. Please stop adding this: it is not a proper quote, or being used as a quotation – see WP:Quotations for the policy on quotes. Two editors have told you this now, so there is clearly also a consensus for its removal (not that there needs to be for a copyright violation).--JohnBlackburnewordsdeeds 08:21, 17 April 2011 (UTC)
- I agree that it was a COPYVIO; quotes of this length are OK but only if marked as quotes with the source given. On the other hand, it should probably have been reworded rather than just removed.--RDBury (talk) 17:48, 17 April 2011 (UTC)
- I might have if I understood the topic well, but I was looking at the source because I couldn't understand it – it seemed to be missing quite a lot of detail – while the rest of the article is even less clear to me. So I had no choice but to remove it. With what's there now being unclear and what was removed a copyvio it could do with rewriting and expanding by someone familiar with the topic.--JohnBlackburnewordsdeeds 18:01, 17 April 2011 (UTC)
- I am simply removing a clear copyright violation, and restoring and ISBN I added which you keep removing for no good reason. Please stop adding this: it is not a proper quote, or being used as a quotation – see WP:Quotations for the policy on quotes. Two editors have told you this now, so there is clearly also a consensus for its removal (not that there needs to be for a copyright violation).--JohnBlackburnewordsdeeds 08:21, 17 April 2011 (UTC)
- It is true that the article is currently short. Why don't you add to it instead of artificially creating problems? Tkuvho (talk) 04:27, 17 April 2011 (UTC)
- To make it clear, quotations are allowed but they should be brief relative to the size of the articel, should be clearly marked as quotes (with attribution and source), should quoted verbatim and should only be used where encyclopaedic content won't do: where they express a particular POV, for example. They should not be used in place of proper encyclopaedic content.--JohnBlackburnewordsdeeds 19:49, 16 April 2011 (UTC)
Kleiner
[edit]Do you have a more precise quote from Kleiner? Tkuvho (talk) 04:06, 27 May 2011 (UTC)
- Sure. I should note he doesn't use the phrase adequality, but use 'approximately equal'.
Fermat's method was severely criticized by some of his contemporaries. They objected to his introduction and subsequent suppression of the mysterious e. Dividing by e meant regarding it as not zero. Discarding e implied treating it as zero. This is inadmissible, they rightly claimed. In a somewhat different context, but with equal justification, Bishop Berkeley in the 18th century would refer to such e's as "the ghosts of departed quantities," arguing that "by virtue of a twofold mistake. . . [one] arrive[d], though not at a science yet at the truth"([13], p. 428).
- Thanks, Thenub. I am interested in the phrase "Discarding e implied treating it as zero. This is inadmissible". If that's the case, wouldn't the standard part function solution to the definition of the derivative, also be inadmissible? What "st" does is, in effect, to discard the "e". Tkuvho (talk) 07:22, 27 May 2011 (UTC)
- I don't see how this relates to the standard part precisely. To begin with Fermat never claimed e was infinitesimal, or even small, so we already already making a big assumption about the past to assume this is what he meant. Even if we accept it you need a reason to discard an infinitesimal quantity. Why is not the answer he gets before he discards e the actual maximum, etc. There is a big difference between applying the standard part function because it is part of your definitions, and discarding unwanted terms. Thenub314 (talk) 04:14, 31 May 2011 (UTC)
- The issue is not the nature of Fermat's e. The issue is Kleiner's claim that to drop this e amounts to setting it equal to zero. This is rejected in strong terms already in the 1968 paper mentioned above. Tkuvho (talk) 04:42, 31 May 2011 (UTC)
- I don't see how this relates to the standard part precisely. To begin with Fermat never claimed e was infinitesimal, or even small, so we already already making a big assumption about the past to assume this is what he meant. Even if we accept it you need a reason to discard an infinitesimal quantity. Why is not the answer he gets before he discards e the actual maximum, etc. There is a big difference between applying the standard part function because it is part of your definitions, and discarding unwanted terms. Thenub314 (talk) 04:14, 31 May 2011 (UTC)
deletion of stillwell reference
[edit]Why did user thenub delete the reference by Stillwell? He is a respected and widely-read author. Tkuvho (talk) 07:43, 3 June 2011 (UTC)
- Same reason I removed Kleiner, we had other references that said more or less the same thing. Specifically, Stillwell was being cited with regaurds to the derivative of y=x2. When I decided to follow some of the other books I was looking and and take Fermat's own example, we weren't using Stillwell to support that part anymore. But I have added it back, I have no particular qualms with the reference. Thenub314 (talk) 08:08, 3 June 2011 (UTC)
- Thanks for this. I would add Kleiner back in, as well. We might as well comment on what Stillwell wrote. I would summarize it as follows: Fermat's technique was well ahead of his time. In fact, it was not fully implemented until the advent of non-standard analysis (which Stillwell mentions explicitly in his comment on adequality). Since you have recently reverted a number of my edits, I prefer to discuss this here rather than engaging in an edit war. Tkuvho (talk) 08:17, 3 June 2011 (UTC)
Snell's law
[edit]If as you claim Grabiner claims that he used adequality to prove Snell's law by a variational argument, wouldn't this imply that he thought of the increment e as a variation? Tkuvho (talk) 07:55, 3 June 2011 (UTC)
- I don't think I would go that far, she says exactly: "Though the considerations that led Fermat to his method may seem surprising to us, he did devise a method of finding extrema that worked, and it gave results that were far from trivial. For instance, Fermat applied his method to optics. Assuming that a ray of light which goes from one medium to another always takes the quickest path (what we now call the Fermat least-time principle), he used his method to compute the path taking minimal time. Thus he showed that his least-time principle yields Snell's law of refraction [7] [12, pp. 387-390]" I can double check what the reference and see what he was actually doing, but if it were variational methods, that would have put all doubt aside as to what his method was about a long time ago. Thenub314 (talk) 08:14, 3 June 2011 (UTC)
- I can't see how it could possibly be anything other than passing from an energy or length extremality to the corresponding Euler-Lagrange equation. On the other hand, I don't think this would put all doubt aside. What did you mean exactly? Why would an Euler-Lagrange interpretation out all doubts aside? Tkuvho (talk) 08:19, 3 June 2011 (UTC)
- Which work by Grabiner are you citing? The reference you added to the article has the page range 195–206 , which is not compatible with the pages you mentioned above. Tkuvho (talk) 08:21, 3 June 2011 (UTC)
- Sorry to be unclear, those are the page numbers for the reference she is citing. (Which is Mahoney in this case.) I am quoting from page 197.
- If Mahoney discusses Fermat's application of adequality to obtain a variational principle, how coherent is it to assert that he thinks adequality purely algebraic? The source of adequality is algebraic, but that's different from what you wrote. Tkuvho (talk) 08:29, 3 June 2011 (UTC)
- Sorry to be unclear, those are the page numbers for the reference she is citing. (Which is Mahoney in this case.) I am quoting from page 197.
- Which work by Grabiner are you citing? The reference you added to the article has the page range 195–206 , which is not compatible with the pages you mentioned above. Tkuvho (talk) 08:21, 3 June 2011 (UTC)
- I can't see how it could possibly be anything other than passing from an energy or length extremality to the corresponding Euler-Lagrange equation. On the other hand, I don't think this would put all doubt aside. What did you mean exactly? Why would an Euler-Lagrange interpretation out all doubts aside? Tkuvho (talk) 08:19, 3 June 2011 (UTC)
- Knowing that the diagram looks like this you can find an algebraic expression for the time it would take light to travel along that path as a function of the intersection point along the interface. You can then minimize this expression. Mahoney is quite clear in several places that (and this is his opinion mind you, not mine) Fermat was not doing calculus either with infinitesimals or limits (and yes some sources claim limits!). If people see calculus problems that people see reading his work, it is because they know calculus. Thenub314 (talk) 15:39, 3 June 2011 (UTC)
Misrepresentation of Mahoney
[edit]Thenub's edit misrepresent Mahoney's position, without even bothering to provide a page number. Tkuvho (talk) 08:08, 3 June 2011 (UTC)
- I added a quote and a page number. Let me know if that is sufficient. Thenub314 (talk) 08:23, 3 June 2011 (UTC)
- Fermat himself said it comes from the theory of equations, namely Diophantus. But he applied it in a different context. As I already mentioned, Mahoney also wrote that approximate equality is one of the meanings of the term, so your presentation is misleading. Tkuvho (talk) 08:25, 3 June 2011 (UTC)
- Well Mahoney has a someone longer version involves a few more ingredients then just Diophantus, but your point is taken. But to listen to Mahoney describe it, the method is still primarily about double roots of polynomials, at least that was the impression I got. I noticed the part about approximate equality, but I thought the more contested part of Mahoney was that he was clearly stated a few times that Fermat's method was not infinitesimal/limit based. He has this opinion that it is much closer to the classical Method of false position which is more or less (he claims) what Diophantus was doing. No particular smallness reasoning required. Thenub314 (talk) 08:43, 3 June 2011 (UTC)
- Fermat himself said it comes from the theory of equations, namely Diophantus. But he applied it in a different context. As I already mentioned, Mahoney also wrote that approximate equality is one of the meanings of the term, so your presentation is misleading. Tkuvho (talk) 08:25, 3 June 2011 (UTC)
maxima
[edit]"Maxima" seems to be the generally accepted plural. Do they use "maximums" in England? Tkuvho (talk) 08:27, 3 June 2011 (UTC)
- Don't know, never lived there. According to Webster's dictionary either form is acceptable, but feel free to change it to maxima if you prefer. (Ironically the dictionary in Firefox recognizes maximums but not maxima, which surprises even me.). Thenub314 (talk) 08:46, 3 June 2011 (UTC)
Syntax
[edit]Not sure if this sentence is correct 'his method with sufficient clarity of completeness to determine' shouldn't that be 'sufficient clarity [or] completeness'? SamCardioNgo (talk) 12:54, 30 October 2012 (UTC)
- This section could be improved, too. Give it a try! Tkuvho (talk) 10:38, 31 October 2012 (UTC)
Dubious Scholarly controversy content
[edit]I just removed the following from the article, as it has a number of issues. It is unsourced and any controversy should be reliably sourced to properly establish the holders of the viewpoints. It's seems to be rather than reporting the controversy putting one particular point of view, describing certain views as 'misleading' and 'nonsense', so is both point of view and unencyclopaedic. And articles should never be signed: signed statements belong on the talk page.--JohnBlackburnewordsdeeds 20:50, 7 February 2013 (UTC)
- H. Breger[1] however holds the view that Fermat used the word adaequare in the sense of "to put equal" and has to be represented by the usual equals sign =. K. Barner[2] shares Breger's view and shows that Fermat uses "adaequabitur" in place of "aequabitur" when the equation describes a relation between two variables which is not a universally valid formula. The misleading introduction of the symbol by Paul Tannery had the consequence that many authors tried to give this symbol a proper name: almost equal, approximately equal, pseudo-equal, counterfactually equal, compared by adégalité, as nearly equal as possible. That, however, is simply all wrong. The meaning is equal. Klaus Barner (talk) 20:13, 7 February 2013 (UTC)
- This is one interpretation found in the recent literature. Giusti's recent article relies exclusively on Latin sources (rather than Tannery's translation and its \backsim) and does not seem to subscribe to the "=" interpretation. Tkuvho (talk) 16:16, 10 February 2013 (UTC)
- I was aware of this. But Giusti is definitely wrong. He shares Mahoney's absurd opinion. I discuss all this in my paper Fermats <<adaequare>> - und kein Ende? I am astonished that so many historians of mathematics are not able to read (not to write or to speak) German which was one of the most important languages in the history of science. I am German, however, I read English, French, Italian, Spanisch, Latin and classical Greek, and sometimes, whith the help of my wife, Russian. I could not do research in that field without being able to do so. If you send me your mail address I will send you the pdf-file of my paper. My address is klaus.barner@uni-kassel.de. Klaus Barner (talk) 18:59, 10 February 2013 (UTC)
I continue the dubious scholarly controversy: Fermat borrowed from Bachet de Meziriac's Latin translation of Diophantus’ Arithmetika the noun adaequalitas and the verb adaequare where they have a meaning in a completely different context, namely solving a special class of arithmetical problems by the method of false position. Fermat, however, uses those words (and the word adaequabitur) in his method of determining maxima and minima of algebraic terms and of computing tangents of conic sections and other algebraic curves. Fermat’s method is purely algebraic. There is no "infinitesimal error term". Fermat uses two different Latin words for "equals": aequabitur and adaequabitur. He uses aequabitur when the equation describes the identity of two constants or is used to determine a solution or represents a universally valid formula. Example:
.
And he uses the word adaequabitur () when the equation describes a relation which is no valid formula. Example (Descartes' folium):
.
Typical examples are:
and
.
Equations which describe relations between two variables (x and y, x and e) were unknown to Vieta. So the 21-year-old Fermat felt compelled to introduce a new concept of equality and called it adaequalitas. Later, when he created his analytic geometry he abandoned this special terminology of his younger days. See my paper Barner, Klaus: Fermats <<adaequare>> - und kein Ende? Math. Semesterber. (2011) 58, 13-45, unfortunately written in German. Klaus Barner (talk) 17:33, 11 February 2013 (UTC)
- I am dubious with the preceding posts. Firstly, as far as I remember my old Latin courses, the prefix "ad" means "to tend toward". Thus the difference between aequabitur and adaequabitur is exactly the same as the difference, in modern mathematics between the = of an identity and the = of an equation (in the latter, things are not equal, but one want to make them equal). Trying to extract more meaning to this difference of terms is simply silly or anachronistic (at that time, mathematics were much less formalized as now).
- Secondly, the assertion that "Fermat’s method is purely algebraic" is a pure anachronism: at that time, mathematicians did not try to classify the methods they use into algebraic, geometric and analytic. The adjectives algebraic and analytic were not even introduced.
- Thirdly, the method that Fermat did use (as described in the article) is exactly the one that is thought in every calculus course to prove the formulas for the derivative. Is that purely algebraic?
- Fourth, at Fermat's time, it was highly common to use geometry for effective numerical computations (graphical abaci, by the way it is strange that WP is almost empty about these historical important tools). It is thus sure that Fermat did use his geometrical intuition to find his method, that is that a tangent is a "line passing through two infinitely close (very close) points". IMHO, the very new idea of Fermat was to transcribe this intuition (which was certainly not new, because abacists did draw many tangents) into a computational method. To decide if this is infinitesimal computation or not is a matter of taste, nothing more.
- All the content of the article is dubious for the same reasons. D.Lazard (talk) 18:07, 13 February 2013 (UTC)
Dear User Lazard, I think that your arguments are worth a reply. Unfortunately I am German and my English is weak. There is much misunderstanding behind your arguments.
Firstly, you are completely right interpreting the prefix "ad" concerning the semantic meaning in the Latin language. But now, here ist your error. It should read: "Thus the difference between aequabitur and adaequabitur is exactly the same as the difference, in modern mathematics between the = of an identity and the = of an equation which describes a relation between to variables (x ad e or, in the case of Descartes' folium, x and y), which is no identity. The algebraic terms and are definitely not equal. However, if you put them equal you get an algebraic curve, the folium cartesii. Fermat considers this equation and writes "Il faudra comparer, par adéquation, le deux cubes CF, FE avec le solide compris sous N, FC, FE." OEuvres, Vol. II, p. 156. However, this equation describes a famous curve. And Fermat succeeded in computing tangents at this curve (Descartes' challenge) which Descartes failed to do. And if you would check all examples where he applies his method of maxima and minima or of computing tangents in Fermat's work you would see: at that moment where he changes from a valid formula to a relation between two variables (A and E) which is not universally valid he changes from aequabitur to adaequabitur. And when he finally arrives at the solution which is a equation between two constants he again changes back to aequabitur. Read Fermat's work in Latin, not Tannery's translation, you will see that I am right. You will probably not believe me until you have seen it with your own eyes.
Secondly, you blame me calling Fermat's method purely algebraic being "a pure anachronism". That is absurd. I do not claime that Fermat himself calls his method purely algebraic. Of course, he did not so. It is the result of my own analysis formulated with my own words using modern terminology. If you blame this then, in your eyes, analysis of historical mathematical texts with modern methods and words is impossible. Let us consider Fermat's usual introductory example. For shortness I will use the symbol for aequabitur and the symbol for adequabitur. Fermat wants to determine the maximum of the term (the concept of function is unknown to him) (i.e. ) in the interval . He replaces by and computes:
- ,
which is a valid mathematical formula. Next he puts the terms and equal:
- .
This is a relation between the variables and which is no valid formula. Substracting on both sides he arrives at:
- .
Now cancelling the common factor Fermat arrives at the relation
- .
Now follows Fermat's final step: he puts (=nihil) which gives the determining equation
- .
Each step is purely algebraic. It is always the same with the applications of Fermat's method, it follows always the same scheme. It is a purely algebraic method.
Thirdly, "the method that Fermat did use (as described in the article) is exactly the one that is thought(?) in every calculus course to prove the formulas for the derivative." Indeed, this claim is a pure anachronism.
Fourth, if one wants to prove the validity of Fermats "method" (especially the last step) it works in all cases with Ulisse Dini's implicit function theorem. But of course: Fermat does not use this theorem. --Klaus Barner (talk) 20:12, 14 February 2013 (UTC)
- I am not a native English speaker. In my preceding post, I have badly expressed my opinion. I'll try to be clearer. Firstly, I am interested in the mathematics of Fermat, not in the philosophy of his mathematics (epistemology). I am not sure that historical epistemology is a field that is sufficiently established to deserve Wikipedia articles. Similarly, the Fermat's thoughts about his methods could be interesting but will never been known. Thus, I'll strictly concentrate on his computations, because his method is a computing method. Also, I'll describe his method in the same way that I describe the content of badly written mathematical articles, which I have frequently to review.
- If one transcripts the computation made by Fermat into the modern language of functions (I agree that Fermat did not have it), we get the following .
- Starting from a function f, we get two functions g and h such that
- (This is a variant of Taylor's theorem for analytic functions.) Then we divide by e to get
- Then, there are two ways to describe the last step: either one simply put e=0 to get g(x); or one makes e tend to 0 to get also g(x).
- Starting from a function f, we get two functions g and h such that
- IMHO, all the discussion about the difference between aequabitur and adaequabitur consists in trying to decide if Fermat did meant "putting e=0" or "making e tend to 0". For me this discussion is irrelevant, because the important thing is what Fermat did, not what he thought (which, in any case, may not be decided). What I see, is that he has introduced a systematic method to apply Taylor's theorem on various examples, more than 50 years before Taylor. D.Lazard (talk) 18:36, 15 February 2013 (UTC)
- Dear Lazard, I definitely like this discussion with you. But sometimes I wish you would more carefully consider my arguments. Fermat had no conception of the continuum which is familar to us since Cantor, Dedekind and Weierstrass. He had no conception of function, of convergence, limit, and continuity. The concept of the local slope of a curve and derivative are far from his world of ideas. There is no infinitesimal in all his treatises and letters on maxima and minima and tangents. So the answer to your question is clear: Fermat ment "putting e=0". He gave a very clear account of how he developed his "method" in his paper Methodus de maxima et minima (OEuvres, vol. I, pp.147-153). His ideas, developed during his study of Viète, are purely algebraic.
- When Fermat did his work on maxima and minima and tangents in 1628 he was about 21 years old and was in Bordeaux, far from Paris, far from the center of scientific activities. He had carefully studied Viète's works in the famous library of his friend Étienne d'Espagnet. However, in Viète's mathematics there are only three kinds of equations: equations where the "aequabitur" (throughout used by Viète) is between two constants, determining equations (for instance quadratic equations), and universally valid equations (Bourbaki would say théorèmes) like
- Fermat however was confronted with equations which were not universally valid but relations describing curves like
- the folium cartesii. Fermat never met an equation like this in Viète's work and did not dare to write aequabitur in this case. So he used the verb adaequare and the noun adaequalitas (and the corresponding French words). Consequently Fermat wrote: "Il faudra comparer, par adéquation, le deux cubes CF, FE avec le solide compris sous N, FC, FE. "Making e tend to 0"??? Of course, also equations like
- are relations of two variables (x and e) and no universally valid formulas. Of course, we would like "making e tend to 0". But Fermat puts e=0. Dear Lazard, don't read the experts, read the original: Fermat! --Klaus Barner (talk) 13:37, 16 February 2013 (UTC)
- Some comments:
- I have never pretended that Fermat did have the notion of function. I have used function in my description of what Fermat did because it was the simplest way to describe his general method without considering explicitly each case of application. In fact, I would have better to use "expression" depending on some variables, which is exactly what Fermat consider.
- IMO, comparer par adéquation should be understood as "finding the condition for having equality" or, in other words "solving the equation in term of an expression". I agree that this was really new for the time of Fermat.
- By the way, you use improperly the word "equation", which means (in modern mathematics) "equality to be solved". Therefore the three kinds of "Viète's equations" are in modern terminology, the equalities between constants, the equations to be solved in term of a constant and the identities (they are not at all theorem, they are only parts of theorems that specifies the set of values for which they are true). Using improperly the mathematical terminology is not the right way to explain Fermat's work. In this case, the correct modern terminology to describe what Fermat did appear to be "solving an equation in term of an expression"
- Putting e=0 or letting e tend to 0: As far as I know (I have not read Fermat, only the article and your comments), Fermat did describe a method of computation, but did not explain nor prove why the result is correct. For the computation, it is clear that he (and anybody else) puts e=0. For the explanation he certainly had in mind, I can not imagine how he could justify his method without any notion of limit. I agree that the notions of limit, derivative, function, ... were totally ignored by the algebraists (by opposition to geometers) of that time. But, the notions of slope and limit were certainly known by the graphical abacists that constructed machines to draw elaborated curves. Before to assert that Fermat had no notion of limit, one should examine his knowledge about abaci and his relations with abacicts. Is there an historian that has considered this aspect of Fermat's biography?
- To conclude, I have to say, that I am not at all an historian of mathematics, but a mathematician more interested in effective computation than in proof of abstract general theorems (what happens in that case rather than what can and can not happen). For this reason, I feel closer from mathematician of XVIIIth century and earlier than from Bourbaki. This the reason why, when I read the description of Fermat method I understand it as a method of computation rather than a proof of theorem, which it is certainly not. I should also confess that my knowledge in history of mathematics is extremely weak. For Fermat's time, it comes mainly from the French habilitation of Dominique Tournès about the graphical computation about which I was a reviewer. The main part of the habilitation was about a more recent period than Fermat's, but he emphasized that the tradition of graphical abaci date from the Middle Age, were it was used to obviate the difficulty of computing with Latin numeration. It appear also that the importance of this tradition and its development until the beginning of XXth century has been strongly underestimated by the historians. D.Lazard (talk) 16:20, 16 February 2013 (UTC)
- Dear Lazard, you have not read Fermat. How can you say all this? I will not comment it at all. I am a historian of mathematics (and a number theorist). I worked on Fermat's life and work since more than 12 years. I have published a series of papers on Fermat's life. Some of them are reviewed in Mathematical Reviews and Zentralblatt. My paper "Fermats <<adaequare>> - und kein Ende?" Math. Semesterber. 58 (2011), 13-45, was checked and aknowledged before handing in for publication by four experts, Professors Herbert Breger (Hannover), Menso Folkerts and Ivo Schneider (both Munich), Michael von Renteln (Karlsruhe). The paper was then peer-reviewed by two experts. One of them, Prof. Niels Jahnke (Bochum), later outed himself to me and wrote: "In the meantime I have read your revised version and find it very compact and stringent. It would be fine if the "thoughtless" descriptions of Fermat's method now would become fewer. Though, I do not expect that." And the leading Fermat expert, Prof. Roshdi Rashed (Paris), wrote to me: "Je tenais à vous remercier pour ce travail de très grande qualité." Unfortunately I feel unable to convince you. --Klaus Barner (talk) 20:00, 16 February 2013 (UTC)
- Editors should keep in mind that work on wiki pages is primarily based on secondary sources, rather than primary sources. According to the rules, User:D.Lazard is entitled to work on the article even if he never studied Fermat in the original. Tkuvho (talk) 14:03, 20 February 2013 (UTC)
- That is formally correct, but not very encouraging for me to work for Wikipedia. I spent much time answering User:D.Lazard and explaining the subject to him. And I took his arguments seriously. --Klaus Barner (talk) 16:30, 20 February 2013 (UTC)
- There might be good reasons for this. The Math. Semesterber. piece suffers from serious weaknesses which make it less convincing. For example, the author's interpretation forces him to assume that Fermat made a systematic mistake in confusing secant and tangent lines in his presentation. Other interpretations do not suffer from such a weakness. Tkuvho (talk) 18:06, 20 February 2013 (UTC)
New version
[edit]I plan to write a completely new text und temporarily "park" some citations here.
Heinrich Wieleitner (1929):[3] "Fermat ersetzt A durch A+E. Er setzt dann den neuen Ausdruck dem alten angenähert gleich, nimmt die gleichen Glieder auf beiden Seiten weg, dividiert durch die höchstmögliche Potenz von E, lässt dann alle mit E behafteten Glieder weg und setzt dann das, was übrig bleibt, wirklich gleich. Daraus ergibt sich A. Auch dass E möglichst klein sein soll, wird nirgends gesagt, und ist höchstens durch den Ausdruck "adaequalitas" ("adegalité") zum Ausdruck gebracht." Wieleitner uses the symbol .
Max Miller (1934):[4] "Sodann setze man, wie Diophant sagt, die beiden das Maximum oder Minimum ausdrückenden Gleichungen einander näherungsweise gleich". Miller uses the symbol .
Jean Itard (1948):[5] "On sait que l'expression <<adégaler>> est reprise par Fermat à Diophante, traduit par Xylander et par Bachet. Il s'agit d'une égalité approximative". Itard uses the symbol .
Joseph Ehrenfried Hofmann (1963):[6] "Fermat wählt eine hinreichend klein gedachte Grösse h und setzt f(x+h) ungefähr gleich f(x). Sein Fachausdruck ist adaequare." Hofmann uses the symbol .
Peer Stromholm (1968):[7] "The basis of Fermat's approach was the comparition of two expressions which, though they had the same form, were not exactly equal. This part of the process he called "comparare par adaequalitatem" or "comparer per adaequalitatem", and it implied that the otherwise strict identity between the two sides of the "equation" was destroyed by the modification of the variable by a small amount:
- .
This, I believe, was the real significance of his use of Diophantos' párison, stressing the smallness of the variation. The ordinary translation of 'adaequalitas' seems to be "approximate equality", but I much prefer "pseudo-equality" to present Fermat's thought at this point."
Claus Jensen (1969)[8] Moreover, in applying the notion of adégalité - which constitutes the basis of Fermat's general method of constructing tangents, and by which is meant a comparition of two magnitudes as if they were equal, although they are in fact not - I will employ the nowdays mor usual symbol .
Ivo Schneider (1971)[9] Der von Fermat als Vorschrift bezeichnete Algorithmus besteht nun aus mehreren Schritten der Umformung einer Art von Gleicheit bzw. Gleichung, die Fermat mit dem Terminus adaequalitas beschreibt. Die begriffliche Scheidung in aequalitas und adaequalitas mußte Fermat vornehmen, weil die einzelnen Schritte seiner Vorschrift Umformungen verlangen, die mit den bekannten für Gleichungen nicht verträglich sind.
Michael Sean Mahoney (1971)[10] "Fermat's Method of maxima and minima, which is clearly applicable to any polynomial P(x), originally rested on purely finitistic algebraic foundations. It assumed, counterfactually, the inequality of two equal roots in order to determine, by Viete's theory of equations, a relation between those roots and one of the coefficients of the polynomial, a relation that was fully general. This relation then led to an extreme-value solution when Fermat removed his counterfactual assumption and set the roots equal. Borrowing a term from Diophantus, Fermat called this counterfactual equality "adequality".
Charles Henry Edwards, Jr. (1979):[11] For example, in order to determine how to subdivide a segment of length into two segments and whose product is maximal, that is to find the rectangle with perimeter that has the maximal area, he [Fermat] proceeds as follows. First he substituted (he used A, E instead of x, e) for the unknown x, and then wrote down the following "pseudo-equality" to compare the resulting expression with the original one:
After canceling terms, he divided through by e to obtain
Finally he discarded the remaining term containg e, transforming the pseudo-equality into the true equality
that gives the value of x which makes maximal. Unfortunately, Fermat never explained the logical basis for this method with sufficient clarity or completeness to prevent disagreements between historical scholars as to precisely what he meant or intended.
Kirsti Anderson (1980):[12] The two expressions of the maximum or minimum are made "adequal", which means something like"as nearly equal as possible".
Herbert Breger (1993):[13] I want to put forward my hypothesis: Fermat used the word "adaequare" in the sense of "to put equal" ... In a mathematical context, the only difference between "aequare" and "adaequare" seems to be that the latter gives more stress on the fact that the equality is achieved. --Klaus Barner (talk) 13:02, 18 February 2013 (UTC)
- Thanks for your input. These quotations are very interesting. The ones that are not in English would have to be translated before inclusion in the article. This is because a wikipedia page is for the general public rather than for historians of mathematics. Any changes to the article should be incremental. Thus, any new material should be added in small increments. Any specific deletions should be discussed at this talkpage first. An attempt to replace the adequality page with an entirely different text may not be helpful, nor necessarily accepted by other editors. Editors should be careful not to impose their preferred interpretation on the topic of the page, but rather seek broader coverage. The page cannot undergo a complete overhaul every time a new research article on Fermat is published. Furthermore, K. Barner's article does not seem to be the last one published on the topic. Tkuvho
- Of course, The quotations that are not in English will be translated. I plan to develop the whole article and to put it forward for discussion here. Before it is not generally accepted I will not copy it into the main page. - Indeed, my article is not the last published on the topic. Mikhail Katz asked me for a copy and I sent him the pdf-file. But he was unable to read it because it is written in German. So I read his paper, however, he did not read mine. The same happened with Enrico Giusti. I read his French and Italian papers, but he could not read my article. I am very astonished that historians of mathematics who work on the mathematics of the 17th century are not in the position to read the language of Gauss, Dirichlet, Riemann, Cantor, Dedekind, and Weierstrass. One should at least have some knowledge of English, French, German, and Latin. Classical Greek, Italian, and Spanish would be fine. Can you read German? If so, have a look at my article about Fermat's life (Leben) in the German Wikipedia! --Klaus Barner (talk) 11:50, 19 February 2013 (UTC)
- From some of your comments I have the impression that you are not entirely familiar with the ways wiki works. Note that new comments should be placed at the bottom of the talk page. The easiest way of doing this is by clicking on the "new section" button at the top of the page. Following this, you are asked to define the title of a new section.
- Furthermore, I think it would be preferable to work with the current version of the article rather than developing an entirely new version. Developing an entirely new version implicitly assumes that there is something irreparably wrong with the current one, which may not be the opinion of the other editors. Granted, in the assumption that the truth about Fermat's adequality is expressed in the 2011 article in Semesterber. Math., the current version is unacceptable. However, I don't think that working on the basis of such an assumption is an appropriate framework for the article. Therefore my suggestion would be to work on the present version, delete material in small doses following discussion on this talkpage, and, similarly, add material in small increments. Tkuvho (talk) 13:14, 20 February 2013 (UTC)
- Dear Tkuvho, this suggestion is not applicable in my case. I understand you well. However, the existing article is extremely short and meaningless. I proposed that I will write a complete new article and put it in here for discussion. Then there are two possibilities, either the article is acceptable (after improvements and corrections following the discussion) or my work was in vain. --Klaus Barner (talk) 16:49, 20 February 2013 (UTC)
- Discussions on talk pages should not be viewed as an attempt by an editor to convince fellow editors of the truth of his way, but rather as a way of developing consensus. A take-it-or-leave-it-attitude is not likely to produce results. Tkuvho (talk) 17:44, 20 February 2013 (UTC)
- I wrote "after improvements and corrections following the discussion". That means, that I will accept corrections and criticism. I do not change my mind. And I will not longer continue this fruitless debate. The following would have been the beginning of my text. However I will not wast my time any more. --Klaus Barner (talk) 20:24, 20 February 2013 (UTC)
Behind the word adequality (Latin: adaequalitas) hides a long story of scholarly interpretations of a technical term used by Pierre de Fermat in his seminal work of extreme values and tangents.
The Latin noun adaequalitas and the accompanying Latin verb adaequare are used by Pierre de Fermat in his treatises and letters about his method of determining maxima and minima of algebraic terms and of computing tangents to algebraic curves (like conic sections). It is a technical term within this method and does not mean the method itself.
The verb adaequare and the noun adaequalitas are used by Fermat in different idioms like adaequentur, adaequabuntur, comparare per adaequalitatem, debet adaequare, fiat per adaequalitatem, and, in his French correspondence, comparer par adéquation, however, most frequently in the form adaequabitur (third person singular passive future) which means "it will be (made) equal" (indefinite tens).
The verb adaequare is synonymous to the verb aequare (Thesaurus Linguae Latinae, Vol. I, p.562), which was used by Viète exclusively to denote equality in place of the symbol =. This symbol was invented by Robert Recorde in 1557. Viète wrote most frequently aequabitur, and Fermat adopted it from him. So Fermat used both words, aequabitur and adaequabitur, in place of the equals sign, obviously systematically and in a subtle difference of meanings. And this is the cause of a long scholarly debate which still goes on. For the purpose of this article we will denote aequabitur by and adaequabitur by . --Klaus Barner (talk) 20:29, 20 February 2013 (UTC)
- The focus on the Latin term and its meaning in Latin is somewhat misplaced because Fermat himself makes the connection with Diophantus's parisotes. For the same reason the meaning of adaequalitat in Viete is of marginal relevance here. Tkuvho (talk) 21:47, 21 February 2013 (UTC)
Breger on Bachet
[edit]The current version states that "Breger questions the correctness of Bachet’s translation of those Greek words". Does User:Klaus.Barner have a source for this claim concerning Breger? Where and in what terms did Breger question the correctness of Bachet's translation? This seems to refer to translating "parisotes" as "adaequalitat" by Bachet. Tkuvho (talk) 09:20, 1 March 2013 (UTC)
- That is not possible in a short answer here. Bregers whole paper (of 27 pages) has only one objective: to show that Fermat's "adaequare" means "to put equal" (that "adaequabitur" means "equals") and that "adaequalitas" and "parisótes" have completely different meanings. "Parisótes", of course, means "approximative equality" and "adaequalitas" means "equality". There is a paragraph Nr.5, The "Diophantus Passage" (pages 199-202), in Breger's paper, where he discusses the completely different context of Diophantus' "parisótes" and Fermat's "adaequalitas". When I was prepairing my paper I visited Herbert Breger in Hannover, and we had a fruitful discussion about this topic. I had understood him well, and he was convinced that my solution of the old riddle of the meaning of "adaequare" would end the discussion. However, this is an error. There is the barrier of the German language. I would be glad if you (or anybody else) would correct my mistakes concerning the English language in my article for Wikipedia. My English ist rather weak. --Klaus Barner (talk) 14:41, 1 March 2013 (UTC)
- I read the pages 199-200 in Breger that you mentioned. I found that, contrary to what you wrote, Breger claims that parisotes is translated by the dictionary as adaequalitat, and, he claims, it means the same thing. We would need a better source for your contention that "Breger questions the correctness of Bachet's translation of those Greek words". The claim that the Greek term "parisotes" was translated incorrectly by Bachet seems to be User:Klaus Barner's, not Breger's, until we see a better source. Do you have such a source? Tkuvho (talk) 20:39, 2 March 2013 (UTC)
The section Analysis of "adequality" meaning in Fermat's work is aimed to give a detailed description of the scholarly controversy and to trying to resolve it. It follows that all this section after the first mention of Bourbaki is original research, having not been previously published elsewhere.
WP:No original research is one of the fundamental policies of Wikipedia. It states "Wikipedia articles must not contain original research. The term "original research" (OR) is used on Wikipedia to refer to material—such as facts, allegations, and ideas—for which no reliable, published sources exist. This includes any analysis or synthesis of published material that serves to advance a position not advanced by the sources. To demonstrate that you are not adding OR, you must be able to cite reliable, published sources that are directly related to the topic of the article, and directly support the material being presented."
As the controversy has not yet been resolved, and as Wikipedia is not the place to resolve it, this section has to be removed.
However it would be useful to use the citations in the section to expand section "Scholarly controversy", by clarifying the description of the different positions. Also, if André Weil has written about Fermat's method (for example in his Mahoney's criticism), his position should be mentioned.
Note that, after removing section Analysis of "adequality" meaning in Fermat's work, its content continues to be accessible through the history of the article, for example to expand section "Scholarly controversy".
D.Lazard (talk) 12:16, 2 March 2013 (UTC)
- User Lazard's claim is completely wrong. The arcticle which Lazard deleted is no "original research". Everything what follows the mention of Bourbaki, has been published in my paper Barner, K. (2011) "Fermats <<adaequare>> - und kein Ende?" Mathematische Semesterberichte (58), pp. 13-45. The problem is that this has been written in German. Of course, I have prepared the subject for the reader of an encyclopedia. I did not cite word-for-word from my paper. --Klaus Barner (talk) 15:11, 2 March 2013 (UTC)
- WP:PRIMARY asserts Wikipedia articles should be based on reliable, published secondary sources. Your article being a primary source, a detailed transcription of its content is original research. Moreover as this transcription has been done by yourself, this is also a conflict of interest. In case of experts, as you are, conflicts of interest are not forbidden but strongly discouraged. This implies that every edit in conflict of interest should strictly follow the other content policies, and particularly WP:Neutral point of view. This means that the place given to your conclusions should not significantly exceed the place devoted to the other scholars, and that it should be in the same section as the others. I had something like this in mind, when I suggested to expand section "Scholarly controversy". D.Lazard (talk) 16:16, 2 March 2013 (UTC)
- Fermat's three examples have been discussed, together with three additional examples, on pages 17-28 (maxima and minima) and 33-42 (tangents) of my paper. In each of these examples I also gave the proof of the validity of Fermat's method by means of the implicit function theorem. "How did Fermat hit upon his method?" is discussed on pages 19 and 20. "Did Fermat prove the validity of his “method?" is dicussed on page 16 of my paper. My answer of the question "Why did Fermat not just write aequabitur instead of adaequabitur?" uses knowledge from my papers on Fermat's life, for instance Barner, K.: Pierre Fermat. Sa vie privée et professionnelle. Annales de la Faculté des Sciences de Toulouse 18, no. Spécial, 2009, pp 119-135 (unfortunately not written in English but in French.) Bourbaki is discussed on pages 43 and 44 of my article. Papers that not have been written in English are obviously not published in the eyes of the English speaking community of Wikipedia. --Klaus Barner (talk) 16:27, 2 March 2013 (UTC)
proposal to restore part of the deleted material
[edit]Recent massive additions to the page have been appropriately reverted on WP:OR grounds. However, I think a small part of the additions can be restored since it does not involve OR. I am referring to the material on scholarly commentary as reproduced below. What do you think? Tkuvho (talk) 14:10, 3 March 2013 (UTC)
Both Newton and Leibniz referred to Fermat's work as an antecedent of infinitesimal calculus. Nevertheless, there is disagreement amongst modern scholars about the exact meaning of Fermat's adequality. Fermat's adequality was analyzed in a number of scholarly studies. In 1896, Paul Tannery published a French translation of Fermat’s Latin treatises on maxima and minima (Fermat, Œuvres, Vol. III, pp. 121-156). Tannery translated Fermat's term as “adégaler” and adopted Fermat’s “adéquation”. Tannery also introduced the symbol for adequality in mathematical formulas.
Heinrich Wieleitner (1929)[14] wrote: "Fermat replaces A with A+E. Then he sets the new expression roughly equal ( angenähert gleich) to the old one, cancels equal terms on both sides, and divides by the highest possible power of E. He then cancels all terms which contain E and sets those that remain equal to each other. From that [the required] A results. That E should be as small as possible is nowhere said and is at best expressed by the word "adaequalitas". (Wieleitner uses the symbol .)
Max Miller (1934)[15] wrote: "Thereupon one should put the both terms, which express the maximum and the minimum, approximately equal (näherungsweise gleich), as Diophantus says." (Miller uses the symbol .)
Jean Itard (1948)[16] wrote: "One knows that the expression "adégaler" is adopted by Fermat from Diophantus, translated by Xylander and by Bachet. It is about an approximate equality (égalité approximative) ". (Itard uses the symbol .)
Joseph Ehrenfried Hofmann (1963)[17] wrote: "Fermat chooses a quantity h, thought as sufficiently small, and puts f(x+h) roughly equal (ungefähr gleich) to f(x). His technical term is adaequare." (Hofmann uses the symbol .)
Peer Strømholm (1968)[18] wrote: "The basis of Fermat's approach was the comparition of two expressions which, though they had the same form, were not exactly equal. This part of the process he called "comparare par adaequalitatem" or "comparer per adaequalitatem", and it implied that the otherwise strict identity between the two sides of the "equation" was destroyed by the modification of the variable by a small amount:
.
This, I believe, was the real significance of his use of Diophantos' πἀρισον, stressing the smallness of the variation. The ordinary translation of 'adaequalitas' seems to be "approximate equality", but I much prefer "pseudo-equality" to present Fermat's thought at this point."
Claus Jensen (1969)[19] wrote: "Moreover, in applying the notion of adégalité - which constitutes the basis of Fermat's general method of constructing tangents, and by which is meant a comparition of two magnitudes as if they were equal, although they are in fact not - I will employ the nowdays mor usual symbol ."
Michael Sean Mahoney (1971)[20] wrote: "Fermat's Method of maxima and minima, which is clearly applicable to any polynomial P(x), originally rested on purely finitistic algebraic foundations. It assumed, counterfactually, the inequality of two equal roots in order to determine, by Viete's theory of equations, a relation between those roots and one of the coefficients of the polynomial, a relation that was fully general. This relation then led to an extreme-value solution when Fermat removed his counterfactual assumption and set the roots equal. Borrowing a term from Diophantus, Fermat called this counterfactual equality 'adequality'." (Mahoney uses the symbol .) On p. 164, end of footnote 46, Mahoney notes that one of the meanings of adequality is approximate equality or equality in the limiting case.
Charles Henry Edwards, Jr. (1979)[21] wrote: "For example, in order to determine how to subdivide a segment of length into two segments and whose product is maximal, that is to find the rectangle with perimeter that has the maximal area, he [Fermat] proceeds as follows. First he substituted (he used A, E instead of x, e) for the unknown x, and then wrote down the following "pseudo-equality" to compare the resulting expression with the original one:
After canceling terms, he divided through by e to obtain Finally he discarded the remaining term containing e, transforming the pseudo-equality into the true equality that gives the value of x which makes maximal. Unfortunately, Fermat never explained the logical basis for this method with sufficient clarity or completeness to prevent disagreements between historical scholars as to precisely what he meant or intended."
Kirsti Andersen (1980)[22] wrote: "The two expressions of the maximum or minimum are made "adequal", which means something like as nearly equal as possible." (Anderson uses the symbol .)
Herbert Breger (1994)[23] wrote: “I want to put forward my hypothesis: Fermat used the word "adaequare" in the sense of "to put equal" ... In a mathematical context, the only difference between "aequare" and "adaequare" seems to be that the latter gives more stress on the fact that the equality is achieved." (Page 197f.)
John Stillwell (Stillwell 2006 p. 91) wrote: "Fermat introduced the idea of adequality in 1630s but he was ahead of his time. His successors were unwilling to give up the convenience of ordinary equations, preferring to use equality loosely rather than to use adequality accurately. The idea of adequality was revived only in the twentieth century, in the so-called non-standard analysis."
Katz, Schaps, Shnider (2013)[24] argue that Fermat's application of the technique to transcendental curves such as the cycloid shows that adequality goes beyond a purely algebraic algorithm, and that, contrary to Breger's interpretation, the terms parisotes and adaequalitat mean "approximate equality". They develop a formalisation of Fermat's technique of adequality in modern mathematics as the standard part function sending a finite hyperreal number to the real number infinitely close to it.
- As I suggested something like that in my post, in which I explained my revert, I may only agree. However, most of these authors are already cited in section "Scholarly controversy". Thus, for not being confusing, this section must be rewritten to include this new material in a coherent way. D.Lazard (talk) 15:37, 3 March 2013 (UTC)
- User:Klaus Barner put in a lot of work in arranging these in chronological order. Also, he presents more detailed quotations than in the current "controversy" section. There is one exception: Mahoney mentions elsewhere in his book that adequality is approximate equality; this appears in the "controversy" section but not in User:Klaus Barner's proposal. I would suggest that we start with his version as the most complete one, and edit and amplify it so as not to lose the current material from "controversy". What do you think? Tkuvho (talk) 15:49, 3 March 2013 (UTC)
- This is fine. What should be avoided is having two parts of the article that present differently the controversy. But the choice of the percentage in the merge is the choice of the merging editor. D.Lazard (talk) 16:29, 3 March 2013 (UTC)
- User:Klaus Barner put in a lot of work in arranging these in chronological order. Also, he presents more detailed quotations than in the current "controversy" section. There is one exception: Mahoney mentions elsewhere in his book that adequality is approximate equality; this appears in the "controversy" section but not in User:Klaus Barner's proposal. I would suggest that we start with his version as the most complete one, and edit and amplify it so as not to lose the current material from "controversy". What do you think? Tkuvho (talk) 15:49, 3 March 2013 (UTC)
bug in article history
[edit]There is some kind of bug in the article history that prevents one from viewing old versions of the article (and displays the current version instead). This makes it difficult to view the recent proposed additions. I therefore copied the material to talk (as was originally proposed by User:Klaus Barner). See below. Tkuvho (talk) 15:24, 4 March 2013 (UTC)
Behind the word adequality (Latin: adaequalitas) hides a long story of scholarly interpretations of a technical term used by Pierre de Fermat in his seminal work of extreme values and tangents.
The Latin noun adaequalitas and the accompanying Latin verb adaequare are used by Fermat in his treatises and letters about his method of determining maxima and minima of algebraic terms and of computing tangents to algebraic curves (like conic sections). It is a technical term within this method and does not mean the method itself.
The verb adaequare and the noun adaequalitas are used by Fermat in different idioms like adaequentur, adaequabuntur, comparare per adaequalitatem, debet adaequare, fiat per adaequalitatem, and, in his French correspondence, comparer par adéquation, however, most frequently in the form adaequabitur (third person singular passive future) which means "it will be (made) equal" (indefinite tens).
The verb adaequare is synonymous with the verb aequare (Thesaurus Linguae Latinae, Vol. I, p.562). The latter word was used by Viète nearly exclusively (with very few exceptions) to denote equality in place of the symbol =. This symbol was invented by Robert Recorde in 1557. Viète wrote most frequently aequabitur, and Fermat adopted it from him. However, Fermat used both words, aequabitur and adaequabitur, in place of the equals sign, obviously systematically and in a subtle difference of meanings.
In Fermat’s work about maxima and minima and tangents there is a place where he says that he adopted the word “adaequentur” from Diophantus. In his treatise “’’Methodus ad disquirendam maximam et minimam’’” (Fermat, Œuvres, Vol. I, pp.133-136) Fermat writes: ‘’Adaequentur, ut loquitur Diophantus, duo homogenia maxima aut minima aequalia …’’ (We make, as Diophantus says, two expressions of maximum or minimum in like manner equal.) But there are more questions than answers what that exactly means. This topic is taken up further below.
And this is the cause of a long scholarly debate which still goes on. For the purpose of this article we will denote aequabitur by and adaequabitur (and its equivalent idioms) by .
Fermat’s example Nr. 1. (Œuvres, Vol. I, p.134) To divide the line by the point this way that the product of the two segments and becomes a maximum.
Fermat’s solution: Let . Next let be one of the two segments. Then the other one will be . And the product, which shall become a maximum, then equals . However, if the first segment is then the second one will be . The product of the segments is then
- .
Next Fermat puts the two terms equal:
- .
Subtracting common terms on both sides yields
Now Fermat [tacitly assuming that is unequal zero] cancels the common factor and gets
Finally Fermat deletes and yields the solution
Fermat then remarks: “The question is answered if we take
Nec potest generalior dari methodus.” (It is impossible to give a more general method.)
There are several questions one would like to ask. What is Fermat’s idea behind his method? Did he explain how he found it? Has Fermat proven the validity of his proceeding? And, if not, is it possible to do this by means of modern analysis? And, above all: what is the precise meaning of “adaequabitur” ()?
Let us first hear the voices of the scholarly experts! When Paul Tannery in 1896 published his French translation of Fermat’s Latin treatises on maxima and minima (Fermat, Œuvres, Vol. III, pp. 121-156) he was obviously insecure of the meaning of adaequare and aequalitas and avoided a translation of these words from Latin into modern French. He invented instead the new French verb “adégaler” and adopted Fermat’s “adéquation”. His introduction of the sign for “adaequabitur” in mathematical formulas, however, had the most serious consequences.
Heinrich Wieleitner (1929):[25] “Fermat replaces A with A+E. Then he puts the new expression roughly equal ( angenähert gleich) to the old one, cancels equal terms on both sides, and divides by the highest possible power of E. He then cancels all terms which contain E and puts that, what remains, really equal. From that A results. That E should be as small as possible is nowhere said and is at best expressed by the word "adaequalitas". (Wieleitner uses the symbol .)
Max Miller (1934):[26] "Thereupon one should put the both terms, which express the maximum and the minimum, approximately equal (näherungsweise gleich), as Diophantus says." (Miller uses the symbol .)
Jean Itard (1948):[27] "One knows that the expression <<adégaler>> is adopted by Fermat from Diophantus, translated by Xylander and by Bachet. It is about an approximate equality (égalité approximative) ". (Itard uses the symbol .)
Joseph Ehrenfried Hofmann (1963):[28] "Fermat chooses a quantity h, thought as sufficiently small, and puts f(x+h) roughly equal (ungefähr gleich) to f(x). His technical term is adaequare." (Hofmann uses the symbol .)
Peer Strømholm (1968):[29] "The basis of Fermat's approach was the comparition of two expressions which, though they had the same form, were not exactly equal. This part of the process he called "comparare par adaequalitatem" or "comparer per adaequalitatem", and it implied that the otherwise strict identity between the two sides of the "equation" was destroyed by the modification of the variable by a small amount: . This, I believe, was the real significance of his use of Diophantos' πἀρισον, stressing the smallness of the variation. The ordinary translation of 'adaequalitas' seems to be "approximate equality", but I much prefer "pseudo-equality" to present Fermat's thought at this point."
Claus Jensen (1969)[30] Moreover, in applying the notion of adégalité - which constitutes the basis of Fermat's general method of constructing tangents, and by which is meant a comparition of two magnitudes as if they were equal, although they are in fact not - I will employ the nowdays mor usual symbol .
Michael Sean Mahoney (1971)[31] "Fermat's Method of maxima and minima, which is clearly applicable to any polynomial P(x), originally rested on purely finitistic algebraic foundations. It assumed, counterfactually, the inequality of two equal roots in order to determine, by Viete's theory of equations, a relation between those roots and one of the coefficients of the polynomial, a relation that was fully general. This relation then led to an extreme-value solution when Fermat removed his counterfactual assumption and set the roots equal. Borrowing a term from Diophantus, Fermat called this counterfactual equality "adequality". (Mahoney uses the symbol .)
Charles Henry Edwards, Jr. (1979):[32] For example, in order to determine how to subdivide a segment of length into two segments and whose product is maximal, that is to find the rectangle with perimeter that has the maximal area, he [Fermat] proceeds as follows. First he substituted (he used A, E instead of x, e) for the unknown x, and then wrote down the following "pseudo-equality" to compare the resulting expression with the original one:
After canceling terms, he divided through by e to obtain
Finally he discarded the remaining term containing e, transforming the pseudo-equality into the true equality
that gives the value of x which makes maximal. Unfortunately, Fermat never explained the logical basis for this method with sufficient clarity or completeness to prevent disagreements between historical scholars as to precisely what he meant or intended.
Kirsti Anderson (1980):[33] “The two expressions of the maximum or minimum are made "adequal", which means something like as nearly equal as possible." (Mrs. Anderson uses the symbol .)
After reading these quotations one must admit that Edwards very precisely describes the state of the art of the research about the meaning of “adaequare” around 1980. No-one of the authors, including Edwards himself, has a well-founded conception what Fermat meant with “adaequare” and “adaequalitas”. And Edwards holds Fermat’s vagueness responsible for that.
The first author, who resolutely contradicts this opinion, is Herbert Breger. “Taking into account that brilliant mathematicians usually are not so very confused when talking about their own central mathematical ideas” he wrote a long paper[34] and proposed a solution of the problem: “I want to put forward my hypothesis: Fermat used the word "adaequare" in the sense of "to put equal" ... In a mathematical context, the only difference between "aequare" and "adaequare" seems to be that the latter gives more stress on the fact that the equality is achieved.” (Page 197f. of his paper.)
Breger’s central considerations are as follows. As mentioned above, Fermat wrote in his treatise “’’Methodus ad disquirendam maximam et minimam’’” (Fermat, Œuvres, Vol. I, pp.133-136): ‘’Adaequentur, ut loquitur Diophantus, duo homogenia maxima aut minima aequalia …’’ (We make, as Diophantus says, two expressions of maximum or minimum in like manner equal.) Indeed, one finds in Diophantus’ Arithmetica several places where Diophantus uses the words παρισὀτης and πἀρισον which Bachet de Méziriac translates as ‘’adaequalitas’’ respectively as ‘’adaequale’’. Both words, which occur in the 11th and 14th problems of the fifth book of the Arithmetica, are used in context of the regula falsi which Diophantus uses to solve a certain class of Diophantine equations. The word παρισὀτης is invented by Diophantus to label this method. Fermat himself does not use these words. The meaning of πἀρισον is “almost equal” and the meaning of παρισὀτης is something like “approximation of the solution” which makes sense in the context of the regula falsi. However, Breger questions the correctness of Bachet’s translation of those Greek words.[dubious – discuss] (Bachet had adopted his own translation from Wilhelm Xylander.) Paul Tannery[35] translates πἀρισον with proximum and παρισὀτης with appropinquatio, which is much better.
The verbs aequare and adaequare are synonymous and mean “to make equal”. All great Latin dictionaries say unanimously: both verbs mean “to make equal”. And Breger concludes that both words, aequabitur and adaequabitur, mean “equals”. He provides many strong arguments for this claim. And he is right, as one will see below. However, he fails to answer the question: why should Fermat use two synonymous verbs obviously and systematically in a different sense? Breger’s answer to this question is completely unsatisfactory.
The only way to resolve this paradoxical situation is to analyze the meaning and the different functions of the equals sign . There are hundreds of books about logic and/or set theory, but almost all of them say no word about the equals sign, they just use it. The notable exception is the work of Fermat’s virtual compatriot Nicolas Bourbaki. In his Elements of Mathematics he devotes a paragraph (of 3 pages) to the equals sign and its proper use. The following quotations are from Bourbaki (Theory of Sets’’. Addison Wesley, Reading Mass.1968, §5.1).
“An equalitarian theory is a theory Ƭ which has a relational sign of weight 2, written (read “equals”).
If and are terms in Ƭ, the assembly is a relation in Ƭ (called the relation of equality). - In practice it is denoted by or .”
“The negation of the relation is denoted by or (where the sign is read is different from).”
“When a relation of the form has been proved in a theory Ƭ, it is often said (by abuse of language) that and are the same or are identical.”
“Likewise, when is true in Ƭ, we say that that and are distinct in place of saying that that is different from .”
Now one should consider a set of relations of equality, one example is from Euler, one from Viète, and the rest is Fermat’s.
Relation of equality Nr.1. (Euler)
This beautiful relation of equality is due to Euler. The equals sign = stands between two constants. They look very different, but they represent the same real number. That has been proven by Euler. So, according to Bourbaki, the two constants in the relation of equality above are the same or identical. If the term is denoted by and the term is denoted by then is true.
Relation of equality Nr.2. (Fermat)
This relation of equality is considered by Fermat (Œuvres, Vol. I, p.155). The letter denotes a constant, the length of a line. This relation may be called a conditional equation. It is neither true nor false. When it has been solved, for instance by the positive solution
and is replaced by the solution the relation of equality above is proved and, according to Bourbaki, the constants on both sides of the relation are the same or identical.
Relation of equality Nr.3. (Fermat)
- .
This relation of equality is from Fermat (Œuvres, Vol. I, p.140). Again, denotes the positive length of a line. This relation is easily proved by the rules of algebra. The relation is universally valid. According to Bourbaki the terms on both sides of the equals sign are the same or identical. If the term is denoted by and the term is denoted by then is true.
Relation of equality Nr.4. (Fermat)
- .
This relation of equality is on the same page as the relation Nr. 3. However, this relation is not universally valid. It is easy to find a counterexample. For instance and yields . This proves, according to Bourbaki, that the two terms on both sides of the relation are distinct. If the term is denoted by and the term is denoted by then .
The relations of equality Nr.5 and Nr.6 follow further below.
Fermat’s example Nr. 2. (Œuvres, Vol. I, p.140) To divide the line by the point this way that the product of the square over and the line is maximal.
Fermat’s solution: Let and so that . If now we replace by then the product, which results by multiplication of the square of and , is
Now Fermat puts this last product equal to the first one:
- ,
word for word explaining: “Id comparo primo solido tanquam essent aequalia , licet revera non sint, et hujus modi comparationem vocavi adaequalitatem.” (I compare this [product] with the first product as if they were equal, even though, in reality, they are not, and I called this kind of comparison adaequalitas.) [It is exactly that case, where Bourbaki writes though is true. It is a relation of equality which describes a relation of two variables, x and e, which are not independent.] After that Fermat cancels those terms which both sides have in common, to wit , in which on one side nothing remains, however, on the other side
Fermat prefers to separate the terms with a minus sign from those with a plus sign (comparando sunt ergo homogenea notata signo + cum iis quae notantur signo - ) yielding the equation
He then cancels the factor :
Fermat deletes all terms, which still contain the factor :
Finally, tacitly assuming that is no sensible solution, Fermat cancels the factor . And he gets
Therefore the line must be divided that way that
Fermat does not always give complete proofs of his results concerning the determination of maxima and minima or of computing tangents. However, in those cases, where he does it, he follows always exactly the same scheme of his “method”. First Fermat prepares the problem for the application of his method. That depends on the specific conditions and assumptions of the problem. The outcome always consists of two different terms of similar structure, one containing only the variable and the other one containing . The terms may be polynomials, quotients of polynomials, and algebraic terms containing roots. These two different terms are than set equal (). If necessary, this equation is then transformed by algebraic operations until Fermat gets a polynomial equation. And, a sheer miracle, all summands of the equation contain the factor or a power of it. Then this factor (the highest common power of ) is cancelled, and finally those remaining terms, which still contain as a factor, are deleted. The result is a conditional equation, which gives, if solved, the solution of the problem. The last equation is the first one where Fermat changes back from adaequabitur to aequabitur. All operations are purely algebraic.
It would be interesting to know, how the adherents of counterfactual equality or almost equality would justify Fermat’s algebraic operations (like cross-multiplying or squaring out roots). However, these guys never give up. But there will be a lucky punch.
Relation of equality Nr.5. (Viète)
Of course, this is a special case of Viète’s more general formula for the factorization of the term . Let be the term and the term . Then the relation of equality is true. That is easily proved (on the basis of the axioms of a commutative ring) and may be noted by means of Bourbaki’s quantifiers as
We now turn to the story of Fermat and Descartes’ folium cartesii, given by the relation of equality
Relation of equality Nr.6. (Fermat)
This relation of equality is found in Fermat’s Œuvres (Vol. II, p.156). It describes a curve which was proposed to him by René Descartes. Let, again, be the term , and the term . We want to show that is true. The relation of equality above is not universally true. If one chooses and one gets the false equation . Therefore
Applying the rule twice we get
which proves that is true.
Fermat’s example Nr. 3. (The lucky punch.) In his letter to Mersenne of 18 January 1638 (Fermat, Œuvres, Vol. III, pp. 126-132) Descartes challenges Fermat to compute the tangent of a new curve, which he had detected and which is nowadays called folium cartesii. On page 129/130 Descartes writes:
“Then, apart from this, his [Fermat’s] alleged rule is not that universal as it seems to him. And it is impossible to extend it to problems which are a little more difficult, but only to the easiest. So he could test it, after having better understood it. He should use it to find, for instance the tangents to the curve which I propose to be the following. At an arbitrary place of the curve take the point . Having drawn the perpendicular the two cubes of side lengths and are, together, equal (égaux) to the rectangular solid formed of the same sides and and the length of a given side.”
If one puts , , and , then one gets the equation of the folium cartesii:
One usually chooses which makes the curve looking nice and the computations easier. Mersenne hesitated for a long time sending a copy of Descartes’ letter to Fermat. But finally he did. And Fermat answered in June 1638 (Œuvres, Vol. II, p.156) and gave the solution of Descartes’ challenge. Fermat formulates the description of the curve, which Descartes had proposed, as follows: “Soit la courbe , de laquelle la propriété est telle que, quelque point qu’on prenne sur la dite courbe, comme , tirant la perpendiculaire , les deux cubes et soient égaux au parallélépipède compris sous une ligne droite donnée, comme , et les deux lignes et .“ Fermat then introduces two variable auxiliary points and , needed for his “method”. He then starts with his “method” and writes : “Il faudra comparer, par adéquation, les deux cubes et avec le solide compris sous . (one must compare, by adequality, the two cubes … ). That means
What may this adequality mean? Approximately equal? Counterfactually equal? As nearly equal as possible? Pseudo-equal? Almost equal?[36] Or put equal? The reader should decide it himself.
Why did Fermat not just write aequabitur instead of adaequabitur? The answer should include some biographical considerations. When Fermat (born November 1607) in 1628 created his “method” he was very young, about 20 or 21 years old. He lived as an âvocat at the parlement de Bordeaux where his friend Etienne d’Espagnet was a conseiller at the same parlement. D’Espagnet possessed a very valuable scientific library which he had inherited from his father, a friend of Viète. In this library Fermat studied the writings of the ancients and Viète’s work. Viète used most frequently the verb aequare and, on some rare occasions, the verb adaequare (8 times) and the noun adaequalitas (once), instead of Recorde’s equals sign. (François Viète, Opera Mathematica. Georg Olms, New York 1970, pp. 80, 134, 135, 137, 141, and 143). In all these cases the meaning of adaequare is to put equal. At that time Fermat had still not studied Diophantus. So he borrowed the verb adaequare and the noun adaequalitas from his admired “example” Viète. Later, in his correspondence with Mersenne and Descartes, he referred to Bachet de Meziriac’s Diophantus. And that was very misleading because Bachet’s translation is false. Viète exclusively dealt with conditional equations and universally valid equations (formulas, theorems), never, however, with relations of equality which describe a relation between two (or more) variables, which are not independent and, occasionally, describe a curve. So Fermat felt that he should give these new relations of equality a different name: adaequabitur. However, when Fermat starts applying his “method” and puts two different terms equal for the first time he prefers to write adaequentur, adaequabuntur, comparare per adaequalitatem, debet adaequare, or fiat per adaequalitatem, and, in his French correspondence, comparer par adéquation.
How did Fermat hit upon his method? Fermat explained that very explicitly in his treatise Methodus de maxima et minima (Œuvres , Vol. I, pp.147-153) which has been preserved as Mersenne’s copy. The following is a concise account in modern mathematical language, nevertheless trying to repeat Fermat’s idea as anadulterated as possible. Let be a term, for instance a polynomial term as like that in the first example. The maximum of this term is to be determined, for instance in the Interval . Now Fermat argues, picking up a remark of Pappus of Alexandria, that the place , where the maximum is attained, that is , is singular (plural: unicae et singulares). That means that the value is not attained at another place of the interval again. Because, if one chooses a value somewhat smaller than then there are two different places in the interval, say and with , for which holds
If one again chooses a constant with , so to this constant will belong and of that kind, that
and and That means that the nearer comes to the closer will be to . Only for the place , where attains its maximum, there exists no other place in the interval where this value is again attained, which corresponds to
This gave Fermat the idea of the following method for computing He puts
and substracting common terms on both sides of this relation of equality all remaining terms contain (or a power of it) as factor. Tacitly assuming he cancels the highest common factor of (that may well be if contains a square root) . In the remaining equation Fermat then puts (equals nihil), which gives him a conditional equation for .
Did Fermat prove the validity of his “method”? If this question means: “gave Fermat a proof which fulfills the standard of modern analysis?” then the answer is – of course – no. Fermat did not possess an idea of the continuum which is familiar to us since Cantor, Dedekind, and Weierstraß. His concept of number could possibly be described by naïve constructivism: if one possesses, for a given quantity, an algorithm which allows him to approximate this quantity arbitrarily precisely by rational numbers then this quantity responds to a number. Fermat had no concept of function, of continuity, of convergence, and of limit. He never considers the local gradient of a curve. (When Fermat determines a tangent he always computes, as a second point of the tangent, the point of intersection of the tangent with an obviously chosen reference line, most often the axis of symmetry of the curve.) Fermat had explained how he hit upon the idea of his “method”. And this method always produced the correct solution. He had, admittedly, some trouble with his attempt to explain to his contemporaries (especially Descartes) his proceeding to compute tangents. However, this had another reason.
Is it possible to prove the validity of Fermat’s “method” by means of modern analysis? (This section is intended to the mathematically inclined reader. A one-year course in calculus will be sufficient. We need, in particular, Ulisse Dini’s implicit function theorem for two variables.) The reader should be sure about the circumstance that every attempt to justify Fermat’s method with the aid of modern real analysis must inevitably be anachronistic. However, one can try to reduce this to a minimum. We will not at all alter Fermat’s equations. We turn our attention to the last three equations in Fermat’s proof. These have always the same structure. We will explain our consideration by taking the example of Fermat’s second problem above. There the third from last equation reads
Then, tacitly assuming , Fermat cancels the factor :
Thus the resulting equation is not valid when . But then Fermat deletes all terms, which still contain the factor , that means that he puts , and the result is the conditional equation
This is the critical point of Fermat’s “method”. The most obvious question is: Is it possible to replace Fermat’s putting by an argument?
The quadratic equation has the solutions and As one easily sees by elementary arguments: is a (relative) minimum of Well, we would like to show: In a neighbourhood of the variable is locally a continuous function with
Temporarily, we write the last relation before deleting in the form
- .
If we put , then we may write
- .
Now we apply the implicit function theorem. The function is a function of and with continuous derivatives and . We note down
We have and . These are the preconditions for the application of the implicit function theorem. According Dini there exists a and a continuous function defined on the interval with the properties
and
- .
This is, written in the initial form,
- .
If we, finally, let in this equation we arrive, taking into account the continuity of all involved functions, at
That is it, what we wanted to achieve. And it justifies Fermat’s “method” in this special case. However, as the reader may check, this kind of using Dini’s theorem works in all cases of determining maxima and minima and of computing tangents which Fermat brings through to the end.
- ^ Breger, H.:The mysteries of adaequare. A vindication of Fermat. Arch. Hist. Exact Sc. 46(1994), 193-219
- ^ Barner, K.:Fermats <<adaequare>> - und kein Ende? Math. Semesterber. 58 (2011), 13-45
- ^ Wieleitner, H.:Bemerkungen zu Fermats Methode der Aufsuchung von Extremwerten und der Berechnung von Kurventangenten. Jahresbericht der Deutschen Mathematiker-Vereinigung 38 (1929)24-35, p.25
- ^ Miller, M.:Pierre de Fermats Abhandlungen über Maxima und Minima. Akademische Verlagsgesellschaft, Leipzig (1934), p.1
- ^ Itard, I: Fermat précurseur du calcul différentiel. Arch Int. Hist. Sci. 27 (1948), 589-610, p.597
- ^ Hofmann, J.E.: Über ein Extremwertproblem des Apollonius und seine Behandlung bei Fermat. Nova Acta Leopoldina (2) 27 (167) (1963), 105-113, p.107
- ^ Stromholm, P.: Fermat's method of maxima and minima and of tangents. A reconstruction. Arch. Hist Exact Sci. 5 (1968), 47-69, p.51
- ^ Jensen, C.: Pierre Fermat's method of determining tangents and its application to the conchoid and the quadratrix. Centaurus 14 (1969), 72-85, p.73
- ^ Schneider, I.: Descartes' Diskussion der Fermat'schen Extremwertmethode - ein Stück Ideengeschichte der Mathematik. Arch. Hist. Eact Sci. 7 (1971), 354-374, p.356
- ^ Mahoney, M.S.: Fermat, Pierre de. Dictionary of Scientific Biography, vol. IV, Charles Scribner's Sons, New York (1971), p.569.
- ^ Edwards, C.H., Jr.:The historical Development of the Calculus. Springer, New York 1979, p.122f
- ^ Anderson, K.: Techniques of the calculus 1630-1660. In: Grattan-Guinness, I. (ed): From the Caculus to Set Theory. An Introductory History. Duckworth, London 1980, 10-48, p.23
- ^ Breger, H.: The mysteries of adaequare: A vindication of Fermat. Arch. Hist. Exact Sci. 46 (1994), 193-219, p.197f
- ^ Wieleitner, H.:Bemerkungen zu Fermats Methode der Aufsuchung von Extremwerten und der Berechnung von Kurventangenten. Jahresbericht der Deutschen Mathematiker-Vereinigung 38 (1929)24-35, p.25
- ^ Miller, M.: Pierre de Fermats Abhandlungen über Maxima und Minima. Akademische Verlagsgesellschaft, Leipzig (1934), p.1
- ^ Itard, I: Fermat précurseur du calcul différentiel. Arch Int. Hist. Sci. 27 (1948), 589-610, p.597
- ^ Hofmann, J.E.: Über ein Extremwertproblem des Apollonius und seine Behandlung bei Fermat. Nova Acta Leopoldina (2) 27 (167) (1963), 105-113, p.107
- ^ Strømholm, P.: Fermat's method of maxima and minima and of tangents. A reconstruction. Arch. Hist Exact Sci. 5 (1968), 47-69, p.51
- ^ Jensen, C.: Pierre Fermat's method of determining tangents and its application to the conchoid and the quadratrix. Centaurus 14 (1969), 72-85, p.73
- ^ Mahoney, M.S.: Fermat, Pierre de. Dictionary of Scientific Biography, vol. IV, Charles Scribner's Sons, New York (1971), p.569.
- ^ Edwards, C.H., Jr.:The historical Development of the Calculus. Springer, New York 1979, p.122f
- ^ Andersen, K.: Techniques of the calculus 1630-1660. In: Grattan-Guinness, I. (ed): From the Calculus to Set Theory. An Introductory History. Duckworth, London 1980, 10-48, p.23
- ^ Breger, H.: The mysteries of adaequare: A vindication of Fermat. Arch. Hist. Exact Sci. 46 (1994), 193-219
- ^ Katz, Mikhail G.; Schaps, David; Shnider, Steve (2013), "Almost Equal: The Method of Adequality from Diophantus to Fermat and Beyond", Perspectives on Science, 21 (3), arXiv:1210.7750
- ^ Wieleitner, H.:Bemerkungen zu Fermats Methode der Aufsuchung von Extremwerten und der Berechnung von Kurventangenten. Jahresbericht der Deutschen Mathematiker-Vereinigung 38 (1929)24-35, p.25
- ^ Miller, M.: Pierre de Fermats Abhandlungen über Maxima und Minima. Akademische Verlagsgesellschaft, Leipzig (1934), p.1
- ^ Itard, I: Fermat précurseur du calcul différentiel. Arch Int. Hist. Sci. 27 (1948), 589-610, p.597
- ^ Hofmann, J.E.: Über ein Extremwertproblem des Apollonius und seine Behandlung bei Fermat. Nova Acta Leopoldina (2) 27 (167) (1963), 105-113, p.107
- ^ Strømholm, P.: Fermat's method of maxima and minima and of tangents. A reconstruction. Arch. Hist Exact Sci. 5 (1968), 47-69, p.51
- ^ Jensen, C.: Pierre Fermat's method of determining tangents and its application to the conchoid and the quadratrix. Centaurus 14 (1969), 72-85, p.73
- ^ Mahoney, M.S.: Fermat, Pierre de. Dictionary of Scientific Biography, vol. IV, Charles Scribner's Sons, New York (1971), p.569.
- ^ Edwards, C.H., Jr.:The historical Development of the Calculus. Springer, New York 1979, p.122f
- ^ Anderson, K.: Techniques of the calculus 1630-1660. In: Grattan-Guinness, I. (ed): From the Calculus to Set Theory. An Introductory History. Duckworth, London 1980, 10-48, p.23
- ^ Breger, H.: The mysteries of adaequare: A vindication of Fermat. Arch. Hist. Exact Sci. 46 (1994), 193-219
- ^ Tannery,Paul (ed.): Diophantus Alexandrinus, Opera Omnia, Vol. I, Teubner, Stuttgart 1974
- ^ Mikhail G. Katz, David M. Schaps, Steven Shnider: Almost equal : Method of adequality from Diophantus to Fermat and beyond. Perspective on Science 21 (2013), no.3, 1-45
Etienne d’Espagnet
[edit]The comments on Etienne d’Espagnet are interesting. It would be good to have a source for this. Tkuvho (talk) 15:46, 4 March 2013 (UTC)
- Here I am referring to the following comment by User:Klaus Barner: D’Espagnet possessed a very valuable scientific library which he had inherited from his father, a friend of Viète. In this library Fermat studied the writings of the ancients and Viète’s work. Viète used most frequently the verb aequare and, on some rare occasions, the verb adaequare (8 times) and the noun adaequalitas (once), instead of Recorde’s equals sign. (François Viète, Opera Mathematica. Georg Olms, New York 1970, pp. 80, 134, 135, 137, 141, and 143). In all these cases the meaning of adaequare is to put equal. At that time Fermat had still not studied Diophantus. So he borrowed the verb adaequare and the noun adaequalitas from his admired “example” Viète. Later, in his correspondence with Mersenne and Descartes, he referred to Bachet de Meziriac’s Diophantus. This seems problematic for the following reason. The earliest version of Fermat's method that we have dates from around 1636, the so-called "methodus". In the methodus, Fermat already attributes the term "adequality" to Diophantus. Whatever version of the method that Fermat may have given to d'Espagnet in 1629 is not extant to the best of my knowledge. The assumption that such a text may have contained the term "adequality" seems to be pure speculation, as well as the claim that such a hypothetical use of the term may have originated from Vieta. Of course, I would be happy to see evidence to the contrary, but short of such evidence the passage above seems to be massaging the facts to fit the desired conclusions. Tkuvho (talk) 14:10, 7 March 2013 (UTC)
pseudoequality
[edit]The description "equating things that are different (the exact meaning is subject to controversy; see below)" is rather paradoxical not very informative, it seems to me. If "approximate equality" does not describe a majority of the opinions cited below, we should try to come up with a more descriptive term that does describe a majority of the opinions, instead of the paradoxical phrase (which is unsourced and so does not reflect any opinion given below). How about "approximate equality or pseudo-equality"? Alternatively, we could rely on Andre Weil's authority (which is beyond dispute) and simply use whichever term he used. Tkuvho (talk) 19:40, 9 March 2013 (UTC)
- I agree that, if he has written on "adequality" and Fermat's method, Weil must be cited in this article and probably in the lead. Unfortunately, I have not an easy access to Weil's work on the subject. On the other hand, I am not so proud of my formulation in the lead. However it is a tentative to solve an apparent contradiction: "Adequality" is a neologism that does not appear in any dictionary. Thus it requires some kind of definition in the lead. But the meaning of the word is controversial; in fact the controversy may be extended to usefulness of the neologism and to know if its denotes or not a mathematical topic. This makes a hard task to simultaneously introduce the context and follow WP:NPOV policy in the lead. I agree that my formulation is not satisfactory. Therefore I have wrote a new version of the lead that is, I hope, purely factual. I'll been bold. Feel free to modify it, if you find a better version.D.Lazard (talk) 15:36, 11 March 2013 (UTC)
- Indeed you made a helpful contribution to the article. I will try to look up what Weil actually wrote. If it is quotable I will replace the current formulation in the lede by his formulation, with a citation, if this is OK with other editors. Tkuvho (talk) 15:47, 11 March 2013 (UTC)
- Weil wrote as follows: "[Fermat] introduces the technical term adaequalitas, adaequare, etc., which he says he has borrowed from Diophantus. As Diophantus V.ll shows, it means an approximate equality, and this is indeed how Fermat explains the word in one of his later writings." Tkuvho (talk) 16:16, 11 March 2013 (UTC)
- Indeed you made a helpful contribution to the article. I will try to look up what Weil actually wrote. If it is quotable I will replace the current formulation in the lede by his formulation, with a citation, if this is OK with other editors. Tkuvho (talk) 15:47, 11 March 2013 (UTC)
- This appears in Weil, A., Book Review: The mathematical career of Pierre de Fermat. Bull. Amer. Math. Soc. 79 (1973), no. 6, 1138--1149. Tkuvho (talk) 16:22, 11 March 2013 (UTC)
- According to Weil, the meaning of the term derives from Diophantus's parisotes, rather than from the Latin term. If so, the focus on the latin term in the current introduction is misplaced. I suggest we cite Weil and skip the part about "controversy", which is not sufficeintly informative for the lede. Tkuvho (talk) 16:34, 11 March 2013 (UTC)
Fermat's allegedly inconsistent procedure
[edit]The page currently contains the following material concerning Barner's article on adequality:
- On page 36, Barner writes: "Why did Fermat continually repeat his inconsistent procedure for all his examples for the method of tangents? Why did he never mention the secant, with which he in fact operated? I do not know."
Editors are invited to comment on the utility of including this citation in the page. Tkuvho (talk) 06:57, 5 October 2014 (UTC)
I think Barner's secant idea is a misinterpretation leading to a straw-man argument, but we can't blame him because Fermat himself was not clear nor consistent. Fermat's methods worked, but he did not completely understand what he was doing, nor the underlying assumptions that made his method work. [comment by Ng F K] — Preceding unsigned comment added by 112.199.248.16 (talk) 22:40, 29 January 2015 (UTC)
- Hi Ng, thanks for your comment. Can you clarify what sources you are basing yourself on? Tkuvho (talk) 09:50, 30 January 2015 (UTC)
- I based it on a comment above from yourself(?). QUOTE The Math. Semesterber. piece suffers from serious weaknesses which make it less convincing. For example, the author's interpretation forces him to assume that Fermat made a systematic mistake in confusing secant and tangent lines in his presentation. Other interpretations do not suffer from such a weakness. Tkuvho (talk) 18:06, 20 February 2013 (UTC) UNQUOTE
Katz's article (reference #17) also describes the controversy well, although I disagree with some parts.
By the way, I am not a registered editor of Wikipedia but I came to the "adequality" article expecting a clean answer to what it meant. I didn't expect that this concept is under debate. I ended up trying to answer my own question on what "adequality" means or should mean (see my section on the link to Big O concept). What I wrote does not require Implicit Function Theorem nor Non-stardard Analysis. I don't think it is original research because I believe the ideas contained therein can be found in any analysis textbook that discusses the Big O notation. I just tried to reformulate them in terms of different degrees of equivalence classes, and to explain why the E 'vanishes' without being contradictory. I hope regular editors would take a look to see if it makes sense and give your feedback. Thanks. [Ng F K] — Preceding unsigned comment added by 220.255.1.172 (talk) 17:41, 30 January 2015 (UTC)
- That's a very long entry down there. Could you summarize your explanation please? A few lines if possible will be helpful. The WP:OR issue is not necessarily that serious because you could have your analysis published and then it could be cited here. Tkuvho (talk) 08:49, 1 February 2015 (UTC)
- The first few lines up to the line before "In mathematics, precision of meaning is important." summarises my idea. The Big O notation is not really necessary, but from what i understand, modern mathematicians and computer scientists express approximate equality by using '=' with some Big O type of notation that specifies the level of precision. The theory is (ought to be) well understood, however it is a kind of abuse of notation. Nevertheless, it presents no problem if the reader knows what it really means.
Even without the Big O notation, we can actually define different levels of "adequality" by different equivalence relations ~1 ~2 ~3 etc in increasing levels of precision which behave like the "equal" relation. In fact, "=" relation can be viewed as "~infinity", as it were, being the most precise. From this point of view, i believe the concept of "adequality" can be explained rigorously. We just need to specify the level of precision, like ~1 ~2 ~3 etc instead of ~, because I believe Fermat just conflated all these different levels of adequality treated them as the same.
In the later sections, I tried to explain the various issues and paradoxes caused by the confusion.
[Ng F K]
- Hi Ng, you are a moving target. Your edits at this page are dispersed amoung about a dozen IP addresses. Would you mind creating a wiki account so as to make it possible to view your edits more easily? This only takes a few seconds and if you don't like it you can always stop using it. Tkuvho (talk) 13:14, 1 February 2015 (UTC)
Link with Big-O Notation
[edit][ modified after reading arXiv paper by Katz reference #17 ]
I believe the concept of adequality can be expressed precisely in modern terms using the Big O notation [1] Namely, that
f(x) ~ f(x + e)
means
f(x+e) = f(x) + O(e^n)
or
| f(x+e) - f(x) | ≤ k.e^n for some positive k
where n=2 for problem of tangents (linear approximation)
n is odd number ≥3 for problem of extrema (maxima & minima)
- In mathematics, precision of meaning is important. Fermat and his critics were not clear on how 'near' is near. Some of the criticisms were straw man arguments.
- Various interpretations mentioned in Katz can be shown to be related or equivalent. "Kinetic approach" is a metaphor but can be linkd to epsilon-delta [2] approach or non-standard [3] approach.
- It can be shown that functions adequately equal or "adequal" under O(e^n)
are reflexive f~f, symmetric (f~g ==> g~f) and transitive (f~g and g~h implies f~h) and therefore ~ is an equivalence relation on functions. Equivalence relations have properties similar to the exact "=" relation, which is also itself an equivalence relation. This explains why ~ can be manipulated algebraically in a way similar to =. In fact that is what some mathematical analysts and computer scientists do nowadays with the Big O.
- I think Fermat basically got the right idea, but he was not clear, nor did he explain it precisely. By being fudgey on "some power of e", he does not seem to appreciate that when terms are expanded to and the dominant power of e is odd, you can get an inflexion point. Maxima and minima can also occur if the dominant power of e is an even power ≥ 2
{{by Ng F K|29 January 2015|220.255.1.137}}
Some further thoughts to resolve the paradox of "equal" vs "pseudo-equal" If we define the relations:
adequal to 1st order i.e. f ~1 g means f - g = O(e^1) adequal to 2nd order i.e. f ~2 g means f - g = O(e^2)
...
adequal to nth order i.e. f ~n g means f - g = O(e^n)
we will notice that these pseudo-equal or approximation relations get more and more stringent as n increases. [The "error" terms get smaller with higher powers, and higher order means better precision.]
If m≥n, then f ~m g implies f ~n g (but converse may not be true)
The ultimate most stringent relation is the exact equal relation "=" which we may think of as ~infinity.
Examples
cos E ~3 1 - E^2/2 i.e. cos E = 1 - E^2/2 + O(E^3)
x + E ~1 x i.e. x + E = x + O(E)
x + E ~0 x i.e. x + E = x + O(1)
x = x i.e. x = x + O(E^infinity, so to speak)
How to explain the "disappearance" of E without saying that E=0? We say that to the required order of approximation x + E is practically the same as x. I think Fermat's mistake was not specifying the order precision. His adequal ~ sometimes means ~2 and sometimes means ~3.
Working out Fermat's example, my way:- Let f(x) = bx - x^2
f(x+e) - f(x) = be - 2ex + e^2
This implies
f(x+e) - f(x) ~3 be - 2ex + e^2 [f(x+e) - f(x)]/e ~2 b - 2x + e
Set LHS to zero to find maximum
0 ~2 b - 2x + e
We "downgrade" the relationship to get
0 ~1 b - 2x
x ~1 b/2
However, e can be made arbitrarily small (as small as we want). If x not= b/2, we can always choose e to be smaller than, say, half of their gap to contradict that. The only way to avoid contradiction is
x = b/2.
I hope this removes the paradox of e being a non-zero quantity that seems to be equated to zero. What Fermat means by "adequate" ~ is a conflation of the ~1, ~2, ~3, ... relationships, which seems to be the source of confusion. Also Fermat did not explain the "arbitrariness" of e, which may be obvious to him, but not to his readers.
[comment by Ng F K]
On the purely algebraic nature of the manipulations
Why can we manipulate adequalities algebraically just like equations?
Once the equivalence relations have been established, we can carry over the algebraic operations to the equivalence classes, the way most things are done in Number Theory, Ring Theory, ... etc. we just need to check that the new algebraic operations are "well-defined" in the sense that if we chose different representatives to the classes and carried out the operations, we still ended up with the same result. Later on, we can 'abuse notation' (as some mathematicians like to do) by replacing equivalence classes by their representatives. For example: from the relation
0 ~2 b - 2x + e
we can write
[0] = [b] - 2[x] + [e]
where [ ] denote equivalence classes under ~2 or up to order O(e^2). Now we abuse notation and write
0 = b - 2x + e
This is how we can make and adequality relation ~2 behave 'as if' it is an equality relation. Was this what Fermat had in mind? Not sure, but probably not. But this is how I would 'repair' what he wrote, and explain the equal vs unequal paradox and to explain why we can just do pure algebraic manipulations without worrying about the element of approximation (it is already taken care of by the equivalence classes).
The 'Formal' nature of E
Why does E appear to be a pseduo-variable? I believe this comes from the Principle of Comparison of Coefficients.
For example: If a + b.E + c.E^2 = p + q.E + r.E^2, then a = p, b = q and c = r.
Why? Field theory [4] says that a polynomial of degree n has at most n real roots.
(a-p) + (b-q).E + (c-r).E^2 = 0
is identically true for an infinite number of values. This is impossible, unless a-p = 0, b - q = 0 and c - r = 0. The upshot of this is, when we see an expression like a + b.E + c.E^2, the coefficients a, b and c stand out and give a vector space-like or ring structure [5]. Because of this a + b.E + c.E^2 |---> (a,b,c) isomorphism , the role of E seems to be merely formal.
Why doesn't the size of E seem to matter One can use non-standard analysis idea of infinitesimal. However, we can also explain it using epsilon-delta type of analysis.
Remember f ~ g means | f - g | ≤ k.E^n for all E>0 (*)
It is not mentioned here that E is meant to be small. However, if you think a bit further: Let's say you have some bigger number E' > E. Then this would imply that
| f - g | ≤ k.E'^n
If (*) can be satisfied by some E, it can definitely be satisfied by some bigger number. This is like if you can score a goal in soccer using narrow goal posts, you can definitely score with wider goal posts. The question is: can you score even if the the goal posts get narrower and narrower. This is implied in the universal quantifier "all". If (*) can be satisfied by _all_ E, it can be satisfied even with the small Es. — Preceding unsigned comment added by 112.199.248.16 (talk) 23:19, 29 January 2015 (UTC)
- I am not sure I understand why you say that n has to be an odd number for the problem of maxima and minima. Isn't it n=2 also for this problem, similarly to the problem of tangency? Tkuvho (talk) 15:00, 2 February 2015 (UTC)
- Referring to the Taylor series [6], solving for the tangent is equivalent to expanding up to an error to the first power, and all the second and higher powers are brought under K.e^2 i.e. O(e^2) using the big O notation. Finding maxima and minima (in non-degenerate cases) is equivalent to expanding up to e^2 and leaving higher powers under K.e^3, and we set the 1st derivative equal to zero (same as setting the coefficient of the e^1 to zero), and then the + or - sign of the coefficient of e^2 (same as the sign of the second derivative) tells us whether it's a maximum or minimum. I guess we can all stick to n=2 always, but we have to infer the maximality or minimality from the context somehow. There is also this problem of degenerate cases e.g. (sin x)^1000 which Fermat probably didn't deal with — Preceding unsigned comment added by Mathducator (talk • contribs) 16:34, 10 February 2015 (UTC)
References
- ^ http://en.wikipedia.org/wiki/Big_O_notation
- ^ http://en.wikipedia.org/wiki/(%CE%B5,_%CE%B4)-definition_of_limit
- ^ http://en.wikipedia.org/wiki/Non-standard_analysis
- ^ http://en.wikipedia.org/wiki/Field_(mathematics)
- ^ http://en.wikipedia.org/wiki/Polynomial_ring
- ^ https://en.wikipedia.org/wiki/Taylor_series#Definition


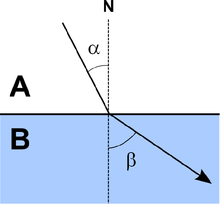











































































































































![{\displaystyle \scriptstyle [0,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f686447e07749ccbe60ab298b068ea7409d0e024)










































