Talk:Proportionality (mathematics)
| This article is rated Start-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
(Does linear imply proportional?)[edit]
If y = kx + c, then would it not be correct to say that y is proportional to x, or y is directly proportional to x irrespective whether or not c = 0 or non-zero?
—Preceding unsigned comment added by 203.97.78.203 (talk) 00:02, 10 June 2005
- I'm pretty sure it is. I was just about to comment on that issue.
—Preceding unsigned comment added by 63.194.211.181 (talk) 04:41, 23 August 2005 (two edits)
- I don't think so. Their change is proportional, but they are not themselves.
--Patrick 12:44, 23 August 2005 (UTC) - No, they're not proportional unless c = 0.
--198.59.188.232 02:44, 24 October 2005 (UTC)
- I don't think so. Their change is proportional, but they are not themselves.
Direct proportionality[edit]
There is no distinction made between merely proportional and directly proportional, in the article. Perhaps one could be made by commenting on the origin graphically.00:36, 1 November 2003 (UTC)
what is the symbol for inverse?[edit]
the article shows that the symbol for directly proportional is α (alpha), but it doesn't say what the symbol for inverse proportional is. can anyone share that with me, i am having trouble remmebering it. I think its either a backwards alpha or an alpha with a line over or under it, something like that. can anyone help?--68.249.39.158 18:18, 14 February 2006 (UTC)
- I thought it was just written as "x is proportional to the reciprocal of y", like this: X α 1/Y capitalist 03:41, 15 February 2006 (UTC)
- The sign of proportionality is not the greek lower case letter alpha (α), but the symbol ∝ (in Arial Unicode MS the symbol is a bit too small, in most type faces it is bigger, as seen in LaTeX: ). In some countries, Sweden for instance, the symbol or ∼ is used instead of ∝. The Unicode-code for ∝ is U+221D (Proportional to) and for ∼ U+223C (Tilde operator). /85.197.143.234 21:51, 27 May 2006 (UTC)
Even more symbols[edit]
- So there is no difference in ∝ and ∼? While checking the Mathematical Operators table at http://www.decodeunicode.org/w3.php?ucHex=2200 i found the character ∽ by the name reversed tilde - maybe this is the inverse proportional sign? By the way, there are many more abstruse characters found in this part of Unicode with most of them hardly to figure out. Maybe someone can help out and expand (that is create redirects) for these characters? Thanks, --Abdull 21:29, 28 May 2006 (UTC)
- I am not too sure about Unicode specifically, but my guess is that it is similar to LaTeX in the sense that there are a lot of characters in LaTeX that can be called or used that do not have predefined meanings in common mathematics nomenclature. These symbols are in LaTeX so that users can define new operations without worrying about creating a new symbol for it and other things like this where it is nice to have a set of undefined, but premade symbols.
Graphs[edit]
Graphs would be helpful here, for examples of an inversely direct and an inversely square relationship. I don't have an SVG editor, so the only thing I can provide is a PNG... Titoxd(?!?) 07:43, 25 June 2006 (UTC)
Proportionality to x^2?[edit]
Should there be a section on proportionality of x^n (n=1,2,3....)? --124.217.57.41 13:19, 4 September 2007 (UTC)BY Mr. Ignacio
That is not, to my knowledge, proportionality. I suppose you could call that "parabolic proportionality", but that would be original research if not a neogolism. dmyersturnbull ⇒ talk 05:15, 3 May 2010 (UTC)
Improving article[edit]
Some suggestions for improving this article include having separate articles for direct and inverse proportion, as they are sufficiently comprehensive and practical topics that deserve separate articles (the redirects will have to be fixed. I must say that I am surprised this article and also ratio are quite short, given their usefulness in real life. I will try to expand the articles once I find the time. I encourage others to help ! Thanks. MP (talk•contribs) 19:20, 19 April 2008 (UTC)
- Given the ubiquity of direct proportion in civilization's systems of rationality, one might expect that that cousin "inverse proportion" would get some attention too. But once you look for sources and experts, books and articles, and real instantiation, the subject slips away into obscurity. Presently I am madly attempting to provide references for the article hyperbolic coordinates which is linked from the paragraph that we have presently. Probably the best evidence for obscurity comes from special relativity, where the hyperbolic curve of inverse proportion is taken for a map of the potential future moment, depending on the speed (or rapidity). The decades it has taken experts to expose the underlying linear algebra of Lorentz' transformations reflects the delicacy of parsing a physical model. Please, yes, if you have some references to build an article, that would be of great assistance.Rgdboer (talk) 20:45, 19 April 2008 (UTC)
In addition, the section Symbols mentions two Unicode proportionality symbols, ∷ and ∺, but doesn't make any attempt to explain what these symbols are used for, other than giving their Unicode names. There should be a better definition of what each means, over and above the Unicode names. For example, the former of the two is simply named 'PROPORTION', which isn't enough to truly define it.. --Ge0nk (talk) 23:45, 28 August 2013 (UTC)
Dispute about factuality[edit]
Two quantities can be directly proportional even if they don't vary by a constant multiple. For example, Newton's law of universal gravitation states that every particle in the universe attracts every other massive particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them[1] This statement can be represented as[2]
- ,
where:
- F is the gravitational force between the two point masses,
- λ is the gravitational constant,
- m is the first mass,
- m′ is the second mass, and
- r is the distance between m and m′
You can find that in about any physics textbook, even a modern one. Because F depends on three variables, m, m′, and r, F does not vary with m⋅m′ by a constant multiple. Yet, they are proportional. Wolfram Mathworld states[3] "If a is (directly) proportional to b, then a/b is a constant. The relationship is written a proportional b, which implies a=cb for some constant c known as the constant of proportionality. What is a good way to explain that other variables may be involved? We could simply say that a∝b does not imply that the only variables involved are a and b, but that is awkward. We need a citation for the definition. I've been looking for one but have had little luck. I'll improve the wording a bit. dmyersturnbull ⇒ talk 02:28, 3 May 2010 (UTC)
- You're just confused by having seen too many examples where the inherent requirement that there are no other variables than the two (i.e., that all other variables are held constant) was not made explicit. In fact, it is implicit that distance be held constant for the first proportionality, and that the product of the masses be held constant for the second.
--Jerzy•t 05:55, 30 September 2010 (UTC)
References[edit]
- ^ Newton, Isaac. Principia Mathematica.
- ^ Alonso, Marcelo; Edward J. Finn (1970). Physics. Menlo Park, California: Addison-Wesley. p. 306.
- ^ Weisstein, Eric. "Proportional".
Lead[edit]
In the lead:
- i removed
- or equivalently if they have a constant ratio
- bcz ratio implies same units, yet for constant speed, distance and time are directly proportional despite different units, and i rem'd
- Proportion also refers to the equality of two ratios.
- bcz a ratio is a quantity, making the statement redundant and inviting confusion about how it could be useful. (If you have some point, show us on this talk page an example of why anyone would care; if you're right, someone will find a less mysterious way to say it.)
--Jerzy•t 06:20, 30 September 2010 (UTC)
Please emphasize direct proportionality can be negative![edit]
Since there NO charts showing negative slopes, some beginning readers might incorrectly think that direct means positive and inverse means negative.
And the examples in the inverse section also involve a negative proportion, so again, we might mislead people that don't read very closely.
Waxmop (talk) 18:36, 1 December 2013 (UTC)
∺[edit]
occurrences of ∺ are required for ∺ is redirected to this page. <STyx @ (I promote Geolocation) 16:13, 1 February 2016 (UTC)
 Done. Petr Matas 00:23, 3 September 2016 (UTC)
Done. Petr Matas 00:23, 3 September 2016 (UTC)
removed section cleanup[edit]
I removed the following part which was party full of format issues but also some of detailed content seem somewhat inappropriate here. It might be ok for its own article though.--Kmhkmh (talk) 09:58, 20 July 2016 (UTC)
Theorem of Joint Variation[edit]
If x ∝ y when z is constant and x ∝ z when y is constant, then x ∝ yz when both y and z vary.
Proof: Since x ∝ y when z is constant Therefore x = ky where k = constant of variation and is independent to the changes of x and y.
Again, x ∝ z when y is constant.
or, ky ∝ z when y is constant (since, x = ky).
or, k ∝ z (y is constant).
or, k = mz where m is a constant which is independent to the changes of k and z.
Now, the value of k is independent to the changes of x and y. Hence, the value of m is independent to the changes of x, y and z.
Therefore x = ky = myz (since, k = mz)
where m is a constant whose value does not depend on x, y and z.
Therefore x ∝ yz when both y and z vary.
Note: (i) The above theorem can be extended for a longer number of variables. For example, if A ∝ B when C and D are constants, A ∝ C when B and D are constants and A ∝ D when B and C are constants, thee A ∝ BCD when B, C and D all vary.
(ii) If x ∝ y when z is constant and x ∝ 1/Z when y is constant, then x ∝ y when both y and z vary.
Some Useful Results:
Theorem of Joint Variation
(i) If A ∝ B, then B ∝ A.
(ii) If A ∝ B and B∝ C, then A ∝ C.
(iii) If A ∝ B, then Ab ∝ Bm where m is a constant.
(iv) If A ∝ BC, then B ∝ A/C and C ∝ A/B.
(v) If A ∝ C and B ∝ C, then A + B ∝ C and AB ∝ C2
(vi) If A ∝ B and C ∝ D, then AC ∝ BD and A/C ∝ B/D
Now we are going to proov the useful results with a step-by-step detailed explanation
Proof: (i) If A ∝ B, then B ∝ A.
Since, A ∝ B Therefore A = kB, where k = constant.
or, B = 1/K ∙ A Therefore B ∝ A. (since,1/K = constant)
Proof: (ii) If A ∝ B and B ∝ C, then A ∝ C.
Since, A ∝ B Therefore A = mB where, m = constant
Again, B ∝ C Therefore B = nC where n= constant.
Therefore A= mB = mnC = kC where k = mn = constant, as m and n are both Constants.
Therefore A ∝ C.
Proof: (iii) If A ∝ B, then Ab ∝ Bm where m is a constant.
Since A ∝ B Therefore A = kB where k= constant.
Am = KmBm = n ∙ Bm where n = km = constant, as k and m are both constants.
Therefore Am ∝ Bm.
Results (iv), (v), and (vi) can be deduced by a similar procedure.
Logarithmic proportionality[edit]
The current logarithmic proportionality definition
is not good, because it can be written as , where . The constant k is clearly superfluous because it can be absorbed into the base a′. Furthermore, if x is exponentially proportional to y according to with , then y will NOT be logarithmically proportional to x, which is not nice.
I think that the logarithmic proportionality definition should be changed to
This will correspond to the exponential proportionality defined with , where . Also, y will be logarithmically proportional to x precisely if x is exponentially proportional to y.
Anyway, a reliable source is really needed for this section. Petr Matas 02:34, 3 September 2016 (UTC)
Equal products[edit]
There was notably the following image. It would be better to explain this incomprehensible deletion. Now it's my turn to click on "undo".
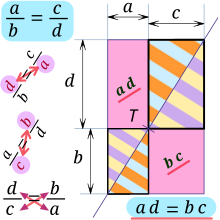
Arthur Baelde (talk) 12:13, 5 June 2018 (UTC)
- Dear Arthur, as you are fairly new here, you may not have absorbed the way things are done on Wikipedia. I deleted your contribution with the comment that it was unsourced. It is one of the pillars of Wikipedia that all contributions must be verifiable, which in this case means that it must be sourced. Unsourced material can be removed at any time– it says so at the top of every edit page. As editors, we do not just write things up, we report on what is available in the literature. While it is not always necessary to delete unsourced material when WP: NOR is violated it is fairly typical to do so. I was persuaded by the spelling errors (now fixed), awkward phrasing, and lack of clarity that this was most likely a case of OR. If this assessment is wrong, it can easily be fixed by providing the source for this material. If this is indeed your own work, you should remove it before some other editor does, just to show that you understand Wikipedia policies. --Bill Cherowitzo (talk) 17:06, 5 June 2018 (UTC)
What specific topic might require to be documented?
Arthur Baelde (talk) 09:42, 6 June 2018 (UTC)
- The whole thing. Yes, you did get the definitions of means and extremes right, but the rest of this is a circular argument. The definition of two fractions being equal is that ad = bc. The equality a/b = c/d = a + c/b + d is based on this definition. Your rectangle illustrates this relation, but it is only valid because of the definition ... it does not prove the definition! You will not be able to find any documentation for this since serious authors would see through this circularity and would never write this. Please remove it. --Bill Cherowitzo (talk) 18:44, 6 June 2018 (UTC)
- "The definition of two fractions being equal" is a very bad beginning, obviously we suppose everybody knows the meaning of an equality. You tangle up the debate. It appears you cannot justify your undo.
Arthur Baelde (talk) 12:14, 7 June 2018 (UTC)
- "The definition of two fractions being equal" is a very bad beginning, obviously we suppose everybody knows the meaning of an equality. You tangle up the debate. It appears you cannot justify your undo.
- I am sorry that you do not understand the mathematical difficulty here. I have been very tolerant and have given you two opportunities to self-revert. I will now do so myself. --Bill Cherowitzo (talk) 16:48, 7 June 2018 (UTC)
- No circular argument in my contributions. Your second deletion is as unjustified as the first one.
Arthur Baelde (talk) 14:52, 8 June 2018 (UTC)
- No circular argument in my contributions. Your second deletion is as unjustified as the first one.
- I will make one more attempt to show you where your error is. You make the statement that the large rectangle is similar to each of the smaller rectangles, in particular for the sake of argument the a × b rectangle. Now, why is this true? You don't say, but I will assume that your reasoning might be that the corresponding sides are in proportion. Algebraically, that is: a/b = a + c/b + d. Why then are these two fractions equal? Well, everyone knows that two fractions are equal if the product of the means equals the product of the extremes, which is just ancient terminology for a × (b + d) = b × (a + c). Now multiplying out and subtracting the common ab leaves you with ad = bc. Thus the fractions are equal and the rectangles are similar only if this equality holds. You use the similar rectangles to "prove" that ad = bc, but if that weren't true the rectangles would not be similar. This is a circular argument, you are proving what you assumed to be true in the first place. If there is something you don't understand or have a question about in this argument, please ask.--Bill Cherowitzo (talk) 23:22, 8 June 2018 (UTC)
What you call the definition of two equal fractions is absolutely irrelevant. When you wrote “the definition of two fractions being equal is that …”, you allude probably to a construction of the field of rationals numbers. However, a coefficient of proportionality in mathematics is not necessarily a rational number. So your third deletion of the same section (10 edits) is as unjustified as the first one and the second one.
Arthur Baelde (talk) 09:28, 9 June 2018 (UTC)
- Circularity issues and sourcing aside, I don't quite see what this section has to do with proportionality or how it helps to understand proportionality. To me the section appears rather alien in the article and if anything possibly confusing or irritating readers.--Kmhkmh (talk) 11:04, 9 June 2018 (UTC)
- Indeed, nothing here about proportionality edited by Bill Cherowitzo, who removed three times a whole section of the article, and claimed to define two equal fractions: an absurdity .
Arthur Baelde (talk) 15:46, 9 June 2018 (UTC) - Bill -- thanks for thinking of me, but Purgy seems to have already taken care of the problem. Rick Norwood (talk) 17:50, 9 June 2018 (UTC)
- Indeed, nothing here about proportionality edited by Bill Cherowitzo, who removed three times a whole section of the article, and claimed to define two equal fractions: an absurdity .
Negative constant of proportionality?[edit]
Currently, the lead and the section on direct proportionality say in a number of places that x and y are directly proportional if y/x equals a non-zero constant. But is it really conventional to call it direct proportionality if y/x is negative? Loraof (talk) 18:56, 17 July 2018 (UTC)
- Text has been changed requiring constant positive per convention. — Rgdboer (talk) 01:05, 1 March 2024 (UTC)
Split Proportion (mathematics)[edit]
Please discuss at Talk:Proportion (mathematics)#Split. fgnievinski (talk) 18:42, 17 March 2023 (UTC)
Inverse proportionality with negative k[edit]
"With inverse proportion, an increase in one variable is associated with a decrease in the other." But what if k, the constant of inverse proportionality, is negative? Perhaps one could add ", when k is positive" or something similar. 94.33.226.183 (talk) 18:20, 27 February 2024 (UTC)
- Proportionality studies select axis for positive constant of proportionality; similarly for inverse proportion. Text now indicates positive constant. — Rgdboer (talk) 01:07, 1 March 2024 (UTC)
Wiki Education assignment: 4A Wikipedia Assignment[edit]
![]() This article is currently the subject of a Wiki Education Foundation-supported course assignment, between 12 February 2024 and 14 June 2024. Further details are available on the course page. Student editor(s): Drinutn (article contribs).
This article is currently the subject of a Wiki Education Foundation-supported course assignment, between 12 February 2024 and 14 June 2024. Further details are available on the course page. Student editor(s): Drinutn (article contribs).
— Assignment last updated by Drinutn (talk) 17:43, 24 April 2024 (UTC)







![{\displaystyle a'={\sqrt[{k}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d93a76b0265b809314835c1ec29479b878d64c69)



