Talk:Trigonometric functions/Archive 3

Archive 1

Archive 2

Archive 3

rules for e.g. sin -x

I'm not entirely sure or I'd edit myself, but I believe there are rules which say that sin x = -sin (pi-x) and cos x = cos (pi-x) that would be very helpful to have here (I'm still looking to confirm them somewhere in fact).. (Just noted that cos (-x) = cos x and sin -x = -sin x, but can't refer to any sources on this one) —Preceding unsigned comment added by 87.96.185.114 (talk) 11:44, 15 November 2010 (UTC)

Unfortunately, because this article (Trigonometric functions) tries to cover so many different functions, it can hardly cover the basics of each of them, so these basics are instead spread over many articles. You're probably looking for List of trigonometric identities. The sine article covers these identities too for the sine function too. —Pengo 12:20, 15 November 2010 (UTC)

Adding Examples of the Series Definitions?

I have worked out examples for the Sine and Cosine series definitions using inputs of 2 radians, and Pi radians. I don't think it would hurt for me to show how you work it out step by step?

It definitely improved my understanding of the Since/Cosine series. (Note: I am speaking about the Taylor Series' of the Sine and Cosine functions)

Tylerp9p (talk) 00:19, 4 February 2009 (UTC)

Wrong Graphs

I don't know who did that, but the graph http://en.wikipedia.org/wiki/Image:Sine_cosine_plot.svg is very very bad -- look at the scale, pi almost equal 1, the slope of sinx at 0 is not 1, etc. Please delete it or fix. The one on http://en.wikipedia.org/wiki/Image:Taylorsine.svg is right. —Preceding unsigned comment added by 72.53.71.84 (talk) 02:47, 22 September 2008 (UTC)

FA status

I think this is in need of review. One thing that strikes me immediately is the shortness of the lead section. I wouldn't even proceed with a GA assessment before the lead was expanded. Richard001 (talk) 09:07, 26 March 2008 (UTC)

Definitions

The article suggests several definitions of trigonometric funcitons, but does not provide any hint to equivalence of these definitions. Why should readers believe, that the function, defined with series, is periodic? dima (talk) 03:56, 25 May 2008 (UTC)

The normal approach in mathematical articles for such uncontroversial facts that are widely known among people familiar with mathematics, since they are taught in undergraduate courses and found in textbooks, is to include one or two references that cover the relevant standard material. I'm not sure the existing references in the article qualify. Alternatively, a proof might be included. I have not yet seen a good discussion of when to include proofs and when not; I'd hoped to work on that myself, but haven't yet found the time to do so. In this case the proof is not deep, but a good exposition may take up more space than is reasonable. If we can start from the fact that the derivative of the sine function is the cosine, and that of the cosine is minus the sine, it is easy to show that their Taylor series are as given.  --Lambiam 02:23, 26 May 2008 (UTC)

Yes, please do it. And periodicity too. dima (talk) 06:03, 26 May 2008 (UTC)

I've no plans to add a proof. As to periodicity: if the series definition and the geometric definition define the same function, then the function defined by the series definition is periodic because it is the same as the "geometric" function, which is obviously periodic.  --Lambiam 23:02, 26 May 2008 (UTC)

Lambiam, it is not obvious, because the "geometric" definition depends on the axioms of Euclidean geometry, so, the properties of trigonometric functions are posulated, not proven. dima (talk) 08:04, 27 May 2008 (UTC)

My statement was conditional (if ... then ...), and holds if the condition is satisfied. You are essentially saying that it is not obvious it is satisfied. It is well-known (and not difficult to prove) that the axioms of Euclid are satisfied in the plane formed by R² endowed with the usual Euclidean metric, and to prove the addition formula you don't need to go beyond the constructible points, which are dense in R, so you don't even need to appeal to the Cantor-Dedekind axiom yet. If you now show that lim_x→0 (sin x)/x = 1 – something that goes beyond Euclid's axioms but should still hold in all models – you are basically done. As I said, a good exposition may take up more space than is reasonable.  --Lambiam 03:09, 28 May 2008 (UTC)

Lambiam, I was not clear, sorry. I wanted to say, that the "geometric definition" does not define any function until we accept the axiom about addition and measuring of angles. I could not understand that axiom, I felt myself stupid. Only after to deduce the periodicity of sin and cos from the differential equations, I realized teachers are wrong; they show things upsidedown. Correctly, first, there should be real numbers, then differential equations, then sin and cos, and only then the concept of angle has sense, it apears as atan2(y,x), and we can speak about constructible numbers; properties of elements in R² can be deduced; there is no need to postulate them as axioms. The article should be rewritten; it should not postulate deducible things. dima (talk) 08:33, 28 May 2008 (UTC)

That goes beyond the purpose of an encyclopedia. We do not "postulate", we report established facts, which for mathematical statements should typically be either commonly accepted definitions or be deducible from such definitions. The relationship between Euclidean geometry and analytic geometry is well known and well established, and if one accepts the latter as the canonical model of the former (basically throwing in completion so as to be able to use analysis), the geometric and analytical definitions are provably equivalent, and it is a matter of convenience and taste which are taken as the definitions and which are deduced.  --Lambiam 17:46, 28 May 2008 (UTC)

Without really reading it, I had suggested this page to a couple of my students. They reported not being entirely happy with it and, upon reading, I can see why. Obviously, this page was a labor of love for at least a couple of people ... who didn't see things in quite the same way with the result that the reading is not as smooth as it could be.

But, rather than edit what is, after all, still a very good page, I will only make a few suggestions and will leave their "defense" to a later occasion, if any,

(1) The first paragraph ought to read something alone the lines of:

There are three aspects to trigonometric functions:

---Originally, trigonometric functions were used to sort of measure angles in a more immediately usable way for computing lengths in a triangle. (Thus, in this case, the use of the word "function" is not legitimate but only a legacy.)

---With the advent of the notion of function, trigonometric functions became really functions, sometimes---and better---called "goniometric functions". They are projection functions, that is the functions which give the coordinates of a point specified on a unit circle by a winding function. In fact, the point specified by the winding function need not move on a circle but on any polygon. See for instance p5 and ff of <http://www.freemathtexts.org/References/AmatycReview/MathUndergroundPDF/10-WhatIsPrecalculus.pdf>, my Spring 99 column in the AMATYC Review.

---The third aspect of trigonometric functions is as solutions of second order differential equations, from which their polynomial approximations (not to be confused with their Taylor series) can be easily derived as well as all their properties. See Serge Lang, A Second Course In Calculus, Appendix 3 or p 72 and ff of Lang's Analysis I. Also, p 147 and ff of Finney, R. L. - Ostbey, D. R. (1984). Elementary differential equations with linear algebra.

(2) There are a number of somewhat unfortunate sentences. For instance, in Unit-cicle definitions, we find "The unit circle definition provides little in the way of practical calculation; indeed it relies on right triangles for most angles". (There are a lot more angles than these.) Schremmer (talk) 19:11, 21 November 2011 (UTC)

Definitions using functional equations?

There is a section of the article claiming that sine and cosine are the unique functions satisfying the angle-addition formulas and a couple of other properties. I added a "citation needed" tag to this a while back, but no one has supplied a reference.

Besides the obvious need for a reference, I'm a little concerned that it may not be true. This definition seems closely related to the definition of the exponential function exp(ix) as the unique unit-magnitude function |f(x)|=1 that satisfies f(x+y)=f(x) f(y), plus some additional constraint to make sure you get exp(ix) and not exp(icx) for some c≠1. However, if you are not careful, such a definition of the exponential can be incomplete [Hewitt & Stromberg, Real and Abstract Analysis (Springer, 1965)]—you typically also need to require that the function be measurable, or alternatively require that it be anywhere-continuous, to exclude crazy non-measurable everywhere-discontinuous functions that can be defined satisfying that condition.

I'm wondering if some analogous requirement of measurability/continuity is required here, or if that is implicit in the inequality $0<x\cos(x)<\sin(x)<x$ for $0<x<1$.

—Steven G. Johnson (talk) 15:41, 12 June 2008 (UTC)

Periodic functions - problematic example

Is anyone else bothered by the square-wave example and the formula:

$x_{\mathrm {square} }(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\sin {\left((2k-1)t\right)} \over (2k-1)}$

given in the article? This formula is rather subtle in its interpretation — it is true almost everywhere, but at the point of the discontinuity the series converges to zero regardless of how the square wave is defined at that point. Of course, if one redefines one's notion of a function to be a distribution, then strict equality holds, but otherwise it is a bit of an odd case.

Maybe it would be better to change this example to, e.g., a triangle wave, which converges pointwise everywhere and has no hidden caveats?

—Steven G. Johnson (talk) 15:49, 12 June 2008 (UTC)

Citations for facts

There seems to be some disagreement over which statements in this article need individual citations, so it's worth reading Wikipedia:When_to_cite. Regarding Relationship to exponential function and complex numbers, it's perhaps also worth following the link to Exponential_function and taking a look at the Exponential_function#On_the_complex_plane section (or better, follow the link to Euler's formula). --catslash (talk) 20:42, 16 June 2008 (UTC)

"Statements based on someone's scientific work should be cited and attributed to their authors in the text," not in the links (Wikipedia:When_to_cite).--Ioannes Pragensis (talk) 21:06, 16 June 2008 (UTC)

The statement "This identity is called Euler's formula." needn't to be cited, as this is a well known fact. The demonstration is obvious from the series definition, as asserted, a citation would be fine but not necessary in my opinion. But I think that there are other sections that critically need to be sourced like "The significance of radians" and "Definitions using functional equations" (see above). Cenarium (talk) 21:27, 16 June 2008 (UTC)

In this place, the Fact was not due to the name "Euler's formula", but due to the formula itself. The article says: "It can be shown from the series definitions..." but does not show it and does not say where it is shown, which is a problem. You cannot expect that an average reader will be able to take the series definitions and derive the nice formula from them - not everybody is Euler. The article tends to be too technical and demanding in places, it should be either avoided or at least supported by citations of literature with detailed proofs.--Ioannes Pragensis (talk) 07:33, 17 June 2008 (UTC)

There is a demonstration in the article Euler's formula, and references there, so I added a note pointing there. (diff) Cenarium (talk) 13:22, 17 June 2008 (UTC)

It is better, but still has two issues: 1. The chapter in Euler's formula is itself unsourced and therefore not easy to check unless one has enough knowledge of math to repeat the computatios himself (and the computation is not given fully there, the proof of absolute convergence is missing!) 2. It is generally not good to make one article directly dependent on another one in sourcing - sources has to be near the content and you cannot expect that the WP articles with sources will be left unchanged over the time; somebody may completely rewrite them one day and the sources disappear. => I would perhaps left the link there, but add a book with the proof. There must be many such books in English.--Ioannes Pragensis (talk) 13:49, 17 June 2008 (UTC)

Agreed that it's not a substitute for a source, but I think that making mathematics articles more dynamic is a good idea. Cenarium (talk) 14:52, 17 June 2008 (UTC)

The citation tag on the series definitions has just been removed and then replaced. I was tempted to remove this tag myself as what was asserted seemed pretty basic and uncontroversial. Perhaps there is a subtlety I have missed. Could the tag be placed more precisely please? Is the problem (1) that these series satisfy the differential equations, or (2) that they are a unique given the x = 0 conditions or (3) that they converge for all real x? --catslash (talk) 17:28, 28 October 2008 (UTC)

Right Triangle Definitions of Sine and Cosine

Something appears to be in error here. The definitions of sine and cosine are identical to those for secant and cosecant. I believe they should be the inverses of how they are defined now, ie. sine = opposite / hypotenuse. The image used to illustrate the definition is wrong as well, which is why I'm not editing it myself. Have to get back to my trig homework. Ravenhearte (talk) 07:29, 5 September 2008 (UTC)

You're right that the definitions were wrong. It looks like the article suffered vandalism (somebody thought it's funny to introduce mistakes), which I now cleaned up. Morale: don't trust Wikipedia blindly. Incidentally, I don't see a mistake in the images. -- Jitse Niesen (talk) 08:55, 5 September 2008 (UTC)

Huh?

I am just an ordinary high school freshman. This does not make sense to me. Can you make it clearer for the simple-minded people like myself? If not, then where should I go for homework help? —Preceding unsigned comment added by 70.137.172.123 (talk) 23:41, 9 October 2008 (UTC)

Amen to the freshman. You need to split / gut / simplify this article. It is too advanced to be useful for those who don't know what the trigonometric functions are, but want to learn. Perhaps have a different page for each of the sine / cosine / tangent functions with more rudimentary information? —Preceding unsigned comment added by 70.192.14.214 (talk) 08:38, 26 October 2008 (UTC)

Though I'm not familiar with the US school system or maths curriculum, I would expect that if the freshman continues to study mathematics he/she will need most of the material in this article before leaving school (excluding History, Definitions using functional equations, Computation, Fourier Analysis and perhaps Definitions via differential equations). Having said that, the size of the article is clearly daunting! Perhaps it would help if the Right-angle triangle definition section was right at the top, above the History. Also, the set-of-zeros stuff is of no relevance to this most elementary section. --catslash (talk) 16:15, 26 October 2008 (UTC)

I would hope that he would learn the material in school, but I think Wikipedia should explain topics at a level aimed to help those people who don't already understand the topic. People like the high-school freshman in trig class - the type or person to do a wikisearch on 'sine'. For example, nowhere in the article is a normal sine curve. I mean, there is a lot of useful (basic) stuff here, but perhaps there should be another page for a more introductory explanation. A page that, for example, has a graph of the cosine curve, that shows why cos(-x)=cos(x) and where the word 'radian' is linked to the radians page. I'm not saying that the info on this page isn't golden - it is - I'm just saying that the topic is much larger than what this article provides information on.

I just looked through the article again and found counterexamples to some of my prior assertions - there is a sine curve, radians are linked to the radian page, etc. It doesn't change my argument: this could be more useful if there was another article "An introduction to Sine, Cosine, and Tangent". The emphasis on important information is lost to the sheer volume of information. Thoughts? Nlspiegel (talk) 21:07, 31 October 2008 (UTC)

I'm afraid if Trigonometric_functions#Sine isn't as clear as day then Wikipedia isn't going to help you. 210.9.143.119 (talk) 11:53, 25 November 2008 (UTC)

As a Ph.D. engineer (yes, I am a rocket scientist having worked on Shuttle and lesser vehicles) with 40+ years experience using trig function, I can tell you that, "The sine function takes an angle and tells the length of the y-component (rise) of that triangle. The cosine function takes an angle and tells the length of x-component (run) of a triangle," is nonsense. If nothing else, sines and cosines are unit less - the above quote would, as stated, gives them the units of length. I stopped reading at this point so have know idea what other useless information is being promulgated here. Pity the poor freshman (or anyone else) who uses Wiki as a guide to anything - it is generally crap (to put it mildly) on just about any subject - think of it as a 6th grade term paper written by a team of mediocre students with no supervision by an accredited teacher. —Preceding unsigned comment added by 69.243.164.201 (talk) 02:29, 24 October 2010 (UTC)

Good find. It's not really nonsense if some context is given. I made some changes to accomodate for this. It's still not ideal, but I think it's better. Please do note that "More precise definitions are detailed below", so perhaps you shouldn't have decided stopping reading after all :-) - DVdm (talk) 18:28, 24 October 2010 (UTC)

History section belongs at the end

I agree with catslash that the history section should not be at the top. Let's move the history section to the end of the article, keeping its first paragraph and the table where they are. With this simple fix, beginners come immediately to the right triangle definitions instead of being intimidated. Any objections? --FactSpewer (talk) 06:18, 11 November 2008 (UTC)

Discovered?

Were functions like chord, sine, etc. really "discovered"? The article's text is oddly disturbing to me. Perhaps the article has a Platonic bias - as if these functions are there just waiting for someone to find them. Would "defined by", or "first used by", or "first studied by" be more accurate?

Not all people know that you can find most trigonometric functions simply by hitting the <COS> key (or equivalent) on a calculator. In order to make this article more accessible to people without mathematic skills, I suggest a new introduction, to be inserted at the start:

Basic use of trigonometric functions

On a basic level, trigonometric functions are useful to calculate the magnitude of forces, for example to calculate the G-forces that work on an airplane when it banks. This can be done through a very simple equation, see below. However, in order to solve the equation, you need to know the function of a specific angle (for example the cosine of a 45° angle). These functions are not straightforward to calculate, but they can be obtained from tables. All calculators except the most rudimentary have these tables built-in (calculators with a <SIN>, <COS>, and <TAN> key). For example, in order to find the cosine of a 45° angle, simply type the number 45 on the calculator and hit the <COS> key. (the cosine of a 45° angle is 0.707)

The equation to calculate the G-forces on a banking airplane (provided that it maintains its altitude) is:

$Gforce={\frac {1}{\cos \theta }}$

Hence, if an airplane banks with a 45° angle and maintains its altitude, it will "pull" ${\frac {1}{0.707}}=1.41G$ 'Mrgalaxy01 (talk) 15:29, 22 January 2010 (UTC)

I don't have a calculator and banking of airplane is a little too particular and away from a lot of peoples experience to stick in never mind into the introduction. Dmcq (talk) 15:53, 23 January 2010 (UTC)

Rise/Run

This article's discussion of "rise/run" is self-referential to the point of uselessness. To understand it, you must already understand it.

Here's the use case with which I approached this article: I've got two points which define a line. I need to shorten the line slightly from both ends. From the points, I can calculate rise/run. From rise/run, I ought to be able to find the sine & cosine of the line's angle relative to the horizontal, from which I ought to be able to find my new line-endpoints. I came to this article to refresh my memory as to how to convert rise/run to sine & cosine.

Consider this paragraph: "Sine is first, rise is first. Sine takes an angle and tells the rise when the length of the line is 1."

- "Sine is first"? What does that mean? The meaning of "first" is completely opaque in this context.

- "Sine takes an angle and tells the rise when the length of the line is 1." I don't need to have sine "tell me" anything. I have the rise/run; I need for it to "tell me" the sine & cosine, not have the sine "tell me" the rise. THAT'S WHY I'M READING THIS SECTION OF THE ARTICLE. If I already had the angle, and needed the rise, I'd be reading some other section of the article.

I suggest that the use case described above is very common for readers of this section of this article, and that the section needs to be re-written to address the needs of that use case.

Please accept my apologies for allowing my frustration to leak into the tone of this suggestion. It is only because I am an avid user of (and occasional contributor of articles to) Wikipedia that I care enough to get emotional about its utility (or lack thereof). —Preceding unsigned comment added by JimPlamondon (talk • contribs) 17:11, 26 January 2010 (UTC)

I'd be inclined to delete this section together with the abbreviated version of it in the lead. Reasons:

1. It's unclear
2. It's redundant
3. The article is rather long and it would benefit from pruning of redundant material
4. The language is archaic; I would guess it's some rote-learned recitation from the 19th century or earlier.

I was already considering deleting the rise/run bit from the lead --catslash (talk) 22:52, 26 January 2010 (UTC)

I'd be a bit more careful if it had a citation, I consider carefully including stuff which has a good citation even if it is silly, but it doesn't so go ahead and remove it is my feeling. I don't think people are too worried about circular reasoning in wikipedia though, it isn't a textbook, it just tries to describe notable stuff. Dmcq (talk) 00:10, 27 January 2010 (UTC)

Non-Euclidean Geometry

What is the change in effect of the trigonometric ratios when one leaves euclidean geometry for shapes on non-planar surfaces? -RadicalOne•^{Contact Me}•_{Chase My Tail} 05:26, 28 January 2010 (UTC)

cotangent

Maybe it's excessively pedantic, but I remember hearing in math class that cot x = 1/tan x, which means it has a removable singularity at pi/2 rather than being 0 there. I wouldn't know what kind of source to rely on for something like this. Maybe some computer algebra systems are affected, or something like that. 66.127.55.192 (talk) 20:06, 1 February 2010 (UTC)

At pi/2, cotangent is ∞^-1; such a value is generally considered to be zero. -RadicalOne•^{Contact Me}•_{Chase My Tail} 20:10, 1 February 2010 (UTC)

$\tan {\pi \over {2}}=\cot 0=\infty$ 68.173.113.106 (talk) 21:56, 22 December 2011 (UTC)

Pros and cons of notations for series

Several equivalent notations can be used for the series characterizations—among them these:

${\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}\\[12pt]\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}x^{2n-1}}{(2n-1)!}}\\[12pt]\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{{\text{odd }}n\geq 1}{\frac {(-1)^{(n-1)/2}x^{n}}{n!}}\end{aligned}}$

Does anyone have specific preferences? Why? Michael Hardy (talk) 05:26, 8 March 2010 (UTC)

• Third one needs too much thinking to understand. First is a tiny bit better than the second because I like 0 more than I like 1; otherwise it is the same. Zero^talk 05:43, 8 March 2010 (UTC)
• I think the first one is more standard.--RDBury (talk) 08:27, 8 March 2010 (UTC)
• Slight preference for the first one. It's marginally simpler than the others. --catslash (talk) 09:00, 8 March 2010 (UTC)
• I prefer the first, for the same reason as User:Zero0000. Ozob (talk) 11:52, 8 March 2010 (UTC)
• I prefer the first one. --Dyaa (talk) 21:18, 8 March 2010 (UTC)
• Comment This was occasioned by a recent edit in which someone tried to switch from the first notation to the second, but forgot to change the lower bound of summation from 0 to 1. A discussion ensued on that person's user talk page, where I posted that I would inquire here on this present page. Michael Hardy (talk) 21:26, 8 March 2010 (UTC)
• One lonely voice for the last, which has fewest operations. —Tamfang (talk) 00:04, 9 March 2010 (UTC)
• I can't say that I care that much, but I find the 0-based sum slightly nicer; somehow i find addition (2n+1) more intuitive than subtraction (2n-1). — Steven G. Johnson (talk) 03:41, 9 March 2010 (UTC)
• I actually also find it more natural to use 2n + 1, but I have read that the general formula is 2n - 1. And of course, I just changed it that time to the form which I thought was standard - and I didn't know that there could be "zeroth" terms. But if you people prefer it this way, then fine - I don't mind. And for cosine, it should of course be 2n, not 2n - 2, so in this case it is mandatory to start at 0. Majopius (talk) 22:13, 9 March 2010 (UTC)
• I'll vote for the first one, because it is more natural to start summation at 0. But of course it makes little difference. The "fundamental(istical)ly correct" form would be

$\sum _{i\in \mathbb {N} }[i{\hbox{ odd}}]\,{\frac {\mathbf {i} ^{i}}{\mathbf {i} }}\,{\frac {x^{i}}{i!}},$

but I don't think that will get much support (and it looks better with n as summation index). Marc van Leeuwen (talk) 14:34, 13 March 2010 (UTC)

• For heaven's sake people, can't you use another letter instead of i as a variable? i is the imaginary unit and that's that. Same goes for e. For the purposes here, you can just use n, its not that difficult. I don't mean to sound pushy, but it annoys me when I see the imaginary unit i used to represent a different number, a variable. And unfortunately, I see it a lot. Majopius (talk) 21:39, 29 March 2010 (UTC)
  • Sure, let's use j and jrrjtate the electrjcal engjneers. —Tamfang (talk) 00:19, 30 March 2010 (UTC)

No Definition or discussion of arctangent, arcsine, etc.

The article refers to the artangent and its use but doesn't really define the term. There is a brief mention of arcsine that just barely defines it as the inverse sine. In general, the article needs to define all the inverse trigonometric functions (arcsine, arccosine, arctangent, etc.), their notation and some basic info about their use. This is an example of a Wikipedia article where the reader already needs to know the subject area before understanding material in the article. Ross Fraser (talk) 09:42, 27 June 2010 (UTC)

Readability of Pi fractions

For readability and consistency I have replaced a number of occurences of

${\tfrac {1}{n}}\pi$

with the more commonly used

${\frac {\pi }{n}}$

DVdm (talk) 08:08, 28 June 2010 (UTC)

I've started a sine article

This is a good diagram, but if you're just trying to learn about the sine function then it's way too overloaded and full of distracting (and intimidating) stuff.

Likewise for this one.

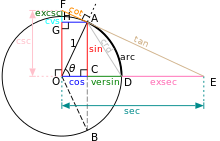
It seems more by accident than by design that there has never been an article on sine on Wikipedia. There are over 250 articles which link to "sine" (not even counting redirects from "sine function", or the many links to "Trigonometric functions#Sine, cosine and tangent). Sine seems like such a basic concept not to have an article. So I've started one. Right now, it's based almost entirely on this article (Trigonometric functions). Please help to build it up and make it clearer and include parts from this article which I've left out. —Pengo 05:10, 9 September 2010 (UTC)

Thank God for that. Well overdue! 128.86.179.86 (talk) 17:52, 30 November 2010 (UTC)

Solving equations with t. f.

Does anyone know, how to solve an equation like cos(x)=x or cos(x)=x² ? Lipedia (talk) 15:43, 9 January 2011 (UTC)

The best place to ask questions like this is the reference desk, especially the maths one: WP:RD/MA. It's a far more active page focussed on answering questions like the above.--JohnBlackburne^words_deeds 15:49, 9 January 2011 (UTC)

Recursive definitions of Maclaurin series

A recursive means of expressing the above series is that

If $p_{1}(x)=x$ and

$p_{n}(x)={\begin{cases}-\int p_{n-1}(x)dx+1,&{\text{if }}n{\text{ is even}}\\\int p_{n-1}(x)dx,&{\text{if }}n{\text{ is odd,}}\end{cases}}$

then $p_{\text{even}}(x)\approx \cos(x)$, $p_{\text{odd}}(x)\approx \sin(x)$, and ${\frac {p_{\text{odd}}(x)}{p_{\text{even}}(x)}}\approx \tan(x)$ provided the above integrals are evaluated without constants of integration.

Can we add the above lines to the section that discusses the Maclaurin series of sine and cosine? Please consider this addition.Maonaqua (talk) 14:12, 12 May 2011 (UTC)

'provided the above integrals are evaluated'? how do you evaluate the integrals? You need p to deduce p which is clearly of little use: it's not like there's a p(0) you start from. More generally this looks like a complicated way to write down the differential equation y´´= -y, i.e. the formula for SHM which does have solutions sin and cos but is not normally used as a definition.--JohnBlackburne^words_deeds 14:23, 12 May 2011 (UTC)

Yes there is a function $p_{1}(x)$ that is used to deduce the successive p-functions. The above algorithm is simply another way to produce the Maclaurin series and it is not connected to the differential equation you speak of. Confirming that this algorithm produces the Maclaurin series of sine and cosine for the first few terms is easy:

$p_{1}(x)=x$

$p_{2}(x)=-{\frac {1}{2}}x^{2}+1$

$p_{3}(x)=-{\frac {1}{6}}x^{3}+x$

$p_{4}(x)={\frac {1}{24}}x^{4}-{\frac {1}{2}}x^{2}+1$

I thought the algorithm should be added because it unifies the Maclaurin series and demonstrates that definitions can be built recursively.Maonaqua (talk) 19:15, 12 May 2011 (UTC)

Of course it is connected to the differential equations of the harmonic oscillator. This is just the Picard iteration for the system $c'(x)=-s(x),\;s'(x)=c(x)\;c(0)=1,\;s(0)=0$. The integration should be definite with boundaries 0 and x.--LutzL (talk) 09:08, 13 May 2011 (UTC)

I see. I'm afraid that is very non-standard use of the notation, both for the integrals which are indefinite ones and the ≈. Looking at it again it's equivalent to the Maclaurin series definition: the way each term is derived, by repeated integration, mirrors the way the terms of the Maclaurin series are derived. Except that is the standard method and more straightforward and general.--JohnBlackburne^words_deeds 19:39, 12 May 2011 (UTC)

I'll admit to non-standard, but I am not so sure about general. You see, there are antiderivative recursion algorithms not just for the standard Maclaurin series of sine and cosine but also for degree-based sine and cosine functions, sine and cosine functions of any desired period, $e^{x}$, general exponential functions of the form $b^{x}$, and even the hyperbolic functions. Antiderivative algorithms can approximate a lot of manipulations that standard Maclaurin and Taylor series cannot handle by themselves. For example, there is no single Taylor or Maclaurin series for exponential functions of the form $b^{x}$ that have a radius of convergence of all real numbers, but there is an antiderivative algorithm for such functions that does have an infinite radius of convergence. I admit that antiderivative recursions are not too straightforward or standard, but they can handle some things that Taylor and Maclaurin series cannot (though thy are are mostly limited to functions that have infinite domains--I will give that nod to Taylor and Maclaurin series as Taylor and Maclaurin series can handle functions with limited domains). Maonaqua (talk) 20:08, 12 May 2011 (UTC)

By 'more general' I mean you can write down the Maclaurin expansion of any function, provided it is infinitely differentiable. And derivatives are known for many functions including b^x, at least for those real values of b that give a useful function. You don't need a special relationship like the one you give involving a pair of derivatives. Instead (in the case of sin and cos) you just observe how the derivatives repeat and plug those into the series.

True, the Maclaurin/Taylor expansion of b^x does exist, by it requires that natural logarithms be calculated. Unfortunately, logarithms do not have very nice Taylor/Maclaurin series expansions (very limited domains) and thus utilizing the Taylor or Maclaurin series for b^x will involve the use of yet another series that approximates natural logarithms. Antiderivative algorithms, on the other hand, do not require the use of another approximation--they are generally self-contained.

Do you have a source for this? It will be easier for you and other editors if you can point to a reference, which might be easier to understand and to see how this all works and relates to other areas.--JohnBlackburne^words_deeds 20:41, 12 May 2011 (UTC)

You can try this article: https://docs.google.com/viewer?a=v&pid=explorer&chrome=true&srcid=0B3Ax_SjQwgpHYmRjOWFmMDgtZjczYi00YTZjLTljZWItZGY4ZTVjZDhlMDdm&hl=en&authkey=CKyY3IoF .

That shares the same problems as the above text: it does say at the start though it "is not meant to present formal methods" which suggests it's not rigorous for a definition. More generally it's not a reliable source from e.g. a textbook or published journal, and it not written as such but is more like an essay. I should have made it clear, but a reference needs to be from a reliable source.--JohnBlackburne^words_deeds 23:47, 12 May 2011 (UTC)

Hmmm--always thought true results were reliable. Anywho, the recursive definition that I proposed is independently verifiable and the author of the article also states that some of the recursive algorithms he generates are indeed verifiable outside of his discourse. Of those recursions that are independently verifiable, the author lists the above recursion, the exponential base e recursion, and the Maclaurin recursion for hyperbolic functions. That is, I gave the source so that the use of recursions could be examined--the recursion itself can be verified by anyone who has studied antiderivatives and Maclaurin series; the recursion formula I proposed meets the requirement of verifiability even without the source I mentioned. —Preceding unsigned comment added by Maonaqua (talk • contribs) 14:24, 13 May 2011 (UTC)

WP:Verifiable on Wikipedia means that it can be looked up in a reliable source. It does not mean that people can work it out for themselves. Stuff that is worked out oneself is called WP:Original research and is not allowed. Wikipedia is for summarizing notable stuff from reliable sources, it is not for telling people ones latest ideas. Wikipedia is an encyclopaedia not a vehicle for new thought no matter how wonderful, see WP:5P for a general overview of what Wikipedia is about. Dmcq (talk) 15:33, 13 May 2011 (UTC)

Yes, I should have linked this before: a reliable source is one not just any source but one from a reliable publisher or authority. In maths that is usually a mainstream academic textbook or a paper from a peer reviewed journal. Occasionally other sources such as newspapers are used but for most maths the sources are recognised academic ones.--JohnBlackburne^words_deeds 15:38, 13 May 2011 (UTC)

Motion defeated, I guess--was worth a shot.

1 / 0

0 is positive or negative? if it tends to 0 as positive the limit of ${\frac {1}{0}}$ tends to infinity. But if the function tends to 0 as negative it tends to minus infinity. I actually don't understand why infinity is the only possible value of some of these trigonometric functions (Trigonometric functions#Special values in trigonometric functions). I just hope that you just take a look at Math World (http://mathworld.wolfram.com/Tangent.html) and see that only on one side tan (90°) is infinity but on the other side it is minus infinity. It is the same with other ${\frac {1}{0}}$. So, basically tan (90°) does not exist. If x=0 and $f(x)={\frac {1}{x}}$, then $f(0)=\infty$? Well, I believe it is not. 176.31.222.33 (talk) 22:55, 23 October 2011 (UTC)

See Real projective line which explains about having a single infinity. Dmcq (talk) 23:16, 23 October 2011 (UTC)

(ec) You can add ∞ in two ways. As detailed at extended real number line it can be added as +∞ and −∞, or just as ∞ so both ends are the same. The former are more useful for limits but for solving problems such as 0x = 1, atan(x) = π/2 only a single infinity is needed. The structure you get is a real projective line, which if formally defined can be easily linked to the trigonometric functions.--JohnBlackburne^words_deeds 23:19, 23 October 2011 (UTC)

I was wondering should we be putting a reference to thatbeside where infinity is used like that? I certainly think it wouldn't be right to put in ±∞, the projective ∞ is the right thing to put in. Dmcq (talk) 23:26, 23 October 2011 (UTC)

Another reason why these values does not exist. For instance the domain of tangent $\tan x={\frac {\sin x}{\cos x}}$ is defined for all $x\neq {\frac {\pi }{2}}+k\pi ,k=0,\pm 1,\pm 2,...$ (Domain of a function#More examples). If you put infinity, you have to put all the context. In any case, it should be explicit that infinity is limit. If x=0 and $f(x)={\frac {x^{2}}{x}}$, you can't say $f(0)=0$, but only that $\lim _{x\to 0}{\frac {x^{2}}{x}}=0$. 176.31.222.33 (talk) 00:06, 24 October 2011 (UTC)

Well that is very interesting if you look at the examples above the one for tan. f(x) = √x is defined only for x ≥ 0 as a function from ℝ to ℝ, but is defined for all x as a function from ℝ to ℂ. The same approach can be used for tan(x): as a function from ℝ to ℝ ∪ {∞} it's defined for all x. The motivation for ℂ is very similar to that for the real projective line: extend ℝ in such a way so the function can be calculated for all real numbers.--JohnBlackburne^words_deeds 00:29, 24 October 2011 (UTC)

Take a look at some books: [1], [2], [3], [4]. 176.31.222.33 (talk) 00:41, 24 October 2011 (UTC)

But those are schoolbooks. There's nothing wrong with them but Wikipedia isn't limited are to what children are taught. As such it's far more encyclopaedic to give the value of infinity rather than saying it's undefined. It may cause readers to think and read beyond what they learned in high school but that's a good thing not a problem.--JohnBlackburne^words_deeds 01:29, 24 October 2011 (UTC)

If you think about it, ⁺∞ = ^–∞ because it is the reciprocal of zero which is both positive and negative (or neither). Cheers, The Doctahedron, 23:50, 20 December 2011 (UTC)

Definitions via differential equations; tangent--unique solution when y(0)=0?

"Definitions via differential equations" ...The tangent function is the unique solution of the nonlinear differential equation

$y'=1+{y}^{2}$

satisfying the initial condition y(0) = 0...

$\tan x$ is not the unique solution. $\tan(x+\pi )$ also satisfies it. So does $\tan(x+2\pi )$

Also, ...There is a very interesting visual proof that the tangent function satisfies this differential equation...

Well, rather than just stating that there is one, the page needs to also show the proof. And besides, there is a very easy way to do it analytically.

$1+{y}^{2}={\frac {{\mbox{d}}y}{{\mbox{d}}x}}$

${\frac {{\mbox{d}}y}{1+{y}^{2}}}=dx$

$\arctan y=x+C$

$y=\tan(x+C)$ — Preceding unsigned comment added by 220.255.2.77 (talk • contribs) 03:43 -- 9 November 2011

First, those functions are all the same due to the periodicity of the trig. functions. Second, one verifies the solution of a differential equation by differentiating the proposed solution and inserting it into the equation. Your reasoning is circular, it assumes the knowledge of the derivative of tan to get the derivative of the inverse function arctan and thus to be able to find the anti-derivative of 1/(1+y^2).--LutzL (talk) 11:49, 9 November 2011 (UTC)

Functions are defined by their values (and types) not by how they are written, x+1 and 2+x-1 are exactly the same function of x. Wikipedia does not and usually should not give proofs, you can look up the references for them. Proofs are only put in when there is something interesting about them or they are short enough not to break the flow. Actually there is a couple of slight problems with saying it is the unique solution in that it isn't defined everywhere and if you do have the real projective line for y (which is one way to say the infinities here are okay) you've still got to show it gets past the infinities all right. So it isn't altogether trivial. Proving you have a unique solution tends to be more difficult than showing you just have a solution. Dmcq (talk) 14:08, 9 November 2011 (UTC)

Cosine redirects here?!?

Hi all,

I can't believe Cosine redirects here. It really should be its own article, or redirect to Sine instead. Could someone please explain why it was moved?

Thanks,

The Doctahedron, 00:26, 18 December 2011 (UTC)

Cosine still redirects here because no one has bothered to make a cosine article in English as yet. Cosine articles exist on 17 other language Wikipedias, but not English. For a long time sine redirected here too. —Pengo 02:49, 18 December 2011 (UTC)

I've created a draft of the new Cosine article, if it's created. See this section of my talk page and leave comments! Cheers, The Doctahedron, 23:17, 22 December 2011 (UTC)

Survey: Should Cosine be its own article?

Update: This survey is not intended as a substitute for consensus. It is only intended to give administrators a good idea of what you think of the move. Please discuss the subject matter as well!

Please vote on whether an article on the cosine function should be created below, by signing beneath the subheading that corresponds to your choice (type four tildes: ~~~~). You do not need to provide a reason for making that choice, but explanations are welcome. It is recommended that you state your opinions above the heading for this section, so as not to confuse the nonexistent bot that is tallying the votes around the clock. You should not vote if you have no opinion of this move. This survey ends on 6 January 2012 at midnight UTC (although you can still contribute to the discussion thereafter).

You may change your vote at any time until this survey expires. You may only vote once.

Those guidelines contradict WP:VOTE. Decisions are not made on the basis of votes on Wikipedia. Each person should say why they want or don't want something, not just vote. And the easiest way of doing that is to put in one contribution not two. Please have a look a how these things are done elsewhere on Wikipedia for instance on the village pump proposals at WP:VPR. Dmcq (talk) 21:22, 20 December 2011 (UTC) Dmcq (talk) 21:22, 20 December 2011 (UTC)

You're absolutely right. Polling is not a substitute for consensus on WP, but it does give admins a good idea of what people generally think about actions. So it's safe to say that voting is a complement to discussion, but should never replace it. Cheers, The Doctahedron, 22:01, 20 December 2011 (UTC)

Internet votes without rationales are almost useless as guidance to anybody. —David Eppstein (talk) 22:14, 7 January 2012 (UTC)

Yes, Cosine should be its own article

• 68.173.113.106 (talk) 21:53, 19 December 2011 (UTC)
• —Pengo 04:34, 20 December 2011 (UTC)

No, it's fine the way it is

• In fact I'd get rid of the sine article and redirect to this article. It already has accumulated ridiculous cruft compared to this article. There is no sine topic, the topic is the trigonometrical functions. Sine is just one of those functions. A name is not the same as a topic. Has anyone made a case for why consine and sine are better off dealt with in separate articles? And we should not just vote on Wikipedia. We should say why we support or oppose something. I am removing the numbering as it encourages vote counting, see WP:VOTE Dmcq (talk) 10:59, 20 December 2011 (UTC)

This is not the graph you should see when you look up cosine, but currently it is.

The sine function has its own attributes which are different to the other trigonometric functions. The majority of the sine article is gathered from existing articles about the topic of sine. Content which could not fit within the "Trigonometric functions" article because it is dealing with six or so functions, which it cycles through over and over again, so cannot cover any one of them in any detail. If they were a single topic, it would not be necessary to structure the trig functions article like that. Sine can be treated independently and it's clearly useful to do so. You can learn about it, understanding it, and use it independently of the other trig functions.

When I raised the topic of starting a sine article (above) there were exactly zero objections in the entirely underwhelming but not unexpected response. If you want to improve the Sine article, by all means go ahead (only a handful have made some small attempts to), but it seems foolhardy to suggest you delete an article that's accessed 1000+ times a day, has hundreds of internal inbound links, and exists on 34 other language Wikipedias, just because you think people need to simultaneously learn cosine, tangent, cotangent, secant, and cosecant. If someone wants to know about sine, let them learn about sine.

Try reading this article with the goal of finding a definition of "sine". First, you have to get to the second sentence of the second paragraph. And then you have to decipher a 443 word sentence. It's absolutely shockingly bad at defining sine, yet you want the hundreds of references to sine to redirect here?

All the same arguments apply equally for cosine. Cosine, although conceptually very similar to sine, has its own properties, some of which are trivial, and others are trivial for sine but more complex for cosine (e.g. fixed point). I really hope I don't have to argue this point further, and I hope no one else has to deal with deletionist trolls when it comes to basic mathematics articles. —Pengo 13:00, 21 December 2011 (UTC)

Pengo, I'm assuming you're not voting "no." But you see, I was thinking that this section would just be for votes, and anyone expecting to see votes would be confused if they saw your signature beneath "Yes" and "No". So as a reminder to everyone else, please don't do anything under "Yes" or "No" but vote (and possibly provide a reason), so as to avoid confusion. And I agree with you, waves are cool. Cheers, The Doctahedron, 01:33, 22 December 2011 (UTC) (This post is not a vote)

Yes!

I think this article and the trigonometric functions in general could use a bit of refactoring. Usually I want to find some specific information (properties) on a function (e.g. cosine, arctan) but I always end on this page a I'm quite confused. I would like as a user to end up on a specific page like the sine one. So think it would be good to have an article of each function (sine, cosins, tan, arctan, ..) and to rethink a bit this article. Now we have sine but not cosine :/ --Jbieler (talk) 11:29, 9 January 2012 (UTC)

Yes, elementary and high school students want a quick definition, not rigor

This page is intimidating for young students. I suggest extremely short articles on sin and cos with links to this page for a rigorous approach. — Preceding unsigned comment added by Nyellin (talk • contribs)

I know Wikipedia isn't supposed to be a dictionary but I think if it could be kept down to the basics like that that would be okay. As well as WP:NOTDICT the WP:NOT policy at the start of content says "In any encyclopedia, information cannot be included solely for being true or useful". However I think some leaning towards dictionary type entries prbably would be a good thing for people loking things up and then they can be directed to the topic article for anything beyond the bare basics. Dmcq (talk) 17:22, 9 January 2012 (UTC)

WP:NOTDICT doesn't mean that you should stick to the basics. It means the polar opposite. It means you should provide as much information as necessary to explain the significance of Cosine. You want to start with the basics in each section, gradually working your way to the more complex stuff. If you start an article with a highly technical explanation, people are more likely to skip the summary and go on to what they think is easier for them to grasp. Wikipedia is not a place where you get deterred because you can't understand it, so that you will use Simple English Wikipedia instead. This is a major problem in many articles currently. There are 13-year-olds (like me) reading Wikipedia! BTW, Nyellin, please remember to sine your posts on talk pages, even if you use a fake username (as do I). I cordially apologize if this post is too lengthy for some people. Cheers, The Doctahedron, 23:16, 19 January 2012 (UTC)

Archive 1

Archive 2

Archive 3