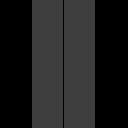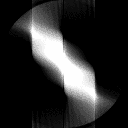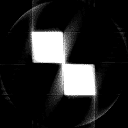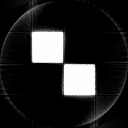Tomographic reconstruction
Tomographic reconstruction is a type of multidimensional inverse problem where the challenge is to yield an estimate of a specific system from a finite number of projections. The mathematical basis for tomographic imaging was laid down by Johann Radon. A notable example of applications is the reconstruction of computed tomography (CT) where cross-sectional images of patients are obtained in non-invasive manner. Recent developments have seen the Radon transform and its inverse used for tasks related to realistic object insertion required for testing and evaluating computed tomography use in airport security.[1]
This article applies in general to reconstruction methods for all kinds of tomography, but some of the terms and physical descriptions refer directly to the reconstruction of X-ray computed tomography.
Introducing formula
[edit]

The projection of an object, resulting from the tomographic measurement process at a given angle , is made up of a set of line integrals (see Fig. 1). A set of many such projections under different angles organized in 2D is called a sinogram (see Fig. 3). In X-ray CT, the line integral represents the total attenuation of the beam of X-rays as it travels in a straight line through the object. As mentioned above, the resulting image is a 2D (or 3D) model of the attenuation coefficient. That is, we wish to find the image . The simplest and easiest way to visualise the method of scanning is the system of parallel projection, as used in the first scanners. For this discussion we consider the data to be collected as a series of parallel rays, at position , across a projection at angle . This is repeated for various angles. Attenuation occurs exponentially in tissue:
where is the attenuation coefficient as a function of position. Therefore, generally the total attenuation of a ray at position , on the projection at angle , is given by the line integral:
Using the coordinate system of Figure 1, the value of onto which the point will be projected at angle is given by:
So the equation above can be rewritten as
where represents and is the Dirac delta function. This function is known as the Radon transform (or sinogram) of the 2D object.
The Fourier Transform of the projection can be written as
- where [2]
- represents a slice of the 2D Fourier transform of at angle . Using the inverse Fourier transform, the inverse Radon transform formula can be easily derived.
where is the derivative of the Hilbert transform of
In theory, the inverse Radon transformation would yield the original image. The projection-slice theorem tells us that if we had an infinite number of one-dimensional projections of an object taken at an infinite number of angles, we could perfectly reconstruct the original object, . However, there will only be a finite number of projections available in practice.
Assuming has effective diameter and desired resolution is , a rule of thumb for the number of projections needed for reconstruction is [2]
Reconstruction algorithms
[edit]Practical reconstruction algorithms have been developed to implement the process of reconstruction of a three-dimensional object from its projections.[3][2] These algorithms are designed largely based on the mathematics of the X-ray transform, statistical knowledge of the data acquisition process and geometry of the data imaging system.
Fourier-domain reconstruction algorithm
[edit]Reconstruction can be made using interpolation. Assume projections of are generated at equally spaced angles, each sampled at the same rate. The discrete Fourier transform (DFT) on each projection yields sampling in the frequency domain. Combining all the frequency-sampled projections generates a polar raster in the frequency domain. The polar raster is sparse, so interpolation is used to fill the unknown DFT points, and reconstruction can be done through the inverse discrete Fourier transform.[4] Reconstruction performance may improve by designing methods to change the sparsity of the polar raster, facilitating the effectiveness of interpolation.
For instance, a concentric square raster in the frequency domain can be obtained by changing the angle between each projection as follow:
where is highest frequency to be evaluated.
The concentric square raster improves computational efficiency by allowing all the interpolation positions to be on rectangular DFT lattice. Furthermore, it reduces the interpolation error.[4] Yet, the Fourier-Transform algorithm has a disadvantage of producing inherently noisy output.
Back projection algorithm
[edit]In practice of tomographic image reconstruction, often a stabilized and discretized version of the inverse Radon transform is used, known as the filtered back projection algorithm.[2]
With a sampled discrete system, the inverse Radon transform is
where is the angular spacing between the projections and is a Radon kernel with frequency response .
The name back-projection comes from the fact that a one-dimensional projection needs to be filtered by a one-dimensional Radon kernel (back-projected) in order to obtain a two-dimensional signal. The filter used does not contain DC gain, so adding DC bias may be desirable. Reconstruction using back-projection allows better resolution than interpolation method described above. However, it induces greater noise because the filter is prone to amplify high-frequency content.
Iterative reconstruction algorithm
[edit]The iterative algorithm is computationally intensive but it allows the inclusion of a priori information about the system .[2]
Let be the number of projections and be the distortion operator for the th projection taken at an angle . are a set of parameters to optimize the conversion of iterations.

An alternative family of recursive tomographic reconstruction algorithms are the algebraic reconstruction techniques and iterative sparse asymptotic minimum variance.
Fan-beam reconstruction
[edit]Use of a noncollimated fan beam is common since a collimated beam of radiation is difficult to obtain. Fan beams will generate series of line integrals, not parallel to each other, as projections. The fan-beam system requires a 360-degree range of angles, which imposes mechanical constraints, but it allows faster signal acquisition time, which may be advantageous in certain settings such as in the field of medicine. Back projection follows a similar two-step procedure that yields reconstruction by computing weighted sum back-projections obtained from filtered projections.
Deep learning reconstruction
[edit]
Deep learning methods are widely applied to image reconstruction nowadays and have achieved impressive results in various image reconstruction tasks, including low-dose denoising, sparse-view reconstruction, limited angle tomography and metal artifact reduction. An excellent overview can be found in the special issue [5] of IEEE Transaction on Medical Imaging. One group of deep learning reconstruction algorithms apply post-processing neural networks to achieve image-to-image reconstruction, where input images are reconstructed by conventional reconstruction methods. Artifact reduction using the U-Net in limited angle tomography is such an example application.[6] However, incorrect structures may occur in an image reconstructed by such a completely data-driven method,[7] as displayed in the figure. Therefore, integration of known operators into the architecture design of neural networks appears beneficial, as described in the concept of precision learning.[8] For example, direct image reconstruction from projection data can be learnt from the framework of filtered back-projection.[9] Another example is to build neural networks by unrolling iterative reconstruction algorithms.[10] Except for precision learning, using conventional reconstruction methods with deep learning reconstruction prior [11] is also an alternative approach to improve the image quality of deep learning reconstruction.
Tomographic reconstruction software
[edit]Tomographic systems have significant variability in their applications and geometries (locations of sources and detectors). This variability creates the need for very specific, tailored implementations of the processing and reconstruction algorithms. Thus, most CT manufacturers provide their own custom proprietary software. This is done not only to protect intellectual property, but may also be enforced by a government regulatory agency. Regardless, there are a number of general purpose tomographic reconstruction software packages that have been developed over the last couple decades, both commercial and open-source.
Most of the commercial software packages that are available for purchase focus on processing data for benchtop cone-beam CT systems. A few of these software packages include Volume Graphics, InstaRecon, iTomography, Livermore Tomography Tools (LTT), and Cone Beam Software Tools (CST).
Some noteworthy examples of open-source reconstruction software include: Reconstruction Toolkit (RTK), [12] CONRAD,[13] TomoPy,[14] the ASTRA toolbox,[15][16] PYRO-NN,[17] ODL,[18] TIGRE,[19] and LEAP.[20]
Gallery
[edit]Shown in the gallery is the complete process for a simple object tomography and the following tomographic reconstruction based on ART.
-
Fig. 2: Phantom object, two kitty-corner squares.
-
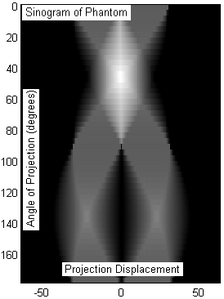
Fig. 3: Sinogram of the phantom object (Fig.2) resulting from tomography. 50 projection slices were taken over 180 degree angle, equidistantly sampled (only by coincidence the x-axis marks displacement at -50/50 units).
-
Fig.4: ART based tomographic reconstruction of the sinogram of Fig.3, presented as animation over the iterative reconstruction process. The original object could be approximatively reconstructed, as the resulting image has some visual artifacts.
See also
[edit]- Operation of computed tomography#Tomographic reconstruction
- Cone beam reconstruction
- Industrial computed tomography
- Industrial Tomography Systems plc
References
[edit]- ^ Najla Megherbi; Toby P. Breckon; Greg T. Flitton; Andre Mouton (October 2013). "Radon Transform based Metal Artefacts Generation in 3D Threat Image Projection" (PDF). Proc. SPIE Optics and Photonics for Counterterrorism, Crime Fighting and Defence. Vol. 8901. SPIE. pp. 1–7. doi:10.1117/12.2028506. S2CID 14001672. Retrieved 5 November 2013.
- ^ a b c d e Dudgeon and Mersereau (1984). Multidimensional digital signal processing. Prentice-Hall.
- ^ Herman, G. T., Fundamentals of computerized tomography: Image reconstruction from projection, 2nd edition, Springer, 2009
- ^ a b R. Mersereau, A. Oppenheim (1974). "Digital reconstruction of multidimensional signals from their projections". Proceedings of the IEEE. 62 (10): 1319–1338. doi:10.1109/proc.1974.9625. hdl:1721.1/13788.
- ^ Wang, Ge; Ye, Jong Chu; Mueller, Klaus; Fessler, Jeffrey A (2018). "Image reconstruction is a new frontier of machine learning". IEEE Transactions on Medical Imaging. 37 (6): 1289–1296. doi:10.1109/TMI.2018.2833635. PMID 29870359. S2CID 46931303.
- ^ Gu, Jawook; Ye, Jong Chul (2017). Multi-scale wavelet domain residual learning for limited-angle CT reconstruction. Fully3D. pp. 443–447.
- ^ Yixing Huang; Tobias Würfl; Katharina Breininger; Ling Liu; Günter Lauritsch; Andreas Maier (2018). Some Investigations on Robustness of Deep Learning in Limited Angle Tomography. MICCAI. doi:10.1007/978-3-030-00928-1_17.
- ^ Maier, Andreas K; Syben, Christopher; Stimpel, Bernhard; Wuerfl, Tobias; Hoffmann, Mathis; Schebesch, Frank; Fu, Weilin; Mill, Leonid; Kling, Lasse; Christiansen, Silke (2019). "Learning with known operators reduces maximum error bounds". Nature Machine Intelligence. 1 (8): 373–380. arXiv:1907.01992. doi:10.1038/s42256-019-0077-5. PMC 6690833. PMID 31406960.
- ^ Tobias Wuerfl; Mathis Hoffmann; Vincent Christlein; Katharina Breininger; Yixing Huang; Mathias Unberath; Andreas Maier (2018). "Deep Learning Computed Tomography: Learning Projection-Domain Weights from Image Domain in Limited Angle Problems". IEEE Transactions on Medical Imaging. 37 (6): 1454–1463. doi:10.1109/TMI.2018.2833499. PMID 29870373. S2CID 46935914.
- ^ J. Adler; O. Öktem (2018). "Learned Primal-Dual Reconstruction". IEEE Transactions on Medical Imaging. 37 (6): 1322–1332. arXiv:1707.06474. doi:10.1109/TMI.2018.2799231. PMID 29870362. S2CID 26897002.
- ^ Yixing Huang; Alexander Preuhs; Guenter Lauritsch; Michael Manhart; Xiaolin Huang; Andreas Maier (2019). Data Consistent Artifact Reduction for Limited Angle Tomography with Deep Learning Prior. Machine Learning for Medical Image Reconstruction. arXiv:1908.06792. doi:10.1007/978-3-030-33843-5_10.
- ^ Reconstruction Toolkit (RTK)
- ^ Maier, Andreas; Hofmann, Hannes G.; Berger, Martin; Fischer, Peter; Schwemmer, Chris; Wu, Haibo; Müller, Kerstin; Hornegger, Joachim; Choi, Jang-Hwan; Riess, Christian; Keil, Andreas; Fahrig, Rebecca (2013). "CONRAD - A software framework for cone-beam imaging in radiology". Medical Physics. 40 (11): 111914. Bibcode:2013MedPh..40k1914M. doi:10.1118/1.4824926. PMC 3820625. PMID 24320447.
- ^ Gürsoy, Doǧa; De Carlo, Francesco; Xiao, Xianghui; Jacobsen, Chris (2014). "TomoPy: A framework for the analysis of synchrotron tomographic data". Journal of Synchrotron Radiation. 22 (5): 1188–1193. Bibcode:2014SPIE.9212E..0NG. doi:10.1107/S1600577514013939. PMC 4181643. PMID 25178011.
- ^ van Aarle, Wim; Palenstijn, Willem Jan; De Beenhouwer, Jan; Altantzis, Thomas; Bals, Sara; Batenburg, K. Joost; Sijbers, Jan (October 2015). "The ASTRA Toolbox: a platform for advanced algorithm development in electron tomography". Ultramicroscopy. 157: 35–47. doi:10.1016/j.ultramic.2015.05.002. hdl:10067/1278340151162165141. PMID 26057688.
- ^ van Aarle, Wim; Palenstijn, Willem Jan; Cant, Jeroen; Janssens, Eline; Bleichrodt, Folkert; Dabravolski, Andrei; De Beenhouwer, Jan; Joost Batenburg, K.; Sijbers, Jan (2016). "Fast and flexible X-ray tomography using the ASTRA toolbox". Optics Express. 24 (22): 35–47. Bibcode:2016OExpr..2425129V. doi:10.1364/OE.24.025129. hdl:10067/1392160151162165141. PMID 27828452.
- ^ Syben, Christopher; Michen, Markus; Stimpel, Bernhard; Seitz, Stephan; Ploner, Stefan; Maier, Andreas (2019). "PYRO-NN: Python Reconstruction Operators in Neural Networks". Medical Physics. 46 (11): 5110–5115. arXiv:1904.13342. Bibcode:2019MedPh..46.5110S. doi:10.1002/mp.13753. PMC 6899669. PMID 31389023.
- ^ "Odlgroup/Odl". GitHub.
- ^ Released by the University of Bath and CERN.
Biguri, Ander; Dosanjh, Manjit; Hancock, Steven; Soleimani, Manuchehr (2016-09-08). "TIGRE: a MATLAB-GPU toolbox for CBCT image reconstruction". Biomedical Physics & Engineering Express. 2 (5): 055010. doi:10.1088/2057-1976/2/5/055010. ISSN 2057-1976. - ^ [1]Kim, Hyojin; Champley, Kyle (2023). "Differentiable Forward Projector for X-ray Computed Tomography". ICML. arXiv:2307.05801.
Further reading
[edit]- Avinash Kak & Malcolm Slaney (1988), Principles of Computerized Tomographic Imaging, IEEE Press, ISBN 0-87942-198-3.
- Bruyant, P.P. "Analytic and iterative reconstruction algorithms in SPECT" Journal of Nuclear Medicine 43(10):1343-1358, 2002
External links
[edit]- Slaney, A. C. Kak and Malcolm. "Principles of Computerized Tomographic Imaging". Slaney.org. Retrieved 7 September 2018.
- Insight ToolKit; open-source tomographic support software
- "TomoPy — TomoPy 1.1.3 documentation". Tomopy.readthedocs.org. Retrieved 7 September 2018.
- ASTRA (All Scales Tomographic Reconstruction Antwerp) toolbox; very flexible, fast open-source software for computed tomographic reconstruction
- NiftyRec; comprehensive open-source tomographic reconstruction software; Matlab and Python scriptable
- Open-source tomographic reconstruction and visualization tool
- "ITS plc - Electrical Process Tomography For Industrial Visualization". Itoms.com. Retrieved 7 September 2018.












![{\displaystyle P_{\theta }(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\exp[-j\omega (x\cos \theta +y\sin \theta )]\,dx\,dy=F(\Omega _{1},\Omega _{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36306c36f50bf7f3e670ee9136027e64f08b056a)





















![{\displaystyle f_{k}(x,y)=f_{k-1}(x,y)+\sum _{i=1}^{N}\lambda _{i}[p_{\theta _{i}}(r)-D_{i}f_{k-1}(x,y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d03e2569148c3e447738b0e62c161e4852051eb6)