Detection limit
The limit of detection (LOD or LoD) is the lowest signal, or the lowest corresponding quantity to be determined (or extracted) from the signal, that can be observed with a sufficient degree of confidence or statistical significance. However, the exact threshold (level of decision) used to decide when a signal significantly emerges above the continuously fluctuating background noise remains arbitrary and is a matter of policy and often of debate among scientists, statisticians and regulators depending on the stakes in different fields.
Significance in analytical chemistry[edit]
In analytical chemistry, the detection limit, lower limit of detection, also termed LOD for limit of detection or analytical sensitivity (not to be confused with statistical sensitivity), is the lowest quantity of a substance that can be distinguished from the absence of that substance (a blank value) with a stated confidence level (generally 99%).[1][2][3] The detection limit is estimated from the mean of the blank, the standard deviation of the blank, the slope (analytical sensitivity) of the calibration plot and a defined confidence factor (e.g. 3.2 being the most accepted value for this arbitrary value).[4] Another consideration that affects the detection limit is the adequacy and the accuracy of the model used to predict concentration from the raw analytical signal.[5]
As a typical example, from a calibration plot following a linear equation taken here as the simplest possible model:
where, corresponds to the signal measured (e.g. voltage, luminescence, energy, etc.), "b" the value in which the straight line cuts the ordinates axis, "a" the sensitivity of the system (i.e., the slope of the line, or the function relating the measured signal to the quantity to be determined) and "x" the value of the quantity (e.g. temperature, concentration, pH, etc.) to be determined from the signal ,[6] the LOD for "x" is calculated as the "x" value in which equals to the average value of blanks "y" plus "t" times its standard deviation "s" (or, if zero, the standard deviation corresponding to the lowest value measured) where "t" is the chosen confidence value (e.g. for a confidence of 95% it can be considered t = 3.2, determined from the limit of blank).[4]
Thus, in this didactic example:
There are a number of concepts derived from the detection limit that are commonly used. These include the instrument detection limit (IDL), the method detection limit (MDL), the practical quantitation limit (PQL), and the limit of quantitation (LOQ). Even when the same terminology is used, there can be differences in the LOD according to nuances of what definition is used and what type of noise contributes to the measurement and calibration.[7]
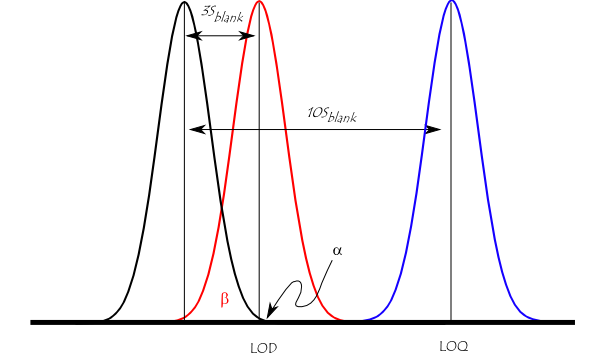
The figure below illustrates the relationship between the blank, the limit of detection (LOD), and the limit of quantitation (LOQ) by showing the probability density function for normally distributed measurements at the blank, at the LOD defined as 3 × standard deviation of the blank, and at the LOQ defined as 10 × standard deviation of the blank. (The identical spread along Abscissa of these two functions is problematic.) For a signal at the LOD, the alpha error (probability of false positive) is small (1%). However, the beta error (probability of a false negative) is 50% for a sample that has a concentration at the LOD (red line). This means a sample could contain an impurity at the LOD, but there is a 50% chance that a measurement would give a result less than the LOD. At the LOQ (blue line), there is minimal chance of a false negative.
Instrument detection limit[edit]
Most analytical instruments produce a signal even when a blank (matrix without analyte) is analyzed. This signal is referred to as the noise level. The instrument detection limit (IDL) is the analyte concentration that is required to produce a signal greater than three times the standard deviation of the noise level. This may be practically measured by analyzing 8 or more standards at the estimated IDL then calculating the standard deviation from the measured concentrations of those standards.
The detection limit (according to IUPAC) is the smallest concentration, or the smallest absolute amount, of analyte that has a signal statistically significantly larger than the signal arising from the repeated measurements of a reagent blank.
Mathematically, the analyte's signal at the detection limit () is given by:
where, is the mean value of the signal for a reagent blank measured multiple times, and is the known standard deviation for the reagent blank's signal.
Other approaches for defining the detection limit have also been developed. In atomic absorption spectrometry usually the detection limit is determined for a certain element by analyzing a diluted solution of this element and recording the corresponding absorbance at a given wavelength. The measurement is repeated 10 times. The 3σ of the recorded absorbance signal can be considered as the detection limit for the specific element under the experimental conditions: selected wavelength, type of flame or graphite oven, chemical matrix, presence of interfering substances, instrument... .
Method detection limit[edit]
Often there is more to the analytical method than just performing a reaction or submitting the analyte to direct analysis. Many analytical methods developed in the laboratory, especially these involving the use of a delicate scientific instrument, require a sample preparation, or a pretreatment of the samples prior to being analysed. For example, it might be necessary to heat a sample that is to be analyzed for a particular metal with the addition of acid first (digestion process). The sample may also be diluted or concentrated prior to analysis by means of a given instrument. Additional steps in an analysis method add additional opportunities for errors. Since detection limits are defined in terms of errors, this will naturally increase the measured detection limit. This "global" detection limit (including all the steps of the analysis method) is called the method detection limit (MDL). The practical way for determining the MDL is to analyze seven samples of concentration near the expected limit of detection. The standard deviation is then determined. The one-sided Student's t-distribution is determined and multiplied versus the determined standard deviation. For seven samples (with six degrees of freedom) the t value for a 99% confidence level is 3.14. Rather than performing the complete analysis of seven identical samples, if the Instrument Detection Limit is known, the MDL may be estimated by multiplying the Instrument Detection Limit, or Lower Level of Detection, by the dilution prior to analyzing the sample solution with the instrument. This estimation, however, ignores any uncertainty that arises from performing the sample preparation and will therefore probably underestimate the true MDL.
Limit of each model[edit]
The issue of limit of detection, or limit of quantification, is encountered in all scientific disciplines. This explains the variety of definitions and the diversity of juridiction specific solutions developed to address preferences. In the simplest cases as in nuclear and chemical measurements, definitions and approaches have probably received the clearer and the simplest solutions. In biochemical tests and in biological experiments depending on many more intricate factors, the situation involving false positive and false negative responses is more delicate to handle. In many other disciplines such as geochemistry, seismology, astronomy, dendrochronology, climatology, life sciences in general, and in many other fields impossible to enumerate extensively, the problem is wider and deals with signal extraction out of a background of noise. It involves complex statistical analysis procedures and therefore it also depends on the models used,[5] the hypotheses and the simplifications or approximations to be made to handle and manage uncertainties. When the data resolution is poor and different signals overlap, different deconvolution procedures are applied to extract parameters. The use of different phenomenological, mathematical and statistical models may also complicate the exact mathematical definition of limit of detection and how it is calculated. This explains why it is not easy to come to a general consensus, if any, about the precise mathematical definition of the expression of limit of detection. However, one thing is clear: it always requires a sufficient number of data (or accumulated data) and a rigorous statistical analysis to render better signification statistically.
Limit of quantification[edit]
The limit of quantification (LoQ, or LOQ) is the lowest value of a signal (or concentration, activity, response...) that can be quantified with acceptable precision and accuracy.
The LoQ is the limit at which the difference between two distinct signals / values can be discerned with a reasonable certainty, i.e., when the signal is statistically different from the background. The LoQ may be drastically different between laboratories, so another detection limit is commonly used that is referred to as the Practical Quantification Limit (PQL).
See also[edit]
- Background noise – Sound other than the sound being monitored (primary sound)
- Background radiation – Measure of ionizing radiation in the environment
- Electronic noise – Random fluctuation in an electrical signal
- Noise (spectral phenomenon) – Types of noise
- Chemometrics – Science of extracting information from chemical systems by data-driven means
- Gamma spectroscopy#Calibration and background radiation – Quantitative study of the energy spectra of gamma-ray sources
- Malmquist bias – Sampling bias in astronomy
- p-value – Function of the observed sample results
- Misuse of p-values – Misinterpretation of statistical significance
- Statistical significance – Concept in inferential statistics
References[edit]
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "detection limit". doi:10.1351/goldbook.L03540
- ^ MacDougall D, Crummett WB, et al. (1980). "Guidelines for Data Acquisition and Data Quality Evaluation in Environmental Chemistry". Analytical Chemistry. 52 (14): 2242–49. doi:10.1021/ac50064a004.
- ^ Saah AJ, Hoover DR (1998). "[Sensitivity and specificity revisited: significance of the terms in analytic and diagnostic language]". Ann Dermatol Venereol. 125 (4): 291–4. PMID 9747274.
- ^ a b Armbruster DA, Pry T (August 2008). "Limit of blank, limit of detection and limit of quantitation". The Clinical Biochemist. Reviews. 29 Suppl 1 (1): S49–S52. PMC 2556583. PMID 18852857.
- ^ a b "R: "Detection" limit for each model". search.r-project.org. Retrieved 2022-01-04.
- ^ Quesada-González D, Stefani C, González I, de la Escosura-Muñiz A, Domingo N, Mutjé P, Merkoçi A (September 2019). "Signal enhancement on gold nanoparticle-based lateral flow tests using cellulose nanofibers". Biosensors & Bioelectronics. 141: 111407. doi:10.1016/j.bios.2019.111407. hdl:10261/201014. PMID 31207571. S2CID 190531742.
- ^ Long, Gary L.; Winefordner, J. D. (1983), "Limit of detection: a closer look at the IUPAC definition", Anal. Chem., 55 (7): 712A–724A, doi:10.1021/ac00258a724
Further reading[edit]
- Altshuler B, Pasternack B (1963-03-01). "Statistical measures of the lower limit of detection of a radioactivity counter". Health Physics. 9 (3): 293–298. doi:10.1097/00004032-196303000-00005. ISSN 0017-9078. PMID 14040764. Retrieved 2022-01-03.
- Currie LA (1968). "Limits for qualitative detection and quantitative determination. Application to radiochemistry". Analytical Chemistry. 40 (3): 586–593. doi:10.1021/ac60259a007. ISSN 0003-2700.
- Long GL, Winefordner JD (1983). "Limit of detection. A closer look at the IUPAC definition". Analytical Chemistry. 55 (7): 712A–724A. doi:10.1021/ac00258a001. ISSN 0003-2700.
- Armbruster DA, Pry T (August 2008). "Limit of blank, limit of detection and limit of quantitation". The Clinical Biochemist. Reviews. 29 (Suppl 1): S49–S52. PMC 2556583. PMID 18852857.
- European Commission. Joint Research Centre. (2016). Guidance document on the estimation of LOD and LOQ for measurements in the field of contaminants in feed and food. Luxembourg: Publications Office. doi:10.2787/8931. ISBN 9789279617683. Retrieved 2022-01-03.
- "DIN 32645 – Chemical analysis – Decision limit, detection limit and determination limit under repeatability conditions – Terms, methods, evaluation. Technical standard. Deutsches Institut für Normung, Berlin (DIN 32645:2008-11) | Via Engineering360" (in German). Published by Beuth Verlag, a subsidiary of the DIN Group. doi:10.31030/1465413. Retrieved 2022-01-03.
{{cite journal}}: Cite journal requires|journal=(help)
External links[edit]
- Evans WC (21 February 2019). "Limit of Detection – Interactive Java applet to illustrate some basic ideas of the limit of detection problem". GeoGebra. Retrieved 2022-01-04.
- "The R Language". search.r-project.org. Retrieved 2022-01-04.
- Garrett RG (2013-11-01). "The 'rgr' package for the R Open Source statistical computing and graphics environment – a tool to support geochemical data interpretation". Geochemistry: Exploration, Environment, Analysis. 13 (4): 355–378. Bibcode:2013GEEA...13..355G. doi:10.1144/geochem2011-106. ISSN 1467-7873. S2CID 129059022. Retrieved 2022-01-04.
- "R: "Detection" limit for each model". search.r-project.org. Retrieved 2022-01-04.
- Deutsches Institut für Normung. "R: Calibration data from DIN 32645 (Package envalysis version 0.5.1)". search.r-project.org. Retrieved 2022-01-04.
- Downloads of articles (a.o. harmonization of concepts by ISO and IUPAC) and an extensive list of references Archived 2009-04-21 at the Wayback Machine