Foliation
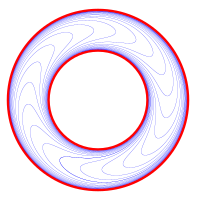

In mathematics (differential geometry), a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation.[1] If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable (of class Cr), or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1 (otherwise, C0 is a topological foliation).[2] The number p (the dimension of the leaves) is called the dimension of the foliation and q = n − p is called its codimension.
In some papers on general relativity by mathematical physicists, the term foliation (or slicing) is used to describe a situation where the relevant Lorentz manifold (a (p+1)-dimensional spacetime) has been decomposed into hypersurfaces of dimension p, specified as the level sets of a real-valued smooth function (scalar field) whose gradient is everywhere non-zero; this smooth function is moreover usually assumed to be a time function, meaning that its gradient is everywhere time-like, so that its level-sets are all space-like hypersurfaces. In deference to standard mathematical terminology, these hypersurface are often called the leaves (or sometimes slices) of the foliation.[3] Note that while this situation does constitute a codimension-1 foliation in the standard mathematical sense, examples of this type are actually globally trivial; while the leaves of a (mathematical) codimension-1 foliation are always locally the level sets of a function, they generally cannot be expressed this way globally,[4][5] as a leaf may pass through a local-trivializing chart infinitely many times, and the holonomy around a leaf may also obstruct the existence of a globally-consistent defining functions for the leaves. For example, while the 3-sphere has a famous codimension-1 foliation discovered by Reeb, a codimension-1 foliation of a closed manifold cannot be given by the level sets of a smooth function, since a smooth function on a closed manifold necessarily has critical points at its maxima and minima.
Foliated charts and atlases[edit]
In order to give a more precise definition of foliation, it is necessary to define some auxiliary elements.
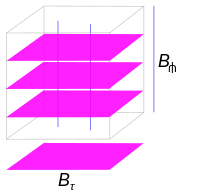
A rectangular neighborhood in Rn is an open subset of the form B = J1 × ⋅⋅⋅ × Jn, where Ji is a (possibly unbounded) relatively open interval in the ith coordinate axis. If J1 is of the form (a,0], it is said that B has boundary[6]
In the following definition, coordinate charts are considered that have values in Rp × Rq, allowing the possibility of manifolds with boundary and (convex) corners.
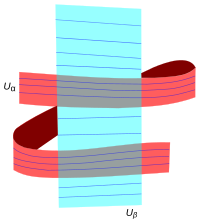
A foliated chart on the n-manifold M of codimension q is a pair (U,φ), where U ⊆ M is open and is a diffeomorphism, being a rectangular neighborhood in Rq and a rectangular neighborhood in Rp. The set Py = φ−1(Bτ × {y}), where , is called a plaque of this foliated chart. For each x ∈ Bτ, the set Sx = φ−1({x} × ) is called a transversal of the foliated chart. The set ∂τU = φ−1(Bτ × (∂)) is called the tangential boundary of U and = φ−1((∂Bτ) × ) is called the transverse boundary of U.[7]
The foliated chart is the basic model for all foliations, the plaques being the leaves. The notation Bτ is read as "B-tangential" and as "B-transverse". There are also various possibilities. If both and Bτ have empty boundary, the foliated chart models codimension-q foliations of n-manifolds without boundary. If one, but not both of these rectangular neighborhoods has boundary, the foliated chart models the various possibilities for foliations of n-manifolds with boundary and without corners. Specifically, if ∂ ≠ ∅ = ∂Bτ, then ∂U = ∂τU is a union of plaques and the foliation by plaques is tangent to the boundary. If ∂Bτ ≠ ∅ = ∂, then ∂U = is a union of transversals and the foliation is transverse to the boundary. Finally, if ∂ ≠ ∅ ≠ ∂Bτ, this is a model of a foliated manifold with a corner separating the tangential boundary from the transverse boundary.[7]

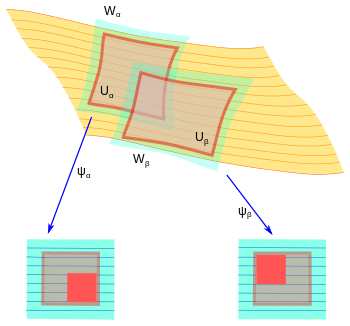
A foliated atlas of codimension q and class Cr (0 ≤ r ≤ ∞) on the n-manifold M is a Cr-atlas of foliated charts of codimension q which are coherently foliated in the sense that, whenever P and Q are plaques in distinct charts of , then P ∩ Q is open both in P and Q.[8]
A useful way to reformulate the notion of coherently foliated charts is to write for w ∈ Uα ∩ Uβ [9]
The notation (Uα,φα) is often written (Uα,xα,yα), with [9]
On φβ(Uα ∩ Uβ) the coordinates formula can be changed as [9]
The condition that (Uα,xα,yα) and (Uβ,xβ,yβ) be coherently foliated means that, if P ⊂ Uα is a plaque, the connected components of P ∩ Uβ lie in (possibly distinct) plaques of Uβ. Equivalently, since the plaques of Uα and Uβ are level sets of the transverse coordinates yα and yβ, respectively, each point z ∈ Uα ∩ Uβ has a neighborhood in which the formula
is independent of xβ.[9]
The main use of foliated atlases is to link their overlapping plaques to form the leaves of a foliation. For this and other purposes, the general definition of foliated atlas above is a bit clumsy. One problem is that a plaque of (Uα,φα) can meet multiple plaques of (Uβ,φβ). It can even happen that a plaque of one chart meets infinitely many plaques of another chart. However, no generality is lost in assuming the situation to be much more regular as shown below.
Two foliated atlases and on M of the same codimension and smoothness class Cr are coherent if is a foliated Cr-atlas. Coherence of foliated atlases is an equivalence relation.[9]
Proof [9] Reflexivity and symmetry are immediate. To prove transitivity let and . Let (Uα,xα,yα) ∈ and (Wλ,xλ,yλ) ∈ and suppose that there is a point w ∈ Uα ∩ Wλ. Choose (Vδ,xδ,yδ) ∈ such that w ∈ Vδ. By the above remarks, there is a neighborhood N of w in Uα ∩ Vδ ∩ Wλ such that
and hence
Since w ∈ Uα ∩ Wλ is arbitrary, it can be concluded that yα(xλ,yλ) is locally independent of xλ. It is thus proven that , hence that coherence is transitive.[10]
Plaques and transversals defined above on open sets are also open. But one can speak also of closed plaques and transversals. Namely, if (U,φ) and (W,ψ) are foliated charts such that (the closure of U) is a subset of W and φ = ψ|U then, if it can be seen that , written , carries diffeomorphically onto
A foliated atlas is said to be regular if
- for each α ∈ A, is a compact subset of a foliated chart (Wα,ψα) and φα = ψα|Uα;
- the cover {Uα | α ∈ A} is locally finite;
- if (Uα,φα) and (Uβ,φβ) are elements of the foliated atlas, then the interior of each closed plaque P ⊂ meets at most one plaque in [11]
By property (1), the coordinates xα and yα extend to coordinates and on and one writes Property (3) is equivalent to requiring that, if Uα ∩ Uβ ≠ ∅, the transverse coordinate changes be independent of That is
has the formula [11]
Similar assertions hold also for open charts (without the overlines). The transverse coordinate map yα can be viewed as a submersion
and the formulas yα = yα(yβ) can be viewed as diffeomorphisms
These satisfy the cocycle conditions. That is, on yδ(Uα ∩ Uβ ∩ Uδ),
and, in particular,[12]
Using the above definitions for coherence and regularity it can be proven that every foliated atlas has a coherent refinement that is regular.[13]
Proof [13] Fix a metric on M and a foliated atlas Passing to a subcover, if necessary, one can assume that is finite. Let ε > 0 be a Lebesgue number for That is, any subset X ⊆ M of diameter < ε lies entirely in some Wj. For each x ∈ M, choose j such that x ∈ Wj and choose a foliated chart (Ux, φx) such that
- x ∈ Ux ⊆ ⊂ Wj,
- φx = ψj|Ux,
- diam(Ux) < ε/2.
Suppose that Ux ⊂ Wk, k ≠ j, and write ψk = (xk,yk) as usual, where yk : Wk → Rq is the transverse coordinate map. This is a submersion having the plaques in Wk as level sets. Thus, yk restricts to a submersion yk : Ux → Rq.
This is locally constant in xj; so choosing Ux smaller, if necessary, one can assume that yk| has the plaques of as its level sets. That is, each plaque of Wk meets (hence contains) at most one (compact) plaque of . Since 1 < k < l < ∞, one can choose Ux so that, whenever Ux ⊂ Wk, distinct plaques of lie in distinct plaques of Wk. Pass to a finite subatlas of {(Ux,φx) | x ∈ M}. If Ui ∩ Uj ≠ 0, then diam(Ui ∪ Uj) < ε, and so there is an index k such that Distinct plaques of (respectively, of ) lie in distinct plaques of Wk. Hence each plaque of has interior meeting at most one plaque of and vice versa. By construction, is a coherent refinement of and is a regular foliated atlas.
If M is not compact, local compactness and second countability allows one to choose a sequence of compact subsets such that Ki ⊂ int Ki+1 for each i ≥ 0 and Passing to a subatlas, it is assumed that is countable and a strictly increasing sequence of positive integers can be found such that covers Kl. Let δl denote the distance from Kl to ∂Kl+1 and choose εl > 0 so small that εl < min{δl/2,εl-1} for l ≥ 1, ε0 < δ0/2, and εl is a Lebesgue number for (as an open cover of Kl) and for (as an open cover of Kl+1). More precisely, if X ⊂ M meets Kl (respectively, Kl+1) and diam X < εl, then X lies in some element of (respectively, ). For each x ∈ Kl int Kl-1, construct (Ux,φx) as for the compact case, requiring that be a compact subset of Wj and that φx = ψj|Ux, some j ≤ nl. Also, require that diam < εl/2. As before, pass to a finite subcover of Kl int Kl-1. (Here, it is taken n−1 = 0.) This creates a regular foliated atlas that refines and is coherent with .
Foliation definitions[edit]
Several alternative definitions of foliation exist depending on the way through which the foliation is achieved. The most common way to achieve a foliation is through decomposition reaching to the following

Definition. A p-dimensional, class Cr foliation of an n-dimensional manifold M is a decomposition of M into a union of disjoint connected submanifolds {Lα}α∈A, called the leaves of the foliation, with the following property: Every point in M has a neighborhood U and a system of local, class Cr coordinates x=(x1, ⋅⋅⋅, xn) : U→Rn such that for each leaf Lα, the components of U ∩ Lα are described by the equations xp+1=constant, ⋅⋅⋅, xn=constant. A foliation is denoted by ={Lα}α∈A.[5]
The notion of leaves allows for an intuitive way of thinking about a foliation. For a slightly more geometrical definition, p-dimensional foliation of an n-manifold M may be thought of as simply a collection {Ma} of pairwise-disjoint, connected, immersed p-dimensional submanifolds (the leaves of the foliation) of M, such that for every point x in M, there is a chart with U homeomorphic to Rn containing x such that every leaf, Ma, meets U in either the empty set or a countable collection of subspaces whose images under in are p-dimensional affine subspaces whose first n − p coordinates are constant.
Locally, every foliation is a submersion allowing the following
Definition. Let M and Q be manifolds of dimension n and q≤n respectively, and let f : M→Q be a submersion, that is, suppose that the rank of the function differential (the Jacobian) is q. It follows from the Implicit Function Theorem that ƒ induces a codimension-q foliation on M where the leaves are defined to be the components of f−1(x) for x ∈ Q.[5]
This definition describes a dimension-p foliation of an n-dimensional manifold M that is a covered by charts Ui together with maps
such that for overlapping pairs Ui, Uj the transition functions φij : Rn → Rn defined by
take the form
where x denotes the first q = n − p coordinates, and y denotes the last p co-ordinates. That is,
The splitting of the transition functions φij into and as a part of the submersion is completely analogous to the splitting of into and as a part of the definition of a regular foliated atlas. This makes possible another definition of foliations in terms of regular foliated atlases. To this end, one has to prove first that every regular foliated atlas of codimension q is associated to a unique foliation of codimension q.[13]
Proof [13] Let be a regular foliated atlas of codimension q. Define an equivalence relation on M by setting x ~ y if and only if either there is a -plaque P0 such that x,y ∈ P0 or there is a sequence L = {P0,P1,⋅⋅⋅,Pp} of -plaques such that x ∈ P0, y ∈ Pp, and Pi ∩ Pi-1 ≠ ∅ with 1 ≤ i ≤ p. The sequence L will be called a plaque chain of length p connecting x and y. In the case that x,y ∈ P0, it is said that {P0} is a plaque chain of length 0 connecting x and y. The fact that ~ is an equivalence relation is clear. It is also clear that each equivalence class L is a union of plaques. Since -plaques can only overlap in open subsets of each other, L is locally a topologically immersed submanifold of dimension n − q. The open subsets of the plaques P ⊂ L form the base of a locally Euclidean topology on L of dimension n − q and L is clearly connected in this topology. It is also trivial to check that L is Hausdorff. The main problem is to show that L is second countable. Since each plaque is 2nd countable, the same will hold for L if it is shown that the set of -plaques in L is at most countably infinite. Fix one such plaque P0. By the definition of a regular, foliated atlas, P0 meets only finitely many other plaques. That is, there are only finitely many plaque chains {P0,Pi} of length 1. By induction on the length p of plaque chains that begin at P0, it is similarly proven that there are only finitely many of length ≤ p. Since every -plaque in L is, by the definition of ~, reached by a finite plaque chain starting at P0, the assertion follows.
As shown in the proof, the leaves of the foliation are equivalence classes of plaque chains of length ≤ p which are also topologically immersed Hausdorff p-dimensional submanifolds. Next, it is shown that the equivalence relation of plaques on a leaf is expressed in equivalence of coherent foliated atlases in respect to their association with a foliation. More specifically, if and are foliated atlases on M and if is associated to a foliation then and are coherent if and only if is also associated to .[10]
Proof [10] If is also associated to , every leaf L is a union of -plaques and of -plaques. These plaques are open subsets in the manifold topology of L, hence intersect in open subsets of each other. Since plaques are connected, a -plaque cannot intersect a -plaque unless they lie in a common leaf; so the foliated atlases are coherent. Conversely, if we only know that is associated to and that , let Q be a -plaque. If L is a leaf of and w ∈ L ∩ Q, let P ∈ L be a -plaque with w ∈ P. Then P ∩ Q is an open neighborhood of w in Q and P ∩ Q ⊂ L ∩ Q. Since w ∈ L ∩ Q is arbitrary, it follows that L ∩ Q is open in Q. Since L is an arbitrary leaf, it follows that Q decomposes into disjoint open subsets, each of which is the intersection of Q with some leaf of . Since Q is connected, L ∩ Q = Q. Finally, Q is an arbitrary -plaque, and so is associated to .
It is now obvious that the correspondence between foliations on M and their associated foliated atlases induces a one-to-one correspondence between the set of foliations on M and the set of coherence classes of foliated atlases or, in other words, a foliation of codimension q and class Cr on M is a coherence class of foliated atlases of codimension q and class Cr on M.[14] By Zorn's lemma, it is obvious that every coherence class of foliated atlases contains a unique maximal foliated atlas. Thus,
Definition. A foliation of codimension q and class Cr on M is a maximal foliated Cr-atlas of codimension q on M.[14]
In practice, a relatively small foliated atlas is generally used to represent a foliation. Usually, it is also required this atlas to be regular.
In the chart Ui, the stripes x = constant match up with the stripes on other charts Uj. These submanifolds piece together from chart to chart to form maximal connected injectively immersed submanifolds called the leaves of the foliation.
If one shrinks the chart Ui it can be written as Uix × Uiy, where Uix ⊂ Rn−p, Uiy ⊂ Rp, Uiy is homeomorphic to the plaques, and the points of Uix parametrize the plaques in Ui. If one picks y0 in Uiy, then Uix × {y0} is a submanifold of Ui that intersects every plaque exactly once. This is called a local transversal section of the foliation. Note that due to monodromy global transversal sections of the foliation might not exist.
The case r = 0 is rather special. Those C0 foliations that arise in practice are usually "smooth-leaved". More precisely, they are of class Cr,0, in the following sense.
Definition. A foliation is of class Cr,k, r > k ≥ 0, if the corresponding coherence class of foliated atlases contains a regular foliated atlas {Uα,xα,yα}α∈A such that the change of coordinate formula
is of class Ck, but xα is of class Cr in the coordinates xβ and its mixed xβ partials of orders ≤ r are Ck in the coordinates (xβ,yβ).[14]
The above definition suggests the more general concept of a foliated space or abstract lamination. One relaxes the condition that the transversals be open, relatively compact subsets of Rq, allowing the transverse coordinates yα to take their values in some more general topological space Z. The plaques are still open, relatively compact subsets of Rp, the change of transverse coordinate formula yα(yβ) is continuous and xα(xβ,yβ) is of class Cr in the coordinates xβ and its mixed xβ partials of orders ≤ r are continuous in the coordinates (xβ,yβ). One usually requires M and Z to be locally compact, second countable and metrizable. This may seem like a rather wild generalization, but there are contexts in which it is useful.[15]
Holonomy[edit]
Let (M, ) be a foliated manifold. If L is a leaf of and s is a path in L, one is interested in the behavior of the foliation in a neighborhood of s in M. Intuitively, an inhabitant of the leaf walks along the path s, keeping an eye on all of the nearby leaves. As they (hereafter denoted by s(t)) proceed, some of these leaves may "peel away", getting out of visual range, others may suddenly come into range and approach L asymptotically, others may follow along in a more or less parallel fashion or wind around L laterally, etc. If s is a loop, then s(t) repeatedly returns to the same point s(t0) as t goes to infinity and each time more and more leaves may have spiraled into view or out of view, etc. This behavior, when appropriately formalized, is called the holonomy of the foliation.
Holonomy is implemented on foliated manifolds in various specific ways: the total holonomy group of foliated bundles, the holonomy pseudogroup of general foliated manifolds, the germinal holonomy groupoid of general foliated manifolds, the germinal holonomy group of a leaf, and the infinitesimal holonomy group of a leaf.
Foliated bundles[edit]
The easiest case of holonomy to understand is the total holonomy of a foliated bundle. This is a generalization of the notion of a Poincaré map.
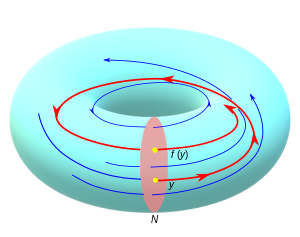
The term "first return (recurrence) map" comes from the theory of dynamical systems. Let Φt be a nonsingular Cr flow (r ≥ 1) on the compact n-manifold M. In applications, one can imagine that M is a cyclotron or some closed loop with fluid flow. If M has a boundary, the flow is assumed to be tangent to the boundary. The flow generates a 1-dimensional foliation . If one remembers the positive direction of flow, but otherwise forgets the parametrization (shape of trajectory, velocity, etc.), the underlying foliation is said to be oriented. Suppose that the flow admits a global cross section N. That is, N is a compact, properly embedded, Cr submanifold of M of dimension n – 1, the foliation is transverse to N, and every flow line meets N. Because the dimensions of N and of the leaves are complementary, the transversality condition is that
Let y ∈ N and consider the ω-limit set ω(y) of all accumulation points in M of all sequences , where tk goes to infinity. It can be shown that ω(y) is compact, nonempty, and a union of flow lines. If there is a value t* ∈ R such that Φt*(z) ∈ N and it follows that
Since N is compact and is transverse to N, it follows that the set {t > 0 | Φt(y) ∈ N} is a monotonically increasing sequence that diverges to infinity.
As y ∈ N varies, let τ(y) = τ1(y), defining in this way a positive function τ ∈ Cr(N) (the first return time) such that, for arbitrary y ∈ N, Φt(y) ∉ N, 0 < t < τ(y), and Φτ(y)(y) ∈ N.
Define f : N → N by the formula f(y) = Φτ(y)(y). This is a Cr map. If the flow is reversed, exactly the same construction provides the inverse f−1; so f ∈ Diffr(N). This diffeomorphism is the first return map and τ is called the first return time. While the first return time depends on the parametrization of the flow, it should be evident that f depends only on the oriented foliation . It is possible to reparametrize the flow Φt, keeping it nonsingular, of class Cr, and not reversing its direction, so that τ ≡ 1.
The assumption that there is a cross section N to the flow is very restrictive, implying that M is the total space of a fiber bundle over S1. Indeed, on R × N, define ~f to be the equivalence relation generated by
Equivalently, this is the orbit equivalence for the action of the additive group Z on R × N defined by
for each k ∈ Z and for each (t,y) ∈ R × N. The mapping cylinder of f is defined to be the Cr manifold
By the definition of the first return map f and the assumption that the first return time is τ ≡ 1, it is immediate that the map
defined by the flow, induces a canonical Cr diffeomorphism
If we make the identification Mf = M, then the projection of R × N onto R induces a Cr map
that makes M into the total space of a fiber bundle over the circle. This is just the projection of S1 × D2 onto S1. The foliation is transverse to the fibers of this bundle and the bundle projection π, restricted to each leaf L, is a covering map π : L → S1. This is called a foliated bundle.
Take as basepoint x0 ∈ S1 the equivalence class 0 + Z; so π−1(x0) is the original cross section N. For each loop s on S1, based at x0, the homotopy class [s] ∈ π1(S1,x0) is uniquely characterized by deg s ∈ Z. The loop s lifts to a path in each flow line and it should be clear that the lift sy that starts at y ∈ N ends at fk(y) ∈ N, where k = deg s. The diffeomorphism fk ∈ Diffr(N) is also denoted by hs and is called the total holonomy of the loop s. Since this depends only on [s], this is a definition of a homomorphism
called the total holonomy homomorphism for the foliated bundle.
Using fiber bundles in a more direct manner, let (M,) be a foliated n-manifold of codimension q. Let π : M → B be a fiber bundle with q-dimensional fiber F and connected base space B. Assume that all of these structures are of class Cr, 0 ≤ r ≤ ∞, with the condition that, if r = 0, B supports a C1 structure. Since every maximal C1 atlas on B contains a C∞ subatlas, no generality is lost in assuming that B is as smooth as desired. Finally, for each x ∈ B, assume that there is a connected, open neighborhood U ⊆ B of x and a local trivialization
where φ is a Cr diffeomorphism (a homeomorphism, if r = 0) that carries to the product foliation {U × {y}}y ∈ F. Here, is the foliation with leaves the connected components of L ∩ π−1(U), where L ranges over the leaves of . This is the general definition of the term "foliated bundle" (M,,π) of class Cr.
is transverse to the fibers of π (it is said that is transverse to the fibration) and that the restriction of π to each leaf L of is a covering map π : L → B. In particular, each fiber Fx = π−1(x) meets every leaf of . The fiber is a cross section of in complete analogy with the notion of a cross section of a flow.
The foliation being transverse to the fibers does not, of itself, guarantee that the leaves are covering spaces of B. A simple version of the problem is a foliation of R2, transverse to the fibration
but with infinitely many leaves missing the y-axis. In the respective figure, it is intended that the "arrowed" leaves, and all above them, are asymptotic to the axis x = 0. One calls such a foliation incomplete relative to the fibration, meaning that some of the leaves "run off to infinity" as the parameter x ∈ B approaches some x0 ∈ B. More precisely, there may be a leaf L and a continuous path s : [0,a) → L such that limt→a−π(s(t)) = x0 ∈ B, but limt→a−s(t) does not exist in the manifold topology of L. This is analogous to the case of incomplete flows, where some flow lines "go to infinity" in finite time. Although such a leaf L may elsewhere meet π−1(x0), it cannot evenly cover a neighborhood of x0, hence cannot be a covering space of B under π. When F is compact, however, it is true that transversality of to the fibration does guarantee completeness, hence that is a foliated bundle.
There is an atlas = {Uα,xα}α∈A on B, consisting of open, connected coordinate charts, together with trivializations φα : π−1(Uα) → Uα × F that carry |π−1(Uα) to the product foliation. Set Wα = π−1(Uα) and write φα = (xα,yα) where (by abuse of notation) xα represents xα ∘ π and yα : π−1(Uα) → F is the submersion obtained by composing φα with the canonical projection Uα × F → F.
The atlas = {Wα,xα,yα}α∈A plays a role analogous to that of a foliated atlas. The plaques of Wα are the level sets of yα and this family of plaques is identical to F via yα. Since B is assumed to support a C∞ structure, according to the Whitehead theorem one can fix a Riemannian metric on B and choose the atlas to be geodesically convex. Thus, Uα ∩ Uβ is always connected. If this intersection is nonempty, each plaque of Wα meets exactly one plaque of Wβ. Then define a holonomy cocycle by setting
Examples[edit]
Flat space[edit]
Consider an n-dimensional space, foliated as a product by subspaces consisting of points whose first n − p coordinates are constant. This can be covered with a single chart. The statement is essentially that Rn = Rn−p × Rp with the leaves or plaques Rp being enumerated by Rn−p. The analogy is seen directly in three dimensions, by taking n = 3 and p = 2: the 2-dimensional leaves of a book are enumerated by a (1-dimensional) page number.
Bundles[edit]
A rather trivial example of foliations are products M = B × F, foliated by the leaves Fb = {b} × F, b ∈ B. (Another foliation of M is given by Bf = B × { f } , f ∈ F.)
A more general class are flat G-bundles with G = Homeo(F) for a manifold F. Given a representation ρ : π1(B) → Homeo(F), the flat Homeo(F)-bundle with monodromy ρ is given by , where π1(B) acts on the universal cover by deck transformations and on F by means of the representation ρ.
Flat bundles fit into the framework of fiber bundles. A map π : M → B between manifolds is a fiber bundle if there is a manifold F such that each b ∈ B has an open neighborhood U such that there is a homeomorphism with , with p1 : U × F → U projection to the first factor. The fiber bundle yields a foliation by fibers . Its space of leaves L is homeomorphic to B, in particular L is a Hausdorff manifold.
Coverings[edit]
If M → N is a covering map between manifolds, and F is a foliation on N, then it pulls back to a foliation on M. More generally, if the map is merely a branched covering, where the branch locus is transverse to the foliation, then the foliation can be pulled back.
Submersions[edit]
If Mn → Nq, (q ≤ n) is a submersion of manifolds, it follows from the inverse function theorem that the connected components of the fibers of the submersion define a codimension q foliation of M. Fiber bundles are an example of this type.
An example of a submersion, which is not a fiber bundle, is given by
This submersion yields a foliation of [−1, 1] × R which is invariant under the Z-actions given by
for (x, y) ∈ [−1, 1] × R and n ∈ Z. The induced foliations of Z \ ([−1, 1] × R) are called the 2-dimensional Reeb foliation (of the annulus) resp. the 2-dimensional nonorientable Reeb foliation (of the Möbius band). Their leaf spaces are not Hausdorff.
Reeb foliations[edit]
Define a submersion
where (r, θ) ∈ [0, 1] × Sn−1 are cylindrical coordinates on the n-dimensional disk Dn. This submersion yields a foliation of Dn × R which is invariant under the Z-actions given by
for (x, y) ∈ Dn × R, z ∈ Z. The induced foliation of Z \ (Dn × R) is called the n-dimensional Reeb foliation. Its leaf space is not Hausdorff.
For n = 2, this gives a foliation of the solid torus which can be used to define the Reeb foliation of the 3-sphere by gluing two solid tori along their boundary. Foliations of odd-dimensional spheres S2n+1 are also explicitly known.[16]
Lie groups[edit]
If G is a Lie group, and H is a Lie subgroup, then G is foliated by cosets of H. When H is closed in G, the quotient space G/H is a smooth (Hausdorff) manifold turning G into a fiber bundle with fiber H and base G/H. This fiber bundle is actually principal, with structure group H.
Lie group actions[edit]
Let G be a Lie group acting smoothly on a manifold M. If the action is a locally free action or free action, then the orbits of G define a foliation of M.
Linear and Kronecker foliations[edit]
If is a nonsingular (i.e., nowhere zero) vector field, then the local flow defined by patches together to define a foliation of dimension 1. Indeed, given an arbitrary point x ∈ M, the fact that is nonsingular allows one to find a coordinate neighborhood (U,x1,...,xn) about x such that
and
Geometrically, the flow lines of are just the level sets
where all Since by convention manifolds are second countable, leaf anomalies like the "long line" are precluded by the second countability of M itself. The difficulty can be sidestepped by requiring that be a complete field (e.g., that M be compact), hence that each leaf be a flow line.
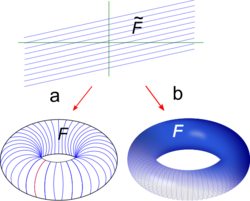

An important class of 1-dimensional foliations on the torus T2 are derived from projecting constant vector fields on T2. A constant vector field
on R2 is invariant by all translations in R2, hence passes to a well-defined vector field X when projected on the torus T2= R2/Z2. It is assumed that a ≠ 0. The foliation on R2 produced by has as leaves the parallel straight lines of slope θ = b/a. This foliation is also invariant under translations and passes to the foliation on T2 produced by X.
Each leaf of is of the form
If the slope is rational then all leaves are closed curves homeomorphic to the circle. In this case, one can take a,b ∈ Z. For fixed t ∈ R, the points of corresponding to values of t ∈ t0 + Z all project to the same point of T2; so the corresponding leaf L of is an embedded circle in T2. Since L is arbitrary, is a foliation of T2 by circles. It follows rather easily that this foliation is actually a fiber bundle π : T2 → S1. This is known as a linear foliation.
When the slope θ = b/a is irrational, the leaves are noncompact, homeomorphic to the non-compactified real line, and dense in the torus (cf Irrational rotation). The trajectory of each point (x0,y0) never returns to the same point, but generates an "everywhere dense" winding about the torus, i.e. approaches arbitrarily close to any given point. Thus the closure to the trajectory is the entire two-dimensional torus. This case is named Kronecker foliation, after Leopold Kronecker and his
Kronecker's Density Theorem. If the real number θ is distinct from each rational multiple of π, then the set {einθ | n ∈ Z} is dense in the unit circle.
Proof To see this, note first that, if a leaf of does not project one-to-one into T2, there must be a real number t ≠ 0 such that ta and tb are both integers. But this would imply that b/a ∈ Q. In order to show that each leaf L of is dense in T2, it is enough to show that, for every v ∈ R2, each leaf of achieves arbitrarily small positive distances from suitable points of the coset v + Z2. A suitable translation in R2 allows one to assume that v = 0; so the task is reduced to showing that passes arbitrarily close to suitable points (n,m) ∈ Z2. The line has slope-intercept equation
So it will suffice to find, for arbitrary η > 0, integers n and m such that
Equivalently, c ∈ R being arbitrary, one is reduced to showing that the set {θn − m}m,n∈Z is dense in R. This is essentially the criterion of Eudoxus that θ and 1 be incommensurable (i.e., that θ be irrational).
A similar construction using a foliation of Rn by parallel lines yields a 1-dimensional foliation of the n-torus Rn/Zn associated with the linear flow on the torus.
Suspension foliations[edit]
A flat bundle has not only its foliation by fibres but also a foliation transverse to the fibers, whose leaves are
where is the canonical projection. This foliation is called the suspension of the representation ρ : π1(B) → Homeo(F).
In particular, if B = S1 and is a homeomorphism of F, then the suspension foliation of is defined to be the suspension foliation of the representation ρ : Z → Homeo(F) given by ρ(z) = Φz. Its space of leaves is L = /~, where x ~ y whenever y = Φn(x) for some n ∈ Z.
The simplest example of foliation by suspension is a manifold X of dimension q. Let f : X → X be a bijection. One defines the suspension M = S1 ×f X as the quotient of [0,1] × X by the equivalence relation (1,x) ~ (0,f(x)).
- M = S1 ×f X = [0,1] × X
Then automatically M carries two foliations: 2 consisting of sets of the form F2,t = {(t,x)~ : x ∈ X} and 1 consisting of sets of the form F2,x0 = {(t,x) : t ∈ [0,1] ,x ∈ Ox0}, where the orbit Ox0 is defined as
- Ox0 = {..., f−2(x0), f−1(x0), x0, f(x0), f2(x0), ...},
where the exponent refers to the number of times the function f is composed with itself. Note that Ox0 = Of(x0) = Of−2(x0), etc., so the same is true for F1,x0. Understanding the foliation 1 is equivalent to understanding the dynamics of the map f. If the manifold X is already foliated, one can use the construction to increase the codimension of the foliation, as long as f maps leaves to leaves.
The Kronecker foliations of the 2-torus are the suspension foliations of the rotations Rα : S1 → S1 by angle α ∈ [0, 2π).

More specifically, if Σ = Σ2 is the two-holed torus with C1,C2 ∈ Σ the two embedded circles let be the product foliation of the 3-manifold M = Σ × S1 with leaves Σ × {y}, y ∈ S1. Note that Ni = Ci × S1 is an embedded torus and that is transverse to Ni, i = 1,2. Let Diff+(S1) denote the group of orientation-preserving diffeomorphisms of S1 and choose f1,f2 ∈ Diff+(S1). Cut M apart along N1 and N2, letting and denote the resulting copies of Ni, i = 1,2. At this point one has a manifold M' = Σ' × S1 with four boundary components The foliation has passed to a foliation transverse to the boundary ∂M' , each leaf of which is of the form Σ' × {y}, y ∈ S1.
This leaf meets ∂M' in four circles If z ∈ Ci, the corresponding points in are denoted by z± and is "reglued" to by the identification
Since f1 and f2 are orientation-preserving diffeomorphisms of S1, they are isotopic to the identity and the manifold obtained by this regluing operation is homeomorphic to M. The leaves of , however, reassemble to produce a new foliation (f1,f2) of M. If a leaf L of (f1,f2) contains a piece Σ' × {y0}, then
where G ⊂ Diff+(S1) is the subgroup generated by {f1,f2}. These copies of Σ' are attached to one another by identifications
- (z−,g(y0)) ≡ (z+,f1(g(y0))) for each z ∈ C1,
- (z−,g(y0)) ≡ (z+,f2(g(y0))) for each z ∈ C2,
where g ranges over G. The leaf is completely determined by the G-orbit of y0 ∈ S1 and can he simple or immensely complicated. For instance, a leaf will be compact precisely if the corresponding G-orbit is finite. As an extreme example, if G is trivial (f1 = f2 = idS1), then (f1,f2) = . If an orbit is dense in S1, the corresponding leaf is dense in M. As an example, if f1 and f2 are rotations through rationally independent multiples of 2π, every leaf will be dense. In other examples, some leaf L has closure that meets each factor {w} × S1 in a Cantor set. Similar constructions can be made on Σ × I, where I is a compact, nondegenerate interval. Here one takes f1,f2 ∈ Diff+(I) and, since ∂I is fixed pointwise by all orientation-preserving diffeomorphisms, one gets a foliation having the two components of ∂M as leaves. When one forms M' in this case, one gets a foliated manifold with corners. In either case, this construction is called the suspension of a pair of diffeomorphisms and is a fertile source of interesting examples of codimension-one foliations.
Foliations and integrability[edit]
There is a close relationship, assuming everything is smooth, with vector fields: given a vector field X on M that is never zero, its integral curves will give a 1-dimensional foliation. (i.e. a codimension n − 1 foliation).
This observation generalises to the Frobenius theorem, saying that the necessary and sufficient conditions for a distribution (i.e. an n − p dimensional subbundle of the tangent bundle of a manifold) to be tangent to the leaves of a foliation, is that the set of vector fields tangent to the distribution are closed under Lie bracket. One can also phrase this differently, as a question of reduction of the structure group of the tangent bundle from GL(n) to a reducible subgroup.
The conditions in the Frobenius theorem appear as integrability conditions; and the assertion is that if those are fulfilled the reduction can take place because local transition functions with the required block structure exist. For example, in the codimension 1 case, we can define the tangent bundle of the foliation as ker(α), for some (non-canonical) α ∈ Ω1 (i.e. a non-zero co-vector field). A given α is integrable iff α ∧ dα = 0 everywhere.
There is a global foliation theory, because topological constraints exist. For example, in the surface case, an everywhere non-zero vector field can exist on an orientable compact surface only for the torus. This is a consequence of the Poincaré–Hopf index theorem, which shows the Euler characteristic will have to be 0. There are many deep connections with contact topology, which is the "opposite" concept, requiring that the integrability condition is never satisfied.
Existence of foliations[edit]
Haefliger (1970) gave a necessary and sufficient condition for a distribution on a connected non-compact manifold to be homotopic to an integrable distribution. Thurston (1974, 1976) showed that any compact manifold with a distribution has a foliation of the same dimension.
See also[edit]
- G-structure – Structure group sub-bundle on a tangent frame bundle
- Haefliger structure – Generalization of a foliation closed under taking pullbacks.
- Lamination – Partitioned topological space
- Reeb foliation – particular foliation of the 3-sphere introduced by the French mathematician Georges Reeb.
- Taut foliation
Notes[edit]
- ^ Candel & Conlon 2000, p. 5
- ^ Anosov 2001
- ^ Gourgoulhon 2012, p. 56
- ^ Reeb, G. (1959), "Remarques sur les structures feuilletées" (PDF), Bull. Soc. Math. France, 87: 445–450, doi:10.24033/bsmf.1539, Zbl 0122.41603
- ^ a b c Lawson 1974
- ^ Candel & Conlon 2000, p. 19
- ^ a b Candel & Conlon 2000, p. 20
- ^ Candel & Conlon 2000, p. 23
- ^ a b c d e f Candel & Conlon 2000, p. 25
- ^ a b c Candel & Conlon 2000, p. 26
- ^ a b Candel & Conlon 2000, p. 27
- ^ Candel & Conlon 2000, p. 28
- ^ a b c d Candel & Conlon 2000, p. 29
- ^ a b c Candel & Conlon 2000, p. 31
- ^ Candel & Conlon 2000, p. 32
- ^ Durfee, A.H. (1972), "Foliations of Odd-Dimensional Spheres", Annals of Mathematics, Second Series, 96 (2): 407–411, doi:10.2307/1970795, JSTOR 1970795
References[edit]
- Anosov, D.V. (2001) [1994], "Foliation", Encyclopedia of Mathematics, EMS Press
- Candel, Alberto; Conlon, Lawrence (2000), Foliations I, Graduate Studies in Mathematics, vol. 23, Providence, Rhode Island: American Mathematical Society, ISBN 0-8218-0809-5
- Candel, Alberto; Conlon, Lawrence (2003), Foliations II, Graduate Studies in Mathematics, vol. 60, Providence, Rhode Island: American Mathematical Society, ISBN 0-8218-0809-5
- Gourgoulhon, Éric (2012), 3+1 Formalism in General Relativity, Lecture Notes in Physics, vol. 846, Heidelberg, New York, Dordrecht, London: Springer, doi:10.1007/978-3-642-24525-1, ISBN 978-3-642-24524-4
- Haefliger, André (1970), "Feuilletages sur les variétés ouvertes", Topology, 9 (2): 183–194, doi:10.1016/0040-9383(70)90040-6, ISSN 0040-9383, MR 0263104
- Lawson, H. Blaine (1974), "Foliations", Bulletin of the American Mathematical Society, 80 (3): 369–418, doi:10.1090/S0002-9904-1974-13432-4, ISSN 0002-9904, MR 0343289
- Moerdijk, Ieke; Mrčun, J. (2003), Introduction to foliations and Lie groupoids, Cambridge Studies in Advanced Mathematics, vol. 91, Cambridge University Press, ISBN 978-0-521-83197-0, MR 2012261
- Reeb, Georges (1952), Sur certaines propriétés topologiques des variétés feuilletées, Actualités Sci. Ind., no. 1183, Hermann & Cie., Paris, MR 0055692
- Thurston, William (1974), "The theory of foliations of codimension greater than one", Commentarii Mathematici Helvetici, 49: 214–231, doi:10.1007/BF02566730, ISSN 0010-2571, MR 0370619, S2CID 120603728
- Thurston, William P. (1976), "Existence of codimension-one foliations", Annals of Mathematics, Second Series, 104 (2): 249–268, doi:10.2307/1971047, ISSN 0003-486X, JSTOR 1971047, MR 0425985
External links[edit]
- Foliations at the Manifold Atlas





































































































![{\displaystyle {\begin{cases}f:[-1,1]\times \mathbb {R} \to \mathbb {R} \\f(x,y)=(x^{2}-1)e^{y}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2485598c9933fa847e7482b4eff219cbd71fc65)


























