Riemann curvature tensor

In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds. It associates a tensor to each point of a Riemannian manifold (i.e., it is a tensor field), that measures the extent to which the metric tensor is not locally isometric to a Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving along a geodesic in a sense made precise by the Jacobi equation.

The curvature tensor is given in terms of the Levi-Civita connection $\nabla$ by the following formula:

$R(u,v)w=\nabla_u\nabla_v w - \nabla_v \nabla_u w - \nabla_{[u,v]} w$

where [u,v] is the Lie bracket of vector fields. For each pair of tangent vectors u, v, R(u,v) is a linear transformation of the tangent space of the manifold. It is linear in u and v, and so defines a tensor. Occasionally, the curvature tensor is defined with the opposite sign.

If $u=\partial/\partial x^i$ and $v=\partial/\partial x^j$ are coordinate vector fields then $[u,v]=0$ and therefore the formula simplifies to

$R(u,v)w=\nabla_u\nabla_v w - \nabla_v \nabla_u w .$

The curvature tensor measures noncommutativity of the covariant derivative, and as such is the integrability obstruction for the existence of an isometry with Euclidean space (called, in this context, flat space). The linear transformation $w\mapsto R(u,v)w$ is also called the curvature transformation or endomorphism.

The curvature formula can also be expressed in terms of the second covariant derivative defined as:

$\nabla^2_{u,v} w = \nabla_u\nabla_v w - \nabla_{\nabla_u v} w$

which is linear in u and v. Then:

$R(u,v)=\nabla^2_{u,v} - \nabla^2_{v,u}$

Thus in the general case of non-coordinate vectors u and v, the curvature tensor measures the noncommutativity of the second covariant derivative.

Geometrical meaning

When a vector in a Euclidean space is parallel transported around a loop, it will again point in the initial direction after returning to its original position. However, this property does not hold in the general case. The Riemann curvature tensor directly measures the failure of this in a general Riemannian manifold. This failure is known as the holonomy of the manifold.

Let x_t be a curve in a Riemannian manifold M. Denote by τ_xt : T_x0M → T_xtM the parallel transport map along x_t. The parallel transport maps are related to the covariant derivative by

$\nabla_{\dot{x}_0} Y = \lim_{h\to 0} \frac{1}{h}\left(Y_{x_0}-\tau^{-1}_{x_h}(Y_{x_h})\right) = \left.\frac{d}{dt}(\tau_{x_t}Y)\right|_{t=0}$

for each vector field Y defined along the curve.

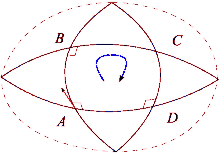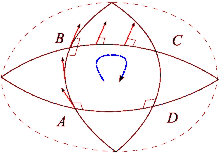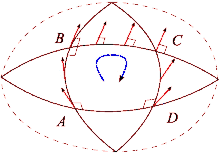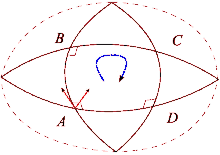
Suppose that X and Y are a pair of commuting vector fields. Each of these fields generates a pair of one-parameter groups of diffeomorphisms in a neighborhood of x₀. Denote by τ_tX and τ_tY, respectively, the parallel transports along the flows of X and Y for time t. Parallel transport of a vector Z ∈ T_x0M around the quadrilateral with sides tY, sX, −tY, −sX is given by

$\tau_{sX}^{-1}\tau_{tY}^{-1}\tau_{sX}\tau_{tY}Z.$

This measures the failure of parallel transport to return Z to its original position in the tangent space T_x0M. Shrinking the loop by sending s, t → 0 gives the infinitesimal description of this deviation:

$\left.\frac{d}{ds}\frac{d}{dt}\tau_{sX}^{-1}\tau_{tY}^{-1}\tau_{sX}\tau_{tY}Z\right|_{s=t=0} = (\nabla_X\nabla_Y - \nabla_Y\nabla_X)Z = R(X,Y)Z$

where R is the Riemann curvature tensor.

Coordinate expression

Converting to the tensor index notation, the Riemann curvature tensor is given by

$R^\rho{}_{\sigma\mu\nu} = dx^\rho(R(\partial_{\mu},\partial_{\nu})\partial_{\sigma})$

where $\partial_{\mu} = \partial/\partial x^{\mu}$ are the coordinate vector fields. The above expression can be written using Christoffel symbols:

$R^\rho{}_{\sigma\mu\nu} = \partial_\mu\Gamma^\rho{}_{\nu\sigma} - \partial_\nu\Gamma^\rho{}_{\mu\sigma} + \Gamma^\rho{}_{\mu\lambda}\Gamma^\lambda{}_{\nu\sigma} - \Gamma^\rho{}_{\nu\lambda}\Gamma^\lambda{}_{\mu\sigma}$

(see also the list of formulas in Riemannian geometry).

The Riemann curvature tensor is also the commutator of the covariant derivative of an arbitrary covector $A_{\nu}\,$ with itself:P. A. M. Dirac (1996). General Theory of Relativity. Princeton University Press. ISBN 0-691-01146-X. 

$A_{\nu ; \rho \sigma} - A_{\nu ; \sigma \rho} = A_{\beta} R^{\beta}{}_{\nu \rho \sigma} \, ,$

since the connection $\Gamma^\alpha{}_{\beta\mu}\,$ is torsionless, which means that the torsion tensor $\Gamma^\lambda{}_{\mu\nu}-\Gamma^\lambda{}_{\nu\mu}\,$ vanishes.

This formula is often called the Ricci identity. This is the classical method used by Ricci and Levi-Civita to obtain an expression for the Riemann curvature tensor. In this way, the tensor character of the set of quantities $R^{\beta}{}_{\nu \rho \sigma}\,$ is proved.

This identity can be generalized to get the commutators for two covariant derivatives of arbitrary tensors as follows

$\begin{align} T^{\alpha_1 \cdots \alpha_r}{}_{\beta_1 \cdots \beta_s ; \gamma \delta} - T^{\alpha_1 \cdots \alpha_r}{}_{\beta_1 \cdots \beta_s ; \delta \gamma} = \, & - R^{\alpha_1}{}_{\rho \gamma \delta} T^{\rho \alpha_2 \cdots \alpha_r}{}_{\beta_1 \cdots \beta_s} - \cdots - R^{\alpha_r}{}_{\rho \gamma \delta} T^{\alpha_1 \cdots \alpha_{r-1} \rho}{}_{\beta_1 \cdots \beta_s} \\ & + \, R^\sigma{}_{\beta_1 \gamma \delta} T^{\alpha_1 \cdots \alpha_r}{}_{\sigma \beta_2 \cdots \beta_s} + \cdots + R^\sigma{}_{\beta_s \gamma \delta} T^{\alpha_1 \cdots \alpha_r}{}_{\beta_1 \cdots \beta_{s-1} \sigma} \,. \end{align}$

This formula also applies to tensor densities without alteration, because for the Levi-Civita (not generic) connection one gets:

$\nabla_{\mu}(\sqrt{g}\,)\equiv (\sqrt{g}\,)_{;\mu}=0 \, , \quad {\mathrm{where}} \quad {g}=|{\mathrm{det}}(g_{\mu\nu})|\, .$

It is sometimes convenient to also define the purely covariant version by

$R_{\rho\sigma\mu\nu} = g_{\rho \zeta} R^\zeta{}_{\sigma\mu\nu} \,.$

Symmetries and identities

The Riemann curvature tensor has the following symmetries:

$R(u,v)=-R(v,u)^{}_{}$

$\langle R(u,v)w,z \rangle=-\langle R(u,v)z,w \rangle^{}_{}$

$R(u,v)w+R(v,w)u+R(w,u)v=0 ^{}_{}.$

The last identity was discovered by Ricci, but is often called the first Bianchi identity or algebraic Bianchi identity, because it is equivalent to the Bianchi identity below. (Also, if there is nonzero torsion, the first Bianchi identity becomes a differential identity of the torsion tensor.) These three identities form a complete list of symmetries of the curvature tensor, i.e. given any tensor which satisfies the identities above, one can find a Riemannian manifold with such a curvature tensor at some point. Simple calculations show that such a tensor has $n^2(n^2-1)/12$ independent components.

Yet another useful identity follows from these three:

$\langle R(u,v)w,z \rangle=\langle R(w,z)u,v \rangle^{}_{}.$

On a Riemannian manifold one has the covariant derivative $\nabla_u R$ and the Bianchi identity (often called the second Bianchi identity or differential Bianchi identity) takes the form:

$(\nabla_uR)(v,w)+(\nabla_vR)(w,u)+(\nabla_w R)(u,v) = 0.$

Given any coordinate chart about some point on the manifold, the above identities may be written in terms of the components of the Riemann tensor at this point as:

Skew symmetry

$R_{abcd}^{}=-R_{bacd}=-R_{abdc}$

Interchange symmetry

$R_{abcd}^{}=R_{cdab}$

First Bianchi identity

$R_{abcd}+R_{acdb}+R_{adbc}^{}=0$

This is often written

$R_{a[bcd]}^{}=0,$

where the brackets denote the antisymmetric part on the indicated indices. This is equivalent to the previous version of the identity because the Riemann tensor is already skew on its last two indices.

Second Bianchi identity

$R_{abcd;e}^{}+R_{abde;c}^{}+R_{abec;d}^{}=0$

The semi-colon denotes a covariant derivative. Equivalently,

$R_{ab[cd;e]}^{}=0$

again using the antisymmetry on the last two indices of R.

The algebraic symmetries are also equivalent to saying that R belongs to the image of the Young symmetrizer corresponding to the partition 2+2.

Special cases

Surfaces

For a two-dimensional surface, the Bianchi identities imply that the Riemann tensor can be expressed as

$R_{abcd}^{}=K(g_{ac}g_{db}- g_{ad}g_{cb}) \,$

where $g_{ab}$ is the metric tensor and $K$ is a function called the Gaussian curvature and a, b, c and d take values either 1 or 2. The Riemann tensor has only one functionally independent component. The Gaussian curvature coincides with the sectional curvature of the surface. It is also exactly half the scalar curvature of the 2-manifold, while the Ricci curvature tensor of the surface is simply given by

$\operatorname{Ric}_{ab} = Kg_{ab}. \,$

Space forms

A Riemannian manifold is a space form if its sectional curvature is equal to a constant K. The Riemann tensor of a space form is given by

$R_{abcd}^{}=K(g_{ac}g_{db}-g_{ad}g_{cb}).$

Conversely, except in dimension 2, if the curvature of a Riemannian manifold has this form for some function K, then the Bianchi identities imply that K is constant and thus that the manifold is (locally) a space form.

See also

• Introduction to mathematics of general relativity
• Decomposition of the Riemann curvature tensor
• Curvature of Riemannian manifolds

References

• Besse, A.L. (1987), Einstein manifolds, Springer 
• Kobayashi, S.; Nomizu, K. (1963), Foundations of differential geometry, vol. 1, Interscience 
• Misner, Charles W.; Thorne, Kip S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0