Family of probability distributions
This article is about the distribution introduced by Diaz and Teruel. For the Tsallis q-Gaussian, see
q-Gaussian .
In mathematical physics and probability and statistics , the Gaussian q -distribution is a family of probability distributions that includes, as limiting cases , the uniform distribution and the normal (Gaussian) distribution . It was introduced by Diaz and Teruel.[clarification needed It is a q-analog of the Gaussian or normal distribution .
The distribution is symmetric about zero and is bounded, except for the limiting case of the normal distribution. The limiting uniform distribution is on the range -1 to +1.
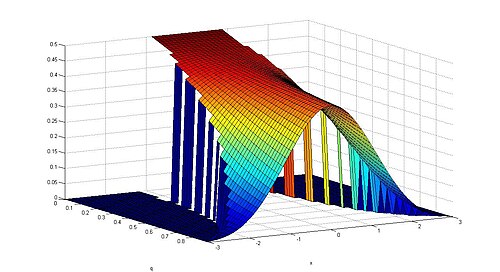
Definition [ edit ] The Gaussian q-density. Let q be a real number in the interval [0, 1). The probability density function of the Gaussian q -distribution is given by
s
q
(
x
)
=
{
0
if
x
<
−
ν
1
c
(
q
)
E
q
2
−
q
2
x
2
[
2
]
q
if
−
ν
≤
x
≤
ν
0
if
x
>
ν
.
{\displaystyle s_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu \\{\frac {1}{c(q)}}E_{q^{2}}^{\frac {-q^{2}x^{2}}{[2]_{q}}}&{\text{if }}-\nu \leq x\leq \nu \\0&{\mbox{if }}x>\nu .\end{cases}}}
where
ν
=
ν
(
q
)
=
1
1
−
q
,
{\displaystyle \nu =\nu (q)={\frac {1}{\sqrt {1-q}}},}
c
(
q
)
=
2
(
1
−
q
)
1
/
2
∑
m
=
0
∞
(
−
1
)
m
q
m
(
m
+
1
)
(
1
−
q
2
m
+
1
)
(
1
−
q
2
)
q
2
m
.
{\displaystyle c(q)=2(1-q)^{1/2}\sum _{m=0}^{\infty }{\frac {(-1)^{m}q^{m(m+1)}}{(1-q^{2m+1})(1-q^{2})_{q^{2}}^{m}}}.}
The q -analogue [t ]q
t
{\displaystyle t}
[
t
]
q
=
q
t
−
1
q
−
1
.
{\displaystyle [t]_{q}={\frac {q^{t}-1}{q-1}}.}
The q -analogue of the exponential function is the q-exponential , E x q
E
q
x
=
∑
j
=
0
∞
q
j
(
j
−
1
)
/
2
x
j
[
j
]
!
{\displaystyle E_{q}^{x}=\sum _{j=0}^{\infty }q^{j(j-1)/2}{\frac {x^{j}}{[j]!}}}
where the q -analogue of the factorial is the q-factorial , [n ]q
[
n
]
q
!
=
[
n
]
q
[
n
−
1
]
q
⋯
[
2
]
q
{\displaystyle [n]_{q}!=[n]_{q}[n-1]_{q}\cdots [2]_{q}\,}
for an integer n > 2 and [1]q q
The Cumulative Gaussian q-distribution. The cumulative distribution function of the Gaussian q -distribution is given by
G
q
(
x
)
=
{
0
if
x
<
−
ν
1
c
(
q
)
∫
−
ν
x
E
q
2
−
q
2
t
2
/
[
2
]
d
q
t
if
−
ν
≤
x
≤
ν
1
if
x
>
ν
{\displaystyle G_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu \\[12pt]\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{x}E_{q^{2}}^{-q^{2}t^{2}/[2]}\,d_{q}t&{\text{if }}-\nu \leq x\leq \nu \\[12pt]1&{\text{if }}x>\nu \end{cases}}}
where the integration symbol denotes the Jackson integral .
The function G q
G
q
(
x
)
=
{
0
if
x
<
−
ν
,
1
2
+
1
−
q
c
(
q
)
∑
n
=
0
∞
q
n
(
n
+
1
)
(
q
−
1
)
n
(
1
−
q
2
n
+
1
)
(
1
−
q
2
)
q
2
n
x
2
n
+
1
if
−
ν
≤
x
≤
ν
1
if
x
>
ν
{\displaystyle G_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu ,\\\displaystyle {\frac {1}{2}}+{\frac {1-q}{c(q)}}\sum _{n=0}^{\infty }{\frac {q^{n(n+1)}(q-1)^{n}}{(1-q^{2n+1})(1-q^{2})_{q^{2}}^{n}}}x^{2n+1}&{\text{if }}-\nu \leq x\leq \nu \\1&{\text{if}}\ x>\nu \end{cases}}}
where
(
a
+
b
)
q
n
=
∏
i
=
0
n
−
1
(
a
+
q
i
b
)
.
{\displaystyle (a+b)_{q}^{n}=\prod _{i=0}^{n-1}(a+q^{i}b).}
Moments [ edit ] The moments of the Gaussian q -distribution are given by
1
c
(
q
)
∫
−
ν
ν
E
q
2
−
q
2
x
2
/
[
2
]
x
2
n
d
q
x
=
[
2
n
−
1
]
!
!
,
{\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{-q^{2}x^{2}/[2]}\,x^{2n}\,d_{q}x=[2n-1]!!,}
1
c
(
q
)
∫
−
ν
ν
E
q
2
−
q
2
x
2
/
[
2
]
x
2
n
+
1
d
q
x
=
0
,
{\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{-q^{2}x^{2}/[2]}\,x^{2n+1}\,d_{q}x=0,}
where the symbol [2n − 1]!! is the q -analogue of the double factorial given by
[
2
n
−
1
]
[
2
n
−
3
]
⋯
[
1
]
=
[
2
n
−
1
]
!
!
.
{\displaystyle [2n-1][2n-3]\cdots [1]=[2n-1]!!.\,}
See also [ edit ] References [ edit ] Díaz, R.; Pariguan, E. (2009). "On the Gaussian q-distribution". Journal of Mathematical Analysis and Applications 358 : 1–9. arXiv :0807.1918 doi :10.1016/j.jmaa.2009.04.046 . S2CID 115175228 . Diaz, R.; Teruel, C. (2005). "q,k-Generalized Gamma and Beta Functions" (PDF) . Journal of Nonlinear Mathematical Physics 12 (1): 118–134. arXiv :math/0405402 Bibcode :2005JNMP...12..118D . doi :10.2991/jnmp.2005.12.1.10 . S2CID 73643153 . van Leeuwen, H.; Maassen, H. (1995). "A q deformation of the Gauss distribution" (PDF) . Journal of Mathematical Physics 36 (9): 4743. Bibcode :1995JMP....36.4743V . CiteSeerX 10.1.1.24.6957 doi :10.1063/1.530917 . hdl :2066/141604 . S2CID 13934946 . Exton, H. (1983), q-Hypergeometric Functions and Applications , New York: Halstead Press, Chichester: Ellis Horwood, 1983, ISBN 0853124914 , ISBN 0470274530 , ISBN 978-0470274538
Discrete
with finite with infinite
Continuous
supported on a supported on a supported with support
Mixed
Multivariate Directional Degenerate singular Families


![{\displaystyle s_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu \\{\frac {1}{c(q)}}E_{q^{2}}^{\frac {-q^{2}x^{2}}{[2]_{q}}}&{\text{if }}-\nu \leq x\leq \nu \\0&{\mbox{if }}x>\nu .\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f4756d8f382ded295f41b2e35a5f6856e88ecbb)



![{\displaystyle [t]_{q}={\frac {q^{t}-1}{q-1}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a356c0354e30a936e10d638ea378c74ead1b6b13)
![{\displaystyle E_{q}^{x}=\sum _{j=0}^{\infty }q^{j(j-1)/2}{\frac {x^{j}}{[j]!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/271b1da4445a1cb1b891e9c3d30099e2e6e99662)
![{\displaystyle [n]_{q}!=[n]_{q}[n-1]_{q}\cdots [2]_{q}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/533b3c41df579ee3f4d41dd6c153ba7e4db42183)
![{\displaystyle G_{q}(x)={\begin{cases}0&{\text{if }}x<-\nu \\[12pt]\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{x}E_{q^{2}}^{-q^{2}t^{2}/[2]}\,d_{q}t&{\text{if }}-\nu \leq x\leq \nu \\[12pt]1&{\text{if }}x>\nu \end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2127f2fe582b05819f37838de70f0b976b4a75d6)


![{\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{-q^{2}x^{2}/[2]}\,x^{2n}\,d_{q}x=[2n-1]!!,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12db0a698d15e9955385a89a2bfd58d6a62a7be7)
![{\displaystyle {\frac {1}{c(q)}}\int _{-\nu }^{\nu }E_{q^{2}}^{-q^{2}x^{2}/[2]}\,x^{2n+1}\,d_{q}x=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b1ba81409d3ee37e51e8b40c38bca8d81bedc4d)
![{\displaystyle [2n-1][2n-3]\cdots [1]=[2n-1]!!.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/044891c4911617a29420b18e032d7fd9c9848714)