Heptadecagon
| Regular heptadecagon | |
|---|---|
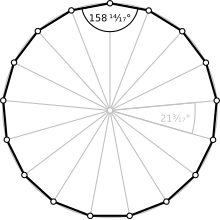 A regular heptadecagon | |
| Type | Regular polygon |
| Edges and vertices | 17 |
| Schläfli symbol | {17} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D17), order 2×17 |
| Internal angle (degrees) | ≈158.82° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, a heptadecagon, septadecagon or 17-gon is a seventeen-sided polygon.
Regular heptadecagon[edit]
A regular heptadecagon is represented by the Schläfli symbol {17}.
Construction[edit]

As 17 is a Fermat prime, the regular heptadecagon is a constructible polygon (that is, one that can be constructed using a compass and unmarked straightedge): this was shown by Carl Friedrich Gauss in 1796 at the age of 19.[1] This proof represented the first progress in regular polygon construction in over 2000 years.[1] Gauss's proof relies firstly on the fact that constructibility is equivalent to expressibility of the trigonometric functions of the common angle in terms of arithmetic operations and square root extractions, and secondly on his proof that this can be done if the odd prime factors of , the number of sides of the regular polygon, are distinct Fermat primes, which are of the form for some nonnegative integer . Constructing a regular heptadecagon thus involves finding the cosine of in terms of square roots. Gauss's book Disquisitiones Arithmeticae[2] gives this (in modern notation) as[3]

Constructions for the regular triangle, pentagon, pentadecagon, and polygons with 2h times as many sides had been given by Euclid, but constructions based on the Fermat primes other than 3 and 5 were unknown to the ancients. (The only known Fermat primes are Fn for n = 0, 1, 2, 3, 4. They are 3, 5, 17, 257, and 65537.)
The explicit construction of a heptadecagon was given by Herbert William Richmond in 1893. The following method of construction uses Carlyle circles, as shown below. Based on the construction of the regular 17-gon, one can readily construct n-gons with n being the product of 17 with 3 or 5 (or both) and any power of 2: a regular 51-gon, 85-gon or 255-gon and any regular n-gon with 2h times as many sides.
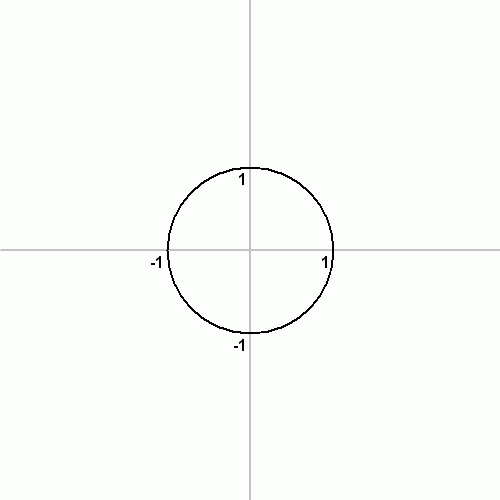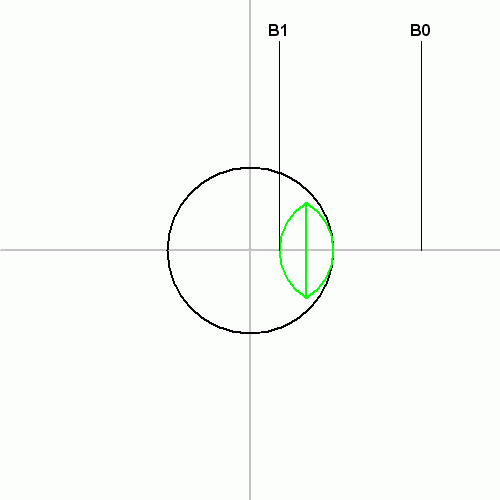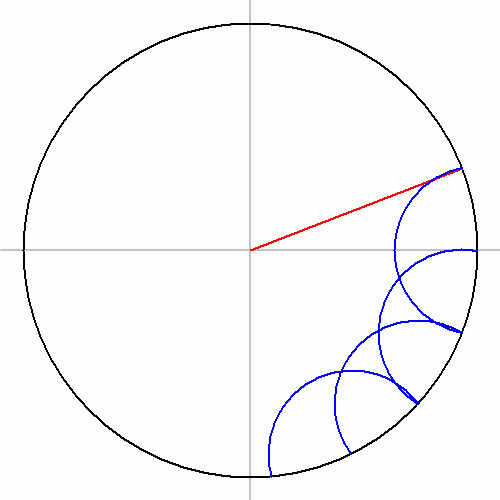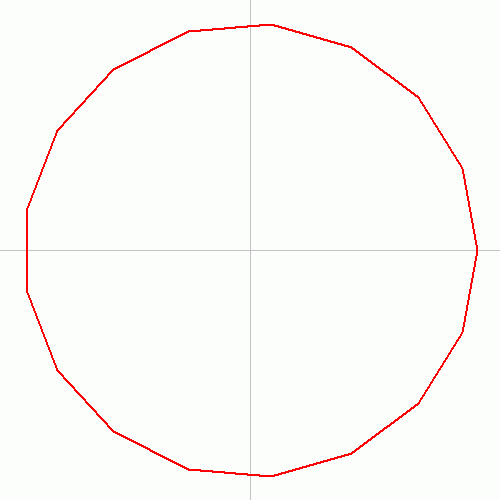

Another construction of the regular heptadecagon using straightedge and compass is the following:

T. P. Stowell of Rochester, N. Y., responded to Query, by W.E. Heal, Wheeling, Indiana in The Analyst in the year 1877:[5]
"To construct a regular polygon of seventeen sides in a circle. Draw the radius CO at right-angles to the diameter AB: On OC and OB, take OQ equal to the half, and OD equal to the eighth part of the radius: Make DE and DF each equal to DQ and EG and FH respectively equal to EQ and FQ; take OK a mean proportional between OH and OQ, and through K, draw KM parallel to AB, meeting the semicircle described on OG in M; draw MN parallel to OC, cutting the given circle in N – the arc AN is the seventeenth part of the whole circumference."

"sent by T. P. Stowell, credited to Leybourn's Math. Repository, 1818".
Added: "take OK a mean proportional between OH and OQ"

"sent by T. P. Stowell, credited to Leybourn's Math. Repository, 1818".
Added: "take OK a mean proportional between OH and OQ", animation
The following simple design comes from Herbert William Richmond from the year 1893:[6]
- "LET OA, OB (fig. 6) be two perpendicular radii of a circle. Make OI one-fourth of OB, and the angle OIE one-fourth of OIA; also find in OA produced a point F such that EIF is 45°. Let the circle on AF as diameter cut OB in K, and let the circle whose centre is E and radius EK cut OA in N3 and N5; then if ordinates N3P3, N5P5 are drawn to the circle, the arcs AP3, AP5 will be 3/17 and 5/17 of the circumference."
- The point N3 is very close to the center point of Thales' theorem over AF.


The following construction is a variation of H. W. Richmond's construction.
The differences to the original:
- The circle k2 determines the point H instead of the bisector w3.
- The circle k4 around the point G' (reflection of the point G at m) yields the point N, which is no longer so close to M, for the construction of the tangent.
- Some names have been changed.

Another more recent construction is given by Callagy.[3]
Trigonometric Derivation using nested Quadratic Equations[edit]
Combine nested double-angle formula with supplementary-angle formula to get the nested quadratic polynomial below.
- , AND
Therefore,
On simplifying and solving for X,
Exact value of sin and cos of mπ/(17 × 2n)[edit]
If , and then, depending on any integer m
For example, if m = 1
Here are the expressions simplified into the following table.
| m | 16 cos (m π / 17) | 8 sin (m π / 17) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Therefore, applying induction with m=1 and starting with n=0:
- and
Symmetry[edit]

The regular heptadecagon has Dih17 symmetry, order 34. Since 17 is a prime number there is one subgroup with dihedral symmetry: Dih1, and 2 cyclic group symmetries: Z17, and Z1.
These 4 symmetries can be seen in 4 distinct symmetries on the heptadecagon. John Conway labels these by a letter and group order.[7] Full symmetry of the regular form is r34 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g17 subgroup has no degrees of freedom but can be seen as directed edges.
Related polygons[edit]
Heptadecagrams[edit]
A heptadecagram is a 17-sided star polygon. There are seven regular forms given by Schläfli symbols: {17/2}, {17/3}, {17/4}, {17/5}, {17/6}, {17/7}, and {17/8}. Since 17 is a prime number, all of these are regular stars and not compound figures.
| Picture |  {17/2} |
 {17/3} |
 {17/4} |
 {17/5} |
 {17/6} |
 {17/7} |
 {17/8} |
|---|---|---|---|---|---|---|---|
| Interior angle | ≈137.647° | ≈116.471° | ≈95.2941° | ≈74.1176° | ≈52.9412° | ≈31.7647° | ≈10.5882° |
Petrie polygons[edit]
The regular heptadecagon is the Petrie polygon for one higher-dimensional regular convex polytope, projected in a skew orthogonal projection:
 16-simplex (16D) |
References[edit]
- ^ a b Arthur Jones, Sidney A. Morris, Kenneth R. Pearson, Abstract Algebra and Famous Impossibilities, Springer, 1991, ISBN 0387976612, p. 178.
- ^ Carl Friedrich Gauss "Disquisitiones Arithmeticae" eod books2ebooks, p. 662 item 365.
- ^ a b Callagy, James J. "The central angle of the regular 17-gon", Mathematical Gazette 67, December 1983, 290–292.
- ^ Duane W. DeTemple "Carlyle Circles and the Lemoine Simplicity of Polygon Constructions" in The American Mathematical Monthly, Volume 98, Issuc 1 (Feb. 1991), 97–108. "4. Construction of the Regular Heptadecagon (17-gon)" pp. 101–104, p.103, web.archive document, selected on 28 January 2017
- ^ Hendricks, J. E. (1877). "Answer to Mr. Heal's Query; T. P. Stowell of Rochester, N. Y." The Analyst: A Monthly Journal of Pure And Applied Mathematicus Vol.1: 94–95. Query, by W. E. Heal, Wheeling, Indiana p. 64; accessdate 30 April 2017
- ^ Herbert W. Richmond, description "A Construction for a regular polygon of seventeen side" illustration (Fig. 6), The Quarterly Journal of Pure and Applied Mathematics 26: pp. 206–207. Retrieved 4 December 2015
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275–278)
Further reading[edit]
- Dunham, William (September 1996). "1996—a triple anniversary". Math Horizons. 4: 8–13. doi:10.1080/10724117.1996.11974982. Retrieved 6 December 2009.
- Klein, Felix et al. Famous Problems and Other Monographs. – Describes the algebraic aspect, by Gauss.
External links[edit]
- Weisstein, Eric W. "Heptadecagon". MathWorld. Contains a description of the construction.
- "Constructing the Heptadecagon". MathPages.com.
- Heptadecagon trigonometric functions
- BBC video of New R&D center for SolarUK
- Archived at Ghostarchive and the Wayback Machine: Eisenbud, David. "The Amazing Heptadecagon (17-gon)" (Video). Brady Haran. Retrieved 2 March 2015.
- OEIS: A210644




































