Score voting: Difference between revisions
remove tag for incorrect merge, see Talk. |
remove Category:Positional electoral systems, no ranking, no fixed points assigned |
||
| Line 241: | Line 241: | ||
[[Category:Single winner electoral systems]] |
[[Category:Single winner electoral systems]] |
||
[[Category:Positional electoral systems]] |
|||
[[de:Rang-Wahl]] |
[[de:Rang-Wahl]] |
||
Revision as of 23:53, 21 December 2007
| A joint Politics and Economics series |
| Social choice and electoral systems |
|---|
 |
|
|
Range voting (also called ratings summation, average voting, cardinal ratings, 0–99 voting, or the score system or point system) is a voting system for one-seat elections under which voters score each candidate, the scores are added up, and the candidate with the highest score wins. It is not presently used in any public election. However, approval voting is range voting with only 2 levels (approved (1) and disapproved (0)) and forms of approval voting have been used for example, in Venice in the 13th century.
Voting system
Range voting uses a ratings ballot; that is, each voter rates each candidate with a number within a specified range, such as 0 to 99 or 1 to 5. Although in cumulative voting voters are not permitted to provide scores for more than some number of candidates, in range voting all candidates can be and should be rated. The scores for each candidate are summed, and the candidate with the highest sum is the winner. If voters are explicitly allowed to abstain from rating certain candidates, as opposed to implicitly giving the lowest number of points to unrated candidates, then a candidate's score would be the average rating from voters who did rate this candidate.
In some competitions subject to judges' scores, a truncated mean is used to remove extreme scores. For example, range voting with truncated means is used in figure skating competitions both to mitigate biases by some judges and to avoid the results of third skaters affecting the relative positions of two skaters who have already finished their performances.
Another method of counting ratings ballots is to find the median score of each candidate, and elect the candidate with the highest median score (see Median Ratings). This could have the effect of reducing the incentive to exaggerate. A potential disadvantage is that multiway exact ties for winner may become common, while in conventional range voting, such ties would be extremely rare. To address this problem it's been proposed to use a linear-interpolated median rather than a conventional median.
Range voting in which only two different votes may be submitted (0 and 1, for example) is equivalent to approval voting. As with approval voting, voters must weigh the adverse impact on their favorite candidate of ranking other candidates highly.
Alternative use
Although no electoral usage of range voting is known, other than the restricted case of Approval voting, the concept can be found in other areas. Sports such as gymnastics rate competitors on a numeric scale, although the fact that judges' ratings are public makes it unlikely for them to engage in tactical voting. On the Web, sites allow users to rate items such as movies (Internet Movie Database), comments (Kuro5hin), recipes, and many other things. Range voting is the primary voting method used and endorsed by the Libertarian Reform Caucus. [1]
Range voting has been used informally by various amateur clubs to determine dates and venues for things like seasonal dinners. In one variant, any club member who wants to propose a date/time or restaurant writes it down on a whiteboard. All other members can each vote once for each new option; either by adding +1 to the total (in favour), casting no vote (neutral), or by subtracting one from the total (disapproval). At the end of the season, the club goes to the restaurant with the most votes, at the date and time with the most votes.
Example
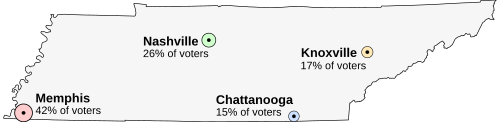
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
- Memphis, the largest city, but far from the others (42% of voters)
- Nashville, near the center of the state (26% of voters)
- Chattanooga, somewhat east (15% of voters)
- Knoxville, far to the northeast (17% of voters)
The preferences of each region's voters are:
| 42% of voters Far-West |
26% of voters Center |
15% of voters Center-East |
17% of voters Far-East |
|---|---|---|---|
|
|
|
|
Suppose that voters each decided to grant from 1 to 10 points to each city such that their most liked choice got 10 points, and least liked choice got 1 point, with the intermediate choices getting 5 points and 2 points.
| Voter from/ City Choice |
Memphis | Nashville | Chattanooga | Knoxville | Total |
|---|---|---|---|---|---|
| Memphis | 420 (42 * 10) | 26 (26 * 1) | 15 (15 * 1) | 17 (17 * 1) | 478 |
| Nashville | 210 (42 * 5) | 260 (26 * 10) | 30 (15 * 2) | 34 (17 * 2) | 534 |
| Chattanooga | 84 (42 * 2) | 130 (26 * 5) | 150 (15 * 10) | 85 (17 * 5) | 449 |
| Knoxville | 42 (42 * 1) | 52 (26 * 2) | 75 (15 * 5) | 170 (17 * 10) | 339 |
Nashville wins. But Memphis would have won if the voters from Memphis had reduced the points they gave Nashville from 5 down to 1 and all other votes had remained the same; voters from Chattanooga or Knoxville could restore Nashville to first place over Memphis if they raised the points they gave Nashville from 2 up to 10.
Properties
Range voting allows voters to express preferences of varying strengths.
Range voting satisfies the monotonicity criterion, i.e. raising your vote's score for a candidate can never hurt his chances of winning. Also, in range voting, casting a sincere vote can never result in a worse election winner (from your point of view) than if you had simply abstained from voting. Range voting passes the favorite betrayal criterion, meaning that it never gives voters an incentive to rate their favorite candidate lower than a candidate they like less. Range voting advocates contend that this is a good property, because it leads to higher average voter satisfaction when voters are honest, and still gives voters the choice to strategically lower their scores for less preferred candidates if they choose.
Range voting is independent of clones in the sense that if there is a set of candidates such that every voter gives the same rating to every candidate in this set, then the probability that the winner is in this set is independent of how many candidates are in the set. Range voting is not a Condorcet method according to the traditional definition of that term.
In summary, range voting satisfies the monotonicity criterion, the favorite betrayal criterion, the participation criterion, the consistency criterion, independence of irrelevant alternatives, resolvability criterion, and reversal symmetry. It is immune to cloning, except for the obvious specific case in which a candidate with clones ties, instead of achieving a unique win. It does not satisfy either the Condorcet criterion (i.e. is not a Condorcet method) or the Condorcet loser criterion. It does not satisfy the majority criterion.
As it satisfies the criteria of a deterministic voting system, with non-imposition, non-dictatorship, monotonicity, and independence of irrelevant alternatives, it may appear that it violates Arrow's impossibility theorem. The reason that range voting is not regarded as a counter-example to Arrow's theorem is that it is a cardinal voting system, while Arrow's theorem is restricted to the processing of ordinal preferences.[2]
Bayesian regret
Many criteria have been proposed for estimating the quality of a voting method, but Bayesian regret[3] is arguably unique in that it represents the aggregate impact of all possible (even as yet undiscovered) criteria, in terms of average voter satisfaction. The mathematical definition of the concept is as follows:
In Bayesian statistics, "regret" is the difference between the maximum possible ideal utility and the actual utility. (Depending on the application, regret can often be more convenient to deal with than utility. This terminology has been used in a large number of papers and is not new from us.) "Social" utility is the sum of utility over all the members of some human population. For voting systems purposes, "Bayesian regret" is the expectation value of social regret. It depends on both the voting system, the number of candidates, the number of voters, and the probabilistic models of utilities, candidates, and voter behaviors.[4]
Some advocates of this yard stick make the analogy to a single person making a choice: a choice is made by assessing the pros and cons of the available options, in order to assign an overall utility value to each one; and then the one with the highest estimated value is selected. Likewise, Bayesian regret is expressed as the difference between the average voter happiness that would be produced by electing the optimum candidate, and the average voter happiness brought about by the actual winner in the specified election system. By using the voting method with the lowest Bayesian regret, a voter maximizes his expected value in the "currency" of satisfation.
Empirical tests
Warren D. Smith has produced some comprehensive Bayesian regret calculations.[5] The calculations were based on computer simulations of hundreds of millions of elections. In those simulations, voting behavior was modeled on five parameters using 720 different tunings. Whether voters were informed or ignorant, honest or strategic, range voting produced the lowest Bayesian regret among common voting methods, in Smith's experiment. The table below shows the results of two sample simulations.
Column A: 5 candidates, 20 voters, random utilities; Each entry averages the regrets from 4000000 simulated elections. Column B: 5 candidates, 50 voters, utilities based on 2 issues, each entry averages the regrets from 2222222 simulated elections.
| Voting System | Regret A | Regret B |
|---|---|---|
| Magically elect optimum winner | 0 | 0 |
| Range (honest voters) | 0.04941 | 0.05368 |
| Borda (honest voters) | 0.13055 | 0.10079 |
| Approval (honest voters) | 0.20575 | 0.16549 |
| Condorcet-LR (honest voters) | 0.22247 | 0.14640 |
| Range & Approval (strategic exaggerating voters) | 0.31554 | 0.23101 |
| IRV (honest voters) | 0.32314 | 0.23786 |
| Plurality (honest voters) | 0.48628 | 0.37884 |
| Borda (strategic exaggerating voters) | 0.70219 | 0.48438 |
| Condorcet-LR (strategic exaggerating voters) | 0.86287 | 0.58958 |
| IRV (strategic exaggerating voters) | 0.91522 | 0.61072 |
| Plurality (strategic voters) | 0.91522 | 0.61072 |
| Elect random winner | 1.50218 | 1.00462 |
Criticisms
Critics of the Bayesian regret metric argue that it is not always fair, and that its inconsistency with majoritarian systems is a flaw. Consider the following scenario, given the honest utility values of three voters for three candidates.
| Candidate 1 | Candidate 2 | Candidate 3 | |
|---|---|---|---|
| Voter 1 | 11 | 9 | 22 |
| Voter 2 | 13 | 11 | 25 |
| Voter 3 | 5 | 8 | 2 |
While it is clear that the election of candidate 3 would produce the greatest average satisfaction in this scenario, this would be at the expense of voter 3. In spite of such lop-sided scenarios, Bayesian regret adherents defend the metric, because it is possible that no voting method (apart from one which reads minds) may prevent them. Range voting advocates point out that under their system, all voters have the same ballots, with the same weight, and the same opportunity to vote strategically, thus making range voting fair.
Strategy
In most cases, ideal range voting strategy for well-informed voters is identical to ideal approval voting strategy, and a voter would want to give his least and most favorite candidates a minimum and a maximum score, respectively. If one candidate's backers engaged in this tactic and other candidates' backers cast sincere rankings for the full range of candidates, then the tactical voters would have a significant advantage over the rest of the electorate. When the population is large and there are two obvious and distinct front-runners, tactical voters seeking to maximize their influence on the result is to give a maximum rating to their preferred candidate, and a minimum rating to the other front-runner; these voters would then give minimum and maximum scores to all other candidates so as to maximize expected utility.
However, there are examples in which voting maximum and minimum scores for all candidates is not optimal.[6] What has been observed to happen in exit poll experiments[7] is that voters tend to vote more sincerely for candidates they perceive have no chance of winning. Thus range voting may yield[8] higher support for third party and independent candidates than other common voting methods, creating what has been called the "nursery effect", unless those candidates become viable.
Because range voting produces lower Bayesian regret than other methods[3], even when voters are strategic, many range voting advocates believe it is the most resistant voting method to strategic voting.
Guy Ottewell, who coined the term approval voting, now endorses range voting[9]. No elected official in the United States is known to endorse range voting.
References
- ^ Shentrup, Clay. "Why alternative parties must get range voting, or die". Libertarian reform caucus. Retrieved 2007-10-09.
{{cite web}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Arrow, Kenneth (August 1950). "A Difficulty in the Concept of Social Welfare". The Journal of Political Economy. 58 (4).
{{cite journal}}: Text "pages 328–346" ignored (help) - ^ a b "Bayesian regret for dummies". The center for range voting.
- ^ "Bayesian regret (mathematical definition". The center for range voting.
- ^ Smith, Warren D. (2000). "Range voting" (PDF).
{{cite web}}: Unknown parameter|month=ignored (help) - ^ "Examples in which best Range Voting strategy is not "approval style" voting". The center for range voting.
- ^ "Honesty and Strategy in real-world voters". The center for range voting.
- ^ "The "Nursery Effect" (Executive summary)". The center for range voting.
- ^ "Endorsement of Range Voting by Guy Ottewell". The center for range voting.
See also
- List of democracy and elections-related topics
- Consensus decision-making
- Decision making
- Democracy
- Hot or Not — a real world example
- Majoritarianism (Majority rule)
- Minoritarianism
External links
- The Center for Range Voting website and CRV simplified entry page
- Range voting discussion list at Yahoo Groups
- FairVote criticism of approval, range voting, and condorcet methods
- Mock 2008 U.S. Presidential Election using range voting
- Simulation of various voting models for close elections Article by Brian Olson.