Schulze method: Difference between revisions
added ballot |
m fixed broken link |
||
| Line 632: | Line 632: | ||
* [[Alma Mater Society of the University of British Columbia|Alma Mater Society of the University of British Columbia (AMS)]] (The AMS uses the Schulze method for its voter-funded media system.) [http://www.votermedia.org/ubc/] |
* [[Alma Mater Society of the University of British Columbia|Alma Mater Society of the University of British Columbia (AMS)]] (The AMS uses the Schulze method for its voter-funded media system.) [http://www.votermedia.org/ubc/] |
||
* [[Annodex|Annodex Association]] [http://www.cs.cornell.edu/w8/~andru/cgi-perl/civs/results.pl?id=E_50cfc592ae8f13d9] |
* [[Annodex|Annodex Association]] [http://www.cs.cornell.edu/w8/~andru/cgi-perl/civs/results.pl?id=E_50cfc592ae8f13d9] |
||
* [ |
* [http://blitzed.org/ Blitzed] [http://wiki.blitzed.org/Condorcet_method_for_admin_voting] |
||
* [[BoardGameGeek]] [http://www.boardgamegeek.com/article/1751505#1751580] |
* [[BoardGameGeek]] [http://www.boardgamegeek.com/article/1751505#1751580] |
||
* [http://0xAA.org Codex Alpe Adria] [http://0xAA.org/competitions/] |
* [http://0xAA.org Codex Alpe Adria] [http://0xAA.org/competitions/] |
||
Revision as of 05:08, 4 June 2008
| A joint Politics and Economics series |
| Social choice and electoral systems |
|---|
 |
|
|
The Schulze method is a voting system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners. The Schulze method is also known as Schwartz Sequential Dropping (SSD), Cloneproof Schwartz Sequential Dropping (CSSD), Beatpath Method, Beatpath Winner, Path Voting, and Path Winner.
If there is a candidate who is preferred pairwise over the other candidates, when compared in turn with each of the others, the Schulze method guarantees that candidate will win. Because of this property, the Schulze method is (by definition) a Condorcet method.
Currently, the Schulze method is the most wide-spread Condorcet method. The Schulze method is used e.g. by Wikimedia, Debian, Gentoo, and Software in the Public Interest.
Many different heuristics for the Schulze method have been proposed. The most important heuristics are the path heuristic and the Schwartz set heuristic that are described below. All heuristics find the same winner and only differ in the details of the computational procedure to determine this winner.
The path heuristic
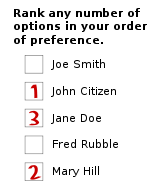
Under the Schulze method (as well as under other preferential single-winner election methods), each ballot contains a complete list of all candidates and the individual voter ranks this list in order of preference. Under a common ballot layout (as shown in the image to the right), ascending numbers are used, whereby the voter places a '1' beside the most preferred candidate, a '2' beside the second-most preferred, and so forth. Voters may give the same preference to more than one candidate and may keep candidates unranked. When a given voter does not rank all candidates, then it is presumed that this voter strictly prefers all ranked candidates to all not ranked candidates and that this voter is indifferent between all not ranked candidates.
Procedure
Suppose d[V,W] is the number of voters who strictly prefer candidate V to candidate W.
A path from candidate X to candidate Y of strength p is a sequence of candidates C(1),...,C(n) with the following properties:
- C(1) = X and C(n) = Y.
- For all i = 1,...,(n-1): d[C(i),C(i+1)] > d[C(i+1),C(i)].
- p is the minimum of all d[C(i),C(i+1)] for i = 1,...,(n-1).
p[A,B], the strength of the strongest path from candidate A to candidate B, is the maximum value such that there is a path from candidate A to candidate B of that strength. If there is no path from candidate A to candidate B at all, then p[A,B] : = 0.
Candidate D is better than candidate E if and only if p[D,E] > p[E,D].
Candidate D is a potential winner if and only if p[D,E] ≥ p[E,D] for every other candidate E.
Implementation
Suppose C is the number of candidates. Then the strengths of the strongest paths can be calculated with the Floyd–Warshall algorithm.
Input: d[i,j] is the number of voters who strictly prefer candidate i to candidate j.
Output: Candidate i is a potential winner if and only if "winner[i] = true".
1 for i : = 1 to C
2 begin
3 for j : = 1 to C
4 begin
5 if ( i ≠ j ) then
6 begin
7 if ( d[i,j] > d[j,i] ) then
8 begin
9 p[i,j] : = d[i,j]
10 end
11 else
12 begin
13 p[i,j] : = 0
14 end
15 end
16 end
17 end
18
19 for i : = 1 to C
20 begin
21 for j : = 1 to C
22 begin
23 if ( i ≠ j ) then
24 begin
25 for k : = 1 to C
26 begin
27 if ( i ≠ k ) then
28 begin
29 if ( j ≠ k ) then
30 begin
31 p[j,k] : = max { p[j,k]; min { p[j,i]; p[i,k] } }
32 end
33 end
34 end
35 end
36 end
37 end
38
39 for i : = 1 to C
40 begin
41 winner[i] : = true
42 end
43
44 for i : = 1 to C
45 begin
46 for j : = 1 to C
47 begin
48 if ( i ≠ j ) then
49 begin
50 if ( p[j,i] > p[i,j] ) then
51 begin
52 winner[i] : = false
53 end
54 end
55 end
56 end
Examples
Example 1
Example (45 voters; 5 candidates):
- 5 ACBED (that is, 5 voters have order of preference: A > C > B > E > D)
- 5 ADECB
- 8 BEDAC
- 3 CABED
- 7 CAEBD
- 2 CBADE
- 7 DCEBA
- 8 EBADC
| d[*,A] | d[*,B] | d[*,C] | d[*,D] | d[*,E] | |
|---|---|---|---|---|---|
| d[A,*] | 20 | 26 | 30 | 22 | |
| d[B,*] | 25 | 16 | 33 | 18 | |
| d[C,*] | 19 | 29 | 17 | 24 | |
| d[D,*] | 15 | 12 | 28 | 14 | |
| d[E,*] | 23 | 27 | 21 | 31 |
The critical defeats of the strongest paths are underlined.
| ... to A | ... to B | ... to C | ... to D | ... to E | |
|---|---|---|---|---|---|
| from A ... | A-(30)-D-(28)-C-(29)-B | A-(30)-D-(28)-C | A-(30)-D | A-(30)-D-(28)-C-(24)-E | |
| from B ... | B-(25)-A | B-(33)-D-(28)-C | B-(33)-D | B-(33)-D-(28)-C-(24)-E | |
| from C ... | C-(29)-B-(25)-A | C-(29)-B | C-(29)-B-(33)-D | C-(24)-E | |
| from D ... | D-(28)-C-(29)-B-(25)-A | D-(28)-C-(29)-B | D-(28)-C | D-(28)-C-(24)-E | |
| from E ... | E-(31)-D-(28)-C-(29)-B-(25)-A | E-(31)-D-(28)-C-(29)-B | E-(31)-D-(28)-C | E-(31)-D |
| p[*,A] | p[*,B] | p[*,C] | p[*,D] | p[*,E] | |
|---|---|---|---|---|---|
| p[A,*] | 28 | 28 | 30 | 24 | |
| p[B,*] | 25 | 28 | 33 | 24 | |
| p[C,*] | 25 | 29 | 29 | 24 | |
| p[D,*] | 25 | 28 | 28 | 24 | |
| p[E,*] | 25 | 28 | 28 | 31 |
Candidate E is a potential winner, because p[E,X] ≥ p[X,E] for every other candidate X.
Example 2
Example (30 voters; 4 candidates):
- 5 ACBD
- 2 ACDB
- 3 ADCB
- 4 BACD
- 3 CBDA
- 3 CDBA
- 1 DACB
- 5 DBAC
- 4 DCBA
| d[*,A] | d[*,B] | d[*,C] | d[*,D] | |
|---|---|---|---|---|
| d[A,*] | 11 | 20 | 14 | |
| d[B,*] | 19 | 9 | 12 | |
| d[C,*] | 10 | 21 | 17 | |
| d[D,*] | 16 | 18 | 13 |
The critical defeats of the strongest paths are underlined.
| ... to A | ... to B | ... to C | ... to D | |
|---|---|---|---|---|
| from A ... | A-(20)-C-(21)-B | A-(20)-C | A-(20)-C-(17)-D | |
| from B ... | B-(19)-A | B-(19)-A-(20)-C | B-(19)-A-(20)-C-(17)-D | |
| from C ... | C-(21)-B-(19)-A | C-(21)-B | C-(17)-D | |
| from D ... | D-(18)-B-(19)-A | D-(18)-B | D-(18)-B-(19)-A-(20)-C |
| p[*,A] | p[*,B] | p[*,C] | p[*,D] | |
|---|---|---|---|---|
| p[A,*] | 20 | 20 | 17 | |
| p[B,*] | 19 | 19 | 17 | |
| p[C,*] | 19 | 21 | 17 | |
| p[D,*] | 18 | 18 | 18 |
Candidate D is a potential winner, because p[D,X] ≥ p[X,D] for every other candidate X.
Example 3
Example (30 voters; 5 candidates):
- 3 ABDEC
- 5 ADEBC
- 1 ADECB
- 2 BADEC
- 2 BDECA
- 4 CABDE
- 6 CBADE
- 2 DBECA
- 5 DECAB
| d[*,A] | d[*,B] | d[*,C] | d[*,D] | d[*,E] | |
|---|---|---|---|---|---|
| d[A,*] | 18 | 11 | 21 | 21 | |
| d[B,*] | 12 | 14 | 17 | 19 | |
| d[C,*] | 19 | 16 | 10 | 10 | |
| d[D,*] | 9 | 13 | 20 | 30 | |
| d[E,*] | 9 | 11 | 20 | 0 |
The critical defeats of the strongest paths are underlined.
| ... to A | ... to B | ... to C | ... to D | ... to E | |
|---|---|---|---|---|---|
| from A ... | A-(18)-B | A-(21)-D-(20)-C | A-(21)-D | A-(21)-E | |
| from B ... | B-(19)-E-(20)-C-(19)-A | B-(19)-E-(20)-C | B-(19)-E-(20)-C-(19)-A-(21)-D | B-(19)-E | |
| from C ... | C-(19)-A | C-(19)-A-(18)-B | C-(19)-A-(21)-D | C-(19)-A-(21)-E | |
| from D ... | D-(20)-C-(19)-A | D-(20)-C-(19)-A-(18)-B | D-(20)-C | D-(30)-E | |
| from E ... | E-(20)-C-(19)-A | E-(20)-C-(19)-A-(18)-B | E-(20)-C | E-(20)-C-(19)-A-(21)-D |
| p[*,A] | p[*,B] | p[*,C] | p[*,D] | p[*,E] | |
|---|---|---|---|---|---|
| p[A,*] | 18 | 20 | 21 | 21 | |
| p[B,*] | 19 | 19 | 19 | 19 | |
| p[C,*] | 19 | 18 | 19 | 19 | |
| p[D,*] | 19 | 18 | 20 | 30 | |
| p[E,*] | 19 | 18 | 20 | 19 |
Candidate B is a potential winner, because p[B,X] ≥ p[X,B] for every other candidate X.
Example 4
Example (9 voters; 4 candidates):
- 3 ABCD
- 2 DABC
- 2 DBCA
- 2 CBDA
| d[*,A] | d[*,B] | d[*,C] | d[*,D] | |
|---|---|---|---|---|
| d[A,*] | 5 | 5 | 3 | |
| d[B,*] | 4 | 7 | 5 | |
| d[C,*] | 4 | 2 | 5 | |
| d[D,*] | 6 | 4 | 4 |
The critical defeats of the strongest paths are underlined.
| ... to A | ... to B | ... to C | ... to D | |
|---|---|---|---|---|
| from A ... | A-(5)-B | A-(5)-C | A-(5)-C-(5)-D | |
| from B ... | B-(5)-D-(6)-A | B-(7)-C | B-(5)-D | |
| from C ... | C-(5)-D-(6)-A | C-(5)-D-(6)-A-(5)-B | C-(5)-D | |
| from D ... | D-(6)-A | D-(6)-A-(5)-B | D-(6)-A-(5)-C |
| p[*,A] | p[*,B] | p[*,C] | p[*,D] | |
|---|---|---|---|---|
| p[A,*] | 5 | 5 | 5 | |
| p[B,*] | 5 | 7 | 5 | |
| p[C,*] | 5 | 5 | 5 | |
| p[D,*] | 6 | 5 | 5 |
Candidate B and candidate D are potential winners, because p[B,X] ≥ p[X,B] for every other candidate X and p[D,Y] ≥ p[Y,D] for every other candidate Y.
The Schwartz set heuristic
The Schwartz set
The definition of a Schwartz set, as used in the Schulze method, is as follows:
- An unbeaten set is a set of candidates of whom none is beaten by anyone outside that set.
- An innermost unbeaten set is an unbeaten set that doesn't contain a smaller unbeaten set.
- The Schwartz set is the set of candidates who are in innermost unbeaten sets.
Procedure
The voters cast their ballots by ranking the candidates according to their preferences, just like for any other Condorcet election.
The Schulze method uses Condorcet pairwise matchups between the candidates and a winner is chosen in each of the matchups.
From there, the Schulze method operates as follows to select a winner (or create a ranked list):
- Calculate the Schwartz set based only on undropped defeats.
- If there are no defeats among the members of that set then they (plural in the case of a tie) win and the count ends.
- Otherwise, drop the weakest defeat(s) (plural in the case of ex æquo defeats) among the candidates of that set. Go to 1.
An example
The situation
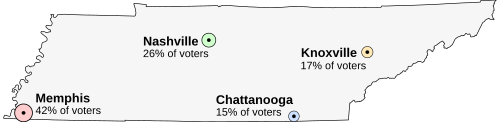
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
- Memphis, the largest city, but far from the others (42% of voters)
- Nashville, near the center of the state (26% of voters)
- Chattanooga, somewhat east (15% of voters)
- Knoxville, far to the northeast (17% of voters)
The preferences of each region's voters are:
| 42% of voters Far-West |
26% of voters Center |
15% of voters Center-East |
17% of voters Far-East |
|---|---|---|---|
|
|
|
|
The results would be tabulated as follows:
| A | |||||
|---|---|---|---|---|---|
| Memphis | Nashville | Chattanooga | Knoxville | ||
| B | Memphis | [A] 58% [B] 42% | [A] 58% [B] 42% | [A] 58% [B] 42% | |
| Nashville | [A] 42% [B] 58% | [A] 32% [B] 68% | [A] 32% [B] 68% | ||
| Chattanooga | [A] 42% [B] 58% | [A] 68% [B] 32% | [A] 17% [B] 83% | ||
| Knoxville | [A] 42% [B] 58% | [A] 68% [B] 32% | [A] 83% [B] 17% | ||
| Pairwise election results (won-lost-tied): | 0-3-0 | 3-0-0 | 2-1-0 | 1-2-0 | |
| Votes against in worst pairwise defeat: | 58% | N/A | 68% | 83% | |
- [A] indicates voters who preferred the candidate listed in the column caption to the candidate listed in the row caption
- [B] indicates voters who preferred the candidate listed in the row caption to the candidate listed in the column caption
Pairwise winners
First, list every pair, and determine the winner:
| Pair | Winner |
|---|---|
| Memphis (42%) vs. Nashville (58%) | Nashville 58% |
| Memphis (42%) vs. Chattanooga (58%) | Chattanooga 58% |
| Memphis (42%) vs. Knoxville (58%) | Knoxville 58% |
| Nashville (68%) vs. Chattanooga (32%) | Nashville 68% |
| Nashville (68%) vs. Knoxville (32%) | Nashville 68% |
| Chattanooga (83%) vs. Knoxville (17%) | Chattanooga: 83% |
Note that absolute counts of votes can be used, or percentages of the total number of votes; it makes no difference.
Dropping
Next we start with our list of cities and their matchup wins/defeats
- Nashville 3-0
- Chattanooga 2-1
- Knoxville 1-2
- Memphis 0-3
Technically, the Schwartz set is simply Nashville as it beat all others 3 to 0.
Therefore, Nashville is the winner.
Ambiguity resolution example
Let's say there was an ambiguity. For a simple situation involving candidates A, B, C, and D.
- A > B 68%
- C > A 52%
- A > D 62%
- B > C 72%
- B > D 84%
- C > D 91%
In this situation the Schwartz set is A, B, and C as they all beat D.
- A > B 68%
- B > C 72%
- C > A 52%
Schulze then says to drop the weakest margin, so we drop C > A and are left with
- A > B 68%
- B > C 72%
The new Schwartz set is now A, as it is unbeaten by anyone outside its set. With A in a Schwartz set by itself, it is now the winner.
Summary
In the (first) example election, the winner is Nashville. This would be true for any Condorcet method. Using the first-past-the-post system and some other systems, Memphis would have won the election by having the most people, even though Nashville won every simulated pairwise election outright. Nashville would also have been the winner in a Borda count. Instant-runoff voting in this example would select Knoxville, even though more people preferred Nashville than Knoxville.
Satisfied and failed criteria
Satisfied criteria
The Schulze method satisfies the following criteria:
- Universality
- Non-imposition (a.k.a. citizen sovereignty)
- Non-dictatorship
- Pareto criterion
- Monotonicity criterion (a.k.a. mono-raise)
- Majority criterion
- Condorcet criterion (a.k.a. Condorcet winner criterion)
- Condorcet loser criterion
- Smith criterion
- Schwartz criterion
- Local independence of irrelevant alternatives
- Mutual majority criterion
- Independence of clones (See clones)
- Reversal symmetry
- Mono-append
- Mono-add-plump
- Resolvability criterion
- Polynomial runtime
If winning votes is used as the definition of defeat strength, it also satisfies:
If margins as defeat strength is used, it also satisfies:
Failed criteria
The Schulze method violates the following criteria:
- All criteria that are incompatible with the Condorcet criterion (e.g. independence of irrelevant alternatives, participation, consistency, invulnerability to compromising, invulnerability to burying, later-no-harm)
Independence of irrelevant alternatives
The Schulze method fails independence of irrelevant alternatives. However, the method adheres to a less strict property that is sometimes called Local independence of irrelevant alternatives. It says that if one candidate (X) wins an election, and a new alternative (Y) is added, X will win the election if Y is not in the Smith set. Local IIA implies the Condorcet criterion.
Comparison with other preferential single-winner election methods
The following table compares the Schulze method with other preferential single-winner election methods:
| Monotonic | Condorcet winner | Condorcet loser | LIIA | Majority | Mutual majority | Clone independence | Reversal symmetry | Polynomial time | |
|---|---|---|---|---|---|---|---|---|---|
| Schulze | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Ranked Pairs | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Kemeny-Young | Yes | Yes | Yes | Yes | Yes | Yes | No | Yes | No |
| MiniMax | Yes | Yes | No | No | Yes | No | No | No | Yes |
| Nanson | No | Yes | Yes | No | Yes | Yes | No | Yes | Yes |
| Baldwin | No | Yes | Yes | No | Yes | Yes | No | No | Yes |
| Instant-runoff voting | No | No | Yes | No | Yes | Yes | Yes | No | Yes |
| Coombs | No | No | Yes | No | Yes | Yes | No | No | Yes |
| Contingent voting | No | No | Yes | No | Yes | No | No | No | Yes |
| Borda | Yes | No | Yes | No | No | No | No | Yes | Yes |
| Bucklin | Yes | No | No | No | Yes | Yes | No | No | Yes |
| Plurality | Yes | No | No | No | Yes | No | No | No | Yes |
| Anti-plurality | Yes | No | No | No | No | No | No | No | Yes |
The difference between the Schulze method and the Ranked Pairs method is discussed in section 9 of this paper.
History of the Schulze method
The Schulze method was developed by Markus Schulze in 1997. The first time, that the Schulze method was discussed in a public mailing list, was in 1998 [1] [2] [3] [4] [5]. In the following years, the Schulze method has been adopted e.g. by Software in the Public Interest (2003), Debian (2003), UserLinux (2003), Gentoo (2005), TopCoder (2005), and Sender Policy Framework (2005). The first books on the Schulze method were written by Tideman (2006) and by Stahl and Johnson (2007).
Use of the Schulze method

The Schulze method is not currently used in government elections. However, it is starting to receive support in some public organizations. Organizations which currently use the Schulze method are:
- Alma Mater Society of the University of British Columbia (AMS) (The AMS uses the Schulze method for its voter-funded media system.) [6]
- Annodex Association [7]
- Blitzed [8]
- BoardGameGeek [9]
- Codex Alpe Adria [10]
- County Highpointers [11]
- Debian [12] [13] [14]
- Furthermore, the fact that the Schulze method is a part of Debian's voting software ("Debian Vote Engine", Devotee) means that it is the standard voting system in all Debian user groups (DUGs).
- EnMasse Forums
- EuroBillTracker [15] [16] [17] [18]
- Fair Trade Northwest (see article XI section 2 of their bylaws)
- Free Software Foundation Latin America (FSFLA) [19] [20]
- Gentoo Foundation [21] [22] [23] [24] [25] [26]
- GNU Privacy Guard (GnuPG) [27]
- Kingman Hall [28] [29]
- Kumoricon [30] [31] [32]
- Libertarian Party at Colorado State University (LPCSU) [33]
- Libre Entreprise [34] [35]
- Lumiera [36]
- Mathematical Knowledge Management Interest Group (MKM-IG) (The MKM-IG uses Condorcet with dual dropping. That means: The Schulze ranking and the ranked pairs ranking are calculated and the winner is the top-ranked candidate of that of these two rankings that has the better Kemeny score.) [37] [38] [39] [40]
- Metalab [41]
- Music Television (MTV) [42]
- North Shore Cyclists (NSC) [43] [44]
- OpenCouchSurfing [45]
- Open Elections [46] / Simply Working Preferential Web Election (SWPWE)
- Pittsburgh Ultimate [47]
- Plant of the Month
- RPMrepo [48]
- Sender Policy Framework (SPF) [49] [50] [51]
- Software in the Public Interest (SPI) [52]
- Students for Free Culture [53] [54]
- TopCoder [55] [56] [57] [58] [59] [60] [61] [62] [63] [64]
- Wikimedia Foundation [65]
- Wikipedia in French (The Schulze method is one of three methods recommended for decision-making.) (see here)
- Wikipedia in Hungarian (see here and here)
- Wikipedia in Spanish (see here)
External resources
Note that these sources may refer to the Schulze method as CSSD, SSD, beatpath, path winner, etc.
General
- Proposed Statutory Rules for the Schulze Single-Winner Election Method by Markus Schulze
- A New Monotonic and Clone-Independent Single-Winner Election Method by Markus Schulze (mirrors: [66] [67])
- A New Monotonic, Clone-Independent, Reversal Symmetric, and Condorcet-Consistent Single-Winner Election Method by Markus Schulze
- Free Riding and Vote Management under Proportional Representation by the Single Transferable Vote by Markus Schulze
- Implementing the Schulze STV Method by Markus Schulze
- A New MMP Method by Markus Schulze
- A New MMP Method (Part 2) by Markus Schulze
Tutorials
Advocacy
- Election Methods Resource by Blake Cretney
- Voting Methods Survey by James Green-Armytage
- Descriptions of ranked-ballot voting methods by Rob LeGrand
- Accurate Democracy by Rob Loring
- Schulze beatpaths method by Warren D. Smith
- Election Methods and Criteria by Kevin Venzke
- The Debian Voting System by Jochen Voss
- election-methods: a mailing list containing technical discussions about election methods
Research papers
- Social Choice Under Incomplete, Cyclic Preferences by Jobst Heitzig
- Voting Systems by Paul E. Johnson
- Distance from Consensus: a Theme and Variations by Tommi Meskanen and Hannu Nurmi
- Analyzing Political Disagreement by Tommi Meskanen and Hannu Nurmi
- Descriptions of voting systems by Warren D. Smith
- Election Systems by Peter A. Taylor
- Personalisierung der Verhältniswahl durch Varianten der Single Transferable Vote Template:De icon by Martin Wilke
- Approaches to Constructing a Stratified Merged Knowledge Base by Anbu Yue, Weiru Liu, and Anthony Hunter
Books
- Understanding Modern Mathematics by Saul Stahl and Paul E. Johnson (ISBN 0-7637-3401-2)
- Collective Decisions and Voting: The Potential for Public Choice [68] by Nicolaus Tideman (ISBN 0-7546-4717-X)
Software
- Voting Software Project by Blake Cretney
- Condorcet with Dual Dropping Perl Scripts by Mathew Goldstein
- Condorcet Voting Calculator by Eric Gorr
- Selectricity and RubyVote by Benjamin Mako Hill
- Java implementation of the Schulze method by Thomas Hirsch
- Electowidget by Rob Lanphier
- Haskell Condorcet Module by Evan Martin
- Condorcet Internet Voting Service (CIVS) by Andrew Myers
- BetterPolls.com by Brian Olson