Laws of Form: Difference between revisions
→References: revise annotation for Meguire (2003) |
→The form (Chapter 1): typographical repairs; add links |
||
| Line 29: | Line 29: | ||
:[[Image:Laws of Form - cross.gif]] |
:[[Image:Laws of Form - cross.gif]] |
||
also called the '''''mark''''' or '''''cross''''', is the |
also called the '''''mark''''' or '''''cross''''', is the essential feature of the Laws of [[Form]]. In Spencer-Brown's inimitable and enigmatic fashion, the Mark symbolizes the root of [[cognition]], i.e., the [[dualism|dualistic]] Mark indicates the [[capability]] of differentiating a "this" from "everything else ''but'' this." |
||
In ''LoF'', a Cross denotes the drawing of a "distinction", and can be thought of as signifying the following, all at once: |
In ''LoF'', a Cross denotes the drawing of a "distinction", and can be thought of as signifying the following, all at once: |
||
| Line 37: | Line 37: | ||
All three ways imply an ''action'' on the part of the cognitive entity (e.g., person) making the distinction. As ''LoF'' puts it: |
All three ways imply an ''action'' on the part of the cognitive entity (e.g., person) making the distinction. As ''LoF'' puts it: |
||
<blockquote>"The first command: |
<blockquote> |
||
"The first command: |
|||
* Draw a distinction |
* Draw a distinction |
||
can well be expressed in such ways as: |
can well be expressed in such ways as: |
||
| Line 46: | Line 47: | ||
* Define a distinction, |
* Define a distinction, |
||
Or: |
Or: |
||
* Let a distinction be drawn." (''LoF'', Notes to chapter 2)</blockquote> |
* Let a distinction be drawn." (''LoF'', Notes to chapter 2) |
||
</blockquote> |
|||
The counterpoint to the Marked state is the Unmarked state, which is simply nothing, the void, represented by a blank space. It is simply the absence of a Cross. No distinction has been made and nothing has been crossed. The Marked state and the void are the two primitive values of the Laws of Form. |
The counterpoint to the Marked state is the Unmarked state, which is simply nothing, the void, represented by a blank space. It is simply the absence of a Cross. No distinction has been made and nothing has been crossed. The Marked state and the void are the two primitive values of the Laws of Form. |
||
The Cross can be seen as denoting the distinction between two states, one "considered as a symbol" and another not so considered. From this fact arises a curious resonance with some theories of consciousness and language. Paradoxically, the Form is at once Observer and Observed, and is also the creative act of making an observation. ''LoF'' (excluding back matter) closes with the words: |
The Cross can be seen as denoting the distinction between two states, one "considered as a symbol" and another not so considered. From this fact arises a curious resonance with some theories of [[consciousness]] and [[language]]. Paradoxically, the Form is at once Observer and Observed, and is also the creative act of making an observation. ''LoF'' (excluding back matter) closes with the words: |
||
"...the first distinction, the Mark and the observer are not only interchangeable, but, in the form, identical." |
"...the first distinction, the Mark and the observer are not only interchangeable, but, in the form, identical." |
||
[[Charles Peirce]] came to a related insight in the 1890s; see Related Work |
[[Charles Peirce]] came to a related insight in the 1890s; see [[#Related Work|Related Work]]. |
||
==The primary arithmetic (Chapter 4)== |
==The primary arithmetic (Chapter 4)== |
||
Revision as of 05:29, 6 November 2007
Laws of Form (hereinafter LoF) is a book by G. Spencer Brown, published in 1969, that straddles the boundary between mathematics and of philosophy. LoF describes three distinct logical systems:
- The primary arithmetic (described in Chapter 4), whose models include Boolean arithmetic;
- The primary algebra (Chapter 6), whose models include two-element Boolean algebra (hereinafter abbreviated 2), Boolean logic, and the classical propositional calculus;
- Equations of the second degree (Chapter 11), whose interpretations include finite automata and Alonzo Church's Restricted Recursive Arithmetic (RRA).
Spencer-Brown referred to the mathematical system of Laws of Form as the "primary algebra" and the "calculus of indications"; others have termed it boundary algebra. "Laws of Form" may refer to LoF or to the primary algebra (hereinafter abbreviated pa).
The book
LoF emerged out of work in electronic engineering its author did around 1960, and from subsequent lectures on mathematical logic he gave under the auspices of the University of London's extension program. LoF has appeared in several editions, the most recent a 1997 German translation, and has never gone out of print.
The mathematics fills only about 55pp and is rather elementary. But LoF's mystical and declamatory prose, and its love of paradox, make it a challenging read for all. Spencer-Brown was influenced by Wittgenstein and R. D. Laing. LoF also echoes a number of themes from the writings of Charles Peirce, Bertrand Russell, and Alfred North Whitehead.
Reception
Ostensibly a work of formal mathematics and philosophy, LoF became something of a cult classic, praised in the Whole Earth Catalog. Those who agree point to LoF as embodying an enigmatic "mathematics of consciousness," its algebraic symbolism capturing an (perhaps even the) implicit root of cognition: the ability to distinguish. LoF argues that the pa reveals striking connections among logic, Boolean algebra, and arithmetic, and the philosophy of language and mind.
Some, e.g. Banaschewski (1977), argue that the pa is nothing but new notation for Boolean algebra. It is true that 2 can be seen as the intended interpretation of the pa. Nevertheless, Meguire (2005) counters that pa notation:
- Fully exploits the duality characterizing not just Boolean algebras but all lattices;
- Highlights how syntactically distinct statements in logic and 2 can have identical semantics;
- Dramatically simplifies Boolean algebra calculations, and proofs in sentential and syllogistic logic.
Moreover, the syntax of the pa can be extended to formal systems other than 2 and sentential logic, resulting in boundary mathematics (see Related Work below).
LoF has influenced, among others, Heinz von Foerster, Louis Kauffman, Niklas Luhmann, Humberto Maturana, Francisco Varela and William Bricken. Some of these authors modified the primary algebra in a variety of interesting ways.
LoF claimed that certain well-known mathematical conjectures of very long standing, such as the Four Color Theorem, Fermat's Last Theorem, and the Goldbach conjecture, are provable using extensions of the pa. Spencer-Brown eventually circulated a purported proof of the Four Color Theorem[1]. The proof met with skepticism and Spencer-Brown's mathematical reputation, as well as that of LoF, went into decline. (The Four Color Theorem and Fermat's Last Theorem were proved in 1976 and 1995, respectively, using methods owing nothing to LoF.)
The form (Chapter 1)
The symbol:
also called the mark or cross, is the essential feature of the Laws of Form. In Spencer-Brown's inimitable and enigmatic fashion, the Mark symbolizes the root of cognition, i.e., the dualistic Mark indicates the capability of differentiating a "this" from "everything else but this."
In LoF, a Cross denotes the drawing of a "distinction", and can be thought of as signifying the following, all at once:
- The act of drawing a boundary around something, thus separating it from everything else;
- That which becomes distinct from everything by drawing the boundary;
- Crossing from one side of the boundary to the other.
All three ways imply an action on the part of the cognitive entity (e.g., person) making the distinction. As LoF puts it:
"The first command:
- Draw a distinction
can well be expressed in such ways as:
- Let there be a distinction,
- Find a distinction,
- See a distinction,
- Describe a distinction,
- Define a distinction,
Or:
- Let a distinction be drawn." (LoF, Notes to chapter 2)
The counterpoint to the Marked state is the Unmarked state, which is simply nothing, the void, represented by a blank space. It is simply the absence of a Cross. No distinction has been made and nothing has been crossed. The Marked state and the void are the two primitive values of the Laws of Form.
The Cross can be seen as denoting the distinction between two states, one "considered as a symbol" and another not so considered. From this fact arises a curious resonance with some theories of consciousness and language. Paradoxically, the Form is at once Observer and Observed, and is also the creative act of making an observation. LoF (excluding back matter) closes with the words:
"...the first distinction, the Mark and the observer are not only interchangeable, but, in the form, identical."
Charles Peirce came to a related insight in the 1890s; see Related Work.
The primary arithmetic (Chapter 4)
LoF often uses the phrase calculus of indications in place of "primary arithmetic".
Begin with the void. Then posit two inductive rules:
- Given any expression, a Cross can be written over it;
- Any two expressions can be concatenated.
Thus the syntax of the primary arithmetic. The semantics of the primary arithmetic are established by the only explicit definition in LoF: Distinction is perfect continence.
The primary arithmetic (and all of the Laws of Form) are grounded in a mere two axioms, A1 and A2.
A1. The law of Calling. To make a distinction twice has the same effect as making it once. For instance, if you say "Let there be light." and then you say "Let there be light." again, it is the same as saying it once. Crossing twice from the unmarked state cannot be distinguished from crossing once. Symbolically:
A2. The law of Crossing. Crossing from the unmarked state takes you to the marked state; crossing again from that marked state takes you back to the unmarked state. To recross is not to cross. Symbolically:
Applying A1 and A2 repeatedly can reduce any expression consisting solely of Crosses to the expression's simplification, either the marked or the unmarked state. The fundamental metatheorem of the primary arithmetic (T3-4 in LoF) states that:
- An expression has a unique simplification;
- The repeated application of A1 and A2 to either the marked or the unmarked state cannot yield an expression whose simplification differs from the initial state.
Hence the relation of logical equivalence partitions all primary arithmetic formulas into two equivalence classes: those that simplify to the Cross, and those that simplify to the void.
A1 and A2 have loose analogs in the properties of series and parallel electrical circuits, and in other ways of diagramming processes, including flowcharting. A1 corresponds to a parallel connection, and A2 to a series connection, with the understanding that making a distinction corresponds to changing how two points in a circuit are connected, and not simply to adding wiring.
More formally, the primary arithmetic is a Dyck language of order 1 with a null alphabet, and the simplest instance of a context-free language in the Chomsky hierarchy.
The notion of 'canon'
The notion of a canon is discussed in the following two excerpts from the Notes to Chapter 2 of LoF:
"The more important structures of command are sometimes called canons. They are the ways in which the guiding injunctions appear to group themselves in constellations, and are thus by no means independent of each other. A canon bears the distinction of being outside (i.e., describing) the system under construction, but a command to construct (e.g., 'draw a distinction'), even though it may be of central importance, is not a canon. A canon is an order, or set of orders, to permit or allow, but not to construct or create."
"...the primary form of mathematical communication is not description but injunction... Music is a similar art form, the composer does not even attempt to describe the set of sounds he has in mind, much less the set of feelings occasioned through them, but writes down a set of commands which, if they are obeyed by the performer, can result in a reproduction, to the listener, of the composer's original experience."
These quotes relate to the distinction in metalogic between the object language, the formal language of the logical system under discussion, and the metalanguage, a language (often a natural language) distinct from the object language, employed to discuss the object language. The first quote seems to assert that the canons are part of the metalanguage. The second quote seems to assert that statements in the object language are essentially commands addressed to the reader by the author. Neither assertion holds in standard metalogic.
The primary algebra (Chapter 6)
The primary algebra is an elegant minimalist notation for the two-element Boolean algebra, very similar to the entitative and existential graphs, and other formal systems Charles Peirce devised in work written 1885-1905. However, Peirce's work that most resembles the pa was not published until after the first edition of Laws of Form.
Syntax
Given any valid primary arithmetic expression, insert into one or more locations any number of Latin letters, with or without numerical subscripts; the result is a pa formula. Letters so employed in mathematics and logic are called variables. A pa variable indicates a location where one can write the primitive value ![]() or its complement
or its complement ![]() . Multiple instances of the same variable indicate multiple locations of the same primitive value. In Boolean algebras, the set of primitive values {
. Multiple instances of the same variable indicate multiple locations of the same primitive value. In Boolean algebras, the set of primitive values {![]() ,
,![]() } is called the carrier.
} is called the carrier.
Rules governing logical equivalence
The sign '=' denotes that what appears to the left and right of = are logically equivalent, i.e., have the same simplification. An expression of the form "A=B" is an equation, meaning that A and B are logically equivalent. Logical equivalence is an equivalence relation over the set of pa formulas, governed by the rules R1 and R2. Let C and D be formulae containing at least one instance of the subformula A:
- R1, Substitution of equals. Replace one or more instances of A in C by B, resulting in E. If A=B, then C=E.
- R2, Uniform replacement. Replace all instances of A in C and D with B. A becomes E and B becomes F. If C=D, then E=F. Note that A=B is not required.
R2 is employed very frequently in pa demonstrations (see below), almost always silently. These rules are routinely yet unwittingly invoked in logic and most of mathematics.
The pa consists of equations, i.e., pairs of formulae linked by an equivalence relation denoted by an infix '='. R1 and R2 enable transforming one equation into another. Hence the pa is an equational formal system, like the many algebraic structures, including Boolean algebra, that are varieties. Mathematical logic consists of tautological formulae, signalled by a prefixed turnstile. Conventional logic adds to variants of R1 and R2 the rule modus ponens; thus conventional logic is ponential. The equational-ponential dichotomy summarizes much of what distinguishes mathematical logic from the rest of mathematics. To indicate that the pa formula A is a tautology, simply write "A =![]() ".
".
Equational logic was common before Principia Mathematica (e.g., Peirce,1,2,3 Johnson 1892), and has present-day advocates (Gries and Schneider 1993).
Initials
An initial is a pa equation verifiable by a decision procedure and as such is not an axiom. LoF lays down the initials:
The absence of anything to the right of the "=" above, is deliberate.
J2 is the familiar distributive law of sentential logic and Boolean algebra.
Another set of initials, friendlier to calculations, is:
It is thanks to C2 that the pa is a lattice. By virtue of J0, it is a complemented lattice whose upper bound and inverse element is (). By J1a, (()) is the corresponding lower bound and identity element. J1a is also an algebraic version of A2 and makes clear the sense in which (()) aliases with the blank page.
T13 in LoF generalizes C2 as follows. Any pa (or sentential logic) formula B can be viewed as an ordered tree with branches. Then:
T13: A subformula A can be copied at will into any depth of B greater than that of A, as long as A and its copy are in the same branch of B. Also, given multiple instances of A in the same branch of B, all instances but the shallowest are redundant.
While a proof of T13 would require induction, the intuition underlying it should be clear.
C2 or its equivalent is named:
- "Generation" in LoF;
- "Exclusion" in Johnson (1892);
- "Pervasion" in the work of William Bricken;
- "Mimesis" in the entry logical nand.
Charles Peirce's existential graphs was perhaps the first formal system to appreciate the power of C2. His Rule of (De)Iteration combined T13 and AA=A.
LoF asserts that concatenation can be read as commuting and associating by default and hence need not be explicitly assumed or demonstrated. (Peirce made a similar assumption in his graphical logic.) Let a period denote grouping. That concatenation commutes and associates may then be demonstrated from the:
- Initial AB.C=BC.A and the consequence AA=A (Byrne 1946). This result holds for all lattices, because AA=A is an easy consequence of the absorption law, which holds for all lattices;
- Initials AB.C=AC.B and J1a. Since J1a holds only for lattices with a lower bound, this method holds only for bounded lattices (which include the pa and 2). Commutativity is trivial; just set A=(()). Associativity: AB.C = BA.C = BC.A = A.BC.
Now that associativity is demonstrated, the period is no longer required.
Proof theory
The pa contains three kinds of proved assertions:
- Consequence is a pa equation verified by a demonstration. A demonstration consists of a sequence of steps, each step justified by an initial or a previously demonstrated consequence.
- Theorem is a statement in the metalanguage verified by a proof, i.e., an argument, formulated in the metalanguage, that is accepted by trained mathematicians and logicians.
- Initial, defined above. Demonstrations and proofs invoke an initial as if it were an axiom.
The distinction between consequence and theorem holds for all formal systems, including mathematics and logic, but is usually not made explicit. A demonstration or decision procedure can be carried out and verified by computer. The proof of a theorem cannot be.
Let A and B be pa formulas. A demonstration of A=B may proceed in either of two ways:
- Modify A in steps until B is obtained, or vice versa;
- Simplify both (A)B and (B)A to
 . This is known as a "calculation".
. This is known as a "calculation".
Once A=B has been demonstrated, A=B can be invoked to justify steps in subsequent demonstrations. pa demonstrations and calculations often require no more than J0, J1, J2, C2, and the consequences ()A=(), ((A))=A, and AA=A (in LoF, C3, C1, and C5, respectively).
The consequence (((A)B)C) = (AC)((B)C), C7 in LoF, enables an algorithm, sketched in LoFs proof of T14, that transforms an arbitrary pa formula to an equivalent formula whose depth does not exceed two. The result is a normal form, the pa analog of the conjunctive normal form. LoF (T14-15) proves the pa analog of the well-known Boolean algebra theorem that every formula has a normal form.
Let A be a subformula of some formula B. When paired with C3, J0 can be viewed as the closure condition for calculations: B is a tautology if and only if A and (A) both appear in depth 0 of B. A related condition appears in some versions of natural deduction. A demonstration by calculation is often little more than:
- Invoking T13 repeatedly to eliminate redundant subformulae;
- Erasing any subformulae having the form ((A)A).
The last step of a calculation always invokes J0.
LoF includes elegant new proofs of the following standard metatheory:
- Completeness: all pa consequences are demonstrable from the initials (T17).
- Independence: J1 cannot be demonstrated from J2 and vice versa (T18).
That sentential logic is complete is taught in every first university course in mathematical logic. But university courses in Boolean algebra seldom mention the completeness of 2.
Interpretations
The Marked and Unmarked states can be read as the Boolean values 1 and 0, or as True and False. The first reading transforms the pa into a notation for 2; the second into a notation for sentential logic. Extending the pa so that it would have standard first-order logic as a model has yet to be done, but Peirce's beta existential graphs suggest that the extension should be straightforward.
Two-element Boolean algebra 2
Let Boolean:
- Meet or join interpret AB;
- The complement of A interpret
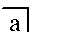 ;
; - 0 or 1 interpret the empty Mark.
If meet interprets AB, then join interprets ~(~A+~B), or vice versa. Hence the pa and 2 are isomorphic, and2 emerges as a model of the primary algebra. The primary arithmetic suggests that 2 can be axiomatized arithmetically by 1+1=1+0=0+1=1=~0, and 0+0=0=~1.
In the language of universal algebra, the pa is the algebraic structure 〈B,--,(-),()〉 of type 〈2,1,0〉, whose identities are J0, J1a, C2, and ABC=BCA. Since the pa and 2 are isomorphic (except that pa complementation can be nullary), 2 can be seen as a 〈B,∪,~,1〉 algebra of type 〈2,1,0〉. This description of 2 is simpler than the conventional one, 〈{0,1},∪,∩.~,1,0〉 of type 〈2,2,1,0,0〉. The expressive adequacy of the Sheffer stroke points to the pa also being a 〈B,(--),()〉 algebra of type 〈2,0〉.
In sum, the pa is an elegant minimalist notation for the two-element Boolean algebra.
Propositional calculus
Let the blank page denote True or False, and let a Cross be read as Not. Then the primary arithmetic has the following sentential reading:
- = False
The pa interprets sentential logic as follows. A letter represents any given sentential expression. Thus:
- and both interpret (A if and only if B).
Thus any expression in sentential logic has a pa translation. Given an assignment of every variable to the Marked or Unmarked states, this pa translation reduces to a primary arithmetic expression, which can be simplified. Repeating this exercise for all possible assignments of the two primitive values to each variable, reveals whether the original expression is tautological or satisfiable. This is an example of a decision procedure, one more or less in the spirit of conventional truth tables. Meguire (2003) sets out a less tedious decision procedure for the pa, more in the spirit of Quine's "truth value analysis".
The interpretations above assume that the Unmarked State is read as False. This reading is wholly arbitrary; the Unmarked state can equally well denote True. All that is required is that the interpretation of concatenation change from OR to AND. IF A THEN B now translates as (A(B)) instead of (A)B. More generally, the pa is "self-dual," meaning that any pa formula has two sentential or Boolean readings, each the dual of the other.
The true nature of the distinction between the pa on the one hand, and 2 and sentential logic on the other, now emerges. In the latter formalisms, complementation/negation with an empty scope is not defined. In the pa, a Cross, interpretable as complementation/negation, with nothing under itself denotes the Marked state, a primitive value. Thus the pa reveals that the heretofore distinct mathematical concepts of operator and operand are in fact merely different facets of a single fundamental action, the making of a distinction.
Syllogism
Appendix 2 of LoF shows how to translate traditional syllogisms and sorites (and hence term and monadic logic, although this is not made explicit) into the pa. A valid syllogism is simply one whose pa translation simplifies to an empty Cross. Let A* denote a literal, i.e., either A or (A), indifferently. It can then be shown that all syllogisms not requiring that some terms be assumed nonempty are one of 24 permutations of a generalization of Barbara, the form (A*B)((B)C*)A*C*. This suggests that monadic logic is also a model of the pa, and that the pa has affinities to the Boolean term schemata of Quine's Methods of Logic.
An example of calculation
The following calculation of Leibniz's nontrivial Praeclarum Theorema exemplifies the demonstrative power of the pa. Let C1 be ((A))=A, and let OI mean that variables and subformulae have been reordered in a way that commutativity and associativity permit. Because the only symmetric connective appearing in the Theorema is conjunction, it is simpler to translate the Theorema into the pa using the dual interpretation. The objective then becomes one of simplifying that translation to (()).
- [(P→R)∧(Q→S)]→[(P∧Q)→(R∧S)] Theorema
- ((P(R))(Q(S))((PQ(RS)))) pa translation
- = ((P(R))P(Q(S))Q(RS)) OI; C1
- = (((R))((S))PQ(RS) C2,2x (C2 eliminates the bold letters in the previous expression); OI
- = (RSPQ(RS)) C1,2x
- = ((RSPQ)RSPQ) C2; OI
- = (()) J1.
Remarks
- C1 and C2 are repeatedly invoked in a fairly mechanical way to eliminate boundaries and variables, respectively. This is typical of calculations;
- A single invocation of J1 (or, in other contexts, J0) terminates the calculation. This too is typical;
- Experienced users of the pa are free to invoke OI silently. OI aside, the demonstration requires a mere 7 steps.
A technical aside
Given some standard notions from mathematical logic and some suggestions in Bostock (1997: 83, fn 11, 12), {} and {{}} may be interpreted as the classical bivalent truth values. Let the extension of an n-place atomic formula be the set of ordered n-tuples of individuals that satisfy it (i.e., for which it comes out true). Let a sentential variable be a 0-place atomic formula, whose extension is a classical truth value, by definition. An ordered 2-tuple is an ordered pair, whose standard set theoretic definition is <a,b> = {{a},{a,b}}, where a,b are individuals. Ordered n-tuples for any n>2 may be obtained from ordered pairs by a well-known recursive construction. Dana Scott has remarked that the extension of a sentential variable can also be seen as the empty ordered pair (ordered 0-tuple), {{},{}} = {{}} because {a,a}={a} for all a. Hence {{}} has the interpretation True. Reading {} as False follows naturally.
Relation to groupoids
The pa can be seen as the logical endpoint of a point noted by Huntington in 1933: Boolean algebra requires two, not three, operations, one binary and one unary. Hence the seldom-noted fact that Boolean algebras are magmas (a.k.a. groupoids). To see this, note that the pa is a commutative:
- Semigroup because pa juxtaposition commutes and associates;
- Monoid with identity element (()), by virtue of J1a.
Groups also require a unary operation, called inverse, whose inverse element is at once the inverse of, and equal to, the identity element. Complementation is the pa unary operation corresponding to group inverse. By J0, the pa inverse element is (). Groups and the pa have signatures of the same form, namely they both are ⟨--,(-),()⟩ algebras of type ⟨2,1,0⟩. Hence the pa is a boundary algebra.
The axioms and initials of the pa distinguish it from an abelian group in two ways:
- While the pa inverse element () and identity element (()) are mutual complements, as group theory requires, A2 rules out their being identical. This follows from B being an ordered set. If the pa were a group, one of (a)a=(()) or a()=a would have to be a pa consequence;
- C2 demarcates the pa from other magmas, because C2 enables demonstrating the defining lattice (order)?lattice property, the absorption law, and the distributive law central to Boolean algebra.
In boundary terms, the defining arithmetical fact of group theory is (())=(). The PA counterpart to that equation is ((()))=().
Equations of the second degree (Chapter 11)
Chapter 11 of LoF introduces equations of the second degree, composed of recursive formulae that can be seen as having "infinite" depth. Some recursive formulae simplify to the marked or unmarked state. Others "oscillate" indefinitely between the two states depending on whether a given depth is even or odd. Specifically, certain recursive formulae can be interpreted as oscillating between true and false over successive intervals of time, in which case a formula is deemed to have an "imaginary" truth value. Thus the flow of time may be introduced into the pa.
Turney (1986) shows how these recursive formulae can be interpreted via Alonzo Church's Restricted Recursive Arithmetic (RRA). Church introduced RRA in 1955 as an axiomatic formalization of finite automata. Turney (1986) presents a general method for translating equations of the second degree into Church's RRA, illustrating his method using the formulae E1, E2, and E4 in chapter 11 of LoF. This translation into RRA sheds light on the names Spencer-Brown gave to E1 and E4, namely "memory" and "counter". RRA thus formalizes and clarifies LoF 's notion of an imaginary truth value.
Resonances in religion, philosophy, and science
The mathematical and logical content of LoF is wholly consistent with a secular point of view. Nevertheless, LoF's "first distinction", and the Notes to its chapter 12, bring to mind the following landmarks in religious belief, and in philosophical and scientific reasoning, presented in rough historical order:
- Vedic, Hindu and Buddhist: Related ideas can be noted in the ancient Vedic Upanishads, which form the monastic foundations of Hinduism and later Buddhism. As stated in the Aitareya Upanishad ("The Microcosm of Man"), the Supreme Atman manifests itself as the objective Universe from one side, and as the subjective individual from the other side. In this process, things which are effects of God's creation become causes of our perceptions, by a reversal of the process. In the Svetasvatara Upanishad, the core concept of Vedicism and Monism is "Thou art That."
- Taoism, (Chinese Traditional Religion): "...The Tao that can be told is not the eternal Tao; The name that can be named is not the eternal name. The nameless is the beginning of heaven and earth..." (Tao Te Ching).
- Zoroastrianism: "This I ask Thee, tell me truly, Ahura. What artist made light and darkness?" (Gathas 44.5)
- Judaism (from the Tanakh, called Old Testament by Christians): "In the beginning when God created the heavens and the earth, the earth was a formless void... Then God said, 'Let there be light'; and there was light. ...God separated the light from the darkness. God called the light Day, and the darkness he called Night.
- "...And God said, 'Let there be a dome in the midst of the waters, and let it separate the waters from the waters.' So God made the dome and separated the waters that were under the dome from the waters that were above the dome.
- "...And God said, 'Let the waters under the sky be gathered together into one place, and let the dry land appear.' ...God called the dry land Earth, and the waters that were gathered together he called Seas.
- "...And God said, 'Let there be lights in the dome of the sky to separate the day from the night...' God made the two great lights... to separate the light from the darkness." (Genesis 1:1-18; Revised Standard Version, emphasis added).
- "And the whole earth was of one language, and of one speech." (Genesis 11:1; emphasis added).
- "I am; that is who I am." (Exodus 3:14)
- Confucianism: Confucius claimed that he sought "a unity all pervading" (Analects XV.3) and that there was "one single thread binding my way together." (Ana. IV.15). The Analects also contain the following remarkable passage on how the social, moral, and aesthetic orders are grounded in right language, grounded in turn in the ability to "rectify names," i.e., to make correct distinctions: "Zilu said, 'What would be master's priority?" The master replied, "Rectifying names! ...If names are not rectified then language will not flow. If language does not flow, then affairs cannot be completed. If affairs are not completed, ritual and music will not flourish. If ritual and music do not flourish, punishments and penalties will miss their mark. When punishments and penalties miss their mark, people lack the wherewithal to control hand and foot." (Ana. XIII.3)
- Heraclitus: Pre-socratic philosopher, credited with forming the idea of logos. "He who hears not me but the logos will say: All is one." Further: "I am as I am not."
- Parmenides: Argued that the every-day perception of reality of the physical world is mistaken, and that the reality of the world is 'One Being': an unchanging, ungenerated, indestructible whole.
- Plato: Logos is also a fundamental technical term in the Platonic worldview.
- Christianity: "In the Beginning was the Word, and the Word was with God, and the Word was God." (John 1:1). "Word" translates logos in the koine original. "If you do not believe that I am, you will die in your sins." (John 8:24). "The Father and I are one." (John 10:30). "That they all may be one; as thou, Father, art in me, and I in thee, that they may also be one in us: that the world may believe that thou has sent me." (John 17:21). (emphases added)
- Islamic philosophy distinguishes essence (Dhat) from attribute (Sifat), which are neither identical nor separate.
- Leibniz: "All creatures derive from God and from nothingness. Their self-being is of God, their nonbeing is of nothing. Numbers too show this in a wonderful way, and the essences of things are like numbers. No creature can be without nonbeing; otherwise it would be God... The only self-knowledge is to distinguish well between our self-being and our nonbeing... Within our selfbeing there lies an infinity, a footprint or reflection of the omniscience and omnipresence of God." ("On the True Theologia Mystica" in Loemker, Leroy, ed. and trans., 1969. Leibniz: Philosophical Papers and Letters. Reidel: 368.)
- Josiah Royce: "Without negation, there is no inference. Without inference, there is no order, in the strictly logical sense of the word. The fundamentally significant position of the idea of negation in determining and controlling our idea of the orderliness of both the natural and the spiritual order, becomes... as momentous as it is, in our ordinary popular views... neglected. ...negation appears as one of the most significant... ideas that lie at the base of all the exact sciences..."
- "When logically analyzed, order turns out to be... inconceivable and incomprehensible to us unless we had the idea which is expressed by the term 'negation'. Thus it is that negation, which is always also something intensely positive, not only aids us in giving order to life, and in finding order in the world, but logically determines the very essence of order." ("Order" in Hasting, J., ed., 1917. Encyclopedia of Religion and Ethics. Scribner's: 540. Reprinted in Robinson, D. S., ed., 1951, Royce's Logical Essays. Dubuque IA: Wm. C. Brown: 230-31.)
Returning to the Bible, the injunction "Let there be light" conveys:
- "… and there was light" — the light itself;
- "… called the light Day" — the manifestation of the light;
- "… morning and evening" — the boundaries of the light.
A Cross denotes a distinction made, and the absence of a Cross means that no distinction has been made. In the Biblical example, light is distinct from the void – the absence of light. The Cross and the Void are, of course, the two primitive values of the Laws of Form.
Related work
Lenzen (2004) reviews in English his extensive work in German showing that Gottfried Leibniz, in memoranda not published until the late 19th and early 20th centuries, invented Boolean logic. Leibniz's notation was isomorphic to that of LoF: concatenation interpreted as conjunction and "non-(X)" interpreted as the complement of X. Leibniz's pioneering role in algebraic logic was adumbrated by Clarence Irving Lewis (1918) and by Rescher (1954). But a full appreciation of Leibniz's accomplishment had to await Lenzen's work in the 1980s.
Charles Peirce (1839-1914) anticipated the pa in three veins of work:
- Two papers he wrote in 1886 proposed a logical algebra employing but one symbol, the streamer, nearly identical to the Cross of LoF. The semantics of the streamer are identical to those of the Cross, except that Peirce never wrote a streamer with nothing under it. An excerpt from one of these papers was published in 19761, but they were not published in full until 19932,3
- A closely related notation appears in an encyclopedia article he published in 1902, reprinted in vol. 4 of his Collected Papers, paragraphs 378-383.
- His alpha existential graphs are isomorphic to the pa (Kauffman 2001).
This work by Peirce was virtually unknown at the time when (1960s) and in the place where (UK) LoF was written. Ironically, LoF cites vol. 4 of Peirce's Collected Papers, where (paragraphs 347-529) the existential graphs are described in detail. Peirce's semiotics may yet shed light on the philosophical aspects of LoF.
The pa and Peirce's graphical logic are instances of boundary mathematics, i.e., mathematics done with boundary notation, one restricted to variables and brackets (enclosing devices). In particular, boundary notation is free of infix, prefix, or postfix operator symbols. The very well-known curly braces of set theory can be seen as a boundary notation.
Kauffman discusses another notation similar to that of LoF, that of a 1917 article by Jean Nicod, a disciple of Bertrand Russell's.
The work of Leibniz, Peirce, and Nicod is innocent of metatheory, as they wrote before Emil Post's landmark 1920 paper (which LoF cites), proving that sentential logic is complete, and before Hilbert and Lukasiewicz showed how to prove axiom independence using models.
That the world, and how humans perceive and interact with that world, has a rich Boolean structure has been noted by at least one orthodox logician, William Craig (1979).
Second-generation cognitive science emerged in the 1970s, after LoF was written. On cognitive science and its relevance to Boolean algebra, logic, and set theory, see:
- Lakoff, George (1987) Women, Fire, and Dangerous Things. University of Chicago Press. See index entries under "Image schema examples: container."
- Lakoff, George, and Rafael E. Núñez (2001) Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being. Basic Books.
Neither book cites LoF.
The biologists and cognitive scientists Humberto Maturana and his student Francisco Varela both discuss LoF in their writings, which identify "distinction" as the fundamental cognitive act. The Berkeley psychologist and cognitive scientist Eleanor Rosch has written extensively on the closely related notion of categorization.
The primary arithmetic and algebra is but one of several minimalist approaches to logic and the foundations of mathematics, or parts thereof. Other, and more powerful, minimalist approaches include:
- The lambda calculus;
- Combinatory logic with S and K as the sole primitive combinators;
- Mathematical logic done with merely three primitive notions: one connective, logical nand (whose pa translation is either (AB) or (A)(B) ), universal quantification, and primitive atomic formulae of one kind, set membership. Willard Quine employed this system in his 1951 Mathematical Logic.
Other formal systems with possible affinities to the Laws of Form are mereology and mereotopology.
Footnotes
- "Qualitative Logic", MS 736 (c. 1886) in Eisele, Carolyn, ed. 1976. The New Elements of Mathematics by Charles S. Peirce. Vol. 4, Mathematical Philosophy. (The Hague) Mouton: 101-15.
- "Qualitative Logic", MS 582 (1886) in Kloesel, Christian et al, eds., 1993. Writings of Charles S. Peirce: A Chronological Edition, Volume 5, 1884-1886. Indiana University Press: 323-71.
- "The Logic of Relatives: Qualitative and Quantitative", MS 584 (1886) in Kloesel, Christian et al, eds., 1993. Writings of Charles S. Peirce: A Chronological Edition, Volume 5, 1884-1886. Indiana University Press: 372-78.
References
- Editions of Laws of Form:
- 1969. London: Allen & Unwin, hardcover.
- 1972. Crown Publishers, hardcover: ISBN 0-517-52776-6
- 1973. Bantam Books, paperback. ISBN 0-553-07782-1
- 1979. E.P. Dutton, paperback. ISBN 0-525-47544-3
- 1994. Portland OR: Cognizer Company, paperback. ISBN 0-9639899-0-1
- 1997 German translation, titled Gesetze der Form. Lübeck: Bohmeier Verlag. ISBN 3-89094-321-7
- Bostock, David, 1997. Intermediate Logic. Oxford Univ. Press.
- Byrne, Lee, 1946, "Two Formulations of Boolean Algebra," Bulletin of the AMS : 268-71.
- Craig, William, 1979, "Boolean Logic and the Everyday Physical World," Proceedings and Addresses of the American Philosophical Association 52: 751-78.
- David Gries, and Schneider, F B, 1993. A Logical Approach to Discrete Math. Springer-Verlag.
- William Ernest Johnson, 1892, "The Logical Calculus," Mind 1 (n.s.): 3-30.
- Louis H. Kauffman, 2001, "The Mathematics of C.S. Peirce", Cybernetics and Human Knowing 8: 79-110.
- ------, 2006, "Reformulating the Map Color Theorem."
- ------, 2006a. "Laws of Form - An Exploration in Mathematics and Foundations." Book draft (hence big).
- Lenzen, Wolfgang, 2004, "Leibniz's Logic" in Gabbay, D., and Woods, J., eds., The Rise of Modern Logic: From Leibniz to Frege (Handbook of the History of Logic - Vol. 3). Amsterdam: Elsevier, 1-83.
- Meguire, P. G., 2003, "Discovering Boundary Algebra: A Simplified Notation for Boolean Algebra and the Truth Functors," International Journal of General Systems 32: 25-87. Revision. This paper is the source for much of the notation of this entry, in that it encloses in parentheses what LoF places under a cross. Steers clear of the more speculative aspects of LoF.
- Nicholas Rescher, 1954, "Leibniz's Interpretation of His Logical Calculi," Journal of Symbolic Logic 18: 1-13.
- Turney, P. D., 1986, "Laws of Form and Finite Automata," International Journal of General Systems 12: 307-18.
See also
- Two-element Boolean algebra
- Boolean algebras canonically defined
- Boolean logic
- List of Boolean algebra topics
- existential graph
- entitative graph
- Propositional calculus
- Zeroth order logic
External links
- Laws of Form web site.
- Spencer-Brown's talks at Esalen, 1973. Self-referential forms are introduced in the section entitled "Degree of Equations and the Theory of Types."
- Louis H. Kauffman, "Box Algebra, Boundary Mathematics, Logic, and Laws of Form."
- Kissel, Matthias, "A nonsystematic but easy to understand introduction to Laws of Form."
- Draw a distinction... The space of imagination based on Spencer-Brown.
- "Diagrammatic Logic of C.S. Peirce." Peirce's existential graphs may give further insights into LoF.
Trivia
- "Philosopher," the German "Lovecraftian" Death Metal Band, pay a musical tribute to G. Spencer-Brown's work on their EP Laws of Form.
- ^ For a sympathetic evaluation, see Kauffman (2001).










