Derivative

For other uses, see derivatives and differentiation in mathematical calculus.

For a non-technical overview of the subject, see Calculus.

The graph of a function, drawn in black, and a tangent line to that function, drawn in red. The slope of the tangent line equals the derivative of the function at the marked point.

In calculus, a branch of mathematics, the derivative is a measurement of how a function changes when the values of its inputs change. The derivative of a function at a chosen input value describes the behavior of the function near that input value. For a real-valued function of a single real variable, the derivative at a point equals the slope of the tangent line to the graph of the function at that point. In general, the derivative of a function at a point determines the best linear approximation to the function at that point.

The process of finding a derivative is called differentiation. The fundamental theorem of calculus states that differentiation is the reverse process to integration.

Differentiation has applications to all quantitative disciplines. In physics, the derivative of the displacement of a moving body with respect to time is the velocity of the body, and the derivative of velocity with respect to time is acceleration. Newton's second law of motion states that the derivative of the momentum of a body equals the force applied to the body. The reaction rate of a chemical reaction is a derivative. In operations research, derivatives determine the most efficient ways to transport materials and design factories. By applying game theory, differentiation can even provide best strategies for competing corporations.

Derivatives are frequently used to find the maxima and minima of a function. Equations involving derivatives are called differential equations and are fundamental in describing natural phenomena. Derivatives and their generalizations appear throughout mathematics, in fields such as complex analysis, functional analysis, differential geometry, and even abstract algebra.

Differentiation and the derivative

Differentiation is a method to compute the rate at which a quantity, y, changes with respect to the change in another quantity, x, upon which it is dependent. This rate of change is called the derivative of y with respect to x. In more precise language, the dependency of y on x means that y is a function of x. If x and y are real numbers, and if the graph of y is plotted against x, the derivative measures the slope of this graph at each point. This functional relationship is often denoted y = f(x), where f denotes the function.

The simplest case is when y is a linear function of x, meaning that the graph of y against x is a straight line. In this case, y = f(x) = m x + c, for real numbers m and c, and the slope m is given by

$m={{\mbox{change in }}y \over {\mbox{change in }}x}={\Delta y \over {\Delta x}}$

where the symbol Δ (The uppercase form of the Greek letter Delta) is an abbreviation for "change in". This formula is true because

y + Δy = f(x+ Δx) = m (x + Δx) + c = m x + c + m Δx = y + mΔx.

It follows that Δy = m Δx.

This gives an exact value for the slope of a straight line. If the function f is not a straight line, however, then the change in y divided by the change in x varies: differentiation is a method to find an exact value for this rate of change at any given value of x.

Figure 1. The tangent line at (x, f(x))

Figure 2. The secant to curve y= f(x) determined by points (x, f(x)) and (x+h, f(x+h)).

Figure 3. The tangent line as limit of secants.

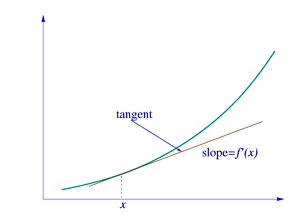
The idea, illustrated by Figures 1-3, is to compute the rate of change as the limiting value of the ratio of the differences Δy / Δx as Δx becomes infinitely small.

In Leibniz's notation, such an infinitesimal change in x is denoted by dx, and the derivative of y with respect to x is written

${\frac {dy}{dx}}\,\!$

suggesting the ratio of two infinitesimal quantities. (The above expression is pronounced in various ways such as "d y by d x" or "d y over d x". The oral form "d y d x" is often used conversationally, although it may lead to confusion.)

The most common approach to turn this intuitive idea into a precise definition uses limits, but there are other methods, such as non-standard analysis.

Definition via difference quotients

Let y=f(x) be a function of x. In classical geometry, the tangent line at a real number a was the unique line through the point (a, f(a)) which did not meet the graph of f transversally, meaning that the line did not pass straight through the graph. The derivative of y with respect to x at a is, geometrically, the slope of the tangent line to the graph of f at a. The slope of the tangent line is very close to the slope of the line through (a, f(a)) and a nearby point on the graph, for example (a + h, f(a + h)). These lines are called secant lines. A value of h close to zero will give a good approximation to the slope of the tangent line, and smaller values (in absolute value) of h will, in general, give better approximations. The slope of the secant line is the difference between the y values of these points divided by the difference between the x values, that is,

${\frac {f(a+h)-f(a)}{h}}.$

This expression is Newton's difference quotient. The derivative is the value of the difference quotient as the secant lines get closer and closer to the tangent line. Formally, the derivative of the function f at a is the limit

$f'(a)=\lim _{h\to 0}{f(a+h)-f(a) \over h}$

of the difference quotient as h approaches zero, if this limit exists. If the limit exists, then f is differentiable at a. Here f '(a) is one of several common notations for the derivative (see below).

Equivalently, the derivative satisfies the property that

$\lim _{h\to 0}{f(a+h)-f(a)-f'(a)\cdot h \over h}=0,$

which has the intuitive interpretation (see Figure 1) that the tangent line to f at a gives the best linear approximation

$f(a+h)\approx f(a)+f'(a)h$

to f near a (i.e., for small h). This interpretation is the most easy to generalize to other settings (see below).

Substituting 0 for h in the difference quotient causes division by zero, so the slope of the tangent line cannot be found directly. Instead, define Q(h) to be the difference quotient as a function of h:

$Q(h)={\frac {f(a+h)-f(a)}{h}}$.

Q(h) is the slope of the secant line between (a, f(a)) and (a + h, f(a + h)). If f is a continuous function, meaning that its graph is an unbroken curve with no gaps, then Q is a continuous function away from the point h = 0. If the limit $\textstyle \lim _{h\to 0}Q(h)$ exists, meaning that there is a way of choosing a value for Q(0) which makes the graph of Q a continuous function, then the function f is differentiable at the point a, and its derivative at a equals Q(0).

In practice, the continuity of the difference quotient Q(h) at h = 0 is shown by modifying the numerator to cancel h in the denominator. This process can be long and tedious for complicated functions, and many short cuts are commonly used to simplify the process.

Example

The squaring function f(x) = x² is differentiable at x = 3, and its derivative there is 6. This is proven by writing the difference quotient as follows:

${f(3+h)-f(3) \over h}={(3+h)^{2}-9 \over {h}}={9+6h+h^{2}-9 \over {h}}={6h+h^{2} \over {h}}=6+h.$

From the last expression, we see that the difference quotient equals 6 + h when h is not zero and is undefined when h is zero. (Remember that in the definition of the difference quotient, we divided by h, so the difference quotient is always undefined when h is zero.) However, there is a natural way of filling in a value for the difference quotient at zero, namely 6. Hence the slope of the graph the squaring function at the point (3, 9) is 6, and so its derivative at x = 3 is f '(3) = 6.

More generally, a similar computation shows that the derivative of the squaring function at x = a is f '(a) = 2a.

Continuity and differentiability

This function does not have a derivative at the marked point.

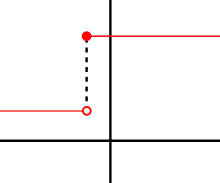
If y = f(x) is differentiable at a, then f must also be continuous at a. As an example, choose a point a and let f be the step function which takes a value, say 1, for all x less than a, and a different value, say 10, for all x greater than or equal to a. f cannot have a derivative at a. If h is negative, then a + h is on the low part of the step, so the secant line from a to a + h will be very steep, and as h tends to zero the slope tends to infinity. If h is positive, then a + h is on the high part of the step, so the secant line from a to a + h will have slope zero. Consequently the secant lines do not approach any single slope, so the limit of the difference quotient does not exist.

However, even if a function is continuous at a point, it may not be differentiable there. For example, the absolute value function y = |x| is continuous at x = 0, but it is not differentiable there. If h is positive, then the slope of the secant line from 0 to h is one, whereas if h is negative, then the slope of the secant line from 0 to h is negative one. This can be seen graphically as a "kink" in the graph at x = 0. Even a function with a smooth graph is not differentiable at a point where its tangent is vertical: For instance the function $y={\sqrt[{3}]{x}}$ is not differentiable at x = 0.

Most functions which occur in practice have derivatives at all points or at almost every point. However, a result of Stefan Banach states that the set of functions which have a derivative at some point is nowhere dense in the space of all continuous functions. Informally, this means that differentiable functions are very atypical among continuous functions. The first known example of a function that is continuous everywhere but differentiable nowhere is the Weierstrass function.

The derivative as a function

Let f be a function that has a derivative at every point a in the domain of f. Because every point a has a derivative, there is a function which sends the point a to the derivative of f at a. This function is written f'(x) and is called the derivative function or the derivative of f. The derivative of f collects all the derivatives of f at all the points in the domain of f.

Sometimes f has a derivative at most, but not all, points of its domain. The function whose value at a equals f'(a) whenever f'(a) is defined and is undefined elsewhere is also called the derivative of f. It is still a function, but its domain is strictly smaller than the domain of f.

Using this idea, differentiation becomes a function of functions: The derivative is an operator whose domain is the set of all functions which have derivatives at every point of their domain and whose range is a set of functions. If we denote this operator by D, then D(f) is the function f'(x). Since D(f) is a function, it can be evaluated at a point a. By the definition of the derivative function, D(f)(a) = f'(a).

For comparison, consider the doubling function f(x) =2x. f is a real-valued function of a real number, meaning that it takes numbers as inputs and has numbers as outputs:

$1\mapsto 2,$

$2\mapsto 4,$

$3\mapsto 6.$

The operator D, however, is not defined on individual numbers. It is only defined on functions:

$(x\mapsto 1)\mapsto (x\mapsto 0),$

$(x\mapsto x)\mapsto (x\mapsto 1),$

$(x\mapsto x^{2})\mapsto (x\mapsto 2x).$

Because the output of D is a function, the output of D can be evaluated at a point. For instance, when D is applied to the squaring function $x\mapsto x^{2}$, D outputs the doubling function f(x). f(x) can then be evaluated to get f(1) = 2, f(2) = 4, and so on.

Higher derivatives

Let f be a differentiable function, and let f'(x) be its derivative. f'(x) is a function, so it might have a derivative. If it does, then the derivative of f'(x) is written f''(x) and is called the second derivative of f. Similarly, the derivative of a second derivative, if it exists, is written f'''(x) and is called the third derivative of f. These repeated derivatives are called higher-order derivatives.

A function f need not have a derivative, for example, if it is not continuous. Similarly, even if f does have a derivative, it may not have a second derivative. For example, let

$f(x)={\begin{cases}x^{2},&{\mbox{if }}x\geq 0\\-x^{2},&{\mbox{if }}x\leq 0\end{cases}}$.

An elementary calculation shows that f is a differentiable function whose derivative is

$f'(x)={\begin{cases}2x,&{\mbox{if }}x\geq 0\\-2x,&{\mbox{if }}x\leq 0\end{cases}}$.

f'(x) is twice the absolute value function, and it does not have a derivative at zero. Similar examples show that a function can have k derivatives for any non-negative integer k but no (k + 1)-order derivative. A function that has k successive derivatives is called k times differentiable. If in addition the kth derivative is continuous, then the function is said to be of differentiability class C^k. (This is a stronger condition than having k derivatives. For an example, see differentiability class.) A function that has infinitely many derivatives is called infinitely differentiable or smooth.

On the real line, every polynomial function is infinitely differentiable. By standard differentiation rules, if a polynomial of degree n is differentiated n times, then it becomes a constant function. All of its subsequent derivatives are identically zero. In particular, they exist, so polynomials are smooth functions.

The derivatives of a function f at a point x provide polynomial approximations to that function near x. For example, if f is twice differentiable, then

$f(x+h)\approx f(x)+f'(x)h+{\tfrac {1}{2}}f''(x)h^{2}$

in the sense that

$\lim _{h\to 0}{\frac {f(x+h)-f(x)-f'(x)h-{\frac {1}{2}}f''(x)h^{2}}{h^{2}}}=0.$

If f is infinitely differentiable, then this is the beginning of the Taylor series for f.

Notations for differentiation

Main article: Notation for differentiation

Leibniz's notation

Main article: Leibniz's notation

The notation for derivatives introduced by Gottfried Leibniz is one of the earliest. It is still commonly used when the equation y=f(x) is viewed as a functional relationship between dependent and independent variables. Then the first derivative is denoted by

${\frac {dy}{dx}},\quad {\frac {d{\bigl (}f(x){\bigr )}}{dx}},\;\;\mathrm {or} \;\;{\frac {d}{dx}}{\bigl (}f(x){\bigr )}.$

Higher derivatives are expressed using the notation

${\frac {d^{n}y}{dx^{n}}},\quad {\frac {d^{n}{\bigl (}f(x){\bigr )}}{dx^{n}}},\;\;\mathrm {or} \;\;{\frac {d^{n}}{dx^{n}}}{\bigl (}f(x){\bigr )}$

for the nth derivative of y=f(x) (with respect to x).

With Leibniz's notation, we can write the derivative of y at the point x=a in two different ways:

${\frac {dy}{dx}}\left.{\!\!{\frac {}{}}}\right|_{x=a}={\frac {dy}{dx}}(a).$

Leibniz's notation allows one to specify the variable for differentiation (in the denominator). This is especially relevant for partial differentiation. It also makes the chain rule easy to remember:

${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}.$

Lagrange's notation

One of the most common modern notations for differentiation is due to Joseph Louis Lagrange and uses the prime mark, so that the derivative of a function $f(x)\,$ is denoted $f'(x)\,$ or simply $f'\,$. Similarly, the second and third derivatives are denoted $(f')'=f''\,$ and $((f')')'=f'''\,$. Beyond this point, some authors use Roman numerals such as $f^{IV}\,$ for the fourth derivative, whereas other authors place the number of derivatives in parentheses: $f^{(4)}\,$ in this case. The latter notation generalizes to yield the notation $f^{(n)}\,$ for the nth derivative of f.

Newton's notation

Main article: Newton's notation

Newton's notation for differentiation, also called the dot notation, places a dot over the function name to represent a derivative. If y = f(t), then ${\dot {y}}$ and denotes the first derivative of y with respect to t and ${\ddot {y}}$ denotes the second derivative. This notation is used almost exclusively for time derivatives, meaning that the independent variable of the function represents time. It is very common in physics and in mathematical disciplines connected with physics such as differential equations. While the notation becomes unmanageable for high-order derivatives, in practice only very few derivatives are needed.

Euler's notation

Euler's notation uses a differential operator D, which is applied to a function f to give the first derivative Df. The second derivative is denoted D²f, and the nth derivative is denoted Dⁿf.

If y=f(x) is a dependent variable, then often the subscript x is attached to the D to clarify the independent variable x. Euler's notation is then written $D_{x}y$ or $D_{x}f(x)$, although this subscript is often omitted when the variable x is understood, for instance when this is the only variable present in the expression.

Euler's notation is useful for stating and solving linear differential equations.

Computing the derivative

The derivative of a function can, in principle, be computed from the definition by considering the difference quotient, and computing its limit. For some examples, see Derivative (examples). In practice, once the derivatives of a few simple functions are known, the derivatives of other functions are more easily computed using rules for obtaining derivatives of more complicated functions from simpler ones.

Rules for finding the derivative

Main article: Differentiation rules

In many cases, complicated limit calculations by direct application of Newton's difference quotient can be avoided using differentiation rules. Some of the most basic rules are the following.

• Constant rule: if f(x) is constant, then

$f'=0\,$

• Linearity:

$(af+bg)'=af'+bg'\,$ for all functions f and g and all real numbers a and b.

• Product rule:

$(fg)'=f'g+fg'\,$ for all functions f and g.

• Chain rule: If $f(x)=h(g(x))$, then

$f'(x)=h'(g(x))g'(x)\,$.

Derivatives of elementary functions

Main article: Table of derivatives

In addition, the derivatives of some common functions are useful to know.

• Derivatives of powers: if $f(x)=x^{r}$, for some non-zero real number r, then

$f'(x)=rx^{r-1},$ wherever this function is defined.

For example, if r = 1/2, then f'(x) = (1/2)x^−1/2 is defined only for non-negative x. When r = 0, this rule recovers the constant rule.

• Exponential and logarithm functions:

${\frac {d}{dx}}\exp(x)=\exp(x).$

${\frac {d}{dx}}\ln(x)=1/x.$

• Trigonometric functions:

${\frac {d}{dx}}\sin(x)=\cos(x).$

${\frac {d}{dx}}\cos(x)=-\sin(x).$

Example computation

The derivative of

$f(x)=x^{4}+\sin(x^{2})-\ln(x)e^{x}+7\,$

is

${\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {d\left(x^{2}\right)}{dx}}\cos(x^{2})-{\frac {d\left(\ln {x}\right)}{dx}}e^{x}-\ln {x}{\frac {d\left(e^{x}\right)}{dx}}+0\\&=4x^{3}+2x\cos(x^{2})-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}$

Here the second term was computed using the chain rule and third using the product rule: the known derivatives of the elementary functions x², x⁴, sin(x), ln(x) and exp(x) = e^x were also used.

Derivatives in higher dimensions

See also: vector calculus and multivariable calculus

Derivatives of vector valued functions

A vector-valued function y(t) of a real variable is a function which sends real numbers to vectors in some vector space Rⁿ. A vector-valued function can be split up into its coordinate functions y₁(t), y₂(t), ..., y_n(t), meaning that y(t) = (y₁(t), ..., y_n(t)). This includes, for example, parametric curves in R² or R³. The coordinate functions are real valued functions, so the above definition of derivative applies to them. The derivative of y(t) is defined to be the vector, called the tangent vector, whose coordinates are the derivatives of the coordinate functions. That is, $\mathbf {y} '(t)=(y'_{1}(t),\ldots ,y'_{n}(t))$. Equivalently,

$\mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},$

if the limit exists. The subtraction in the numerator is subtraction of vectors, not scalars. If the derivative of y exists for every value of t, then y' is another vector valued function.

If e₁, ..., e_n is the standard basis for Rⁿ, then y(t) can also be written as y₁(t)e₁ + ... + y_n(t)e_n. If we assume that the derivative of a vector-valued function retains the linearity property, then the derivative of y(t) must be $y'_{1}(t)\mathbf {e} _{1}+\cdots +y'_{n}(t)\mathbf {e} _{n}$, because each of the basis vectors is a constant.

This generalization is useful, for example, if y(t) is the position vector of a particle at time t; then the derivative y'(t) is the velocity vector of the particle at time t.

Partial derivatives

Main article: Partial derivative

Suppose that f is a function that depends on more than one variable. For instance,

$f(x,y)=x^{2}+xy+y^{2}.$

f can be reinterpreted as a family of functions of one variable indexed by the other variables:

$f(x,y)=f_{x}(y)=x^{2}+xy+y^{2}.$

In other words, every value of x chooses a function, denoted f_x, which is a function of one real number. That is,

$x\mapsto f_{x},$

$f_{x}(y)=x^{2}+xy+y^{2}.$

Once a value of x is chosen, say a, then f(x,y) determines a function f_a which sends y to a² + ay + y²:

$f_{a}(y)=a^{2}+ay+y^{2}.$

In this expression, a is a constant, not a variable, so f_a is a function of only one real variable. Consequently the definition of the derivative for a function of one variable applies:

$f_{a}'(y)=a+2y.$

The above procedure can be performed for any choice of a. Assembling the derivatives together into a function gives a function which describes the variation of f in the y direction:

${\frac {\partial f}{\partial y}}(x,y)=x+2y.$

This is the partial derivative of f with respect to y. Here ∂ is a rounded d called the partial derivative symbol. To distinguish it from the letter d, ∂ is sometimes pronounced "der", "del", or "partial" instead of "dee".

In general, the partial derivative of a function f(x₁,...,x_n) in the direction x_i at the point (a₁,...,a_n) is defined to be:

${\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{n})}{h}}.$

In the above difference quotient, all the variables except x_i are held fixed. That choice of fixed values determines a function of one variable $f_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}(x_{i})=f(a_{1},\ldots ,a_{i-1},x_{i},a_{i+1},\ldots ,a_{n})$, and by definition,

${\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(a_{1},\ldots ,a_{n})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).$

In other words, the different choices of a index a family of one-variable functions just as in the example above. This expression also shows that the computation of partial derivatives reduces to the computation of one-variable derivatives.

An important example of a function of several variables is the case of a scalar-valued function f(x₁,...x_n) on a domain in Euclidean space Rⁿ (e.g., on R² or R³). In this case f has a partial derivative ∂f/∂x_j with respect to each variable x_j. At the point a, these partial derivatives define the vector

$\nabla f(a)=\left({\frac {\partial f}{\partial x_{1}}}(a),\ldots ,{\frac {\partial f}{\partial x_{n}}}(a)\right).$

This vector is called the gradient of f at a. If f is differentiable at every point in some domain, then the gradient is a vector-valued function ∇f which takes the point a to the vector ∇f(a). Consequently the gradient determines a vector field.

Directional derivatives

Main article: directional derivative

If f is a real-valued function on Rⁿ, then the partial derivatives of f measure its variation in the direction of the coordinate axes. For instance, if f is a function of x and y, then its partial derivatives measure the variation in f in the x direction and the y direction. They do not, however, directly measure the variation of f in any other direction, such as along the diagonal line y = x. These are measured using directional derivatives. Choose a vector

$\mathbf {v} =(v_{1},\ldots ,v_{n}).$

The directional derivative of f in the direction of v at the point x is the limit

$D_{\mathbf {v} }{f}({\boldsymbol {x}})=\lim _{h\rightarrow 0}{\frac {f({\boldsymbol {x}}+h\mathbf {v} )-f({\boldsymbol {x}})}{h}}.$

Let λ be a scalar. The substitution of h/λ for h changes the λv direction's difference quotient into λ times the v direction's difference quotient. Consequently, the directional derivative in the λv direction is λ times the directional derivative in the v direction. Because of this, directional derivatives are often considered only for unit vectors v.

If all the partial derivatives of f exist and are continuous at x, then they determine the directional derivative of f in the direction v by the formula:

$D_{\mathbf {v} }{f}({\boldsymbol {x}})=\sum _{j=1}^{n}v_{j}{\frac {\partial f}{\partial x_{j}}}.$

This is a consequence of the definition of the total derivative. It follows that the directional derivative is linear in v.

The same definition also works when f is a function with values in R^m. In this case, the directional derivative is a vector in R^m.

The total derivative, the Jacobian, and the differential

Main article: total derivative

Suppose f is a function from a domain in Rⁿ to R^m (for instance a scalar or vector valued function on R³). Then f has components (f₁,f₂,...f_m). If the partial derivatives of all of these components exist (at a point x), they form an m by n matrix, called the Jacobian matrix J_x(f) of f (at x), whose (i,j) entry is the partial derivative

$(J_{\boldsymbol {x}}f)_{ij}={\frac {\partial f_{i}}{\partial x_{j}}}.$

Matrix multiplication by the Jacobian defines a linear map from Rⁿ to R^m sending a vector v=(v₁,... v_n) to the vector whose ith component is

$\sum _{j=1}^{n}(J_{\boldsymbol {x}}f)_{ij}v_{j}=\sum _{j=1}^{n}v_{j}{\frac {\partial f_{i}}{\partial x_{j}}}.$

As long as the partial derivatives are continuous, this vector is the directional derivative df_x(v). By the definition of the directional derivative, the linear map df_x has the property that

$\lim _{h\to 0}{\frac {f({\boldsymbol {x}}+h\mathbf {v} )-f({\boldsymbol {x}})-\mathrm {d} f_{\boldsymbol {x}}(\mathbf {v} )h}{h}}=0.$

The intuitive interpretation of this property is that df_x is the best linear approximation to f at x. If function which has a best linear approximation in this sense is said to differentiable at x, and df_x is called the total derivative or differential of f at x, and is the linear map whose matrix is the Jacobian matrix of partial derivatives.

This generalizes the characterization of the one-dimensional derivative as the best linear approximation: if f is a function from R to R, then the differential of f exists at x if and only if the derivative of f exists at x, and the matrix of df_x is the 1×1 matrix whose only entry is f '(x). This 1×1 matrix defines a (linear) function from R to R, sending h to f '(x)h and the linear approximation already discussed may be written

$f(x+h)\approx f(x)+{\mathrm {d} }f_{x}(h).\,$

History of differentiation

Main article: History of calculus

The concept of a derivative in the sense of a tangent line is a very old one, familiar to Greek geometers such as Euclid (c. 300 BCE), Archimedes (c. 287 BCE – 212 BCE) and Apollonius of Perga (c. 262 BCE – c. 190 BCE). Archimedes also introduced the use of infinitesimals, although these were primarily used to study areas and volumes rather than derivatives and tangents — see Archimedes' use of infinitesimals.

The use of infinitesimals to study rates of change can be found in Indian mathematics, perhaps as early as 500 CE, when the astronomer and mathematician Aryabhata (476 – 550) used infinitesimals to study the motion of the moon. The use of infinitesimals to compute rates of change was developed significantly by Bhaskara (1114-1185): indeed, it has been argued that many of the key notions of differential calculus can be found in his work.

The modern development of calculus is usually credited to Isaac Newton (1643 – 1727) and Gottfried Leibniz (1646 – 1716), who provided independent and unified approaches to differentiation and derivatives. The key insight, however, that earned them this credit, was the fundamental theorem of calculus relating differentiation and integration: this rendered obsolete most previous methods for computing areas and volumes, which had not been significantly extended since the time of Archimedes. For their ideas on derivatives, both Newton and Leibniz built on significant earlier work by mathematicians such as Isaac Barrow (1630 – 1677), René Descartes (1596 – 1650), Christiaan Huygens (1629 – 1695), Blaise Pascal (1623 – 1662) and John Wallis (1616 – 1703). In particular, Isaac Barrow is often credited with the early development of the derivative. Nevertheless, Newton and Leibniz remain key figures in the history of differentiation, not least because Newton was the first to apply differentiation to theoretical physics, while Leibniz systematically developed much of the notation still used today.

Since the 17th century many mathematicians have contributed to the theory of differentiation. In the 19th century, calculus was put on a much more rigorous footing by mathematicians such as Augustin Louis Cauchy (1789 – 1857), Bernhard Riemann (1826 – 1866), and Karl Weierstrass (1815 – 1897). It was also during this period that the differentiation was generalized to Euclidean space and the complex plane.

Applications of derivatives

Maxima, minima and critical points

If f is a differentiable function on R (or an open interval) and x is a local maximum or a local minimum of f, then the derivative of f at x is zero; points where f '(x) = 0 are called critical points or stationary points (and the value of f at x is called a critical value). (The definition of a critical point is sometimes extended to include points where the derivative does not exist.) Conversely, a critical point x of f can be analysed by considering the second derivative of f at x:

• if it is positive, x is a local minimum;
• if it is negative, x is a local maximum;
• if it is zero, then x could be a local minimum, a local maximum, or neither. (For example, f(x)=x³ has a critical point at x=0, but it has neither a maximum nor a minimum there.)

This is called the second derivative test. An alternative approach, called the first derivative test, involves considering the sign of the f ' on each side of the critical point.

Taking derivatives and solving for critical points is therefore often a simple way to find local minima or maxima, which can be useful in optimization. By the extreme value theorem, a continuous function on a closed interval must attain its minimum and maximum values at least once. If the function is differentiable, the minima and maxima can only occur at critical points or endpoints.

This also has applications in graph sketching: once the local minima and maxima of a differentiable function have been found, a rough plot of the graph can be obtained from the observation that it will be either increasing or decreasing between critical points.

In higher dimensions, a critical point of a scalar valued function is a point at which the gradient is zero. The second derivative test can still be used to analyse critical points by considering the eigenvalues of the Hessian matrix of second partial derivatives of the function at the critical point. If all of the eigenvalues are positive, then the point is a local minimum; if all are negative, it is a local maximum. If there are some positive and some negative eigenvalues, then the critical point is a saddle point, and if none of these cases hold (i.e., some of the eigenvalues are zero) then the test is inconclusive.

Physics

Calculus is of vital importance in physics: many physical processes are described by equations involving derivatives, called differential equations. Physics is particularly concerned with the way quantities change and evolve over time, and the concept of the "time derivative" — the rate of change over time — is essential for the precise definition of several important concepts. In particular, the time derivatives of an object's position are significant in Newtonian physics:

• velocity is the derivative (with respect to time) of an object's displacement (distance from the original position)
• acceleration is the derivative (with respect to time) of an object's velocity, that is, the second derivative (with respect to time) of an object's position.

For example, if an object's position on a line is given by

$x(t)=-16t^{2}+16t+32,\,\!$

then the object's velocity is

${\dot {x}}(t)=x'(t)=-32t+16,\,\!$

and the object's acceleration is

${\ddot {x}}(t)=x''(t)=-32,\,\!$

which is constant.

Generalizations

Main article: Derivative (generalizations)

The concept of a derivative can be extended to many other settings. The common thread is that the derivative of a function at a point serves as a linear approximation of the function at that point.

• An important generalization of the derivative concerns complex functions of complex variables, such as functions from (a domain in) the complex numbers C to C. The notion of the derivative of such a function is obtained by replacing real variables with complex variables in the definition. However, this innocent definition hides some very deep properties. If C is identified with R² by writing a complex number z as x + i y, then a differentiable function from C to C is certainly differentiable as a function from R² to R² (in the sense that its partial derivatives all exist), but the converse is not true in general: the complex derivative only exists if the real derivative is complex linear and this imposes relations between the partial derivatives called the Cauchy Riemann equations — see holomorphic functions.

• Another generalization concerns functions between differentiable or smooth manifolds. Intuitively speaking such a manifold M is a space which can be approximated near each point x by a vector space called its tangent space: the prototypical example is a smooth surface in R³. The derivative (or differential) of a (differentiable) map f: M → N between manifolds, at a point x in M, is then a linear map from the tangent space of M at x to the tangent space of N at f(x). The derivative function becomes a map between the tangent bundles of M and N. This definition is fundamental in differential geometry and has many uses — see pushforward (differential) and pullback (differential geometry).

• Differentiation can also be defined for maps between infinite dimensional vector spaces such as Banach spaces and Fréchet spaces. There is a generalization both of the directional derivative, called the Gâteaux derivative, and of the differential, called the Fréchet derivative.

• One deficiency of the classical derivative is that not very many functions are differentiable. Nevertheless, there is a way of extending the notion of the derivative so that all continuous functions and many other functions can be differentiated using a concept known as the weak derivative. The idea is to embed the continuous functions in a larger space called the space of distributions and only require that a function is differentiable "on average".

• The properties of the derivative have inspired the introduction and study of many similar objects in algebra and topology — see, for example, differential algebra.

See also

• Automatic differentiation
• Differentiability class
• Differintegral
• Linearization
• Numerical differentiation
• Techniques for differentiation

References

Print

• Anton, Howard; Bivens, Irl; Davis, Stephen (February 2, 2005), Calculus: Early Transcendentals Single and Multivariable (8th ed.), New York: Wiley, ISBN 978-0471472445
• Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra, vol. 1 (2nd ed.), Wiley, ISBN 978-0471000051
• Apostol, Tom M. (June 1969), Calculus, Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications, vol. 1 (2nd ed.), Wiley, ISBN 978-0471000075
• Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (6th ed.), Brooks Cole, ISBN 978-0030295584
• Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (4th ed.), Houghton Mifflin Company, ISBN 978-0618606245
• Spivak, Michael (September 1994), Calculus (3rd ed.), Publish or Perish, ISBN 978-0914098898
• Stewart, James (December 24, 2002), Calculus (5th ed.), Brooks Cole, ISBN 978-0534393397
• Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy (Revised, Updated, Expanded ed.), New York: St. Martin's Press, ISBN 978-0312185480

Online books

• Crowell, Benjamin (2003), Calculus
• Garrett, Paul (2004), Notes on First-Year Calculus
• Hussain, Faraz (2006), Understanding Calculus
• Keisler, H. Jerome (2000), Elementary Calculus: An Approach Using Infinitesimals
• Mauch, Sean (2004), Unabridged Version of Sean's Applied Math Book
• Sloughter, Dan (2000), Difference Equations to Differential Equations
• Stroyan, Keith D. (1997), A Brief Introduction to Infinitesimal Calculus
• Wikibooks, Calculus

External links

• WIMS Function Calculator makes online calculation of derivatives; this software also enables interactive exercises.

• ADIFF online symbolic derivatives calculator.

• Proving Derivatives from First Principles.