Polynomial

In mathematics, a polynomial is an expression that is constructed from one or more variables and constants, using only the operations of addition, subtraction, multiplication, and constant positive whole number exponents. For example, $x^{2}-4x+7\,$ is a polynomial, but $x^{2}-4/x+7x^{3/2}\,$ is not a polynomial because it involves division by a variable and also because it has an exponent that is not a positive whole number.

Polynomials are one of the most important concepts in algebra and throughout mathematics and science. To mention just a few of their many applications, polynomial equations are used to solve word problems, polynomial functions appear in basic chemistry and physics, in calculus polynomials are used to approximate other functions, in economics polynomials are used to describe financial transactions.

Overview

A polynomial is either 0, or the sum of one or more terms called monomials. These monomials consist of a non-zero constant (called the coefficient of the monomial) multiplied by zero or more variables (which are usually represented by letters). Each variable may have a constant positive whole number exponent. The exponent on a variable in a monomial is equal to the degree of that variable in that monomial. Since $x=x^{1}$ , the degree of a variable without a written exponent is one. A monomial with no variables is called a constant monomial, or just a constant. The degree of a constant monomial is 0. The coefficient of a monomial may be any number, including fractions, irrational numbers, and negative numbers.

For example,

-5x^{2}y\,

is a monomial. The coefficient is -5, the variables are x and y, the degree of x is two, and the degree of y is one.

The degree of the entire monomial is the sum of the degrees of each variable in it. In the example above, the degree is 2 + 1 = 3.

A polynomial is a sum of zero or more monomial terms. For example, the following is a polynomial:

3x^{2}-5x+4\,.

It consists of three monomials: the first is degree two, the second is degree one, and the third is degree zero. Here "

" stands for "

", so the coefficient of the middle monomial is −5.

When a polynomial is arranged in the traditional order, the terms of higher degree come before the terms of lower degree. In the first term, the coefficient is 3, the variable is x, and the exponent is two. In the second term, the coefficient is -5. The third term is a constant. The degree of a polynomial is the largest degree of any one term. In the example, the polynomial has degree two.

A polynomial of degree one is called linear, of degree two is called quadratic, and of degree three is called cubic. Less commonly used, degree four is called quartic and degree five quintic.

A polynomial with one term is called a monomial, two terms a binomial, and three terms a trinomial. The polynomial 0, which has zero terms, is called the zero polynomial.

A polynomial whose term of highest degree has a coefficient of 1 is called monic.

An expression that can be converted to polynomial form through a sequence of applications of the commutative, associative, and distributive laws is usually considered to be a polynomial.

For example

{\frac {x^{3}}{12}}

is considered a polynomial because it is equivalent to ${\tfrac {1}{12}}x^{3}$ . The coefficient is ${\tfrac {1}{12}}$ .

Division by an expression containing a variable is not generally allowed in polynomials.^[1] For example,

{1 \over x^{2}+1}\,

is not a polynomial because it includes division by a variable. Similarly,

(5+y)^{x},\,

is not a polynomial, because it has a variable exponent.

Since subtraction can be treated as addition of the additive opposite, and since exponentiation to a constant positive whole number power can be treated as repeated multiplication, polynomials can be constructed from constants and variables with just the two operations addition and multiplication.

A polynomial function is a function defined by evaluating a polynomial. For example, the function f defined by

f(x)=x^{3}-x\,

is a polynomial function. Polynomial functions are an important class of smooth functions.

A polynomial equation is an equation in which a polynomial is set equal to another polynomial.

3x^{2}+4x-5=0\,

is a polynomial equation.

Elementary properties of polynomials

A sum of polynomials is a polynomial
A product of polynomials is a polynomial
The derivative of a polynomial is a polynomial
A primitive or antiderivative of a polynomial is a polynomial

Polynomials serve to approximate other functions, such as sine, cosine, and exponential.

All polynomials have an expanded form, in which the distributive law has been used to remove all parentheses. All polynomials also have a factored form in which the polynomial is written as a product of linear polynomials. For example, the polynomial

x^{2}-2x-3\,

is the expanded form of the polynomial

(x-3)(x+1)\,

,

which is written in factored form. Note that the constants in the linear polynomials (like -3 and +1 in the above example) may be complex numbers in certain cases.

In school algebra, students learn to move easily from one form to the other (see: factoring).

Every polynomial in one variable is equivalent to a polynomial with the form

a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{2}x^{2}+a_{1}x+a_{0}

.

This form is sometimes taken as the definition of a polynomial in one variable.

Evaluation of a polynomial consists of assigning a number to each variable and carrying out the indicated multiplications and additions. Evaluation is sometimes performed more efficiently using the Horner scheme

((\ldots (a_{n}x+a_{n-1})x+...+a_{2})x+a_{1})x+a_{0}\,

.

In elementary algebra, methods are given for solving all first degree and second degree polynomial equations in one variable. In the case of polynomial equations, the variable is often called an unknown. The number of solutions may not exceed the degree, and will equal the degree when multiplicity of solutions and complex number solutions are counted. This fact is called the fundamental theorem of algebra.

A system of polynomial equations is a set of equations in which a given variable must take on the same value everywhere it appears in any of the equations. Systems of equations are usually grouped with a single open brace on the left. In elementary algebra, methods are given for solving a system of linear equations in several unknowns. To get a unique solution, the number of equations should equal the number of unknowns. If there are more unknowns than equations, the system is called underdetermined. If there are more equations than unknowns, the system is called overdetermined. This important subject is studied extensively in the area of mathematics known as linear algebra. Overdetermined systems are common in practical applications. For example, one U.S. mapping survey used computers to solve 2.5 million equations in 400,000 unknowns. ^[2]

More advanced examples of polynomials

In linear algebra, the characteristic polynomial of a square matrix encodes several important properties of the matrix.

In graph theory the chromatic polynomial of a graph encodes the different ways to vertex color the graph using x colors.

In abstract algebra, one may define polynomials with coefficients in any ring.

In knot theory the Alexander polynomial, the Jones polynomial, and the HOMFLY polynomial are important knot invariants.

History

Determining the roots of polynomials, or "solving algebraic equations", is among the oldest problems in mathematics. However, the elegant and practical notation we use today only developed beginning in the 15th century. Before that, equations are written out in words. For example, an algebra problem from the Chinese Arithmetic in Nine Sections, circa 200 BCE, begins "Three sheafs of good crop, two sheafs of mediocre crop, and one sheaf of bad crop are sold for 29 dou." We would write $3x+2y+z=29$ .

Notation

The earliest known use of the equal sign is in Robert Recorde's The Whetstone of Witte, 1557. The signs + for addition, − for subtraction, and the use of a letter for an unknown appear in Michael Stifel's Arithemetica integra, 1544. René Descartes, in La geometrie, 1637, introduced the concept of the graph of a polynomial equation. He also popularized the use of letters from the beginning of the alphabet to denote constants and letters from the end of the alphabet to denote variables, as can be seen above, in the general formula for a polynomial in one variable, where the a 's denote constants and x denotes a variable. Descartes introduced the use of superscripts to denote exponents as well. ^[3]

Solving polynomial equations

Every polynomial corresponds to a polynomial function, where f(x) is set equal to the polynomial, and to a polynomial equation, where the polynomial is set equal to zero. The solutions to the equation are called the roots of the polynomial and they are the zeroes of the function and the x-intercepts of its graph. If x = a is a root of a polynomial, then (x - a) is a factor of that polynomial.

Some polynomials, such as f(x) = x² + 1, do not have any roots among the real numbers. If, however, the set of allowed candidates is expanded to the complex numbers, every (non-constant) polynomial has at least one distinct root; this follows from the fundamental theorem of algebra.

There is a difference between approximating roots and finding exact roots. Formulas for the roots of polynomials up to a degree of 2 have been known since ancient times (see quadratic equation) and up to a degree of 4 since the 16th century (see Gerolamo Cardano, Niccolo Fontana Tartaglia). But formulas for degree 5 eluded researchers. In 1824, Niels Henrik Abel proved the striking result that there can be no general formula (involving only the arithmetical operations and radicals) for the roots of a polynomial of degree 5 or greater in terms of its coefficients (see Abel-Ruffini theorem). This result marked the start of Galois theory which engages in a detailed study of relationships among roots of polynomials.

Approximate solutions to any polynomial equation can be found either by Newton's method or by one of the many more modern methods of approximating solutions. For a polynomial in Chebyshev form the Clenshaw algorithm can be used. As a practical matter, an approximate solution that is accurate to a desired precision may be as useful as an exact solution.

The difference engine of Charles Babbage was designed to create large tables of approximate values of logarithms and trigonometric functions automatically, by evaluating approximating polynomials at many points using Newton's method.

Numerically solving a polynomial equation in one unknown is easily done on computer by the Durand-Kerner method or by some other root-finding algorithm. The reduction of equations in several unknowns to equations each in one unknown is discussed in the article on the Buchberger's algorithm. The special case where all the polynomials are of degree one is called a system of linear equations, for which a range of different solution methods exist, including the classical gaussian elimination.

It has been shown by Richard Birkeland and Karl Meyr that the roots of any polynomial may be expressed in terms of multivariate hypergeometric functions. Ferdinand von Lindemann and Hiroshi Umemura showed that the roots may also be expressed in terms of Siegel modular functions, generalizations of the theta functions that appear in the theory of elliptic functions. These characterizations of the roots of arbitrary polynomials are generalizations of the methods previously discovered to solve the quintic equation.

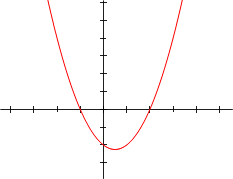
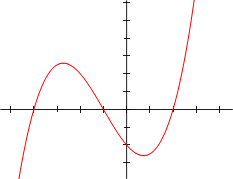
Graphs

A polynomial function in one real variable can be represented by a graph.

The graph of the zero polynomial

f(x) = 0

is the x-axis.

The graph of a degree 0 polynomial

f(x) = a₀ , where a₀ ≠ 0,

is a horizontal line with y-intercept a₀

The graph of a degree 1 polynomial (or linear function)

f(x) = a₀ + a₁x , where a₁ ≠ 0,

is an oblique line with y-intercept a₀ and slope a₁.

The graph of a degree 2 polynomial

f(x) = a₀ + a₁x + a₂x², where a₂ ≠ 0

is a parabola.

The graph of any polynomial with degree 2 or greater

f(x) = a₀ + a₁x + a₂x² + . . . + a_nxⁿ , where a_n ≠ 0 and n ≥ 2

is a continuous non-linear curve.

Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior.

The illustrations below show graphs of polynomials.

Polynomial of degree 2: f(x) = x² - x - 2 = (x+1)(x-2)	Polynomial of degree 3: f(x) = x³/5 + 4x²/5 - 7x/5 - 2 = 1/5 (x+5)(x+1)(x-2)
Polynomial of degree 4: f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5	Polynomial of degree 5: f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2

Polynomials and calculus

One important aspect of calculus is the project of analyzing complicated functions by means of approximating them with polynomials. The culmination of these efforts is Taylor's theorem, which roughly states that every differentiable function locally looks like a polynomial, and the Stone-Weierstrass theorem, which states that every continuous function defined on a compact interval of the real axis can be approximated on the whole interval as closely as desired by a polynomial. Polynomials are also frequently used to interpolate functions.

Quotients of polynomials are called rational expressions, and functions that evaluate rational expressions are called rational functions. Piecewise rationals are the only functions that can be evaluated directly on a computer, since typically only the operations of addition, multiplication, division and comparison are implemented in hardware. All the other functions that computers need to evaluate, such as trigonometric functions, logarithms and exponential functions, must then be approximated in software by suitable piecewise rational functions.

Calculating derivatives and integrals of polynomials is particularly simple. For the polynomial

\sum _{i=0}^{n}a_{i}x^{i}

the derivative with respect to x is

\sum _{i=1}^{n}a_{i}ix^{i-1}

and the indefinite integral is

\sum _{i=0}^{n}{a_{i} \over i+1}x^{i+1}+c

.

Abstract algebra

Main article: polynomial ring.

In abstract algebra, one must take care to distinguish between polynomials and polynomial functions. A polynomial f is defined to be a formal expression of the form

f=a_{n}X^{n}+a_{n-1}X^{n-1}+\cdots +a_{1}X+a_{0}

where the coefficients a₀, ..., a_n are elements of some ring R and X is considered to be a formal symbol. Two polynomials are considered to be equal if and only if the sequences of their coefficients are equal. Polynomials with coefficients in R can be added by simply adding corresponding coefficients and multiplied using the distributive law and the rules

X\;a=a\;X

for all elements a of the ring R

X^{k}\;X^{l}=X^{k+l}

for all natural numbers k and l.

One can then check that the set of all polynomials with coefficients in the ring R forms itself a ring, the ring of polynomials over R, which is denoted by R[X]. If R is commutative, then R[X] is an algebra over R.

One can think of the ring R[X] as arising from R by adding one new element X to R and only requiring that X commute with all elements of R. In order for R[X] to form a ring, all sums of powers of X have to be included as well. Formation of the polynomial ring, together with forming factor rings by factoring out ideals, are important tools for constructing new rings out of known ones. For instance, the clean construction of finite fields involves the use of those operations, starting out with the field of integers modulo some prime number as the coefficient ring R (see modular arithmetic).

To every polynomial f in R[X], one can associate a polynomial function with domain and range equal to R. One obtains the value of this function for a given argument r by everywhere replacing the symbol X in f’s expression by r. The reason that algebraists have to distinguish between polynomials and polynomial functions is that over some rings R, two different polynomials may give rise to the same polynomial function (see Fermat's little theorem for an example where R is the integers modulo p). This is not the case over the real or complex numbers and therefore many analysts often don't separate the two concepts.

Divisibility

In commutative algebra, one major focus of study is divisibility among polynomials. If R is an integral domain and f and g are polynomials in R[X], it is said that f divides g if there exists a polynomial q in R[X] such that f q = g. One can then show that "every zero gives rise to a linear factor", or more formally: if f is a polynomial in R[X] and r is an element of R such that f(r) = 0, then the polynomial (X − r) divides f. The converse is also true. The quotient can be computed using the Horner scheme.

If F is a field and f and g are polynomials in F[X] with g ≠ 0, then there exist unique polynomials q and r in F[X] with

f=q\,g+r

and such that the degree of r is smaller than the degree of g. The polynomials q and r are uniquely determined by f and g. This is called "division with remainder" or "polynomial long division" and shows that the ring F[X] is a Euclidean domain.

Analogously, polynomial "primes" (more correctly, irreducible polynomials) can be defined which cannot be factorized into the product of two polynomials of lesser degree. It is not easy to determine if a given polynomial is irreducible. One can start by simply checking if the polynomial has linear factors. Then, one can check divisibility by some other irreducible polynomials. Eisenstein's criterion can also be used in some cases to determine irreducibility.

Extensions of the concept of a polynomial

One also speaks of polynomials in several variables, obtained by taking the ring of polynomials of a ring of polynomials: R[X,Y] = (R[X])[Y] = (R[Y])[X]. These are of fundamental importance in algebraic geometry which studies the simultaneous zero sets of several such multivariate polynomials.

Polynomials are frequently used to encode information about some other object. The characteristic polynomial of a matrix or linear operator contains information about the operator's eigenvalues. The minimal polynomial of an algebraic element records the simplest algebraic relation satisfied by that element.

Other related objects studied in abstract algebra are formal power series, which are like polynomials but may have infinite degree, and the rational functions, which are ratios of polynomials.

References

^ Peter H. Selby, Steve Slavin, Practical Algebra: A Self-Teaching Guide, 2nd Edition, Wiley, ISBN-10 0471530123 ISBN-13 978-0471530121
^ Gilbert Strang, Linear Algebra and its Applications, Fourth Edition, Thompson Brooks/Cole, ISBN 0030105676.
^ Howard Eves, An Introduction to the History of Mathematics, Sixth Edition, Saunders, ISBN 0030295580

R. Birkeland. Über die Auflösung algebraischer Gleichungen durch hypergeometrische Funktionen. Mathematische Zeitschrift vol. 26, (1927) pp. 565-578. Shows that the roots of any polynomial may be written in terms of multivariate hypergeometric functions. Paper is available here.
F. von Lindemann. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen. Nachrichten von der Königl. Gesellschaft der Wissenschaften, vol. 7, 1884. Polynomial solutions in terms of theta functions. Paper available here.
F. von Lindemann. Über die Auflösung der algebraischen Gleichungen durch transcendente Functionen II. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, 1892 edition. Paper available here.
K. Mayr. Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen. Monatshefte für Mathematik und Physik vol. 45, (1937) pp. 280-313.
H. Umemura. Solution of algebraic equations in terms of theta constants. In D. Mumford, Tata Lectures on Theta II, Progress in Mathematics 43, Birkhäuser, Boston, 1984.

External links

[1] Peter H. Selby, Steve Slavin, Practical Algebra: A Self-Teaching Guide, 2nd Edition, Wiley, ISBN-10 0471530123 ISBN-13 978-0471530121

[2] Gilbert Strang, Linear Algebra and its Applications, Fourth Edition, Thompson Brooks/Cole, ISBN 0030105676.

[3] Howard Eves, An Introduction to the History of Mathematics, Sixth Edition, Saunders, ISBN 0030295580

[1]

[2]

[3]