Jump to content

Photonic crystal

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by DMB (talk | contribs) at 14:03, 3 February 2009 (→History of photonic crystals). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

The opal in this bracelet contains a natural periodic microstructure responsible for its iridescent color. It is essentially a natural photonic crystal, although it does not have a complete photonic band gap.

Photonic crystals are periodic optical nanostructures that are designed to affect the motion of photons in a similar way that periodicity of a semiconductor crystal affects the motion of electrons. Photonic crystals occur in nature and in various forms have been studied scientifically for the last 100 years.

Introduction

Photonic crystals are composed of periodic dielectric or metallo-dielectric nanostructures that affect the propagation of electromagnetic waves (EM) in the same way as the periodic potential in a semiconductor crystal affects the electron motion by defining allowed and forbidden electronic energy bands. Essentially, photonic crystals contain regularly repeating internal regions of high and low dielectric constant. Photons (behaving as waves) propagate through this structure - or not - depending on their wavelength. Wavelengths of light that are allowed to travel are known as modes, and groups of allowed modes form bands. Disallowed bands of wavelengths are called photonic band gaps. This gives rise to distinct optical phenomena such as inhibition of spontaneous emission, high-reflecting omni-directional mirrors and low-loss-waveguiding, amongst others.

Since the basic physical phenomenon is based on diffraction, the periodicity of the photonic crystal structure has to be of the same length-scale as half the wavelength of the EM waves i.e. ~200 nm (blue) to 350 nm (red) for photonic crystals operating in the visible part of the spectrum - the repeating regions of high and low dielectric constants have to be of this dimension. This makes the fabrication of optical photonic crystals cumbersome and complex.


History of photonic crystals

Although photonic crystals have been studied in one form or another since 1887, the term “photonic crystal” was first used over 100 years later, after Eli Yablonovitch and Sajeev John published two milestone papers on photonic crystals in 1987.[1][2]

Before 1987, one-dimensional photonic crystals in the form of periodic multi-layers dielectric stacks (such as the Bragg mirror) were studied extensively. Lord Rayleigh started their study in 1887[3], by showing that such systems have a one-dimensional photonic band-gap, a spectral range of large reflectivity, known as a stop-band. Today, such structures are used in a diverse range of applications; from reflective coatings to enhancing the efficiency of LEDs to highly reflective mirrors in certain laser cavities (see, for example, VCSEL). A detailed theoretical study of one-dimensional optical structures was performed by Bykov[4], who was the first to investigate the effect of a photonic band-gap on the spontaneous emission from atoms and molecules embedded within the photonic structure. Bykov also speculated as to what could happen if two- or three-dimensional periodic optical structures were used[5]. However, these ideas did not take off until after the publication of two milestone papers in 1987 by Yablonovitch and John. Both these papers concerned high dimensional periodic optical structures – photonic crystals. Yablonovitch’s main motivation was to engineer the photonic density of states, in order to control the spontaneous emission of materials embedded within the photonic crystal; John’s idea was to use photonic crystals to affect the localisation and control of light.

After 1987, the number of research papers concerning photonic crystals began to grow exponentially. However, due to the difficulty of actually fabricating these structures at optical scales (see Fabrication Challenges), early studies were either theoretical or in the microwave regime, where photonic crystals can be built on the far more readily accessible centimetre scale. (This fact is due to a property of the electromagnetic fields known as scale invariance – in essence, the electromagnetic fields, as the solutions to Maxwell's equations, has no natural length scale, and so solutions for centimetre scale structure at microwave frequencies are the same as for nanometre scale structures at optical frequencies.) By 1991, Yablonovitch had demonstrated the first three-dimensional photonic band-gap in the microwave regime.[6]

In 1996, Thomas Krauss made the first demonstration of a two-dimensional photonic crystal at optical wavelengths.[7] This opened up the way for photonic crystals to be fabricated in semiconductor materials by borrowing the methods used in the semiconductor industry. Today, such techniques use photonic crystal slabs, which are two dimensional photonic crystals “etched” into slabs of semiconductor; total internal reflection confines light to the slab, and allows photonic crystal effects, such as engineering the photonic dispersion to be used in the slab. Research is underway around the world to use photonic crystal slabs in integrated computer chips, in order to improve the optical processing of communications both on-chip and between chips.

Although such techniques are still to mature into commercial applications, two-dimensional photonic crystals have found commercial use in the form of photonic crystal fibres (otherwise known as holey fibres, because of the air holes that run through them). Photonic crystal fibres were first developed by Philip Russell in 1998, and can be designed to possess enhanced properties over (normal) optical fibres.

The study of three-dimensional photonic crystals has proceeded more slowly then their two-dimensional counterparts. This is because of the increased difficulty in fabrication; there was no inheritance of readily applicable techniques from the semiconductor industry for fabricators of three-dimensional photonic crystals to draw on. Attempts have been made, however, to adapt some of the same techniques, and quite advanced examples have been demonstrated[8], for example in the construction of "woodpile" structures constructed on a planar layer-by-layer basis. Another strand of research has been to try and construct three-dimensional photonic structures from self-assembly – essentially allowing a mixture of dielectric nano-spheres to settle from solution into three-dimensionally periodic structures possessing photonic band-gaps (see colloidal crystals, below).

Fabrication challenges

The major challenge for higher dimensional photonic crystals is in fabrication of these structures, with sufficient precision to prevent scattering losses blurring the crystal properties and with processes that can be robustly mass produced. One promising method of fabrication for two-dimensionally periodic photonic crystals is a photonic-crystal fiber, such as a "holey fiber". Using fiber draw techniques developed for communications fiber it meets these two requirements, and photonic crystal fibres are commercially available. Another promising method for developing two-dimensional photonic crystals is the so-called photonic crystal slab. These structures consist of a slab of material (such as silicon) which can be patterned using techniques borrowed from the semiconductor industry. Such chips offer the potential to combine photonic processing with electronic processing on a single chip.

For three dimensional photonic crystals various techniques[8] have been used including photolithography and etching techniques similar to those used for integrated circuits. Some of these techniques are already commercially available like Nanoscribe's Direct Laser Writing system.[9] To circumvent nanotechnological methods with their complex machinery, alternate approaches have been followed to grow photonic crystals as self-assembled structures from colloidal crystals.

Colloidal Crystals

Main article: colloidal crystal

File:Coll 3.jpg
300px Bulk microstructure of a colloidal crystal composed of submicron amorphous hydrated colloidal silica. SEM Micrograph: R.M. Allman III, UCLA School of Engr. & Applied Science, 1983

A colloidal crystal is a highly ordered array of particles which can be formed over a very long range (from a few millimeters to one centimeter) in length, and which appear analogous to their atomic or molecular counterparts (1). One of the finest natural examples of this phenomenon can be found in precious opal, where brilliant regions of pure spectral color result form from close-packed domains of amorphous colloidal spheres of silicon dioxide (or silica, SiO2). (2) The spherical particles precipitate in highly siliceous pools in Australia and elsewhere, and form highly ordered arrays after years of sedimentation and compression under hydrostatic and gravitational forces. The periodic arrays of spherical particles make similar arrays of interstitial voids, which act as a natural diffraction grating for visible light waves, espacialy when the interstitial spacing is of the same order of magnitude as the incident lightwave. (15 - 28)

Thus, it has been known for many years that, due to repulsive Coulombic interactions, electrically charged macromolecules in an aqueous environment can exhibit long-range crystal-like correlations with interparticle separation distances often being considerably greater than the individual particle diameter. In all of these cases in nature, the same brilliant iridescence (or play of colors)can be attributed to the diffraction and constructive interference of visible lightwaves which satisfy Bragg’s law, in a matter analogous to the scattering of X-rays in crystalline solids.

Due to both the rarity and pathological properties, neither precious opal nor any of the organic viruses have been very popular in the scientific laboratory. The large number of experiments exploring the physics and chemistry of these so-called “colloidal crystals” has emerged as a result of the relatively simple methods which have evolved in the last 20 years for preparing synthetic monodisperse colloids (both polymer and mineral) and, through various mechanisms, implementing and preserving their long-range order formation.

Technologically, colloidal crystals have found recent application in the world of optics as photonic band gap (PBG) materials (or photonic crystals). Synthetic Opals as well as inverse Opal configurations are being formed either by natural sedimentation or applied forces, both achieving similar results : long-range ordered structures which provide a natural diffraction grating for lightwaves of wavelength comparable to the particle size.

Novel PBG materials are being formed from opal-semiconductor-polymer composites, typically utilizing the ordered lattice to create an ordered array of holes (or pores) which is left behind after removal (or decomposition) of the original particles. Residual hollow honeycomb structures provide a relative index of refraction (ratio of matrix to air) sufficient for selective filters. Variable index liquids or liguid crystals injected into the network alter the ratio and band gap.

Such frequency-sensitive devices may be ideal for optical switching and frequency selective filters in the ultraviolet, visible or infrared portions of the spectrum, as well as higher efficiency antennae at microwave and millimeter wave frequencies Such photonic devices may be instrumental in the evolution of the next generation of optical circuits used in microchips, biochips, and other chemical sensing applications.

Historical origins of colloidal crystals

The origins of colloidal crystals trace back to the unique mechanical properties of bentonite sols, and the interesting optical properties of Schiller layers in iron oxide sols. The properties were supposed to be due to the ordering of monodisperse inorganic particles (5). It was clear then that monodisperse colloids, capable of forming long-range ordered arrays, existed in nature. In particular, the discovery by W.M. Stanley of the crystalline forms of the tobacco and tomato viruses provided excellent examples of this (Nobel Prize in Chemistry, 1946). (6)

Using X-ray diffraction methods, it was subsequently determined that when concentrated by centrifuging from dilute water suspensions, these virus particles often organized themselves into highly ordered arrays. (7) E.G. Rod-shaped particles in the tobacco mosaic virus (TMV) could form a two-dimensional triangular lattice, while a body-centered cubic (BCC) structure was formed from the nearly spherical particles in the tomato Bushy Stunt Virus.

In 1957, a brief letter describing the discovery of "A Crystallizable Insect Virus" was published in the journal Nature. Known now as the Tipula Iridiscent Virus (TIV), from both square and triangular arrays occuring on crystal faces, the authors deduced the face-centered cubic (FCC) close-packing of virus particles. (8)

This type of ordered array has also been observed in cell suspensions, where the symmetry is particularly well adapted to the mode of reproduction of the organism. (9) The limited content of genetic material places a restriction on the size of the protein to be coded by it. The use of a large number of identical proteins to build a protective shell is consistent with this limited length of RNA or DNA content.

A prominent example of a photonic crystal is the naturally occurring gemstone opal. Its play of colours is essentially a photonic crystal phenomenon based on Bragg diffraction of light on the crystal's lattice planes. Another well-known photonic crystal is found on the wings of some butterflies such as those of genus Morpho.[10][11]

Computing photonic band structure

The photonic band gap (PBG) is essentially the gap between the air-line and the dielectric-line in the relation of the PBG system. To design photonic crystal systems, it is essential to engineer the location and size of the bandgap; this is done by computational modeling using any of the following methods.

  1. Plane wave expansion method.
  2. Finite Difference Time Domain method
  3. Order-N spectral method[12][13]
  4. KKR method

Essentially these methods solve for the frequencies (normal models) of the photonic crystal for each value of the propagation direction given by the wave vector, or vice-versa. The various lines in the band structure, correspond to the different cases of n, the band index. For an introduction to photonic band structure, see Joannopoulos.[14]

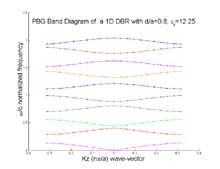
Band structure of a 1D Photonic Crystal, DBR air-core calculated using plane wave expansion technique with 101 planewaves, for d/a=0.8, and dielectric contrast of 12.250.

The plane wave expansion method, can be used to calculate the band structure using an eigen formulation of the Maxwell's equations, and thus solving for the eigen frequencies for each of the propagation directions, of the wave vectors. It directly solves for the dispersion diagram. Electric field strength values can also be calculated over the spatial domain of the problem using the eigen vectors of the same problem. For the picture shown to the right, corresponds to the band-structure of a 1D DBR with air-core interleaved with a dielectric material of relative permittivity 12.25, and a lattice period to air-core thickness ratio (d/a) of 0.8, is solved using 101 planewaves over the first irreducible Brillouin zone.

Applications

Photonic crystals are attractive optical materials for controlling and manipulating the flow of light. One dimensional photonic crystals are already in widespread use in the form of thin-film optics with applications ranging from low and high reflection coatings on lenses and mirrors to colour changing paints and inks. Higher dimensional photonic crystals are of great interest for both fundamental and applied research, and the two dimensional ones are beginning to find commercial applications. The first commercial products involving two-dimensionally periodic photonic crystals are already available in the form of photonic-crystal fibers, which use a microscale structure to confine light with radically different characteristics compared to conventional optical fiber for applications in nonlinear devices and guiding exotic wavelengths. The three-dimensional counterparts are still far from commercialization but offer additional features possibly leading to new device concepts (e.g. optical computers), when some technological aspects such as manufacturability and principal difficulties such as disorder are under control.

See also


References

  1. ^ E. Yablonovitch (1987), "Inhibited Spontaneous Emission in Solid-State Physics and Electronics" (PDF), Physical Review Letters, 58 (20): 2059–2062, doi:10.1103/PhysRevLett.58.2059
  2. ^ S. John (1987), "Strong localization of photons in certain disordered dielectric superlattices" (PDF), Physical Review Letters, 58 (23): 2486–2489, doi:10.1103/PhysRevLett.58.2486
  3. ^ J. W. S. Rayleigh (1888), "On the remarkable phenomenon of crystalline reflexion described by Prof. Stokes" (PDF), Phil. Mag, 26: 256–265
  4. ^ V. P. Bykov (1972), "Spontaneous Emission in a Periodic Structure", Soviet Journal of Experimental and Theoretical Physics, 35
  5. ^ V. P. Bykov (1975), "Spontaneous emission from a medium with a band spectrum", Quantum Electronics, 4 (7): 861–871, doi:10.1070/QE1975v004n07ABEH009654
  6. ^ E. Yablonovitch, T.J. Gmitter, K.M. Leung (1991), "Photonic band structure: the face-centered-cubic case employing nonspherical atoms" (PDF), Physical Review Letters, 67 (17): 2295–2298, doi:10.1103/PhysRevLett.67.2295{{citation}}: CS1 maint: multiple names: authors list (link)
  7. ^ T. F. Krauss, R. M. DeLaRue, S. Brand (1996), "Two-dimensional photonic-bandgap structures operating at near-infrared wavelengths", Nature, 383 (6602): 699–702, doi:10.1038/383699a0{{citation}}: CS1 maint: multiple names: authors list (link)
  8. ^ a b Review: S. Johnson (MIT) Lecture 3: Fabrication technologies for 3d photonic crystals, a survey
  9. ^ Homepage of Nanoscribe - a spin-off enterprise of the Karlsruhe Institute of Technology http://www.nanoscribe.de
  10. ^ P. Vukusic and J. R. Sambles (2003), "Photonic structures in biology" (PDF), Nature, 424 (6950): 852–855, doi:10.1038/nature01941
  11. ^ S. Kinoshita, S. Yoshioka and K. Kawagoe (2002), "Mechanisms of structural colour in the Morpho butterfly: cooperation of regularity and irregularity" (PDF), Proceedings of the Royal Society B: Biological Sciences, 269 (1499): 1417–1421, doi:10.1098/rspb.2002.2019
  12. ^ P. Ordejon (1998), "Order-N tight-binding methods for electronic-structure and molecular dynamics", Computational materials science, 12 (3): 157–191, doi:10.1016/S0927-0256(98)00027-5
  13. ^ Richard M Martin, Linear Scaling ‘Order-N’ Methods in Electronic Structure Theory
  14. ^ John D Joannopoulos, Johnson SG, Winn JN & Meade RD (2008). Photonic Crystals: Molding the Flow of Light (2nd Edition ed.). Princeton NJ: Princeton University Press. ISBN 978-0-691-12456-8. {{cite book}}: |edition= has extra text (help)CS1 maint: multiple names: authors list (link)

15. Luck, W. et al., Ber. Busenges Phys. Chem. , Vol. 67, p.84 (1963)

16. Hiltner, P.A. and Krieger, I.M., Diffraction of Light by Ordered Suspensions, J. Phys. Chem., Vol.73, p.2306 (1969)

17. Langmuir, I., J. Chem. Phys., Vol.6, p.873 (1938)

18. Stanley, W.M., Crystalline Form of the Tobacco Mosaic Virus, Am. J. Botany, Vol.24, p.59 (1937); Nobel Lecture: The Isolation and Properties of Crystalline TMV (1946); http://nobelprize.org/nobel_prizes/chemistry/laureates/1946/stanley-lecture.pdf

19. Bernal. J.D. and Fankuchen, I., J. Gen. Physiol., Vol.25, p.111 (1941)

20. Williams, R.C. and Smith, K., Nature (Lond.), Vol. 119, p.4551 (1957)

21. Watson, J.D., Molecular Biology of the Gene, Benjamin, Inc. (1970)

22. Sanders, J.V., Structure of Opal, Nature, Vol.204, p.1151, 1964); Darragh, P.J., et al., Scientific American, Vol. 234, p. 84, (1976)

23. http://www.profoundglass.com/current_gilson.html

24. Pieranski, P., Contemp. Phys., Colloidal Crystals, Vol.24, p.25 (1983)

25. Allman III, R.M., Structural Variations in Colloidal Crystals, M.S. Thesis, UCLA (1983). See Ref.14 in Mangels, J.A. and Messing, G.L., Eds., Forming of Ceramics, Microstructural Control Through Colloidal Consolidation, I.A. Aksay, Advances in Ceramics, Vol.9, p.94, Proc. Amer. Ceramic Soc. (1984)

26. Allman III, R.M. and Onoda, G.Y., Jr. (IBM T.J. Watson Research Center, 1984)

27. Whitesides, G.M., et al., Molecular Self-Assembly and Nanochemistry: A Chemical Strategy for the Synthesis of Nanostructures, Science, Vol. 254, p.1312 (1991)

28. Aksay, I.A., et al., Self-Assembled Ceramics, Ann. Rev. Phys. Chem., Vol. 51, p.601 (2000)


Retrieved from "https://en.wikipedia.org/w/index.php?title=Photonic_crystal&oldid=268248712"