Jump to content

Network theory

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by Bhny (talk | contribs) at 14:21, 11 February 2015 (Undid revision 646643398 by Lightgodsy (talk) why are you doing this??). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

For the theory regarding the regulation of the adaptive immune system, see immune network theory. For the sociological theory, see social network.
A small example network with eight vertices and ten edges.
Part of a series on
Network science
Internet_map_1024.jpg
Network types
Graphs
Features
Types
Models
Topology
Dynamics
  • Lists
  • Categories

In computer and network science, network theory is the study of graphs as a representation of either symmetric relations or, more generally, of asymmetric relations between discrete objects. Network theory is a part of graph theory.

It has applications in many disciplines including statistical physics, particle physics, computer science, electrical engineering, biology, economics, operations research, and sociology. Applications of network theory include logistical networks, the World Wide Web, Internet, gene regulatory networks, metabolic networks, social networks, epistemological networks, etc; see List of network theory topics for more examples.

Euler's solution of the Seven Bridges of Königsberg problem is considered to be the first true proof in the theory of networks.[1]

Network optimization

Network problems that involve finding an optimal way of doing something are studied under the name combinatorial optimization. Examples include network flow, shortest path problem, transport problem, transshipment problem, location problem, matching problem, assignment problem, packing problem, routing problem, Critical Path Analysis and PERT (Program Evaluation & Review Technique).

Network analysis

Social network analysis

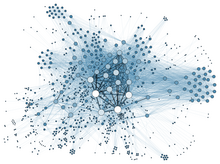
Visualization of social network analysis.[2]

Social network analysis examines the structure of relationships between social entities.[3] These entities are often persons, but may also be groups, organizations, nation states, web sites, scholarly publications.

Since the 1970s, the empirical study of networks has played a central role in social science, and many of the mathematical and statistical tools used for studying networks have been first developed in sociology.[4] Amongst many other applications, social network analysis has been used to understand the diffusion of innovations, news and rumors. Similarly, it has been used to examine the spread of both diseases and health-related behaviors. It has also been applied to the study of markets, where it has been used to examine the role of trust in exchange relationships and of social mechanisms in setting prices. Similarly, it has been used to study recruitment into political movements and social organizations. It has also been used to conceptualize scientific disagreements as well as academic prestige. More recently, network analysis (and its close cousin traffic analysis) has gained a significant use in military intelligence, for uncovering insurgent networks of both hierarchical and leaderless nature.

Biological network analysis

With the recent explosion of publicly available high throughput biological data, the analysis of molecular networks has gained significant interest. The type of analysis in this context is closely related to social network analysis, but often focusing on local patterns in the network. For example network motifs are small subgraphs that are over-represented in the network. Similarly, activity motifs are patterns in the attributes of nodes and edges in the network that are over-represented given the network structure. The analysis of biological networks with respect to diseases has led to the development of the field of network medicine.[5]

Link analysis is a subset of network analysis, exploring associations between objects. An example may be examining the addresses of suspects and victims, the telephone numbers they have dialed and financial transactions that they have partaken in during a given timeframe, and the familial relationships between these subjects as a part of police investigation. Link analysis here provides the crucial relationships and associations between very many objects of different types that are not apparent from isolated pieces of information. Computer-assisted or fully automatic computer-based link analysis is increasingly employed by banks and insurance agencies in fraud detection, by telecommunication operators in telecommunication network analysis, by medical sector in epidemiology and pharmacology, in law enforcement investigations, by search engines for relevance rating (and conversely by the spammers for spamdexing and by business owners for search engine optimization), and everywhere else where relationships between many objects have to be analyzed.

Network robustness

The structural robustness of networks [6] is studied using percolation theory. When a critical fraction of nodes (or links) is removed the network becomes fragmented into small disconnected clusters. This phenomenon is called percolation [7] and it represents an order-disorder type of phase transition with critical exponents.

Several Web search ranking algorithms use link-based centrality metrics, including Google's PageRank, Kleinberg's HITS algorithm, the CheiRank and TrustRank algorithms. Link analysis is also conducted in information science and communication science in order to understand and extract information from the structure of collections of web pages. For example the analysis might be of the interlinking between politicians' web sites or blogs. Another use is for classifying pages according to their mention in other pages.[8]

Centrality measures

Information about the relative importance of nodes and edges in a graph can be obtained through centrality measures, widely used in disciplines like sociology. For example, eigenvector centrality uses the eigenvectors of the adjacency matrix corresponding to a network, to determine nodes that tend to be frequently visited. Formally established measures of centrality are degree centrality, closeness centrality, betweenness centrality, eigenvector centrality, subgraph centrality and Katz centrality. The purpose or objective of analysis generally determines the type of centrality measure to be used. For example, if one is interested in dynamics on networks or the robustness of a network to node/link removal, often the dynamical importance [9] of a node is the most relevant centrality measure.

Assortative and disassortative mixing

These concepts were made because of the nature of hubs in a network. Hubs are nodes which have lots of links. If we see one link in the hub, there is no difference between the hubs, however, some differences are exited between those nodes; some hubs tend to link to the other nodes and other hubs avoid connecting to the other nodes. We say a hub is assortative when it tends to connect to the other hubs. A dissortative hub avoids connecting to other hubs. If some nodes have some connections with the expected random probabilities, the hubs are neutral. There are three methods to quantify degree correlations.

Spread

Content in a complex network can spread via two major methods: conserved spread and non-conserved spread.[10] In conserved spread, the total amount of content that enters a complex network remains constant as it passes through. The model of conserved spread can best be represented by a pitcher containing a fixed amount of water being poured into a series of funnels connected by tubes . Here, the pitcher represents the original source and the water is the content being spread. The funnels and connecting tubing represent the nodes and the connections between nodes, respectively. As the water passes from one funnel into another, the water disappears instantly from the funnel that was previously exposed to the water. In non-conserved spread, the amount of content changes as it enters and passes through a complex network. The model of non-conserved spread can best be represented by a continuously running faucet running through a series of funnels connected by tubes. Here, the amount of water from the original source is infinite. Also, any funnels that have been exposed to the water continue to experience the water even as it passes into successive funnels. The non-conserved model is the most suitable for explaining the transmission of most infectious diseases, neural excitation, information and rumors, etc.

Interdependent networks

Interdependent networks is a system of coupled networks where nodes of one or more networks depend on nodes in other networks. Such dependencies are enhanced by the developments in modern technology. Dependencies may lead to cascading failures between the networks and a relatively small failure can lead to a catastrophic breakdown of the system. Blackouts are a fascinating demonstration of the important role played by the dependencies between networks. A recent study developed a framework to study the cascading failures in an interdependent networks system.[11][12]

Implementations

See also

Column-generating template families

The templates listed here are not interchangeable. For example, using {{col-float}} with {{col-end}} instead of {{col-float-end}} would leave a <div>...</div> open, potentially harming any subsequent formatting.

Column templates
Type Family
Handles wiki
table code?†
 Responsive/
mobile suited 		Start template Column divider End template
Float "col-float" Yes Yes {{col-float}} {{col-float-break}} {{col-float-end}}
"columns-start" Yes Yes {{columns-start}} {{column}} {{columns-end}}
Columns "div col" Yes Yes {{div col}} – {{div col end}}
"columns-list" No Yes {{columns-list}} (wraps div col) – –
Flexbox "flex columns" No Yes {{flex columns}} – –
Table "col" Yes No {{col-begin}},
{{col-begin-fixed}} or
{{col-begin-small}} 		{{col-break}} or
{{col-2}} .. {{col-5}} 		{{col-end}}

† Can template handle the basic wiki markup {| | || |- |} used to create tables? If not, special templates that produce these elements (such as {{(!}}, {{!}}, {{!!}}, {{!-}}, {{!)}})—or HTML tags (<table>...</table>, <tr>...</tr>, etc.)—need to be used instead.

References

  1. ^ Newman, M. E. J. "The structure and function of complex networks" (PDF). Department of Physics, University of Michigan. {{cite journal}}: Cite journal requires |journal= (help)
  2. ^ Published in Grandjean, Martin (2014). "La connaissance est un réseau". Les Cahiers du Numérique. 10 (3): 37–54. Retrieved 2014-10-15.
  3. ^ Wasserman, Stanley and Katherine Faust. 1994. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.
  4. ^ Newman, M.E.J. Networks: An Introduction. Oxford University Press. 2010
  5. ^ Barabási, A. L., Gulbahce, N., & Loscalzo, J. (2011). Network medicine: a network-based approach to human disease. Nature Reviews Genetics, 12(1), 56-68.
  6. ^ R. Cohen, S. Havlin (2010). Complex Networks: Structure, Robustness and Function. Cambridge University Press.
  7. ^ A. Bunde, S. Havlin (1996). Fractals and Disordered Systems. Springer.
  8. ^ Attardi, G.; S. Di Marco; D. Salvi (1998). "Categorization by Context" (PDF). Journal of Universal Computer Science. 4 (9): 719–736.
  9. ^ Restrepo, Juan, E. Ott, B. R. Hunt (2006). "Characterizing the Dynamical Importance of Network Nodes and Links". Phys. Rev. Lett. 97 (9): 094102. doi:10.1103/PhysRevLett.97.094102. PMID 17026366. {{cite journal}}: |first2= missing |last2= (help); |first3= missing |last3= (help)CS1 maint: multiple names: authors list (link)
  10. ^ Newman, M., Barabási, A.-L., Watts, D.J. [eds.] (2006) The Structure and Dynamics of Networks. Princeton, N.J.: Princeton University Press.
  11. ^ S. V. Buldyrev, R. Parshani, G. Paul, H. E. Stanley, S. Havlin (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–28. doi:10.1038/nature08932. PMID 20393559.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  12. ^ Jianxi Gao, Sergey V. Buldyrev3, Shlomo Havlin4, and H. Eugene Stanley (2011). "Robustness of a Network of Networks". Phys. Rev. Lett. 107 (19): 195701. doi:10.1103/PhysRevLett.107.195701. PMID 22181627. {{cite journal}}: |first2= missing |last2= (help); |first3= missing |last3= (help); |first4= missing |last4= (help)CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)

Books

  • S.N. Dorogovtsev and J.F.F. Mendes, Evolution of Networks: from biological networks to the Internet and WWW, Oxford University Press, 2003, ISBN 0-19-851590-1
  • G. Caldarelli, "Scale-Free Networks", Oxford University Press, 2007, ISBN 978-0-19-921151-7
  • A. Barrat, M. Barthelemy, A. Vespignani , "Dynamical Processes on Complex Networks", Cambridge University Press, 2008, ISBN 978-0521879507
  • E. Estrada, "The Structure of Complex Networks: Theory and Applications", Oxford University Press, 2011, ISBN 978-0-199-59175-6
Retrieved from "https://en.wikipedia.org/w/index.php?title=Network_theory&oldid=646649328"