Centered octagonal number

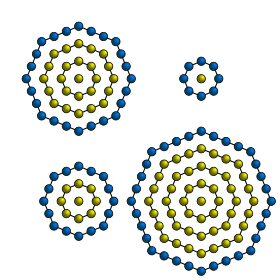
A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers. The centered octagonal numbers are the same as the odd square numbers. Thus, the nth centered octagonal number is given by the formula

$(2n-1)^{2}=4n^{2}-4n+1.$

The first few centered octagonal numbers are

1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089.

Calculating Ramanujan's tau function on a centered octagonal number yields an odd number, whereas for any other number the function yields an even number.

See also

• Octagonal number