Aristotle's wheel paradox

Aristotle's wheel paradox is a paradox or problem appearing in the pseudo-Aristotelian Greek work Mechanica. It states as follows: A wheel is depicted in two-dimensional space as two circles. Its larger, outer circle is tangential to a horizontal surface (e.g. a road that it rolls on), while the smaller, inner one has the same center and is rigidly affixed to the larger. (The smaller circle could be the bead of a tire, the rim it is mounted upon, or the axle.) Assuming the larger circle rolls without slipping (or skidding) for one full revolution, the distances moved by both circles' circumferences are the same. The distance travelled by the larger circle is equal to its circumference, but for the smaller it is greater than its circumference, thereby creating a paradox.
The paradox is not limited to wheels: other things depicted in two dimensions display the same behavior such as a roll of tape, or a typical round bottle or jar rolled on its side (the smaller circle would be the mouth or neck of the jar or bottle).
In an alternative version of the problem, the smaller circle, rather than the larger one, is in contact with the horizontal surface. Examples include a typical train wheel, which has a flange, or a barbell straddling a bench. American educator and philosopher Israel Drabkin called these Case II versions of the paradox,[1] and a similar, but unidentical, analysis applies.
History of the paradox
[edit]In antiquity
[edit]In antiquity, the wheel problem was described in the Greek work Mechanica, traditionally attributed to Aristotle, but widely believed to have been written by a later member of his school.[2] (Thomas Winter has made the alternative proposal that it was written by Archytas.[3]) It also appears in the Mechanica of Hero of Alexandria.[1][4] In the Aristotelian version it appears as "Problem 24", where the description of the wheel is given as follows:
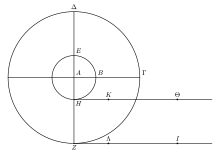
For let there be a larger circle ΔZΓ a smaller EHB, and A at the centre of both; let ZI be the line which the greater unrolls on its own, and HK that which the smaller unrolls on its own, equal to ZΛ. When I move the smaller circle, I move the same centre, that is A; let the larger be attached to it. When AB becomes perpendicular to HK, at the same time AΓ becomes perpendicular to ZΛ, so that it will always have completed an equal distance, namely HK for the circumference HB, and ZΛ for ZΓ. If the quarter unrolls an equal distance, it is clear that the whole circle will unroll an equal distance to the whole circle so that when the line BH comes to K, the circumference ZΓ will be ZΛ, and the whole circle will be unrolled. In the same way, when I move the large circle, fitting the small one to it, their centre being the same, AB will be perpendicular and at right angles simultaneously with AΓ, the latter to ZI, the former to HΘ. So that, when the one will have completed a line equal to HΘ, and the other to ZI, and ZA becomes again perpendicular to ZΛ, and HA to HK, so that they will be as in the beginning at Θ and I.[5]
The problem is then stated:
Now since there is no stopping of the greater for the smaller so that it [the greater] remains for an interval of time at the same point, and since the smaller does not leap over any point, it is strange that the greater traverses a path equal to that of the smaller, and again that the smaller traverses a path equal to that of the larger. Furthermore, it is remarkable that, though in each case there is only one movement, the center that is moved in one case rolls a great distance and in the other a smaller distance.[1]
In the Scientific Revolution
[edit]The mathematician Gerolamo Cardano discusses the problem of the wheel in his 1570 Opus novum de proportionibus numerorum,[6] taking issue with the presumption of its analysis in terms of motion.[1] Mersenne further discussed it in his 1623 Quaestiones Celeberrimae in Genesim,[7] where he suggests that the problem can be analysed by a process of expansion and contraction of the two circles. But Mersenne remained unsatisfied with his understanding, writing:
Indeed I have never been able to discover, and I do not think any one else has been able to discover whether the smaller circle touches the same point twice, or proceeds by leaps and sliding.[1]
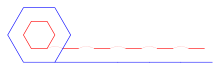
In his Two New Sciences, Galileo uses the wheel problem to argue for a certain kind of atomism. He begins his analysis by considering a pair of concentric hexagons, as opposed to circles. Imagining this hexagon "rolling" on a surface, Galileo notices that the inner hexagon "jumps" a little space with each roll of the outer onto a new face.[8] He then imagines what would happen to the limit as the number of faces on a polygon becomes very large, and finds that the little space that is "jumped" by the inner polygon becomes smaller and smaller. He writes:
Therefore a larger polygon having a thousand sides passes over and measures a straight line equal to its perimeter, while at the same time the smaller one passes an approximately equal line, but one interruptedly composed of a thousand little particles equal to its thousand sides with a thousand little void spaces interposed — for we may call these "void" in relation to the thousand linelets touched by the sides of the polygon.[8]
Since a circle is just the limit in which the number of faces on the polygon becomes infinite, Galileo finds that Aristotle's wheel contains material that is filled with infinitesimal spaces or "voids", and that "the interposed voids are not quantified, but are infinitely many".[8] This leads him to conclude that a belief in atoms – in the sense that matter is "composed of infinitely many unquantifiable atoms" – is sufficient to explain the phenomenon.[8] Gilles de Roberval (1602–1675) is also associated with this analysis.
In the 19th century
[edit]Bernard Bolzano discussed Aristotle's wheel in The Paradoxes of the Infinite (1851), a book that influenced Georg Cantor and subsequent thinkers about the mathematics of infinity. Bolzano observes that there is a bijection between the points of any two similar arcs, which can be implemented by drawing a radius, remarking that the history of this apparently paradoxical fact dates back to Aristotle.[1]
In the 20th century
[edit]The author of Mathematical Fallacies and Paradoxes uses a dime glued to a half-dollar (representing smaller and larger circles, respectively) with their centers aligned and both fixed to an axle, as a model for the paradox. He writes:
This is the solution, then, or the key to it. Although you are careful not to let the half-dollar slip on the tabletop, the “point” tracing the line segment at the foot of the dime is both rotating and slipping all the time. It is slipping with respect to the tabletop. Since the dime does not touch the table top, you do not notice the slipping. If you can roll the half-dollar along the table and at the same time roll the dime (or better yet the axle) along a block of wood, you can actually observe the slipping. If you have ever parked too close to the curb, you have noticed the screech made by your hubcap as it slips (and rolls) on the curb while your tire merely rolls on the pavement. The smaller the small circle relative to the large circle, the more the small one slips. Of course the center of the two circles does not rotate at all, so it slides the whole way.[9]
Analysis and solutions
[edit]
The paradox is that the smaller inner circle moves 2πR, the circumference of the larger outer circle with radius R, rather than its own circumference. If the inner circle were rolled separately, it would move 2πr, its own circumference with radius r. The inner circle is not separate but rigidly connected to the larger.
First solution
[edit]If the smaller circle depends on the larger one (Case I), the larger circle's motion forces the smaller to traverse the larger’s circumference. If the larger circle depends on the smaller one (Case II), then the smaller circle's motion forces the larger circle to traverse the smaller circle’s circumference. This is the simplest solution.
Second solution
[edit]
This solution considers the transition from the starting to ending positions. Let Pb be a point on the bigger circle and Ps be a point on the smaller circle, both on the same radius. For convenience, assume they are both directly below the center, analogous to both hands of a clock pointing towards six. Both Pb and Ps travel in a cycloid path as they roll together one revolution.[10]
While each travels 2πR horizontally from start to end, Ps's cycloid path is shorter and more efficient than Pb's. Pb travels farther above and farther below the center's path – the only straight one – than does Ps.
If Pb and Ps were anywhere else on their respective circles, the curved paths would be the same length. Summarizing, the smaller circle moves horizontally 2πR because any point on the smaller circle travels a shorter, and thus more direct path than any point on the larger circle.
See also
[edit]References
[edit]- ^ a b c d e f Drabkin, Israel E. (1950). "Aristotle's Wheel: Notes on the History of a Paradox". Osiris. 9: 162–198. doi:10.1086/368528. JSTOR 301848. S2CID 144387607.
- ^ Heath, Thomas Little (2003) [1931]. A Manual of Greek Mathematics. Mineola, NY: Dover Publications. p. 199. ISBN 978-0486432311.
- ^ Thomas Nelson Winter, "The Mechanical Problems in the Corpus of Aristotle," DigitalCommons@University of Nebraska – Lincoln, 2007.
- ^ "Heron Alexandrinus Mechanica". Translated by Miller, Jutta. 1999. Problem 7. Retrieved 27 July 2023.
- ^ Leeuwen, Joyce van (2016-03-17). The Aristotelian Mechanics: Text and Diagrams. Springer. ISBN 9783319259253.
- ^ Cardano, Geronimo (1570). Opus novum de proportionibus numerorum ...: Praeterea Artis magnae sive de regulis algebraicis liber unus ... Item De regula liber ...
- ^ Mersenne, Marin (1623). Quaestiones celeberrimae in Genesim ... (in Latin).
- ^ a b c d Galilei, Galileo; Drake, Stillman (2000). Two New Sciences: Including Centers of Gravity & Force of Percussion. Wall & Emerson. ISBN 9780921332503.
- ^ Bunch, Bryan H. (1982). Mathematical Fallacies and Paradoxes. Van Nostrand Reinhold. pp. 3–9. ISBN 0-442-24905-5.
- ^ The two paths are pictured here: http://mathworld.wolfram.com/Cycloid.html and http://mathworld.wolfram.com/CurtateCycloid.html
Further reading
[edit]- Hutton, Charles (1795). "Rota Aristotelica". Mathematical and Philosophical Dictionary. Vol. 2. p. 398. Archived from the original on 2017-07-02.
- Weisstein, Eric W. "Aristotle's Wheel Paradox". MathWorld.
