Dodecagon

Regular dodecagon
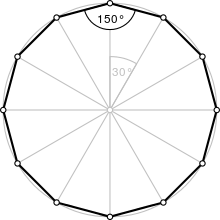A regular dodecagon
Type	Regular polygon
Edges and vertices	12
Schläfli symbol	{12}, t{6}, tt{3}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D12), order 2×12
Internal angle (degrees)	150°
Properties	Convex, cyclic, equilateral, isogonal, isotoxal
Dual polygon	Self

In geometry, a dodecagon is any twelve-sided polygon or 12-gon.

Regular dodecagon

A regular dodecagon has Schläfli symbol {12} and can be constructed as a truncated hexagon, t{6}, or a twice-truncated triangle, tt{3}.

It has all sides of equal length and all angles equal to 150°. It has 12 lines of symmetry and rotational symmetry of order 12. Its Schläfli symbol is {12}.

The area of a regular dodecagon with side a is given by:

${\begin{aligned}A&=3\cot \left({\frac {\pi }{12}}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}\\&\simeq 11.19615242\,a^{2}.\end{aligned}}$

Or, if R is the radius of the circumscribed circle,

$A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2}.$

And, if r is the radius of the inscribed circle,

${\begin{aligned}A&=12\tan \left({\frac {\pi }{12}}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}\\&\simeq 3.2153903\,r^{2}.\end{aligned}}$

A simple formula for area (given the two measurements) is: $\scriptstyle A\,=\,3ad$ where d is the distance between parallel sides.

Length d is the height of the dodecagon when it sits on a side as base, and the diameter of the inscribed circle.

By simple trigonometry, $\scriptstyle d\,=\,a(1\,+\,2cos{30^{\circ }}\,+\,2cos{60^{\circ }})$.

The perimeter for an inscribed dodecagon of radius 1 is 12√(2 - √3), or approximately 6.21165708246.

The perimeter for a circumscribed dodecagon of radius 1 is 24(2 – √3), or approximately 6.43078061835. Interestingly, this is double the value of the area of the inscribed dodecagon of radius 1.

With respect to the above-listed equations for area and perimeter, when the radius of the inscribed dodecagon is 1, note that the area of the inscribed dodecagon is 12(2 – √3) and the perimeter of this same inscribed dodecagon is 12√(2 - √3).

Dodecagon construction

As 12 = 2² × 3, regular dodecagon is constructible using compass and straightedge:

Construction of a regular dodecagon

Dissection

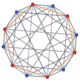
Coxeter states that every parallel-sided 2m-gon can be divided into m(m-1)/2 rhombs. For the dodecagon, m=6, and it can be divided into 15 rhombs, with one example shown below. This decomposition is based on a Petrie polygon projection of a 6-cube, with 15 of 240 faces.

Regular dodecagons dissected

With hexagons, squares, and triangles

pattern blocks

With 15 rhombs from 6-cube

With 15 rhombs

One of the ways the mathematical manipulative pattern blocks are used is in creating a number of different dodecagons.

Symmetry

The symmetries of a regular dodecagon as shown with colors on edges and vertices. John Conway labels these lower symmetries with a letter and order of the symmetry follows the letter. He gives d (diagonal) with mirror lines through vertices, p with mirror lines through edges (perpendicular), i with mirror lines through both vertices and edges, and g for rotational symmetry. a1 labels no symmetry. These lower symmetries allows degrees of freedoms in defining irregular dodecagons.

The regular dodecagon has Dih₁₂ symmetry, order 24. There are 15 distinct subgroup dihedral and cyclic symmetries. Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g12 subgroup has no degrees of freedom but can seen as directed edges.

Example dodecagons by symmetry

r24
d12	g12	p12		i8
d6	g6	p6		d4	g4	p4
g3				d2	g2	p2
a1

Occurrence

Tiling

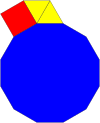
A regular dodecagon can fill a plane vertex with other regular polygons in 4 ways:

3.12.12	4.6.12	3.3.4.12	3.4.3.12

Here are 3 example periodic plane tilings that use regular dodecagons, defined by their vertex configuration:

1-uniform		2-uniform
3.12.12	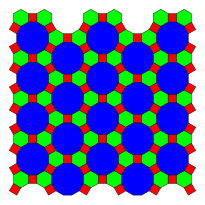4.6.12	3.12.12; 3.4.3.12

Skew dodecagon

A regular skew dodecagon seen as zig-zagging edges of a hexagonal antiprism.

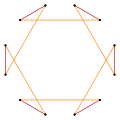
A skew dodecagon is a skew polygon with 12 vertices and edges but not existing on the same plane. The interior of such an dodecagon is not generally defined. A skew zig-zag dodecagon has vertices alternating between two parallel planes.

A regular skew dodecagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew dodecagon and can be seen in the vertices and side edges of a hexagonal antiprism with the same D_5d, [2⁺,10] symmetry, order 20. The dodecagrammic antiprism, s{2,24/5} and dodecagrammic crossed-antiprism, s{2,24/7} also have regular skew dodecagons.

Petrie polygons

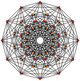
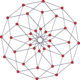
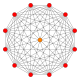
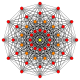
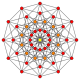
The regular dodecagon is the Petrie polygon for many higher-dimensional polytopes, seen as orthogonal projections in Coxeter planes. Examples in 4 dimensionare the 24-cell, snub 24-cell, 6-6 duoprism, 6-6 duopyramid. In 6 dimensions 6-cube, 6-orthoplex, 2₂₁, 1₂₂. It is also the Petrie polygon for the grand 120-cell and great stellated 120-cell.

Regular skew dodecagons in higher dimensions E6 F4 2G2 (4D) 221 122 24-cell Snub 24-cell 6-6 duopyramid 6-6 duoprism A11 D7 B6 11-simplex (411) 141 6-orthoplex 6-cube

Related figures

A dodecagram is a 12-sided star polygon, represented by symbol {12/n}. There is one regular star polygon: {12/5}, using the same vertices, but connecting every fifth point. There are also three compounds: {12/2} is reduced to 2{6} as two hexagons, and {12/3} is reduced to 3{4} as three squares, {12/4} is reduced to 4{3} as four triangles, and {12/6} is reduced to 6{2} as six degenerate digons.

Stars and compounds

n	1	2	3	4	5	6
Form	Polygon	Compounds			Star polygon	Compound
Image	{12/1} = {12}	{12/2} or 2{6}	{12/3} or 3{4}	{12/4} or 4{3}	{12/5}	{12/6} or 6{2}

Deeper truncations of the regular dodecagon and dodecagrams can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths. A truncated hexagon is a dodecagon, t{6}={12}. A quasitruncated hexagon, inverted as {6/5}, is a dodecagram: t{6/5}={12/5}.

As truncated hexagons

Vertex-transitive truncations of the hexagon

Quasiregular	Isogonal		Quasiregular
t{6}={12}			t{6/5}={12/5}

Examples in use

In block capitals, the letters E, H and X (and I in a slab serif font) have dodecagonal outlines. A cross is a dodecagon.

The Vera Cruz church in Segovia

The regular dodecagon features prominently in many buildings. The Torre del Oro is a dodecagonal military watchtower in Seville, southern Spain, built by the Almohad dynasty. The early thirteenth century Vera Cruz church in Segovia, Spain is dodecagonal. Another example is the Porta di Venere (Venus' Gate), in Spello, Italy, built in the 1st century BC has two dodecagonal towers, called "Propertius' Towers".

A 1942 British threepence, reverse

Regular dodecagonal coins include:

• British threepenny bit from 1937 to 1971, when it ceased to be legal tender.
• British One Pound Coin to be introduced in 2017.
• Australian 50-cent coin
• Fijian 50 cents
• Tongan 50-seniti, since 1974
• Solomon Islands 50 cents
• Croatian 25 kuna
• Romanian 5000 lei, 2001–2005
• Canadian penny, 1982–1996
• South Vietnamese 25 đồng, 1968–1975
• Zambian 50 ngwee, 1969–1992
• Malawian 50 tambala, 1986–1995
• Mexican 20 centavos, 1992-2009

See also

• Dodecagonal number
• Dodecahedron – a regular polyhedron with 12 pentagonal faces.
• Dodecagram

External links

• Weisstein, Eric W. "Dodecagon". MathWorld.
• Kürschak's Tile and Theorem
• Definition and properties of a dodecagon With interactive animation