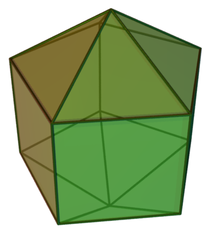
Elongated pentagonal bipyramid
| Elongated pentagonal bipyramid | |
|---|---|
 | |
| Type | Johnson J15 – J16 – J17 |
| Faces | 10 triangles 5 squares |
| Edges | 25 |
| Vertices | 12 |
| Vertex configuration | 10(32.42) 2(35) |
| Symmetry group | D5h, [5,2], (*522) |
| Rotation group | D5, [5,2]+, (522) |
| Dual polyhedron | Pentagonal bifrustum |
| Properties | convex |
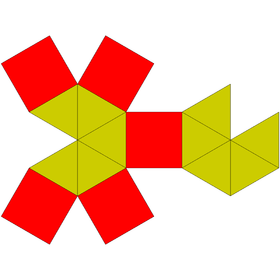
| Net | |
 | |
In geometry, the elongated pentagonal bipyramid is a polyhedron constructed by attaching two pentagonal pyramids onto the base of a pentagonal prism. It is an example of Johnson solid.
Construction
[edit]The elongated pentagonal bipyramid is constructed from a pentagonal prism by attaching two pentagonal pyramids onto its bases, a process called elongation. These pyramids cover the pentagonal faces so that the resulting polyhedron ten equilateral triangles and five squares.[1][2] A convex polyhedron in which all of the faces are regular polygons is the Johnson solid. The elongated pentagonal bipyramid is among them, enumerated as the sixteenth Johnson solid .[3]
Properties
[edit]The surface area of an elongated pentagonal bipyramid is the sum of all polygonal faces' area: ten equilateral triangles, and five squares. Its volume can be ascertained by dissecting it into two pentagonal pyramids and one regular pentagonal prism and then adding its volume. Given an elongated pentagonal bipyramid with edge length , they can be formulated as:[2]

It has the same three-dimensional symmetry group as the pentagonal prism, the dihedral group of order 20. Its dihedral angle can be calculated by adding the angle of the pentagonal pyramid and pentagonal prism:[4]
- the dihedral angle of an elongated pentagonal bipyramid between two adjacent triangular faces is that of a pentagonal pyramid between those, 138.19°.
- the dihedral angle of an elongated pentagonal bipyramid between two adjacent square faces is that of a regular pentagonal prism, the internal angle of a regular pentagon, 108°.
- the dihedral angle of an elongated pentagonal bipyramid between square-to-triangle is the sum of the dihedral angle of a pentagonal pyramid between triangle-to-pentagon with that of a pentagonal prism between square-to-pentagon, 37.38° + 90° = 127.38°.
The dual of the elongated square bipyramid is a pentagonal bifrustum.
References
[edit]- ^ Rajwade, A. R. (2001), Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem, Texts and Readings in Mathematics, Hindustan Book Agency, doi:10.1007/978-93-86279-06-4, ISBN 978-93-86279-06-4.
- ^ a b Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
- ^ Francis, Darryl (August 2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177.
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, S2CID 122006114, Zbl 0132.14603.






