Pinhole camera

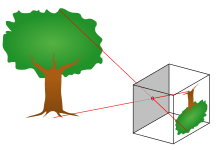
A pinhole camera is a simple camera without a lens but with a tiny aperture (the so-called pinhole)—effectively a light-proof box with a small hole in one side. Light from a scene passes through the aperture and projects an inverted image on the opposite side of the box, which is known as the camera obscura effect. The size of the images depends on the distance between the object and the pinhole.
A Worldwide Pinhole Photography Day is observed on the last Sunday of April, every year.[1]
History
[edit]Camera obscura
[edit]The camera obscura or pinhole image is a natural optical phenomenon. Early known descriptions are found in the Chinese Mozi writings (circa 500 BCE)[2] and the Aristotelian Problems (circa 300 BCE – 600 CE).[3]
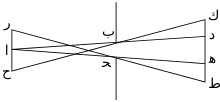
Ibn al-Haytham (965–1039), an Arab physicist also known as Alhazen, described the camera obscura effect. Over the centuries others started to experiment with it, mainly in dark rooms with a small opening in shutters, mostly to study the nature of light and to safely watch solar eclipses.[5]
Giambattista Della Porta wrote in 1558 in his Magia Naturalis about using a concave mirror to project the image onto paper and to use this as a drawing aid.[6] However, at about the same time, the use of a lens instead of a pinhole was introduced. In the 17th century, the camera obscura with a lens became a popular drawing aid that was further developed into a mobile device, first in a little tent and later in a box. The photographic camera, as developed early in the 19th century, was basically an adaptation of the box-type camera obscura with a lens.
The term "pin-hole" in the context of optics was found in James Ferguson's 1764 book Lectures on select subjects in mechanics, hydrostatics, pneumatics, and optics.[7][8]
Early pinhole photography
[edit]The first known description of pinhole photography is found in the 1856 book The Stereoscope by Scottish inventor David Brewster, including the description of the idea as "a camera without lenses, and with only a pin-hole".
Sir William Crookes and William de Wiveleslie Abney were other early photographers to try the pinhole technique.[9]
Film and integral photography experiments
[edit]According to inventor William Kennedy Dickson, the first experiments directed at moving pictures by Thomas Edison and his researchers took place around 1887 and involved "microscopic pin-point photographs, placed on a cylindrical shell". The size of the cylinder corresponded with their phonograph cylinder as they wanted to combine the moving images with sound recordings. Problems arose in recording clear pictures "with phenomenal speed" and the "coarseness" of the photographic emulsion when the pictures were enlarged. The microscopic pin-point photographs were soon abandoned.[10] In 1893 the Kinetoscope was finally introduced with moving pictures on celluloid film strips. The camera that recorded the images, dubbed Kinetograph, was fitted with a lens.
Eugène Estanave experimented with integral photography, exhibiting a result in 1925 and publishing his findings in La Nature. After 1930 he chose to continue his experiments with pinholes replacing the lenticular screen.[11]
Usage
[edit]The image of a pinhole camera may be projected onto a translucent screen for a real-time viewing (used for safe observation of solar eclipses) or to trace the image on paper. But it is more often used without a translucent screen for pinhole photography with photographic film or photographic paper placed on the surface opposite to the pinhole aperture.
A common use of pinhole photography is to capture the movement of the sun over a long period of time. This type of photography is called solarigraphy. Pinhole photography is used for artistic reasons, but also for educational purposes to let pupils learn about, and experiment with, the basics of photography.
Pinhole cameras with CCDs (charge-coupled devices) are sometimes used for surveillance because they are difficult to detect.
Related cameras, image forming devices, or developments from it include Franke's widefield pinhole camera, the pinspeck camera, and the pinhead mirror.
Modern manufacturing has enabled the production of high quality pinhole lenses[12] that can be applied to digital cameras.
Construction
[edit]
Pinhole cameras can be handmade by the photographer for a particular purpose. In its simplest form, the photographic pinhole camera can consist of a light-tight box with a pinhole in one end, and a piece of film or photographic paper wedged or taped into the other end. A flap of cardboard with a tape hinge can be used as a shutter. The pinhole may be punched or drilled using a sewing needle or small diameter bit through a piece of tinfoil or thin aluminum or brass sheet. This piece is then taped to the inside of the light-tight box behind a hole cut through the box. A cylindrical oatmeal container may be made into a pinhole camera.
The interior of an effective pinhole camera is black to avoid any reflection of the entering light onto the photographic material or viewing screen.[13]
Pinhole cameras can be constructed with a sliding film holder or back so the distance between the film and the pinhole can be adjusted. This allows the angle of view of the camera to be changed and also the effective f-stop ratio of the camera. Moving the film closer to the pinhole will result in a wide angle field of view and shorter exposure time. Moving the film farther away from the pinhole will result in a telephoto or narrow-angle view and longer exposure time.
Pinhole cameras can also be constructed by replacing the lens assembly in a conventional camera with a pinhole. In particular, compact 35 mm cameras whose lens and focusing assembly have been damaged can be reused as pinhole cameras—maintaining the use of the shutter and film winding mechanisms. As a result of the enormous increase in f-number, while maintaining the same exposure time, one must use a fast film in direct sunshine.
Pinholes (homemade or commercial) can be used in place of the lens on an SLR. Use with a digital SLR allows metering and composition by trial and error, and is effectively free, so is a popular way to try pinhole photography.[14]
Selection of pinhole size
[edit]Up to a certain point, the smaller the hole, the sharper the image, but the dimmer the projected image. Optimally, the size of the aperture should be 1/100 or less of the distance between it and the projected image.
Within limits, a small pinhole through a thin surface will result in a sharper image resolution because the projected circle of confusion at the image plane is practically the same size as the pinhole. An extremely small hole, however, can produce significant diffraction effects and a less clear image due to the wave properties of light.[15] Additionally, vignetting occurs as the diameter of the hole approaches the thickness of the material in which it is punched, because the sides of the hole obstruct the light entering at anything other than 90 degrees.
The best pinhole is perfectly round (since irregularities cause higher-order diffraction effects) and in an extremely thin piece of material. Industrially produced pinholes benefit from laser etching, but a hobbyist can still produce pinholes of sufficiently high quality for photographic work.
A method of calculating the optimal pinhole diameter was first published by Joseph Petzval in 1857. The smallest possible diameter of the image point and therefore the highest possible image resolution and the sharpest image are given when:[16]
(Where d is the pinhole diameter, f is the distance from pinhole to image plane or “focal length” and λ is the wavelength of light.)
The first to apply wave theory to the problem was Lord Rayleigh in 1891. But due to some incorrect and arbitrary deductions he arrived at:[17]
So his optimal pinhole was approximatively 1/3 bigger than Petzval’s.
The correct optimum can be found with Fraunhofer approximation of the diffraction pattern behind a circular aperture at:
This may be shortened to: (When d and f in millimetres and λ = 550 nm = 0.00055 mm, corresponding to yellow-green.)
For a pinhole-to-film distance of 1 inch or 25.4 mm, this works out to a pinhole of 0.185 mm (185 microns) in diameter. For f= 50 mm the optimal diameter is 0.259 mm.
The depth of field is basically infinite, but this does not mean that no optical blurring occurs. The infinite depth of field means that image blur depends not on object distance but on other factors, such as the distance from the aperture to the film plane, the aperture size, the wavelength(s) of the light source, and motion of the subject or canvas. Additionally, pinhole photography can not avoid the effects of haze.

In the 1970s, Young measured the resolution limit of the pinhole camera as a function of pinhole diameter[18] and later published a tutorial in The Physics Teacher.[19] Partly to enable a variety of diameters and focal lengths, he defined two normalized variables: resolution limit divided by the pinhole radius, and focal length divided by the quantity s2/λ, where s is the radius of the pinhole and λ is the wavelength of the light, typically about 550 nm. His results are plotted in the figure.
On the left-side of the graph, the pinhole is large, and geometric optics applies; the resolution limit is about 1.5 times the radius of the pinhole. (Spurious resolution is also seen in the geometric-optics limit.) On the right-side, the pinhole is small, and Fraunhofer diffraction applies; the resolution limit is given by the far-field diffraction formula shown in the graph and now increases as the pinhole is made smaller. In this formula, the radius of the pinhole is used instead of its diameter, that's why the constant is 0.61 instead of the more usual 1.22. In the region of near-field diffraction (or Fresnel diffraction), the pinhole focuses the light slightly, and the resolution limit is minimized when the focal length f (the distance between the pinhole and the film plane) is given by f = s2/λ. At this focal length, the pinhole focuses the light slightly, and the resolution limit is about 2/3 of the radius of the pinhole. The pinhole, in this case, is equivalent to a Fresnel zone plate with a single zone. The value s2/λ is in a sense the natural focal length of the pinhole.[citation needed]
The relation f = s2/λ yields an optimum pinhole diameter d = 2√fλ, so the experimental value differs slightly from the estimate of Petzval, above.
Calculating the f-number and required exposure
[edit]
The f-number of the camera may be calculated by dividing the distance from the pinhole to the imaging plane (the focal length) by the diameter of the pinhole. For example, a camera with a 0.5 mm diameter pinhole, and a 50 mm focal length would have an f-number of 50/0.5, or 100 (f/100 in conventional notation).
Due to the large f-number of a pinhole camera, exposures will often encounter reciprocity failure.[20] Once exposure time has exceeded about 1 second for film or 30 seconds for paper, one must compensate for the breakdown in linear response of the film/paper to intensity of illumination by using longer exposures.
Exposures projected on to modern light-sensitive photographic film can typically range from five seconds up to as much as several hours, with smaller pinholes requiring longer exposures to produce the same size image. Because a pinhole camera requires a lengthy exposure, its shutter may be manually operated, as with a flap made of opaque material to cover and uncover the pinhole.
Natural pinhole phenomenon
[edit]
A pinhole camera effect can sometimes occur naturally. Small "pinholes" formed by the gaps between overlapping tree leaves will create replica images of the sun on flat surfaces. During an eclipse, this produces small crescents in the case of a partial eclipse, or hollow rings in the case of an annular eclipse. Disco balls can also function as natural reflective pinhole cameras (also known as a pinhead mirror).[21]
Photographers using the technique
[edit]See also
[edit]| Alternative photography |
|---|
 |
- Camera obscura (usually employs a lens)
- Dirkon
- Henry Fox Talbot
- Ibn al-Haytham
- Nautilus (whose pinhole eye functions as a camera obscura)
- Pinhole camera model
- Pinhole glasses
- Pinhole occluder, a similar device used by ophthalmologists
- Spatial filter
- The Great Picture
- Zone plate
References
[edit]- ^ "Worldwide Pinhole Photography Day". pinholeday.org.
- ^ "CS194-26: proj2". inst.eecs.berkeley.edu. Retrieved 2022-01-07.
- ^ "Camera Obscura: Ancestor of Modern Photography | Encyclopedia.com". www.encyclopedia.com. Retrieved 2022-01-07.
- ^ Kirkpatrick, Larry D.; Francis, Gregory E. (2007). "Light". Physics: A World View (6 ed.). Belmont, California: Thomson Brooks/Cole. p. 339. ISBN 978-0-495-01088-3.
- ^ Plott, John C. (1984). Global History of Philosophy: The Period of scholasticism (part one). Motilal Banarsidass Publ. p. 460. ISBN 978-0-89581-678-8.
- ^ Zik, Yaakov; Hon, Giora (10 February 2019). "Claudius Ptolemy and Giambattista Della Porta: Two Contrasting Conceptions of Optics". arXiv:1902.03627 [physics.hist-ph].
- ^ "Nick's pinhole photography". idea.uwosh.edu. Archived from the original on 30 September 2018. Retrieved 29 January 2018.
- ^ Ferguson, James (1764). Lectures on select subjects in mechanics, hydrostatics, pneumatics, and optics with the use of the globes, the art of dialing, and the calculation of the mean times of new and full moone and eclipses.
- ^ "Pinhole photography history". photo.net. Archived from the original on 2017-02-02. Retrieved 29 January 2018.
- ^ History of the kinetograph, kinetoscope, & kinetophonograph [by] W. K. L. Dickson and Antonia Dickson. Literature of cinema. Arno Press. 1970. hdl:2027/mdp.39015002595158. ISBN 978-0-405-01611-0.
- ^ Timby, Kim (31 July 2015). 3D and Animated Lenticular Photography. Walter de Gruyter GmbH & Co KG. ISBN 978-3-11-044806-1.
- ^ "Pinhole Pro Lens by Thingyfy". 2018.
- ^ "How to Make and Use a Pinhole Camera". Archived from the original on 2016-03-05.
- ^ "V3 - digital transformation news, analysis and insight". v3.co.uk. Archived from the original on 19 April 2009. Retrieved 18 October 2018.
- ^ Hecht, Eugene (1998). "5.7.6 The Camera". Optics (3rd ed.). Addison-Wesley. ISBN 0-201-30425-2.
- ^ Petzval, J. (1857). Bericht über dioptrische Untersuchungen [Report on dioptric examinations]. Sitzungsberichte der kaiserlichen Akademie der Wissenschaften, mathematisch-naturwissenschaftliche Classe (in German). Vol. 26. Aus der Kais. Kön. Hof- und Staatsdruckerei, in commission bei Karl Gerold's Sohn. pp. 33–90. OCLC 16122711.
- ^ Rayleigh, Lord (February 1891). "X. On pin-hole photography" (PDF). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 31 (189): 87–99. doi:10.1080/14786449108620080.
- ^ Young, M. (1 December 1971). "Pinhole Optics". Applied Optics. 10 (12): 2763–2767. Bibcode:1971ApOpt..10.2763Y. doi:10.1364/ao.10.002763. PMID 20111427.
- ^ Young, Matt (December 1989). "The pinhole camera: Imaging without lenses or mirrors". The Physics Teacher. 27 (9): 648–655. Bibcode:1989PhTea..27..648Y. doi:10.1119/1.2342908.
- ^ breslin, nancy a. "Nancy Breslin's pinhole camera exposure tips". www.nancybreslin.com. Retrieved 29 January 2018.
- ^ Cumming, Robert J; Pietrow, Alexander G M; Pietrow, Livia; Cavallius, Maria; Petit dit de la Roche, Dominique; Pietrow, Casper; Schroetter, Ilane; Skan, Moa (March 2024). "Why every observatory needs a disco ball". Physics Education. 59 (2): 025012. arXiv:2309.14173. Bibcode:2024PhyEd..59b5012C. doi:10.1088/1361-6552/ad1fa0.
Further reading
[edit]- Renner, Eric (2012). Pinhole Photography: From Historic Technique to Digital Application. CRC Press. ISBN 978-1-136-09534-4.
- Handojo, Andrianto (15 October 1989). "Solar eclipse observation: some simple devices". Applied Optics. 28 (20): 4293–4297. Bibcode:1989ApOpt..28.4293H. doi:10.1364/AO.28.004293. PMID 20555865.
- Maithong, Wiraporn; Pancharoen, Warisa (2020). "Creation of Pinhole Camera for Solar Eclipse Using STEM Education". 2020 5th International STEM Education Conference (ISTEM-Ed). pp. 131–133. doi:10.1109/iSTEM-Ed50324.2020.9332718. ISBN 978-1-7281-9570-4.
- Straker, Stephen (1981). "Kepler, Tycho, and the 'Optical Part of Astronomy': the genesis of Kepler's theory of pinhole images". Archive for History of Exact Sciences. 24 (4): 267–293. doi:10.1007/BF00357311.
- Bakich, Michael E. (2016). "Projects for Observing the Sun (And the Eclipse)". Your Guide to the 2017 Total Solar Eclipse. The Patrick Moore Practical Astronomy Series. pp. 195–221. doi:10.1007/978-3-319-27632-8_18. ISBN 978-3-319-27630-4.
External links
[edit]![]() Media related to Pinhole cameras at Wikimedia Commons
Media related to Pinhole cameras at Wikimedia Commons
- pinhole.cz
- Pinhole Photography by Vladimir Zivkovic
- Worldwide Pinhole Photography Day website
- An easy way to convert a DSLR to a pinhole camera
- Pinhole Photography and Camera Design Calculators
- Oregon Art Beat: Pinhole Photos by Zeb Andrews
- Civil War 150 Pinhole Project by Michael Falco
- https://vaidasphotos.com/pinhole






