Sigmoid function
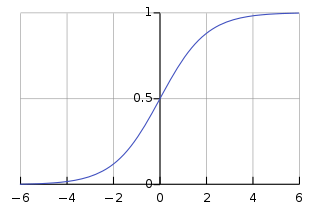
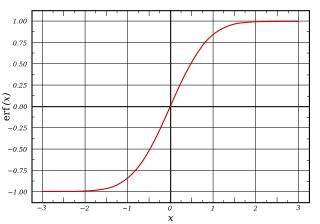
A sigmoid function is any mathematical function whose graph has a characteristic S-shaped or sigmoid curve.
A common example of a sigmoid function is the logistic function shown in the first figure and defined by the formula:[1]
Other standard sigmoid functions are given in the Examples section. In some fields, most notably in the context of artificial neural networks, the term "sigmoid function" is used as an alias for the logistic function.
Special cases of the sigmoid function include the Gompertz curve (used in modeling systems that saturate at large values of x) and the ogee curve (used in the spillway of some dams). Sigmoid functions have domain of all real numbers, with return (response) value commonly monotonically increasing but could be decreasing. Sigmoid functions most often show a return value (y axis) in the range 0 to 1. Another commonly used range is from −1 to 1.
A wide variety of sigmoid functions including the logistic and hyperbolic tangent functions have been used as the activation function of artificial neurons. Sigmoid curves are also common in statistics as cumulative distribution functions (which go from 0 to 1), such as the integrals of the logistic density, the normal density, and Student's t probability density functions. The logistic sigmoid function is invertible, and its inverse is the logit function.
Definition[edit]
A sigmoid function is a bounded, differentiable, real function that is defined for all real input values and has a non-negative derivative at each point[1] [2] and exactly one inflection point.
Properties[edit]
In general, a sigmoid function is monotonic, and has a first derivative which is bell shaped. Conversely, the integral of any continuous, non-negative, bell-shaped function (with one local maximum and no local minimum, unless degenerate) will be sigmoidal. Thus the cumulative distribution functions for many common probability distributions are sigmoidal. One such example is the error function, which is related to the cumulative distribution function of a normal distribution; another is the arctan function, which is related to the cumulative distribution function of a Cauchy distribution.
A sigmoid function is constrained by a pair of horizontal asymptotes as .
A sigmoid function is convex for values less than a particular point, and it is concave for values greater than that point: in many of the examples here, that point is 0.
Examples[edit]

- Logistic function
- Hyperbolic tangent (shifted and scaled version of the logistic function, above)
- Arctangent function
- Gudermannian function
- Error function
- Generalised logistic function
- Smoothstep function
- Some algebraic functions, for example
- and in a more general form[3]
- Up to shifts and scaling, many sigmoids are special cases of whereis the inverse of the negative Box–Cox transformation, and and are shape parameters.[4]
- Smooth transition function[5] normalized to (-1,1):
Applications[edit]
Many natural processes, such as those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a specific mathematical model is lacking, a sigmoid function is often used.[6]
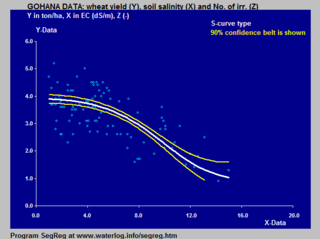
The van Genuchten–Gupta model is based on an inverted S-curve and applied to the response of crop yield to soil salinity.
Examples of the application of the logistic S-curve to the response of crop yield (wheat) to both the soil salinity and depth to water table in the soil are shown in modeling crop response in agriculture.
In artificial neural networks, sometimes non-smooth functions are used instead for efficiency; these are known as hard sigmoids.
In audio signal processing, sigmoid functions are used as waveshaper transfer functions to emulate the sound of analog circuitry clipping.[7]
In biochemistry and pharmacology, the Hill and Hill–Langmuir equations are sigmoid functions.
In computer graphics and real-time rendering, some of the sigmoid functions are used to blend colors or geometry between two values, smoothly and without visible seams or discontinuities.
Titration curves between strong acids and strong bases have a sigmoid shape due to the logarithmic nature of the pH scale.
The logistic function can be calculated efficiently by utilizing type III Unums.[8]
See also[edit]
- Step function – Linear combination of indicator functions of real intervals
- Sign function – Mathematical function returning -1, 0 or 1
- Heaviside step function – Indicator function of positive numbers
- Logistic regression – Statistical model for a binary dependent variable
- Logit – Function in statistics
- Softplus function – Activation function
- Soboleva modified hyperbolic tangent – Mathematical activation function in data analysis
- Softmax function – Smooth approximation of one-hot arg max
- Swish function – Mathematical activation function in data analysis
- Weibull distribution – Continuous probability distribution
- Fermi–Dirac statistics – Statistical description for the behavior of fermions
References[edit]
- ^ a b Han, Jun; Morag, Claudio (1995). "The influence of the sigmoid function parameters on the speed of backpropagation learning". In Mira, José; Sandoval, Francisco (eds.). From Natural to Artificial Neural Computation. Lecture Notes in Computer Science. Vol. 930. pp. 195–201. doi:10.1007/3-540-59497-3_175. ISBN 978-3-540-59497-0.
- ^ Ling, Yibei; He, Bin (December 1993). "Entropic analysis of biological growth models". IEEE Transactions on Biomedical Engineering. 40 (12): 1193–2000. doi:10.1109/10.250574. PMID 8125495.
- ^ Dunning, Andrew J.; Kensler, Jennifer; Coudeville, Laurent; Bailleux, Fabrice (2015-12-28). "Some extensions in continuous methods for immunological correlates of protection". BMC Medical Research Methodology. 15 (107): 107. doi:10.1186/s12874-015-0096-9. PMC 4692073. PMID 26707389.
- ^ "grex --- Growth-curve Explorer". GitHub. 2022-07-09. Archived from the original on 2022-08-25. Retrieved 2022-08-25.
- ^ EpsilonDelta (2022-08-16). "Smooth Transition Function in One Dimension | Smooth Transition Function Series Part 1". 13:29/14:04 – via www.youtube.com.
- ^ Gibbs, Mark N.; Mackay, D. (November 2000). "Variational Gaussian process classifiers". IEEE Transactions on Neural Networks. 11 (6): 1458–1464. doi:10.1109/72.883477. PMID 18249869. S2CID 14456885.
- ^ Smith, Julius O. (2010). Physical Audio Signal Processing (2010 ed.). W3K Publishing. ISBN 978-0-9745607-2-4. Archived from the original on 2022-07-14. Retrieved 2020-03-28.
- ^ Gustafson, John L.; Yonemoto, Isaac (2017-06-12). "Beating Floating Point at its Own Game: Posit Arithmetic" (PDF). Archived (PDF) from the original on 2022-07-14. Retrieved 2019-12-28.
Further reading[edit]
- Mitchell, Tom M. (1997). Machine Learning. WCB McGraw–Hill. ISBN 978-0-07-042807-2.. (NB. In particular see "Chapter 4: Artificial Neural Networks" (in particular pp. 96–97) where Mitchell uses the word "logistic function" and the "sigmoid function" synonymously – this function he also calls the "squashing function" – and the sigmoid (aka logistic) function is used to compress the outputs of the "neurons" in multi-layer neural nets.)
- Humphrys, Mark. "Continuous output, the sigmoid function". Archived from the original on 2022-07-14. Retrieved 2022-07-14. (NB. Properties of the sigmoid, including how it can shift along axes and how its domain may be transformed.)
External links[edit]
- "Fitting of logistic S-curves (sigmoids) to data using SegRegA". Archived from the original on 2022-07-14.























