Talk:Golden ratio/Archive 7
| This is an archive of past discussions about Golden ratio. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | ← | Archive 5 | Archive 6 | Archive 7 | Archive 8 | Archive 9 |
Semi-protected edit request on 6 July 2017
This edit request to Golden ratio has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
I would appreciate it if you could add this novel and cited continued fraction for the Golden ratio below the heading "Alternative forms" and below the other two continued fractions. Below is the coding.
An alternative generalized continued fraction of the Golden Ratio consists of the squares of the Fibonacci numbers and the Golden Rectangle areas. [1]
- 74.192.56.20 (talk) 15:49, 6 July 2017 (UTC)
 Not done: please provide reliable sources that support the change you want to be made. Eggishorn (talk) (contrib) 19:25, 6 July 2017 (UTC)
Not done: please provide reliable sources that support the change you want to be made. Eggishorn (talk) (contrib) 19:25, 6 July 2017 (UTC)
References
- ^ Foster, Tony (July 6, 2017). "Theorem of the Day: Theorem no. 203". Robin Whitty. Retrieved July 6, 2017.
Semi-protected edit request on 11 October 2017
This edit request to Golden ratio has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
Top equation should have "proportional to" symbols (alpha) instead of the equals sign symbols. 68.3.121.10 (talk) 17:44, 11 October 2017 (UTC)
 Not done. Equal signs are correct, so using proportional-to signs would make the equation unnecessarily more general. Gap9551 (talk) 22:18, 11 October 2017 (UTC)
Not done. Equal signs are correct, so using proportional-to signs would make the equation unnecessarily more general. Gap9551 (talk) 22:18, 11 October 2017 (UTC)
Negative root in the evaluation.
The article says:
---
Because φ is the ratio between positive quantities φ is necessarily positive::
Because φ is the ratio between positive quantities φ is necessarily positive: --- Is that necessarily right, because if you take the -0.6180 as a vector you still get a golden rectangle but the other way round because -0.6180 = -1/φ? -- Q Chris (talk) 12:25, 7 November 2017 (UTC)
- I think you have copied it incorrectly. The article is correct. The golden ratio is normally considered to be a positive number, as it’s the ratio of lengths and a length, and lengths are always positive. A quadratic has two roots, so you take the positive one. The other negative root also satisfies the equation, and is related to the golden ratio in the way you describe. But it’s not the solution we are looking for.--JohnBlackburnewordsdeeds 12:44, 7 November 2017 (UTC)
The Greeks learned from the educators in Khemet (today called Egypt)
It is crucial to edit the article to reflect the fact that the Golden Ratio was taught to Greeks by Africans in Egypt. Further, there are early signs of fractals (created via the golden ratio) in homes of African kings. See: http://www.academia.edu/3164223/Follow_the_Golden_Ratio_from_Africa_to_the_Bauhaus_for_a_Cross-Cultural_Aesthetic_for_Images — Preceding unsigned comment added by 2604:2000:DDC7:1700:B917:9804:2C3A:E2AE (talk) 09:55, 18 November 2017 (UTC)
Removed section
I just removed a section that demonstrated the value is (1 + √5) / 2 as it made no sense. In particular the first step is to use the Dividing a line segment by exterior division method, but the value can be trivially deduced from that, as the line MC has length √5 / 2. It then used a rather elaborate construction to make everything 2 times as big, before dividing by 2 in the final calculation. But as the result can be deduced from the first step the rest is redundant. It was not possible to refer to any sources to see what was meant by it, as there were no sources, so the only thing to do was remove it.--JohnBlackburnewordsdeeds 12:54, 19 August 2017 (UTC)
- There was a similar discussion on the German side. As I understand it the intent is to provide derivation of the value of the golden ratio by geometric rather than algebraic means. So instead solving a quadratic equation, one does a simply compute lengths of line segments, a geometric derivation if you will.
- However the drawing and the explanation mix this basic idea with a ruler and compass construction aspects, i.e. showing in parallel that a line segment with the length of the golden ratio can be constructed with a classic Greek ruler and compass construction. As a result the idea of simple geometric derivation becomes rather muddled and instead of being a potentially helpful alternative to the algebraic derivation it probably just confuses readers.--Kmhkmh (talk) 14:09, 19 August 2017 (UTC)
- Improvement
- This derivation can also be found with a compass-and-straightedge construction:

- The initial situation is the dividing a line segment by exterior division with the longer side . This results in the right triangle with the cathetuses and the hypotenuse such as . From the segment follows
- ---
- I hope the improvement has succeeded me.--Petrus3743 (talk) 19:45, 19 August 2017 (UTC)
- It's still unclear to me whether you are trying to (1) describe how to construct the golden ratio using compass and straightedge, (2) derive the algebraic value of the golden ratio using analytic geometry, (3) prove that the extreme-and-mean definition of the golden ratio is equivalent to some other definition, (4) something else. —David Eppstein (talk) 20:00, 19 August 2017 (UTC)
- @David Eppstein, to (1) the description is described in dividing a line segment by exterior division.
- I want to illustrate the value of only graphically on a number line. I would also like to reach readers with less mathmatical knowledge, but with geometric knowledge. The previous construction had only one fault, it was much too long!--Petrus3743 (talk) 20:32, 19 August 2017 (UTC)
- φ is a constructible number, a simple one, so is easy to construct with compass and straight edge. But that’s already demonstrated here (though it could do with cleaning up a bit). I don’t see what else what I removed or the above adds to this.--JohnBlackburnewordsdeeds 21:27, 19 August 2017 (UTC)
- Text improvement (attempt)
- This derivation can also be found with a compass-and-straightedge construction:
- The initial situation is the construction of the dividing a line segment by exterior division with the longer side . The adjoining representation shows again, the right triangle with the cathetuses and with according to Pythagorean theorem the hypotenuse is . The circular arc around with the radius produces on a number line the shorter side and thus with the equivalent length . In summary, this also results
- ---
- I hope you can understand it, because my English isn't good! --Petrus3743 (talk) 12:10, 20 August 2017 (UTC)
It does not change what I wrote: I still don’t see what this adds to the fact that it is constructible, as is already demonstrated in the article.--JohnBlackburnewordsdeeds 12:49, 20 August 2017 (UTC)
- Here the algebraic and the geometric derivation are shown... Geometrische Herleitung des Zahlenwertes--Petrus3743 (talk) 07:23, 7 December 2017 (UTC)
- That is the German Wikipedia, so not a useful or reliable source, and does not explain anything for those of us who do not understand German.--JohnBlackburnewordsdeeds 08:25, 7 December 2017 (UTC)
Incorrect Number in "History" Section?
Hi everyone, I am using this paper for research and noticed that under the "History" section, it states that the Golden Ratio is equal to 0.6180340. Am I missing something, or should it be 1.6180340? — Preceding unsigned comment added by 66.160.201.63 (talk) 03:31, 20 April 2018 (UTC)
- It does say "(inverse) golden ratio", The inverse, 1/ φ = φ - 1, is effectively the same ratio but the other way round: b/a instead of a/b. And you just need to add 1 to get the number we use today.--JohnBlackburnewordsdeeds 03:41, 20 April 2018 (UTC)
Superstition and pareidolia/apophenia
What does this nonsense in the article even mean: "Both Egyptian pyramids and the regular square pyramids that resemble them can be analyzed with respect to the golden ratio and other ratios."
One could just as wel write: "Both Egyptian pyramids and the regular square pyramids that resemble them can be analyzed with respect to the football scores of the holy year 1983."
If all that can be found is that there are two distances with ratio that is approximately 2, 3, 4, 5, 7, pi, e, golden ratio, square root of two, ... you have found nothing of interest. Because that is also the case for any flower pot, toilet, or hair dryer. Try it out yourself.
Please label phantasies of higher meaning as such, and warn readers of the trap of apophenia.
109.131.19.153 (talk) 16:49, 9 June 2018 (UTC)
- It is merely a brief introductory summary of the two well-sourced and much more detailed sections that follow this sentence. —David Eppstein (talk) 16:52, 9 June 2018 (UTC)
10,000,000 digits of Phi
I recently computed 10,000,000 digits of Phi. It seems like it's the most digits available on the Internet (I searched alone, so I may have missed some intel though). I figured out it would be nice to post the link here:
https://phi.nodot.fr/ — Preceding unsigned comment added by 80.215.198.247 (talk) 08:50, 16 July 2018 (UTC)
Missing Value
The text or image following "It is an irrational number with a value of: " does not render on my screen (and probably also does not render for some other users as well). Thus, this article does not adequately inform all users of the value of the golden ratio. — Preceding unsigned comment added by Cowlinator (talk • contribs) 08:15, 27 August 2018 (UTC)
- Please look at your user preferences tab, under appearance &rarrow; mathematics. If you can't view this formula, then the way your browser displays mathematical formulas in Wikipedia is broken, and you need to change to a different display option. There is nothing unusual about how this particular formula in this particular article is formatted. —David Eppstein (talk) 14:22, 27 August 2018 (UTC)
Hull and core of the stellated dodecahedra
I just made this table for Kepler–Poinsot polyhedron, and thought it might also be a nice example for Golden ratio.
It shows that the hull of the small stellated dodecahedron is times bigger than the core,
and the hull of the great stellated dodecahedron is times bigger than the core.
(The midradius is a common measure to compare the size of a dodecahedron and an icosahedron.)
| hull | star polyhedron | core | ||
|---|---|---|---|---|

|

|

|
||

|

|

|
||
| difference 1 | sum 1 | |||
| Same numbers for decagram and pentagram | ||||
|---|---|---|---|---|
| hull | star polygon | core | ||

|

|

|
||

|

|

|
||
| difference 1 | sum 1 | |||
Greetings, Watchduck (quack) 22:45, 15 September 2018 (UTC)
- I think the first one follows directly from the ratios of lengths in a pentagram, as illustrated by a diagram in the article. I suspect something similar is happening in the second case though it‘s less obvious. Both stellated shapes have pentagram faces.--JohnBlackburnewordsdeeds 01:03, 16 September 2018 (UTC)
- I doubt that something genuinely 3D can follow directly from something 2D. I realized that pentagram and decagram have the same ratios of hull to core, and added the table above. Watchduck (quack) 12:13, 16 September 2018 (UTC)
- It does though. The polyhedra are connected by the stellated polyhedra. The stellated polyhedra have pentagrams for faces. The ratios of all lengths, e.g. all sides of triangles, in a pentagram is the golden ratio. In particular the innermost and outmost pentagons are connected by the golden ratio, and the edges of these coincide with the edges of the inner and outer polyhedra.
- So this result is not that surprising. Just as π arises in many situations which have an underlying circular or spherical aspect, the golden ratio arises in many places where shapes with 5-fold symmetry are involved. So many that adding them to the article would be excessive, unless they are particularly interesting and notable, according to reliable sources.--JohnBlackburnewordsdeeds 20:28, 16 September 2018 (UTC)
- In the context of discussing the Kepler-Poinsot solids, this might be of more interest, but I think it would be better there if we used the actual great dodecahedron {5, 5/2} as the core of {5/2, 3} instead of the icosahedron which shares its vertices and edges. Then the stellation sequence of {5, 3} is shown more clearly, passing through {5/2, 5} and {5, 5/2} on the way to the final stellation {5/2, 3}. Double sharp (talk) 04:58, 18 September 2018 (UTC)
- Feel free to bring it up on the right talk page. But I have to say that I find your argument extremely esoteric. You could just as well argue, that the core of a pentagram should be something other than a small pentagon. Watchduck (quack) 18:34, 18 September 2018 (UTC)
inconsistent phi symbol
Both and appear in the article. Is there a reason to not change all instances (after the place in the introduction that shows both forms) to use the same symbol?
Jmichael ll (talk) 08:45, 25 November 2018 (UTC)
- It should be more consistent. In my opinion, the varphi form seems appropriate for equations, but standard prose should just use phi. UpdateNerd (talk) 08:50, 25 November 2018 (UTC)
- I'm not sure this is technically possible except for within
<math>...</math>tags. Otherwise, different fonts may render phi differently. Even just looking at this article, one of phis in text mode renders as a normal \phi for me, but then I see it as a \varphi when I go to edit. I don't know if there's really a good solution here. –Deacon Vorbis (carbon • videos) 17:46, 26 November 2018 (UTC)- The solution is to use the same style of mathematics formatting for all formulas throughout the article, so that markup that is intended to render the same really does render the same. I think varphi is the one we should be using, but it's more important to be consistent. —David Eppstein (talk) 17:50, 26 November 2018 (UTC)
Section d'Or
In the article it is mentioned: "However, despite this general interest in mathematical harmony, the paintings featured in the celebrated 1912 Salon de la Section d'Or exhibition did not use the golden ratio itself in their compositions." (Livio 2003, p. 169)
However, upon close examination, the painting reproduced below by Albert Gleizes, exhibited at the 1912 Salon de la Section d'Or (catalogue no. 40), most conspicuously did employ the golden ratio. The proportions of the canvas correspond exactly to the golden rectangle (a ratio of 1 to 1.618 ± 0.01). The probability this is a chance occurrence would be exceedingly small. This work has a rare dimension of 105 x 171 cm. Gleizes, as most artists at the time, generally used standard format chassis (stretchers), which are not golden rectangles:

Unfortunately, observers have long attributed the golden ratio to works where nothing of the kind was used (arbitrarily placing the grid or spiral in the preferred section of the composition), and when it was used, it's not alway easy to identify. Here however, the fact is, the canvas itself corresponds to the golden rectangle. I have sent an email to a Gleizes expert (Peter Brooke)[1] on this topic who responded: "it wouldn't surprise me if Gleizes would have experimented with the section d'Or, indeed it would rather surprise me if he didn't." So too, "Gris and Villon". Because Liovio's statement is likely inaccurate (and he provides no verifiable source to back his claim), it should be removed from the article, and replace with something more inline with, "the extent to which these artists engaged in the such mathematical formalism is not known, or difficult to discern..." If need be, I can search for a another source that states something similar. Coldcreation (talk) 08:32, 30 November 2018 (UTC)
- The golden rectangle frame size in that one is convincing enough. And it's easy to believe that some artists of that time started deliberately using golden ratios in their work. But throwing a spiral on top and saying "see how the features line up" (when they don't) is unhelpful pareidolia. See XKCD for more examples that are equally (not) convincing. —David Eppstein (talk) 18:58, 30 November 2018 (UTC)
- It fits quite nicely flipped horizontally too. Coldcreation (talk) 19:33, 30 November 2018 (UTC)
- Yes, the spiral fits nicely into the rectangle, but that has nothing to do with the painting. And if you can't even tell which way up the spiral goes, you might consider that to be evidence that the artist did not use the spiral as a compositional principle. —David Eppstein (talk) 20:54, 30 November 2018 (UTC)
- A new version will be rolling out shortly. Coldcreation (talk) 21:25, 30 November 2018 (UTC)
- Yes, the spiral fits nicely into the rectangle, but that has nothing to do with the painting. And if you can't even tell which way up the spiral goes, you might consider that to be evidence that the artist did not use the spiral as a compositional principle. —David Eppstein (talk) 20:54, 30 November 2018 (UTC)
- It fits quite nicely flipped horizontally too. Coldcreation (talk) 19:33, 30 November 2018 (UTC)
- The golden rectangle frame size in that one is convincing enough. And it's easy to believe that some artists of that time started deliberately using golden ratios in their work. But throwing a spiral on top and saying "see how the features line up" (when they don't) is unhelpful pareidolia. See XKCD for more examples that are equally (not) convincing. —David Eppstein (talk) 18:58, 30 November 2018 (UTC)
- The 1912 compositions of Juan gris, according to art historian Christopher Green, were often "modular and regular... easily fitted to the demands of Golden Section composing in the pictures of the summer, such as Man in a Café and The Watch." The "synthetic and analytic were visibly fused. In the Golden Section paintings... he laid the grids like systems of fault-lines across things, faut-lines on either side of which view-points switch.[2][3][4]

- While Gris' Man in a Café canvas/stretcher format and ratio do not correspond to a golden rectangle, an overlay clearly does match multiple golden ratio points, lines and intersections of the composition. I have examined, but not yet uploaded the Golden ratio overlay version of this painting. I will if anyone is interested in seeing the close relationship. Evidently, several works at the Section d'Or exhibit were based on the ratio; incorporating it within the standard stretcher formats at their disposition, and personalized golden section formats. Gleizes, as seen above, made a concerted effort to make sure his canvas was equal in proportion to the golden ratio. (See references below) Coldcreation (talk) 10:55, 30 November 2018 (UTC)

This early 1912 painting by Juan Gris, Still Life with Flowers (above), also exhibited at the salon, corresponds precisely to the golden rectangle (a ratio of 1 to 1.618 ± 0.01), measuring 112.1 x 70.2 cm. Not only that, there are elements of at least two grids that line up with parts of the structural composition, one is a 6/4 grid, the other varieties of golden sections (from the the outer stretcher, and from the inner painted frame). I can upload the golden ratio overlay version if need be. This stretcher was likely custom built to the golden rectangle ratio, since, again, it was not a standard format.
These observations, and those referenced above and below, disprove Livio's claim that "the paintings featured in the celebrated 1912 Salon de la Section d'Or exhibition did not use the golden ratio itself in their compositions." (Livio 2003, p. 169) Coldcreation (talk) 15:38, 30 November 2018 (UTC)
References
- ^ Peter Brooke, private communication
- ^ Christopher Green, Juan Gris, Whitechapel Art Gallery, London, 18 September - 29 November 1992 ; Staatsgalerie Stuttgart 18 December 1992-14 February 1993 ; Rijksmuseum Kröller-Müller, Otterlo, 6 March - 2 May 1993, Yale University Press, 1992, pp. 37-38, ISBN 0300053746
- ^ William A. Camfield, Juan Gris and the Golden Section, Art Bulletin, 47, no. 1, March 1965, 128-34. 68
- ^ David Cottington, Cubism and Its Histories, Barber Institute's critical perspectives in art history series, Critical Perspectives in Art History, Manchester University Press, 2004, pp. 112, 142, ISBN 0719050049
This entire topic would by now be better served by writing an analysis for another venue that could, eventually, in turn benefit Wikipedia. We spill over into WP:OR every which way. Of the cases mentioned so far, the most interesting (in terms of print sources that can actually be evaluated) may be Juan Gris. The references appear to be originally dependent upon Camfield (1965), who is at least cautious and careful to distinguish mathematics from metaphor. His placement of the golden section at La Section d'Or is rather tentative:
- A few of these paintings were moreover based on simple geometrical compositions. Yet, not a single artist there displayed a serious commitment to geometrical proportions with the one exception of Juan Gris. [...] Although all of the Puteaux artists were interested in mathematics (Marcel Duchamp, interview with the author, April 4, 1961), neither Marcel Duchamp (ibid.) nor Jacques Villon, who suggested the title for "La Section d'Or" (Dora Vallier, Jacques Villon, Paris, 1957, pp. 60-62), believes that the golden section was actually used in their paintings. And in Du Cubisme (1st English translation), London, 1913, p. 64) Gleizes and Metzinger chastise those painters who would rely on mathematics for certitude.
Camfield says that neither of the paintings he analyses "can be definitively identified with "La Section d'Or" paintings", only that the "stylistic evidence" places them in that period and they "would almost certainly have been shown" there. So, it is really a question of what later observers have claimed about the art, and we may have to content ourselves with the "not known, or difficult to discern" kind of language. XOR'easter (talk) 18:22, 30 November 2018 (UTC)
- Good points. I'm in the process of gathering more sourced information. I'll be back. Coldcreation (talk) 18:35, 30 November 2018 (UTC)
- In Du "Cubisme" it was argued that Cubism itself was not based on any geometrical theory, but that non-Euclidean geometry corresponded better than classical, or Euclidean geometry, to what the Cubists were doing: "If we wished to relate the space of the [Cubist] painters to geometry, we should have to refer it to the non-Euclidean mathematicians; we should have to study, at some length, certain of Riemann's theorems." In fact, they were free do overlap multiple methods including the golden section (or non at all). That is what some of them they did. Coldcreation (talk) 18:46, 30 November 2018 (UTC)
- Quoting the Cottington book (p. 112),
- It will be remembered that Du "Cubisme", written probably as these paintings were being made, gestured somewhat obscurely to non-Euclidean concepts, and Riemann's theorems; as Linda Henderson has shown, these references betray not an informed understanding of modern mathematics but a shaky hold on some of their principles, culled (indeed plagiarised) from Henri Poincaré's La Science et l'Hypothèse. The authors themselves had little clear idea of how such mathematics related to their art, except as a vague synecdoche for "modern science".
- As mathematicians, they were great artists. XOR'easter (talk) 21:23, 30 November 2018 (UTC)
- Today their 'equations' are on the expensive side. Coldcreation (talk) 23:18, 30 November 2018 (UTC)
- Quoting the Cottington book (p. 112),
- In Du "Cubisme" it was argued that Cubism itself was not based on any geometrical theory, but that non-Euclidean geometry corresponded better than classical, or Euclidean geometry, to what the Cubists were doing: "If we wished to relate the space of the [Cubist] painters to geometry, we should have to refer it to the non-Euclidean mathematicians; we should have to study, at some length, certain of Riemann's theorems." In fact, they were free do overlap multiple methods including the golden section (or non at all). That is what some of them they did. Coldcreation (talk) 18:46, 30 November 2018 (UTC)
- Good points. I'm in the process of gathering more sourced information. I'll be back. Coldcreation (talk) 18:35, 30 November 2018 (UTC)
Stepping back a bit for perspective, I think it's important to record what Livio has to say about this topic, since his book is one of the standard references — possibly the treatment of the subject at the popularized or semi-popularized level. The fact that such a work takes a position itself makes that position worth noting. We're outlining the history of an idea, not merely giving the "final word" on it. XOR'easter (talk) 00:44, 1 December 2018 (UTC)
- Fair points, but Livio apparently did not bother to measure the paintings, or analyze their geometric structural elements. (Instead, he seems to have relied on what others had written on the topic, without citing his sources). Had he done so, he would have seen that some of the paintings featured in the 1912 Salon de la Section d'Or exhibition did in fact use the golden ratio itself in their compositions. Theses artists were more than just interested in the golden ratio, some actually experimented with it to varying degrees. From the literature, it is evident that, notwithstanding, the Groupe de Puteaux felt no need to limit themselves to any such formula. Mentioning Livio's view in the article will only serve, at best, to show how capable the Cubists were at dissimulating their strategies; at worst, to highlight Livio's mistake. That said, Wikipedia readers might be well served to have access to this information. And the best place for elaborating on it would likely be in the article dedicated to it: Section d'Or. As for this article, the reader now has enough information, and more if needed. Coldcreation (talk) 06:54, 1 December 2018 (UTC)
- Another point about Livio's inability to 'definitively identify' the works shown at the 1912 show (thus leading to his erroneous claim). From the titles, dates and previous exhibitions listed in the 1912 Salon de la Section d'Or catalogue, many are easily identifiable, e.g., Les Baigneuses (The Bathers) and Le goûter (Tea Time), and many more works by Gleizes, Metzinger and others. The main exception is for the works of Juan Gris, since no titles are given for his submissions in the catalogue. However, it is now known, from published correspondence between the artist and the dealer Léonce Rosenberg that 13 paintings by Gris were shown (Green 1992), most of which have been identified by their titles, dates, and dimensions. Coldcreation (talk) 07:16, 1 December 2018 (UTC)
Question
I realize that there are many supposed golden ratio attributions that lack rigor or are simply false. Is it possible to identify the golden ratio in a figure that is not, say, a golden rectangle, e.g., a square, as shown here, or some rectangle between the two? Coldcreation (talk) 07:43, 1 December 2018 (UTC)
- The obvious answer is that it's the ratio between side and diagonal of a regular pentagon (the main reason the Greeks studied it). —David Eppstein (talk) 07:45, 1 December 2018 (UTC)
- My objective here is to be able to determine if a painting has been constructed with the golden ratio in mind, or not, regardless of its format, e.g., Juan Gris' Man in a Café (shown above). Coldcreation (talk) 09:06, 1 December 2018 (UTC)
- The better question is, once you overlay a grid of some sort on an artwork of some sort, what is your criterion for determining how good a fit it is? And where is your null hypothesis? —David Eppstein (talk) 18:15, 1 December 2018 (UTC)
- Here is an example:
- The better question is, once you overlay a grid of some sort on an artwork of some sort, what is your criterion for determining how good a fit it is? And where is your null hypothesis? —David Eppstein (talk) 18:15, 1 December 2018 (UTC)
- My objective here is to be able to determine if a painting has been constructed with the golden ratio in mind, or not, regardless of its format, e.g., Juan Gris' Man in a Café (shown above). Coldcreation (talk) 09:06, 1 December 2018 (UTC)
-
Golden rhombus
-
Georges Braque, 1917, Guitare et verre (Guitar and Glass), oil on canvas, 60.1 x 91.5 cm, Kröller-Müller Museum
Here, shown side by side rather than overlaid (I have not uploaded the overlay version) it is clear that Braque used the Golden rhombus in the design of this 1917 painting. The match is exact (assuming the Commons image is correct). The angles and sides should line up to within a margin of error (± 0.01): equal to (a close approximation) the width of the edges of the painting hidden by the frame, and/or cropped off in the photo. The stretcher of Braque's painting is a golden rectangle (ratio of 1 to 1.618 ± 0.02). The ± 0.02 is attributed to frame overlap/cropping. That is the criteria. I found plenty of Null hypotheses (I tested about 50 paintings today, not just from the 1912 exhibition), until I tested the 1917 Braque. It actually surprised me that Braque used rhombus, as he was not a member of the Section d'Or (though from 1919 they exhibited together at Rosenberg's gallery l'Effort moderne). Coldcreation (talk) 20:34, 1 December 2018 (UTC)
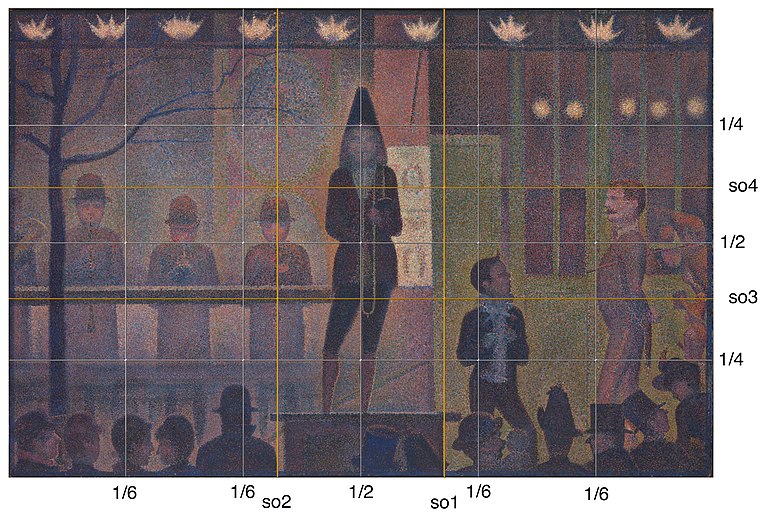
- Georges Seurat's, 1887–88, Parade de Cirque (Circus Sideshow) is an interesting case study:
-
Georges Seurat, 1887–88, Circus Sideshow (Parade de Cirque), oil on canvas, 99.7 × 140.9 cm, Metropolitan Museum of Art. Golden mean overlay (section d'or, so1 - so4) and 4 : 6 ratio grid
- The golden section (golden/yellow grid, so1 - so4) does not govern Parade's geometric structure. Modern consensus is that Seurat never used the 'divine proportion'. Parade is shown here divided horizontally into fourths and vertically into sixths. The 4 : 6 ratio corresponds to the dimensions of the canvas (one-half times wider than its vertical dimension). The ratio of Seurat's painting/stretcher corresponded to a ratio of 1 to 1.502, ± 0.002 (as opposed to the golden ratio of 1 to 1.618). The compositional axes in the painting correspond to basic mathematical divisions (simple ratios that appear to approximate the golden section). Coldcreation (talk) 09:47, 2 December 2018 (UTC)
I don't understand the point of this section, nor what you have done. See WP:NOTFORUM, item 4, which says "bear in mind that article talk pages exist solely to discuss how to improve articles; they are not for general discussion about the subject of the article, nor are they a help desk for obtaining instructions or technical assistance". Dicklyon (talk) 16:22, 2 December 2018 (UTC)
- Actually, it's a subsection of the previous. In the article it was mentioned: "...despite this general interest in mathematical harmony, the paintings featured in the celebrated 1912 Salon de la Section d'Or exhibition did not use the golden ratio itself in their compositions." (Livio 2003, p. 169) Several sources contradicted that statement. While examining some of the works exhibited, mentioned in the latter references, it was confirmed that indeed Livio's claim was erroneous. This subsection was set up to test more works (those that were not constructed in a golden rectangle format). The question has been resolved. The Art section of the article has now been improved, with a statement that reflects the actual 1912 developments. Coldcreation (talk) 16:31, 2 December 2018 (UTC)
- Thanks for making it a subsection to clarify. I still don't understand what the section is for. You seem to be presenting your original research, while may be interesting, but not really relevant here. Why don't you get it published in a journal, and then let us know? Dicklyon (talk) 19:33, 2 December 2018 (UTC)
- We had several sources with conflicting statements regarding the use (or not) of the golden ratio in 1911-12 works. Livio, nor Camfield, could identify the paintings exhibited. Others have identified the works. They are well-known works. I posted a couple of them above. The dimensions correspond to golden rectangles. We now know, and have conveyed in the article, the correct statement. Before, we had no way of knowing which source was correct. While some original research to verify the sources was involved here at Talk, reliable sources back the current claims in the article. The Seurat info above is well documented. So all is well and good. Coldcreation (talk) 19:44, 2 December 2018 (UTC)
- Got it. I'm all for representing both sides in such disagreements, as long as we don't do our own OR and editorializing about which source is correct. I'll try to catch up on what's happening... Dicklyon (talk) 19:55, 2 December 2018 (UTC)
- We had several sources with conflicting statements regarding the use (or not) of the golden ratio in 1911-12 works. Livio, nor Camfield, could identify the paintings exhibited. Others have identified the works. They are well-known works. I posted a couple of them above. The dimensions correspond to golden rectangles. We now know, and have conveyed in the article, the correct statement. Before, we had no way of knowing which source was correct. While some original research to verify the sources was involved here at Talk, reliable sources back the current claims in the article. The Seurat info above is well documented. So all is well and good. Coldcreation (talk) 19:44, 2 December 2018 (UTC)
- Thanks for making it a subsection to clarify. I still don't understand what the section is for. You seem to be presenting your original research, while may be interesting, but not really relevant here. Why don't you get it published in a journal, and then let us know? Dicklyon (talk) 19:33, 2 December 2018 (UTC)
This section got wiped out in the massive rollback to the Nov 1 version. I have a moderately copy-edited version on my draft under 'Disputed claims'. Before it was just under Art with no subsection. UpdateNerd (talk) 10:05, 27 January 2019 (UTC)
Wholesale changes
@UpdateNerd: – With no discussion, this editor has made about a hundred edits, reinstating a lot of the kind of POV that we took years to weed out. For example, he writes "The Great Pyramid of Giza (c. 2560 BC) has properties which closely approximate the golden ratio, and the Babylonian Tablet of Shamash (c. 888–855 BC) can be superimposed with two orders of golden rectangles", referencing a golden ratio hype book. This is unnecessarily misleading, suggesting as it does that a few observations of ratios near phi might mean something. I reverted one day's changes, but he put it all back and carried on with more. How can we deal with this rate of flux? Is anyone up for giving these changes the critical review they need, or should we roll back and take it slowly as I had suggested? Dicklyon (talk) 00:26, 12 January 2019 (UTC)
- I haven't studied the changes but the lead should not define the golden ratio as a number then detour with observations about self similarity. I'm inclined to roll everything back and proceed slowly, one section at a time, with the lead last. Slowly means that edits to one section should occur, then wait three days for responses before starting on another section. Bold editing is great, but rolling everything back is also a bold edit and will happen if it has consensus. Johnuniq (talk) 00:57, 12 January 2019 (UTC)
- Well, I'm happy to walk away from working on the article while other editors vet it, but my only request is that this be done constructively, by bringing up new/existing reliable sources and reflecting what the majority of them say; not rolling back a lot of sourced work indiscriminately. Look at the actual references; many of them are linked. If you want something in particular removed, e.g. the Tablet of Shamash, why not start a discussion about that one point? Rolling everything back is unproductive. I used Livio as my main source and the other refs bring up points he never addresses, but can easily be verified by the reader. Please let's discuss this one topic at a time, and make consensus changes, rather than making wholesale accusations and disruptive rollbacks. UpdateNerd (talk) 01:37, 12 January 2019 (UTC)
I'm inclined to roll everything back and proceed slowly, one section at a time, with the lead last.
Sounds sensible to me. (I find that intros and leads and abstracts are, often, good things to do last. One has to establish the content to be summarized before attempting the summary. I know this isn't how everyone writes, but it seems the appropriate method to follow here.) Cheers, XOR'easter (talk) 18:11, 12 January 2019 (UTC)- Per WP:STATUSQUO: "Reverting is appropriate mostly for vandalism or other disruptive edits. The Wikipedia edit warring policy forbids repetitive reverting. If you see a good-faith edit which you feel does not improve the article, make a good-faith effort to reword instead of reverting it." If you wish to dispute material recently added to the article you should do so with consensus. Or, if you see material added by User:UpdateNerd that could be improved, be bold, and improve it. Coldcreation (talk) 18:35, 12 January 2019 (UTC)
- "reinstating a lot of the kind of POV that we took years to weed out" sounds like disruptive editing to me. And your link is an essay describing some editors' editing philosophy; it is not policy or even a guideline. I think a more appropriate editing philosophy is to roll back edits that are clear disimprovements, regardless of the good faith of the editor, and not put the onus on cleaning up someone's mess on someone else. I think the number of edits involved is significantly greater than 100; the last version prior to UpdateNerd's revisions appears to be this one. —David Eppstein (talk) 20:05, 12 January 2019 (UTC)
- If my edits had been "reinstating a lot of the kind of POV that we took years to weed out" I would agree with reverting them! But nothing I added was copied from an old version, it was directly sourced. For now, I've removed the controversial information from the lead and History section; I think this way the improvements that I've made can be compared to old versions without appearing POV. Implications that the golden ratio was intentionally included in pre-Pythagorean objects gives the perception of POV, but that was not my intent. It's fair not to include them since enough RS question their intentional use. If anyone's looking for the validity of ancient objects with golden ratio properties, they can look for the information in the more detailed section or article without having it emblazened in the golden ratio's lead. Please, before reinstating any old work, compare how the individual references are being used. Making claims with missing page numbers, or misrepresenting what they say is WP:SYNTH and another form of POV. UpdateNerd (talk) 20:59, 12 January 2019 (UTC)
- "reinstating a lot of the kind of POV that we took years to weed out" sounds like disruptive editing to me. And your link is an essay describing some editors' editing philosophy; it is not policy or even a guideline. I think a more appropriate editing philosophy is to roll back edits that are clear disimprovements, regardless of the good faith of the editor, and not put the onus on cleaning up someone's mess on someone else. I think the number of edits involved is significantly greater than 100; the last version prior to UpdateNerd's revisions appears to be this one. —David Eppstein (talk) 20:05, 12 January 2019 (UTC)
- Per WP:STATUSQUO: "Reverting is appropriate mostly for vandalism or other disruptive edits. The Wikipedia edit warring policy forbids repetitive reverting. If you see a good-faith edit which you feel does not improve the article, make a good-faith effort to reword instead of reverting it." If you wish to dispute material recently added to the article you should do so with consensus. Or, if you see material added by User:UpdateNerd that could be improved, be bold, and improve it. Coldcreation (talk) 18:35, 12 January 2019 (UTC)
- Well, I'm happy to walk away from working on the article while other editors vet it, but my only request is that this be done constructively, by bringing up new/existing reliable sources and reflecting what the majority of them say; not rolling back a lot of sourced work indiscriminately. Look at the actual references; many of them are linked. If you want something in particular removed, e.g. the Tablet of Shamash, why not start a discussion about that one point? Rolling everything back is unproductive. I used Livio as my main source and the other refs bring up points he never addresses, but can easily be verified by the reader. Please let's discuss this one topic at a time, and make consensus changes, rather than making wholesale accusations and disruptive rollbacks. UpdateNerd (talk) 01:37, 12 January 2019 (UTC)
@David Eppstein: This is Wikipedia:Editing policy: Instead of removing content from an article, consider: WP:FIXTHEPROBLEM. Coldcreation (talk) 00:05, 13 January 2019 (UTC)
- The material you link is about material that is appropriate but merely badly written. But in this case "the problem" is reinstatement of debunked claims about pyramids and off-topic material about whether the Egyptians knew the Pythagorean theorem, and the like, and the correct solution to the problem is bulk removal. The simplest way of doing that would be to revert to the last clean version. —David Eppstein (talk) 00:32, 13 January 2019 (UTC)
- Another aspect of the problem is that it will be a monumental effort to find all the errors, with edits done in a way that the diff tool and undo are hard to use. Going back to his very first edit, the very first word he inserts is wrong. Should I fix that and move to the next one? Maybe it's not even there in the present version. If I work from the present instead, there nothing to guide the inspection of this huge complicated article, so that's not likely to take care of the problem either. It's best if we proceed incrementally, vetting changes made at a moderate pace, rather than having to contend with this sort of wholesale rewrite via hundreds of ad-hoc steps. Dicklyon (talk) 00:36, 13 January 2019 (UTC)
- At some point the quoted phrase "extreme and mean ratio" was removed; now it appears only in a quote and in the lead in a way that's disconnected and meaningless. Dicklyon (talk) 00:52, 13 January 2019 (UTC)
- It appears in the Euclid quote; in what other context is it more relevant? The Kepler triangle? UpdateNerd (talk) 01:36, 13 January 2019 (UTC)
Here is the diff that I propose we revert. It starts with an in appropriate hatnote, continues through an ill-advised lead rewrite ("the golden ratio is an irrational number represented by the Greek letter ..." doesn't tell you anything useful or interesting), includes a wrong definition of golden spiral in a figure caption, and then gets harder to understand from there as not much lines up. If there are improvements in it, we can work on finding them and putting them back. Perhaps some of the ref detailing. It looks like 4 us of agree this is the best course of action. Dicklyon (talk) 00:58, 13 January 2019 (UTC)
He's also got Kepler connected to art in the lead, but not in the body, and I don't find anything in Livio or elsewhere supporting that. And did we really need a second image of Kepler's solar system model? Dicklyon (talk) 01:13, 13 January 2019 (UTC)
- I don't see why we need even the first image. The connection to the golden ratio is indirect and unexplained. —David Eppstein (talk) 01:19, 13 January 2019 (UTC)
- I fixed the Kepler & golden spiral misphrasing in the lead & replaced the first solar system image with a simple dodecahedron, which produces less ambiguity. I really think that this process of pointing out the issues and working to fix them is more productive than a rollback. Please continue to raise concerns and I'll provide what info I can to address them. UpdateNerd (talk) 02:11, 13 January 2019 (UTC)
The pyramid info sourced to Maor and referencing the Rhind papyrus also got dropped and replaced by speculation. Dicklyon (talk) 01:21, 13 January 2019 (UTC)
- The Maor ref never had a page number, and I couldn't find the info in the source that it was supposed to represent. I don't see how the Rhine Papyrus was ever relevant, but the Pythagorean theorem notes certainly are in the context of the Kepler triangle/related pyramid. Everything else is sourced, not speculation. UpdateNerd (talk) 01:34, 13 January 2019 (UTC)
- It is not difficult to find pirated copies of Maor. And with a copy in hand it is also not difficult to determine that the appropriate page number range is 7–9. It is relevant because it provides evidence against the use of the golden ratio, by explaining the Egyptian pyramid shape in a different way that fits much better with what we know of Egyptian mathematics. —David Eppstein (talk) 02:14, 13 January 2019 (UTC)
- According to my email records, I bought a copy in 2006, which is when we started a long hard de-bullshitting phase on this article. I went to the NY Public Library to look at books about the Rhind papyrus, too. Sorry I didn't get the page numbers in at that time, but UpdateNerd, you can ask; don't remove refs for lack of understanding their details. Dicklyon (talk) 04:54, 13 January 2019 (UTC)
- Page numbers help. The most relevant information I can find in the article citing Maor is that the 3:4:5 triangle is described in the Rhind papyrus... but which source claims that the Great Pyramid of Giza might be based on that triangle, or that it is a "nearly similar pyramid shape", as asserted in the Nov. 1 version of the article? The reinstated version of the article synthesizes a bunch of poor citations such as this offline personal site, while ignoring the very informative Bartlett. UpdateNerd (talk) 06:15, 13 January 2019 (UTC)
- According to my email records, I bought a copy in 2006, which is when we started a long hard de-bullshitting phase on this article. I went to the NY Public Library to look at books about the Rhind papyrus, too. Sorry I didn't get the page numbers in at that time, but UpdateNerd, you can ask; don't remove refs for lack of understanding their details. Dicklyon (talk) 04:54, 13 January 2019 (UTC)
- It is not difficult to find pirated copies of Maor. And with a copy in hand it is also not difficult to determine that the appropriate page number range is 7–9. It is relevant because it provides evidence against the use of the golden ratio, by explaining the Egyptian pyramid shape in a different way that fits much better with what we know of Egyptian mathematics. —David Eppstein (talk) 02:14, 13 January 2019 (UTC)
The proposal is to revert all edits back to this permalink: 00:17, 2 November 2018. The diff of edits since then was given by Dicklyon but it is too complex to digest. Instead, I put the two versions (then and now) side-by-side and scanned them. The original is superior in several ways, starting with the lead and Calculation section which tell the reader what the golden ratio is. The current version moved Calculation into the Mathematics section which has a consistency appeal but which fails to define the topic somewhere near the top of the article. Other adjustments of that nature weakened the article IMHO. I support a revert. People wanting the new version need to justify it, section-by-section. WP:FIXTHEPROBLEM is not relevant as explained by David Eppstein above. Johnuniq (talk) 01:58, 13 January 2019 (UTC)
- I've restored the calculation to the lead (minus the footnote of the derivation of -0.618, which I feel is overly detailed and should remain only in the body). Please feel free to improve it if you can. UpdateNerd (talk) 02:17, 13 January 2019 (UTC)
I've done the revert. UpdateNerd, I hope you'll help us identify and retrieve the good parts of your edits. Dicklyon (talk) 04:48, 13 January 2019 (UTC)
- I don't think so, as I attempted to improve the article in the public eye for anyone to individually revert/revise/add to. I'm happy to continue discussing which part of my revisions were in error, perhaps in a draft, and reinstating it from the status-quo revision you rolled back to once common ground can be found. Thanks UpdateNerd (talk) 05:15, 13 January 2019 (UTC)
Working through the changes
I added back the Livio refs to the history from you first edit. At second edit, I'm stumped already. It's not clear why Plato's divided line analogy is worth a mention, as it works for arbitrary ratios; nothing relevant to golden ratio there. Also not clear why so much name unlinking in that edit, or why you go to the trouble of asking for nowrap on hyphenated terms. Mixing so many issues in an edit makes it hard on us. I'll skip that one and move forward. Dicklyon (talk) 17:28, 13 January 2019 (UTC)
- I know of no other ratio Plato's analogy is true for. It's relevant because his definition precedes Euclid's. UpdateNerd (talk) 20:11, 13 January 2019 (UTC)
- This reply makes no sense to me, and seems symptomatic of the kind of fuzzy thinking that got us into this mess. First, what mathematical fact is expressed in Plato's analogy that might be true for some ratios and false for others? And second, in what way is it more true for the golden ratio than for simple rational (but unequal) ratios like 1:2? —David Eppstein (talk) 20:21, 13 January 2019 (UTC)
- It's a simple but not "fuzzy" concept. A line with the golden cut has parts proportional to each other in the same ratio as the larger is to the whole; it is self-similar. That is not true of the 1:2 ratio. It is not self-similar in any way that I can think of. UpdateNerd (talk) 20:27, 13 January 2019 (UTC)
- There is nothing in analogy of the divided line about comparing the part to the whole. It is only about comparing one subdivided part to another subdivided part with the same proportions. And your attempt to view this as an example of self-similarity is extremely anachronistic; that's a 20th-century concept. —David Eppstein (talk) 20:34, 13 January 2019 (UTC)
- You're correct on the misattribution. I think Plato describes a similar concept in the Republic about geometrical self-similarity, but not in his Analogy, which is a metaphysical model. I'll see if I can find the other quote, and sorry for the confusion (I should have caught this lapse in citations). UpdateNerd (talk) 20:57, 13 January 2019 (UTC)
- The self-similarity quote is from Timaeus; if I can find a source linking it to the history of the golden ratio, I will share it. UpdateNerd (talk) 21:40, 13 January 2019 (UTC)
- It doesn't look like there's anything there either. Sounds more like the usual fan hype of trying to connect golden ratio to everything (which is always possible, of course). Dicklyon (talk) 22:31, 13 January 2019 (UTC)
- I agree with the StackExchange user who posted that question — it's hard to see the golden ratio anywhere in that passage. To me, it looks like a statement about the conditions for arithmetic and geometric means being equal, maybe garbled a bit by a translator not knowing enough math (though I can't be sure about that). XOR'easter (talk) 23:57, 13 January 2019 (UTC)
- It doesn't look like there's anything there either. Sounds more like the usual fan hype of trying to connect golden ratio to everything (which is always possible, of course). Dicklyon (talk) 22:31, 13 January 2019 (UTC)
- There is nothing in analogy of the divided line about comparing the part to the whole. It is only about comparing one subdivided part to another subdivided part with the same proportions. And your attempt to view this as an example of self-similarity is extremely anachronistic; that's a 20th-century concept. —David Eppstein (talk) 20:34, 13 January 2019 (UTC)
- It's a simple but not "fuzzy" concept. A line with the golden cut has parts proportional to each other in the same ratio as the larger is to the whole; it is self-similar. That is not true of the 1:2 ratio. It is not self-similar in any way that I can think of. UpdateNerd (talk) 20:27, 13 January 2019 (UTC)
- This reply makes no sense to me, and seems symptomatic of the kind of fuzzy thinking that got us into this mess. First, what mathematical fact is expressed in Plato's analogy that might be true for some ratios and false for others? And second, in what way is it more true for the golden ratio than for simple rational (but unequal) ratios like 1:2? —David Eppstein (talk) 20:21, 13 January 2019 (UTC)
Your third edit suggests that the name tau went out as the twentieth century came in. This is not so; it just gradually became less common. So I'll skip that one, too. In this edit you remove all the &dq= info from book-search links, which removes highlighting that can be very useful for readers looking for the cited content; is there consensus that this is a good direction to go? Let me know. Dicklyon (talk) 17:37, 13 January 2019 (UTC)
- I tend to prefer only the &pg= parameter in Google Books links (so that the preview goes directly to the chosen page), omitting &dq and other parameters. But I don't know of official guidelines on that issue. The {{Google books}} template does have a parameter corresponding to dq, suggesting that it's ok to continue including it. —David Eppstein (talk) 18:51, 13 January 2019 (UTC)
This edit added the sentence, The ratio of Lucas numbers to Fibonacci numbers appears to converge to , which is strongly related to the golden ratio.
There are two problems with this. First, we shouldn't say "appears to": either , or it doesn't. There are oodles of relations between Lucas and Fibonacci numbers, and this statement can actually be proven, so if it's worth including, we need to make clear that it is not an unresolved conjecture. Second, "strongly related" is vague. Are all numbers that can be obtained from by an integer addition and a multiplication "strongly related" to it? Or, are we reserving "strongly related" for something more specific yet esoteric, e.g., is "strongly related" to if is a fundamental unit in the field ? I'm not convinced it's significant enough to warrant inclusion, but I wouldn't strongly object, provided it were rewritten for clarity.
To be honest, the preceding sentence isn't that great, either (I don't know how long it has been in the article). It doesn't make clear why working in the field is meaningful, as opposed to working in . XOR'easter (talk) 19:59, 13 January 2019 (UTC)
- That reflects the reference, but by "appears to" it means that it does so increasingly, beyond doubt, but how exactly this would be 'proven' isn't in the ref. UpdateNerd (talk) 20:11, 13 January 2019 (UTC)
- Indeed, that ref has little to say, and the "strongly related" is a jump. At your next edit you elided a digit, change pp. 86–87 to pp. 86–7. This is really not OK. Dicklyon (talk) 22:11, 13 January 2019 (UTC)
Draft
I've worked on a draft which incorporates various feedback. You can see what's changed in the edit history. Notably, I moved the Egyptian pyramids to 'disputed claims' and removed some of the irrelevant history. I'm happy to address any other feedback for a potential "goal" article. Also, I think it's simpler to look at than stepping through individual edits, particularly after weeding out some false/disputed claims. I'm happy to slowly reintroduce changes for public scrutiny, but if you wish to help in the planning process, please take a look. Thanks UpdateNerd (talk) 08:22, 18 January 2019 (UTC)
- UN, that 2014 Chistopher Bartlett article is a sham. In getting from "most reliable" measurements to exact golden ratio he says "I began by taking the averages of the most reliable published data from three highly respected surveyors/researchers, Cole (1925), Dorner (1981) and Lehner (1997)." Here the Dorner and Lehner numbers are modern and identical, and the old Cole numbers, off from these by more than a part per thousand, are just about what's needed to make the part per 2000 to 3000 (one to two minutes of arc) correction to the modern data needed to arrive at the remarkable result. The Herz book is a more more objective/unbiased analysis of actual data and theories instead of cooked averages. I suggest we don't use Bartlett at all (do we even have reason to trust a word he says? who is he? Affiliation is listed as "Hunt ValleyUSA"), or if we use it, presenting it as this guy's claims, not as you have with a statement of factoid like "Based on the most reliable measurements of the Great Pyramid of Giza (c. 2560 BC), the slant height of one of its faces divided by half its base width (semi-base) is φ". That's all I've looked at so far Dicklyon (talk) 19:04, 19 January 2019 (UTC)
- And your draft is based off the version we all agreed to get away from, so looking at diffs there is not going to be useful. We need to work forward from where we are, slowly. It's hard to see what changes you think are most important. If it's page numbers, I'l happy to work with you on that; I have Herz and others. Since the entire Herz book is what we're summarizing, it's not clear page numbers are really needed, but I can find some if you like. I'm not very familiar with how to convert the ref style to accommodate page numbers, though; if you can stub in new-style refs with dummy numbers to show me how, I'll put in actual numbers. Dicklyon (talk) 19:11, 19 January 2019 (UTC)
- Ah, here's how you did it. I can copy that. Dicklyon (talk) 19:15, 19 January 2019 (UTC)
- Yeah, that was pretty much my take-away from the Bartlett (2014) article, too. XOR'easter (talk) 20:25, 19 January 2019 (UTC)
- I agree that any inclusion of Bartlett should attribute the claims more specifically, probably using direct quotes. But Bartlett does have some useful information even if the claims of the first paragraph are generally disputed (he argues for alternatives further into the article). Since it's now under disputed claims, it's not placing Bartlett as more important than the discreditation of related claims; we should simply present all the views with the appropriate balance.
- The draft has many other improvements, like focusing on sourced info, not synthesized claims, and has a well-sourced History section instead of a flimsy list. It's also more logically organized into parent sections. I'm listening to all the feedback and eliminating problems to make it better than the version that was reverted and fix problems on the live article. You can also edit it yourself if you wish. UpdateNerd (talk) 21:30, 19 January 2019 (UTC)
- The live version of the article is plagued with reference issues, which now include stray "</ref>" tags and missing refs that were removed. This type of editing should be avoided, but I also insist that more be done to verify that the functional refs actually support what is being claimed. Not including page numbers because "the whole book says that" is WP:SYNTH, as I've already said, and I hope my draft can be useful in fixing that. If there are issues as to its arrangement, I'd be happy to discuss how it could be improved. Per feedback, I made the Calculation section more prominent again. UpdateNerd (talk) 07:54, 20 January 2019 (UTC)
- I apologize if I messed up on trying to improve the refs. I'd be happy to have your help. But we need to proceed from where we are. It's hard to see how to leverage your separate branch to do that. Dicklyon (talk) 17:16, 20 January 2019 (UTC)
- OK, I fixed the ref errors. Got suggestions for what's a next good step or two? Dicklyon (talk) 18:01, 20 January 2019 (UTC)
- I suggest merging the redundant Timeline section with History so we can start seeing what's missing from the prose content. Lists like the timeline should be avoided when equally good or better prose can be written. UpdateNerd (talk) 22:23, 20 January 2019 (UTC)
- I agree that any inclusion of Bartlett should attribute the claims more specifically, probably using direct quotes. But Bartlett does have some useful information even if the claims of the first paragraph are generally disputed (he argues for alternatives further into the article). Since it's now under disputed claims, it's not placing Bartlett as more important than the discreditation of related claims; we should simply present all the views with the appropriate balance.
- Yeah, that was pretty much my take-away from the Bartlett (2014) article, too. XOR'easter (talk) 20:25, 19 January 2019 (UTC)
The same pattern of edits that got us into this mess is continuing, with UpdateNerd going back to the same pattern of making dozens and dozens of consecutive edits to this article, many of them innocuous, others that turn something that used to make sense into a garbled mess of disconnected half-thoughts. UpdateNerd: Can you explain clearly here in talk what you are trying to accomplish? Because to me it looks like you have no plan. I think you should stop making these edits until you have one. —David Eppstein (talk) 08:42, 27 January 2019 (UTC)
- Well, it's fine that you reverted my recent edits, because the entire point of the recent rollback was so that edits could be reviewed on a case-by-case basis. I'm doing my best to make the minimum number of edits that are able to be easily compared. This has nothing to do with what "got us into this mess", because you intervened this time. If I make all the changes I envision in a single edit, then it's harder to see what changed. UpdateNerd (talk) 08:47, 27 January 2019 (UTC)
- It would help if you rather than making many changes all over the article or providing a new draft for the complete article, simply were to post the new content and sources you want to have added as short sections. Then merit of those can be discussed in a focussed fashion. But a large number of changes who overall improve little and contain occasional problematic stuff, will at some point just trigger categorical resets by other editors and increasingly hostile attitudes (as such edits cause a lot of work for others maintaining the article), in other words you won't be able to contribute that way.--Kmhkmh (talk) 09:43, 27 January 2019 (UTC)
- Based on the feedback, I will make a greater effort to keep my BOLD edits innocuous, and bring anything more controversial up for discussion. It might also generally help if others focus on fixing problems; you can use my draft to grab some of the reference page numbers which are still missing, or information which clears up some of the WP:SYNTH issues. UpdateNerd (talk) 09:49, 27 January 2019 (UTC)
- It would help if you rather than making many changes all over the article or providing a new draft for the complete article, simply were to post the new content and sources you want to have added as short sections. Then merit of those can be discussed in a focussed fashion. But a large number of changes who overall improve little and contain occasional problematic stuff, will at some point just trigger categorical resets by other editors and increasingly hostile attitudes (as such edits cause a lot of work for others maintaining the article), in other words you won't be able to contribute that way.--Kmhkmh (talk) 09:43, 27 January 2019 (UTC)
Egyptian pyramids
For anyone interested, I've incorporated some of my more recent finds concerning Röber's discussion of Egyptian pyramids to the draft, and copyedited the rest for simplicity. I think this helps put Bartlett et al. into context, and clears up some of the misinformation. Incidentally, I haven't seen any modern historian sources saying that the Great Pyramid doesn't have golden ratio properties, only that it's the result of chance. Hopefully we can build up a quality argument and address any outstanding issues on the draft so we can replace the sketchy version that is currently being synthesized. UpdateNerd (talk) 11:33, 27 January 2019 (UTC)
I was able to find that Taylor indeed misrepresented Herodotus; Livio traces this error. I also reworded my version so that it's not actually saying that φ or the Kepler triangle appear in the Great Pyramid, only that they are closely approximated—according to the cited estimates. I also added a Livio quote that affirms that the Egyptians had no knowledge of the golden ratio, and even re-added the Rhind Mathematical Papyrus as the source of pi's fractional approximation. Please let me know your thoughts, as I think it's now much clearer to a first-time reader... without misrepresenting sources! UpdateNerd (talk) 09:08, 28 January 2019 (UTC)
- I don't like that section at all to be honest, imho the whole pyramid thing only deserves a bullet point under disputed claims.--Kmhkmh (talk) 19:11, 11 February 2019 (UTC)
- I like the bullet point idea since it doesn't merit anything but a disputed claim, and those are about a paragraph in length. I'm now just using the draft as a repository and skipping stuff not explicitly related to the golden ratio—I've updated the paragraph on Egyptian pyramids if you care to see a condensed approach. UpdateNerd (talk) 20:53, 11 February 2019 (UTC)
- I'm not so sure. There's been so much writing on this speculation that some discussion may be in order. Dicklyon (talk) 04:31, 12 February 2019 (UTC)
- I'm all for discussion. One thing I eliminated from the draft is the mention of mathematical phrases which would be unclear to the common reader. E.g. "secant of the angle θ" or "face angle 52° 20". (What does the second number in an angle represent?)
- I've also updated the draft to sample what listing the disputed claims as bullet points would look like. UpdateNerd (talk) 06:28, 12 February 2019 (UTC)
- I'm not so sure. There's been so much writing on this speculation that some discussion may be in order. Dicklyon (talk) 04:31, 12 February 2019 (UTC)
- I like the bullet point idea since it doesn't merit anything but a disputed claim, and those are about a paragraph in length. I'm now just using the draft as a repository and skipping stuff not explicitly related to the golden ratio—I've updated the paragraph on Egyptian pyramids if you care to see a condensed approach. UpdateNerd (talk) 20:53, 11 February 2019 (UTC)
Reversion
In response to this revert and request for explanation: all I did was make Section D'or a bullet point for consistency with the rest of the section as well as remove some unclear/irrelevant statements which seem to be copy-pasted from the subpage—having nothing to do with the golden ratio. The changes related to the Parthenon were also to clean up some of the off-topic nonsense and put it in its due place under 'Disputed observations', as throwing it under Architecture (on the golden ratio article) is misleading. Let me know if that clears it up. UpdateNerd (talk) 06:59, 21 February 2019 (UTC)
THe golden ratio is also 2×sin(54°) or 2×cos(36°). — Preceding unsigned comment added by 27.33.8.157 (talk) 08:47, 5 March 2019 (UTC)
Dürer

@Deacon Vorbis: The source clearly states that the vanishing point divides the diameter of the rainbow in the golden proportion, and that could also not be more apparent from the actual measurement. Since the illustration in question is quite literally full of riddles/mathematical puzzles, it would seem highly unlikely that the vanishing point underlying the entire composition would be placed at this location by accident. The article is chock-full of other reliable information, so at least with attribution, it would be appropriate to include. And as far as I'm aware Dürer didn't leave notebooks of his intentions lying around (as Da Vinci did). UpdateNerd (talk) 13:43, 2 May 2019 (UTC)
- (edit conflict) The source says "divine proption", not "golden proportion" or even "golden ratio". While I realize that this term is sometimes used instead, the author never did so anywhere else in the source, despite using "golden ratio" five times explicitly. In any case, I'm very hesitant to put in a single "this one person says this one painter did something in the golden ratio this one time" kind of thing, even if the source is otherwise more or less reliable. It starts to get kind of WP:CRUFTy for one thing. But also, if you're specifically looking for φ, and you make enough measurements, you're going to find it all over the place – a point which is made elsewhere in the article even. Without some kind of corroboration or quote from the artist or something providing some context, we can't just WP:INDISCRIMINATEly include these. –Deacon Vorbis (carbon • videos) 14:15, 2 May 2019 (UTC)
- Considering there was an edit conflict, did you see the image I mocked up? Also, "divine proportion" explicitly refers to the golden ratio in pretty much all contexts, expecially during the Renaissance when Pacioli (whom the article is primarily about) advocated for calling it that. Yes, it is a single source making an extraordinary claim, so if we include it we should attribute it to "one source" or something like that. There isn't likely to be a bunch of articles repeating such esoterica on the interweb, but if there was, that would make the guideline-stringest case for including this much stronger... but likely without adding any insight. But I don't see how your cruft/indiscriminate arguments apply. This is particularly discriminate on what to include (a rare strong-case use of the golden ratio during the Renaissance, of which there are only 1 or 2 other highly significant examples—currently missing from the article). I agree it would help to find corroboration, but making the point so obvious might not have been the artist's intent. :) UpdateNerd (talk) 14:42, 2 May 2019 (UTC)
- Granted about the terminology, but that was the lesser of my concerns really. As for the image, using lines so close together is going to introduce extra uncertainty in determining the vanishing point. Even in the author's diagram, where he used a couple more, one of them didn't intersect the others, yet there was no indication of how much uncertainty there was in his measurements, just a blanket "omgz golden ratio!". Even in your diagram, I see that you've used the outside of the rainbow, rather than the inside. Why? Why not the center? Using one of those will doubtless give a better match than the others. How much other subtle little fudging is made in these sorts of measurements?
- Could the artist have done this intentionally? Of course. Did he? Who knows; the author certainly doesn't make any sort of case that he did. And if it was unintentional, then it shouldn't be included. We need to stick to cases where there's some sort of corroboration about intentional use, or at the very least some sort of robust discussion about it, rather than including any questionable case of finding something that was specifically being sought, too obscure to have attracted any other attention. –Deacon Vorbis (carbon • videos) 15:17, 2 May 2019 (UTC)
Ahmes papyrus
While I agree that a letter to editor is not the most reliable source per se, it replicates the quoted portion of the papyrus included in Alger's Mathematics for Science and Engineering, which doesn't make any other outlandish claims related to the golden ratio. It mentions in the same section that the golden ratio was not known until Euclid, which could be added as a quote in the reference (I'll post it when I have time tomorrow). Including the information in the article gives insight as to the more scholarly views that have existed about the golden ratio and the pyramids, without saying that they're true. UpdateNerd (talk) 04:01, 6 June 2019 (UTC)
- Please refrain from using bad sources. This article has been infested with woo too much already, you don't need to make it worse. Seked is apparently just a word for the slope of a pyramid; different pyramids had different slopes, and the imputation that the slope is the golden ratio is modern. As the more respectable sources already say. Including this information does not give more insight; it merely makes it look like Wikipedia editors are credulous and unscholarly. —David Eppstein (talk) 05:10, 6 June 2019 (UTC)
- I didn't realize they were referring to seked. I figured the translation could have been a weasly one (although slopes derived from two side measurements aren't totally unrelated from ratios). There is nothing wrong with pointing out different views—perhaps mentioning that that's the word transliterated seqt—but I don't see a need for that now. UpdateNerd (talk) 05:59, 6 June 2019 (UTC)