Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is transient on its vertices (i.e. there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent, and the polyhedron has a high degree of reflectional and rotational symmetry.

Uniform polyhedra may be regular, quasi-regular or semi-regular. The faces and vertices need not be convex, so many of the Uniform polyhedra are also star polyhedra.

Excluding the infinite sets there are 75 uniform polyhedra (or 76 if edges are allowed to coincide).

Categories include:

Infinite set of uniform prisms (including star prisms)
Infinite set of uniform antiprisms (including star antiprisms)
5 Platonic solids - regular convex polyhedra
4 Kepler-Poinsot polyhedra - regular nonconvex polyhedra
13 Archimedean solids - quasiregular and semiregular convex polyhedra
14 nonconvex polyhedra with convex faces
39 nonconvex polyhedra with nonconvex faces
1 polyhedron found by John Skilling with pairs of edges that coincide.

They can also be grouped by their symmetry group, which is done below.

History

The Platonic solids date back to the classical Greeks and were studied by Plato, Theaetetus and Euclid.
Johannes Kepler (1571-1630) was the first to publish the complete list of Archimedean solids after the original work of Archimedes was lost.
Kepler (1619) discovered two of the regular Kepler-Poinsot polyhedra and Louis Poinsot (1809) discovered the other two.
Of the remaining 37 were discoved by Badoureau (1881). Edmund Hess (1878) discovered 2 more and Pitsch (1881) independently discovered 18, not all previously discovered.
The famous geometer Donald Coxeter discovered the remaining twelve in collaboration with J.C.P. Miller (1930-1932) but did not publish. M.S. and H.C. Longuet-Higgins and independently discovered 11 of these.
In 1954 H.S.M. Coxeter, M.S. Longuet-Higgins, J.C.P. Miller published the list of uniform polyhedra.
In 1970 S. P. Sopov proved their conjecture that the list was complete.
In 1974, Magnus Wenninger published his book, Polyhedron models, which is the first published list of all 75 nonprismatic uniform polyhedra, with many previously unpublished names given to them by Norman Johnson (mathematician).
In 1975, John Skilling independently proved the completeness, and showed that if the definition of uniform polyhedron is relaxed to allow edges to coincide then there is just one extra possibility.
In 1993, Zvi Har'El produced a complete computer construction of the uniform polyhedra and duals via their Kaleidoscopic construction via a comptuter program called Kaleido, and summarized in a paper Uniform Solution for Uniform Polyhedra., counting figures 1-80.
Also in 1993, R. Mäder ported this Kaleido solution to Mathematica with a slightly different indexing system.

Indexing

There are four major published indexing efforts from the works above. To distinguish them, they are given by indexing different letters, C for Coxeter 1954 first enumeration figures, W for the 1974 book Polyhedron models by Wenninger, K for the 1993 Kaleido solution, and U for the Maeder solution used by Mathematica and extensively reproduced elsewhere.

[C] 1954: This paper listed the uniform polyhedra by figures in the paper from 15-92. Starting with 15-32 for the convex forms, 33-35 for 3 infinite prismatic sets, and ending with 36-92 for the nonconvex forms.
[W] 1974: Wenninger's book Polyhedron model numbered figures 1-119: 1-5 for the Platonic solids, 6-18 for the Archimedean solids, 19-66 for stellated forms including the 4 regular nonconvex polyhedra, and ended with 67-119 for the nonconvex uniform polyhedra.
[K] 1993 Kaleido: The 80 figures given in the Kaleido solution were grouped by symmetry, numbered 1-80: 1-5 as representatives for the infinite families of prismatic forms with dihedral symmetry, 6-9 with tetrahedral symmetry, 10-26 with Octahedral symmetry, 46-80 with icosahedral symmetry.
[U] 1993 Mathematica: This listing followed the Kaleido one, but moved the 5 prismatic forms to last, shifting the nonprismatic forms back 5, and now 1-75.

References

Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germany: Teubner, 1900. [1]
H.S.M. Coxeter, M.S. Longuet-Higgins, J.C.P. Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401-50 [2]
S. P. Sopov A proof of the completeness on the list of elementary homogeneous polyhedra. (Russian) Ukrain. Geometr. Sb. No. 8, (1970), 139-156
Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
John Skilling, The complete set of uniform polyhedra., Philos. Trans. Roy. Soc. London Ser. A 278 (1975), 111-135 [3]
Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El [4], Kaleido software, Images, dual images
Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993. [5]

Convex forms and fundamental vertex arrangements

The convex uniform polyhedra can be named by Wythoff construction operations upon a parent form.

Note: Dihedra are members of an infinite set of two-sided polyhedra (2 identical polygons) which generate the prisms as truncated forms.

Each of these convex forms define set of vertices that can be identified for the nonconvex forms in the next section.

	Parent	Truncated	Rectified	Bitruncated (truncated dual)	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Extended Schläfli symbol	${\begin{Bmatrix}p,q\end{Bmatrix}}$	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	${\begin{Bmatrix}q,p\end{Bmatrix}}$	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$
Extended Schläfli symbol	t₀{p,q}	t_0,1{p,q}	t₁{p,q}	t_1,2{p,q}	t₂{p,q}	t_0,2{p,q}	t_0,1,2{p,q}	s{p,q}
Wythoff symbol p-q-2	q \| p 2	2 q \| p	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Coxeter-Dynkin diagram (variations)

	(o)-p-o-q-o	(o)-p-(o)-q-o	o-p-(o)-q-o	o-p-(o)-q-(o)	o-p-o-q-(o)	(o)-p-o-q-(o)	(o)-p-(o)-q-(o)	( )-p-( )-q-( )
	xPoQo	xPxQo	oPxQo	oPxQx	oPoQx	xPoQx	xPxQx	sPsQs
	[p,q]:001	[p,q]:011	[p,q]:010	[p,q]:110	[p,q]:100	[p,q]:101	[p,q]:111	[p,q]:111s
Vertex figure	p^q	(q.2p.2p)	(p.q.p.q)	(p.2q.2q)	q^p	(p.4.q.4)	(4.2p.2q)	(3.3.p.3.q)
Tetrahedral 3-3-2	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	{3,3}	(3.4.3.4)	(4.6.6)	(3.3.3.3.3)
Octahedral 4-3-2	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4.4)	(4.6.8)	(3.3.3.3.4)
Icosahedral 5-3-2	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3.3.5)
Dihedral p-2-2 Example p=5	{5,2}	2.10.10	2.5.2.5	4.4.5	{2,5}	2.4.5.4	4.4.10	3.3.3.5

Definition of operations

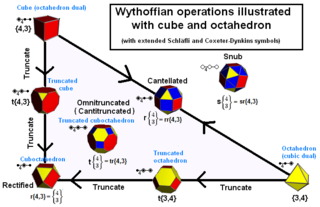Example forms from the cube and octahedron

Operation	Extended Schläfli symbols		Coxeter- Dynkin diagram	Description
Parent	t_{0_{p,q}}	${\begin{Bmatrix}p,q\end{Bmatrix}}$	File:Dynkins-100.png	Any regular polyhedron or tiling
Rectified	t_{1_{p,q}}	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	File:Dynkins-010.png	The edges are fully-truncated into single points. The polyhedron now has the combined faces of the parent and dual.
Birectified Also Dual	t_{2_{p,q}}	${\begin{Bmatrix}q,p\end{Bmatrix}}$	File:Dynkins-001.png	The birectified (dual) is a further truncation so that the original faces are reduced to points. New faces are formed under each parent vertex. The number of edges is unchanged and are rotated 90 degrees. The dual of the regular polyhedron {p, q} is also a regular polyhedron {q, p}.
Truncated	t_{0,1_{p,q}}	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	File:Dynkins-110.png	Each original vertex is cut off, with new faces filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated polyhedron. The polyhedron has its original faces doubled in sides, and contains the faces of the dual. File:Cube truncation sequence.png
Bitruncated	t_{1,2_{p,q}}	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	File:Dynkins-011.png	Same as truncated dual.
Cantellated (or rhombated) (Also expanded)	t_{0,2_{p,q}}	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	File:Dynkins-101.png	In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place, as well as the original vertices are also truncated. A uniform cantellation is half way between both the parent and dual forms.
Omnitruncated (or cantitruncated) (or rhombitruncated)	t_{0,1,2_{p,q}}	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	File:Dynkins-111.png	The truncation and cantellation operations are applied together create an omnitruncated form which has the parent's faces doubled in sides, the duals faces doubled in sides, and squares where the original edges existed.
Snub	s{p,q}	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$	File:Dynkins-sss.png	The snub takes the omnitruncated form and rectifies alternate vertices. (This operation is only possible for polyhedra with all even-sided faces.) All the original faces end up with half as many sides, and the square degenerate into edges. Since the omnitruncated forms have 3 faces/vertex, new triangles are formed. Usually these alternated faceting forms are slightly deformed thereafter in order to end again as uniform polyhedra. The possibility of the latter variation depends on the degree of freedom.

Nonconvex forms listed by symmetry groups and vertex arrangements

All the uniform polyhedra are listed below by their symmetry groups and subgrouped by their vertex arrangements.

Regular polyhedra are labeled by their Schläfli symbol. Other nonregular uniform polyhedra are listed by their vertex configuration or their Uniform polyhedron index U(1-80).

Note: For nonconvex forms below an additional descriptor Nonuniform is used when the convex hull of the vertex arrangement has same topology as one of these, but has nonregular faces. For example an nonuniform cantellated form may have rectangles created in place of the edges rather than squares.

Tetrahedral symmetry

There are 2 convex uniform polyhedra, the tetrahedron and truncated tetrahedron, and one nonconvex form, the tetrahemihexahedron which have tetrahedral symmetry. The tetrahedron is self dual.

In addition the octahedron, truncated octahedron, cuboctahedron, and icosahedron have tetrahedral symmetry as well as higher symmetry. They are added for completeness below, although their nonconvex forms with octahedral symmetry are not included here.

Vertex group	Convex	Nonconvex
(Tetrahedral)	{3,3}
Truncated (*)	(3.6.6)
Rectified (*)	{3,4}	(4.3/2.4.3)
Cantellated (*)	(3.4.3.4)
Omnitruncated (*)	(4.6.6)
Snub (*)	{3,5}

Octahedral symmetry

There are 8 convex forms, and 10 nonconvex forms with octahedral symmetry.

Vertex group	Convex	Nonconvex
(Octahedral)	{3,4}
Truncated (*)	(4.6.6)
Rectified (*)	(3.4.3.4)	(6.4/3.6.4)	(6.3/2.6.3)
Truncated dual (*)	(3.8.8)	(4.8/3.4/3.8/5)	(8/3.3.8/3.4)	(4.3/2.4.4)
Dual (*)	{4,3}
Cantellated (*)	(3.4.4.4)	(4.8.4/3.8)	(8.3/2.8.4)	(8/3.8/3.3)
Omnitruncated (*)	(4.6.8)
Nonuniform omnitruncated (*)	(4.6.8)	(8/3.4.6)	(8/3.6.8)
Snub (*)	(3.3.3.3.4)

Icosahedral symmetry

There are 8 convex forms and 46 nonconvex forms with icosahedral symmetry (or 47 nonconvex forms if Skilling's figure is included). Some of the nonconvex snub forms have nonuniform chiral symmetry, and some have achiral symmetry.

There are many nonuniform forms of varied degrees of truncation and cantellation.

Vertex group	Convex	Nonconvex
(Icosahedral)	{3,5}	{5/2,5}	{5,5/2}	{3,5/2}
Truncated (*)	(5.6.6)
Nonuniform truncated (*)	(5.6.6)	U32	U37	U61	U38	U44	U56	U67	U73
Rectified (*)	(3.5.3.5)	U49	U51	U54	U70	U71	U36	U62	U65
Truncated dual (*)	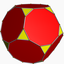(3.10.10)	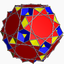U42	U48	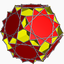U63
Nonuniform truncated dual (*)	(3.10.10)	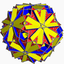U68	U72	U45
Dual (*)	{5,3}	{5/2,3}	U30	U41	U47
Cantellated (*)	(3.4.5.4)	U33	U39
Nonuniform Cantellated (*)	(3.4.5.4)	U31	U43	U50	U55	U58	U75	U64	U66
Omnitruncated (*)	(4.6.10)
Nonuniform omnitruncated (*)	(4.6.10)	U59
Snub (*)	(3.3.3.3.5)
Nonuniform Snub (*)	(3.3.3.3.5)	U40	U46	U57	U69	U60	U74

Skilling's figure

One further nonconvex polyhedron is the Great disnub dirhombidodecahedron, also known as Skilling's figure, which is vertex-uniform, but has pairs of edges which coincide in space such that four faces meet at some edges. It is sometimes but not always counted as a uniform polyhedron. It has I_h symmetry.

Dihedral symmetry

There are two infinite sets of uniform polyhedra with dihedral symmetry:

prisms, for each rational number p/q > 2, with symmetry group D_ph;
antiprisms, for each rational number p/q > 3/2, with symmetry group D_pd if q is odd, D_ph if q is even.

If p/q is an integer, i.e. if q = 1, the prism or antiprism is convex. (The fraction is always assumed to be stated in lowest terms.)

The difference between the prismatic and antiprismatic dihedral symmetry groups is that D_ph has a reflection plane perpendicular to its p-fold axis (parallel to the {p/q} polygon), while D_pd has none. Each has p reflection planes which contain the p-fold axis.

An antiprism with p/q < 2 is crossed; its vertex figure resembles a bowtie. If p/q ≤ 3/2 no antiprism can exist, as its vertex figure would violate the triangle inequality.

Note: The cube and octahedron are listed here with dihedral symmetry (as a tetragonal prism and trigonal antiprism respectively), although if uniformly colored, they also have octahedral symmetry.

Symmetry group	Convex	Nonconvex
d_3h	3.3.4
d_3d	3.3.3.3
d_4h	4.4.4
d_4d	3.3.3.4
d_5h	4.4.5	4.4.5/2	3.3.3.5/2
d_5d	3.3.3.5	3.3.3.5/3
d_6h	4.4.6
d_6d	3.3.3.6
d_7h	4.4.7	4.4.7/2	4.4.7/3	3.3.3.7/2	3.3.3.7/4
d_7d	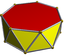3.3.3.7	3.3.3.7/3
d_8h	4.4.8	4.4.4.8/3
d_8d	3.3.3.8	3.3.3.8/3 3.3.3.8/5
d_9h	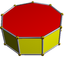4.4.9	4.4.9/2	3.3.3.9/2	3.3.3.9/4
d_9d	3.3.3.9	3.3.3.9/5
d_10h	4.4.10	4.4.10/3
d_10d	3.3.3.10	3.3.3.10/3
d_11h	4.4.11	4.4.11/2 4.4.11/3 4.4.11/4 4.4.11/5	3.3.3.11/2 3.3.3.11/4 3.3.3.11/6
d_11d	3.3.3.11	3.3.3.11/3 3.3.3.11/5 3.3.3.11/7
d_12h	4.4.12	4.4.12/5	3.3.3.12/7
d_12d	3.3.3.12	3.3.3.12/5
...