User:Purgy Purgatorio/sandbox
In mathematics, a field is a set on which are defined addition, subtraction, multiplication, and division, which behave as they do when applied to rational and real numbers. A field is thus a fundamental algebraic structure, which is widely used in algebra, number theory and many other areas of mathematics.
The best known fields are the field of rational numbers and the field of real numbers. The field of complex numbers is also widely used, not only in mathematics, but also in many areas of science and engineering. Many other fields, such as fields of rational functions, algebraic function fields, algebraic number fields, and p-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Finite fields are used in most cryptographic protocols used for computer security.
Any field may be used as the scalars for a vector space, which is the standard general context for linear algebra. The theory of field extensions (including Galois theory) involves the roots of polynomials with coefficients in a field; among other results, this theory leads to impossibility proofs for the classical problems of angle trisection and squaring the circle with a compass and straightedge, as well as a proof of the Abel–Ruffini theorem on the algebraic insolubility of quintic equations.
Definition
[edit]In a nutshell, a field is a set on which are defined an addition and a multiplication that behave similarly as they behave for rational numbers and real numbers, including the existence of a multiplicative inverse for every nonzero element.
Formally, a field is a set together with two operations the addition and the multiplication.[1] An operation is a mapping that associates an element of the set to every pair of its elements. The result of the addition of a and b is called the sum of a and b and denoted a + b. Similarly, the result of the multiplication of a and b is called the product of a and b, and denoted ab or a⋅b. These operations are required to satisfy the following properties, referred to as field axioms. In the sequel, a, b and c are arbitrary elements of F.
- a + (b + c) = (a + b) + c and a · (b · c) = (a · b) · c (associativity of addition and multiplication)
- a + b = b + a and a · b = b · a (commutativity of addition and multiplication)
- There exist two different elements 0 (called additive identity) and 1 (the multiplicative identity) in F such that a + 0 = a and a . 1 = a.
- For every a in F, there exists an element in F, denoted −a, called additive inverse, such that a + (−a) = 0.
- For every a ≠ 0 in F, there exists an element in F, denoted a−1, 1/a, or 1/a, and referred to as multiplicative inverse such that a · a−1 = 1
- a · (b + c) = (a · b) + (a · c) (distributivity of multiplication over addition).
A subtraction and a division are defined in every field by
Alternative definition
[edit]As with other algebraic structures, there are several equivalent definitions. One can alternatively define a field by four binary operations (add, subtract, multiply, divide), and the properties that they must have. As existential quantifiers are problematic in constructive mathematics and computing, fields are often defined by two binary operations (add and multiply), two unary operations (additive inverse and multiplicative inverse), and two nullary operations (0 and 1); this implies that the axioms that the operations must satisfy contain only universal quantifiers.
The axioms of a field can also be packaged using other algebraic notions. As was mentioned above, the existence of the binary operation "·", together with its commutativity, associativity, (multiplicative) identity element and inverses are precisely the axioms for an abelian group. The structure of a field is the same as specifying such two group structures (on the same set), obeying the distributivity.[2]
Fundamental examples
[edit]The rational numbers
[edit]Rational numbers have been widely used a long time before the elaboration of the concept of field. They are numbers which can be written as fractions a/b, where a and b are integers, and b ≠ 0. The additive inverse of such a fraction is −a/b, and the multiplicative inverse (provided that a ≠ 0) is b/a, which can be seen as follows:
The abstractly required field axioms reduce to standard properties of rational numbers, such as the law of distributivity
or the law of commutativity and law of associativity.[3]
Real and complex numbers
[edit]The real numbers R, with the usual operations of addition and multiplication, also form a field. The complex numbers C consist of expressions
- a + bi
where i is the imaginary unit, i.e., a (non-real) number satisfying i2 = −1. Addition and multiplication of real numbers are defined in such a way that all field axioms hold for C. For example, the distributive law enforces
- (a + bi)·(c + di) = ac + bci + adi + bdi2, which equals ac−bd + (bc + ad)i.
The complex numbers form a field. Complex numbers can be geometrically represented as points in the plane, and addition resp. multiplication of such numbers then corresponds to adding resp. rotating and scaling points. The fields of real and complex numbers are used throughout mathematics, physics, engineering, statistics, and many other scientific disciplines.
Constructible numbers
[edit]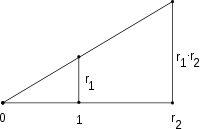
In antiquity, several geometric problems concerned the (in)feasibility of constructing certain numbers with compass and straightedge. For example, it was unknown to the Greeks that it is in general impossible to trisect a given angle. Using the field notion and field theory allows these problems to be settled. To do so, the field of constructible numbers is considered. It contains, on the plane, the points 0 and 1, and all complex numbers that can be constructed from these two by a finite number of construction steps using only compass and straightedge. This set, endowed with the usual addition and multiplication of complex numbers does form a field. For example, multiplying two (real) numbers r1 and r2 that have already been constructed can be done using construction at the right, based on the intercept theorem. This way, the obtained field F contains all rational numbers, but is bigger than Q, because for any f ∈ F, the square root of f is also a constructible number.
A closely related concept is that of a Euclidean field, namely an ordered field whose positive elements are closed under square root. The real constructible numbers form the least Euclidean field, and the Euclidean fields are precisely the ordered extensions thereof.
A field with four elements
[edit]| Addition | Multiplication | ||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
In addition to familiar number systems such as the rationals, there are other, less immediate examples of fields. The following example is a field consisting of four elements called O, I, A, and B. The notation is chosen such that O plays the role of the additive identity element (denoted 0 in the axioms above), and I is the multiplicative identity (denoted 1 in the axioms above). One can check that all field axioms are satisfied. For example:
- A · (B + A) = A · I = A, which equals A · B + A · A = I + B = A, as required by the distributivity.
This field is called a finite field with four elements, and is denoted F4 or GF(4). The subset consisting of O and I (highlighted in red in the tables at the right) is also a field, known as the binary field or GF(2). In the context of computer science and Boolean algebra, O and I are often denoted respectively by false and true, the addition is then denoted XOR (exclusive or), and the multiplication is denoted AND. In other words, the structure of the binary field is the basic structure that allows computing with bits.
Properties
[edit]In this section, F denotes an arbitrary field.
Elementary consequences of the definition
[edit]For every a in F, one has a · 0 = 0 and −a = (−1) · a.[4] In particular, one may deduce the additive inverse of every element as soon as one knows –1.
If a ≠ 0 and b belong to a field, then the equation ax = b has a unique solution in the field, which is b/a. This is the starting point of linear algebra.
If a ≠ 0 then ab = 0 implies b = 0. This follows from 0 = a–1⋅0 = a–1(ab) = (a–1a)b = b. This means that every field is an integral domain.
The additive and the multiplicative group of a field
[edit]The subset of nonzero elements F \ {0} together with the multiplication operation is an abelian group. It is also denoted F× and called the multiplicative group of F. Likewise (F, +) is an abelian group, known as the additive group. Some elementary statements about fields can therefore be obtained by applying general facts of groups. For example, the additive and multiplicative inverses −a and a−1 are uniquely determined by a.
One of the main reasons for requiring 1 ≠ 0, is that a group has at least one element and thus that the trivial ring does not have a multiplicative group.
Every finite subgroup of the multiplicative group of a field is cyclic. See Root of unity § Cyclic groups.
Characteristic
[edit]Beware, in this section the token 0 denotes the integer 0 as well as the field element 0, and the token "" stands for the newly introduced "product" as well as for the multiplication within the field.
The "product" of an arbitrary element a of F by any integer n, yielding a field element, can be defined as
- when n is positive, by
- for and by
- for n negative ("(-n)" referring in this case to a positive integer).
Depending on the field F in question, there may be a positive integer n such that the expression
- n ⋅ 1 = 0.
In this case, there is a smallest such integer, which can be shown to be a prime number, often denoted by p. The field is said to have characteristic p in this case. It follows from the field axioms that
- p ⋅ a = 0 for any element a in F.
For example, the field F4 mentioned above has characteristic 2 since 2 ⋅ a = 0, i.e. a + a = 0, for any element in this field.
If there is no positive integer such that n ⋅ 1 = 0, then F is said to have characteristic 0. For example, Q has characteristic 0.
Subfields and prime fields
[edit]Informally, a subfield E is a field contained in another field F. More precisely, E is a subset of F that contains 1, and is closed under addition, multiplication, additive inverse and multiplicative inverse of a nonzero element. This means that that, for all one has and and that, for all in E, one has and It is straightforward to verify that a subfield is indeed a field.
For any field F, the subset of expressions , where n is an integer, forms the so-called prime field of F. This subfield is minimal in the sense that every subfield of F contains it, since 1 and all its "products" must be in all subfields of F. If the characteristic of F is p (a prime number), the prime fields consists of the p elements j ⋅ 1 (with 0 ≤ j < p). Otherwise, it is infinite.
Finite fields
[edit]Finite fields (also called Galois fields) are fields with finitely many elements, whose number is also referred to as the order of the field. The above introductory example F4 is a field with four elements. F2 consists of two elements, 0 and 1. This is the smallest field, because by definition a field has at least two distinct elements 1 ≠ 0.
A basic class of finite fields are the fields Fp with p elements (p a prime number):
- Fp = Z/pZ = {0, 1, ..., p − 1},
where the operations are defined by performing the operation in the set of integers Z, dividing by p and taking the remainder; see modular arithmetic. A field K of characteristic p necessarily contains Fp,[5] and therefore may be viewed as a vector space over Fp, of finite dimension if K is finite. Thus a finite field K has prime power order, i.e., K has q = pn elements (where n > 0 is the number of elements in a basis of K over Fp). By developing more field theory, in particular the notion of the splitting field of a polynomial f over a field K, which is the smallest field containing K and all roots of f, one can show that two finite fields with the same number of elements are isomorphic, i.e., there is a one-to-one mapping of one field onto the other that preserves multiplication and addition. Thus we may speak of the finite field with q elements, usually denoted by Fq or GF(q).
History
[edit]Both Niels Henrik Abel (1802–1829) and Évariste Galois (1811–1832) used the concept of field implicitly in their work on the solvability of polynomial equations with rational coefficients of degree five or higher.
In 1857 Karl von Staudt published his concept of Algebra of Throws, which provided a geometric model satisfying the axioms of a field.[6] This construction has been frequently recalled as a contribution to the foundations of mathematics.[citation needed]
In 1871 Richard Dedekind introduced, for a set of real or complex numbers which is closed under the four arithmetic operations, the German word Körper, which means "body" or "corpus" (to suggest an organically closed entity),[7] hence the common use of the letter K to denote a field. He also defined rings (then called order or order-modul). Hilbert invented the term "a ring" (Zahlring).[8] In 1893, Eliakim Hastings Moore called the concept "field" in English.[9][10]
In 1881 Leopold Kronecker defined what he called a "domain of rationality", which is indeed a field of rational fractions in modern terms. In 1893 Heinrich M. Weber gave the first clear definition of an abstract field.[11] In 1910, Ernst Steinitz published the very influential paper Algebraische Theorie der Körper (English: Algebraic Theory of Fields).[12] In this paper he axiomatically studies the properties of fields and defines many important field-theoretic concepts like prime field, perfect field and the transcendence degree of a field extension.
Emil Artin developed the relationship between groups and fields in great detail from 1928 through 1942.
Related algebraic structures
[edit]Dropping one or several axioms in the definition of a field leads to other algebraic structures. Commutative rings have already been mentioned above. A ring in which division is possible but commutativity is not assumed (such as the quaternions) is called a division ring or skew field.[13]
Fields can be characterized as those commutative rings R which have precisely two ideals, (0) and the R. Similarly, fields are precisely those commutative rings in which (0) is a prime ideal, and is the only (and therefore maximal) one.
Constructing fields
[edit]Constructing fields from rings
[edit]In various situations, all the axioms of a field are satisfied, except for the existence of multiplicative inverses . Such an algebraic structure is called a commutative ring. For example, the integers Z form a commutative ring, but not a field since the reciprocal of an n is not itself an integer (unless ). There are two important methods to construct a field from a given commutative ring R, i.e., to find a field (related to R) where all elements become invertible (which is not necessarily the case in a ring): forming the field of fractions, and forming residue fields. The field of fractions of Z is Q, the rationals, while the residue fields of Z are the finite fields Fp'.
Field of fractions
[edit]Given an integral domain R, its field of fractions Q(R) is built with the fractions of two elements of R exactly as is constructed from the integers. More precisely, the elements of Q(R) are the fractions a/b where a and b are in R, and b ≠ 0. Two fractions a/b and c/d are equal if and only if ad = bc. The operation on the fractions work exactly as usual. For example
It is straightforward to show that, if the ring is an integral domain, the set of the fractions form a field.
Further examples of this are
- The field k(x) of the rational fractions over a field (or an integral domain) k is the field of fractions of the polynomial ring k[x].
- The field k((x)) of the Laurent series over a field k is the field of fractions of the ring k[[x]] of the power series. In this case, the representation as fractions is not used, as one can show that every fraction is equal to a fraction which has a power of x as a denominator.
Residue fields
[edit]Another method to obtain a field from a commutative ring R is taking the quotient R / m, where m is any maximal ideal of R. This field is called the residue field of R and m. An important example is
- F = E[X] / (p(X)),
where p is an irreducible polynomial in E, i.e., a polynomial which can not be expressed as the product of two polynomials of smaller degree. The irreducibility of p is equivalent to the maximality of the ideal generated by this polynomial.
Field extensions
[edit]The notion of a subfield can also be regarded from the opposite point of view, by referring to F being a field extension (or just extension) of E, denoted by
- F / E (read F over E).
For example, the real numbers are an extension of any of the following subfields: the real algebraic numbers, the computable numbers and the rational numbers are examples. Field extensions are a crucial concept in field theory and appear in many other mathematical domains. Given a field E, field extensions F / E can be constructed by "adding new elements" or adjoining elements to E.
As was mentioned above, the field F = E(X) of rational functions is the field of fractions of the polynomial ring E[X], i.e., its elements are fractions
where p(X) and q(X) are polynomials with coefficients in E, and q is not the zero polynomial. In this example, the added symbol X and its powers do not interact with elements of E: there is no polynomial equation with coefficients in E whose zero is X. Such an extension is called purely transcendental.
It is possible however that the adjoined symbol may interact with E. For example, as was explained above, C is an extension of R and can be obtained from R by adjoining the imaginary symbol i which satisfies i2 = −1. The result is that R[i]=C. This is different from adjoining the symbol X to R, because in that case, the powers of X are all distinct objects, but here, i2=−1 is actually an element of R. This field extension can also be constructed as follows: since i is a zero of the polynomial p(X) = X2 + 1, there is an isomorphism
The polynomial X2+1 is irreducible over R. Therefore the principal ideal generated by this polynomial is maximal, so that the quotient ring is a field. The above nonzero ring map from the quotient to C is necessarily an isomorphism of rings.
The above construction generalises to any irreducible polynomial p in the polynomial ring E[X], i.e., a polynomial p(X) that cannot be written as a product of non-constant polynomials with coefficients in E. The quotient ring F = E[X] / (p(X)), is again a field. The field extension F / E obtained in this way is an algebraic extension.
Alternatively, field extensions can also be constructed, if a bigger container field is already given. Suppose given a field E, and a field G containing E as a subfield. (In many situations, G is an algebraic closure of E). For any element x of G, there is a smallest subfield of G containing E and x, denoted F = E(x) and called field extension F / E generated by x in G.[14] Such extensions are called simple extensions. The primitive element theorem asserts that any finite separable extension is simple. For instance, Q(i) is the subfield of C consisting of all numbers of the form a + bi where both a and b are rational numbers.
A related construction is the compositum of two subfields E and E' of some field G.
Example: Algebraic numbers
[edit]The most important class of fields in number theory are algebraic number fields. We will first give an example, namely the field Q(ζ) consisting of numbers of the form
- a + bζ
with a, b ∈ Q, where ζ is a primitive third root of unity, i.e., a complex number satisfying ζ3 = 1, ζ ≠ 1. This field extension can be used to prove a special case of Fermat's last theorem, which asserts the non-existence of rational nonzero solutions to the equation
- x3 + y3 = z3.
In the language of field extensions detailed below, Q(ζ) is a field extension of degree 2. Algebraic number fields are by definition finite field extensions of Q, that is, fields containing Q having finite dimension as a Q-vector space.
Closure operations
[edit]A field is algebraically closed if any polynomial equation
- fnxn + fn−1xn−1 + ··· + f1x + f0 = 0, with coefficients fn, ..., f0 ∈ F, n>0,
has a solution . The fields of rational or real numbers are not algebraically closed since the equation
- x2 + 1 = 0
does not have any rational or real solution. There is, however, a complex solution to this equation, namely x=i, the imaginary unit. What is more, by the fundamental theorem of algebra, any polynomial equation with complex coefficients has a complex solution. In other words, C is algebraically closed.
Assuming the axiom of choice, for every field F, there exists a field F, called an algebraic closure of F, which contains F, is algebraic over F, which means that any element x of F satisfies a polynomial equation with coefficients in F, as above (roughly speaking, F is not too big compared to F), and which is algebraically closed (big enough to contain solutions of all polynomial equations). For example, C is an algebraic closure of R. (In other words C is the smallest field which both contains the reals and is algebraically closed.) Moreover, any other field G which has the same properties as F is isomorphic to F, but the isomorphism is not unique.
The algebraic closure Q is also called field of algebraic numbers. The field of algebraic numbers is an example of an algebraically closed field of characteristic zero; as such it satisfies the same first-order sentences as the field of complex numbers C. The algebraic closure of the field C((t)) of Laurent series is the field of Puiseux series.
A similar concept is the separable closure, containing all roots of separable polynomials, instead of all polynomials.
Ultraproducts
[edit]If I is an index set, U is an ultrafilter on I, and Fi is a field for every i in I, the ultraproduct of the Fi with respect to U is a field.
For example, a non-principal ultraproduct of finite fields is a pseudo finite field; i.e., a PAC field having exactly one extension of any degree.
Fields with modified structures
[edit]Since fields are ubiquitous in mathematics and beyond, there are several refinements of the concept which are adapted to the needs of a particular mathematical area.
Ordered fields
[edit]A field F is called an ordered field if there any two elements can be compared, in a way that is compatible with the multiplication and addition. For example, the reals form an ordered field, with the usual ordering <. A field being ordered is equivalent to being formally real, i.e., the existence of an ordering is equivalent to the condition that −1 is not a square in F.
An Archimedean field is an ordered field such that for each element there exists a finite expression
- 1 + 1 + ··· + 1
whose value is greater than that element, that is, there are no infinite elements. Equivalently, the field contains no infinitesimals; or, the field is isomorphic to a subfield of the reals R. The hyperreals R* are an extension of the reals obtained by including infinite and infinitesimal numbers. These are larger, respectively smaller than any real number. The hyperreals form the foundational basis of non-standard analysis.
The reals form the smallest ordered field that contains the integers, and is complete, in the sense that every upper bound, lower bound (see Dedekind cut) and limit (see Cauchy sequence), which should exist, exist effectively. These properties of the reals form the foundation of calculus.
A necessary condition for an ordered field to be complete is that it be Archimedean, since in any non-Archimedean field there is neither a greatest infinitesimal nor a least positive rational, whence the sequence 1/2, 1/3, 1/4, …, every element of which is greater than every infinitesimal, has no limit. (And since every proper subfield of the reals also contains such gaps, up to isomorphism the reals form the unique complete ordered field.)
Topological fields
[edit]Another refinement of the notion of a field is a topological field, which combines the algebraic structure of a field with the topological concept of nearness.
Field of functions
[edit]Functions on a topological space X can be added and multiplied pointwise, i.e.,
- (f ⋅ g)(x) = f(x) ⋅ g(x).
In order to have multiplicative inverses requires considering ratios of functions, i.e., expressions of the form
where . Such ratios form a field, called the function field of X. This concept is used in different mathematical areas:
- if X is an algebraic variety, the relevant class of functions are of polynomial nature. Their ratios are known as rational functions. For example, the function field of the n-dimensional space over a field k is , i.e., the field consisting of ratios of polynomials f and g in n indeterminates.
- if X is a complex manifold, the relevant class of functions are holomorphic functions, i.e., complex differentiable functions. Their ratios are referred to as meromorphic functions.
The function field of X captures important geometric information about X. For smooth projective algebraic curves, and similarly for compact Riemann surfaces, the surface can actually be reconstructed from this field. The study of these function fields and their goemetric meaning in higher dimensions is referred to as birational geometry.
Local fields
[edit]The real numbers mentioned above can be constructed by completing the rational numbers, i.e., filling the "gaps": for example √2 is such a gap. A formally very similar procedure, namely the completion with respect to a different notion of distance (the p-adic valuation), leads to the field of p-adic numbers Qp. It is used in number theory and p-adic analysis.
The following fields are called local fields:
- R and C (called archimedian local fields),
- finite extensions of Qp (non-archimedian local fields of characteristic zero)
- finite extensions of Fp((t)), the field of Laurent series over Fp (non-archimedian local fields of characteristic p).
Non-archimedian local fields in characteristic 0 and characteristic p share some fundamental similarities. In this relation, the elements and (referred to as uniformizer) correspond to each other. The first manifestation of this is at an elementary level: the elements of both fields can be expressed as power series in the uniformizer, with coefficients in Fp. (However, since the addition in Qp is done using carrying, which is not the case in Fp((t)), these fields are not isomorphic.) The following facts show that this superficial similarity goes much deeper:
- any first order statement which is true for almost all Qp is also true for almost all Fp((t)). An application of this is the Ax-Kochen theorem describing zeros of homogeneous polynomials in Qp.
- tamely ramified extensions of both fields are in bijection to one another.
- Adjoining arbitrary p-power roots of p (in Qp), respectively of t (in Fp((t))), yields (infinite) extensions of these fields known as perfectoid fields. Strikingly, the Galois groups of these two fields are isomorphic, which is the first glimpse of a remarkable parallel between these two fields:[15]
Global fields
[edit]Global fields are, by definition, algebraic number fields or function fields over Fq, i.e., finite extensions of Fq(t). Local fields are completions of global fields at a given place. For example, the local fields attached to Q are Qp and R, by Ostrowski's theorem. Studying arithmetic questions in global fields may sometimes be done by looking at the corresponding questions locally—this technique is called local-global principle. For example, the Hasse–Minkowski theorem reduces the problem of finding rational solutions of quadratic equations to solving these equations in R and Qp, whose solutions can easily be described.
Differential fields
[edit]Differential fields are fields equipped with a derivation, i.e., allow to take derivatives of elements in the field. For example, the field R(X), together with the standard derivative of polynomials forms a differential field. These fields are central to differential Galois theory.
Fields (with capital F)
[edit]There are also proper classes with field structure, which are sometimes called Fields, with a capital F:
- The surreal numbers form a Field containing the reals, and would be a field except for the fact that they are a proper class, not a set.
- The nimbers form a Field. The set of nimbers with birthday smaller than 22n, the nimbers with birthday smaller than any infinite cardinal are all examples of fields.
Exponential fields
[edit]Exponential fields are fields equipped with an exponential function, i.e., a group homomorphism
For example, the real and complex numbers, equipped with their usual exponential function, are exponential fields.
One does not in general study generalizations of fields with three binary operations. The familiar addition/subtraction, multiplication/division, exponentiation/root-extraction/logarithm operations from the natural numbers to the reals, each built up in terms of iteration of the last, mean that generalizing exponentiation as a binary operation is tempting, but has generally not proven fruitful; instead, an exponential field assumes a unary exponential function from the additive group to the multiplicative group, not a partially defined binary function. Note that the exponential operation of is neither associative nor commutative, nor has a unique inverse ( are both square roots of 4, for instance), unlike addition and multiplication, and further is not defined for many pairs—for example, does not define a single number. These all show that even for rational numbers exponentiation is not nearly as well-behaved as addition and multiplication, which is why one does not in general axiomatize exponentiation.
Galois theory
[edit]Galois theory aims to study the algebraic extensions of a field by studying the symmetry in the arithmetic operations of addition and multiplication. The fundamental theorem of Galois theory shows that there is a strong relation between the structure of the symmetry group and the set of algebraic extensions.
In the case where F / E is a finite (Galois) extension, Galois theory studies the algebraic extensions of E that are subfields of F. Such fields are called intermediate extensions. Specifically, the Galois group of F over E, denoted Gal(F/E), is the group of field automorphisms of F that are trivial on E (i.e., the bijections σ : F → F that preserve addition and multiplication and that send elements of E to themselves), and the fundamental theorem of Galois theory states that there is a one-to-one correspondence between subgroups of Gal(F/E) and the set of intermediate extensions of the extension F/E. The theorem, in fact, gives an explicit correspondence and further properties.
To study all (separable) algebraic extensions of E at once, one must consider the absolute Galois group of E, defined as the Galois group of the separable closure, Esep, of E over E i.e., Gal(Esep/E). It is possible that the degree of this extension is infinite (as in the case of E = Q). It is thus necessary to have a notion of Galois group for an infinite algebraic extension. The Galois group in this case is obtained as a "limit" (specifically an inverse limit) of the Galois groups of the finite Galois extensions of E. In this way, it acquires a topology.[note 1] The fundamental theorem of Galois theory can be generalized to the case of infinite Galois extensions by taking into consideration the topology of the Galois group, and in the case of Esep/E it states that there this a one-to-one correspondence between closed subgroups of Gal(Esep/E) and the set of all separable algebraic extensions of E (technically, one only obtains those separable algebraic extensions of E that occur as subfields of the chosen separable closure Esep, but since all separable closures of E are isomorphic, choosing a different separable closure would give the same Galois group and thus an "equivalent" set of algebraic extensions).
Applications
[edit]The concept of a field is of use, for example, in defining vectors and matrices, two structures in linear algebra whose components can be elements of an arbitrary field.
Finite fields are used in number theory, Galois theory, cryptography, coding theory and combinatorics; and again the notion of algebraic extension is an important tool.
See also
[edit]- Category of fields
- Glossary of field theory for more definitions in field theory.
- Heyting field
- Lefschetz principle
- Puiseux series
- Ring
- Vector space
- Vector spaces without fields
- Differential field
- Isomorphism extension theorem
- field with one element
- tensor product of fields
- algebra over a field
- real-closed field
Notes
[edit]- ^ As an inverse limit of finite discrete groups, it is equipped with the profinite topology, making it a profinite topological group
References
[edit]This article includes a list of general references, but it lacks sufficient corresponding inline citations. (March 2009) |
- ^ Definition 4.1.1, p181, Chapter 4.1 FIELDS: ROOTS OF POLYNOMIALS, Abstract Algebra, 3rd Edition (2006), by John A. Beachy, William D. Blair, Northern Illinois University, Waveland Press INC. www.waveland.com, ISBN 1-57766-443-4
- ^ Equivalently, a field is an algebraic structure 〈F, +, ·, −, −1, 0, 1〉; of type 〈2, 2, 1, 1, 0, 0〉, consisting of two abelian groups:
- F under +, −, and 0;
- F ∖ {0} under ·, −1, and 1, with 0 ≠ 1,
- ^ Second row at p120, Chapter 3 GROUPS, Abstract Algebra, 3rd Edition (2006), by John A. Beachy, William D. Blair, Northern Illinois University, Waveland Press INC. www.waveland.com, ISBN 1-57766-443-4
- ^ p120, Chapter 3 GROUPS, Abstract Algebra, 3rd Edition (2006), by John A. Beachy, William D. Blair, Northern Illinois University, Waveland Press INC. www.waveland.com, ISBN 1-57766-443-4
- ^ Jacobson (2009), p. 213
- ^ Karl Georg Christian v. Staudt, Beiträge zur Geometrie der Lage (Contributions to the Geometry of Position), volume 2 (Nürnberg, (Germany): Bauer and Raspe, 1857). See: "Summen von Würfen" (sums of throws), pp. 166-171 ; "Produkte aus Würfen" (products of throws), pp. 171-176 ; "Potenzen von Würfen" (powers of throws), pp. 176-182.
- ^ Peter Gustav Lejeune Dirichlet with R. Dedekind, Vorlesungen über Zahlentheorie von P. G. Lejeune Dirichlet (Lectures on Number Theory by P.G. Lejeune Dirichlet), 2nd ed., volume 1 (Braunschweig, Germany: Friedrich Vieweg und Sohn, 1871), p. 424. From page 424: "Unter einem Körper wollen wir jedes System von unendlich vielen reellen oder complexen Zahlen verstehen, welches in sich so abgeschlossen und vollständig ist, dass die Addition, Subtraction, Multiplication und Division von je zwei dieser Zahlen immer wieder eine Zahl desselben Systems hervorbringt." (By a "field" we will understand any system of infinitely many real or complex numbers, which is so closed and complete that the addition, subtraction, multiplication, and division of any two of these numbers always again produces a number of the same system.)
- ^ J J O'Connor and E F Robertson, The development of Ring Theory, September 2004.
- ^ Moore, E. Hastings (1893), "A doubly-infinite system of simple groups", Bulletin of the New York Mathematical Society, 3 (3): 73–78, doi:10.1090/S0002-9904-1893-00178-X, JFM 25.0198.01. From page 75: "Such a system of s marks [i.e., a finite field with s elements] we call a field of order s."
- ^ Earliest Known Uses of Some of the Words of Mathematics (F)
- ^ Fricke, Robert; Weber, Heinrich Martin (1924), Lehrbuch der Algebra, Vieweg, JFM 50.0042.03
- ^ Steinitz, Ernst (1910), "Algebraische Theorie der Körper", Journal für die reine und angewandte Mathematik, 137: 167–309, doi:10.1515/crll.1910.137.167, ISSN 0075-4102, JFM 41.0445.03
- ^ Historically, division rings were sometimes referred to as fields, while fields were called commutative fields.
- ^ Jacobson (2009, p. 213)
- ^ Scholze, Peter (2014), "Perfectoid spaces and their Applications" (PDF), Proceedings of the International Congress of Mathematicians 2014, ISBN 978-89-6105-804-9
Sources
[edit]- Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-13-004763-2, especially Chapter 13
- Allenby, R.B.J.T. (1991), Rings, Fields and Groups, Butterworth-Heinemann, ISBN 978-0-340-54440-2
- Blyth, T.S.; Robertson, E. F. (1985), Groups, rings and fields: Algebra through practice, Cambridge University Press. See especially Book 3 (ISBN 0-521-27288-2) and Book 6 (ISBN 0-521-27291-2).
- Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
- James Ax (1968), The elementary theory of finite fields, Ann. of Math. (2), 88, 239–271
External links
[edit]- "Field", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Field Theory Q&A
- Fields at ProvenMath definition and basic properties.
- "Field". PlanetMath.
xxxx
[edit]Statement and derivation
[edit]For a collection of N point particles, the scalar moment of inertia I about the origin is defined by the equation
where mk and rk represent the mass and position of the kth particle. rk=|rk| is the position vector magnitude. The scalar G is defined by the equation
where pk is the momentum vector of the kth particle. Assuming that the masses are constant, G is one-half the time derivative of this moment of inertia
In turn, the time derivative of G can be written
where mk is the mass of the k-th particle, is the net force on that particle, and T is the total kinetic energy of the system
Connection with the potential energy between particles
[edit]The total force on particle k is the sum of all the forces from the other particles j in the system
where is the force applied by particle j on particle k. Hence, the virial can be written
Since no particle acts on itself (i.e., for ), we split the sum in terms below and above this diagonal:
where we have assumed that Newton's third law of motion holds, i.e., (equal and opposite reaction).
The double summation in the two parts of the penultimate expression can be restated to
Exchanging the free variable names in the second sum and contracting the now identical summations leads to
where applying the mentioned Newton's third law yields the final result
_________________________________________________
It often happens that the forces can be derived from a potential function V, which is a linear superposition of N potentials Vk, each being spherically symmetric around particle k. A spherical symmetry requires that the value of the potential at any arbitrary point in space is independent of e.g. polar and azimuthal angles with respect to the center at particle k, i.e, the potential enacted by particle k at the location of particle j depends only on the absolute distance of particle j from particle k, which is given by
- , and thus
- for some single variable potential function .
The forces are given by the well known relations
- which, in these specific spherical coordinate systems with radii , turn to
- .
The magnitude of these force vectors is determined by the , which degenerates to a single variable derivative with respect to and vanishing derivatives in the other directions of these specific coordinates, and the respective directions are along the lines from particle k to particle j, expressed by the unit vectors in the last term above.
______________________________________________________________________________
It often happens that the forces can be derived from a potential energy V that is a function only of the distance rjk between the point particles j and k. Since the force is the negative gradient of the potential energy, we have in this case
which is equal and opposite to , the force applied by particle on particle j, as may be confirmed by explicit calculation. Hence,
Thus, we have
Special case of power-law forces
[edit]In a common special case, the potential energy V between two particles is proportional to a power n of their distance r
where the coefficient α and the exponent n are constants. In such cases, the virial is given by the equation
where VTOT is the total potential energy of the system
Thus, we have
For gravitating systems the exponent n equals −1, giving Lagrange's identity
which was derived by Lagrange and extended by Jacobi.
Time averaging
[edit]The average of this derivative over a time, τ, is defined as
from which we obtain the exact equation
The virial theorem states that, if , then
There are many reasons why the average of the time derivative might vanish, i.e., . One often-cited reason applies to stably bound systems, i.e., systems that hang together forever and whose parameters are finite. In that case, velocities and coordinates of the particles of the system have upper and lower limits so that Gbound, is bounded between two extremes, Gmin and Gmax, and the average goes to zero in the limit of very long times τ
Even if the average of the time derivative of G is only approximately zero, the virial theorem holds to the same degree of approximation.
For power-law forces with an exponent n, the general equation holds
For gravitational attraction, n equals −1 and the average kinetic energy equals half of the average negative potential energy
This general result is useful for complex gravitating systems such as solar systems or galaxies.
A simple application of the virial theorem concerns galaxy clusters. If a region of space is unusually full of galaxies, it is safe to assume that they have been together for a long time, and the virial theorem can be applied. Doppler measurements give lower bounds for their relative velocities, and the virial theorem gives a lower bound for the total mass of the cluster, including any dark matter.
The averaging need not be taken over time; an ensemble average can also be taken, with equivalent results.
==
[edit]Introduction
[edit]Statement of the Einstein summation convention
[edit]Any term containing an index variable once as subscript and once as superscript is expanded to a sum running over all the values of the range of this index of this term. For example, if the index ranges over the set {1, 2, 3},
is expanded by this convention to:
Note that the upper indices are not interpreted as exponents but are indices in superscript notation, indexing e.g. coefficients or basis vectors. So in this context x2 should be read as "x-two", not "x squared", and typically (x1, x2, x3) would be equivalent to the traditional (x, y, z).
Application
[edit]When dealing with covariant and contravariant vectors, the down/up position of an index indicates the type of this vector. Coordinates of covariant vectors are usually indexed with subscripts and their basis vectors use superscripts, and in the opposite for contravariant vectors and their basis. In this way the duality pairing of dual vector spaces can be expressed very simply by contractinga covariant vector with a contravariant vector; see below.
In settings where the co- and contravariance is of no importance, e.g. euclidean space, all indices may be written as subscripts and the convention applies still.[2]
In settings where a metric is available in the space the metric tensor associated with the musical isomorphisms allows to interchange covariant and contravariant indices.
In general relativity, a common convention is that
- the Greek alphabet is used for both time and spatial components, where indices take values 0,1,2,3 (frequently used letters are μ, ν, ...),
- the Latin alphabet is used for just spatial components, where indices take values 1,2,3 (frequently used letters are i, j, ...).
All indices that are summed over in an expression are called summation indices, in the above example i is this index. These are also called dummy indices since they may be reneamed by any symbol without changing the meaning of the expression, provided that it does not collide with the other index symbols in the same expression or equation.
An index that is not summed over is called free index. Compare free indices and dummy indices with free variables and bound variables: the summation indices are always bound by the whole range of their index variable, whereas the range of free indices does not need to coincide with the whole range of the summation indices and must be stated seperately for the concerned formula.
Einstein notation is sometimes applied in slightly different ways. Typically, each index occurs once in an upper (superscript) and once in a lower (subscript) position in a term; however, the convention can be applied more generally to any repeated indices within a term.
Vector representations
[edit]Superscripts and subscripts vs. only subscripts
[edit]In terms of covariance and contravariance of vectors,
- upper indices represent components (vi) of contravariant vectors (vectors), or index the basis vectors of the space of the covectors (e*i).
- lower indices represent components (wi) of covariant vectors (covectors), or index the basis vectors of the space of the vectors (ei).
The components transform contravariantly, resp. covariantly, with respect to change of basis.
In recognition of this fact, the following notation uses the same symbol both for a (co)vector and for its components, as in:
where v is the vector and vi are its components (not the ith covector v), w is the covector and wi are its components, whereas ei and e*iare the i-th basisvectors of their respective spaces.
In the presence of a non-degenerate, symmetric bilinear form (an isomorphism , for instance a Riemannian metric or Minkowski metric), one can raise and lower indices.
A basis gives such a form (via the dual basis), hence when working on Rn with a Euclidian metric and a fixed orthonormal basis, one can work with only subscripts.
However, if one changes coordinates, the way that coefficients change depends on the variance of the object, and one cannot ignore the distinction; see covariance and contravariance of vectors.
Mnemonics
[edit]In the above example, vectors are represented as n×1 matrices (column vectors), while covectors are represented as 1×n matrices (row covectors).
When using the column vector convention
- "Upper indices go up to down; lower indices go left to right"
- "COvariant tensors are ROW vectors that have indices that are belOW. Co-below-row
- Vectors can be stacked (column matrices) side-by-side:
- Hence the lower index indicates which column you are in.
- You can stack covectors (row matrices) top-to-bottom:
- Hence the upper index indicates which row you are in.
Abstract description
[edit]The virtue of Einstein notation is that it represents the invariant quantities with a simple notation.
Any scalar is invariant under transformations of basis; the individual terms in the sum are not. When the basis is changed, the components of a vector change by a linear transformation described by a matrix. This led Einstein to propose the convention that repeated indices imply the summation is to be done.
As for covectors, they change by the inverse matrix. This is designed to guarantee that the linear function associated with the covector, the sum above, is the same no matter what the basis is.
The value of the Einstein convention is that it applies to other vector spaces built from V using the tensor product and duality. For example, , the tensor product of V with itself, has a basis consisting of tensors of the form . Any tensor in can be written as:
- .
, the dual of , has a basis e1, e2, ..., en which obeys the rule
where is the Kronecker delta. As
the row-column coordinates on a matrix correspond to the upper-lower indices on the tensor product.
Common operations in this notation
[edit]In Einstein notation, the usual element reference for the mth row and nth column of matrix A becomes . We can then write the following operations in Einstein notation as follows.
- Inner product (hence also Vector dot product)
Using an orthogonal basis, the inner product is the sum of corresponding components multiplied together:
This can also be calculated by multiplying the covector on the vector.
Again using an orthogonal basis (in 3d) the cross product intrinsically involves summations over permutations of components:
where
and is the Levi-Civita symbol. Based on this definition of , there is no difference between and but the position of indices.
The matrix product of two matrices and is:
equivalent to
For a square matrix , the trace is the sum of the diagonal elements, hence the sum over a common index .
The outer product of the column vector by the row vector yields an m×n matrix A:
Since i and j represent two different indices, there is no summation and the indices are not eliminated by the multiplication.
Given a tensor, one can raise an index or lower an index by contracting the tensor with the metric tensor, . For example, take the tensor , one can raise an index:
Or one can lower an index:
See also
[edit]- Ricci calculus
- Tensor
- Abstract index notation
- Bra–ket notation
- Penrose graphical notation
- Kronecker delta
- Levi-Civita symbol
Notes
[edit]- This applies only for numerical indices. The situation is the opposite for abstract indices. Then, vectors themselves carry upper abstract indices and covectors carry lower abstract indices, as per the example in the introduction of this article. Elements of a basis of vectors may carry a lower numerical index and an upper abstract index.
References
[edit]- ^ Proof of this equation
- ^ "Einstein Summation". Wolfram Mathworld. Retrieved 13 April 2011.
Bibliography
[edit]- Kuptsov, L.P. (2001) [1994], "Einstein rule", Encyclopedia of Mathematics, EMS Press.
External links
[edit]- Rawlings, Steve (2007-02-01). "Lecture 10 - Einstein Summation Convention and Vector Identities". Oxford University.
Category:Mathematical notation Category:Multilinear algebra Category:Tensors Category:Riemannian geometry Category:Mathematical physics Category:Albert Einstein
__________________________________________________________________________________________________________________________
[[User:{{{1}}}|{{{1}}}]]
- The ...
- High-powered ....
- Emergency ....
- A ...
- apply ...
- apply ...
______________________________________
- The changing of the gear, especially with a foot-operated clutch, offers well known examples: although the accelerating force is bounded by the engine, an inexperienced driver lets you experience severe jerk.
- High-powered sports cars offer the feeling of being pressed into the cushioning, but this is the force of the acceleration. Only in the very first moments, when the torque of the engine grows with the rotational speed, a whiplash effect is noticeable in the neck.
- Emergency braking (not to talk about a collision!) lets the body whip forward faster as the acceleration value alone would accomplish, but this is not apt to an experiment.
- A highly reproducible experiment to demonstrate jerk is as follows: Brake a car starting at a modest speed in two different ways:
- apply a constant, modest force on the pedal till the car comes to a halt, than release the pedal;
- apply the same, constant, modest force on the pedal, but almost before the halt, reduce the force on the pedal, optimally, releasing the pedal fully, exactly when the car stops.
- The reason for the big jerk in the first way to brake is the discontinuity of the acceleration, which is initially constant due to the constant force on the pedal and drops to zero immediately, when the wheels stop to rotate. See also below in the motion profile, segment 7: Deceleration ramp-down. Every experienced driver knows how to start and how to stop braking with small jerk.




![{\displaystyle {\begin{aligned}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}+{\frac {e}{f}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}\cdot {\frac {f}{f}}+{\frac {e}{f}}\cdot {\frac {d}{d}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {cf}{df}}+{\frac {ed}{fd}}\right)={\frac {a}{b}}\cdot {\frac {cf+ed}{df}}\\[6pt]={}&{\frac {a(cf+ed)}{bdf}}={\frac {acf}{bdf}}+{\frac {aed}{bdf}}={\frac {ac}{bd}}+{\frac {ae}{bf}}\\[6pt]={}&{\frac {a}{b}}\cdot {\frac {c}{d}}+{\frac {a}{b}}\cdot {\frac {e}{f}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e98a7025c1876787eb0614cda3cb72084b76af3)




















![{\displaystyle \mathbb {R} [X]/(X^{2}+1){\stackrel {\cong }{\rightarrow }}\mathbb {C} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7311d27fe245a1950d7140583b6fd3b3b3869046)




























































































