3D symmetry group
Selected point groups in three dimensions
Involutional symmetry s , (*)Cyclic symmetry nv , (*nn)Dihedral symmetry nh , (*n22)
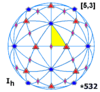
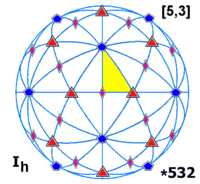
Polyhedral group , [n,3], (*n32)
Tetrahedral symmetry d , (*332)Octahedral symmetry h , (*432)Icosahedral symmetry h , (*532)
Icosahedral symmetry fundamental domains A soccer ball , a common example of a spherical truncated icosahedron , has full icosahedral symmetry. Rotations and reflections form the symmetry group of a great icosahedron . In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron . Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual of the icosahedron) and the rhombic triacontahedron .
Every polyhedron with icosahedral symmetry has 60 rotational (or orientation-preserving) symmetries and 60 orientation-reversing symmetries (that combine a rotation and a reflection ), for a total symmetry order of 120. The full symmetry group is the Coxeter group of type H3 . It may be represented by Coxeter notation [5,3] and Coxeter diagram alternating group A5 on 5 letters.
Description [ edit ] Icosahedral symmetry is a mathematical property of objects indicating that an object has the same symmetries as a regular icosahedron .
As point group [ edit ] Apart from the two infinite series of prismatic and antiprismatic symmetry, rotational icosahedral symmetry or chiral icosahedral symmetry of chiral objects and full icosahedral symmetry or achiral icosahedral symmetry are the discrete point symmetries (or equivalently, symmetries on the sphere ) with the largest symmetry groups .
Icosahedral symmetry is not compatible with translational symmetry , so there are no associated crystallographic point groups or space groups .
Presentations corresponding to the above are:
I
:
⟨
s
,
t
∣
s
2
,
t
3
,
(
s
t
)
5
⟩
{\displaystyle I:\langle s,t\mid s^{2},t^{3},(st)^{5}\rangle \ }
I
h
:
⟨
s
,
t
∣
s
3
(
s
t
)
−
2
,
t
5
(
s
t
)
−
2
⟩
.
{\displaystyle I_{h}:\langle s,t\mid s^{3}(st)^{-2},t^{5}(st)^{-2}\rangle .\ }
These correspond to the icosahedral groups (rotational and full) being the (2,3,5) triangle groups .
The first presentation was given by William Rowan Hamilton in 1856, in his paper on icosian calculus .[1]
Note that other presentations are possible, for instance as an alternating group (for I ).
Visualizations [ edit ] The full symmetry group is the Coxeter group of type H3 . It may be represented by Coxeter notation [5,3] and Coxeter diagram alternating group A5 on 5 letters.
Group structure [ edit ] Every polyhedron with icosahedral symmetry has 60 rotational (or orientation-preserving) symmetries and 60 orientation-reversing symmetries (that combine a rotation and a reflection ), for a total symmetry order of 120.
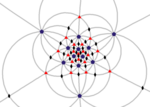
The edges of a spherical compound of five octahedra represent the 15 mirror planes as colored great circles. Each octahedron can represent 3 orthogonal mirror planes by its edges.
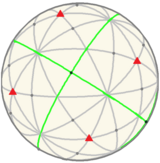
The pyritohedral symmetry is an index 5 subgroup of icosahedral symmetry, with 3 orthogonal green reflection lines and 8 red order-3 gyration points. There are 5 different orientations of pyritohedral symmetry.
The icosahedral rotation group I I is isomorphic to A 5 , the alternating group of even permutations of five objects. This isomorphism can be realized by I acting on various compounds, notably the compound of five cubes (which inscribe in the dodecahedron ), the compound of five octahedra , or either of the two compounds of five tetrahedra (which are enantiomorphs , and inscribe in the dodecahedron). The group contains 5 versions of T h with 20 versions of D3 (10 axes, 2 per axis), and 6 versions of D5 .
The full icosahedral group Ih I as normal subgroup of index 2. The group Ih is isomorphic to I × Z 2 , or A 5 × Z 2 , with the inversion in the center corresponding to element (identity,-1), where Z 2 is written multiplicatively.
Ih acts on the compound of five cubes and the compound of five octahedra , but −1 acts as the identity (as cubes and octahedra are centrally symmetric). It acts on the compound of ten tetrahedra : I acts on the two chiral halves (compounds of five tetrahedra ), and −1 interchanges the two halves.
Notably, it does not act as S5 , and these groups are not isomorphic; see below for details.
The group contains 10 versions of D3d and 6 versions of D5d (symmetries like antiprisms).
I is also isomorphic to PSL2 (5), but Ih is not isomorphic to SL2 (5).
Isomorphism of I with A5 [ edit ] It is useful to describe explicitly what the isomorphism between I and A5 looks like. In the following table, permutations Pi and Qi act on 5 and 12 elements respectively, while the rotation matrices Mi are the elements of I . If Pk is the product of taking the permutation Pi and applying Pj to it, then for the same values of i , j and k , it is also true that Qk is the product of taking Qi and applying Qj , and also that premultiplying a vector by Mk is the same as premultiplying that vector by Mi and then premultiplying that result with Mj , that is Mk = Mj × Mi . Since the permutations Pi are all the 60 even permutations of 12345, the one-to-one correspondence is made explicit, therefore the isomorphism too.
Rotation matrix
Permutation of 5
Permutation of 12
M
1
=
[
1
0
0
0
1
0
0
0
1
]
{\displaystyle M_{1}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}}
P
1
{\displaystyle P_{1}}
Q
1
{\displaystyle Q_{1}}
M
2
=
[
−
1
2
1
2
ϕ
ϕ
2
−
1
2
ϕ
ϕ
2
−
1
2
−
ϕ
2
−
1
2
−
1
2
ϕ
]
{\displaystyle M_{2}={\begin{bmatrix}-{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
2
{\displaystyle P_{2}}
Q
2
{\displaystyle Q_{2}}
M
3
=
[
−
1
2
−
1
2
ϕ
−
ϕ
2
1
2
ϕ
ϕ
2
−
1
2
ϕ
2
−
1
2
−
1
2
ϕ
]
{\displaystyle M_{3}={\begin{bmatrix}-{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
3
{\displaystyle P_{3}}
Q
3
{\displaystyle Q_{3}}
M
4
=
[
−
1
2
1
2
ϕ
−
ϕ
2
1
2
ϕ
−
ϕ
2
−
1
2
−
ϕ
2
−
1
2
1
2
ϕ
]
{\displaystyle M_{4}={\begin{bmatrix}-{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
4
{\displaystyle P_{4}}
Q
4
{\displaystyle Q_{4}}
M
5
=
[
ϕ
2
1
2
1
2
ϕ
1
2
−
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
ϕ
2
−
1
2
]
{\displaystyle M_{5}={\begin{bmatrix}{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
5
{\displaystyle P_{5}}
Q
5
{\displaystyle Q_{5}}
M
6
=
[
−
1
2
ϕ
−
ϕ
2
1
2
ϕ
2
−
1
2
−
1
2
ϕ
1
2
1
2
ϕ
ϕ
2
]
{\displaystyle M_{6}={\begin{bmatrix}-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
6
{\displaystyle P_{6}}
Q
6
{\displaystyle Q_{6}}
M
7
=
[
ϕ
2
1
2
−
1
2
ϕ
1
2
−
1
2
ϕ
ϕ
2
1
2
ϕ
−
ϕ
2
−
1
2
]
{\displaystyle M_{7}={\begin{bmatrix}{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
7
{\displaystyle P_{7}}
Q
7
{\displaystyle Q_{7}}
M
8
=
[
0
−
1
0
0
0
1
−
1
0
0
]
{\displaystyle M_{8}={\begin{bmatrix}0&-1&0\\0&0&1\\-1&0&0\end{bmatrix}}}
P
8
{\displaystyle P_{8}}
Q
8
{\displaystyle Q_{8}}
M
9
=
[
−
ϕ
2
1
2
1
2
ϕ
1
2
1
2
ϕ
ϕ
2
1
2
ϕ
ϕ
2
−
1
2
]
{\displaystyle M_{9}={\begin{bmatrix}-{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
9
{\displaystyle P_{9}}
Q
9
{\displaystyle Q_{9}}
M
10
=
[
−
1
2
ϕ
ϕ
2
1
2
−
ϕ
2
−
1
2
1
2
ϕ
1
2
−
1
2
ϕ
ϕ
2
]
{\displaystyle M_{10}={\begin{bmatrix}-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
10
{\displaystyle P_{10}}
Q
10
{\displaystyle Q_{10}}
M
11
=
[
0
0
−
1
−
1
0
0
0
1
0
]
{\displaystyle M_{11}={\begin{bmatrix}0&0&-1\\-1&0&0\\0&1&0\end{bmatrix}}}
P
11
{\displaystyle P_{11}}
Q
11
{\displaystyle Q_{11}}
M
12
=
[
1
2
ϕ
−
ϕ
2
1
2
−
ϕ
2
−
1
2
−
1
2
ϕ
1
2
−
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{12}={\begin{bmatrix}{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
12
{\displaystyle P_{12}}
Q
12
{\displaystyle Q_{12}}
M
13
=
[
1
0
0
0
−
1
0
0
0
−
1
]
{\displaystyle M_{13}={\begin{bmatrix}1&0&0\\0&-1&0\\0&0&-1\end{bmatrix}}}
P
13
{\displaystyle P_{13}}
Q
13
{\displaystyle Q_{13}}
M
14
=
[
−
1
2
1
2
ϕ
ϕ
2
1
2
ϕ
−
ϕ
2
1
2
ϕ
2
1
2
1
2
ϕ
]
{\displaystyle M_{14}={\begin{bmatrix}-{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
14
{\displaystyle P_{14}}
Q
14
{\displaystyle Q_{14}}
M
15
=
[
−
1
2
−
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
−
ϕ
2
1
2
−
ϕ
2
1
2
1
2
ϕ
]
{\displaystyle M_{15}={\begin{bmatrix}-{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
15
{\displaystyle P_{15}}
Q
15
{\displaystyle Q_{15}}
M
16
=
[
−
1
2
−
1
2
ϕ
ϕ
2
1
2
ϕ
ϕ
2
1
2
−
ϕ
2
1
2
−
1
2
ϕ
]
{\displaystyle M_{16}={\begin{bmatrix}-{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
16
{\displaystyle P_{16}}
Q
16
{\displaystyle Q_{16}}
M
17
=
[
−
1
2
ϕ
ϕ
2
−
1
2
ϕ
2
1
2
1
2
ϕ
1
2
−
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{17}={\begin{bmatrix}-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
17
{\displaystyle P_{17}}
Q
17
{\displaystyle Q_{17}}
M
18
=
[
ϕ
2
−
1
2
−
1
2
ϕ
1
2
1
2
ϕ
ϕ
2
−
1
2
ϕ
−
ϕ
2
1
2
]
{\displaystyle M_{18}={\begin{bmatrix}{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
18
{\displaystyle P_{18}}
Q
18
{\displaystyle Q_{18}}
M
19
=
[
−
1
2
ϕ
−
ϕ
2
−
1
2
−
ϕ
2
1
2
−
1
2
ϕ
1
2
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{19}={\begin{bmatrix}-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
19
{\displaystyle P_{19}}
Q
19
{\displaystyle Q_{19}}
M
20
=
[
0
0
1
−
1
0
0
0
−
1
0
]
{\displaystyle M_{20}={\begin{bmatrix}0&0&1\\-1&0&0\\0&-1&0\end{bmatrix}}}
P
20
{\displaystyle P_{20}}
Q
20
{\displaystyle Q_{20}}
M
21
=
[
1
2
ϕ
ϕ
2
−
1
2
−
ϕ
2
1
2
1
2
ϕ
1
2
1
2
ϕ
ϕ
2
]
{\displaystyle M_{21}={\begin{bmatrix}{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
21
{\displaystyle P_{21}}
Q
21
{\displaystyle Q_{21}}
M
22
=
[
ϕ
2
−
1
2
1
2
ϕ
1
2
1
2
ϕ
−
ϕ
2
1
2
ϕ
ϕ
2
1
2
]
{\displaystyle M_{22}={\begin{bmatrix}{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
22
{\displaystyle P_{22}}
Q
22
{\displaystyle Q_{22}}
M
23
=
[
0
1
0
0
0
−
1
−
1
0
0
]
{\displaystyle M_{23}={\begin{bmatrix}0&1&0\\0&0&-1\\-1&0&0\end{bmatrix}}}
P
23
{\displaystyle P_{23}}
Q
23
{\displaystyle Q_{23}}
M
24
=
[
−
ϕ
2
−
1
2
−
1
2
ϕ
1
2
−
1
2
ϕ
−
ϕ
2
1
2
ϕ
−
ϕ
2
1
2
]
{\displaystyle M_{24}={\begin{bmatrix}-{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
24
{\displaystyle P_{24}}
Q
24
{\displaystyle Q_{24}}
M
25
=
[
−
1
2
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
ϕ
2
1
2
ϕ
2
1
2
−
1
2
ϕ
]
{\displaystyle M_{25}={\begin{bmatrix}-{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
25
{\displaystyle P_{25}}
Q
25
{\displaystyle Q_{25}}
M
26
=
[
ϕ
2
1
2
1
2
ϕ
−
1
2
1
2
ϕ
ϕ
2
1
2
ϕ
−
ϕ
2
1
2
]
{\displaystyle M_{26}={\begin{bmatrix}{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
26
{\displaystyle P_{26}}
Q
26
{\displaystyle Q_{26}}
M
27
=
[
−
1
2
ϕ
−
ϕ
2
1
2
−
ϕ
2
1
2
1
2
ϕ
−
1
2
−
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{27}={\begin{bmatrix}-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
27
{\displaystyle P_{27}}
Q
27
{\displaystyle Q_{27}}
M
28
=
[
−
1
2
−
1
2
ϕ
ϕ
2
−
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
2
−
1
2
1
2
ϕ
]
{\displaystyle M_{28}={\begin{bmatrix}-{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
28
{\displaystyle P_{28}}
Q
28
{\displaystyle Q_{28}}
M
29
=
[
−
1
2
ϕ
ϕ
2
−
1
2
−
ϕ
2
−
1
2
−
1
2
ϕ
−
1
2
1
2
ϕ
ϕ
2
]
{\displaystyle M_{29}={\begin{bmatrix}-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
29
{\displaystyle P_{29}}
Q
29
{\displaystyle Q_{29}}
M
30
=
[
ϕ
2
−
1
2
−
1
2
ϕ
−
1
2
−
1
2
ϕ
−
ϕ
2
1
2
ϕ
ϕ
2
−
1
2
]
{\displaystyle M_{30}={\begin{bmatrix}{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
30
{\displaystyle P_{30}}
Q
30
{\displaystyle Q_{30}}
M
31
=
[
−
ϕ
2
1
2
−
1
2
ϕ
1
2
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
−
ϕ
2
−
1
2
]
{\displaystyle M_{31}={\begin{bmatrix}-{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
31
{\displaystyle P_{31}}
Q
31
{\displaystyle Q_{31}}
M
32
=
[
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
2
1
2
−
1
2
ϕ
1
2
−
1
2
ϕ
ϕ
2
]
{\displaystyle M_{32}={\begin{bmatrix}{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
32
{\displaystyle P_{32}}
Q
32
{\displaystyle Q_{32}}
M
33
=
[
1
2
1
2
ϕ
ϕ
2
1
2
ϕ
ϕ
2
−
1
2
−
ϕ
2
1
2
1
2
ϕ
]
{\displaystyle M_{33}={\begin{bmatrix}{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
33
{\displaystyle P_{33}}
Q
33
{\displaystyle Q_{33}}
M
34
=
[
1
2
ϕ
ϕ
2
1
2
ϕ
2
−
1
2
1
2
ϕ
1
2
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{34}={\begin{bmatrix}{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
34
{\displaystyle P_{34}}
Q
34
{\displaystyle Q_{34}}
M
35
=
[
−
ϕ
2
−
1
2
1
2
ϕ
1
2
−
1
2
ϕ
ϕ
2
−
1
2
ϕ
ϕ
2
1
2
]
{\displaystyle M_{35}={\begin{bmatrix}-{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
35
{\displaystyle P_{35}}
Q
35
{\displaystyle Q_{35}}
M
36
=
[
1
2
−
1
2
ϕ
−
ϕ
2
1
2
ϕ
−
ϕ
2
1
2
−
ϕ
2
−
1
2
−
1
2
ϕ
]
{\displaystyle M_{36}={\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
36
{\displaystyle P_{36}}
Q
36
{\displaystyle Q_{36}}
M
37
=
[
ϕ
2
1
2
−
1
2
ϕ
−
1
2
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
ϕ
2
1
2
]
{\displaystyle M_{37}={\begin{bmatrix}{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
37
{\displaystyle P_{37}}
Q
37
{\displaystyle Q_{37}}
M
38
=
[
0
−
1
0
0
0
−
1
1
0
0
]
{\displaystyle M_{38}={\begin{bmatrix}0&-1&0\\0&0&-1\\1&0&0\end{bmatrix}}}
P
38
{\displaystyle P_{38}}
Q
38
{\displaystyle Q_{38}}
M
39
=
[
−
ϕ
2
1
2
1
2
ϕ
−
1
2
−
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
−
ϕ
2
1
2
]
{\displaystyle M_{39}={\begin{bmatrix}-{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
39
{\displaystyle P_{39}}
Q
39
{\displaystyle Q_{39}}
M
40
=
[
−
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
2
−
1
2
1
2
ϕ
−
1
2
−
1
2
ϕ
ϕ
2
]
{\displaystyle M_{40}={\begin{bmatrix}-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
40
{\displaystyle P_{40}}
Q
40
{\displaystyle Q_{40}}
M
41
=
[
0
0
1
1
0
0
0
1
0
]
{\displaystyle M_{41}={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}}}
P
41
{\displaystyle P_{41}}
Q
41
{\displaystyle Q_{41}}
M
42
=
[
1
2
ϕ
ϕ
2
−
1
2
ϕ
2
−
1
2
−
1
2
ϕ
−
1
2
−
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{42}={\begin{bmatrix}{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
42
{\displaystyle P_{42}}
Q
42
{\displaystyle Q_{42}}
M
43
=
[
−
ϕ
2
1
2
−
1
2
ϕ
−
1
2
−
1
2
ϕ
ϕ
2
1
2
ϕ
ϕ
2
1
2
]
{\displaystyle M_{43}={\begin{bmatrix}-{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\end{bmatrix}}}
P
43
{\displaystyle P_{43}}
Q
43
{\displaystyle Q_{43}}
M
44
=
[
1
2
ϕ
−
ϕ
2
−
1
2
−
ϕ
2
−
1
2
1
2
ϕ
−
1
2
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{44}={\begin{bmatrix}{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
44
{\displaystyle P_{44}}
Q
44
{\displaystyle Q_{44}}
M
45
=
[
1
2
1
2
ϕ
ϕ
2
−
1
2
ϕ
−
ϕ
2
1
2
ϕ
2
−
1
2
−
1
2
ϕ
]
{\displaystyle M_{45}={\begin{bmatrix}{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
45
{\displaystyle P_{45}}
Q
45
{\displaystyle Q_{45}}
M
46
=
[
1
2
1
2
ϕ
−
ϕ
2
1
2
ϕ
ϕ
2
1
2
ϕ
2
−
1
2
1
2
ϕ
]
{\displaystyle M_{46}={\begin{bmatrix}{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
46
{\displaystyle P_{46}}
Q
46
{\displaystyle Q_{46}}
M
47
=
[
1
2
−
1
2
ϕ
ϕ
2
−
1
2
ϕ
ϕ
2
1
2
−
ϕ
2
−
1
2
1
2
ϕ
]
{\displaystyle M_{47}={\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
47
{\displaystyle P_{47}}
Q
47
{\displaystyle Q_{47}}
M
48
=
[
−
1
0
0
0
1
0
0
0
−
1
]
{\displaystyle M_{48}={\begin{bmatrix}-1&0&0\\0&1&0\\0&0&-1\end{bmatrix}}}
P
48
{\displaystyle P_{48}}
Q
48
{\displaystyle Q_{48}}
M
49
=
[
−
1
2
ϕ
ϕ
2
1
2
ϕ
2
1
2
−
1
2
ϕ
−
1
2
1
2
ϕ
−
ϕ
2
]
{\displaystyle M_{49}={\begin{bmatrix}-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\end{bmatrix}}}
P
49
{\displaystyle P_{49}}
Q
49
{\displaystyle Q_{49}}
M
50
=
[
0
0
−
1
1
0
0
0
−
1
0
]
{\displaystyle M_{50}={\begin{bmatrix}0&0&-1\\1&0&0\\0&-1&0\end{bmatrix}}}
P
50
{\displaystyle P_{50}}
Q
50
{\displaystyle Q_{50}}
M
51
=
[
1
2
ϕ
−
ϕ
2
1
2
ϕ
2
1
2
1
2
ϕ
−
1
2
1
2
ϕ
ϕ
2
]
{\displaystyle M_{51}={\begin{bmatrix}{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
51
{\displaystyle P_{51}}
Q
51
{\displaystyle Q_{51}}
M
52
=
[
ϕ
2
−
1
2
1
2
ϕ
−
1
2
−
1
2
ϕ
ϕ
2
−
1
2
ϕ
−
ϕ
2
−
1
2
]
{\displaystyle M_{52}={\begin{bmatrix}{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
52
{\displaystyle P_{52}}
Q
52
{\displaystyle Q_{52}}
M
53
=
[
0
1
0
0
0
1
1
0
0
]
{\displaystyle M_{53}={\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}}}
P
53
{\displaystyle P_{53}}
Q
53
{\displaystyle Q_{53}}
M
54
=
[
−
ϕ
2
−
1
2
−
1
2
ϕ
−
1
2
1
2
ϕ
ϕ
2
−
1
2
ϕ
ϕ
2
−
1
2
]
{\displaystyle M_{54}={\begin{bmatrix}-{\frac {\phi }{2}}&-{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
54
{\displaystyle P_{54}}
Q
54
{\displaystyle Q_{54}}
M
55
=
[
1
2
ϕ
ϕ
2
1
2
−
ϕ
2
1
2
−
1
2
ϕ
−
1
2
−
1
2
ϕ
ϕ
2
]
{\displaystyle M_{55}={\begin{bmatrix}{\frac {1}{2\phi }}&{\frac {\phi }{2}}&{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\\-{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\end{bmatrix}}}
P
55
{\displaystyle P_{55}}
Q
55
{\displaystyle Q_{55}}
M
56
=
[
−
ϕ
2
−
1
2
1
2
ϕ
−
1
2
1
2
ϕ
−
ϕ
2
1
2
ϕ
−
ϕ
2
−
1
2
]
{\displaystyle M_{56}={\begin{bmatrix}-{\frac {\phi }{2}}&-{\frac {1}{2}}&{\frac {1}{2\phi }}\\-{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\end{bmatrix}}}
P
56
{\displaystyle P_{56}}
Q
56
{\displaystyle Q_{56}}
M
57
=
[
1
2
−
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
ϕ
2
−
1
2
ϕ
2
1
2
1
2
ϕ
]
{\displaystyle M_{57}={\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&{\frac {1}{2\phi }}\end{bmatrix}}}
P
57
{\displaystyle P_{57}}
Q
57
{\displaystyle Q_{57}}
M
58
=
[
1
2
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
−
ϕ
2
−
1
2
−
ϕ
2
1
2
−
1
2
ϕ
]
{\displaystyle M_{58}={\begin{bmatrix}{\frac {1}{2}}&{\frac {1}{2\phi }}&-{\frac {\phi }{2}}\\-{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\-{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
58
{\displaystyle P_{58}}
Q
58
{\displaystyle Q_{58}}
M
59
=
[
1
2
−
1
2
ϕ
ϕ
2
1
2
ϕ
−
ϕ
2
−
1
2
ϕ
2
1
2
−
1
2
ϕ
]
{\displaystyle M_{59}={\begin{bmatrix}{\frac {1}{2}}&-{\frac {1}{2\phi }}&{\frac {\phi }{2}}\\{\frac {1}{2\phi }}&-{\frac {\phi }{2}}&-{\frac {1}{2}}\\{\frac {\phi }{2}}&{\frac {1}{2}}&-{\frac {1}{2\phi }}\end{bmatrix}}}
P
59
{\displaystyle P_{59}}
Q
59
{\displaystyle Q_{59}}
M
60
=
[
−
1
0
0
0
−
1
0
0
0
1
]
{\displaystyle M_{60}={\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\end{bmatrix}}}
P
60
{\displaystyle P_{60}}
Q
60
{\displaystyle Q_{60}}
Commonly confused groups [ edit ] The following groups all have order 120, but are not isomorphic:
They correspond to the following short exact sequences (the latter of which does not split) and product
1
→
A
5
→
S
5
→
Z
2
→
1
{\displaystyle 1\to A_{5}\to S_{5}\to Z_{2}\to 1}
I
h
=
A
5
×
Z
2
{\displaystyle I_{h}=A_{5}\times Z_{2}}
1
→
Z
2
→
2
I
→
A
5
→
1
{\displaystyle 1\to Z_{2}\to 2I\to A_{5}\to 1}
In words,
A
5
{\displaystyle A_{5}}
normal subgroup
S
5
{\displaystyle S_{5}}
A
5
{\displaystyle A_{5}}
factor of
I
h
{\displaystyle I_{h}}
direct product
A
5
{\displaystyle A_{5}}
quotient group
2
I
{\displaystyle 2I}
Note that
A
5
{\displaystyle A_{5}}
exceptional irreducible 3-dimensional representation (as the icosahedral rotation group), but
S
5
{\displaystyle S_{5}}
These can also be related to linear groups over the finite field with five elements, which exhibit the subgroups and covering groups directly; none of these are the full icosahedral group:
A
5
≅
PSL
(
2
,
5
)
,
{\displaystyle A_{5}\cong \operatorname {PSL} (2,5),}
projective special linear group , see here for a proof;
S
5
≅
PGL
(
2
,
5
)
,
{\displaystyle S_{5}\cong \operatorname {PGL} (2,5),}
projective general linear group ;
2
I
≅
SL
(
2
,
5
)
,
{\displaystyle 2I\cong \operatorname {SL} (2,5),}
special linear group .Conjugacy classes [ edit ] The 120 symmetries fall into 10 conjugacy classes.
conjugacy classes
I
additional classes of Ih
identity, order 1
12 × rotation by ±72°, order 5, around the 6 axes through the face centers of the dodecahedron
12 × rotation by ±144°, order 5, around the 6 axes through the face centers of the dodecahedron
20 × rotation by ±120°, order 3, around the 10 axes through vertices of the dodecahedron
15 × rotation by 180°, order 2, around the 15 axes through midpoints of edges of the dodecahedron
central inversion, order 2
12 × rotoreflection by ±36°, order 10, around the 6 axes through the face centers of the dodecahedron
12 × rotoreflection by ±108°, order 10, around the 6 axes through the face centers of the dodecahedron
20 × rotoreflection by ±60°, order 6, around the 10 axes through the vertices of the dodecahedron
15 × reflection, order 2, at 15 planes through edges of the dodecahedron
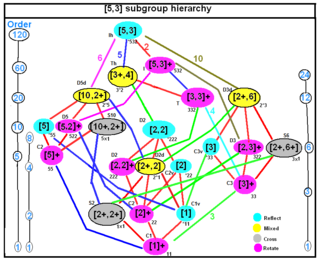
Subgroups of the full icosahedral symmetry group [ edit ] Subgroup relations Chiral subgroup relations Each line in the following table represents one class of conjugate (i.e., geometrically equivalent) subgroups. The column "Mult." (multiplicity) gives the number of different subgroups in the conjugacy class.
Explanation of colors: green = the groups that are generated by reflections, red = the chiral (orientation-preserving) groups, which contain only rotations.
The groups are described geometrically in terms of the dodecahedron.
The abbreviation "h.t.s.(edge)" means "halfturn swapping this edge with its opposite edge", and similarly for "face" and "vertex".
Schön. Coxeter Orb. H-M Structure Cyc. Order Index Mult.
Description
Ih
[5,3]
*532
53 2/mA5 ×Z2 120
1
1
full group
D2h
[2,2]
*222
mmm
D4 ×D2 =D2 3 8
15
5
fixing two opposite edges, possibly swapping them
C5v
[5]
*55
5m
D10
10
12
6
fixing a face
C3v
[3]
*33
3m
D6 =S3
6
20
10
fixing a vertex
C2v
[2]
*22
2mm
D4 =D2 2
4
30
15
fixing an edge
Cs
[ ]
*
2 or mD2
2
60
15
reflection swapping two endpoints of an edge
Th
[3+ ,4]
3*2
m3
A4 ×Z2
24
5
5
pyritohedral group
D5d
[2+ ,10]
2*5
10 m2D20 =Z2 ×D10
20
6
6
fixing two opposite faces, possibly swapping them
D3d
[2+ ,6]
2*3
3 mD12 =Z2 ×D6
12
10
10
fixing two opposite vertices, possibly swapping them
D1d = C2h
[2+ ,2]
2*
2/m
D4 =Z2 ×D2
4
30
15
halfturn around edge midpoint, plus central inversion
S10
[2+ ,10+ ]
5×
5 Z10 =Z2 ×Z5
10
12
6
rotations of a face, plus central inversion
S6
[2+ ,6+ ]
3×
3 Z6 =Z2 ×Z3
6
20
10
rotations about a vertex, plus central inversion
S2
[2+ ,2+ ]
×
1 Z2
2
60
1
central inversion
I
[5,3]+
532
532
A5
60
2
1
all rotations
T
[3,3]+
332
332
A4
12
10
5
rotations of a contained tetrahedron
D5
[2,5]+
522
522
D10
10
12
6
rotations around the center of a face, and h.t.s.(face)
D3
[2,3]+
322
322
D6 =S3
6
20
10
rotations around a vertex, and h.t.s.(vertex)
D2
[2,2]+
222
222
D4 =Z2 2
4
30
15
halfturn around edge midpoint, and h.t.s.(edge)
C5
[5]+
55
5
Z5
5
24
6
rotations around a face center
C3
[3]+
33
3
Z3 =A3
3
40
10
rotations around a vertex
C2
[2]+
22
2
Z2
2
60
15
half-turn around edge midpoint
C1
[ ]+
11
1
Z1
1
120
1
trivial group
Vertex stabilizers [ edit ] Stabilizers of an opposite pair of vertices can be interpreted as stabilizers of the axis they generate.
vertex stabilizers in I give cyclic groups C 3
vertex stabilizers in Ih give dihedral groups D 3
stabilizers of an opposite pair of vertices in I give dihedral groups D 3
stabilizers of an opposite pair of vertices in Ih give
D
3
×
±
1
{\displaystyle D_{3}\times \pm 1}
Edge stabilizers [ edit ] Stabilizers of an opposite pair of edges can be interpreted as stabilizers of the rectangle they generate.
edges stabilizers in I give cyclic groups Z 2
edges stabilizers in Ih give Klein four-groups
Z
2
×
Z
2
{\displaystyle Z_{2}\times Z_{2}}
stabilizers of a pair of edges in I give Klein four-groups
Z
2
×
Z
2
{\displaystyle Z_{2}\times Z_{2}}
stabilizers of a pair of edges in Ih give
Z
2
×
Z
2
×
Z
2
{\displaystyle Z_{2}\times Z_{2}\times Z_{2}}
Face stabilizers [ edit ] Stabilizers of an opposite pair of faces can be interpreted as stabilizers of the antiprism they generate.
face stabilizers in I give cyclic groups C 5
face stabilizers in Ih give dihedral groups D 5
stabilizers of an opposite pair of faces in I give dihedral groups D 5
stabilizers of an opposite pair of faces in Ih give
D
5
×
±
1
{\displaystyle D_{5}\times \pm 1}
Polyhedron stabilizers [ edit ] For each of these, there are 5 conjugate copies, and the conjugation action gives a map, indeed an isomorphism,
I
→
∼
A
5
<
S
5
{\displaystyle I{\stackrel {\sim }{\to }}A_{5}<S_{5}}
stabilizers of the inscribed tetrahedra in I are a copy of T
stabilizers of the inscribed tetrahedra in Ih are a copy of T
stabilizers of the inscribed cubes (or opposite pair of tetrahedra, or octahedra) in I are a copy of T
stabilizers of the inscribed cubes (or opposite pair of tetrahedra, or octahedra) in Ih are a copy of Th Coxeter group generators [ edit ] The full icosahedral symmetry group [5,3] (0 , R1 , R2 below, with relations R0 2 = R1 2 = R2 2 = (R0 ×R1 )5 = (R1 ×R2 )3 = (R0 ×R2 )2 = Identity. The group [5,3]+ (0,1 , S1,2 , S0,2 . A rotoreflection of order 10 is generated by V0,1,2 , the product of all 3 reflections. Here
ϕ
=
5
+
1
2
{\displaystyle \phi ={\tfrac {{\sqrt {5}}+1}{2}}}
golden ratio .
[5,3],
Reflections
Rotations
Rotoreflection
Name
R0
R1
R2
S0,1
S1,2
S0,2
V0,1,2
Group
Order
2
2
2
5
3
2
10
Matrix
[
−
1
0
0
0
1
0
0
0
1
]
{\displaystyle \left[{\begin{smallmatrix}-1&0&0\\0&1&0\\0&0&1\end{smallmatrix}}\right]}
[
1
−
ϕ
2
−
ϕ
2
−
1
2
−
ϕ
2
1
2
1
−
ϕ
2
−
1
2
1
−
ϕ
2
ϕ
2
]
{\displaystyle \left[{\begin{smallmatrix}{\frac {1-\phi }{2}}&{\frac {-\phi }{2}}&{\frac {-1}{2}}\\{\frac {-\phi }{2}}&{\frac {1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {1-\phi }{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}
[
1
0
0
0
−
1
0
0
0
1
]
{\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\end{smallmatrix}}\right]}
[
ϕ
−
1
2
ϕ
2
1
2
−
ϕ
2
1
2
1
−
ϕ
2
−
1
2
1
−
ϕ
2
ϕ
2
]
{\displaystyle \left[{\begin{smallmatrix}{\frac {\phi -1}{2}}&{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {-\phi }{2}}&{\frac {1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {1-\phi }{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}
[
1
−
ϕ
2
ϕ
2
−
1
2
−
ϕ
2
−
1
2
1
−
ϕ
2
−
1
2
ϕ
−
1
2
ϕ
2
]
{\displaystyle \left[{\begin{smallmatrix}{\frac {1-\phi }{2}}&{\frac {\phi }{2}}&{\frac {-1}{2}}\\{\frac {-\phi }{2}}&{\frac {-1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {\phi -1}{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}
[
−
1
0
0
0
−
1
0
0
0
1
]
{\displaystyle \left[{\begin{smallmatrix}-1&0&0\\0&-1&0\\0&0&1\end{smallmatrix}}\right]}
[
ϕ
−
1
2
−
ϕ
2
1
2
−
ϕ
2
−
1
2
1
−
ϕ
2
−
1
2
ϕ
−
1
2
ϕ
2
]
{\displaystyle \left[{\begin{smallmatrix}{\frac {\phi -1}{2}}&{\frac {-\phi }{2}}&{\frac {1}{2}}\\{\frac {-\phi }{2}}&{\frac {-1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {\phi -1}{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}
(1,0,0)n
(
ϕ
2
,
1
2
,
ϕ
−
1
2
)
{\displaystyle ({\begin{smallmatrix}{\frac {\phi }{2}},{\frac {1}{2}},{\frac {\phi -1}{2}}\end{smallmatrix}})}
n
(0,1,0)n
(
0
,
−
1
,
ϕ
)
{\displaystyle (0,-1,\phi )}
axis
(
1
−
ϕ
,
0
,
ϕ
)
{\displaystyle (1-\phi ,0,\phi )}
axis
(
0
,
0
,
1
)
{\displaystyle (0,0,1)}
axis
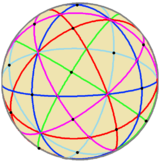
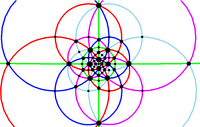
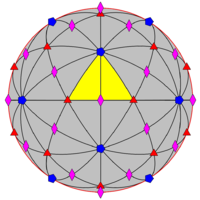
Fundamental domain [ edit ] Fundamental domains for the icosahedral rotation group and the full icosahedral group are given by:
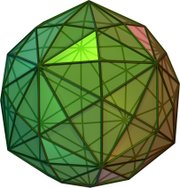
In the disdyakis triacontahedron one full face is a fundamental domain; other solids with the same symmetry can be obtained by adjusting the orientation of the faces, e.g. flattening selected subsets of faces to combine each subset into one face, or replacing each face by multiple faces, or a curved surface.
Polyhedra with icosahedral symmetry [ edit ] Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual of the icosahedron) and the rhombic triacontahedron .
Chiral polyhedra [ edit ] Full icosahedral symmetry [ edit ]
Platonic solid Kepler–Poinsot polyhedra
Archimedean solids
{5,3} {5/2,5} {5/2,3} t{5,3} t{3,5} r{3,5} rr{3,5} tr{3,5}
Platonic solid
Kepler–Poinsot polyhedra
Catalan solids
{3,5} {5,5/2} {3,5/2} V3.10.10 V5.6.6 V3.5.3.5 V3.4.5.4 V4.6.10
Other objects with icosahedral symmetry [ edit ] Liquid crystals with icosahedral symmetry [ edit ] For the intermediate material phase called liquid crystals the existence of icosahedral symmetry was proposed by H. Kleinert and K. Maki[2] here .
In aluminum, the icosahedral structure was discovered experimentally three years after this
by Dan Shechtman , which earned him the Nobel Prize in 2011.
Related geometries [ edit ] Icosahedral symmetry is equivalently the projective special linear group PSL(2,5), and is the symmetry group of the modular curve X(5), and more generally PSL(2,p ) is the symmetry group of the modular curve X(p ). The modular curve X(5) is geometrically a dodecahedron with a cusp at the center of each polygonal face, which demonstrates the symmetry group.
This geometry, and associated symmetry group, was studied by Felix Klein as the monodromy groups of a Belyi surface – a Riemann surface with a holomorphic map to the Riemann sphere, ramified only at 0, 1, and infinity (a Belyi function ) – the cusps are the points lying over infinity, while the vertices and the centers of each edge lie over 0 and 1; the degree of the covering (number of sheets) equals 5.
This arose from his efforts to give a geometric setting for why icosahedral symmetry arose in the solution of the quintic equation , with the theory given in the famous (Klein 1888 ); a modern exposition is given in (Tóth 2002 , Section 1.6, Additional Topic: Klein's Theory of the Icosahedron, p. 66 ).
Klein's investigations continued with his discovery of order 7 and order 11 symmetries in (Klein 1878 ) and (Klein 1879 ) (and associated coverings of degree 7 and 11) and dessins d'enfants , the first yielding the Klein quartic , whose associated geometry has a tiling by 24 heptagons (with a cusp at the center of each).
Similar geometries occur for PSL(2,n ) and more general groups for other modular curves.
More exotically, there are special connections between the groups PSL(2,5) (order 60), PSL(2,7) (order 168) and PSL(2,11) (order 660), which also admit geometric interpretations – PSL(2,5) is the symmetries of the icosahedron (genus 0), PSL(2,7) of the Klein quartic (genus 3), and PSL(2,11) the buckyball surface (genus 70). These groups form a "trinity " in the sense of Vladimir Arnold , which gives a framework for the various relationships; see trinities
There is a close relationship to other Platonic solids .
See also [ edit ] References [ edit ]
Klein, F. (1878). "Ueber die Transformation siebenter Ordnung der elliptischen Functionen" [On the order-seven transformation of elliptic functions]. Mathematische Annalen . 14 (3): 428–471. doi :10.1007/BF01677143 . S2CID 121407539 .Levy, Silvio, ed. (1999). The Eightfold Way ISBN 978-0-521-66066-2 MR 1722410 . Klein, F. (1879), "Ueber die Transformation elfter Ordnung der elliptischen Functionen (On the eleventh order transformation of elliptic functions)" , Mathematische Annalen , 15 (3–4): 533–555, doi :10.1007/BF02086276 , S2CID 120316938 Oeuvres, Tome 3 Klein, Felix (1888), Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree , Trübner & Co., ISBN 0-486-49528-0 trans {{citation }}: CS1 maint: postscript (link )Tóth, Gábor (2002), Finite Möbius groups, minimal immersions of spheres, and moduli Peter R. Cromwell, Polyhedra (1997), p. 296
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 Kaleidoscopes: Selected Writings of H.S.M. Coxeter , edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] N.W. Johnson : Geometries and Transformations , (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups , 11.5 Spherical Coxeter groups
External links [ edit ] 







![]()
![]()
![]()
![]()
![]() . The set of rotational symmetries forms a subgroup that is isomorphic to the alternating group A5 on 5 letters.
. The set of rotational symmetries forms a subgroup that is isomorphic to the alternating group A5 on 5 letters.
![]()
![]()
![]()
![]()
![]() . The set of rotational symmetries forms a subgroup that is isomorphic to the alternating group A5 on 5 letters.
. The set of rotational symmetries forms a subgroup that is isomorphic to the alternating group A5 on 5 letters.









![]()
![]()
![]()
![]()
![]() ) of order 120 has generators represented by the reflection matrices R0, R1, R2 below, with relations R02 = R12 = R22 = (R0×R1)5 = (R1×R2)3 = (R0×R2)2 = Identity. The group [5,3]+ (
) of order 120 has generators represented by the reflection matrices R0, R1, R2 below, with relations R02 = R12 = R22 = (R0×R1)5 = (R1×R2)3 = (R0×R2)2 = Identity. The group [5,3]+ (![]()
![]()
![]()
![]()
![]() ) of order 60 is generated by any two of the rotations S0,1, S1,2, S0,2. A rotoreflection of order 10 is generated by V0,1,2, the product of all 3 reflections. Here denotes the golden ratio.
) of order 60 is generated by any two of the rotations S0,1, S1,2, S0,2. A rotoreflection of order 10 is generated by V0,1,2, the product of all 3 reflections. Here denotes the golden ratio.





















































































































































































































![{\displaystyle \left[{\begin{smallmatrix}-1&0&0\\0&1&0\\0&0&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b81bf2648cef2b0f3cb2f82f0f0bcba89c595af1)
![{\displaystyle \left[{\begin{smallmatrix}{\frac {1-\phi }{2}}&{\frac {-\phi }{2}}&{\frac {-1}{2}}\\{\frac {-\phi }{2}}&{\frac {1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {1-\phi }{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94a2f124af793abcdec2a757fa54eacd8e12183f)
![{\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d98311a57b2d6575867fb3100199be36b656299)
![{\displaystyle \left[{\begin{smallmatrix}{\frac {\phi -1}{2}}&{\frac {\phi }{2}}&{\frac {1}{2}}\\{\frac {-\phi }{2}}&{\frac {1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {1-\phi }{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bef78ac2c56b1aeecf4b2ee91fa450dd1b0bbc29)
![{\displaystyle \left[{\begin{smallmatrix}{\frac {1-\phi }{2}}&{\frac {\phi }{2}}&{\frac {-1}{2}}\\{\frac {-\phi }{2}}&{\frac {-1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {\phi -1}{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c62a981424dfb7bce1a413d58b0ee62a9322924)
![{\displaystyle \left[{\begin{smallmatrix}-1&0&0\\0&-1&0\\0&0&1\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29ecfba65b611468342e533ba54ae7b9f240f3bb)
![{\displaystyle \left[{\begin{smallmatrix}{\frac {\phi -1}{2}}&{\frac {-\phi }{2}}&{\frac {1}{2}}\\{\frac {-\phi }{2}}&{\frac {-1}{2}}&{\frac {1-\phi }{2}}\\{\frac {-1}{2}}&{\frac {\phi -1}{2}}&{\frac {\phi }{2}}\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f358516e6f6d9c29e3ca1c9f6bac53e18019636)