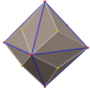
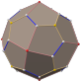
Triakis icosahedron
| Triakis icosahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kI |
| Face type | V3.10.10 isosceles triangle |
| Faces | 60 |
| Edges | 90 |
| Vertices | 32 |
| Vertices by type | 20{3}+12{10} |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 160°36′45″ arccos(−24 + 15√5/61) |
| Properties | convex, face-transitive |
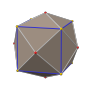
 Truncated dodecahedron (dual polyhedron) |
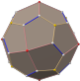
 Net |
In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid, with 60 isosceles triangle faces. Its dual is the truncated dodecahedron. It has also been called the kisicosahedron.[1] It was first depicted, in a non-convex form with equilateral triangle faces, by Leonardo da Vinci in Luca Pacioli's Divina proportione, where it was named the icosahedron elevatum.[2] The capsid of the Hepatitis A virus has the shape of a triakis icosahedron.[3]
As a Kleetope[edit]
The triakis icosahedron can be formed by gluing triangular pyramids to each face of a regular icosahedron. Depending on the height of these pyramids relative to their base, the result can be either convex or non-convex. This construction, of gluing pyramids to each face, is an instance of a general construction called the Kleetope; the triakis icosahedron is the Kleetope of the icosahedron.[2] This interpretation is also expressed in the name, triakis, which is used for the Kleetopes of polyhedra with triangular faces.[1]
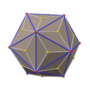
When depicted in Leonardo's form, with equilateral triangle faces, it is an example of a non-convex deltahedron, one of the few known deltahedra that are isohedral (meaning that all faces are symmetric to each other).[4] In another of the non-convex forms of the triakis icosahedron, the three triangles adjacent to each pyramid are coplanar, and can be thought of as instead forming the visible parts of a convex hexagon, in a self-intersecting polyhedron with 20 hexagonal faces that has been called the small triambic icosahedron.[5] Alternatively, for the same form of the triakis icosahedron, the triples of coplanar isosceles triangles form the faces of the first stellation of the icosahedron.[6] Yet another non-convex form, with golden isosceles triangle faces, forms the outer shell of the great stellated dodecahedron, a Kepler–Poinsot polyhedron with twelve pentagram faces.[7]
Each edge of the triakis icosahedron has endpoints of total degree at least 13. By Kotzig's theorem, this is the most possible for any polyhedron. The same total degree is obtained from the Kleetope of any polyhedron with minimum degree five, but the triakis icosahedron is the simplest example of this construction.[8] Although this Kleetope has isosceles triangle faces, iterating the Kleetope construction on it produces convex polyhedra with triangular faces that cannot all be isosceles.[9]
As a Catalan solid[edit]


The triakis icosahedron is a Catalan solid, the dual polyhedron of the truncated dodecahedron. The truncated dodecahedron is an Archimedean solid, with faces that are regular decagons and equilateral triangles, and with all edges having unit length; its vertices lie on a common sphere, the circumsphere of the truncated decahedron. The polar reciprocation of this solid through this sphere is a convex form of the triakis icosahedron, with all faces tangent to the same sphere, now an inscribed sphere, with coordinates and dimensions that can be calculated as follows.
Let denote the golden ratio. The short edges of this form of the triakis icosahedron have length
and the long edges have length
Its faces are isosceles triangles with one obtuse angle of
and two acute angles of
As a Catalan solid, its dihedral angles are all equal, 160°36'45.188". One possible set of 32 Cartesian coordinates for the vertices of the triakis icosahedron centered at the origin (scaled differently than the one above) can be generated by combining the vertices of two appropriately scaled Platonic solids, the regular icosahedron and a regular dodecahedron:[12]
- Twelve vertices of a regular icosahedron, scaled to have a unit circumradius, with the coordinates
- Twenty vertices of a regular dodecahedron, scaled to have circumradius with the coordinatesand
Symmetry[edit]
In any of its standard convex or non-convex forms, the triakis icosahedron has the same symmetries as a regular icosahedron.[4] The three types of symmetry axes of the icosahedron, through two opposite vertices, edge midpoints, and face centroids, become respectively axes through opposite pairs of degree-ten vertices of the triakis icosahedron, through opposite midpoints of edges between degree-ten vertices, and through opposite pairs of degree-three vertices.
See also[edit]
- Triakis triangular tiling for other "triakis" polyhedral forms.
- Great triakis icosahedron
References[edit]
- ^ a b Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. AK Peters. p. 284. ISBN 978-1-56881-220-5.
- ^ a b Brigaglia, Aldo; Palladino, Nicla; Vaccaro, Maria Alessandra (2018). "Historical notes on star geometry in mathematics, art and nature". In Emmer, Michele; Abate, Marco (eds.). Imagine Math 6: Between Culture and Mathematics. Springer International Publishing. pp. 197–211. doi:10.1007/978-3-319-93949-0_17.
- ^ Zhu, Ling; Zhang, Xiaoxue (October 2014). "Hepatitis A virus exhibits a structure unique among picornaviruses". Protein & Cell. 6 (2): 79–80. doi:10.1007/s13238-014-0103-7. PMC 4312766.
- ^ a b Shephard, G. C. (1999). "Isohedral deltahedra". Periodica Mathematica Hungarica. 39 (1–3): 83–106. doi:10.1023/A:1004838806529.
- ^ Grünbaum, Branko (2008). "Can every face of a polyhedron have many sides?". Geometry, games, graphs and education. The Joe Malkevitch Festschrift. Papers from Joe Fest 2008, York College–The City University of New York (CUNY), Jamaica, NY, USA, November 8, 2008. Bedford, MA: Comap, Inc. pp. 9–26. hdl:1773/4593. ISBN 978-1-933223-17-9. Zbl 1185.52009.
- ^ Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 270. ISBN 0-521-66405-5.
- ^ Wenninger, Magnus (1974). "22: The great stellated dodecahedron". Polyhedron Models. Cambridge University Press. pp. 40–42. ISBN 0-521-09859-9.
- ^ Zaks, Joseph (1983). "Extending Kotzig's theorem". Israel Journal of Mathematics. 45 (4): 281–296. doi:10.1007/BF02804013. hdl:10338.dmlcz/127504. MR 0720304.
- ^ Eppstein, David (2021). "On polyhedral realization with isosceles triangles". Graphs and Combinatorics. 37 (4): 1247–1269. arXiv:2009.00116. doi:10.1007/s00373-021-02314-9.
- ^ Weisstein, Eric W. "Triakis icosahedron". MathWorld.
- ^ Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 89. ISBN 0-486-23729-X.
- ^ Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). "Catalan Solids Derived From 3D-Root Systems and Quaternions". Journal of Mathematical Physics. 51 (4). arXiv:0908.3272. doi:10.1063/1.3356985.