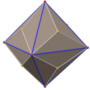
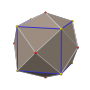
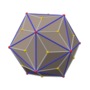
Pentakis dodecahedron

Pentakis dodecahedron
(Click here for rotating model)
Type	Catalan solid
Face type	isosceles triangle
Faces	60
Edges	90
Vertices	32
Vertices by type	20{6}+12{5}
Face configuration	V5.6.6
Symmetry group	Ih, [5,3], *532
Dihedral angle	156°43'7" $\arccos ( -\frac{80 + 9\sqrt{5}}{109} )$
Properties	convex, face-transitive
Truncated icosahedron (dual polyhedron)	Net

In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.

It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron. This interpretation is expressed in its name.

Geometric variations

Its construction is topologically the same as that of:

1. The small stellated dodecahedron (with very tall pyramids).
2. Great pentakis dodecahedron (with extremely tall pyramids)
3. Wenninger's third stellation of icosahedron (with inverted pyramids).

If one affixes pentagrammic pyramids into Wenninger's third stellation of icosahedron one obtains the great icosahedron.

Chemistry

The pentakis dodecahedron in a model of buckminsterfullerene: each surface segment represents a carbon atom.

Cultural references

• Spaceship Earth in Walt Disney World's Epcot is based on one.
• The shape of the "Crystal Dome" used in the popular TV game show The Crystal Maze was based on a pentakis dodecahedron.
• In Doctor Atomic, the shape of the first atomic bomb detonated in New Mexico was a pentakis dodecahedron.[1]
• In De Blob 2 in the Prison Zoo, domes are made up of parts of a Pentakis Dodecahedron. These Domes also appear whenever the player transforms on a dome in the Hypno Ray level.
• Some Geodomes in which people play on are Pentakis Dodecahedra.

References

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Section 3-9)
• Sellars, Peter (2005). "Doctor Atomic Libretto". Boosey & Hawkes. http://www.scribd.com/doc/7817182/Doctor-Atomic-Libretto. "We surround the plutonium core from thirty two points spaced equally around its surface, the thirty-two points are the centers of the twenty triangular faces of an icosahedron interwoven with the twelve pentagonal faces of a dodecahedron." 
• Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR730208  (The thirteen semiregular convex polyhedra and their duals, Page 18, Pentakisdodecahedron)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [2] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Pentakis dodecahedron )

External links

• Eric W. Weisstein, Pentakis dodecahedron (Catalan solid) at MathWorld.
• Pentakis Dodecahedron – Interactive Polyhedron Model