Radiative forcing
![Warming contributions of various GHGs, agents, factors [name the year that the contributions pertain to] [*correct reference given under the 'Talk' tab*]. Plus, the figure is inaccurate; at least wrt. to methane.](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a0/Physical_Drivers_of_climate_change.svg/300px-Physical_Drivers_of_climate_change.svg.png)
Radiative forcing (or climate forcing[2]) is a concept used in climate science to quantify the change in energy balance in Earth's atmosphere. Various factors contribute to this change in energy balance, such as concentrations of greenhouse gases and aerosols, and changes in surface albedo and solar irradiance. In more technical terms, it is defined as "the change in the net, downward minus upward, radiative flux (expressed in W/m2) due to a change in an external driver of climate change."[3]: 2245 These external drivers are distinguished from feedbacks and variability that are internal to the climate system, and that further influence the direction and magnitude of imbalance. Radiative forcing on Earth is meaningfully evaluated at the tropopause and at the top of the stratosphere. It is quantified in units of watts per square meter, and often summarized as an average over the total surface area of the globe.
A planet in radiative equilibrium with its parent star and the rest of space can be characterized by net zero radiative forcing and by a planetary equilibrium temperature.[4]
Radiative forcing is not a thing in the sense that a single instrument can independently measure it. Rather it is a scientific concept and entity whose strength can be estimated from more fundamental physics principles. Scientists use measurements of changes in atmospheric parameters to calculate the radiative forcing.[5]: 1–4
The IPCC summarized the current scientific consensus about radiative forcing changes as follows: "Human-caused radiative forcing of 2.72 W/m2 in 2019 relative to 1750 has warmed the climate system. This warming is mainly due to increased GHG concentrations, partly reduced by cooling due to increased aerosol concentrations".[1]: 11
The atmospheric burden of greenhouse gases due to human activity has grown especially rapidly during the last several decades (since about year 1950). For carbon dioxide, the 50% increase (C/C0 = 1.5) realized as of year 2020 since 1750 corresponds to a cumulative radiative forcing change (ΔF) of +2.17 W/m2.[6] Assuming no change in the emissions growth path, a doubling of concentrations (C/C0 = 2) within the next several decades would correspond to a cumulative radiative forcing change (ΔF) of +3.71 W/m2.
Radiative forcing can be a useful way to compare the growing warming influence of different anthropogenic greenhouse gases over time. The radiative forcing of long-lived and well-mixed greenhouse gases have been increasing in earth's atmosphere since the industrial revolution.[6] Carbon dioxide has the biggest impact on total forcing, while methane and chlorofluorocarbons (CFCs) play smaller roles as time goes on.[6] The five major greenhouse gases account for about 96% of the direct radiative forcing by long-lived greenhouse gas increases since 1750. The remaining 4% is contributed by the 15 minor halogenated gases.
Definition and fundamentals[edit]
Radiative forcing is defined in the IPCC Sixth Assessment Report as follows: "The change in the net, downward minus upward, radiative flux (expressed in W/m2) due to a change in an external driver of climate change, such as a change in the concentration of carbon dioxide (CO2), the concentration of volcanic aerosols or the output of the Sun."[3]: 2245
There are some different types of radiative forcing as defined in the literature:[3]: 2245
- Stratospherically adjusted radiative forcing: "when all tropospheric properties held fixed at their unperturbed values, and after allowing for stratospheric temperatures, if perturbed, to readjust to radiative-dynamical equilibrium."
- Instantaneous radiative forcing: "if no change in stratospheric temperature is accounted for".
- Effective radiative forcing: "once both stratospheric and tropospheric adjustments are accounted for".
The radiation balance of the Earth (i.e. the balance between absorbed and radiated energy) determines the average global temperature. This balance is also called Earth's energy balance. Changes to this balance occur due to factors such as the intensity of solar energy, reflectivity of clouds or gases, absorption by various greenhouse gases or surfaces and heat emission by various materials. Any such alteration is a radiative forcing, which along with its climate feedbacks, ultimately changes the balance. This happens continuously as sunlight hits the surface of Earth, clouds and aerosols form, the concentrations of atmospheric gases vary and seasons alter the groundcover.
Positive radiative forcing means Earth receives more incoming energy from sunlight than it radiates to space. This net gain of energy will cause global warming. Conversely, negative radiative forcing means that Earth loses more energy to space than it receives from the Sun, which produces cooling (global dimming).
Related metrics[edit]
The concept of radiative forcing has been evolving from the initial proposal, named nowadays instantaneous radiative forcing (IRF), to other proposals that aim to relate better the radiative imbalance with global warming (global surface mean temperature). For example, researchers explained in 2003 how the adjusted troposphere and stratosphere forcing can be used in general circulation models.[7]
The adjusted radiative forcing, in its different calculation methodologies, estimates the imbalance once the stratosphere temperatures has been modified to achieve a radiative equilibrium in the stratosphere (in the sense of zero radiative heating rates). This new methodology is not estimating any adjustment or feedback that could be produced on the troposphere (in addition to stratospheric temperature adjustments), for that goal another definition, named effective radiative forcing has been introduced.[8] In general the ERF is the recommendation of the CMIP6 radiative forcing analysis [9] although the stratospherically adjusted methodologies are still being applied in those cases where the adjustments and feedbacks on the troposphere are considered not critical, like in the well mixed greenhouse gases and ozone.[10][11] A methodology named radiative kernel approach allows to estimate the climate feedbacks within an offline calculation based on a linear approximation [12]
Uses[edit]

Climate change attribution[edit]
Radiative forcing is used to quantify the strengths of different natural and man-made drivers of Earth's energy imbalance over time. The detailed physical mechanisms by which these drivers cause the planet to warm or cool are varied. Radiative forcing allows the contribution of any one driver to be compared against others.
Another metric called effective radiative forcing or ERF removes the effect of rapid adjustments (so-called "fast feedbacks") within the atmosphere that are unrelated to longer term surface temperature responses. ERF means that climate change drivers can be placed onto a more level playing field to enable comparison of their effects and a more consistent view of how global surface temperature responds to various types of human forcing.[14]
Climate sensitivity[edit]
Radiative forcing and climate feedbacks can be used together to estimate a subsequent change in steady-state (often denoted "equilibrium") surface temperature (ΔTs) via the equation:
where is commonly denoted the climate sensitivity parameter, usually with units K/(W/m2), and ΔF is the radiative forcing in W/m2.[15] An estimate for is obtained from the inverse of the climate feedback parameter having units (W/m2)/K. An estimated value of gives an increase in global temperature of about 1.6 K above the 1750 reference temperature due to the increase in CO2 over that time (278 to 405 ppm, for a forcing of 2.0 W/m2), and predicts a further warming of 1.4 K above present temperatures if the CO2 mixing ratio in the atmosphere were to become double its pre-industrial value. Both of these calculations assume no other forcings.[16]
Historically, radiative forcing displays the best predictive capacity for specific types of forcing such as greenhouse gases. It is less effective for other anthropogenic influences like soot.[14]
Calculations and measurements[edit]
Atmospheric observation[edit]
Earth's global radiation balance fluctuates as the planet rotates and orbits the Sun, and as global-scale thermal anomalies arise and dissipate within the terrestrial, oceanic and atmospheric systems (e.g. ENSO).[17] Consequently, the planet's 'instantaneous radiative forcing' (IRF) is also dynamic and naturally fluctuates between states of overall warming and cooling. The combination of periodic and complex processes that give rise to these natural variations will typically revert over periods lasting as long as a few years to produce a net-zero average IRF. Such fluctuations also mask the longer-term (decade-long) forcing trends due to human activities, and thus make direct observation of such trends challenging.[18]

Earth's radiation balance has been continuously monitored by NASA's Clouds and the Earth's Radiant Energy System (CERES) instruments since year 1998.[20][21] Each scan of the globe provides an estimate of the total (all-sky) instantaneous radiation balance. This data record captures both the natural fluctuations and human influences on IRF; including changes in greenhouse gases, aerosols, land surface, etc. The record also includes the lagging radiative responses to the radiative imbalances; occurring mainly by way of Earth system feedbacks in temperature, surface albedo, atmospheric water vapor and clouds.[22][23]
Researchers have used measurements from CERES, AIRS, CloudSat and other satellite-based instruments within NASA's Earth Observing System to parse out contributions by the natural fluctuations and system feedbacks. Removing these contributions within the multi-year data record allows observation of the anthropogenic trend in top-of-atmosphere (TOA) IRF. The data analysis has also been done in a way that is computationally efficient and independent of most related modelling methods and results. Radiative forcing was thus directly observed to have risen by +0.53 W m−2 (±0.11 W m−2) from years 2003 to 2018. About 20% of the increase was associated with a reduction in the atmospheric aerosol burden, and most of the remaining 80% was attributed to the rising burden of greenhouse gases.[18][24][25]
A rising trend in the radiative imbalance due to increasing global CO2 has been previously observed by ground-based instruments. For example, such measurements have been separately gathered under clear-sky conditions at two Atmospheric Radiation Measurement (ARM) sites in Oklahoma and Alaska.[26] Each direct observation found that the associated radiative (infrared) heating experienced by surface dwellers rose by +0.2 W m−2 (±0.07 W m−2) during the decade ending 2010.[27][28] In addition to its focus on longwave radiation and the most influential forcing gas (CO2) only, this result is proportionally less than the TOA forcing due to its buffering by atmospheric absorption.
Basic estimates[edit]
Radiative forcing can be evaluated for its dependence on different factors which are external to the climate system.[29] Basic estimates summarized in the following sections have been derived (assembled) in accordance with first principles of the physics of matter and energy. Forcings (ΔF) are expressed as changes over the total surface of the planet and over a specified time interval. Estimates may be significant in the context of global climate forcing for times spanning decades or longer.[5] Gas forcing estimates presented in the IPCC's AR6 report have been adjusted to include so-called "fast" feedbacks (positive or negative) which occur via atmospheric responses (i.e. effective radiative forcing).
Forcing due to changes in atmospheric gases[edit]

For a well-mixed greenhouse gas, radiative transfer codes that examine each spectral line for atmospheric conditions can be used to calculate the forcing ΔF as a function of a change in its concentration. These calculations may be simplified into an algebraic formulation that is specific to that gas.
Carbon dioxide[edit]
A simplified first-order approximation expression for carbon dioxide (CO2) is:[30]
- ,
where C0 is a reference concentration in parts per million (ppm) by volume and ΔC is the concentration change in ppm. For the purpose of some studies (e.g. climate sensitivity), C0 is taken as the concentration prior to substantial anthropogenic changes and has a value of 278 ppm as estimated for the year 1750.
| Baseline concentration, C0 | Concentration change, ΔC | Radiative forcing change, ΔF (W m−2) | |
|---|---|---|---|
| 1979-1989 | 336.8 | +16.0 | +0.248 |
| 1989-1999 | 352.8 | +15.0 | +0.222 |
| 1999-2009 | 367.8 | +18.7 | +0.266 |
| 2009-2019 | 386.5 | +23.6 | +0.316 |
The atmospheric burden of greenhouse gases due to human activity has grown especially rapidly during the last several decades (since about year 1950). For carbon dioxide, the 50% increase (C/C0 = 1.5) realized as of year 2020 since 1750 corresponds to a cumulative radiative forcing change (delta F) of +2.17 W/m2.[6] Assuming no change in the emissions growth path, a doubling of concentrations (C/C0 = 2) within the next several decades would correspond to a cumulative radiative forcing change (delta F) of +3.71 W/m2.
The relationship between CO2 and radiative forcing is logarithmic at concentrations up to around eight times the current value.[31] Constant concentration increases thus have a progressively smaller warming effect. However, the first-order approximation is inaccurate at higher concentrations and there is no saturation in the absorption of infrared radiation by CO2.[32]
Other trace gases[edit]
Somewhat different formulae apply for other trace greenhouse gases such as methane and N
2O (square-root dependence) or CFCs (linear), with coefficients that may be found for example in the IPCC reports.[33] A year 2016 study suggests a significant revision to the methane IPCC formula.[34] Forcings by the most influential trace gases in Earth's atmosphere are included in the section describing recent growth trends, and in the IPCC list of greenhouse gases.
Water vapor[edit]
Water vapor is Earth's primary greenhouse gas currently responsible for about half of all atmospheric gas forcing. Its overall atmospheric concentration depends almost entirely on the average planetary temperature, and has the potential to increase by as much as 7% with every degree (°C) of temperature rise (see also: Clausius–Clapeyron relation).[35] Thus over long time scales, water vapor behaves as a system feedback that amplifies the radiative forcing driven by the growth of carbon dioxide and other trace gases.[36][37]
Forcing due to changes in solar irradiance[edit]
The intensity of solar irradiance including all wavelengths is the Total Solar Irradiance (TSI) and on average is the solar constant. It is equal to about 1361 W m−2 at the distance of Earth's annual-mean orbital radius of one astronomical unit and as measured at the top of the atmosphere.[38] Earth TSI varies with both solar activity and planetary orbital dynamics. Multiple satellite-based instruments including ERB, ACRIM 1-3, VIRGO, and TIM[39][40] have continuously measured TSI with improving accuracy and precision since 1978.[41]
Approximating Earth as a sphere, the cross-sectional area exposed to the Sun () is equal to one quarter the area of the planet's surface (). The globally and annually averaged amount of solar irradiance per square meter of Earth's atmospheric surface () is therefore equal to one quarter of TSI, and has a nearly constant value of .
Annual cycles[edit]
Earth follows an elliptical orbit around the Sun, so that the TSI received at any instant fluctuates between about 1321 W m−2 (at aphelion in early July) and 1412 W m−2 (at perihelion in early January), and thus by about ±3.4% over each year.[42] This change in irradiance has minor influences on Earth's seasonal weather patterns and its climate zones, which primarily result from the annual cycling in Earth's relative tilt direction.[43] Such repeating cycles contribute a net-zero forcing (by definition) in the context of decades-long climate changes.
Sunspot activity[edit]
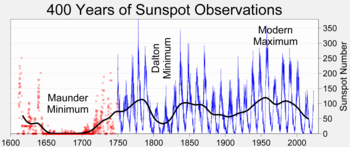
Average annual TSI varies between about 1360 W m−2 and 1362 W m−2 (±0.05%) over the course of a typical 11-year sunspot activity cycle.[44] Sunspot observations have been recorded since about year 1600 and show evidence of lengthier oscillations (Gleissberg cycle, Devries/Seuss cycle, etc.) which modulate the 11-year cycle (Schwabe cycle). Despite such complex behavior, the amplitude of the 11-year cycle has been the most prominent variation throughout this long-term observation record.[45]
TSI variations associated with sunspots contribute a small but non-zero net forcing in the context of decadal climate changes.[41] Some research suggests they may have partly influenced climate shifts during the Little Ice Age, along with concurrent changes in volcanic activity and deforestation.[46] Since the late 20th century, average TSI has trended slightly lower along with a downward trend in sunspot activity.[47]
Milankovitch shifts[edit]
Climate forcing caused by variations in solar irradiance have occurred during Milankovitch cycles, which span periods of about 40,000 to 100,000 years. Milankovitch cycles consist of long-duration cycles in Earth's orbital eccentricity (or ellipticity), cycles in its orbital obliquity (or axial tilt), and precession of its relative tilt direction.[48] Among these, the 100,000 year cycle in eccentricity causes TSI to fluctuate by about ±0.2%.[49] Currently, Earth's eccentricity is nearing its least elliptic (most circular) causing average annual TSI to very slowly decrease.[48] Simulations also indicate that Earth's orbital dynamics will remain stable including these variations for least the next 10 million years.[50]
Sun aging[edit]
The Sun has consumed about half its hydrogen fuel since forming approximately 4.5 billion years ago.[51] TSI will continue to slowly increase during the aging process at a rate of about 1% each 100 million years. Such rate of change is far too small to be detectable within measurements and is insignificant on human timescales.
Total Solar Irradiance (TSI) forcing summary[edit]
| Δτ | Radiative forcing change ΔF (W m−2) | |
|---|---|---|
| Annual cycle | ±0.034 [42] | 0 (net) |
| Sunspot activity | ±5×10−4 [44] | ±0.1 [47][52] |
| Orbital shift | −4×10−7 [49] | −1×10−4 |
| Sun aging | +1×10−9 [51] | +2×10−7 |
The maximum fractional variations (Δτ) in Earth's solar irradiance during the last decade are summarized in the accompanying table. Each variation previously discussed contributes a forcing of:
- ,
where R=0.30 is Earth's reflectivity. The radiative and climate forcings arising from changes in the Sun's insolation are expected to continue to be minor, notwithstanding some as-of-yet undiscovered solar physics.[47][53]
Forcing due to changes in albedo and aerosols[edit]
This article needs to be updated. (April 2024) |
A fraction of incident solar radiation is reflected by clouds and aerosols, oceans and landforms, snow and ice, vegetation, and other natural and man-made surface features. The reflected fraction is known as Earth's bond albedo (R), is evaluated at the top of the atmosphere, and has an average annual global value of about 0.30 (30%). The overall fraction of solar power absorbed by Earth is then (1−R) or 0.70 (70%).[54]
Atmospheric components contribute about three-quarters of Earth albedo, and clouds alone are responsible for half. The major roles of clouds and water vapor are linked with the majority presence of liquid water covering the planet's crust. Global patterns in cloud formation and circulation are highly complex, with couplings to ocean heat flows, and with jet streams assisting their rapid transport. Moreover, the albedos of Earth's northern and southern hemispheres have been observed to be essentially equal (within 0.2%). This is noteworthy since more than two-thirds of land and 85% of the human population are in the north.[55]
Multiple satellite-based instruments including MODIS, VIIRs, and CERES have continuously monitored Earth's albedo since 1998.[56] Landsat imagery, available since 1972, has also been used in some studies.[57] Measurement accuracy has improved and results have converged in recent years, enabling more confident assessment of the recent decadal forcing influence of planetary albedo.[55] Nevertheless, the existing data record is still too short to support longer-term predictions or to address other related questions.
Annual cycles[edit]
Seasonal variations in planetary albedo can be understood as a set of system feedbacks that occur largely in response to the yearly cycling of Earth's relative tilt direction. Along with the atmospheric responses, most apparent to surface dwellers are the changes in vegetation, snow, and sea-ice coverage. Intra-annual variations of about ±0.02 (± 7%) around Earth's mean albedo have been observed throughout the course of a year, with maxima occurring twice per year near the time of each solar equinox.[55] This repeating cycle contributes net-zero forcing in the context of decades-long climate changes.
Interannual variability[edit]

Regional albedos change from year to year due to shifts arising from natural processes, human actions, and system feedbacks. For example, human acts of deforestion typically raise Earth's reflectivity while introducing water storage and irrigation to arid lands may lower it. Likewise considering feedbacks, ice loss in arctic regions decreases albedo while expanding desertification at low to middle latitudes increases it.
During years 2000-2012, no overall trend in Earth's albedo was discernible within the 0.1% standard deviation of values measured by CERES.[55] Along with the hemispherical equivalence, some researchers interpret the remarkably small interannual differences as evidence that planetary albedo may currently be constrained by the action of complex system feedbacks. Nevertheless, historical evidence also suggests that infrequent events such as major volcanic eruptions can significantly perturb the planetary albedo for several years or longer.[58]
Albedo forcing summary[edit]
| Fractional variations (Δα) in Earth's albedo | Radiative forcing change ΔF (W m−2) | |
|---|---|---|
| Annual cycle | ± 0.07[55] | 0 (net) |
| Interannual variation | ± 0.001[55] | ∓ 0.1 |
The measured fractional variations (Δα) in Earth's albedo during the first decade of the 21st century are summarized in the accompanying table. Similar to TSI, the radiative forcing due to a fractional change in planetary albedo (Δα) is:
- .
Satellite observations show that various Earth system feedbacks have stabilized planetary albedo despite recent natural and human-caused shifts.[56] On longer timescales, it is more uncertain whether the net forcing which results from such external changes will remain minor.
Recent growth trends[edit]
The IPCC summarized the current scientific consensus about radiative forcing changes as follows: "Human-caused radiative forcing of 2.72 [1.96 to 3.48] W/m2 in 2019 relative to 1750 has warmed the climate system. This warming is mainly due to increased GHG concentrations, partly reduced by cooling due to increased aerosol concentrations".[1]: 11
Radiative forcing can be a useful way to compare the growing warming influence of different anthropogenic greenhouse gases over time.
The radiative forcing of long-lived and well-mixed greenhouse gases have been increasing in earth's atmosphere since the industrial revolution.[6] The table includes the direct forcing contributions from carbon dioxide (CO2), methane (CH
4), nitrous oxide (N
2O); chlorofluorocarbons (CFCs) 12 and 11;[failed verification] and fifteen other halogenated gases.[61] These data do not include the significant forcing contributions from shorter-lived and less-well-mixed gases or aerosols; including those indirect forcings from the decay of methane and some halogens. They also do not account for changes in land use or solar activity.
Click at right to show/hide table
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
These data show that CO2 dominates the total forcing, with methane and chlorofluorocarbons (CFC) becoming relatively smaller contributors to the total forcing over time.[6] The five major greenhouse gases account for about 96% of the direct radiative forcing by long-lived greenhouse gas increases since 1750. The remaining 4% is contributed by the 15 minor halogenated gases.
It might be observed that the total forcing for year 2016, 3.027 W m−2, together with the commonly accepted value of climate sensitivity parameter λ, 0.8 K /(W m−2), results in an increase in global temperature of 2.4 K, much greater than the observed increase, about 1.2 K.[62][failed verification] Part of this difference is due to lag in the global temperature achieving steady state with the forcing. The remainder of the difference is due to negative aerosol forcing (compare climate effects of particulates), climate sensitivity being less than the commonly accepted value, or some combination thereof.[63]
The table also includes an "Annual Greenhouse Gas Index" (AGGI), which is defined as the ratio of the total direct radiative forcing due to long-lived greenhouse gases for any year for which adequate global measurements exist to that which was present in 1990.[6] 1990 was chosen because it is the baseline year for the Kyoto Protocol. This index is a measure of the inter-annual changes in conditions that affect carbon dioxide emission and uptake, methane and nitrous oxide sources and sinks, the decline in the atmospheric abundance of ozone-depleting chemicals related to the Montreal Protocol. and the increase in their substitutes (hydrogenated CFCs (HCFCs) and hydrofluorocarbons (HFC). Most of this increase is related to CO2. For 2013, the AGGI was 1.34 (representing an increase in total direct radiative forcing of 34% since 1990). The increase in CO2 forcing alone since 1990 was about 46%. The decline in CFCs considerably tempered the increase in net radiative forcing.
An alternative table prepared for use in climate model intercomparisons conducted under the auspices of IPCC and including all forcings, not just those of greenhouse gases.[64]
See also[edit]
References[edit]
- ^ a b c IPCC, 2021: Summary for Policymakers. In: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte, V., P. Zhai, A. Pirani, S.L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M.I. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J.B.R. Matthews, T.K. Maycock, T. Waterfield, O. Yelekçi, R. Yu, and B. Zhou (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp. 3−32, doi:10.1017/9781009157896.001.
- ^ Rebecca, Lindsey (14 January 2009). "Climate and Earth's Energy Budget: Feature Articles". earthobservatory.nasa.gov. Archived from the original on 10 April 2020. Retrieved 3 April 2018.
- ^ a b c IPCC, 2021: Annex VII: Glossary [Matthews, J.B.R., V. Möller, R. van Diemen, J.S. Fuglestvedt, V. Masson-Delmotte, C. Méndez, S. Semenov, A. Reisinger (eds.)]. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte, V., P. Zhai, A. Pirani, S.L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M.I. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J.B.R. Matthews, T.K. Maycock, T. Waterfield, O. Yelekçi, R. Yu, and B. Zhou (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp. 2215–2256, doi:10.1017/9781009157896.022.
- ^ Lissauer, Jack Jonathan; De Pater, Imke (16 September 2013). Fundamental planetary science: physics, chemistry, and habitability. New York City. ISBN 9780521853309. OCLC 808009225.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ a b National Research Council (2005). Radiative Forcing of Climate Change: Expanding the Concept and Addressing Uncertainties. The National Academic Press. doi:10.17226/11175. ISBN 978-0-309-09506-8.
- ^ a b c d e f g h i j
 This article incorporates public domain material from Butler, James H. and Montzka, Steven J. (2022). THE NOAA ANNUAL GREENHOUSE GAS INDEX (AGGI). NOAA/ESRL. Retrieved 7 March 2023.
This article incorporates public domain material from Butler, James H. and Montzka, Steven J. (2022). THE NOAA ANNUAL GREENHOUSE GAS INDEX (AGGI). NOAA/ESRL. Retrieved 7 March 2023.{{citation}}: CS1 maint: multiple names: authors list (link) - ^ Shine, Keith P.; Cook, Jolene; Highwood, Eleanor J.; Joshi, Manoj M. (23 October 2003). "An alternative to radiative forcing for estimating the relative importance of climate change mechanisms". Geophysical Research Letters. 30 (20): 2047. Bibcode:2003GeoRL..30.2047S. doi:10.1029/2003GL018141. S2CID 59514371.
- ^ Sherwood, Steven C.; Bony, Sandrine; Boucher, Olivier; Bretherton, Chris; Forster, Piers M.; Gregory, Jonathan M.; Stevens, Bjorn (2015-02-01). "Adjustments in the Forcing-Feedback Framework for Understanding Climate Change" (PDF). Bulletin of the American Meteorological Society. 96 (2): 217–228. Bibcode:2015BAMS...96..217S. doi:10.1175/bams-d-13-00167.1. ISSN 0003-0007. S2CID 12515303. Archived (PDF) from the original on 2019-04-28. Retrieved 2019-12-16.
- ^ Forster, Piers M.; Richardson, Thomas; Maycock, Amanda C.; Smith, Christopher J.; Samset, Bjorn H.; Myhre, Gunnar; Andrews, Timothy; Pincus, Robert; Schulz, Michael (2016-10-27). "Recommendations for diagnosing effective radiative forcing from climate models for CMIP6" (PDF). Journal of Geophysical Research: Atmospheres. 121 (20): 12, 460–12, 475. Bibcode:2016JGRD..12112460F. doi:10.1002/2016jd025320. ISSN 2169-897X. S2CID 59367633. Archived (PDF) from the original on 2019-09-25. Retrieved 2019-09-25.
- ^ Stevenson, D. S.; Young, P. J.; Naik, V.; Lamarque, J.-F.; Shindell, D. T.; Voulgarakis, A.; Skeie, R. B.; Dalsoren, S. B.; Myhre, G. (2013-03-15). "Tropospheric ozone changes, radiative forcing and attribution to emissions in the Atmospheric Chemistry and Climate Model Intercomparison Project (ACCMIP)" (PDF). Atmospheric Chemistry and Physics. 13 (6): 3063–3085. Bibcode:2013ACP....13.3063S. doi:10.5194/acp-13-3063-2013. ISSN 1680-7316. S2CID 15347857. Archived (PDF) from the original on 2021-11-21. Retrieved 2019-09-04.
- ^ Checa-Garcia, Ramiro; Hegglin, Michaela I.; Kinnison, Douglas; Plummer, David A.; Shine, Keith P. (2018-04-06). "Historical Tropospheric and Stratospheric Ozone Radiative Forcing Using the CMIP6 Database" (PDF). Geophysical Research Letters. 45 (7): 3264–3273. Bibcode:2018GeoRL..45.3264C. doi:10.1002/2017gl076770. ISSN 0094-8276. S2CID 53471515. Archived (PDF) from the original on 2019-04-30. Retrieved 2019-12-16.
- ^ Soden, Brian J.; Held, Isaac M.; Colman, Robert; Shell, Karen M.; Kiehl, Jeffrey T.; Shields, Christine A. (2008-07-01). "Quantifying Climate Feedbacks Using Radiative Kernels". Journal of Climate. 21 (14): 3504–3520. Bibcode:2008JCli...21.3504S. CiteSeerX 10.1.1.141.653. doi:10.1175/2007jcli2110.1. ISSN 0894-8755. S2CID 14679991.
- ^ Forster, Piers M.; Smith, Christopher J.; Walsh, Tristram; et al. (2023). "Indicators of Global Climate Change 2022: annual update of large-scale indicators of the state of the climate system and human influence". Earth System Science Data. 15 (15): 2295–2327. Bibcode:2023ESSD...15.2295F. doi:10.5194/essd-15-2295-2023.
- ^ a b Nauels, A.; Rosen, D.; Mauritsen, T.; Maycock, A.; McKenna, C.; Rogelj, J.; Schleussner, C.-F.; Smith, E.; Smith, C. (2019-12-02). "ZERO IN ON the remaining carbon budget and decadal warming rates. The CONSTRAIN Project Annual Report 2019". constrain-eu.org. doi:10.5518/100/20. Archived from the original (PDF) on 2019-12-09. Retrieved 2020-01-20.
- ^ "IPCC Third Assessment Report - Climate Change 2001". Archived from the original on 30 June 2009.
- ^ "Atmosphere Changes". Archived from the original on 10 May 2009.
- ^ Rebecca, Lindsey (14 January 2009). "Climate and Earth's Energy Budget". earthobservatory.nasa.gov. Archived from the original on 21 January 2021. Retrieved 15 April 2021.
- ^ a b Kramer, R.J., H. He, B.J. Soden, L. Oreopoulos, G. Myhre, P.M. Forster, and C.J. Smith (2021-03-25). "Observational Evidence of Increasing Global Radiative Forcing". Geophysical Research Letters. 48 (7): e91585. Bibcode:2021GeoRL..4891585K. doi:10.1029/2020GL091585. hdl:11250/2788616. S2CID 233684244. Archived from the original on 2021-11-21. Retrieved 2021-04-17.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ "NASA's Earth Observing System homepage". NASA EOS Project Science Office. Archived from the original on 2021-03-18. Retrieved 2021-04-16.
- ^ Loeb, N.G., S. Kato, K. Loukachine, and N. Manalo-Smith (2005-04-01). "Angular Distribution Models for Top-of-Atmosphere Radiative Flux Estimation from the Clouds and the Earth's Radiant Energy System Instrument on the Terra Satellite. Part I: Methodology". Journal of Atmospheric and Oceanic Technology. 22 (4): 338–351. Bibcode:2005JAtOT..22..338L. doi:10.1175/JTECH1712.1.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Loeb, N.G., F.G. Rose, S. Kato, D.A. Rutan, W. Su, H. Wang, D.R. Doelling, W.L. Smith, and A. Gettelman (2020-01-01). "Toward a Consistent Definition between Satellite and Model Clear-Sky Radiative Fluxes". Journal of Climate. 33 (1): 61–75. Bibcode:2020JCli...33...61L. doi:10.1175/JCLI-D-19-0381.1.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Sherwood, S.C., S. Bony, O. Boucher, C. Bretherton, P.M. Forster, J.M. Gregory, and B. Stevens (2015-02-01). "Adjustments in the Forcing-Feedback Framework for Understanding Climate Change". Bulletin of the American Meteorological Society. 96 (2): 217–228. Bibcode:2015BAMS...96..217S. doi:10.1175/BAMS-D-13-00167.1. hdl:11858/00-001M-0000-0015-79FA-A. S2CID 12515303.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Wielicki, B.A., R.D. Cess, M.D. King, D.A. Randall, and E.F. Harrison (1995-11-01). "Mission to Planet Earth: Role of Clouds and Radiation in Climate". Bulletin of the American Meteorological Society. 76 (11): 2125–2154. Bibcode:1995BAMS...76.2125W. doi:10.1175/1520-0477(1995)076<2125:MTPERO>2.0.CO;2.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Sarah Hansen (12 April 2021). "UMBC's Ryan Kramer confirms human-caused climate change with direct evidence for first time". University of Maryland, Baltimore County. Archived from the original on 17 April 2021. Retrieved 17 April 2021.
- ^ "Direct observations confirm that humans are throwing Earth's energy budget off balance". phys.org. 26 March 2021. Archived from the original on 18 April 2021. Retrieved 17 April 2021.
- ^ "ARM Capabilities - Atmospheric Observatories". U.S. Department of Energy - Office of Science. Archived from the original on 2021-04-25. Retrieved 2021-04-25.
- ^ Feldman, D.R., W.D. Collins, P.J. Gero, M.S. Torn, E.J. Mlawer, and T.R. Shippert (2015-02-25). "Observational determination of surface radiative forcing by CO2 from 2000 to 2010". Nature. 519 (7543): 339–343. Bibcode:2015Natur.519..339F. doi:10.1038/nature14240. PMID 25731165. S2CID 2137527. Archived from the original on 2021-04-05. Retrieved 2021-04-25.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Robert McSweeney (2015-02-25). "New study directly measures greenhouse effect at Earth's surface". Carbon Brief. Archived from the original on 2021-04-18. Retrieved 2021-04-25.
- ^ "The Study of Earth as an Integrated System". NASA. Archived from the original on 2016-11-02. Retrieved 2021-05-20.
- ^ Myhre, G.; Highwood, E.J.; Shine, K.P.; Stordal, F. (1998). "New estimates of radiative forcing due to well mixed greenhouse gases". Geophysical Research Letters. 25 (14): 2715–8. Bibcode:1998GeoRL..25.2715M. doi:10.1029/98GL01908. S2CID 128895348.
- ^ Huang, Yi; Bani Shahabadi, Maziar (28 November 2014). "Why logarithmic?". J. Geophys. Res. Atmos. 119 (24): 13, 683–89. Bibcode:2014JGRD..11913683H. doi:10.1002/2014JD022466. S2CID 129640693.
- ^ Zhong, Wenyi; Haigh, Joanna D. (27 March 2013). "The greenhouse effect and carbon dioxide". Weather. 68 (4): 100–5. Bibcode:2013Wthr...68..100Z. doi:10.1002/wea.2072. ISSN 1477-8696. S2CID 121741093.
- ^ IPCC WG-1 Archived 13 December 2007 at the Wayback Machine report
- ^ Etminan, M.; Myhre, G.; Highwood, E. J.; Shine, K. P. (2016-12-27). "Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing". Geophysical Research Letters. 43 (24): 12, 614–12, 623. Bibcode:2016GeoRL..4312614E. doi:10.1002/2016gl071930. ISSN 0094-8276.
- ^ Gavin Schmidt (2010-10-01). "Taking the Measure of the Greenhouse Effect". NASA Goddard Institute for Space Studies - Science Briefs. Archived from the original on 2021-04-21. Retrieved 2021-05-24.
- ^ "It's Water Vapor, Not the CO2". American Chemical Society. Archived from the original on 2021-05-11. Retrieved 2021-05-20.
- ^ Lacis, Andrew A.; Schmidt, Gavin A.; Rind, David; Ruedy, Reto A. (15 October 2010). "Atmospheric CO2: Principal Control Knob Governing Earth's Temperature". Science. 330 (6002): 356–359. doi:10.1126/science.1190653. PMID 20947761. S2CID 20076916.
- ^ Gregg Kopp; Judith L. Lean (2011-01-14). "A new, lower value of total solar irradiance: Evidence and climate significance". Geophysical Research Letters. 38 (1): n/a. Bibcode:2011GeoRL..38.1706K. doi:10.1029/2010GL045777. S2CID 8190208.
- ^ "Solar Radiation and Climate Experiment". University of Colorado, Laboratory for Atmospheric and Space Physics. Archived from the original on 2021-05-19. Retrieved 2021-05-15.
- ^ "TSIS-1 Mission Overview". NASA. 28 November 2017. Archived from the original on 2021-07-18. Retrieved 2021-05-20.
- ^ a b Gregg Kopp (2014-04-24). "Solar variability, solar forcing, and coupling mechanisms in the terrestrial atmosphere". Journal of Space Weather and Space Climate. 4 (A14): 1–9. Bibcode:2014JSWSC...4A..14K. doi:10.1051/swsc/2014012. Archived from the original on 2021-05-06. Retrieved 2021-05-24.
- ^ a b Sophie Lewis (2021-01-02). "Earth reaches perihelion, closer to the sun than any other day". CBS News. Archived from the original on 2021-05-24. Retrieved 2021-05-24.
- ^ "The Seasons, the Equinox, and the Solstices". National Weather Service. Archived from the original on 2021-05-24. Retrieved 2021-05-20.
- ^ a b Claus Fröhlich & Judith Lean (2004-12-01). "Solar radiative output and its variability: evidence and mechanisms". The Astronomy and Astrophysics Review. 12 (4): 273–320. Bibcode:2004A&ARv..12..273F. doi:10.1007/s00159-004-0024-1. S2CID 121558685. Archived from the original on 2021-05-25. Retrieved 2021-05-24.
- ^ David H. Hathaway (2015-09-21). "The Solar Cycle" (PDF). Living Reviews in Solar Physics. 12 (12): 4. arXiv:1502.07020. Bibcode:2015LRSP...12....4H. doi:10.1007/lrsp-2015-4. ISSN 1614-4961. PMC 4841188. PMID 27194958. Archived (PDF) from the original on 2021-05-23. Retrieved 2021-05-24.
- ^ Lean, Judith; Rind, David (1999-01-01). "Evaluating sun–climate relationships since the Little Ice Age". Journal of Atmospheric and Solar-Terrestrial Physics. 61 (1–2): 25–36. Bibcode:1999JASTP..61...25L. doi:10.1016/S1364-6826(98)00113-8. ISSN 1364-6826. Archived from the original on 2021-05-10. Retrieved 2021-05-24.
- ^ a b c Gareth S. Jones, Mike Lockwood, Peter A. Stott (2012-03-16). "What influence will future solar activity changes over the 21st century have on projected global near-surface temperature changes?". Journal of Geophysical Research: Atmospheres. 117 (D5): n/a. Bibcode:2012JGRD..117.5103J. doi:10.1029/2011JD017013.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b Alan Buis (2020-02-27). "Milankovitch (Orbital) Cycles and Their Role in Earth's Climate". NASA Jet Propulsion Laboratory. Archived from the original on 2020-10-30. Retrieved 2021-05-24.
- ^ a b Marie-France Loutre, Didier Paillard, Françoise Vimeux, Elsa Cortijo (2004-04-30). "Does mean annual insolation have the potential to change the climate?". Earth and Planetary Science Letters. 221 (1–4): 1–14. Bibcode:2004E&PSL.221....1L. doi:10.1016/S0012-821X(04)00108-6. Archived from the original on 2021-05-14. Retrieved 2021-05-24.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ J. Laskar (1989-03-16). "A numerical experiment on the chaotic behaviour of the Solar System". Nature. 338 (6212): 237–238. Bibcode:1989Natur.338..237L. doi:10.1038/338237a0. S2CID 4321705. Archived from the original on 2021-03-11. Retrieved 2021-05-24.
- ^ a b "NASA Solar System Exploration - Our Sun". NASA. Archived from the original on 2021-05-15. Retrieved 2021-05-15.
- ^ "There Is No Impending 'Mini Ice Age'". NASA Global Climate Change. 2020-02-13. Archived from the original on 2021-05-28. Retrieved 2021-05-28.
- ^ "What Is the Sun's Role in Climate Change?". NASA. 2019-09-06. Archived from the original on 2021-05-26. Retrieved 2021-05-24.
- ^ Bida Jian, Jiming Li, Guoyin Wang, Yongli He, Ying Han, Min Zhang, and Jianping Huang (2018-11-01). "The Impacts of Atmospheric and Surface Parameters on Long-Term Variations in the Planetary Albedo". Journal of Climate. 31 (21): 8705–8718. Bibcode:2018JCli...31.8705J. doi:10.1175/JCLI-D-17-0848.1. S2CID 133651731.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b c d e f Graeme L. Stephens, Denis O'Brien, Peter J. Webster, Peter Pilewski, Seiji Kato, Jui-lin Li (2015-01-25). "The albedo of Earth". Reviews of Geophysics. 53 (1): 141–163. Bibcode:2015RvGeo..53..141S. doi:10.1002/2014RG000449. S2CID 12536954. Archived from the original on 2021-05-24. Retrieved 2021-05-24.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b "Measuring Earth's Albedo". NASA Earth Observatory. 21 October 2014. Archived from the original on 2021-05-06. Retrieved 2021-05-15.
- ^ "Landsat Science Team's Crystal Schaaf Discusses Albedo, Its Importance, and How It Can Affect Climate". U.S. Geological Survey. 2021-01-12. Archived from the original on 2021-05-24. Retrieved 2021-05-24.
- ^ Robock, Alan (2000-05-01). "Volcanic eruptions and climate". Reviews of Geophysics. 38 (2): 191–219. Bibcode:2000RvGeo..38..191R. doi:10.1029/1998RG000054. S2CID 1299888.
- ^ "The NOAA Annual Greenhouse Gas Index (AGGI)". NOAA.gov. National Oceanic and Atmospheric Administration (NOAA). Spring 2023. Archived from the original on 24 May 2023.
- ^ "The NOAA Annual Greenhouse Gas Index - Figure 5". NOAA. 2020. Archived from the original on 2009-08-25. Retrieved 2009-07-30.
- ^
CFC-113, tetrachloromethane (CCl
4), 1,1,1-trichloroethane (CH
3CCl
3); hydrochlorofluorocarbons (HCFCs) 22, 141b and 142b; hydrofluorocarbons (HFCs) 134a, 152a, 23, 143a, and 125; sulfur hexafluoride (SF
6), and halons 1211, 1301 and 2402) - ^ Hansen, J.E.; et al. "GISS Surface Temperature Analysis: Analysis Graphs and Plots". Goddard Institute for Space Studies, National Aeronautics and Space Administration. Archived from the original on 2018-01-18. Retrieved 2018-01-25.
- ^ Schwartz, Stephen E.; Charlson, Robert J.; Kahn, Ralph A.; Ogren, John A.; Rodhe, Henning (2010). "Why hasn't Earth warmed as much as expected?" (PDF). Journal of Climate. 23 (10) (published 15 May 2010): 2453–64. Bibcode:2010JCli...23.2453S. doi:10.1175/2009JCLI3461.1. S2CID 14309074. Archived (PDF) from the original on 8 March 2021. Retrieved 24 September 2019.
- ^ Stocker, Thomas (24 March 2014). Climate change 2013 : the physical science basis : Working Group I contribution to the Fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press. ISBN 978-1-107-66182-0. OCLC 1120509660. Archived from the original on 19 April 2021. Retrieved 18 April 2021. datafile Archived 2017-09-30 at the Wayback Machine
External links[edit]
- United States National Research Council (2005), Radiative Forcing of Climate Change: Expanding the Concept and Addressing Uncertainties, Board on Atmospheric Sciences and Climate
- Small volcanoes add up to cooler climate; Airborne particles help explain why temperatures rose less last decade Archived 2012-10-03 at the Wayback Machine August 13, 2011; Vol.180 #4 (p. 5) Science News
- NASA: The Atmosphere's Energy Budget















