Talk:Monty Hall problem: Difference between revisions
→Focus on the article: new section |
|||
| Line 1,930: | Line 1,930: | ||
::I am not clear exactly what you mean by the word. We can take the W/vS statement to indicate symmetry with respect to door number and goat number by noting that no information is given which breaks this symmetry but this is just the Bayesian understanding of the problem, so why not just say that? [[User:Martin Hogbin|Martin Hogbin]] ([[User talk:Martin Hogbin|talk]]) 12:17, 5 October 2012 (UTC) |
::I am not clear exactly what you mean by the word. We can take the W/vS statement to indicate symmetry with respect to door number and goat number by noting that no information is given which breaks this symmetry but this is just the Bayesian understanding of the problem, so why not just say that? [[User:Martin Hogbin|Martin Hogbin]] ([[User talk:Martin Hogbin|talk]]) 12:17, 5 October 2012 (UTC) |
||
== Focus on the article == |
|||
While I'm sure all this debate is fascinating, could I remind everyone that '''''This is the talk page for discussing changes to the Monty Hall problem article itself. Please place discussions on the underlying mathematical issues on the Arguments page.''''' |
|||
You guys are all starting to sound like a bunch of turkeycocks in a dust up - and this page is not for trying to persuade each other that your own approach to the problem is the right one. Can we return focus on the article. Does it in fact need any changes? Where does it need changes? What changes would make it better. Or do most of the folks here just prefer to keep this endless argument going? --[[User:Elen of the Roads|Elen of the Roads]] ([[User talk:Elen of the Roads|talk]]) 12:31, 5 October 2012 (UTC) |
|||
Revision as of 12:31, 5 October 2012
| This is the talk page for discussing changes to the Monty Hall problem article itself. Please place discussions on the underlying mathematical issues on the Arguments page. If you just have a question, try Wikipedia:Reference desk/Mathematics instead. |
Error: The code letter for the topic area in this contentious topics talk notice is not recognised or declared. Please check the documentation.
| Monty Hall problem is a former featured article. Please see the links under Article milestones below for its original nomination page (for older articles, check the nomination archive) and why it was removed. | |||||||||||||||||||||||||
| This article appeared on Wikipedia's Main Page as Today's featured article on July 23, 2005. | |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| This article is of interest to the following WikiProjects: | |||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||
|
|
This page has archives. Sections older than 14 days may be automatically archived by Lowercase sigmabot III when more than 4 sections are present. |
Jerrywickey says:
++ A far simpler and more intuitive explanation ++
for the solution to the Monty Hall Problem might be needed. Readers struggling with understanding probabilities need an explanation that they can "feel" in their gut. The text below is such and if no one objects or if someone encourages me to do so, I will post it to the page. After all helping readers who consult Wikipedia is and should be contributor's goal.
simple clear intuitive explanation
The chance that the prize door will be chosen from three doors at random is 33% (1/3) But more importantly the choice has a 67% (2/3) chance of being the wrong door. Removing one door does not change that 67% chance that the chosen door is wrong. Even if both other doors were not opened but instead removed, there still remains the same 67% chance that opening the chosen door will reveal it to be empty.
When one other door is opened to reveal it to be empty, new information is added to the system that can be exploited to recalculate the odds that the remaining door is hiding the prize. The chosen door still has a 67% chance of being wrong. That can't change. This implies that the remaining door has only a 33% chance of being wrong while it has a 67% chance not 50% of being the prize door.
The intuitive argument against this is that "removal of one door reassigns the odds for both doors to 50% 50%; not just reassigns the chance for the door not chosen without effecting the odds of the chosen door." The error of this false assumption is easily demonstrated if the number of doors is increased.
The chance that the prize door will be chosen from ten doors at random is 10% (1/10) But more importantly the choice has a 90% (9/10) chance of being the wrong door. Removing eight doors does not change the 90% chance that the chosen door is wrong, but since the removal was selective, removing only empty doors, but not removing the chosen door nor the prize door, it becomes easy to see intuitively that which ever door remains after eight empty doors are removed has a far greater than 50% chance of being the prize door. It doesn't make sense that the prize is just as likely to be behind the chosen door as the last remaining door, because the removal was selective. The original choice was not selective. The remover knew which door held the prize, causing the remover to not remove the prize door while the chooser did not have this knowledge and made his or her choice .
This is because when making the original choice with the information available before any doors were removed, the chosen door was very unlikely to be the correct choice, 90% chance of being wrong. That chance isn't changed by the removal of eight other doors. However, if it is known that all eight removed doors were empty, then the chance that the remaining, unchosen door, is the prize door is very high. Much higher than 50%. It has a 90% chance of holding the prize because the chance of the chosen being wrong is 90%.
Jerrywickey (talk) 18:54, 25 May 2012 (UTC)
- Jerrywickey, please start a new sections after earlier discussions. It is a fact that some editors follow Morgan et al. in claiming that the chance of the door first selected by the guest could be changed by the special behavior of the host in opening a losing door. If he should be extremely biased e.g. to open his preferred door if ever possible, then he can do that in 2/3, but if in 1/3 his preferred door hides the car he then would be forced to open his strictly avoided door, showing that the chance by switching to his preferred but still closed door is max. 1 and the chance of the door first selected by the guest could converge to zero. So there is some desire to first of all show by Bayes' formula that "which one" of his two doors the host has actually opened could be of influence on the probability to win by switching. Please read also the archive of this talk page. --Gerhardvalentin (talk) 19:49, 25 May 2012 (UTC)
- Jerrywickey, your explanation still does nothing for me. I can't '"feel" it in my gut' at all. You remove the wrong doors... and leave 2, it's therefore down to 50/50. But I'm a linguist, not a mathematician. What do I know? Oh yeah... I'm meant to "feel it in my gut". Malick78 (talk) 22:57, 26 May 2012 (UTC)
- Perhaps I can offer some insight into this. For some time I have been incorporating this into some training (on an unrelated topic) that I have been giving to scientists and engineers. Here is what I do:
- First I ask anyone who has heard of this problem before to silently watch what I am about to do.
- Then I hand out the (fully unambiguous, mathematically explicit version of the standard problem) Krauss and Wang description from this page, in writing, and ask everyone to read it and put their answers on paper (unsigned) and hand it back. I count the answers and write that on a whiteboard. Usually, "no advantage to switching" is way ahead.
- Then I open it up for discussion. There is always a spirited debate with much certainty on both sides. I have never seen anyone, ever, change their position based upon hearing arguments from the other side. Ever.
- Then I prove who is right using the cups simulation described on the page, moving to ten cups if needed. In my experience, this is the best way to convince engineers. (I use toy cars and toy goats - had to buy ten packages of toy barnyard animals at the 99 cent store to get the goats.) I have also found that playing with me as Monty and someone from the audience as the contestant and having the contestant never switch if he thinks there is no advantage to switching works best. I have never had anyone remain unconvinced that they should switch after choosing cups and keeping score.
- My point in the training is that actual data trumps logical argument, no matter how sure you are that you are right. but here is an interesting thing I have observed: a significant number of those who got it wrong and argued vigorously that they were right blame the problem description. and it doesn't matter whether I presented the Vos Savant version or the Krauss and Wang version! Just as something about the human mind makes engineers get the wrong answer and defend it to the end, something about the human mind makes engineers reject the notion that they were wrong and blame the problem description. We tend to "feel" things that are not true. --Guy Macon (talk) 02:48, 27 May 2012 (UTC)
- Excellent work Guy, perhaps you should try to get it published somewhere so that we can report it here. It is also a sad fact that not one person has changed their mind on the disputed issues here. Martin Hogbin (talk) 13:24, 27 May 2012 (UTC)
- Jerrywickey, your explanation still does nothing for me. I can't '"feel" it in my gut' at all. You remove the wrong doors... and leave 2, it's therefore down to 50/50. But I'm a linguist, not a mathematician. What do I know? Oh yeah... I'm meant to "feel it in my gut". Malick78 (talk) 22:57, 26 May 2012 (UTC)
- Points well taken.
- However, removing only empty doors is an assumption of the riddle. Any examination which explores other possibilities is not an exploration of the Monty Hall Problem. If the prize could be removed, the Mony Hall game makes no sense. It is this selectivity on which the solution must be based. If you didn't "feel" the one before then try this.
- When making the original choice one has only a one third chance of choosing the winning door. What is more important to understanding the problem, however, is that also means that the choice has a two thirds chance of being wrong. No later event, removing one door included, changes those odds. After the removal of one door, or any other event aside from exposing the winning door, the chance the chosen door is wrong remains two thirds. Nothing can change that.
- With the removal of one door only one other door remains. Since the winning door must be one of the two as an assumption of the riddle, then the chance that the chosen door is wrong is still two thirds, which implies that the chance that the single remaining door could be wrong is only one third. Meaning that the remaining, unchosen door, has a two thirds chance, not fifty fifty, of being the winning door.
- Some might argue that "removing one door can not change the odds for one of the remaining doors, but not the other. Just designating one door as chosen doesn't give it preferential treatment." This is an erroneous assumption. The error becomes intuitively obvious if more than three doors are used.
- If one were choosing from a hundred doors instead of just three, then the chance that the chosen door is wrong is 99 out of 100. Removing 98 doors does not change that probability. It does not give the chooser any more confidence that his chosen door is correct, but he does intuitively realize that the door he chose still has a ninety nine percent chance of being wrong. He also intuitively realizes that since only wrong doors were removed the one single door that remains has a much greater chance, much greater than 50% 50%, of being the winning door. How much? 99/100 Why? Because the one he chose had and still has a 99/100 chance of being wrong. After all, it was selected from a hundred choices. The selectivity of the removal of 98 wrong doors changes the odds for the one remaining door, but not for the chosen door. — Preceding unsigned comment added by Jerrywickey (talk • contribs) 13:59, 27 May 2012 (UTC)
- Curiously, you are both wrong. Jerywickey, you say, 'When making the original choice one has only a one third chance of choosing the winning door. ... No later event, removing one door included, changes those odds'. That is not necessarily true, although under the standard assumptions made about the problem it is true that the odds do not change.
- To take a really obvious example first, suppose that Monty tells you that the car is behind door number 2. The odds change then for sure.
- Now consider a more interesting and instructive case. Suppose that Monty does not know where the car is and opens one of the two doors that you have not chosen at random and it happens to reveal goat. What are the odds then that the car is behind the door that you originally chose?
- The important point to consider is whether any event that occurs after you have chosen your door but before you decide whether to swap or not gives you any information about the whereabouts of the car. Under the standard assumptions you know the Monty will reveal a goat, because he must do under the rules, you also gain no information from his choice of door when you happen to have originally chosen the door hiding the car because the host must choose randomly between the two doors available to him under the standard assumptions in that case. So, the host opening, say door 3 to reveal a goat tells you nothing you do not already know, thus your original odds of having chosen the car cannot change. In the standard version of the problem you have a 2/3 chance of winning if you swap. Martin Hogbin (talk) 16:02, 27 May 2012 (UTC)
Thank you Martin, you are absolutely correct, and you clearly articulate the dilemma of the article: -- Not sure who left this comment
So, what difference does it make if you get a new choice each time a door is opened? Sure, the odds are 1-in-3 when you have three doors. But when you get a new choice from 2 doors, the odds are even. So why do people even talk about the door that isn't part of the problem anymore? I am faced with a new choice that is only about two doors. Why so much ink spilled for a simple choice? -- Avanu (talk) 14:15, 9 September 2012 (UTC)
Conditional or Simple solutions for the Monty Hall problem?
|
Should the Monty Hall problem page be edited according to the 'Simple' or the 'Conditional' solutions? --Guy Macon (talk) 21:18, 6 September 2012 (UTC)
The aim of this RfC is to resolve a longstanding and ongoing conflict involving multiple editors concerning the relative importance and prominence within the Monty Hall problem article of the 'simple' and the more complex 'conditional' solutions to the problem.
The 'simple' solutions do not consider which specific door the host opens to reveal a goat (see examples here and here). The 'conditional' solutions use conditional probability to solve the problem in the case that the host has opened a specific door to reveal a goat (see example here).
One group of editors considers that the 'simple' solutions are perfectly correct and easier to understand and that the more complex, 'conditional' solutions are an unimportant academic extension to the problem.
The other group believes that the 'simple' solutions are essentially incomplete or do not answer the question as posed and that the 'conditional' solutions are necessary to solve the problem. Both sides claim sources support their views.
That argument is unlikely to ever be resolved but two proposals have been made to resolve the dispute. Both proposals aim to give equal prominence and weight to the two types of solution.
One of the points of contention is whether either of the proposals below violates any Wikipedia policies and guidelines (in particular WP:NPOV, WP:NOR, WP:V, WP:WEIGHT, WP:EP, MOS:JARGON, WP:MOSINTRO, WP:MTAA and WP:OPINION). See the individual editor's comments below for arguments on both sides of this issue.
Proposal 1 is for the initial sections including 'Solution' and 'Aids to understanding' to be based exclusively on 'simple' solutions (with no disclaimers that they do not solve the right problem or are incomplete) then to follow that, for those interested, with a section at the same heading level giving a full and scholarly exposition of the 'conditional' solutions.
Proposal 2 is for the article to include in the initial 'Solution' section both one or more 'simple' solutions and an approachable 'conditional' solution (showing the conditional probability the car is behind Door 2 given the player picks Door 1 and the host opens Door 3 is 2/3) with neither presented as "more correct" than the other, and to include in some later section of the article a discussion of the criticism of the 'simple' solutions.
Proposal 1, Proposal 2, or Neither? (or Abstain.)
Considering all Wikipedia policies and guidelines, should the Monty Hall problem page be edited according to Proposal 1, Proposal 2, or neither? Abstain is also an acceptable answer.
Note: Because prior attempts to resolve this conflict have resulted in long discussions with many endless back and forth comments, please place any responses to other editor's comments in your own "Comments from user X" section and limit your comments to no more than 500 words. If you wish to have a threaded discussion, feel free to start a new section on this talk page but outside of this RfC or on your own talk page.
Comments from Elen of the Roads
(327 of 500 words)
Note: I am assigning Neither to the comments below. If this is incorrect, please indicate "Proposal #1", "Proposal #2", or "Abstain". --Guy Macon (talk) 20:16, 20 September 2012 (UTC)
- Neither is my starting position on this - I believe the dichotomy is artificial and the structure of the article needs looking at in a different way. Being an Arb (lol) I would say Proposal #1 is a second choice, with Proposal #3 being an oppose.--Elen of the Roads (talk) 14:04, 21 September 2012 (UTC)
Commenting so there's no danger of ever being asked to close this, or PD a rerun Arbcom !! Seriously, the Monty Hall problem was originally presented as a parlour teaser for folks with a bit of mathematical knowledge who were familiar with game shows like Opportunity Knocks. The question was - should the contestant stick with his door or switch, and the utterly non-intuitive answer is that he should always switch, regardless of whether Monty knows where the goat is, whether Monty prefers the red door, or what Monty had for breakfast. The article has to present the puzzle and the answer in this light first. The conditional mathematicians contentions that the answer has the potential to be different if Monty has had his Weetabix must come separated, later in the article, for those who have an interest in such things. --Elen of the Roads (talk) 23:02, 6 September 2012 (UTC)
@Guy Macon - I've always liked the ten goats explanation. Surely the actual, unspoken condition is that Monty always knows where the goats are. Everyone takes this as read, because they extrapolate from how real game shows work, and if he opened the door on the car, the show will end ten minutes early. All of the other potential conditions - whether Monty opens the door on the left first, or prefers the blue door, are not part of the original problem, and do not affect the solution to the original problem. --Elen of the Roads (talk) 15:29, 7 September 2012 (UTC)
See section below Talk:Monty_Hall_problem#Does_this_version_work. Uses the approach taken in Zebra Puzzle, ie that it is the statement of the puzzle that is faulty, not the solution. Does this remove the divide? It is not true (for any given value of true) that "all the simple solutions are wrong" but it is true that Vos Savant's statement of the puzzle is incomplete, and anything claiming to be a solution to that version of the puzzle is incomplete if it does not highlight the missing assumption. --Elen of the Roads (talk) 14:18, 15 September 2012 (UTC)
Comments from Glrx
(63 of 500 words)
Neither. I'll second Elen's comments. Unfortunately, this article has taken a mathematician's viewpoint much too seriously. For WP, it is an interesting puzzle and not a graduate level exercise in probability/statistics. The simple stuff must be first and the academic views much later. There should not be an overly precise description of the problem at the beginning. I'll explain the neither vote later. Glrx (talk) 23:40, 6 September 2012 (UTC)
Comments from Ebe123
(6 of 500 words)
Neither. I echo Elen on this. ~~Ebe123~~ → report 00:50, 7 September 2012 (UTC)
Comments from czarkoff
(197 of 500 words)
Proposal 1. Though I share the view by Elen of the Roads that the first things to present readers are the problem and the counter-intuitive solution, this is exactly the purpose of the lead section. I reject the notion that the math is taken too seriously in this article – it is the subject, not a side discussion, so it should be presented and explained in the article's body. By analogy with WP:WEIGHT I would present the material to the reader in order of complexity increase, so that the solutions involving less logical operations or iterations are placed on top of more complex material.
That said, I would suggest to move the current lead section (I generally prefer the word "lede" over the phrase "lead section", but in this article it is indeed a magazine's lede, not a summary one would expect) into a first named section, which I would call "Background"; in the lead section I would overview the problem and state the solution in the first paragraph. In the second paragraph I would provide the brief descriptions of the solutions, as general as possible. The proposal 1 should be implemented in sections 2 and onward. — Dmitrij D. Czarkoff (talk•track) 01:48, 7 September 2012 (UTC)
Comments from Noleander
(187 of 500 words)
Neither. Splitting the solutions into Simple and non-Simple seems like it would just perpetuate the underlying conflict for several more years. Is it not possible to simply enumerate the several different approaches to the problem? I suggest:
- Just list the approaches, one after another. The approaches could be grouped based on similarity, but no need to name them as "Simple" or not.
- There is no reason to treat some approaches (e.g. the so-called simple ones) as "better" than others, more deserving of being in the lead. The lead should summarize all the approaches (or at least all classes of approches).
- Consider using the word "approach" instead of "solution", to indicate that some solutions may not be considered to be full or accurate.
- Emphasize (earlier) that the analysis depends heavily on the host's behavior (e.g. whether the host deliberately avoids the car when opening doors, vs. opening random doors) ... I know that is in the article body already, but it should be emphasized in the lead.
Bottom line: don't divide the approaches into two categories that could perpetuate the civil war. (Maybe this is Option 2?). --Noleander (talk) 02:28, 7 September 2012 (UTC)
Comments from ChrisGualtieri
(152 of 500 words)
Neither - Clearly the problem and show's ORIGINAL problem diverge into a thought experiment along the way. First, go with the simple answer in no uncertain terms, with the most prevalent rules without behavior such as 'evil or angelic' Monty. The problem as classically postulated. Then get into the counters and thought process behind that. Once that is done, the 'complex' matter can be dealt with separately assuming X or X case, but by all means, each of these have to be explicit in their terms about the ideology (and not math) which goes into it. I'll end up doing it myself if this can't get resolved. Either way... this conflict is going to end shortly. ChrisGualtieri (talk) 02:31, 7 September 2012 (UTC)
- Additional note: Crunching the data seems to support that. If things get really long winded we can probably collapse complicated sections. Seems to be quite a lot of material after all. ChrisGualtieri (talk) 03:05, 7 September 2012 (UTC)
Comments from Rick Block
(468 of 500 words)
Proposal 2 This is a POV dispute, plain and simple.
POV 1) "Simple" solutions are the "right" way to solve the problem.
POV 2) The "right" solution is to compute the conditional probabilities the car is behind Door 1 and Door 2, given the player has selected Door 1 and the host has opened Door 3.
Proposal 1's "compromise" is to give "simple" solutions far greater WP:WEIGHT, and structurally endorse POV 1. Proposal 2 gives equal WEIGHT and endorses neither POV, remaining strictly NPOV.
Regarding WEIGHT: many, many sources present "simple" solutions. But the vast majority of these are popular, not academic, sources and many of them uncritically parrot vos Savant's ("simple") solution. Within the field of probability, the textbook solution (literally and figuratively, meaning both appears in numerous textbooks and is completely standard) is to compute the conditional probabilities. This solution, presented by the preponderance of sources in the most relevant academic field, should have at least equal WEIGHT to any other.
Regarding STRUCTURE: there is a controversial, but by no means fringe, POV expressed by numerous sources, e.g. [1] [2] [3] [4] [5] [6], criticizing "simple" solutions. To be NPOV the article must not endorse this POV (as it arguably did at one point, which is perhaps the actual source of much of the conflict). But it equally must not endorse the opposite view that "simple" solutions are universally accepted as "perfectly correct". Proposal 1 does exactly this, presenting "simple" solutions as "the solution" ("with no disclaimers that they do not solve the right problem or are incomplete") and relegating "conditional" solutions to a later section "for those interested". This creates a strong structural POV suggesting the "simple" solutions are true and undisputed, which (hardly coincidentally) exactly matches the POV of certain editors involved in this conflict.

Furthermore, the claim "simple" solutions are easier to understand is at best dubious. Krauss and Wang say 97% of their test subjects drew an image of the (conditional!) situation where the player picked Door 1 and the host opened Door 3 (like the image to the right), and that once formed this image "prevents the problem solver from gaining access to the intuitive [simple] solution". We know vos Savant's solution was not convincing (she received thousands of letters after publishing it). As Eisenhauer says "what could and should have been a correct and enlightening answer to the problem was made unconvincing and misleading."
The resolution here is simple. Follow Wikipedia's core content policy of NPOV. Include BOTH "simple" and approachable "conditional" solutions in an initial "Solution" section, presenting both as equally valid. Discuss the differences between these types of solutions in a later section "for those interested". I.e. Proposal 2. -- Rick Block (talk) 04:30, 7 September 2012 (UTC)
Comments from Trovatore
(209 of 500 words)
Note: I am assigning Abstain to the comments below. If this is incorrect, please indicate "Proposal #1", "Proposal #2", or "Neither". --Guy Macon (talk) 20:16, 20 September 2012 (UTC)
The problem with Elen's take is that there is no such thing as an answer independent of Monty. There are ("simple") answers that are based on certain assumptions of neutrality regarding Monty's strategy, assumptions that are arguably not unnatural, but are certainly not the way Monty in fact behaved.
This is not "the mathematician's view"; this is simply the fact.
That said, I think a mixture of Proposal 1 and Proposal 2 is probably appropriate. The bulk of the coverage has indeed been on the "simple" answers, with all their unexamined assumptions, and it should probably come first. However, to leave the qualification out of the lead paragraph is not reasonable. To fail to point out the hidden (and certainly inaccurate, compared to the real-life model) assumptions, is to be just plain incorrect. --Trovatore (talk) 09:32, 7 September 2012 (UTC)
- Hope this is OK since I have space left. I'd like to respond to Guy Macon's point below about simulation. There is no mystery about what a given simulation will show. The question is, how do you make your simulated Monty behave? If for example you make him always show an unchosen empty door, then yes, you will get the "simple" answer. But the statement of the problem gives no warrant at all for that choice. --Trovatore (talk) 17:37, 7 September 2012 (UTC)
Comments from Guy Macon
(420 of 500 words)
Neither. The article should start with a description of what the MHP is (using the Krauss and Wang version) and the "better to switch" question without (in the lead) saying what the answer is or why. Just present the problem in the lead and let the reader decide what the answer is.
Next should be a history section, still not saying what the answer is but instead documenting what various letter writers to the American Statistician wrote in 1975, Marilyn vos Savant's answer, the answer of the 1,000 PhDs who disagreed with her, etc. The key here is not to say what the answer is, but rather to document (with citations) what various notable people say it is.
Next should be a section on simulation starting with clear instructions on how to do the simulation yourself using plastic cups (better than playing cards; goats are indistinguishable). This has a huge advantage over the other "solutions" and "aids to understanding", which often end up with two people talking past each other, each convinced that they understand the problem and have the solution and that the other person isn't thinking clearly. Again, we shouldn't give the answer but rather should report (with citations) on the result of people running simulations. One big advantage of a physical simulation (or a computer simulation that you wrote yourself) is that Monty's behavior must be defined for it to work, and alternative Monty behaviors can be easily tested.
Finally, after the Lead, History and Simulation sections, the other approaches should have a section or sections, with simple first followed by conditional. Here, for the first time, we should reveal what Wikipedia says the answer is, along with answers to different but related questions.
I have gone through physical simulations many times (mostly with engineers and scientists, and with ten cups if they assert that there is no advantage to switching even if there are ten cups), and have found it to be a reliable way to convince even the most stubborn that switching is better, and to do so in a way that no amount of verbal argument can accomplish. Furthermore, watching "Monty" select which eight cups to turn over leads to understanding -- clearly "Monty" is choosing cups with goats and avoiding the car. This also makes it easy to understand variations like "random choice Monty", where sometimes he opens the door on the car and the player loses immediately without being given a choice to switch. --Guy Macon (talk) 19:04, 8 September 2012 (UTC)
Comments from Martin Hogbin
(381 of 500 words)
I am the proposer of Proposal 1.
Firstly let me say that I completely agree with Elen of the roads that, 'Monty Hall problem was originally presented as a parlour teaser for folks with a bit of mathematical knowledge who were familiar with game shows...', and I and many other editors have long argued that the article should concentrate on this aspect. However there are some who believe that the more esoteric mathematical aspects are important and who have pressed for what they see as the only 'correct' solutions' to dominate this article. That battle has raged for years with no sign of resolution and my proposal is a compromise which should be acceptable to all.
My proposal makes no claim that any one solution is the 'correct' one and I am suggesting that we give both types of solution equal weight but:
First, we treat the problem as a simple mathematical puzzle and give the 'simple' solutions to this puzzle. This is what 90% of our readers want. We need to concentrate on making the solutions convincing and the explanations understandable. There are two things that fool most people: that the answer is 2/3 and not 1/2, and that it matters that the host knows where the car is. Once we have fully resolved these two issues most readers will be satisfied.
After we have done that, for the remaining 10% of readers and for mathematical completeness we should mention that some sources say that the simple solutions are defective in some way. We should then have a full and scholarly discussion of that claim, based on reliable sources.
- Glrx says 'The simple stuff must be first and the academic views much later'. Yes! That is exactly what I am proposing.
- Final attempt to explain my compromise proposal.
- Like most others, I think the 'simple' solutions are the best and that they should be given more weight in the article, with the 'conditional' solutions being treated as an academic sideline. However, in the interests of peace and cooperation, I am suggesting that we give both equal prominence in the article but that we start the simple (even if there is some loss of rigour) and then explain the details later, just as most good text books and encyclopedia articles do. — Preceding unsigned comment added by Martin Hogbin (talk • contribs) 14:30, 12 September 2012 (UTC)
Comments from Richard Gill
(491 of 500 words.)
Neither. The important distinction is between informal, heuristic, verbal solutions which anyone can understand, and formal solutions appropriate within some academic context. If there are simple verbal equivalents of solutions based on conditional probability then they can appear early in the article alongside other simple solutions.
Marylin vos Savant's question was "should you switch?", not "what is the (this, that or another) probability?" What most readers need is to gain the intuition through being shown how to see the problem from another angle, that switching offers a huge advantage. MHP is carefully formulated so as to throw the newcomer off track. It's a trick question. It's fun. A classic brainteaser. Conditional probability is justs one of many ways to solve the problem, after just one of many possible formalizations of it has been chosen.
Another important distiction for me is that between an argument being correct and incorrect. I see no need at all that the article should reproduce arguments which are logically wrong. With careful wording, we can stick to the Truth. Richard Gill (talk) 13:44, 27 September 2012 (UTC)
Comments from Gerhard Valentin
(486 of 500 words)
Proposal 1. For the reader, it's easy to follow that "any group" of two doors has double chance to hide the prize, compared to one single door. The tricky story tells a brilliant honest puzzle. It is not so much important what is *the* original question and its "possible" ambiguity, but it is on the certainly *intended* paradox of a *confidential* host who observes *secrecy* regarding the car-hiding door in that one-time problem. — It is on helping people, *by modern reliable sources*, to decode and understand the puzzle.
- The charm of the world famous paradox: Two still closed doors, one door hiding the prize for sure, the other door hiding a nullity for sure,
but – in one special given perspicuous scenario as per Krauss and Wang, Henze and many others – the chances are not 1/2:1/2,
but the chance of the door first selected by the guest is and remains exactly 1/3 in each and every game,
while the chance of the still closed door offered by the host is exactly 2/3 in that plausible and honest scenario.
The paradox can be decoded by careful evaluation, by game theory, principle of dominance and other approaches as per the sources, that all say that “staying” forever will diminish your probability to win the prize.
The article first should show the common assumptions: All doors are initially equally likely to hide the car in this one-time problem.
The door selected by the player has 1/3 chance, and the group of unselected doors, although there is at least one goat behind, has 2/3 chance to hide the car. And Monty, observing secrecy regarding the car-hiding door, is equally likely to open either of his two doors if he should have a choice, in intentionally having to reveal a goat. By this *symmetry* it is unimportant which one of his doors the host has opened, specific door numbers is irrelevant. The player's initial choice still hides the car with probability 1/3, and the other door left closed by the host therefore has probability 2/3 to hide the car in this one-time problem.
- This common and well known honest scenario (*secrecy*) should be shown first, together with a Bayes' theorem in the "posterior odds = prior odds times likelihood" version.
And then in contrast, as an eye-opener, immediately followed by the *strange variant* of a forgetful host who is showing the car in 1/3 by just randomly opening one of his two doors, deleting the probability to win by switching in that 1/3, while in the remaining 2/3 ("goat:car" and "car:goat"), the chance of both still closed doors is 1/2:1/2 then, as per the most intuitive common appraisal.
Conditional probability theory is not "needed" to decode the paradox. Show in later sections that the MHP is often used in textbooks and in teaching conditional probability theory, with adventuresome presumptions. What matters most is a clear structure of the article. Gerhardvalentin (talk) 14:26, 21 September 2012 (UTC)
Comments from Tom Hulse
(484 of 500 words)
Proposal 2
I'm sorry Guy Macon, but I really think you should scrap this whole Rfc and start again. You've overestimated our group ability to understand what a "conditional solution" is. :) You have two groups arguing past each other on two very different questions. Comments from Elen of the Roads highlight the misunderstanding. I don't mean to pick on you Ellen, but several are following you when you believe that a "conditional solution" involves one of the tortured conditions to make the traditional "yes-you-should-switch" answer wrong. No. Instead, a conditional solution still arrives at the same yes-switch answer, but it is reached differently, with conditional probability. It says Marilyn's answer was right but her math explanation to get there was wrong.
So right now all comments from Elen, Grix, Ebe123, czarkoff, ChrisGualtieri, Trovatore, Richard Gill, & Gerhard Valentin should all be disregarded as irrelvant since they don't even understand the basic premise of this Rfc. A conditional solution is using conditional probability to get the same final answer, not changing the conditions to get a different answer.
Once you understand that, read Rick Block's comments for an overview of Proposal 2, and Martin Hogbin's for a review of proposal 1. I switched my view to Proposal 2 actually when reading Martin's idea that we could admit later in the article that the simple solutions may be wrong in their math (though not in their final answer). Wrong is wrong, and the more reliable academic sources have enough weight to at least give them an equal footing, even with the massive numbers of internet parrots that just blindly repeat Marilyn's simple solution.
I do agree with Guy and the others above that the article could also benefit from a little more emphasis on simulation--Tom Hulse (talk) 07:44, 8 September 2012 (UTC)
I'll add Lambian to the long list of users who's comments are 100% irrelevant here and should not be considered, since he, like the others I mentioned, doesn't understand what this Rfc is about. He also thinks Position 2 is about about variations in the conditions of the problem (it's not at all). Boris Tsirelson misunderstands too, commenting about 'starting with the ideal case'. Both simple & conditional solutions start with the IDENTICAL PROBLEM. There is no variations in the conditions. Look more carefully. Ya'll are alsleep, lol! Condtional probability, not conditions in the problem. --Tom Hulse (talk) 07:55, 9 September 2012 (UTC)
Lambian, my opinion on Marilyn's correctness is irrelvant, as is yours. Only sources matter here, and many of the highest quality ones disagree with you, see Rick Block's post with many quality examples. He only asks for parity in discussion because of their quality weight. Regardless, you still don't understand the very premise of this whole Rfc! You refer twice to "variations" in the problem. No, that is not what this Rfc (or Position 2) is about. Please try harder to look closer at what I've said. --Tom Hulse (talk) 09:48, 9 September 2012 (UTC)
Comments from Salix alba
(218 of 500)
Proposal 1 My inclination is to stick with the status quo, this topic has been discussed to death. However I do fid the condition probability section has been poorly written and is confusing. Effort should go into fixing that. Condition probability can be explain better than it is.--Salix (talk): 17:59, 8 September 2012 (UTC)
For all its flaws the Vos Savant explanation gives the gist of the problem and a simple means when the probabilities turn out to be. Before trying for a major overhall work need to be done on expanding the Decision tree section so that readers with only basic statistical background can undersand it. Its not made clear that the tree diagram really has conditional probabilites in it with each branch of the tree representing P(car at location 1 AND host opens door 2) = P(car at location) * P(host opens door 2 | car at location). The formal solution section is just a mass of symbols making it look more complicated than it really is. In has the effect of making the whole section incomprehensible to anyone who is not familier with Bayes theorem. Fix this before going on about the order of presentation.--Salix (talk): 16:19, 15 September 2012 (UTC)
Oh the latest xkcd seems to capture some of the effect of these discussions.--Salix (talk): 16:24, 15 September 2012 (UTC)
Comments from 203.171.197.35
(48 of 500 words)
Proposal 2
Some readers may want just an overview of the problem, but most readers will want a rigorous solution. The so-called "simple solutions" are unconvincing and, at present, the only mathematically rigorous solution in the article is the one based on conditional probability; no way should we downplay that. -- 203.171.197.35 (talk) 01:50, 9 September 2012 (UTC)
Comments from Boris Tsirelson
(73 of 500 words)
I replace my original comments; hope this does not violate the rules of RfC.
Abstain.
The first solution in the article should be the most simple (that is, accessible for the widest possible audience) among all available correct solutions. (Fortunately simple and correct solutions exist!)
And I do not care, whether or not (and to what extent, and in which sense) this solution may be called "conditional", or "unconditional", or both, or neither.
Boris Tsirelson (talk) 15:48, 13 September 2012 (UTC)
Comments from Lambiam
(302 of 500 words)
Proposal 1. In the terminology of User:Martin Hogbin/Monty Hall History, I'm a card-carrying simplist. Let me repeat what I proposed on this talk page on 2 March 2008:
- What about this two-part approach:
- Present the simple solution to the "main version" of the problem, with the least amount of fussing over the problem statement we can get away with to make it into a solution. Also present some other analysis methods of the problem, leading to the same solution. Following these presentations of the solution, briefly discuss unintended interpretations of the problem statement, and the difficulty in ruling them out unambiguously, while referring to a later section on variations.
- Have (like now) a section with variations on the problem, such as those in which the player may know more than in the main version, depending on the host's behaviour.
- The terminology "unconditional solution" is unfortunate. The notion of a "conditional" solution has no meaning for the main problem version. It is only in variations of the main version that conditional issues arise. --Lambiam 08:28, 2 March 2008 (UTC)
I'd like to add that I gave an "unconditional" mathematically solid simple proof on Richard Gill's talk page of a proposition he has dubbed "the Holy Grail of MHP studies", namely that the 2/3 chance of success on switching can't be beaten by any strategy, even if the player's initial choice and the host's choice are not necessarily random. This shows conclusively that the conditionalism is an unnecessary complication. --Lambiam 07:38, 9 September 2012 (UTC)
Tom Hulse wrote: "Marilyn's answer was right but her math explanation to get there was wrong". Well, no, her answer was right and so was her explanation. The simple explanation is perfectly adequate, and we should not torture and confuse the reader with unnecessarily complications, or at least postpone their introduction as long as possible. --Lambiam 09:08, 9 September 2012 (UTC)
Comments from Coffee2theorems
(500 of 500 words)
Proposal 2. I think an approachable conditional solution is doable, if care is taken not to dot every i and cross every t in sight, and maybe starting with a very short introduction to conditional probability and explanation of why it's relevant here (in the vein: if you want to guess a man's height, use statistics for men, not for all people). More sophisticated and rigorous discussion coming in a later section would be in line with WP:UPFRONT.
The problem with the unconditional solutions is that they take considerable liberties with the problem. There are people who are just sophisticated enough to sense the holes in the argument and so fail to be convinced, yet are not sophisticated enough to see how the holes can be mended and the solutions salvaged by the symmetry proof. (concrete example: me when I was in high school)
Those readers need the conditional solutions, and they need to be mentioned before some "aids to understanding section", or the readers will likely go away thinking that the article has no real solutions to offer. Incidentally, for all its simplicity, the symmetry proof is actually more sophisticated than the conditional one. It's the kind of shortcut you can take in a recipe once you know how to cook, not when you're struggling with the basic recipe ("what does it even mean that probabilities can change?!"). -- Coffee2theorems (talk) 10:57, 9 September 2012 (UTC)
Boris: The "conditional proof" is a very straightforward application of the definition of conditional probability, so it can be understood with absolutely minimal prerequisites of probability theory, and the correspondence of the decision tree with the original problem is clear and explicit. It solves the "standard MHP" by directly computing the conditional probability which decision theory says you should compute, brooking no argument and being economical in the amount theory the reader needs to understand. It's also a very standard approach to such problems.
The symmetry argument gives you another way of obtaining the conditional probability, by showing that it is equal to the unconditional probability here. It requires all the same concepts as the proof by direct computation, and more besides. The symmetry proof sections in the article use statistical independence at least. They are also even less clear than the conditional proof sections of the article, and I think the reasoning is fundamentally more sophisticated, and thereby fundamentally less accessible.
The symmetry argument certainly should remain in the article. All I'm saying is that the conditional solution should be presented along with the unconditional solution, not much later in the article. The other proposal where no mention at all of conditional probabilities is made in the main "Solution" section would amount to presenting a lie to children as a full solution, which is clearly undesirable. Most of the "unconditionalists" don't want an "unconditional solution + symmetry argument", they want just the unconditional solution, with any mention of conditional probabilities ("unimportant academic extension") omitted, or as a "compromise" at least hidden as much out of sight as at all possible. -- Coffee2theorems (talk) 03:33, 10 September 2012 (UTC)
Comments from User:Dicklyon
(79 of 500 words)
Proposal 1 – Rick Block's description of the 2 POVs is accurate enough, but his long-time insistence to putting so much weight on the minority POV 2 is what has kept this problem from being resolved. Readers would be better served by presenting the simple POV 1 solution first, without complications. Then, a later section can pay homage to those mathematicians who like to formalize the solution more carefully by appeal to conditional probabilities using conditions that don't matter. Dicklyon (talk) 18:50, 9 September 2012 (UTC)
And of course, as others have noted, every time you invite comment on this article you'll be swamped by the noise by people who don't understand the basics of it and so can't even get close to the question at hand. Dicklyon (talk) 04:44, 11 September 2012 (UTC)
Comments from Nijdam
(331 of 500 words)
Proposal 2, being, as Rick Block explained, in compliance with Wikipedia policy, as both the simple "solutions" and the conditional solution are widely sourced. I find it however very difficult, to accept the sources of the simple "solutions", being evidently mistaken, as reliable sources. I furthermore agree with Rick Block and Tom Hulse in their analysis of the situation. The latter also clearly shows where the problem lies. I would like to add to Proposal 2, at the point where the "conditional solution" is introduced, also the (well sourced) reason (need) for this solution. At this point the simple (vos Savant) solution, may be called an acceptable intuitive explanation.
To Richard Gill I would say: Don't be naive, Vos Savant indeed asked: "Would you switch?" and the direct answer to this question would be: a yes or a no. In that way neither the simple nor the conditional solution is the answer. However, immediately following the answer "Yes, I'll switch" , will be the question "Why?". And it is this 'why' that is the core of the problem. And ... it will not surprise you, the answer is: because the conditional probability ...., etc. Or equivalently, because the odds are ...Nijdam (talk) 19:25, 9 September 2012 (UTC)
- Well Richard I thought you weren't, but you seem to show different here. I did study the sources and strangely enough you yourself immediately admit the interesting question, is the "why". From scientific points of view there may be many ways to approach this question. Our discussion here however is which approach is appropriate for the common Wikipedia reader. I hope you agree with me that the game theoretic approach is not especially suited for this purpose. I, and I hope all the participants here, concentrate on a probabilistic analysis. All that's said here has to be place in that context. I hope you also restrict yourself to this. Even then a lot of missionary work has to be done. And, Richard, the only relevant probabilistic solution is the conditional one. Nijdam (talk) 20:52, 12 September 2012 (UTC)
Comments from Linas
(177 of 500 words)
Note: I am assigning Proposal #1 to the comments below. If this is incorrect, please indicate "Proposal #2", "Neither", or "Abstain". --Guy Macon (talk) 20:16, 20 September 2012 (UTC)
Both :-) Leaning to proposal 1. There is nothing 'mathematically' wrong with the 'simple' explanations, and they should come first. The Bayes Thm variant is a worthy exercise, but wow ... the current article presents it very badly, maximizing the total possible confusion. On first read, my knee-jerk reaction was that it was just flat out wrong; I fought off an urge to edit. I had to re-read the 'conditional' explanation a few times before I got it -- and I do math (& probability) for a living. After this stumbling block, I currently find it dubious that the Bayes variant is somehow 'more correct' -- mostly it just seems 'more difficult', and little else. First and foremost with math topics, explanations must be simple, easy, approachable. Don't confuse dense formulas with mathematical rigor. linas (talk) 16:01, 10 September 2012 (UTC)
BTW: Appeal to authority: I edit little here on WP except for higher math articles. I recognize Trovatore, salix alba, Boris Tsirelson and Lambiam as other regulars in my edit circles, and I find it damning that they all lean to proposal 1. linas (talk) 16:10, 10 September 2012 (UTC)
Joe Decker: Don't confuse counting arguments with frequentism. The 'simple' explanations here are counting arguments, not frequentist arguments. This has nothing to do with Bayesianism; there's no need to invoke 'priors' or 'ill-explicated pre-conditions': if something is 'ill-explicated', then turning it into a Bayesian prior doesn't magically make it 'well-explicated', nor any less 'hidden'. There is nothing wrong with using this problem to illustrate Bayesian-style reasoning, and indeed, the article already has an (opaque) section on this; none of the proposals are suggesting its removal. linas (talk) 18:25, 11 September 2012 (UTC)
Comments from Joe Decker
(113 of 500 words)
Abstain (Previous material struck as I'd misunderstood the question the RfC was asking.) --j⚛e deckertalk 16:25, 15 September 2012 (UTC)
Not including a Bayesian explanation somewhere would make me, Duda and Hart, and Baby Bayes sad. It is a particularly clean way of looking at the problem that is certainly not the simplest explanation, but which tends to get people who use it to the right answer without the sort of ill-explicated preconditions hidden within the simpler and more accessible frequentist explanations. --j⚛e deckertalk 02:05, 11 September 2012 (UTC)
linas: The RfC was a bit unclear, but I gather you're correct that nothing is intending to remove the formal Bayesian argument, which was the primary point I intended to make. --j⚛e deckertalk 19:47, 14 September 2012 (UTC)
Comments from Ningauble
(432 of 500 words)
Neither proposal directly solves the problem which has plagued this article for years: attempting to give due weight to differing POVs has resulted in giving UNDUE weight to the dispute itself – a tempest in a teapot. Proposal 2 is "more worse" in this respect.
Even the most strident and widely cited critic of vos Savant's "simple" solution, (Morgan et al. (1991), cited in the article) acknowledges in a rejoinder (printed in the same issue but not cited in the article) that if it is stipulated that Monty chooses goats uniformly at random (as is stipulated in most subsequent academic literature, and in this very article) then that is a legitimate basis for her "unconditional" solution, as he terms it. Taking their criticism out of this context is POV cherry picking.
More fundamentally, there are different "frequentist" (statistical) and "Bayesian" (information theoretic) interpretations of probability. See §3 of Richard Gill's paper for Statistica Neerlandica,[7] which contrasts these perspectives as applied to MHP. Some who deny the validity of the "simple" solutions appear to be either unaware of this difference or to be dogmatic about only one being the "true" meaning of "probability". This epistemological distinction is probably too abstruse for the general readership of this article, and is seldom directly addressed in the literature on MHP. Presenting them as conflicting views rather than complementary approaches unduly makes a mountain out of a molehill. ~ Ningauble (talk) 00:41, 12 September 2012 (UTC)
- Re. Rick Block's six examples of sources criticizing "simple" solutions: [1] as discussed above, Morgan et al. (1991) is cherry picked; [2] Gillman (1992) says it depends on Monty's selection strategy, but the current "standard" problem specifies uniform random selection; [3] Eisenhauer (2000) bases his criticism on ambiguity about Monty's behavior, long since resolved by the "standard" problem; [4] Rosenthal (2005a) explicitly states that the "simple" solution is correct, and only criticizes it for not being general enough to evaluate variant host behaviors; [5] Grinstead & Snell (2006) claim to prove that the "simple" solution does not answer the equal-goat-frequency problem by showing that it fails for the unequal-goat-frequency problem, which is simply non sequitur; and [6] Lucas et al. (2006) say that the conditional probability method handles a broad class of variant host behaviors, and do not at any point say the "simple" solution to the "standard" problem is incorrect.
Taking these sources as expressing the POV that the "simple" solutions are incorrect is a grossly distorted reading of what the sources actually say. If any of these "criticisms" of solutions merit inclusion at all, they must be contextualized by reference to the questions to which they apply. ~ Ningauble (talk) 01:08, 12 September 2012 (UTC)
Comments from User:Jouster
(162 of 500 words)
Note: I am assigning Abstain to the comments below. If this is incorrect, please indicate "Proposal #1", "Proposal #2", or "Neither". --Guy Macon (talk) 20:16, 20 September 2012 (UTC)
Object Strongly to this Being an RfC—Wikipedia is not a democracy, principles of mathematics are not subject to being voted upon, and articles should be written in the way that best communicates the most correct information to the widest possible audience. If anyone does not support the implementation of these guidelines, they should discontinue editing the article. If there's a genuine desire to reach this, on the other hand, then a scientific approach is easiest adopted: find a trusted, neutral third party, have them run A/B comparisons between the two suggested complete articles, and then test for comprehension afterwards.
Is this a terrible lot of effort? Of course! But so is me typing this. The reason I am typing it is because the readers' time, in aggregate, monstrously outweighs my own. Consequently, we owe it to the readers to spend more of our time making a better article from the readers' perspective(s), not from the perspective of a plurality of the editors.
Jouster (whisper) 02:46, 12 September 2012 (UTC)
Comments from User Albtal
(413 of 500 words)
Proposal 1 But surely start with the MvS version which caused the "furor" around the world, and state that the crucial rule there was missing, and clearly formulate this rule (K&W not needed), and then explain the solution based on:
A strong argument for the simple solution - "strong" because it even holds for weaker conditions than those in the "standard problem":
Forget The car and the goats were placed randomly, and forget he chooses one [uniformly] at random.
The following holds: If the contestant has chosen door 1, he will win the car by switching in two of three cases: If the host opens door 2, he will choose door 3, and if the host opens door 3, he will choose door 2. So he will win the car, if it is behind door 2 or door 3. Therefore switching has a 2/3-chance of winning the car.
We all know that we don't know the strategy of the host, neither in placing the car nor in choosing his door if he has a choice. So we have to decide without this knowledge. If now somebody says But it may be that the host does not choose symmetric strategies, we say Yes, it may be, but if so, we can't know; and therefore we have to decide without this knowledge.
But if we don't know the strategies of the host, we cannot compute the conditional probabilities. May be, but we don't have to compute conditional probabilities to know that the contestant has a 2/3-chance with switching. Imagine you are the coach of the contestant, and (may be just before his final choice or earlier) he asks you: What shall I do? Do you say now: Sorry, I can't compute my conditional probabilities; I cannot help you? Or would you say, as another coach would do: Take the switch. Then you have a 2/3-chance of winning.
(I think that these considerations belong to elementary game theory, and are as simple as the "game" Have I a coin in my hand?, which is even too simple to occur in elementary books there.)
...and in a separate section: Three doors, one car, two goats; two possible "Jokers": 1. The host must open a door with a goat before the contestant picks his door. 2. The contestant determines two doors of which the host has to open one with a goat. Then picking. Which Joker should he choose? --Albtal (talk) 07:39, 13 September 2012 (UTC)
@JohnSRoberts99: The show never happened in the "MHP" mode. Monty Hall was free in his actions, and never offered a switch. And a show with the crucial MHP rule that the contestant has to determine two doors of which Monty has to open one with a goat is too boring not only for Monty Hall. And if taken place frequently results would be the same as if you throw a die counting "1 or 2" / "3, 4, 5, or 6".--Albtal (talk) 20:41, 14 September 2012 (UTC)
Comments from JohnSRoberts99
(33 of 500 words)
Note: I am assigning Abstain to the comments below. If this is incorrect, please indicate "Proposal #1", "Proposal #2", or "Neither". --Guy Macon (talk) 20:16, 20 September 2012 (UTC) (Oops. cut and pasted to the wrong section. Sorry about that.) --Guy Macon (talk) 07:30, 21 September 2012 (UTC)
Does anyone have statistics from the show itself? That might be a bit more useful than trying to look at all the way people have calculated potential outcomes. I would back Proposal 2. JSR (talk) 19:33, 14 September 2012 (UTC)
Looks like I was in favor of Proposal 2.JSR (talk) 20:46, 20 September 2012 (UTC)
Comments from Wehwalt
(50 of 500 words)
Proposal 1 Agree with Elen. The game show host knows everything. That's part of the background assumption, along with the sun rising that morning, the end of the universe not yet having occurred, and the stagehands aren't leading the goat from door to door depending on what the contestant says.--Wehwalt (talk) 22:22, 20 September 2012 (UTC)
Comments from CBM
(106 of 500 words)
I don't think I have commented yet. I prefer proposal 1, because I think it captures the spirit of the actual problem better. In general, Richard Gill's published analysis of the problem is very apt and I would be glad to see us follow it. It it matters, just to respond to something I saw on this page: I am an academic and I think the conditional probability is "a somewhat unimportant academic extension to the problem" - where "somewhat unimportant" means that it should be treated in later sections of the article and explicitly as an extension rather than something that addresses the original question. — Carl (CBM · talk) 23:03, 20 September 2012 (UTC)
Comments from Mike409
(28 of 500 words)
I hate to do this, but I have to go with Proposal 1.
Wikipedia is not meant to be first Mathematically rigorous (MTAA), unfortunate as that may be.
Mike409 (talk) 04:40, 21 September 2012 (UTC)
Comments from JonRichfield
(439 of 500 words)
Responding to this RFC is about as tricky as the MHP. If I am not doing it correctly, too bad. I certainly agree with Tom Hulse about re-thinking the RFC and probably with his reasons.
- Neither. The article as it stands is better than either of the two alternatives. It may not be elegant, but it is about as near to comprehensive as most reasonable readers could demand. It also starts with simple concepts, so that impatient or naive readers can do the TLDR trick without failing to read a compelling answer. Such an impatient reader might miss some of the more interesting material further down, but that is his choice; we can't force him to stay in after class and clean the dusters. To omit any of the material further down (such as unspecified details of the host from hell/heaven) would leave a mutilated article and discussion, both betraying naive readers who try to apply the principle (well, we can't force them to read and understand -- that is their problem, but if we fail to supply salient considerations, then selling the reader short is our responsibility) and letting down readers who would like some depth of treatment. In short, we should take seriously the duty of thoroughly treating material that demands thorough treatment. The question of whether WP is supposed to be mathematically rigorous is totally different; the discussion as it stands is not primarily mathematical, and inserting a few elementary mathematical remarks and equal signs in an article on a basically mathematical topic is not to sin in terms of mathematical rigour. As it stands the article is nothing like formally demanding; the discussion is light and any symbolic expressions are highly visible and easily skimmed or skipped.
- A totally different question is whether the article needs re-writing (always assuming that there is no sacrifice of depth of treatment). I don't feel strongly about that; I don't think that the current version sins seriously on any of the usual niggles about OR, POV etc, but if anyone can demonstrate a better layout or improved didactics etc, then good luck. All I say is that pruning of either the historical or theoretical content would be totally improper. If someone really feels that the article covers too wide a field, it could be split, to avoid stampeding the livestock. For example, it might calm the waters a bit to treat material such as discussed below in the Rules for Monty section. I don't specially want that, but I suspect that some people might like it. At all events however, first demonstrate that everything is in place, then split. JonRichfield (talk) 09:53, 25 September 2012 (UTC)
Comments from User 31
Comments from User 32
Comments from User 33
Comments from User 34
Comments from User 35
Comments from User X
Please create a new section or two if you use up the last one.
End of RfC
Post-dated check to avoid archiving Glrx (talk) 23:35, 31 October 2012 (UTC)
How has that been working out for you?
Looking at the recent history of this talk page, I am once again struck by the large number of comments and with the net result of pretty much nobody shifting their position even slightly. (This, of course, includes me and my comments.) This has been going on for ten years and 1.3 million talk page words. Is there anyone here who can make a reasonable argument that, if only we spend another year and put another 100,000 words on this talk page, the dispute will be resolved? Now obviously, I am right, anyone who disagrees with me is wrong, and if they would only realize this and agree with me the dispute would be resolved. Alas, there are a bunch of misguided individuals who imagine that they are right, I am wrong, and everyone should agree with them! How crazy is that? I know what to do -- I will post another thousand or so words. That should do it! Just because it didn't work the last thousand or so times, is that any reason not to keep trying it forever?
So, other than talking at each other until we all die of old age, does anyone have any idea at all of a way out of this mess? --Guy Macon (talk) 19:25, 17 September 2012 (UTC)
- It has worked very badly for me to. I thought the plan was to ask users to chose between two ways of ending the long-standing conflict, which is only about the validity of the 'simple' solutions. Instead people started bringing up all sorts of other issues, which may be important, but are not the issue that has been dogging the article for years and are issues which will probably be resolved perfectly well by the normal WP processes of discussion and cooperative editing.
- Hardly anyone seemed to understand the problem that Rick and I were trying to solve which was, 'How do we deal the dispute between two groups of editors, one who thing the simple solutions are OK and the other group who think they are incomplete/answer the wrong question?'. Note, we were not trying to resolve the dispute itself for, as you say, not a single person has changed their mind on that subject, rather we were trying to find a way that the two groups could agree to differ but still edit the article cooperatively. That process has clearly failed.
- The only way forward now is to ask users to decide on the dispute itself, are the simple solutions (individually if you like) 'satisfactory'. satisfactory in this context implying that they can be used freely within the article without disclaimers or proximity to 'better' solutions.
- Accept strictly only 'yes' or 'no' answers with no comments at all and count the supporters for each side. Abstainers should simply not vote or comment. All comments, in fact anything other than the words 'yes' or 'no', should be deleted or moved to a 'Invalid replies' section. Martin Hogbin (talk) 20:00, 17 September 2012 (UTC)
- There are two separate issues here; the RfC and the outside-the-RfC comments.
- I actually think the RfC is going fairly well. Yes, there are irrelevant comments, but I plan on asking an experienced, uninvolved admin to evaluate all the comments and post her/his finding as to what the consensus is, then I am going to ask another couple of experienced and uninvolved admins to review that finding and confirm that it is good. That way nobody has cause to question the result. I will make sure that these admins are well aware of the specific question we are addressing and I am sure that they will have no problem separating the wheat from the chaff, so I see no need to remove any comments. The good news is that each person is limited to 500 words in the RfC. I have seen enough of you (Martin and Rick) in action -- both reasonable people who want the best for the encyclopedia but disagree on what is best -- that I am fairly confident that this will put an end to the Rick/Martin dispute once and for all.
- As for the outside-the-RfC comments, as I expected, my efforts to widely advertise this among those with an interest in math and those with an interest in dispute resolution brought in a bunch of comments from folks who are new to the topic or who had given up long ago. Also as I expected, there has been Yet Another Wall Of Text That Accomplishes Nothing. Everybody has an opinion, nobody has been convinced to change their position, and no faction seems to have a strong consensus. The good news is that the Martin/Rick dispute can be resolved while ignoring all comments that are not in the RfC. The bad news is that whoever comes out of that process as the "winner" will be faced with a new dispute with a new set of editors. --Guy Macon (talk) 23:30, 17 September 2012 (UTC)
- I'm not sure if Martin is being tongue in cheek above, but if he's seriously suggesting we should attempt to resolve this dispute with a poll such as he suggests IMO he seriously misunderstands Wikipedia policies. The question is not and hasn't been for several years what editors think about "simple" solutions vs. "conditional" solutions, but how the article should present what sources say about the problem and its solution. The orgy of WP:OR this RfC has spawned above (and Guy's clearly tongue in cheek comments starting this thread) is completely consistent with a nearly universal refusal to approach this issue from a perspective of what sources say, as opposed to what editors think, about the problem. -- Rick Block (talk) 02:02, 18 September 2012 (UTC)
- I am being perfectly serious. You always insist an talking as though the sources support your POV on this subject; they do not.
- Existing WP policies and dispute resolution methods have failed to resolve the longstanding argument so now is the time to try something new. I am not remotely suggesting that we abandon any of the WP core policies, especially verifiability but community consensus has always been the final arbiter in content disputes. Asking for consensus on a complex question, as we have just done, has failed completely. Now is the time to ask for consensus on a very simple question. Editors will be free to look at what the sources say in making their yes/no decisions but there simply is no useful purpose in discussing the matter here, we have done that for years and got nowhere. Martin Hogbin (talk) 08:34, 18 September 2012 (UTC)
- Guy, if you can extract a clear consensus for one of the proposals from the replies then then good on you, that would suit me fine. I make it 9 for proposal 1, 6, for proposal 2, and 10 other, which even from my perspective must be a 'no consensus', which leaves us with the question, 'What now?'. Martin Hogbin (talk) 08:46, 18 September 2012 (UTC)
- Remember, The RfC is a long way from day 30, so don't assume we have all the data. As for the "What now?" question, "If either proposal is accepted that will be a consensus decision. If neither proposal is accepted then anyone else is quite free to make their own proposal and have an RfC on it." (Quote from Martin Hogbin, posted here at 23:40, 8 August 2012) Perhaps someone else can write an RfC that ends in a consensus.
- Certainly a "no consensus" will put some arguments to bed. Want to claim that the majority supports your position? Not if the result was no consensus. Want to claim that you are following the sources and the other fellow isn't? You presented that argument to multiple editors and there was no consensus that it was a compelling argument. This, of course presumes that we know what the result will be... --Guy Macon (talk) 14:01, 18 September 2012 (UTC)
- No. that is completely wrong. No consensus does not mean consensus not to. Martin Hogbin (talk) 14:34, 18 September 2012 (UTC)
- I thought that one brilliant original suggestion did come out of all this discussion: don't call a solution a solution, call it an argument, approach, guide to understanding. At the same time the material on the Bayes approach should be made a whole lot more accessible, and it should not be presented in a confrontational way ("now here is the proper way to solve the problem"). So the extremists on both sides give a little, and we have a neutral framework within which any editor with knowledge of relevant sources can work to improve the article locally. Richard Gill (talk) 12:20, 18 September 2012 (UTC)
- I see no reason why we should not use the term 'solution' for the simple arguments but if calling them 'arguments', for example, allows us to structure the article sensibly then I would not object. I would object if we gave the impression that these arguments were in any way defective or second rate though. Martin Hogbin (talk) 14:34, 18 September 2012 (UTC)
- Richard's suggestion is actually fairly close to Proposal 2 (which, again, does not say anything like "conditional solutions are to be presented as the only correct approach"). Martin's claim above that I "always insist an talking as though the sources support your POV on this subject" is incorrect. What I insist is that there are lots of sources from the academic field of probability (a preponderance, I claim) that present only conditional solutions, and that there are numerous (I've cited 6, but there are more) that are critical of "simple" solutions. Proposal 2 does not say we include what the critical sources say early in the article, but that we include a conditional solution and present both "simple" and "conditional" solutions as equally correct. If we only present "simple" solutions early in the article, we're completely ignoring the sources that criticize these kinds of solutions and taking an editorial stance that these sources are wrong. We don't have to say in the article every time a "simple" solution is presented that there are sources that criticize such solutions, but the article can't present "simple" solutions as if they are universally understood to be complete and correct without taking the POV that sources that disagree with this are wrong. Presenting both "simple" and "conditional" as simply two different, even complementary, approaches (neither "more correct" than the other) allows us to remain neutral about this. Presenting just one (whichever one it is) is not neutral. -- Rick Block (talk) 15:08, 18 September 2012 (UTC)
Here we are, a week later, and still multiple editors are adding text to the Great Wall Of Text and making what mostly appear to be reasonable arguments.
And the result of all of this Sturm und Drang? Not a single editor has changed his or her position in any way. Not even slightly. Exactly as it has been for the last ten years. Insanity is doing the same thing over and over and expecting different results.
(Misattributed to various people, including Albert Einstein and Mark Twain. Earliest occurrence appears to have been at University of California, Irvine in social science lectures in the late 1960s.) --Guy Macon (talk) 00:39, 26 September 2012 (UTC)
- Unfortunately, it does appear some people haven't changed their position at all. But you're painting with too broad of a brush.
- Boris changed from "Proposal 1" to "neither". Richard seems to be changing from "Proposal 1" to "neither", and is saying things that sound remarkably like "Proposal 2". Elen currently lists herself as "neither" but is also saying things that sound remarkably like "Proposal 2". I've moved from "must include inline what various sources say about 'simple' solutions" to "must be NPOV" (years ago), and continue to offer revisions in the direction of what any reasonable persons suggests (latest, here, doesn't even mention the words "conditional probability").
- It seems to me some people are trying to reach a resolution. -- Rick Block (talk) 01:31, 26 September 2012 (UTC)
Combining purses
Two men together have 20 pounds in their purses. At the cinema one of them opens his purse and sees it's empty. How much is in the other man's purse? Piece of cake. But now the real story. Two men, heading for the cinema, leave home with each one of them 10 pounds in his purse. Together they have 20 pounds with them. At the cinema one of them opens his purse and sees it's empty. Would you believe the other man saying: no problem, together we had 20 pounds, so your 10 pounds must have jumped into my purse, opens his purse and indeed finds 20 pounds????? Nijdam (talk) 09:46, 18 September 2012 (UTC)
To be sure it's understood, notice the similarity with the combining doors solution. Nijdam (talk) 15:54, 18 September 2012 (UTC)
- See False analogy. hydnjo (talk) 13:02, 18 September 2012 (UTC)
- The "answer" to the problem (should you switch) can be demonstrated easily. And the answer is "even though it doesn't appear to make sense: Yes". Anything else is argument over -why- it makes sense to switch or if there are extra conditions (which door was opened? Is the host lying? Was something not stated in the original problem?) that can be debated. 83.70.170.48 (talk) 14:45, 18 September 2012 (UTC)
- Nijdam, since you seem completely obsessed with this, can you expound on which of the published sources actually gives the answer you want. And if the answer is 'none', have you considered getting published yourself, as you so clearly do have what you believe to be the answer, and it could then be the latest addition to the references. --Elen of the Roads (talk) 22:00, 18 September 2012 (UTC)
I retracted some reliable sources from the reference list:
- Gillman, Leonard (1992). "The Car and the Goats," American Mathematical Monthly 99: 3–7.
- Grinstead, Charles M. and Snell, J. Laurie (2006-07-04). Grinstead and Snell’s Introduction to Probability (PDF). Retrieved 2008-04-02.
{{cite book}}: CS1 maint: multiple names: authors list (link) Online version of Introduction to Probability, 2nd edition, published by the American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell. - Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma," American Statistician 45: 284-287.
- Mueser, Peter R. and Granberg, Donald (May 1999). "The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making", University of Missouri Working Paper 99-06. Retrieved June 10, 2010.
- Rosenhouse, Jason: The Monty Hall Problem. Oxford University Press 2009, ISBN 978-0-19-536789-8 (online copy of the first chapter, preprint).
Nijdam (talk) 10:32, 20 September 2012 (UTC)
Not much comment here. Afraid one has to admit the misleading way of arguing in the so called 'combining doors solution'? Nijdam (talk) 10:04, 25 September 2012 (UTC)
- We are still awaiting the source (please indicate page) for the lost 10 pounds, saying that any group of two doors having better chance than one single door cannot help to decode the obvious paradox (2/3 and not 1/2). Gerhardvalentin (talk) 23:30, 27 September 2012 (UTC)
Devlin's probability theory
I had a better look at the 2005 article of Devlin, that Richard added to the literature. In the proposed variant Devlin comes to the conclusion that the second player wins with probability 1/3 and loses also with probability 1/3. Got it! Nijdam (talk) 16:27, 18 September 2012 (UTC)
- Nijdam, why are you showing here Devlin's variant of "the forgetful host" who does not know where the prize is, and subsequently, in opening one of his two doors at random, in 1/3 inevitably will show the prize, and in that 1/3 destroys the possibility to win by switching, while in the remaining 2/3 ("car:goat" and "goat:car") the chances of the two still closed doors are "1:1" now. What is your argument? The "second player" had a choice only between 2 of 3 doors, both with 1/3 chance to hide the prize. Gerhardvalentin (talk) 17:23, 18 September 2012 (UTC)
- @Nijdam: Yes, here the text of an email which I wrote to Devlin at 8th May 2012:
- <start email text>
- I think that your following phrase for the "variant game" is wrong:
- The probability that she loses is likewise 1/2 x 2/3 = 1/3. And that's the probability that you win if you switch. Exactly the same as if you did not.
- My consideration:
- The probability that "she" wins is 1/3; and - of course - the probability that she loses is 2/3.
- And the probability that "you win if you switch" is 1/2, not 1/3. "Exactly the same as if you did not".
- The difference between the (well formulated) original game and the variant game is the following:
- In the original game the probability that the host opens door t is twice as much if the contestant has chosen a door with a goat (1/3 * 1 = 1/3) as if she has chosen the car (1/3 *1/2 = 1/6)).
- In the variant game the probability that the host opens door t in both cases is 1/3 * 1/2 = 1/6.
- The "shock" in the variant game only arises if you believe in the following argumentation for the original game:
- [1] The probability that the prize is behind door B or C (i.e., not behind door A) is 2/3.
- [2] The prize is not behind door C.
- Combining these two pieces of information, you conclude that the probability that the prize is behind door B is 2/3.
- Indeed you could apply this argumentation to the variant game - which leads to the proof that the argumentation is wrong. The real reason why in the original game the probability for switching is 2/3 is that (1/3)/(1/3 + 1/6) = 2/3. For the variant game we have (1/6)/(1/6 + 1/6) = 1/2.
- <end email text>
- --Albtal (talk) 17:57, 18 September 2012 (UTC)
- He didn't answer. And I only placed this comment here after having said good bye above, because my already existing email exactly matches your hint (and more). So concerning the following comments here: No ban is necessary for me. But since I am here once again I allow myself to write the following last lines here: In this German article we can find an analogous variant as Übungsaufgabe 1, placed there as a hint, that the consent to the 2/3-solution of the original MvS-problem almost always was not only superficial but wrong; and that the problem, combined with the 2/3-solution, which had been going around the world as a "paradox", really was a joke.--Albtal (talk) 06:34, 19 September 2012 (UTC)
NO ORIGINAL RESEARCH PLEASE. NO CITING EMAILS FROM EXPERTS, PAPERS YOU FOUND IN YOUR GRANNY'S ATTIC, OR PERSONAL GNOSIS FROM YOUR TALKING TOASTER. Elen of the Roads (talk) 20:53, 18 September 2012 (UTC)
- What's the problem? I don't think Albtal has the intention to show this in the article itself. Nijdam (talk) 21:02, 18 September 2012 (UTC)
- See below. Or try citing personal emails on any other talkpage and see where it gets you. Elen of the Roads (talk) 21:14, 18 September 2012 (UTC)
- Re. Nijdam's original post in this thread: Yes, that is an inexplicable mistake. It probably shows the hazards of not using a copy editor who knows the subject matter. However, like Gerhardvalentin, I fail to see the relevance of dwelling on the variant problem. ~ Ningauble (talk) 21:18, 18 September 2012 (UTC)
- Well, I don't comment on GerhardValentine, but the relevance is the reliability of Devlin as a source. Nijdam (talk) 21:29, 18 September 2012 (UTC)
- Only in the respect that it potentially shows a lack of proper peer review, and not just a dumb typesetter and a sloppy proofreader. It would be a good source for how vos Savant isn't the only one to publish duff stuff where this problem is concerned. Elen of the Roads (talk) 21:57, 18 September 2012 (UTC)
- Well, I don't comment on GerhardValentine, but the relevance is the reliability of Devlin as a source. Nijdam (talk) 21:29, 18 September 2012 (UTC)
- Keith Devlin is a reliable source according to Wikipedia standards: a mathematician and popularizer of mathematics (but not a probabilist or a statistician or a games theorist). His pretty little solution -- not an academic publication but a chatty newsletter column -- to MHP had a tiny little gap in it. He got a lot of letters telling him he'd screwed up so he got scared and gave the full Bayes calculation which at least (as he said) is a reliable way to get the right answer without actually using your head, provided you are careful and patient. However, the little gap in his proof is child's play to patch and Richard Gill did that in articles on Citizendium and StatProb; the latter had peer review. No doubt other sources did it too. Richard Gill (talk) 07:14, 19 September 2012 (UTC)
- So much then for Wikipedia standards. The itsy bitsy tiny winy little gap is in fact nothing more than the complete solution. Indeed child's play for a statistician, nothing to brag about. However, combining doors is highly misleading, as the basic idea is wrong. Have a look at the combining purses. Nijdam (talk) 09:21, 19 September 2012 (UTC)
- On Wikipedia, Wikipedia standards rule. On the Annals of Statistics, Annals of Statistics standards rule. Here we're on Wikipedia. Next: Nijdam, your opinion is that the basic idea of combining doors is wrong. My opinion is that it's brilliant. On Wikipedia, neither of our opinions has any relevance whatsoever. "Truth" is not relevant. If you want the Truth to influence what's in Wikipedia, go and publush papers expounding the truth in major academic journals, and then sit back and wait 20 years for this info to trickle down into the standard textbooks. Richard Gill (talk) 19:04, 19 September 2012 (UTC)
Ban all the mathematicians
OK, so I'm only partly serious, but LOOK at this talkpage. A whole bunch of mathematicians trying to convince each other that THEIR solution is the right one, that all the others are wrong, and that no-one else is clever enough to understand them.
Wikipedia:Arbitration/Requests/Case/Monty Hall problem contains the following principle
Mathematics (use of sources)
11.4) If editors disagree on how to express a problem and/or solution in mathematics, citations to reliable published sources that both are directly related to the topic of the article and directly support the material as presented must be supplied by the editor(s) who wishes to include the material. Novel derivations, applications or conclusions that cannot be supported by sources are likely to constitute original research within the definition used by the English Wikipedia.
So there should be no maths on this page that you cannot reference to a source suitable for inclusion in the article, and it should only be on this page to discuss whether the layout works, how to use Math Jax or similar. If I went through and hatted off all the non-sourced solutions, we might get a talkpage that focused on how to lay out the article in accordance with Wikipedia policies, ie by describing what the different sources say, since none of them agree with each other.
It is apparent that there is not a single agreed iteration of the problem, and there is not a single agreed solution. The sources seem to go forward in time, each disagreeing with all the previous ones, lets go thru it in iterations from vos Savant forwards in time. I know this is a physics model, not a maths one, but it gets everything in, and it MAKES NO DIFFERENCE if one of you thinks a particular 'solution' is 'wrong' because if there is a source that says it is wrong, it can't have been written until after the offending solution came out, so it is obvious that it should be placed in the article in a section subsequent to the section with the offending solution in it. Elen of the Roads (talk) 21:13, 18 September 2012 (UTC)
- Hi Elen, if you look above, at how all of the mathematicians chimed in on this debate, you will notice that they all agreed with your positions, more or less. The people who are arguing against you are not mathematicians, they are average, ordinary users who are simply trying to grapple with this problem using whatever means they can. Unfortunately, they mis-use the mathematics, because, I'm presuming, they never got good at it, because, I guess, its just plain taught badly in school. Thus is the plight. Coping the attitude that you do certainly doesn't make anything any better; it just adds to the illiteracy problem. linas (talk) 03:37, 19 September 2012 (UTC)
- Elen might not be right with her notion there, but your reply is definitely wrong. Most people are active here are not just ordinary users but have science backgrounds, some of them are mathematicians in particular the one Elen reacted to.--Kmhkmh (talk) 06:18, 19 September 2012 (UTC)
- Who, exactly? I've been editing math articles here for years, and I have a pretty good idea who the mathematicians are on WP. I recognize a handful of names above, but the vast majority of people arguing here, including those arguing incorrectly, simply never edit any math articles. This, coupled with the fact that many of the arguments above are rather childish, when not flat-out wrong, and I must conclude they are math-illiterate. linas (talk) 13:16, 21 September 2012 (UTC)
- Nijdam is a mathematician (so are Richard, Boris and myself among possibly others). If you look at edits of involved editors or their use pages (assuming they do anything else than MHP), you can quickly see that many/most seem to have a background in math/sciences/engineering. As far as "childish" (or occasionally flat out wrong) arguments/opinions/reactions go mathematicians/academics are capable of them as well and in fact have produced plenty on this subject, starting with some of the letters to vos Savant all to the way to some peer reviewed publications (an error in Morgan's paper got corrected almost 20 years later). In some way much of the ongoing discussion here is just mimicking the ongoing (academic) arguments/struggles outside WP.--Kmhkmh (talk) 06:07, 22 September 2012 (UTC)
- Who, exactly? I've been editing math articles here for years, and I have a pretty good idea who the mathematicians are on WP. I recognize a handful of names above, but the vast majority of people arguing here, including those arguing incorrectly, simply never edit any math articles. This, coupled with the fact that many of the arguments above are rather childish, when not flat-out wrong, and I must conclude they are math-illiterate. linas (talk) 13:16, 21 September 2012 (UTC)
- Elen might not be right with her notion there, but your reply is definitely wrong. Most people are active here are not just ordinary users but have science backgrounds, some of them are mathematicians in particular the one Elen reacted to.--Kmhkmh (talk) 06:18, 19 September 2012 (UTC)
- Note that it says "If editors disagree [...] must be supplied by the editor(s) who wishes to include the material." Most of the discussions you are referring to are not about trying to include material in the article, but about trying to reach consensus. Once that is reached, the first part, i.e. "If editors disagree", becomes false, and the point moot. Most of the discussions appear friendly and honestly aimed at finding consensus, too. It's quite usual on talk pages to not source every claim, because most of that will be a part of the iceberg that will not reach the article, and the editors agree on most of those points anyway, perhaps after a bit of discussion. Editorial judgement on how to tie the sources together to form a good article is also not something that can be sourced and requires common understanding of the material.
- One might argue that trying to reach consensus is a futile quest, but obviously not everyone has given up on it. It's only because the discussion has taken so long that people lose patience with the usual consensus building process. Consider, though, that the world will not end even if it takes another ten years to resolve the dispute, and we're not on a deadline here. In the large scheme of things, the MHP is just a curiosity, nothing more. A good-sized jug of coffee with a sugary lump of MHP in it ought to put things in the right perspective :) -- Coffee2theorems (talk) 05:26, 19 September 2012 (UTC)
- Spot on, Coffee2theorems: "Editorial judgement on how to tie the sources together to form a good article is also not something that can be sourced and requires common understanding of the material". Especially since the number of sources is huge, they are written in hugely varying contexts (for hugely varying audiences with hugely varying backgrounds), and finally because some of them appear to disagree with one another vehemently. It is very hard to come up with genuinely new maths on MHP. A.V. Gnedin did it, his new solution was reported on in the newspapers. His research was triggered by mine, and that was triggered by the discussions here (but I only wrote up the elementary facts which everyone with a maths background agrees on, most of it well known and/or well sourceable). Richard Gill (talk) 07:28, 19 September 2012 (UTC)
Really, a good idea. I, a mathematician, ban myself for 3 years. Hey, mathematicians, follow me! Find a better hobby. We'll see what will happen here. :-) Boris Tsirelson (talk) 06:25, 19 September 2012 (UTC)
Re: "Consider, though, that the world will not end even if it takes another ten years to resolve the dispute, and we're not on a deadline here.", is there anyone here who is willing to make the argument that 20 years of discussion will reach a resolution that 10 years of discussion has utterly failed to reach? --08:33, 19 September 2012 (UTC) (Edit of Guy Macon)
Many of you seem not to have understood the two proposals here
For the reason Richard quotes above, '...the number of sources is huge, they are written in hugely varying contexts (for hugely varying audiences with hugely varying backgrounds), and finally because some of them appear to disagree with one another vehemently.' it is not possible to resolve the argument as to which solutions are correct. For that reason the proposals made by both myself and Rick accept this fact and both proposals aim to give the 'simple' and 'conditional' solution equal prominence within the article. Neither claims that either solution is better than the other.
The difference between the two proposals is only the editorial decision as to how the article is structured. As Coffe2Theorems, quoted by Richard, says, "Editorial judgement on how to tie the sources together to form a good article is also not something that can be sourced and requires common understanding of the material".
Can I as those of you who have not made a decision on the two proposals to go back and re-read them both. As you will see, it is not the case that I am proposing that the simple solutions are 'right' or 'sufficient' and Rick is saying that they are 'incorrect' or 'deficient', that is a fight that we have both withdrawn from (well I certainly have) as it can never been resolved. The question is, 'How can we as editors use our own judgement to structure the article to make it of most use and benefit to our readers without making any judgement over the 'sufficiency' of the simple sources. Simple first is what WP:technical suggests and whay most text books and encyclopedia articles do so that is my proposal. It does not in any way assert that the simple solutions are 'correct' in fact we will specifically mention the claimed deficiencies in them in the article. Martin Hogbin (talk) 09:29, 19 September 2012 (UTC)
- You do not quite say but imply that "simple first" is what distinguishes the two proposals. That is not so. Rick's proposal does not say outright that the simple solution(s) should come first in the "Solution" section, but that is probably the intent (like it currently is in the article), and in any case it does not say that conditional solutions should come first! So both proposals would put simple solutions first. What you want is to leave the conditional solutions out of the main "Solution" section altogether, and Rick does not. -- Coffee2theorems (talk) 09:53, 19 September 2012 (UTC)
- Imho the discussion here has developed very well in the matter. The article should be useful and "gettable" for the reader. For years it has been a tohu-bohu, concealing more than it explains. The clear "paradox" (two doors having double chance than one door) was told by a "story". For the story that had been told there are reams of variants to interpret / reinterpret /misinterpret. The article should show the clean paradox, and it should show variants where the paradox simply doesn't exist. The principal duty is to distinguish those variants and to keep them very clearly apart, and not to present a mingle-mangle as before, completely inapprehensible for the reader. The discussion here did help a lot to come closer to attain that goal. Gerhardvalentin (talk) 11:02, 19 September 2012 (UTC)
- Coffee2theorems. where do I even say that there will be a main "solution" section? All I am asking is that we give the simple solutions first, with a reasonable and simple discussion of the other issues (such as the host knowing where the car is before we discuss in full' criticism of the simple solutions, and all other solutions and variants. Martin Hogbin (talk) 18:27, 19 September 2012 (UTC)
- I didn't say that you said there would be one, it was my own assessment of the proposal. If there is a section called "Solution" (no qualifications), after which comes a lengthy section called "Aids to understanding", and after that comes a section that is called something else than "Solution" (no qualifications), as I understood your proposal to be, then I think it is fair to call the "Solution" section the "main" solution section.
- The other proposal isn't about "discuss[ing] in full criticism of the simple solutions, and all other solutions and variants" before "a reasonable and simple discussion of the other issues" — it says that would go in a later section. Again you characterize your proposal in a way that is not characteristic of it, but characteristic of both proposals. When you are pitting off two alternative proposals, that is misleading, because people easily assume that you are talking about differences, not shared qualities. -- Coffee2theorems (talk) 10:24, 22 September 2012 (UTC)
To be absolutely clear, in Proposal 2 simple solutions would (of course) come first. The major difference in the two proposals is whether there is an initial section called "Solution" followed by one or more other sections (e.g. "Aids to understanding") mentioning only simple solutions ("with no disclaimers that they do not solve the right problem or are incomplete" - Martin has previously rejected even a forward reference to any other kind of solution) as opposed to a more inclusive initial "Solution" section with both simple and conditional solutions ("with neither presented as 'more correct' than the other"). Martin's claim that both proposals aim to give the 'simple' and 'conditional' solution equal prominence within the article is, IMO, obviously untrue. Proposal 2 does (it even says this), but Proposal 1 clearly gives much more prominence to simple solutions and furthermore creates an editorial stance that these solutions are "perfectly correct" (also implying conditional solutions "are an unimportant academic extension to the problem"). Anyone who has followed this page knows that this is precisely Martin's and Gerhard's POV (not even the POV of any particular published source), and that this POV conflicts with the POV published by numerous reliable sources that simple solutions are insufficient (not wrong per se - anyone who may be interested in this should read the discussion Martin and I has about these sources here). -- Rick Block (talk) 17:26, 19 September 2012 (UTC)
- Rick the wording that you have challenged was agreed by both of us, after a very length discussion. You seem unable to distinguish between my own POV (which is that the simple solutions are what the MHP is all about) and my proposed compromise (which gives both POV's equal prominence within the article). It is pointless to say that this is untrue because it is true by definition. If my suggestion is accepted all editors could hold me to that statement by insuring that your POV gets equal prominence, provided that the simple solutions come first, unfettered. Martin Hogbin (talk) 18:23, 19 September 2012 (UTC)
All this fixation on solutions. All this fixation on right and wrong. Different sources have given different analyses, different arguments (making different assumptions, writing for different audiences). If someone can compose three or four simple English sentences which correspond to a clever derivation of a conditional probability under, say, K&W conditions, (and which moreover paraphrase a published reliable source) then this belongs right at the beginning of the article alongside other simple intuitive arguments and explanations. I begin to shift my allegiances from "Proposal 1" to "Neither" since both proposals put undue weight on the POV that there is some kind of conflict. I think that this (the opinion there is a conflict and it's important) is a minority opinion as far as reliable sources are concerned. Richard Gill (talk) 19:22, 19 September 2012 (UTC)
- Richard - Proposal 2 avoids the conflict (in the article) and does precisely what you're suggesting. One reason to structure the article this way is because there are conflicting opinions (both in sources and among editors), but this conflict in no way is emphasized in the article text under Proposal 2 (the conflict "informs" the presentation, but is not mentioned). A suggestion for the three or four simple English sentences (doesn't have to be these - this is just a suggestion) are the two paragraphs and figures currently in the article starting here, up to (not including) the subsequent "Formal solution" section. This text says nothing even remotely like "simple solutions are wrong" or "conditional solutions such as this one are the only right solution". -- Rick Block (talk) 20:36, 19 September 2012 (UTC)
- Two paragraphs and several figures are much more than a couple of sentences of plain English, Rick! Your specific suggestion only works for people who take the trouble to get pencil and paper and work all their way through the calculations. It'll take them half an hour. It does not provide instant insight. My favourite three sentences would be: Suppose all doors are initially equally likely to hide the car, and that Monty is equally likely to open either door to reveal a goat, if he has a choice. By symmetry, specific door numbers are now irrelevant to the problem. The player's initial choice hides the car with probability 1/3, and the other door left closed by the host therefore has probability 2/3 to hide the car. — Preceding unsigned comment added by Gill110951 (talk • contribs)
- Richard - I think you're seriously underestimating the difficulty of transitioning from the mental model of having picked door 1 and seeing the host open door 3, to a more abstract mental model considering other alternatives (I've cited what K&W say about this numerous times - search for "once formed" in the archives). Your sentences make perfect sense, but they require far more from the reader than slogging through a few extremely simple calculations. I really don't understand the reluctance to address the conditional probability head-on. The text in the "Decision tree" section uses only high school level probability concepts (not even Bayes) and 6th grade math (addition and division of fractions) - and directly addresses the mental model K&W say nearly all readers form after reading the problem statement (97%, 35 out of their sample of 36). What you're effectively asking the reader to do is to put this mental model on hold, shift back to thinking about the probability the car is behind door 1 before the host opens a door (obviously 1/3), and understand that this must remain the same after the host opens a door if the host is equally likely to open either door (and must open a door). This seems to me to be a far more sophisticated (and complicated) way to look at the problem than the straightforward computation. We can certainly say this (it can definitely be sourced), but isn't the direct computation far more prevalent - and even easier to understand? -- Rick Block (talk) 15:47, 20 September 2012 (UTC)
- This is a good point Rick. Yes, I *am* asking the reader to put their earlier formed mental model on hold, and try to create another. Remember, MHP is a *trick* question (it's famous, and so there's a big article on it on Wikipedia, because it's a very popular brain-teaser; not because it's a standard exercise in a conventional Probability 101 course, from the lecture on Bayes' theorem). Vos Savant's question is deliberately posed to entice the reader/listener into forming the mental picture which so dominates his/her brain that (s)he jumps to the wrong conclusion (the static picture of two doors closed, one goat and one car behind them, no point in switching). So, helping people to get deep understanding of MHP involves helping them see a different mental model which leads to the opposite conclusion. After that they may be prepared to slog through some calculations, figure out some subtelties. Different people's minds work in different ways. I saw the light with a flash of insight after realizing that a stayer/switcher wins/loses according to whether or not the car is behind the initial door. I personally didn't see the light from doing some algebra or arithmetic. Maybe some readers will appreciate your solution. Still, for me, it doesn't fall in the category "intuitive arguments which open your eyes to an alternative reality", different from the one (the false one) which Vos Savant's carefully crafted words trapped you in. Richard Gill (talk) 19:55, 20 September 2012 (UTC)
- Proposal 2 is also materially different from Proposal 1 in expressly calling for a section on "criticism of the 'simple' solutions". I strongly oppose this because it is a tendentiously non-neutral way to characterize sources that are talking about different interpretations and definitions of what the question is. Execrably so when a source says solution S1 does answer problem P1 but not problem P2.
These differences are essential context for the solutions but, unfortunately, attempts to contextualize solutions in the article have been met with strenuous objections about "health warnings" or "disclaimers" about the relevance of the solutions. This is why I cannot support Proposal 1 either: it simply does not settle the dispute.
Using the colorful example in Rosenthal (2005a) where Monty opens door #3 unintentionally because he slips on a banana peel, one side appears to be insisting that simple solutions must be criticized because they don't work when Monty slips on a banana peel, and the other side appears to be insisting we must not mention that simple solutions do work if Monty doesn't slip on a banana peel. This is nutty as a fruitcake.
I fully endorse Richard Gill's remark that "both proposals put undue weight on the POV that there is some kind of conflict." The conflict is between the contributors, not between the substance of the sources (notwithstanding the uncollegial tone adopted by at least one of the sources). ~ Ningauble (talk) 18:55, 20 September 2012 (UTC)
- I agree with Ningauble and Richard Gill on this one. For those who haven't been following this for years, a bit of history might be of interest. When I saw this dispute after the arbcom decision, I figured that Wikipedia's standard dispute resolution process should be given a fair chance. This has been through a number of the steps (third party mediation, ect.) but at the time I determined that the specific dispute had not been the subject of an RfC. It took months to get that to happen. The problem? Rick and Martin would not accept any description of the dispute written by the other. No matter what either of them wrote, the response from the other disputant was was "that's not what this dispute is about! This is what the dispute is about!" Finally, after taking several long wikibreaks from trying, I was finally able to get them to agree on RfC wording.
- Each of them was pretty confident that the consensus would support their proposal, and both of them made a commitment to stop disputing if the consensus was against them. The RfC is still young, and things may change, but it is pretty clear that there is not going to be a clear consensus for either proposal. It hasn't happened yet, but a clear consensus for "neither" could emerge. If it does, both Martin and Rick should graciously accept that consensus and stop fighting over two positions that have both been rejected by the community.
- I am really hoping that comments like "Many of you seem not to have understood the two proposals here" are not precursors for a future position of "because many here did not understand the two proposals I will now ignore the lack of consensus for my position and continue battling" or "because my opponent mischaracterized my proposal I will now ignore the lack of consensus for my position and continue battling" --Guy Macon (talk) 19:58, 20 September 2012 (UTC)
- Guy, as I have already said to you, I accept that there is no consensus for my compromise proposal or for Rick's proposal and if that is the final result of this RfC I am quite happy not to propose it again. I will stick to my original POV from now on.
- It is extremely uncharitable for you to attempt to characterise this dispute as a fight between myself and Rick. We both tried to find compromise solutions to an ongoing battle between two groups of editors and we were the only two who actually produced concrete proposals that could be comment upon. You mentioned the history of this dispute. Here is the history of the dispute. As you will see many other editors have argued over which are the best solutions for this article and over a considerable period of time. I (and Rick) tried to find a way to resolve this dispute but accept that we have failed. The problem now is that the original dispute continues with no sign of any resolution or consensus. Martin Hogbin (talk) 20:58, 20 September 2012 (UTC)
- @Ningauble - if you're objecting to calling the section "criticism" how about if we call this section "Detailed discussion of solutions" (or some such). The intent of Proposal 2 is that this is essentially the same as the section Proposal 1 characterizes as "a full and scholarly exposition of the 'conditional' solutions" and is where the specific differences between "simple" and "conditional" solutions would be described (of course in neutral terms). -- Rick Block (talk) 20:14, 21 September 2012 (UTC)
- It is unfortunate that the proposals (and sometimes the proposers) aren't entirely clear on what is the same and what is different about the two. Would it be too late to add some clarifications on that to the RfC? -- Coffee2theorems (talk) 11:09, 22 September 2012 (UTC)
- @Rick: – A rose by any other name would be as thorny. Rather than a discussion of the merits of various solutions, or some such, I would like to see a discussion of various ways of interpreting the problem. I think the "Criticism of the simple solutions" section should be gone; and the "History" section (which should lose the mere mentions that do not contribute to or illustrate the historical development of the problem, or at least move them to "In popular culture") should be re-cast to show various perspectives on such matters as, e.g., the initial ambiguity about whether Monty must open an unchosen door revealing a goat, the issue of the objective(-ist) significance Monty's choice of goats, and the issue of the subjective(-ist) insignificance of, say, door numbers.
What I am earnestly opposed to is placing undue weight on disputation about solutions, thereby obscuring the very thing that complementary views might help to illuminate, to wit, understanding the Monty Hall problem. ~ Ningauble (talk) 17:57, 28 September 2012 (UTC)
- @Rick: – A rose by any other name would be as thorny. Rather than a discussion of the merits of various solutions, or some such, I would like to see a discussion of various ways of interpreting the problem. I think the "Criticism of the simple solutions" section should be gone; and the "History" section (which should lose the mere mentions that do not contribute to or illustrate the historical development of the problem, or at least move them to "In popular culture") should be re-cast to show various perspectives on such matters as, e.g., the initial ambiguity about whether Monty must open an unchosen door revealing a goat, the issue of the objective(-ist) significance Monty's choice of goats, and the issue of the subjective(-ist) insignificance of, say, door numbers.
OK, I give up
I have made it as clear as it is possible to do that my proposal does not claim that any solution is right or wrong yet even Richard is now saying that I have a fixation with right and wrong. It seems that words no longer carry any meaning and that this is percieved purely as a battle between the 'simplists' and the 'conditionalists' who both claim to have absolute right on their side. It is rather like a debate on law and order. No matter what anyone says there are only two views that a person can be perceived to take, 'hard liner' or 'liberal'. Rational discussion is no longer possible. Whatever happened to WP:assume good faith? Martin Hogbin (talk) 08:32, 20 September 2012 (UTC)
- Martin, I do not accuse you of having such a fixation, nor lack of good faith. My point is that the discussion degenerates into a debate on whether some "solutions" are "right" and some are "wrong". I think that informal arguments, intuitive arguments, arguments which aid insight and intuition, should go first in the article. We should restrict ourselves to arguments which are actually *correct*, even though this is a concept alien to Wikipedia policies. But I do hope everyone here agrees that it is correct to say that if your initial choice has 1/3 chance of hitting the car, then the chance the car is behind one of the other two doors is 2/3. This argument is found all over the literature, not difficult to source it. Notice: I do not say that this is a "solution" to MHP. I say: this is what many notable sources have written about MHP, and many readers of Wikipedia will find it illuminating, and it is correct. Some readers will see it as a solution, some won't, who cares.
- I would like to ban the word "solution" from the first sections of the article. If there is a simple and correct argument, which can be expressed in one or two sentences only, and which most readers will understand, and which actually (for the insiders) corresponds to a derivation of a conditional probability, then it can be there in the beginning of the article (I think there are several such). Again you see I am veering to Boris Tsirelson's opinion that the article should start simple, without being incorrect. It's my opinion that this would allow some variants of "the full solution" (including an informal version of the notion of conditioning) to also be present in the early part of the article.
- I'd like to see mathematicians and non-mathematicians to be able to work together on the article, and both mathematicians and non-mathematicians to find it a fabulous resource. Richard Gill (talk) 12:02, 20 September 2012 (UTC)
- I really do not understand you. You say, 'All this fixation on right and wrong.', then you insist that, 'the article should start simple, without being incorrect'. It would seem that my attempt to find a compromise has failed so the fight is likely to go on for a few more years. Martin Hogbin (talk) 20:32, 20 September 2012 (UTC)
- Dr Gill, I'm with you. Martin, I think he's saying 'correct' only as in 'the arithmetic/logic is correct', 'Sooty's magic wand is not invoked' or (I would add) 'correct allowing that the puzzle specification was incomplete' (for vos Savant). Not 'correct' as in whatever Nijdam's 'correct' explanation is that he will never tell us, or Rick Block's correct explanation that probably is correct but requires a four paragraph exposition of the problem and three screens of maths to set out the answer. Elen of the Roads (talk) 21:25, 20 September 2012 (UTC)
- Elen, I think you will find that Richard has a rather stricter idea of 'correct' than you think, but let us not speculate. Richard, would you say the following solutions are correct, exactly as they are (these are solutions copied from various versions of this article)?
- User:Martin_Hogbin/MHP - Combining doors
- User:Martin_Hogbin/MHP - Parade
- User:Martin_Hogbin/MHP - Economist Martin Hogbin (talk) 22:05, 20 September 2012 (UTC)
- I'll comment per example later this weekend. But you use the word "solutions". We can't discuss whether a solution is right or wrong till we have fixed the problem it is supposed to address, and the level of detail which is acceptable for the context. I prefer to study the presented argument. Is each step in the argument logically correct? If assumptions are needed to justify argument steps, are they stated explicitly? If assumptions are made explicitly, are they used in some step of the argument? Is the stated conclusion of the argument the same as the actually justified conclusion? A completely separate question is whether or not a given, correct, argument can be considered to be a solution of the original problem.
- Elen, I think you will find that Richard has a rather stricter idea of 'correct' than you think, but let us not speculate. Richard, would you say the following solutions are correct, exactly as they are (these are solutions copied from various versions of this article)?
- Dr Gill, I'm with you. Martin, I think he's saying 'correct' only as in 'the arithmetic/logic is correct', 'Sooty's magic wand is not invoked' or (I would add) 'correct allowing that the puzzle specification was incomplete' (for vos Savant). Not 'correct' as in whatever Nijdam's 'correct' explanation is that he will never tell us, or Rick Block's correct explanation that probably is correct but requires a four paragraph exposition of the problem and three screens of maths to set out the answer. Elen of the Roads (talk) 21:25, 20 September 2012 (UTC)
- One can evaluate the correctness of a written argument without use of external information, objectively. One simply inspects the internal logical coherence of the argument. One clearly cannot evaluate the correctness of a solution to Vos Savant's question objectively, since it's a matter of taste how the informal verbal question should be converted into an unambiguously mathematically formalizable question. Richard Gill (talk) 08:04, 22 September 2012 (UTC)
- The argument of the Economist is a correct argument for the statement that the player who chooses a door at random and then switches, whichever door is opened by the host, will win the car with probability 2/3, while the player who chooses his door at random and then stays, whichever door is opened, wins with probability 1/3. Note: no K&W assumptions! Randomness is in the choice of the player! I like this.
- The argument is also given by several academic mathematics sources, in particular by your truly. It's the important part of a game-theoretic (decision theoretic) argument. The specialist can go on to remark that no strategy whatsoever can do better than 2/3 (there are of course a whole lot of more complicated strategies than the two particular ones "choose at random, always switch" and "choose at random, always stay").Richard Gill (talk) 16:04, 22 September 2012 (UTC)
- The argument called combining doors seems to take a subjectivist notion of probability. The only assumption which is used, is that the car is equally likely behind any of the three doors. (The competitor's choice is fixed). It ignores the possibility that you might want to do something different depending on whether the host opened door 2 or door 3. It's a good argument for lazy competitors who are not interested in which door is chosen. If they switch they'll get the car with probability 2/3. Competitors who are not so lazy might wonder about whether or not it could be useful to do something different in case the host opens door 2 and in case the host opens door 3. However, if indeed they are using probability in the subjectivist sense, they'll correctly consider the specific door number irrelevant. Their prior information is symmetric in the door numbers so the specific door numbers opened in a specific case are irrelevant. Possibly this is in the back of the mind of all those who only compare "always switch" with "always stay". The door numbers are arbitrary labels, nothings is changed in the problem by renumbering then. Hence we need only consider strategies which are the same however the doors are numbered. Laziness is completely justified. It seems to be a matter of taste whether one explicitly mentions that one has reduced the problem by symmetry, or not, and many writers probably do it subconsciously. Richard Gill (talk) 16:25, 22 September 2012 (UTC)
- The argument from Parade uses the same assumption as the combining doors argument: the car is initially equally likely behind any of the three doors; the competitor's choice is fixed. It shows completely correctly that by switching (whatever door is opened) you'll get the car with probability 2/3. The possibility that it might be to your advantage to switch in one case but to stay in the other (depending on which door is opened) is not raised. Of course, once you've seen that always staying and always switching have success probabilities of 1/3 and 2/3 respectively, it would seem quite inconceivable that a mixed strategy could go above 2/3; one would very naturally suppose that it would do something in between. The mathematician might like to add a little mathematical analysis which shows that this is indeed the case. For instance, Gnedin's dominance argument shows very easily that it is a waste of time to consider staying in any situation whatsoever. Richard Gill (talk) 16:34, 22 September 2012 (UTC)
- In summary, the arguments presented in all three sources are correct, it seems to me. By this I mean that the author's derivation of the author's stated conclusion under the author's stated assumptions is correct. The assumptions are different and the arguments are different and the conclusions are different! What do we learn from this? The controversy here has arisen from earlier wikipedia editors who created the false impression that there's only one MH problem, namely that "Marylin is asking for a conditional probability", and hence that solutions can be classified right or wrong according to whether or not they present a logically correct and explicit derivation of a conditional probability. No. Stupid. Each different source converts Marilyn's words into a different problem and solves it in an appropriate way. (Morgan et al even deliberately misquoted Marilyn in order to twist the problem towards their solution. And imposed a frequentist interpretation on probability, thus making the problem more difficult). One of the three arguments here is decision theoretic (and makes the competitor also active in his choice of door choice strategy). The other two use subjective probability and symmetry, partly explicitly partly implicitly. All the argumentments are simple, intuitive, insight-increasing... and correct. Richard Gill (talk) 05:35, 23 September 2012 (UTC)
- Just to clarify (since I've inadvertantly upset him) - I'm not criticizing Rick because his solution is long, and I apologise if he thought I was. It takes as much space as it needs (and I was exaggerating a tad). My concern is that I don't think it's particularly intelligible for the reader. In terms of the described outcome, it's plainly not any more 'right' than vos Savant's original solution(they both say you'll win twice as many times by switching), so in that sense it's just a more complicated way of getting to the same answer.Elen of the Roads (talk) 22:25, 21 September 2012 (UTC)
- Apology accepted. However, the point is not whether one solution is more 'right' than another, and how intelligible the conditional solution night be is mostly irrelevant. Per WP:MTAA "It is important not to oversimplify material in the effort to make it more accessible", but we should of course make it as intelligible as is humanly possible. The point is how often and in what kind of sources these solutions appear. The fact is that many, many sources publish conditional solutions. In addition, sources keep being published distinguishing "simple" and conditional solutions, and explicitly expressing a preference for conditional solutions (Morgan et al. in 1991, Gillman in 1992, Eisenhauer in 2001, Rosenthal in 2005, Grinstead and Snell in 2006, Lucas et al in 2009). Per NPOV the article must represent "fairly, proportionately, and as far as possible without bias, all significant views that have been published by reliable sources". Omitting a conditional solution from the initial "Solution" section (as Proposal 1 would) IMO creates a strong bias. -- Rick Block (talk) 03:25, 22 September 2012 (UTC)
- And other sources keep criticizing the sources you've named for deliberately misrepresenting Vos Savant, narrow-mindedness regarding interpretation of the the problem, dogmatism, and apparent unawareness of alternative ways to express a simple argument in more formal mathematical terms. If door numbers are irrelevant by symmetry then insisting on emphasizing that the 2/3 chance of winning by switching is also the conditional chance of wining by switching given ... is obfuscation. But, if there are short sharp insight-increasing simple solutions built around conditional probability (there are: the Bayes theorem odds form argument) then they belong at the front of the article. (Simple Bayes: Assume symmetry. Initially the odds are 1:1 that the car is behind your chosen door, door 1, or behind door 2. The host is twice as likely to open door 3 in the second case than in the first case: in the second cases he's certain to do so, in the first case there's only a 50% chance he'll do so. So after he's opened door 3 the odds on door 1 versus door 2 have changed to 1:2, by Bayes' rule. The reader who doesn't know what odds are and what Bayes' rule is, is hopefully enticed to read on and learn more. There are reliable sources aplenty who give this argument.) Richard Gill (talk) 06:00, 23 September 2012 (UTC)
- The Lucas et al. paper is excellent. It does *not* say that unconditional solutions are wrong. It *is* all about conditioning and about showing how Bayes helps you solve all kinds of complicated variants of MHP. It does have a short verbal argument in the intro. Assume symmetry. Given: you chose door 1. The probability the car is behind door 1 and the host opens door 3 is 1/3 * 1/2 = 1/6. The probability that the car is behind door 2 and the host opens door 3 is 1/3 x 1 = 1/3. These are the only two possibilities. The second probability is twice the first. So you should switch. This is a correct argument and it's simple. It belongs among the "simple solutions". Richard Gill (talk) 06:41, 23 September 2012 (UTC)
- Which "other sources keep criticizing the sources [I've] named for ..."? Please be specific. Even if you can cite such sources my point remains valid. In your opinion (and presumably the opinion of any sources you might be able to cite), the sources I'm citing are full of crap. However, this simply further demonstrates the fact that this is a POV issue. Wikipedia simply cannot take sides, regardless of what anyone (even Richard Gill) thinks (unless we're talking fringe opinions, which we're not). "Many sources say 'simple' solutions are inadequate" is a true statement. This is not the same as saying "simple solutions are inadequate" - which seems to be a matter of opinion. Do you agree? -- Rick Block (talk) 07:01, 23 September 2012 (UTC)
- A number of the published discussion contributions to Morgan et al. criticised them soundly. Also, if I remember correctly, Jason Rosenhouse criticises them too. So does R.D. Gill. And finally, Morgan et al. retracted their original harsh criticism of Vos Savant. I do not say that the sources you are citing are full of crap. They contain much that is of value. What they say should be taken in context. I agree that it's a matter of opinion as to whether or not simple solutions are inadequate. And depends very much on which simple solution you are talking about. They are not all the same. A guy called Bell in the discussion of Morgan's original paper already wrote that it was a matter of taste whether or not one was explicit about symmetry assumptions. And of course Wikipedia can't take sides. The question is how much weight should be paid to this "matter of taste". In my opinion, not a great deal. I would prefer to treat Wikipedia readers as intelligent persons who can do any judging for themselves. The level of precision and expliciteness which one might require in a probability class is not the same as the level of precision and expliciteness which one requires in a popular discussion of a popular brain-teaser. Moreover we saw again when comparing the arguments given by the Economist and by Parade, that writers from economics and decision theory have a very different way of looking at MHP. No K&P assumptions at all, probability is entirely in the hands of the contestant! I'd say that it's up to those who are fond of the conditional solution to present it as attractively and accessibly as possible to the readers. Preferably at two levels; first short and informal/intuitive, among the other short informal/intuitive arguments; secondly at greater length and with the level of mathematical precision one would find in an introductory probability text. If this had been done long ago we wouldn't be arguing about these things today. Richard Gill (talk) 12:24, 23 September 2012 (UTC)
Proposal: Rewrite the section on conditional probability!
Yes, I agree, it was difficult to tell apart the two proposals, which is why I voted "both". I suspect that other votes were spurious, due to the confusing wording in the proposals. To be practical, I see two issues:
- The section in this article, on conditional probability, is written very badly, and is very difficult to understand, even if one is an expert in probability theory. This needs to be fixed.
- It becomes clear from the arguments above that many supporters of the "conditional probability" solution have a rather weak grasp on how probability calculations are done, or even the place of conditional probability in the historical sweep of the subject. There is a failure to see how various solutions are in fact equivalent, and how different solutions can be transformed into one-another. This confuses the issues.
If the section on conditional probability is fixed so as to be clear, then perhaps much of the argumentation will fall away. So, I propose: focus on editing the conditional probability section so that ordinary readers can understand it, and then all of the other issues will fall away.
How bad is it? Its bad. Really bad. When I first read it, it seemed obviously full of errors, and I was about to start editing to fix all of them. On closer read, I saw that it was, in fact, more or less correct. But its developed in such a totally confusing, obtuse fashion, that most readers will be utterly perplexed by the "explanation" given there. And so they will react badly to it. Fix that section so that it is at least coherent. The rest will follow. linas (talk) 14:29, 21 September 2012 (UTC)
- Can you clarify? Are you talking about the initial text (and figures) in Decision tree, the text (mostly formulas) in Formal solution, the text in Odds, the text in Simple solution and symmetry proof, the text in Total symmetry proof, or the text plus formulas in Bayes' theorem? These sections together have no particular flow or coherence (i.e. no one has made any attempt to consolidate them into a single section presenting them as various equivalent ways to arrive at the conditional probability). Under Proposal 2 the suggestion is to include in an initial "Solution" section only the most accessible conditional solution(s), which I think would be something like the initial text and figures in Decision tree. Would you say this section, in isolation, is "Really bad"? -- Rick Block (talk) 16:15, 21 September 2012 (UTC)
- One thing that might be an improvement is to use just one figure, instead of two equivalent ones (less is more). That way the reader could concentrate on just one, and the text could refer to its parts more explicitly.
- The text starts calculating "conditional probability of winning by switching given which door the host opens" without explaining what that means, and how it differs from the unconditional probability. I think you end up providing the reader yet another number whose meaning they don't really understand! To understand the meaning of the unconditional and conditional probabilities here, you need to understand the difference, or you probably didn't actually understand either. I suggested a way of doing that in the "Simpler (if longer) description of the conditional solution by simulation" section, which can probably be condensed quite a bit if you don't want to actually go into simulations. Essentially, think of going to the show and filtering out the cases that match the problem description in all particulars and look at the frequency of winning among those cases, vs. doing the same without filtering. That is understandable to anyone.
- The meat of the section is this paragraph:
- Assuming the player picks door 1, the car is behind door 2 and the host opens door 3 with probability 1/3. The car is behind door 1 and the host opens door 3 with probability 1/6. These are the only possibilities given the player picks door 1 and the host opens door 3. Therefore, the conditional probability of winning by switching is (1/3)/(1/3 + 1/6), which is 2/3.
- Taken alone, this is confusing, and no reference is made to the diagrams, so the reader is left to puzzle out that too for themselves. It would probably be clearest if we could use more concrete terminology, even if it doesn't sound all formal-like. E.g. "Consider what happens in the long run when you go on a simulated game show many times and always pick Door One yourself. If the host opens Door Three as described, there are only two possible explanations:
- the car is behind Door One (your door), and the host opened Door Three by sheer chance. Switching loses.
- the car is behind Door Two (not your door), and the host had no choice but to open Door Three. Switching wins.
- Explanation (1) is clearly less likely, as it can only occur by sheer chance. The decision tree diagram (right) shows case (1) on the first bolded path and case (2) on the second bolded path, and that case (1) occurs 1/6 of the time and case (2) occurs 1/3 of the time. Case (2) occurs twice as often as case (1), because 1/3 is twice 1/6. This means that if you keep a record of the simulated show, then among the cases that exactly match the problem description (the cases (1) and (2) where the host opens Door Three), case (2) where switching wins occurs twice as often as case (1) where it loses. Therefore switching wins with probability 2/3 in the problem as described." You'd need to bold the two relevant paths in the diagram and it would be good to explain how to read the thing in the figure text, too ("The number at each branching point shows the probability that the branch is taken. One of the branches is always taken, so at each branching point the probabilities sum to one (1/3+1/3+1/3 = 1 and 1/2+1/2 = 1).", and something about the joint probabilities on the right). -- Coffee2theorems (talk) 10:04, 22 September 2012 (UTC)
- The meat of the section is this paragraph:
- The section 'formal solution' is the one that really set me off. I had skimmed the one right before, 'decision tree', because I couldn't follow it; coffee2theorems explains why. The section 'formal solution', if written correctly, would probably look like 'Bayes theorem', at the very end of the article. The title 'formal solution' is misleading; one does not need Bayes thm to solve the problem, nor is the solution somehow 'better' or 'more formal' by using it. Perhaps deleting the entire section called 'formal solution' would be best. linas (talk) 13:58, 23 September 2012 (UTC)
Proposed text for Solution section
While there's widespread interest, can I get comments on the following proposed text (motivated to some extent by Linas's comments above)?
Proposed text for Solution section
| ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
There are two main approaches to solving the Monty Hall problem. One is to compare a strategy of switching (always switching to whichever door the host doesn't open) with a strategy of staying. The other is to evaluate the conditional probability the car is behind door 2 given the player picks door 1 and the host opens door 3. Because the problem is symmetrical, these two approaches show (and must show) the same result - switching wins the car 2/3 of the time. Most popular sources present solutions comparing a strategy of always switching with a strategy of always staying with the player's initial choice. For example, the solution presented by vos Savant in Parade (vos Savant 1990b) shows the three possible arrangements of one car and two goats behind three doors and the result of staying or switching after initially picking door 1 in each case:
A player who stays with the initial choice wins in only one out of three of these equally likely possibilities, while a player who switches wins in two out of three. Thus, a player who picks door 1 should switch to whichever of door 2 or door 3 the host doesn't open, and by doing so will win the car with probability 2/3. The other main approach to solving the problem, used primarily in academic sources, is to treat it as a conditional probability problem. The probability the car is behind any one of the doors before the host opens a door is 1/3. The probability the car is behind Door 2 after the player picks Door 1 and the host opens Door 3 is the conditional probability the car is behind Door 2, usually written as: 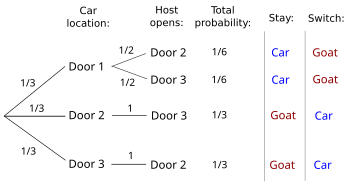 This conditional probability can be determined referring to the figure below, or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138). In each figure, it is assumed that the contestant initially chooses door 1. The probability can also be formally derived as in the mathematical formulation shown in the appendix. If the player picks door 1, the car is behind door 2 and the host opens door 3 with joint probability 1/3. The car is behind door 1 and the host opens door 3 with joint probability 1/6. These are the only possibilities given the player picks door 1 and the host opens door 3. Therefore, the conditional probability the car is behind door 2 is (1/3)/(1/3 + 1/6), which is 2/3. (Morgan et al. 1991) The intuition behind this solution is that the host must always open Door 3 if the car is behind Door 2, but opens Door 3 only half the time the car is behind Door 1 - so a player who switches wins twice as often as a player who doesn't. |
Comments on the proposed text
This is intended to follow the Proposal 2 approach (both "simple" and "conditional" in one Solution section, with neither presented as "more correct" than the other). In the article this would follow the "Extended description" section (replacing the entirety of what is now the "Solutions" section), and like any other article content here would (of course) be able to be edited at will. If you read this, could you at least add a quick "I like it" (it's in the right ballpark, you'd be able to live with this without a complete rewrite), "I hate it" (needs to be completely rewritten), "meh" (might be OK - doesn't thrill you but doesn't offend you either) sort of comment? Thanks. -- Rick Block (talk) 03:44, 22 September 2012 (UTC)
- I like it <user sig here>
- I hate it <user sig here>
- meh <user sig here>
I'll say I like it, because it's broadly speaking in the right direction, but there's nevertheless much that I would change in it. It's good in that it attempts to explain the sources' POVs about the "standard MHP" in a coherent and understandable manner with due weight, and that's the right thing to do. It's the "attempts" part that I have some comments about. In addition to what I said in the Proposal: Rewrite the section on conditional probability! section, I'll say these:
- The "strategy" thing doesn't actually distinguish between conditional and unconditional solutions, and readers will probably fail to understand it that way. You can follow a "always switch" strategy regardless of whether someone is going to analyze your chances of winning using an unconditional or conditional probability calculation. I'll reiterate that explanation using a simulation is probably the only way to get the difference understood properly.
- "The problem is symmetrical" is not enlightening. Symmetrical how? Why does that matter? Something along the lines "It can be shown (see section [symmetry section]) that the two approaches necessarily produce the same result, because the problem and the answer remain the same if the door numbers are permuted in the problem description, making the door numbers irrelevant." would be more like it, but do we really need to even add the "because" part here and is it helpful? "It is shown in section [symmetry] that ..." would suffice, IMO.
- The P(... | ...) is not used anywhere so mentioning it is rather pointless.
- Here it is even more painfully obvious that the conditional solution should only have one diagram (I prefer the decision tree), as it takes up so much space in comparison to the MvS table.
- Wikipedia article with an appendix? Ow. Rather just link to the formal solution section, and that can come as the last sentence in the text, just like "Further Reading" is usually at the bottom.
The material here is not rocket science. It can be written in a way understandable to anyone. -- Coffee2theorems (talk) 11:51, 22 September 2012 (UTC)
As it stands, it's way too complicated to be the section you use to explain the answer. Coffee2theorems I think is right that it can be written much better, so in addition to Coffee's points above, all of which are good, here's what doesn't work for me
- putting the conditional probability tree and vos Savant's table near to each other, because they appear to contradict each other. Of course the little 1/6 and 1/3s mean that it doesn't, but put next to each other it looks as if it does, because one appears to show there is no advantage to switching. Moving them apart or laying the table out differently would both work, but I gather the table layout appears in books that way, so a redraw may suffer from the accusation of OR.
- I found the picture table to be just incomprehensible. Putting a section in with a note 'this hasn't happened' isn't at all clear. You would need to sit down with a pencil and paper and redraw it yourself to understand it.
- The text from "If the player picks door 1..." is equally unclear. If that's how sources write it, then we have a problem, because the average reader won't understand either 'joint probability' or 'intuition' (indeed, I'm not convinced intuition is at all the right word here, unless it has some specific meaning in maths).
- No appendices. But the Bayes write out can comfortably go in another section.
So, too complicated as is, but I'm sure I can see the light. Elen of the Roads (talk) 17:30, 22 September 2012 (UTC)
- I hate it because it is far too complicated.
- Proposal: instead of the tree, imo it was better to show the very clear answer of this table in en.citizendium.org, section "Explicit Computations", btw this article having been cited repeatedly by academic sources meanwhile. Gerhardvalentin (talk) 18:01, 22 September 2012 (UTC)
I suck at markup, but I agree with Gerhardvalentin about using a table not a tree. The contrast between the two solution then looks something like
| Your door | The door Monty opens | The other door has the | result if switching | result if staying |
|---|---|---|---|---|
| Car | Goat | Goat | Goat | Car |
| Goat | Goat | Car | Car | Goat |
| Goat | Goat | Car | Car | Goat |
| Door 1 | Door 2 | Door 3 | result if switching | result if staying |
|---|---|---|---|---|
| Your door has the car | Monty opens to show a goat | has a goat | goat | car |
| has a goat | Monty opens to show a goat | |||
| Your door has a goat | Monty opens to show a goat | has the car | car | goat |
| Your door has a goat | has the car | Monty opens to show a goat | Car | Goat |
If you take table 2 and put the probabilities in, it has a chance of making sense.Elen of the Roads (talk) 18:23, 22 September 2012 (UTC)
- Strange, to me the tree is much clearer than a table — it contains the same information in essentially the same format, but the structure is visually more obvious. I'd just bold the two relevant paths (and corresponding texts) so that the reader knows what to compare with what, and add more explanation to the figure text. Also, the citizendium version's use of 1/3×1/2 and 1/3×1 instead of 1/6 and 1/3 is actually a good idea, as it shows how the values were obtained and makes it clearer that one is twice as big as the other.
- If one were really going for eye candy, one could make a separate, animated figure of a simulation, where the path taken by the simulation is slowly highlighted on the tree and next to it a log of what happened and a running tally shows how the winning frequency approaches 2/3. That might be asking for too much, though :) -- Coffee2theorems (talk) 18:51, 22 September 2012 (UTC)
- You're going to need a better coder than me (not hard!). I think the tree can be improved - it's the present format that troubles me. Is the use of 1/3*1/2 an issue source wise (surely not - anyone using 1/6 must have derived it). The more you start from the beginning, the clearer it is. Incidentally, is table 1 pure OR or has a published source phrased it that way (no door numbers, just 'your door', 'Monty's door' and 'the other door') Elen of the Roads (talk) 19:20, 22 September 2012 (UTC)
- The content in Elen's first table is at least usually presented the way vos Savant did, i.e. with door numbers (which is the table already in the article). Using door numbers both connects it to the example given in the problem statement ("You pick a door, say No. 1, ...") and makes it clear why there are three rows (the repeating rows 2 and 3 seem very strange). Vos Savant's table makes it very difficult to see what happens in the case where the host opens door 3. The point of the conditional solution is to address this specific case, so perhaps a table like this (similar to tables I've suggested before):
| Situation before the host opens a door | Situation after the host opens a door | ||||||
|---|---|---|---|---|---|---|---|
| Door 1 (your door) | Door 2 | Door 3 | probability | host opens Door 2 | host opens Door 3 | ||
| probability | result if switching | probability | result if switching | ||||
| Car | Goat | Goat | 1/3 | 1/3 x 1/2 = 1/6 | Goat | 1/3 x 1/2 = 1/6 | Goat |
| Goat | Car | Goat | 1/3 | 0 | N/A | 1/3 | Car |
| Goat | Goat | Car | 1/3 | 1/3 | Car | 0 | N/A |
- This table is equivalent to the tree diagram (and the large figure as well). It shows that whatever door you see the host open, you win with probability 1/6 if you stay with your initial choice but with probability 1/3 (twice as often) if you switch (which, expressed as conditional probabilities are 1/3 and 2/3). If you're only interested in the "host opens door 3 case" you ignore the "host opens door 2" column. -- Rick Block (talk) 21:43, 22 September 2012 (UTC)
My proposal
Taking into account Richards comments, this is what I propose to follow the problem section. It is simple, and makes no special claims of correctness. I do not care about the order of the explanation and, do doubt, we could come up with some more imaginative titles.
Proposed text for Solution section
| ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
AnswerThe contestant should always switch to the other door; contestants who switch double their chances of winning the car by switching. Simple explanationsExplanation 1A simple and intuitive explanation is to reason that a player whose strategy is to switch loses if and only if the player initially picks the car, which happens with probability 1/3, so switching must win with probability 2/3 (Carlton 2005). Explanation 2The analysis can be illustrated in terms of the equally likely events that the player has initially chosen the car, goat A, or goat B (Economist 1999): Explanation 3The solution presented by vos Savant in Parade (vos Savant 1990b) shows the three possible arrangements of one car and two goats behind three doors and the result of staying or switching after initially picking door 1 in each case:
A player who stays with the initial choice wins in only one out of three of these equally likely possibilities, while a player who switches wins in two out of three. The probability of winning by staying with the initial choice is therefore 1/3, while the probability of winning by switching is 2/3. Explanation 4Another way to understand the solution is to consider the two original unchosen doors together. Instead of one door being opened and shown to be a losing door, an equivalent action is to combine the two unchosen doors into one since the player cannot choose the opened door (Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008). As Cecil Adams puts it (Adams 1990), "Monty is saying in effect: you can keep your one door or you can have the other two doors." The player therefore has the choice of either sticking with the original choice of door, or choosing the sum of the contents of the two other doors, as the 2/3 chance of hiding the car has not been changed by the opening of one of these doors. As Keith Devlin says (Devlin 2003), "By opening his door, Monty is saying to the contestant 'There are two doors you did not choose, and the probability that the prize is behind one of them is 2/3. I'll help you by using my knowledge of where the prize is to open one of those two doors to show you that it does not hide the prize. You can now take advantage of this additional information. Your choice of door A has a chance of 1 in 3 of being the winner. I have not changed that. But by eliminating door C, I have shown you that the probability that door B hides the prize is 2 in 3.'" |
— Preceding unsigned comment added by Martin Hogbin (talk • contribs)
Comments on Martin's proposal
My comments on this one:
- It starts simple, which I like. In particular, stating up front the simple fact that switching doubles the chances of winning is good, and so is Carlton's explanation.
- I don't like the Economist explanation much, and would remove it. It's a minor and less complete variant of vos Savant's solution that doesn't match the problem description as well. vos Savant assumes that the player picks door 1 (as described) and that the car might be anywhere. The Economist assumes that the player picks any door instead of always door 1, and assumes that car is always behind door 1 (what??). Certainly it is easily completed ("cases where the car is behind other doors are similar"), but there's no reason to use it when vos Savant's version doesn't have these problems. (randomizing player's choice is necessary for optimality in certain game theoretic extensions of the problem, but that subtlety is going to be totally lost on the reader unless explicitly pointed out, whereas the car always being behind door 1 in the diagram might actually confuse someone)
- vos Savant's solution could be made clearer by replacing the table with a diagram similar to the one in the Economist solution, except that it should of course be equivalent to vos Savant's table. It could incidentally double as an illustration for Carlton's argument.
- "Explanation 4" section should just be deleted. There's no point in turning this into a gallery of every solution ever proposed, and these do not provide any additional insight.
- The conditional solutions are missing, which is both a POV problem and results in lack of discussion of many of the issues involved which I'll not rehash again here.
- Having simulations covered in this section would be good.
In short: instead of having a zillion minor variants of the same unconditional solution, have just one and explain it well, and then do the same for the conditional solution. Quantity is no substitute for quality! The text has a distinct "Oh sorry that explanation sucked so let me try again.. oh not that one either, so how about if I tweak here a little.. bear with me, I'll get around to a good one any time now!" feel to it, and that's bad. The unconditional solution would probably best be explained by a combination of Carlton's short statement and vos Savant's solution illustrated using a nice picture instead of an equivalent table. -- Coffee2theorems (talk) 11:08, 23 September 2012 (UTC)
- The Economist's solution is not a minor variant of the same unconditional solution. It is a different approach, common in the economic and decision theoretic literature. It does not assume that the car is always behind Door 1. It calls the door behind which the car is located, Door 1.
- Incidentally, many wikipedia editors have in the past spontaneously come up with the same approach. It represents a way of thinking about MHP (strategic/decision oriented) which is common and legitimate and different from the usual subjectivist (probabilistic) approach. Richard Gill (talk) 12:33, 23 September 2012 (UTC)
- ... OK. That's interesting, but most people are probably going to think of the doors numbered 1, 2, 3 from left to right on stage. The figure also has the doors ordered from left to right, and the car is always behind the leftmost door in it. It would need some kind of disclaimer that no actual spatial relationship is implied by the figure ("the leftmost door in this figure is not necessarily the leftmost door on the stage, it's instead the door we call 'door 1'"). I think that's an additional source of confusion we don't need, at least not in the first solution section. -- Coffee2theorems (talk) 21:58, 23 September 2012 (UTC)
- I agree with Coffee2theorems that we don't want a zillion minor alternatives. I think we want representatives of some main classes of alternatives. I would also want to see an informal/intuitive short and snappy form of a solution based on the conditional probability approach here too. e.g.. paraphrased from Lucas et al (2009) Assume symmetry. Given: you chose door 1. The probability the car is behind door 1 and the host opens door 3 is 1/3 * 1/2 = 1/6. The probability that the car is behind door 2 and the host opens door 3 is 1/3 x 1 = 1/3. These are the only two possibilities. The second probability is twice the first. So you should switch. Richard Gill (talk) 12:38, 23 September 2012 (UTC)
- I rather like this argument. It's almost as simple as Carlton's simple argument. I'd leave the rather cryptic "Assume symmetry." out and just rely on the K&W assumptions, though. (symmetry implies K&W and the other way around, so it's equivalent anyway! except that the reader can actually understand how to get the numbers "1/3" and "1/2" from the latter) -- Coffee2theorems (talk) 00:04, 24 September 2012 (UTC)
- Yes, symmetry implies K&W and the other way around, so it's equivalent anyway!. This is fully correct, yes. But consider that the simple common argument of K&W ("host chooses randomly" if in 1/3 he has got "two goats" to show), what implies symmetry (Henze calls it "secrecy" regarding the car-hiding door) for years has completely been faded down, a permanent conflict. Meanwhile we know from the sources that symmetry a priori is implicit in the paradox, so that K&W and Henze more or less only are a concession to new readers who did not check that yet. But: just to avoid confusion, imo all three wordings should explicitly be mentioned: "at random", as well as "secrecy" and "symmetry". This is just my thought, and as said, just to avoid ongoing confusion and ongoing argument "can only correctly be solved by conditional probability". I would be happy if that wasn't necessary . . . Gerhardvalentin (talk) 17:26, 24 September 2012 (UTC)
- My thoughts.
- I like Carlton's initial statement and agree with Coffee2theorems that one diagram - vos Savant's table with pictures - plus Carlton's statement, is a good 'simple explanation'
- I think you could introduce a conditional here - 'many mathematicians prefer to write out the solution taking into account which goat monty shows if you pick the car'..... with either a table or a diagram that shows clearly that it comes to the same answer.
- Simulations, explanations in terms of game theory or strategy, and answers written in Bayesian notation should each have their own heading which describes the approach taken, avoiding falling into the trap C2t described.
- I also think (and I seem to be alone in this) that the first section should explain why the missing assumption in vos Savant's statement of the puzzle (that Monty is forced to show a goat/that Monty will never show the car) is vital, because if Monty always picks a door at random and can show the car, there's no advantage in switching. Elen of the Roads (talk) 13:02, 23 September 2012 (UTC)
- +1, my thoughts, too. - For the readers, "The article first should show the common assumptions"). Even if, for the expert, never necessary as a presupposition.
Because what one has down in black and white, it is a comfort to take home at night. Gerhardvalentin (talk) 13:35, 23 September 2012 (UTC)- I think we need a number of simple alternatives because different explanations work for different people. Explanation 4 is one that may work for people who do not like the others. If any I would drop the vos Savant table.
- +1, my thoughts, too. - For the readers, "The article first should show the common assumptions"). Even if, for the expert, never necessary as a presupposition.
- I am not remotely suggesting that these are the only solutions. My suggestion is that we could follow Explanation 4 with a discussion of why it matters that the host knows the position of the car as this follows naturally, from the 'Combining doors' section. From there we could lead into the possibility that the host might not choose evenly as another demonstration of the significance of conditional probability to this problem. Martin Hogbin (talk) 13:48, 23 September 2012 (UTC)
- That the MHP quite often is used in textbooks teaching conditional probability theory, with various adventuresome "assumptions" for getting different values of probability to win by switching within the firm scale of 1/2 to 1 and a firm average of unchangeable 2/3 (as each "result" corresponds to the optional "adoption"), should be shown in later sections. Conditional probability theory is not "needed" to decode the paradox, but the MHP is a useful example in training conditional probability theory. And: just in order to very clearly show that a host, in exceptionally opening of that special one door that he usually is "strictly avoiding to open, if ever possible", does give the additional info that his preferred but closed door actually is most likely to hide the prize, doesn't need Bayes formula, either. Gerhardvalentin (talk) 14:45, 23 September 2012 (UTC)
- vos Savant's table fits the way I would guess most schoolchildren are taught simple probability theory - you write out all the options and count 'em up, then Teech shows how you can achieve the same effect with some simple multiplication (provided you can multiply fractions). The much argued over 'conditional solution' does exactly the same thing, only allows for the fact that if your door has the car behind it, Monty has a choice of doors he can open. Using 'write out all the options' and some simple multiplication, and you really can show both solutions at the same time, because they use the same approach. This is why I think all the other approaches deserve their own sections, where you can if you like add in a bit of context for the approach. Elen of the Roads (talk) 15:11, 23 September 2012 (UTC)
- I nearly completely agree with Coffee2theorems. I'm not sure it's any more clear than the table, but here's a figure version of vos Savant's table. -- Rick Block (talk) 17:12, 23 September 2012 (UTC)
Figure version of vos Savant's table
| |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||
Rick, above I read a hint, a plausible statement to "decoding" the paradox. It says
- partitioning the doors between "your door" and "Monty's doors" is the most persuasive explanation, and just suggesting the partition is often enough of a hint.
I would like to suggest, in your above clear visualization, to "enframe" all seven groups of two host's doors on the right side, as per Martin's visualization. Just to help the reader from the start to distinguish those two groups:
- "group of just only one door selected" versus
- "group of two unselected host's doors"
Imo such hint will help the article, and could assist the reader to "decode" the paradox, as one editor expressed above. Gerhardvalentin (talk) 19:03, 23 September 2012 (UTC)
- Comment on the new figure: This may be just me and probably sounds a bit silly, but I think the Economist's format for the figure is clearer. I think it's partly because in it you have the cases stacked vertically instead of horizontally. We read from left to right and then top to bottom, and in Economist's format that tendency results in you naturally considering each case one at a time, and then looking at the whole picture once you've read all of it (also, time usually goes from left to right, not top to bottom). The arrows, the black bars separating the cases, and the numbers on the left also probably help. -- Coffee2theorems (talk) 21:34, 23 September 2012 (UTC)
- Seems like this has come up before. The columnar format allows their widths to be proportional to their probability (essentially regardless of browser window size) - a fairly subtle effect but I think it helps comprehension (doing this with rows in html is much harder). Feel free to try if you want. And (BTW) I'm not sure how similar the other figure is to the actual diagram from the Economist. The online version [8] omits the figure. I believe the figure here was created independently by user:Father Goose and sourced (after the fact) to the Economist. -- Rick Block (talk) 22:05, 23 September 2012 (UTC)
- How about with thick lines between the columns, per above? Another reason for this columnar orientation is it transitions very nicely to the conditional view (as shown in the next section). If we're going to have multiple figures I think it's important to pick an orientation and stick with it. -- Rick Block (talk) 15:31, 24 September 2012 (UTC)
- It actually helps a bit. BTW, Krauss and Wang had plenty of suggestions about how to describe the problem. What do you think about the modified figure below?
Modified figure using K&W (&Carlton) suggestions
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||
- I tried to make it similar to both vos Savant's table and K&W figure 1, and count cases instead of using probabilities as K&W say is better psychologically (note that not elaborating on Monty's behavior in case 1 is a point of theirs, presumably because splitting it into two cases might confuse when counting cases). I also tried to tie this in with Carlton's explanation by always "switching away from" whatever is behind door 1. -- Coffee2theorems (talk) 18:16, 25 September 2012 (UTC)
Towards agreement?
Although 1 and 2 are not exactly the same perhaps we could combine them in one section for brevity. I prefer the figure to the table for vos Savant's explanation. I think 4 is essential because it comes at the problem from a different angle. It also relies on the probability that door 1 hides the car remaining 1/3 after the host has opened a door. This is not the case if the host has opened an unchosen door randomly and this just happens to hide a goat to we can use this difference to show that it matters that the host knows where the car is and to lead on to discuss conditional probability. Martin Hogbin (talk) 19:45, 23 September 2012 (UTC)
- The article has been opaque for years now. Please observe that the common incorrect first intuitive common appraisal of "1:1" should explicitly be addressed, immediately after section one, in showing the strange variant of a "forgetful host".
- You don't need conditional probability to show that such forgetful host, by just randomly opening one of his two doors, be it the car in 1/3 or be it a goat in 2/3, inevitably will be "showing the car in 1/3", and by that is deleting the possibility to win by switching in that 1/3.
- Result: probability to win by switching has been reduced to 1:1 in the remaining 2/3 ("car:goat" and "goat:car"). This should very clearly and very prominently be shown as an eye-opener. You don't need Bayes, to show that. Gerhardvalentin (talk) 20:44, 23 September 2012 (UTC)
- IMO, 4 belongs in an "aids to understanding" section, not the initial explanation section. And a conditional solution needs to be included with the simple solutions. How about the following for an accessible conditional view (please note how symmetrical the figure is)? -- Rick Block (talk) 21:03, 23 September 2012 (UTC)
transition to a conditional probability view
| ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
A player who picks door 1 and switches to whichever door the host doesn't open wins the car with probability 2/3. But what about a player who picks door 1 and sees the host open door 3? [NOTE: this is here to connect to the mental model the reader almost certainly has in his/her head. We can talk about this if anyone's going to seriously be perturbed by this.] After the player picks door 1, the host must open either door 2 or door 3. What happens in each of these two cases can be seen by rearranging one of the figures above as follows:
Whichever door the host opens, switching wins the car with twice the probability of staying with the initial pick. For example, if the host opens door 3 either the car is behind door 2 (this occurs with probability 1/3) or the car is behind door 1 and the host randomly chose to open door 3 (this occurs with probability 1/3 x 1/2 = 1/6). | ||||||||||||||||||||||||
We are getting there I feel. Elen of the Roads (talk) 21:09, 23 September 2012 (UTC)
- NIce. I suggest rewriting the two "punchlines" in the table as "If the player picks door 1, then the host opens door 2 and switching wins with probability 1/3 and loses with probability 1/6", and "If the player picks door 1, then the host opens door 3 and switching wins with probability 1/3 and loses with probability 1/6". The point is that the probabilities you give of 1/3 and 1/6 are probabilities given the player picks door 1, of events which include the host's choice. Richard Gill (talk) 04:13, 24 September 2012 (UTC)
- Question for those more familiar with the sources: Have you seen this kind of variant of the above kind of table somewhere? (I'm sort of betting on being unable to come up with anything original about the MHP here.. :)
Door 1 Door 2 Door 3 Host's coin toss Host's door choice Result if switching Possible Car Goat Goat Heads Door 2 Loss No Car Goat Goat Tails Door 3 Loss Yes Goat Car Goat Heads Door 3 Win Yes Goat Car Goat Tails Door 3 Win Yes Goat Goat Car Heads Door 2 Win No Goat Goat Car Tails Door 2 Win No
- You always pick door 1. The host always tosses a coin, and picks door 2 if heads and door 3 if tails, except when he is forced to pick a particular door. There are only three possibilities that match the problem description, of which two win, so the probability of winning by switching is 2/3.
- The reason I'm asking this is that K&W says that counting cases is more intuitive than dealing with probabilities as such, and the former can be made possible by using a little trick like this. Otherwise it's pretty much the same thing. -- Coffee2theorems (talk) 21:03, 25 September 2012 (UTC)
- This is conceptually identical to the wheel diagram used here. This particular source has been criticized earlier as perhaps not the most reliable (its an unsigned subpage of the homepage of a university course - probably created by some grad student). It's similar to the 6 mental model representation K&W describes (attributed by them to a 1999 paper I don't have by Johnson-Laird, Legrenzi, Girotto, Legrenzi, and Caverni). -- Rick Block (talk) 01:06, 26 September 2012 (UTC)
- Right, such a web page is unfortunately not a stellar source. Another way to avoid probabilities would be to count the number (or proportion) of people doing something instead, and that would avoid changing the solution. Something like the following maybe?
Trying to count players instead of probabilities
| ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||
- In addition to counting players instead of probabilities, I also tried removing and de-emphasizing (where removal would be more confusing) material that does not answer the question at hand (host opens door 3 case) because of the "less-is-more effect" K&W mentioned. That way, when you are trying to look where the numbers etc. came from in the next step, you're not so distracted by irrelevancies. What do you think? (there are a few modifications here, and it may also be that some are good and some bad) -- Coffee2theorems (talk) 10:16, 26 September 2012 (UTC)
Back to where we started
We are now pretty much back where we started with, as Gerhard says, an opaque article which confuses the reader with conditional probability before addressing the crucial issue of why it matters that the host knows where the car is. If you look through the talk pages you will see that that issue comes up time after time. On the other hand the door opened by the host is never mentioned.
I am not saying that Rick's table should not be in the article just that we need to address the most common questions that newcomers wish answered. Conditional probability is of much more interest to the more expert reader and in my opinion it should be addressed in a more scholarly manner. Martin Hogbin (talk) 15:02, 24 September 2012 (UTC)
- I think it is important to address conditional probability in an unscholarly manner! Make it accessible to all. Rick's table shows that the probability of winning by switching is twice the probability of winning by staying, both when the host opens door 2 and when the host opens door 3. There is no mention of conditional probability. If this is considered too much detail early on in the article, why not just reproduce the Lucas, Rosenhouse, and Schepler (2009) verbal argument: Given: you chose door 1. The probability the car is behind door 1 and the host opens door 3 is 1/3 * 1/2 = 1/6; the "times half" is here because the host has two alternative choices! The probability that the car is behind door 2 and the host opens door 3 is 1/3 x 1 = 1/3; the "times one" is here because the host has no choice in this case. These are the only two possibilities. The second probability is twice the first. So you should switch. Note that Rosenhouse is the guy who wrote a whole book on MHP, also appeared in 2009. Richard Gill (talk) 16:40, 24 September 2012 (UTC)
- Richard - you are sounding more and more like a Proposal 2 kind of guy. Can I ask you to review your response to the RfC? AFAICT, if you think it is important to address conditional probability (in any manner, scholarly or not) you are not in favor of Proposal 1. -- Rick Block (talk) 18:35, 24 September 2012 (UTC)
- I am veering more and more to a "neither" guy as far as proposal 1 versus proposal 2 is concerned. I would like to see the initial parts of the article present various *different* arguments, all of them accessible to a broad audience, and all of them correct: these should represent the broad range of ways that different people have approached MHP. It would be obvious that the different arguments make *different* assumptions. If reliable sources have presented simple arguments which from a mathematician's point of view are actually formalizations of a conditional probability argument, then I fail to see why they should be excluded from the early part of the article. Richard Gill (talk) 11:59, 25 September 2012 (UTC)
- Richard - you are sounding more and more like a Proposal 2 kind of guy. Can I ask you to review your response to the RfC? AFAICT, if you think it is important to address conditional probability (in any manner, scholarly or not) you are not in favor of Proposal 1. -- Rick Block (talk) 18:35, 24 September 2012 (UTC)
- This is an article on the MHP not a text book on probability. 95% of those who read this article will not have any interest in conditional probability at all but they will want to know the probability of winning by switching and why it matters what the host knows. Martin Hogbin (talk) 19:45, 24 September 2012 (UTC)
- Martin, all this is doing is saying "...mathematicians prefer to write out a longer version of the solution, that takes into account that if the contestant picks the door with the car behind it, Monty has two goats to choose from. Whether you use the simple version or this more detailed explanation, the result is still the same..." It's not mentioning conditional probability (as an academic discipline) at the moment. Elen of the Roads (talk) 20:16, 24 September 2012 (UTC)
- This is an article on the MHP not a text book on probability. 95% of those who read this article will not have any interest in conditional probability at all but they will want to know the probability of winning by switching and why it matters what the host knows. Martin Hogbin (talk) 19:45, 24 September 2012 (UTC)
- I agree with you Martin on the needs of 95% of the readers. Do you think that the Lucas et al. argument is too difficult for 95% of our readers? Richard Gill (talk) 12:24, 25 September 2012 (UTC)
- Yes, it is far too complicated to start with. The argument needs to be convincing and therefore very simple or there is no point in going on. If the reader does not believe that the answer is 2/3 they are not going to read through an argument that is more complicated but which has no more explanatory or convincing power than the simple ones do. Once the reader has been convinced, and also understood why the host's knowledge matters, then the Lucas explanation is fine, along with many others. The Morgan argument is then quite straightforward to understand and believe. As Morgan did in their paper, the argument for taking account of the host's choice of door is most easily introduced by considering a variant of the problem in which the host does not choose evenly. That the conventional formulation can be considered as a special case of this is trivial for anyone who gets this far. To introduce that piece of pointless pedantry at too early a stage can only put people off. We should never underestimate the power of the basic problem to confuse. Martin Hogbin (talk) 12:55, 25 September 2012 (UTC)
- I agree with you Martin on the needs of 95% of the readers. Do you think that the Lucas et al. argument is too difficult for 95% of our readers? Richard Gill (talk) 12:24, 25 September 2012 (UTC)
- Elen, I do not accept that, '...mathematicians prefer to write out a longer version of the solution'. Some may do in some circumstances, but why do we need to make that at the start. It is of far less interest to nearly all readers than is the startling difficulty of the main problem. The problem here is that the article is being written by editors in order to prove some point or other rather than being written for the benefit of our readers. Martin Hogbin (talk) 12:55, 25 September 2012 (UTC)
- Real mathematicians prefer to write a short verbal solution which uses mathematical insight and which at the same time is complete and easily (for the professional) formalizable. Unreal mathematicians prefer to write out a long explicit formal calculation. For instance, if you want a subjectivist probability solution, then this particular mathematician would write the following: if we have no a priori knowledge about how the game show organizers hide the car or how the host chooses a door to open when he has a choice, then the problem is symmetric in the door numbers, and the specific door numbers in a particular instance are irrelevant. The only question are the relationships between the door chosen by the player, the door hiding the car, the door opened by the host, and the door left closed by the host. By symmetry there is probability 1/3 that the competitors initial choice is the same as the door hiding the car. In that case, the other closed door hides a goat, otherwise, the other closed door hides a car. Therefore the probability that the other closed door hides a car is 2/3, independently of the specific door numbers involved in any particular instance.
- On the other hand, if you want a strategic/decision oriented solution, like the writer of the Economist, then this particular mathematician would write the following: if you choose your door initially completely at random and then switch you'll get the car 2/3 of the time. It's an easy exercise to show that this is the minimax solution, i.e., no other strategy is guaranteed to win at least 2/3 of the time.
- Please note: the real mathematician has different solutions to offer, depending on the taste of his client, the consumer so to speak. They make different assumptions, they are both short and sweet and a professional easily fills in any details. As a class-room exercise in a course on elementary probability or on elementary game theory (or mathematical economics) one might write some things out in more detail. Richard Gill (talk) 13:52, 26 September 2012 (UTC)
- Richard I like your subjectivist probability solution and I think we need to say this somewhere in the article, but not at the start. At the start we need some very clear diagrams, as I have proposed. Martin Hogbin (talk) 18:04, 27 September 2012 (UTC)
- Who is the audience for this? Martin Hogbin (talk) 08:38, 25 September 2012 (UTC)
- The article should show that, for the common scenario, conditional probability is not *needed*. In the common scenario, it is futile to use it, but of course you can use it.
The conflict here for years has been: Is the claim that conditional probability being "the only correct approach to solve the paradox" relevant or irrelevant in the common scenario. Gerhardvalentin (talk) 09:37, 25 September 2012 (UTC)
- The article should show that, for the common scenario, conditional probability is not *needed*. In the common scenario, it is futile to use it, but of course you can use it.
- Who is the audience for this? Martin Hogbin (talk) 08:38, 25 September 2012 (UTC)
- The notion of "probability of winning by switching" is ambiguous. There are three common meanings of it here: (1) what proportion of all switchers win?, (2) what proportion of switchers who choose door 1 win?, and (3) what proportion of switchers who choose door 1 and see host open door 3 to show a goat win?. Given what most non-mathematicians would consider to be mild assumptions (i.e. K&W), these are all 2/3. Many people think (3) is the quantity they want to know after reading the problem description. The simple solutions show that the answer to (1) or (2) is 2/3 and leave the step of going from there to (3) as "obvious", but it isn't obvious to everyone, so connecting the dots for them is nice.
- As to why it matters that the host knows (and is constrained to pick a goat), the simple conditional solution answers it easily: if the host knows, the alternatives are 1/3×1/2 and 1/3×1 (explained already), whereas if the host doesn't know, they are 1/3×1/2 and 1/3×1/2 (the host always has two 50:50 options). -- Coffee2theorems (talk) 21:20, 24 September 2012 (UTC)
Or in my seriously clunky table version
| Door 1 | Monty opens door 2 | Door 3 | result if switching | result if staying |
|---|---|---|---|---|
| Car | Goat | Goat | Goat | Car |
| Goat | Car | Goat | Goat | Goat |
| Goat | Goat | Car | Car | Goat |
| Door 1 | Door 2 | Monty opens door 3 | result if switching | result if staying |
|---|---|---|---|---|
| Car | Goat | Goat | Goat | Car |
| Goat | Goat | Car | Goat | Goat |
| Goat | Goat | Car | Car | Goat |
If Monty doesn't know where the car is, there is no advantage to switching.Elen of the Roads (talk) 22:45, 24 September 2012 (UTC)
- If Monty doesn't know where the car is, then the common intuitive answer will be the case (1:1, no difference).
- In one out of three the host got two goats, he will show one goat and switching loses the already first selected car.
- In one out of three the host got the car and a goat, and (in that one out of three) inevitably, by chance, will show the goat, and switching wins.
- But: in one out of three the host got a goat and the car, and (in that one out of three) inevitably will show the car, and *game-over*.
- If Monty doesn't know where the car is, then the common intuitive answer will be the case (1:1, no difference).
| Door A | Door B | Monty opens door C | result if switching | result if staying |
|---|---|---|---|---|
| Car | Goat | Goat | Goat | Car |
| Goat | Car | Goat | Car | Goat |
| Goat | Goat | Car | game-over | game-over |
- If Monty doesn't know where the car is, there is no advantage to switching, the common intuitive estimation (1:1) applies, irrespective of the location of the doors and irrespective of any door numbers. Regardless whether the doors have numbers or the door first selected by the guest has been "called" #1, regardless whether the car is behind door 1, 2 or 3. Regardless whether the guest first selected door 1, 2 or 3. And regardless whether the host has opened door 1, 2 or 3. It is useless to distinguish and to condition on the location of the doors or to condition on door numbers.
- It applies for the case that the guest has selected door 1 and the host has opened any other door, so it also applies for the case that the guest has selected door 1 and the host has opened door 3. It applies in any case, so it applies in every case and it applies for "always" switching / staying also. Distinguishing "before" the host has opened a door and "thereafter" is pointless. In the given scenario, that the host knows the location of the car, probability to win by switching 2/3 applies for any permutation. And if the host does "not" know the location of the car, probability to win by switching 1/2 "also applies for any permutation". To distinguish "before" the host has opened a door and "thereafter", in the given scenario, shapes up as an error in reasoning. Gerhardvalentin (talk) 01:15, 25 September 2012 (UTC)
- You're right. I couldn't figure out if that presentation was adequate, but it is very effective. You can eliminate the door designations - I tried this above, but some folks found it even more confusing. What do you think --Elen of the Roads (talk) 15:44, 25 September 2012 (UTC)
- It applies for the case that the guest has selected door 1 and the host has opened any other door, so it also applies for the case that the guest has selected door 1 and the host has opened door 3. It applies in any case, so it applies in every case and it applies for "always" switching / staying also. Distinguishing "before" the host has opened a door and "thereafter" is pointless. In the given scenario, that the host knows the location of the car, probability to win by switching 2/3 applies for any permutation. And if the host does "not" know the location of the car, probability to win by switching 1/2 "also applies for any permutation". To distinguish "before" the host has opened a door and "thereafter", in the given scenario, shapes up as an error in reasoning. Gerhardvalentin (talk) 01:15, 25 September 2012 (UTC)
| You pick a | The other door has a | Monty Picks a | result if switching | result if staying |
|---|---|---|---|---|
| Car | Goat | Goat | Goat | Car |
| Goat | Car | Goat | Car | Goat |
| Goat | Goat | Car | game-over | game-over |
Yes, this is exactly was Richard once said: Not "door numbers" are of relevance, but relevant it is the role / the function of a door: Door first selected / door opened by the host / and door offered as an alternative to switch on.
And as to me, the question was about a "one time problem", as Tom did underline. "This show", in exactly this way, never occurred in reality, and the famous question is a tricky brain teaser. Now IMO you can regard the problem with the view of a subjectivist / Bayesian, or with a frequentist's view, both is okay. But IMO Morgan et al. did overshoot the mark by telling that in observing "available log lists" (perormance-lists) regarding the host's behaviour in opening one of his two doors, you can detect whether he "had" resp. still "has" some special preference to open just only one of his two doors. (Not to forget: The famous question is about a "one time problem" that never happened in exactly this way in reality, where "secrecy" regarding the car-hiding door is implied therefore: One-Time-Problem). MCDD said that the host could have been telling additional info on the actual location of the car, additional info revealed by "which-one" of his two door he actually did open: "No secrecy" regarding the actual car-hiding door.
In exceptionally opening of his "strictly avoided door", he could divulge e.g. the additional information that the car actually is very likely to be behind his second still closed door, that he usually prefers to open, if any possible, but actually had to left it closed. Imo no more "frequentist's view", but a complete new story of some quite OTHER game show that since long has been ongoing. Nothing to do with the famous "one time problem". But the article insolently pretends MDCC did address the "original" scenario as per MvS.
All of that "conditioning on door numbers" is interesting and helpful in class rooms and textbooks teaching probability theory, but without impact on the famous question "Is it to your advantage to switch". So that quite "other scenario" should be shown, yes, but should be shown later, saying that all of this addresses quite another "problem", that this addresses not MvS, but addresses repeated shows. Yes, "conditioning" on door numbers may be shown, but never mingle-mangled with first of all helping the reader in decoding the famous paradox. Gerhardvalentin (talk) 17:28, 25 September 2012 (UTC)
- Yes indeed. All of that guff needs to be relegated to a section headed "Variations" or "Exploring the possibilities" or some such. It's a one shot puzzle - what isthe answer to this one occurrence. Since it's the same answer in simple or conditional versions, let's put in both. No suggestion that the simple one is wrong - it's not - just that the conditional one is a bit more detailed. Morgan and his fantasies about Monty's motivations belong right down at the bottom of the article....or maybe in another article Variations on the Monty Hall problem --Elen of the Roads (talk) 15:19, 26 September 2012 (UTC)
Who are we writing this for?
There is a lot of discussion above that seems aimed at convincing other editors here of some subtle point or other.
WP is intended to be an encyclopedia, not a debating forum. Disputes on the benefits various solutions may be OK in the talk pages but they should not spill over into the article. There we should be only addressing the needs of our readers, not trying to prove some mathematical point.
How do we know that problems our readers will have? In the case of the MHP this is easy, we have two sources of information, the talk pages here and reports of the many letters that vos Savant received. In both cases the problems were: believing that the answer is 2/3; and understanding why it matters that the host knows where the car is. There is no record of a single person saying to vS, 'but what if Monty had opened door 2 to reveal a goat?'; for nearly everyone this is a non-issue. That is not to say that we should never mention this possibility but it can only ever be of interest to those that have completely understood the first two points. Martin Hogbin (talk) 09:49, 25 September 2012 (UTC)
- The point of the article is not to convince our readers of anything, but to be (per WP:NOT) "a summary of accepted knowledge regarding its subject". It is accepted knowledge that in the standard version of the MHP 2/3 is both the overall probability of winning the car by switching (per many published "simple" solutions) and the probability of winning the car by switching from door 1 to door 2 if the host opens door 3 (per many published "conditional" solutions).
- Vos Savant's explanations all said in one way or another that 2/3 is the overall probability of winning by switching (with or without having picked door 1, i.e. what Coffee2theorems describes above as the proportion of all switchers or the proportion of switchers who choose door 1). This is the characteristic that effectively defines your notion of "simple". We know for a fact that Vos Savant found this kind of explanation not convincing and resorted to challenging her readers to do a simulation.
- Yet you keep insisting that "simple" explanations are, if not easy to understand, at least obviously easier to understand than a solution explaining the probabilities in the specific case where the player picks door 1 and the host opens door 3. What is this insistence based on? Are there any sources that say this? K&W say the problem statement creates a mental model that prevents "access" to a "simple" solution. Have you considered the possibility that your mental model of the problem is not that same as the mental model of most of our readers? It seems to me you want to structure the article based on your mental model, with an extensive selection of solutions none of which fit the mental model K&W say nearly all people (97%!!) have after reading the problem statement, all similar to solutions vos Savant's readers (for whatever reason) couldn't accept. Don't you think it might be better to include a solution that addresses the mental model 97% of our readers will have? -- Rick Block (talk) 18:06, 25 September 2012 (UTC)
- If readers are not persuaded that the article gives the correct answer they will disregard any information that we present to them. Do you think this serves our encyclopedic purpose.
- My understanding of K&W is diametrically opposed to yours. Nowhere does it say that readers consider it important which (of the legal possibilities) door the host opens. If you want to discuss this I suggest we do it on my or your talk pages.
- Can you present any evidence that clearly and unambiguously says that a more complex solution is more convincing? Martin Hogbin (talk) 18:32, 25 September 2012 (UTC)
- It just is not true that an article about conditional probability theory can help the reader to easily decode the famous simple paradox that has been presented in the form of a story about the sequence of a one-time problem: Devolution brought forth "two still closed doors", one hiding the prize, the other door hiding a nullity. But in the given scenario, and by the given sequence, one door has double chance to hide the prize than the other door. It could easily be decoded by the reader if the article addresses this very aim. But for years now the article never says clearly what it is just talking about. Concealing more than it explains. Presenting a textbook in conditional probability theory, showing that a duad / a fixed combined group of two host's doors never can nor will have a better chance compared to one single door (see the story of the host's two "purses" above, it just depicts the conflict in the article).
Help the reader first to decode the paradox, and stop claiming that conditional probability is the only way to grasp that the group of the host's two doors has a better chance to hide the prize than one single door first selected.
Look at the archive of this talk page, confused readers have been left helpless and alone, thanks to the position of few incorrigible editors. Stop the article to be a textbook on unimportant negligibility. Gerhardvalentin (talk) 19:50, 25 September 2012 (UTC)
- It just is not true that an article about conditional probability theory can help the reader to easily decode the famous simple paradox that has been presented in the form of a story about the sequence of a one-time problem: Devolution brought forth "two still closed doors", one hiding the prize, the other door hiding a nullity. But in the given scenario, and by the given sequence, one door has double chance to hide the prize than the other door. It could easily be decoded by the reader if the article addresses this very aim. But for years now the article never says clearly what it is just talking about. Concealing more than it explains. Presenting a textbook in conditional probability theory, showing that a duad / a fixed combined group of two host's doors never can nor will have a better chance compared to one single door (see the story of the host's two "purses" above, it just depicts the conflict in the article).
- FWIW, I took K&W to mean the same as Rick did, I think. Assuming that we expose the reader to the standard version (with door numbers) before the solution section, it would make sense to backtrack at the beginning of the solution section and tell the reader to ignore the "door 3" part and to consider the proportion of winners among all switchers who pick door 1 instead. It is easily established that this is 2/3. Then, we can consider the proportion of winners among all switchers who pick door 1 and see door 3 opened in a simple way (what Gill calls the Lucas version here, suitably illustrated so that it is easy to understand). At that point, we will have addressed the question the reader was thinking of, whichever it was. K&W do suggest that it is the latter one:
- "Although, semantically, door 3 in the standard version is merely named as an example ('Monty Hall opens another door, say number 3"), most participants take the opening of door 3 for granted and base their reasoning on this fact. [...] Note that once formed, this assumption prevents the problem solver from gaining access to the intuitive solution illustrated in Figure 1 [essentially the vos Savant solution].",
- and
- "The additional specification of the door opened by Monty Hall in the standard version of the problem leaves only two of the three arrangements [...] (A1 and A2). [Ax is the situation where you picked door 1 and the car is behind door x]. A3 is impossible because Monty Hall cannot open the door concealing the car. As a result, one cannot simply count and compare [...], but rather one has to reason in probability terms to reach the Bayesian solution. That is, Monty Hall's opening door 3 has a lower probability in A1 than A2, because in A1 he could have opened either door 2 or door 3, whereas in A2 he had to open door 3."
- The reasoning in the last part here is essentially the "Lucas solution", and they are essentially suggesting that you have to use it for the standard version because of the mental model it induces.
- The reason I suggested backtracking is this part from their article:
- "The easiest way to make sure that participants' reasoning processes are not impeded by knowing which door Monty Hall opens, is simply not to give them this information. The corresponding formulation would be: 'Monty Hall now opens another door and reveals a goat."
- If we have to use the standard version from the beginning (and I suppose we do, due weight and all that), then the next best thing to doing as K&W suggest is to tell the reader to put the mental model they have on hold for a moment, right? But just for a moment; the conditional solution should follow immediately after. Telling people to put a thought on hold like that for a long time tends not sit in well with many people (and it needs to be worded properly, not literally "ignore this part for now" but "one interpretation of the question is..." or something, so it's more palatable). -- Coffee2theorems (talk) 19:52, 25 September 2012 (UTC)
- Yes yes. One of my monumentally clunky tables was an attempt to explain just as 'your door' 'Monty's door' 'the other door' without door numbers. I think it's possible to go "here's the problem....the significant thing to remember is that Monty can't show the car. If Monty just picked a door at random, there would be no benefit to switching, but because he can't show the car.....(cue simple tables)" Then (as I rather keep saying - sorry) - mathematically you can write this out in a more detailed way (one of the conditional tables above). Now I have realised that the reason I couldn't originally understand the conditional version was because of the way it was written out (sorry Rick or whoever constructed it), I am convinced it can be written out clearly enough for anyone with a decent maths GCSE to follow. I think that sequence, followed by the other iterations of the problem, the other approaches to a solution (formal or thought experiment) is far clearer that presenting the editor with half a dozen apparently different 'solutions' immediately. Elen of the Roads (talk) 22:04, 25 September 2012 (UTC)
- FWIW, I took K&W to mean the same as Rick did, I think. Assuming that we expose the reader to the standard version (with door numbers) before the solution section, it would make sense to backtrack at the beginning of the solution section and tell the reader to ignore the "door 3" part and to consider the proportion of winners among all switchers who pick door 1 instead. It is easily established that this is 2/3. Then, we can consider the proportion of winners among all switchers who pick door 1 and see door 3 opened in a simple way (what Gill calls the Lucas version here, suitably illustrated so that it is easy to understand). At that point, we will have addressed the question the reader was thinking of, whichever it was. K&W do suggest that it is the latter one:
Are we there yet?
Summarising the discussion so far, it seems that we get something like the below - possibly with the tables replaced by graphics or the graphics replaced by tables, and probably with changes to the wording. The sections below the 'solution' section then seem to fall naturally to me as shown - again this can be discussed further.
The Solution
Vos Savant's solution only works if - like a typical game show host - Monty Hall knows what's behind the doors only reveals the prize at the end. To do this, he must make sure never to open the door with the car behind it.
If Monty pick's his door at random, he will pick the car 1/3 of the time, and you will pick the car 1/3 of the time. There is no advantage to switching
| You pick | Monty picks | The other door has the | result if switching | result if staying |
|---|---|---|---|---|
| Car | Goat | Goat | Goat | Car |
| Goat | Goat | Car | Car | Goat |
| Goat | Car | Goat | Goat | Goat |
However, if Monty knows what's behind the doors, and is only going to reveal the prize at the end, he has to pick a door with a goat. This gives quite a different result. In this case, if you have picked a goat, Monty has to pick the other goat and leave the car hidden. You still only have a 1/3 chance of picking the car to start with, but if you switch, 2/3 of the time (the two times you picked the goat) the other door will have the car behind it.
| You pick | Monty picks | The other door has the | result if switching | result if staying |
|---|---|---|---|---|
| Car | Goat | Goat | Goat | Car |
| Goat | Goat | Car | Car | Goat |
| Goat | Goat | Car | Car | Goat |
This is true even if you use the more detailed mathematical technique known as conditional probability, which takes into account that if you pick the car, Monty has two goats to choose from.
| Car hidden behind door 3 (Probability 1/3) |
Car hidden behind door 1 (Probability 1/3) |
Car hidden behind door 2 (Probability 1/3) | |
|---|---|---|---|
Player picks door 1 
|
Player picks door 1
|
Player picks door 1
| |
| Host must open door 2 | Host randomly opens door 2 | Host randomly opens door 3 | Host must open door 3 |
 Switching wins |
 Switching loses |
 Switching loses |
 Switching wins |
| Probability 1/3 | Probability 1/6 (=1/3 x 1/2) | Probability 1/6 (=1/3 x 1/2) | Probability 1/3 |
| If the player picks door 1 and the host opens door 2, switching wins with probability 1/3 and loses with probability 1/6 | If the player picks door 1 and the host opens door 3, switching wins with probability 1/3 and loses with probability 1/6 | ||
Other versions of the original problem
Other approaches to explaining the problem
The solution using mathematical notation
Variations on the problem
Comments
Thoughts folks --Elen of the Roads (talk) 15:47, 26 September 2012 (UTC)
- I guess I'd say much the same as for Rick's proposal: "I like it, because it's broadly speaking in the right direction, but there's nevertheless much that I would change in it" :) Just different things. (both are in the "I could live with it without a complete rewrite" realm) Comments
- Do we need to have the ignorant host case here? IMO it would fit better after the standard case has been dealt with. Immediately after (next section/subsection) would be just fine. The reason I'd put it after the solutions is that it mainly serves as a check that the reader understood the subtleties. There are people who are familiar with the MHP and yet are surprised when they hear about the ignorant host case, so it's not necessary for basic understanding of the MHP itself. It seems to me like one of those fine points one can discuss after the solution.
- Even if we do talk about the ignorant host case, isn't starting with it a bit much? It's a different problem, after all, and modern wordings take care to exclude that interpretation.
- I think the solutions without door numbers are hard to understand. Even if you replaced the second table with the "Economist figure" of Martin's proposal (which is much clearer), it's still confusing for the reasons I explained there. The reader is probably thinking in terms of the door numbers (1, 2, 3 from left to right on stage) anyway, and there are good solutions (vos Savant..) with them, so why not use them?
- Emphasizing the mathematical-ness of the conditional solutions and in general making it sound difficult is not desirable. When people feel that they are expected to not understand something, it reduces the chances that they will.
- The post-solution sections are probably best discussed after we succeed in getting consensus about the solution section :)
- That's about it. -- Coffee2theorems (talk) 19:11, 26 September 2012 (UTC)
- See notes below as well. Based on my limited pool of test subjects, everyone looks at (or imagines) the two remaining doors (theirs and the one Monty hasn't opened) and says "Well, it's 50/50 innit.It's either here or there." Showing that the special provision that Monty won't show the car alters the outcome is what makes the lightbulb come on. Other than that, happy to go with a different placement, and whatever others think best on the table layouts. I like the three cell display you use below. --Elen of the Roads (talk) 22:20, 26 September 2012 (UTC)
Proposed text for Solution section
Proposed text for Solution section
| ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
SolutionThe player should switch. Switching wins twice as often as staying. Simple explanationSwitching loses if and only if the player initially picks the car door, which happens 1/3 of the time, so switching must win 2/3 of the time (Carlton 2005).
The situation can also be analyzed by cases, as illustrated above. Switching loses in only one of the three equally likely cases, and wins in the other two (vos Savant 1990b; Krauss and Wang, 2003). Many people find the situation intuitively easier to understand by considering the same problem with 1,000,000 doors instead of just three (vos Savant 1990; Krauss and Wang, 2003). In this case there are 999,999 doors with goats behind them, and the player's chances of picking the car door are 1 out of 1,000,000. The game host goes down the line of doors, opening each one to show 999,998 goats in total, skipping over only the player's door and one other door. The host then offers the player the chance to switch to the only other unopened door. On average, in 999,999 out of 1,000,000 times (i.e. the times the player initially picked a goat) the other door will contain the prize. Explanation with door 3 openMost people take it for granted that the host opens door 3, and base their reasoning on that fact. That assumption is incompatible with the simple explanation illustrated above, because in case 3 the host does not open door 3. Once case 3 is excluded as impossible, simple case counting results in the common incorrect answer that only two cases (case 1 with door 3 open and case 2) are possible and therefore the chances are 50:50 either way (Krauss and Wang, 2003). It is true that when door 3 is open, there are only two possible cases: either the car is behind door 1 or it is behind door 2. These two cases, however, are not equally likely! This is illustrated in the alternative explanation below, with the two relevant cases on the left side of the thick line.
The above illustration shows everything that can happen to players who pick door 1. On average, three in six end up in the exact situation described in the problem statement (door 3 is opened; left of the thick line). Two of the three win and one loses by switching; therefore the probability that switching wins in that situation is 2/3 (Chun 1991; Grinstead and Snell 2006; Morgan et al. 1991). | ||||||||||||||||||||||||||||
Comments on the proposed text
Since I criticized the other proposals, I felt it is only fair if I put one up for criticism, too. This contains material from both, the article, and some my own. The referencing could probably be improved. How do you like it?
It's intentionally somewhat minimalistic, and adding a "Discussion" subsection or something to it where things like the ignorant host variant could be covered is certainly possible. This is only meant to get the "answer to the standard problem is 2/3; switch!" part done with before the article proceeds on to other stuff. -- Coffee2theorems (talk) 17:07, 26 September 2012 (UTC)
- I do not like it, for reasons discussed at length above. Martin Hogbin (talk) 18:39, 26 September 2012 (UTC)
- The explanation about the most common mental model is pretty unintelligible - I guess I just don't think that way. Can we have a do over on that. And I don't think the million goats belongs in there. Perhaps the next section should be Still having trouble? which could include the million goats.--Elen of the Roads (talk) 18:45, 26 September 2012 (UTC)
- I'm not too attached to the million goats thing, but I put it in there because while it isn't a solution it's certainly an explanation, and it seems to be an effective one. It's often mentioned that it helps people "get" the MHP, and K&W had this to say about it:
- "Hell and Heinrichs (2000) obtained 65% switch decisions by investigating a variant of the problem with 30 doors, where 28 doors were opened after the first choice.", which is big compared to "Most studies on the Monty Hall problem only report the percentage of switch decisions, usually around 10-15%." It's actually more effective than their carefully constructed "guided intuition" version with three doors (59%).
- I'm loath to include any lengthy "aids to understanding" material before the conditional solution (I'm for proposal 2, after all :), but this one was fairly short and the bang for the buck high, so if there was going to be any then that was the obvious candidate. Do you have any specific reasons why it doesn't belong?
- Which part of the mental model explanation is unintelligible? The paragraph before the figure? The figure? The paragraph after it? Is there anything there that is understandable? -- Coffee2theorems (talk) 19:37, 26 September 2012 (UTC)
- I think it's the way it's written above. You've run a number of things together and my thought chain goes something like
- I'm not too attached to the million goats thing, but I put it in there because while it isn't a solution it's certainly an explanation, and it seems to be an effective one. It's often mentioned that it helps people "get" the MHP, and K&W had this to say about it:
- "After reading the standard version of the problem, most people form a mental model I've never formed a mental model that looks anything like that
- The solution illustrated above is incompatible with this mental model Why the hell are you showing it to me then
- Instead of switching to a compatible mental model, it is also possible to solve the problem in a way consistent with the common one by considering only cases where door 3 is opened (left of the thick line below) OK, I'm giving up at this point
- I think that the idea of mental models may go some way to explain why people get confused, and certainly belongs in the article somewhere. Interestingly, it's not the actual reason everybody I ever show this puzzle gives for thinking it makes no difference to switch. They all mentally look at the two remaining doors (their pick and the one Monty hasn't opened) and say "Well, it's fifty fifty isn't it. The car's either behind my door or that door. What's the point of switching." Every time (admittedly small sample). That's why I put the version where Monty picks at random into my layout above - it can indeed go below vos Savant's solution, but it's that which seems to convince everyone - showing that the outcome is differend because Monty won't show the car. Elen of the Roads (talk) 22:15, 26 September 2012 (UTC)
- I rewrote that part now. At the same time I ditched the "mental model" wording; it wasn't even used in the same sense as in the K&W paper. Their meaning is one definite arrangement (e.g. "Car / Goat / Open door" is a mental model in their sense), whereas I used it in the sense of a model that you can mentally simulate. Better? -- Coffee2theorems (talk) 00:10, 27 September 2012 (UTC)
I like it. Except for the first paragraph of the "with door 3 open" bit. It can be deleted. Start straight away with "it is true that with door 3 opened there are two cases".
References: Selvin's (1975b) second letter to the editor has this solution. It's the second oldest solution on record. His first letter to the editor (1975a) has the other solution. Since he invented the problem I think these references are good reasons to put both these solutions right at the start of the article. Both give useful insight, probably both will appeal to many readers. Some readers will have no use for one or the other. So what?
I would like to see the Economist solution here as well. That too appeals to many people. Editors have repeatedly put it forward spontaneously. Richard Gill (talk) 07:14, 27 September 2012 (UTC)
- Isn't starting with "It is true that when door 3 is open" a bit sudden? The first paragraph ties that section into the bigger picture. I think that the first sentence is fairly good at least, even if the rest of the paragraph could be improved.
- What I'm trying to get across to the reader is essentially these points (without necessarily explicitly spending ink on all of them):
- Most people (such as you the reader, in all probability) initially reason based on the assumption that door 3 is open, and that leads to this common fallacious argument and this wrong conclusion (two cases, 50:50).
- The common fallacious argument is actually salvageable, and here's how to fix it (two cases yes, 50:50 no).
- Now that the argument is fixed, it should be obvious what went wrong. (host is sometimes constrained, sometimes not, and that matters)
- I think that showing what went wrong, not just this is how to do it right, is an important part of the solution in a paradoxical problem. Certainly there are other reasons to put the conditional solution in, but this is the one that I think has the most immediate relevance to the reader.
- Maybe it would be better if the paragraph didn't refer to the previous solution? Maybe something like the following (replacing both paragraphs)?
- Most people take it for granted that the host opens door 3, and base their reasoning on that assumption, imagining door 3 as already open. That leads to considering only two cases as possible - the car is either behind door 1 or door 2 - and incorrectly concluding that the chances are 50:50 either way (Krauss and Wang, 2003). The two cases are indeed the only ones possible when door 3 is open, but they are not equally likely! This is illustrated in the alternative explanation below, with the two relevant cases on the left side of the thick line.
- Any better? One might also throw in an extra sentence right after the vos Savant solution, saying that
- Therefore, the strategy of picking door 1 and then switching no matter what happens wins 2/3 of the time.
- so that if the reader goes back and is confused about what the explanation actually does show, then they are gently nudged in the right direction (there exists an interpretation of that sentence which is true, and it's the most natural interpretation). -- Coffee2theorems (talk) 09:21, 27 September 2012 (UTC)
- As to the received impression "Two still closed doors, and one of them hides the car", Ningauble said above:
partitioning the doors between "your door" and "Monty's doors" is the most persuasive explanation, and just suggesting the partition is often enough of a hint. - Being able to see two "groups of doors" (1 door + 2 doors), to distinguish and to help keep them apart: Why not saying just in the beginning:
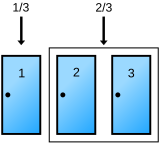 Three doors, and one of them will hide the car. (Instead of "1/3 2/3" we should write "Player Host") and instead of "1 2 3" we should say (or add) "1/3 1/3 1/3"
Three doors, and one of them will hide the car. (Instead of "1/3 2/3" we should write "Player Host") and instead of "1 2 3" we should say (or add) "1/3 1/3 1/3"- Gerhardvalentin (talk) 10:27, 27 September 2012 (UTC)
- As to the received impression "Two still closed doors, and one of them hides the car", Ningauble said above:
- Three doors, and just only one of them will hide the car. Only one.
Note: After the guest first has selected "his" door, the entity of three doors has irrevocably been divided into two opposing groups.
The reader should be "aware" of this fact, because it is useful to examine those two groups. Each group can hide one car at most.The guest's group can hide one goat at most, and the host's group can hide two goats at most, but the host's group "must" hide one goat at least. (At this stage, the "biased" host who in the million doors variant leaves only #777'777 of his doors closed, because he NEVER uses to open #777'777 if any possible, is still not "necessary" in this step.)
What the article should do, but never does: Helping to "decode the picture" that the tricky "story" and its course / sequence / devolution tells / leaves behind, resulting in a given obvious paradox.
Help to correctly distinguish, to single out, to decompose the elements and to put them together again in an insightful manner.
Help the reader to understand and to "decode" the paradox, imo he should be able to *vary* his first impression from different perspectives. Why rejecting to offer him this support? The article could be much better than it has been for years now. Gerhardvalentin (talk) 11:31, 29 September 2012 (UTC)
- Three doors, and just only one of them will hide the car. Only one.
- Coffee2theorems, you wrote "Most people take it for granted that the host opens door 3, and base their reasoning on that assumption, imagining door 3 as already open". I find this a very odd statement. We were told that the host opened door 3! (Not opens door 3). Of course one imagines door 3 as being open. Yes, because it was opened. That's why I find this intro superfluous but also confusing since there are maybe some subtleties implied by present versus past tense. But if so, they are too subtle to come across (to me, at least). How about: Because door 3 has been opened to reveal a goat and we see two doors left closed, most people automatically imagine that the two remaining possibilities for the location of the car must be equally likely. Richard Gill (talk) 12:11, 27 September 2012 (UTC)
- That seems to be what people do. And if Monty had opened a door at random, they would be right. The trick is to show them that by avoiding showing the car, Monty has made it more likely that the other door has the car behind it. Elen of the Roads (talk) 12:52, 27 September 2012 (UTC)
- Exactly! And the reason why it is more likely, twice as likely in fact, is because Monty is twice as likely to open door 3 when he has no choice, as when he does have a choice. Richard Gill (talk) 13:36, 27 September 2012 (UTC)
- Incidentally, the ignorant host version is easy enough to explain using the "explanation with door 3 open" figure, too. When the host chooses randomly even when the car is behind door 2, one of the two players who would win in the standard setting ends up being shown the car behind door 2. Only two in six are shown a goat behind door 3, one of who wins and another one who loses. -- Coffee2theorems (talk) 14:31, 27 September 2012 (UTC)
- That seems to be what people do. And if Monty had opened a door at random, they would be right. The trick is to show them that by avoiding showing the car, Monty has made it more likely that the other door has the car behind it. Elen of the Roads (talk) 12:52, 27 September 2012 (UTC)
- Coffee2theorems, you wrote "Most people take it for granted that the host opens door 3, and base their reasoning on that assumption, imagining door 3 as already open". I find this a very odd statement. We were told that the host opened door 3! (Not opens door 3). Of course one imagines door 3 as being open. Yes, because it was opened. That's why I find this intro superfluous but also confusing since there are maybe some subtleties implied by present versus past tense. But if so, they are too subtle to come across (to me, at least). How about: Because door 3 has been opened to reveal a goat and we see two doors left closed, most people automatically imagine that the two remaining possibilities for the location of the car must be equally likely. Richard Gill (talk) 12:11, 27 September 2012 (UTC)
- The first sentence is that way because it was based on this one in K&W:
- "Although, semantically, door 3 in the standard version is merely named as an example ('Monty Hall opens another door, say number 3"), most participants take the opening of door 3 for granted and base their reasoning on this fact."
- I just took that as the basis, nothing deep implied (FWIW, the word is "opens" in the standard problem descriptions, not "opened", and the vos Savant version doesn't use past tense anywhere; you can imagine yourself doing the analysis in front of the closed doors if you want). They also say:
- "34 out of the remaining 35 participants (97%) indeed drew an open door 3, and only a single participant (3%) indicated that other constellations also remain possible according to the wording of the standard version."
- So there are a few who do see it otherwise, too. It might be fine to say "Because door 3 has been opened" despite that, if we started our article with the conditional solution, but we don't! The simple solutions describe things from another point of view (you analyzing cases in front of closed doors), where it is still possible that door 2 is opened. I think the reader should be told when we are changing the point of view back to door 3 being already open, and why. Trying again:
- Most people consider only the situation where door 3 is open, leaving only two possibilities: the car is either behind door 1 or door 2. They then incorrectly conclude that the chances are 50:50 either way (Krauss and Wang, 2003). These are indeed the only possibilities when door 3 is open, but they are not equally likely! This is illustrated in the alternative explanation below, with these two possibilities on the left side of the thick line.
- I'm not dead set against stating that door 3 has been opened as a matter of fact instead of saying merely that most people analyze the problem from that POV, but that seems slightly presumptuous as it is not the only way to analyze it. -- Coffee2theorems (talk) 13:59, 27 September 2012 (UTC)
- This is all interesting stuff an worthy of a place in the article but first we have to convince our readers of the right answer. It seems we are going round in circles and the 'combing doors' explanation is coming back into fashion. I agree with all those above, that it has great explanatory and convincing power. We need it near the start. Martin Hogbin (talk) 17:59, 27 September 2012 (UTC)
- Well, I've almost lost track of where we stand, but the 'combining doors' explanation is a very bad one and as I wrote above: highly misleading. For your interest again: There is nothing to combine. Each of the not chosen doors has 1/3 chance on the car. Combining them means adding 1/3+1/3 =2/3. I have not the slightest clue how this may be helpful in any solution. Why not read what I wrote on combining purses? Easy to understand for anyone! Nijdam (talk) 22:18, 27 September 2012 (UTC)
- This is about convincing readers of the right answer. I think many have this incorrect argument ("two cases, 50:50") lodged in their brain and some won't listen to anything that doesn't point out the flaw in their reasoning. The conditional explanation addresses this directly - you have the two cases, and it shows why they aren't 50:50. I hope that what looks like going in circles is actually going in spirals - steadily, if slowly, upward. -- Coffee2theorems (talk) 23:02, 27 September 2012 (UTC)
- The combining doors argument is a correct argument for what it delivers, namely that switching gives the car 2/3 of the time. For many newcomers to MHP, it's *the* eye-opener. It's used by many sources, both popular and academic. Some academic mathematical sources even use it as a step towards the kind of solution some editors want to see (namely, a conditional probability statement). Because if we add symmetry to the argument, the door numbers are irrelevant, and 2/3 is a conditional as well as an unconditional probability. Equivalently, door numbers are independent of door roles and we can ignore the numbers; the only thing that is relevant is the roles of the doors. Richard Gill (talk) 07:31, 28 September 2012 (UTC)
- This is all interesting stuff an worthy of a place in the article but first we have to convince our readers of the right answer. It seems we are going round in circles and the 'combing doors' explanation is coming back into fashion. I agree with all those above, that it has great explanatory and convincing power. We need it near the start. Martin Hogbin (talk) 17:59, 27 September 2012 (UTC)
- The first sentence is that way because it was based on this one in K&W:
Nijdam, we discussed this earlier and, I thought, came to some form of understanding. The crucial, sometimes unstated, fact in the 'combining doors' solution is that the host's actions of revealing a goat do not affect the probability that the car is behind the originally chosen door.
My suggestion, which I thought you had agreed to, was to state, initially without proof or justification, that the probability the car is behind door 1 is not changed by the host showing a goat.
Having done this, we can then compare this with the case where the host reveals a goat by chance. It is easy to explain how that action gives us us information which can be used to revise our probability that the car is behind door 1, resulting in no advantage in switching. We can the proceed to justify our original statement that in the standard case no information is revealed and the probability that the car is behind door 1 is unchanged.
If we make this explanation the last of the simple ones we achieve three worthy objectives: we keep the explanations simple at the start, we explain why it matters that the host knows where the car is, and we show how, in some circumstances, the probability the car is behind the originally chosen door can be changed by the host's actions, thus providing a lead into conditional probability and the Morgan solutions. Martin Hogbin (talk) 14:20, 28 September 2012 (UTC)
- It seems to me that the others wanted to use the combined doors solution to illustrate the same thing as the other simple solutions do: that 2/3 of all switchers (who choose door 1) win. That is a very different usage from the one where we claim "no information is revealed". What you are talking about is something like this going into the "Explanation with door 3 open" section:
- One intuitive argument groups the doors into the player's doors (door 1) and the host's doors (doors 2 and 3), as illustrated below. Initially, the chances of the car being behind the player's door are 1/3, and the chances of it being behind one of the host's doors is 2/3. This remains true after the host opens door 3, because doing so provides the player no new information about what is behind the player's door — regardless of what is behind the player's door, the host's choice appears completely random to the player.

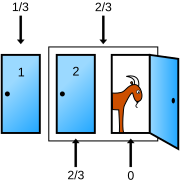
- What the others seem to be talking about is something that would go in the beginning of the "Simple explanation" section. For example, one could replace the Carlton blurb with this:
- If the player is determined to always stick to their initial choice, they might as well not be offered the chance to switch at all. Sticking wins exactly when the player initially picks the car, which happens 1/3 of the time. Switching wins the other 2/3 of the time. This may be easier to grasp if the doors are grouped into player's doors (door 1) and host's doors (doors 2 and 3), as below:

- The player is effectively given the choice of keeping what's behind their door, or taking everything behind the host's two doors. The host opens one of his doors to show a goat, but that doesn't change the fact that switchers always get all cars behind the host's two doors, and stickers get all cars behind their one door.
- I'm sure both wordings could be improved. I think the latter approach is somewhat better, as the "information" thinking is notorious for causing various kinds of confusion, and that concept is not necessary for solving the problem. The notion of no new information being revealed about what is behind the player's door is also somewhat complicated compared to the simple case counting used in most approaches. -- Coffee2theorems (talk) 16:05, 28 September 2012 (UTC)
Let me make this crystal clear, especially for the defenders of this explanation, i.e. the combining doors. It goes like this:
- the chosen door has 1/3 chance on the car
- hence the other doors have together 2/3 chance on the car
- one of these other doors is opened by the host showing a goat
- this door clearly has 0 chance on the car
- as both doors together has 2/3 chance, the remaining door must have 2/3 chance on the car
Many will find it very "logically", and may think they now understand the paradox. This explanation is indeed found in several (reliable??) sources. It is impossible to repair this kind of reasoning, as the basic idea, the combining of two chances of 1/3 into 2/3, gives the wrong suggestion, and does not contribute to any understanding. It especially lacks the explanation why the chance of 1/3 for the remaining door magically changes into 2/3.
- It is *easy* to complete/repair the reasoning. And the repair job is in the published literature.
- @Richard: There is nothing to complete/repair, as the basic idea is wrong. Of course you may see the equivalence with the simple solution, and complete it, but this does not repair the wrong idea of combining the doors. Combining may seem to bring understanding, but what is understood is wrong. The step from 4. to 5. is not logical, and to prove 5. the combining is superfluous and of no help.Tell me what insight the combining brings you. Does it enlighten you that 1/3+1/3 = 2/3 ?! Nijdam (talk) 22:47, 28 September 2012 (UTC)
- The competitor chooses door 1. With probability 2/3 there is a goat behind it. The host opens a different door revealing a goat but does not inform you which door he has opened. Probability 2/3 your initial door 1 hides a goat since you have gained no new information. Finally the host informs you that it was door 3 he opened. Still probability 2/3 that your initial door 1 hides a goat because *which* door he opens is independent of whether or not your door hides a goat, by symmetry.
- And indeed what effectively is going on is that the host is offering you the possiblity of a car behind doors 2 and 3 in exchange for the possibility of a car behind door 1. Richard Gill (talk) 17:53, 28 September 2012 (UTC)
- While the symmetry arguments are neat and all, I do not think they help the general reader. It's just so much mumbo jumbo they could parrot to a mathematician to get them to shut up, and that's about all the mileage they will ever get out of it. You can fill in the details. I can fill in the details. Nijdam can fill in the details. But the general reader can't!
- A simple test to check whether the reader understood the argument: "Prove that 2/3 of switchers who pick door 1 and see door 3 opened to show a goat end up getting the car. Show your work." (and maybe same for the ignorant host case) If you have hand-waved something about symmetry, do you seriously believe the reader can turn that into an actual proof showing true understanding? Even assuming a high-school student fairly good at math?
- The second illustration in my proposal should impart that level of understanding, at least to that high school student. Much more difficult problems are usually tackled in high school, and that explanation does not even require any understanding of probability theory (much less something like non-trivial statistical independence or conditional probability; are those even covered in high school?). The more complicated alternative mathematical material can well go in a later section (which could cover all non-K&W cases and "reverse mathematics" of MHP investigating necessity of assumptions etc. — all very interesting — to your satisfaction).
- Even if you don't require standards of proof that would satisfy a high school math teacher, the "no information" thing is tricky enough. I did try to argue it in the combined doors example above, but it's probably pretty opaque, even though it is the most intuitive approach I can think of (i.e. some way of expressing the line of thought "case 1: car behind your door, host behavior seems random", "case 2: goat behind your door, host behavior seems random"; host behavior indistinguishable in the two cases, he has "perfect poker face", you are none the wiser about what's behind your door). -- Coffee2theorems (talk) 19:23, 28 September 2012 (UTC)
NB. By using random doors, a kind of combining doors solution is possible, but that is not what generally is understood as the combining doors solution.Nijdam (talk) 16:29, 28 September 2012 (UTC)
- I agree that in this type of combined doors solution (the first one of the two I illustrated above), the combining of doors is superfluous. Once you show door 3 open, the argument of "taking everything the other guy has" loses its force, because both of you now equally 'own' one closed door! Then we go down the rabbit hole of arguing why it's not 50:50 even though there are only two places the car could be, and I don't see how combining doors helps there at all. It's a "no information revealed" argument in disguise.
- If all doors are shown closed, then the host has two closed doors, and that's why taking what he has looks like such a sweet deal. I think that is where the intuitive force of the second type of this argument comes from. Showing an open door ruins the argument; one must instead show them closed and say that "no matter what the host does, you get all cars behind his two doors" or something like that. -- Coffee2theorems (talk) 17:14, 28 September 2012 (UTC)
- I think the reason combining doors is *such* an eye-opener is that nobody is taken in by a cardsharp who, accused of hiding the ace of spades in his sleeves, rolls up one sleeve (say, the left one) and declares "see, nothing up my sleeve." Everybody knows this is not evidence about whether he is hiding the purloined card. None whatsoever.
Some professor (or sophomore) might note that if the accused has a tendency to roll up his right sleeve whenever possible then choosing the left one would be highly suspicious, so therefore an objective probability for sleeve preference must be taken into account. To a subjectivist this putative unknown probability is immaterial, and the sleeve chosen does not contribute any evidence about whether he is hiding the card. None. What. So. Ever. However, as a sop to those who think it makes a difference, one could stipulate in advance that the accused is completely ambidextrous and utterly dyslexic. If the professor now wants to plug a 50:50 distribution into some formula then that is his prerogative; however, if he says that one must do so, and that it is illogical to simply use the stipulation as indicating the choice of sleeve makes no difference, then I think it just illustrates what Turing laureate Richard Hamming said in The Art of Probability for Scientists and Engineers (1991), p. 4:
- "Probability is too important to be left to the experts. [...] The experts, by their very expert training and practice, often miss the obvious and distort reality seriously. [...] The desire of the experts to publish and gain credit in the eyes of their peers has distorted the development of probability theory from the needs of the average user. The comparatively late rise of the theory of probability shows how hard it is to grasp, and the many paradoxes show clearly that we, as humans, lack a well grounded intuition in the matter. Neither the intuition of the man in the street, nor the sophisticated results of the experts provides a safe basis for important actions in the world we live in." [emphasis in original]
- Some mathematicians might prefer adding the words "by symmetry" to the explanation. I doubt many laypersons would find the addition of a five dollar word particularly illuminating. Personally, I think it is a *virtue* of the combined-doors approach that lumping them together points out the symmetry to laypersons without reference to abstract ideas. It is a real eye-opener, and ought not be omitted from the article. ~ Ningauble (talk) 17:43, 28 September 2012 (UTC)
- I think the reason combining doors is *such* an eye-opener is that nobody is taken in by a cardsharp who, accused of hiding the ace of spades in his sleeves, rolls up one sleeve (say, the left one) and declares "see, nothing up my sleeve." Everybody knows this is not evidence about whether he is hiding the purloined card. None whatsoever.
- Laypersons omit the door numbers from their explanations because they instinctively and correctly appreciate symmetry, and because they are intuitively using probability in its classical sense. They should be applauded for their sound intuition. I'm all behind Richard Hamming here.
- If the word "symmetry" is superfluous for laypersons, no hard done in using it. At least it will keep the pedants among the professionals quiet, and it will delight the others. Alternatively, how about the word "independent"? Whether the host opens door 2 or door 3 is independent of whether there is a car or a goat behind door 1. That is both intuitive and true (and easily proven, using symmetry, if you feel a proof is needed). And it's in the literature, in the discussion of Morgan et al. Richard Gill (talk) 17:58, 28 September 2012 (UTC)
- Ninguable, I am with you on this one, 'The experts, by their very expert training and practice, often miss the obvious and distort reality seriously'. Morgan is a classic example of where experts use what is essentially a conjuring trick to ruin a simple puzzle. Martin Hogbin (talk) 22:13, 28 September 2012 (UTC)
- I agree that name-dropping a cryptic word like "symmetry" doesn't help. The conditional solution needs to be explained in a way that is actually understood; that is done in the "Explanation with door 3 open" section of the proposal.
- The "nothing up my sleeve" analogy is interesting, I didn't think of it like that. Yet if we show one of the doors open or talk about the probability of one door changing, I think we are going to confuse many people. I've often enough seen people say that probabilities don't change and get all confused about that, and explicitly showing two closed doors is just begging for the "two doors, 50:50!" knee-jerk response. Would showing the three closed doors figure and closely following the Adams explanation like this be suggestive enough?
- The player is basically given the choice of keeping what's behind their door, or taking everything behind the host's two doors. The host is saying in effect: "You can keep your one door or you can have the other two doors, one of which (a goat door) I'll open for you."
- This explicitly mentions opening the goat door, but leaves making the connection to sleeve-rolling (or to whatever analogy they think of) to the reader. -- Coffee2theorems (talk) 23:01, 28 September 2012 (UTC)
- Once upon a time I went looking for a FA-class reference for the "combining doors" solution. The best I could come up with was Devlin (who, as has been mentioned repeatedly here, botched it and in a follow-up column resorted to a Bayes' Theorem solution). If anyone can come up with a FA-class reference (no blogs, not some random guy with a web page) presenting this solution in a way that is better, please let us know what it is. Perhaps obvious, but I'm fine with the overall approach Coffee2theorems is suggesting here. It sounds like Elen is OK with it, Richard is OK with it, C2T (obviously) is, I am - are Martin and possibly Gerhard the only naysayers? -- Rick Block (talk) 05:06, 29 September 2012 (UTC)
- A certain RD Gill fixed K Devlin's solution in print. He did not use any scary words like symmetry. [9], middle of page 5; this is an article in the online statistics and probability encyclopedia of the big national and international statistics societies, and peer review is part of the procedure of publication. The contestant initially chooses door number 1. Initially, his odds that the car is behind this door are 2 to 1 against: it is two times as likely for him that his choice is wrong as that it is right.The host opens one of the other two doors, revealing a goat. Let’s suppose that for the moment, the contestant doesn’t take any notice of which door was opened. Since the host is certain to open a door revealing a goat whether or not the car is behind door 1, the information that an unspecified door is opened revealing a goat cannot change the contestant’s odds that the car is indeed behind door 1; they are still 2 to 1 against. Now here comes the further detail which we will take account of in this solution: the contestant also gets informed which specific door was opened by the host – let’s say it was door 3. Does this piece of information influence his odds that the car is behind door 1? No: from the contestant’s point of view, the chance that the car is behind door 1 obviously can’t depend on whether the host opens door 2 or door 3 – the door numbers are arbitrary, exchangeable. Therefore, also knowing that the host opened specifically door 3 to reveal a goat, the contestant’s odds on the car being behind his initially chosen door 1 still remain 2 to 1 against. He had better switch to door 2. Richard Gill (talk) 09:42, 29 September 2012 (UTC)
- I could see a section called "Explanation with a door open" going in there, explaining (without an illustration showing door 3 open) how nothing changes for a contestant who does not notice which door was opened - maybe they are blind and are told that a door was opened but not which - and then saying something like:
- Many people find it intuitively clear that further being told the door number reveals no new information about what is behind the player's door. However, this is only true when the host chooses randomly among his allowed choices. In a variant where the host even slightly favors one of the doors when possible, new information is revealed by his choice and the probability does change.
- Trying to actually show that no new information is revealed to those whom it is not intuitive would get way too complicated, IMO, so leaving it at "many people find it intuitive" seems best. I also feel that pointing out the dependence on the unbiased host assumption is necessary if we go down this route, because readers otherwise probably won't notice and are thus misled to think that this applies to the biased host variant as well. That is entirely analogous to people not noticing the dependence on host's restricted choice assumption and assuming the simple solutions apply to the ignorant host variant as well.
- This would be the only part of the "Solution" section that actually explicitly uses belief update and has "changing probabilities". I'm worried that this is unnecessarily confusing with little gain. Many peple are not familiar with the idea that probabilities can change and some resist it. The probability interpretations also rear their thorny head. That said, it's not an impossible idea. -- Coffee2theorems (talk) 10:02, 29 September 2012 (UTC)
- I could see a section called "Explanation with a door open" going in there, explaining (without an illustration showing door 3 open) how nothing changes for a contestant who does not notice which door was opened - maybe they are blind and are told that a door was opened but not which - and then saying something like:
- Coffee2theorems, I notice that you are not appreciating Devlin's solution because you apparently have a frequentist mind-set. You seem to think that we can only use symmetry if we know the host is unbiased. No. We weren't told anything at all. We don't know whether the host is biased or not. If he's biased we don't know which direction he's biased in. All in all, for us it is equally likely that he'll open Door 2 or Door 3 when he has that choice because we have been given no information to the contrary. And Vos Savant underlined the fact that we are supposed to take the door numbers as mere labels, of no significance at all, in her wording say Door 1 etc.
- I notice that many mathematicians have a frequentist mind-set and I suspect this is because they have been exposed to academic probability which is usually taught from a frequentist perspective. The rest of the world is still just as Bayesian as ever.
- Long ago Martin said a very wise thing: no one can think seriously about MHP without pondering on the meaning of probability. Probability interpretations raise their head, thorny or not, the moment you start to solve a popular brain-teaser by using probability notions. You had better be aware that there are different interpretations, all of them legitimate, and that there is a big mismatch between the more common (subconscious) popular interpretations (which are the same as those of the founders of probability: Huygens, Pascal, Laplace, Boole ...) and the more common present day academic interpretations.
- Like it or not, probability does not belong exclusively to the experts. We need meta-experts here, not experts. Richard Gill (talk) 13:35, 29 September 2012 (UTC)
- I'm actually Bayesian; I'm just trying to avoid unnecessarily imposing that on the reader at the outset. If the reader understood common notation, we could bash P(gobbledy) = gook at them with impunity and be interpretation-agnostic, confusing nobody regardless of their personal interpretation of probability. We can't do that, but we can use counting of "equally possible" (sic!) cases and easily understood frequencies ("2 people out of 3") while still remaining basically interpretation-agnostic (it's not like we are using confidence intervals or p-values here). In fact, with K&W assumptions, (almost) everyone agrees regardless of interpretation! That's as close to confusing nobody as we can reasonably expect to get.
- You seem to think that laypersons are Bayesians. That is indeed the Bayesian party line, but to be honest, I don't think laypersons actually have a consistent interpretation of probability that a statistician or a philosopher would recognize. It probably also varies quite a bit from person to person. People have different backgrounds, and the use of Bayesian language confuses some people (even if they perhaps think in a quasi-Bayesian way at some level). What little exposure to probability theory people have is also usually explained in frequentist terms, even if nothing inherently frequentist is actually covered. That's one reason I wrote the "However, ..." part in those terms (another is that the K&W assumptions are in those terms as well); it is easily enough re-expressed in Bayesian terms if need be. Having to make a choice of interpretation this way is IMO a major drawback of this explanation. -- Coffee2theorems (talk) 17:27, 29 September 2012 (UTC)
- Hear, hear, a certain Nijdam does not consider this a fix of the combining doors "explanation". It's a solution to the MHP, but it does not fix the fundamentally wrong idea behind the combining doors. There simply is nothing to combine in making the paradox better understandable. Nijdam (talk) 08:08, 29 September 2012 (UTC)
- Let me explain to dear Nijdam why this is a fix of the combining doors explanation. It focusses on what is behind Door 1. A car or a goat. That means that it lumps together what is behind Doors 2 and 3. We focus on the question: is the car behind Door 1, or is it behind Doors 2 and 3 combined? Secondly it splits up the information which we get from the host's actions into pieces. What information do we get from the host about the question whether or not the car is behind Door 1? The answer: no information. Devlin was a bit careless about this. For those who might still be worried that he did not tell the hold story, my solution discusses what information, about the question whether or not the car is behind Door 1, is given it by being revealed *which* door, Door 2 or Door 3, is opened by the host. Answer: none, by symmetry. Or if you find that word to scary: none, because we are given to understand that the door numbers are just arbitrary labels. There is nothing special about any of the doors. Richard Gill (talk) 09:42, 29 September 2012 (UTC)
- So, maybe some editors don't understand some solutions: that doesn't mean those solutions are wrong. It might mean that some editors' powers of imagination, or understanding of common English language, or knowledge of the sources, are too limited. The first important issue is whether or not those solutions are published in reliable sources. The second important issue is whether there is a consensus among editors that they might be useful to our readers. The third important issue is whether or not there is a concensus among editors that thy are notable enough that we have to inform the readers about them. If an editor disagrees with a solution then he or she should point to a reliable source which supports his point of view. Richard Gill (talk) 09:36, 29 September 2012 (UTC)
- Well dearest Richard, do you, with all your knowledge of the English language, understand what the fundamentally wrong idea behind the combining doors argumentation is? BTW: what do you think of the combining purses example? Nijdam (talk) 12:16, 29 September 2012 (UTC)
- In this early stage of receiving what (picture) the tricky one-time-story of devolution has left in the end, it is not necessary to imply that the "paradox" that it has left can only be viewed under one single slight aspect, and in this early stage it is never necessary to imply the unimportant illusion that the overall chance to win by switching could be "enhanced by staying" in one special "repetition" that was never implied to ever follow. Never necessary in that stage. Gerhardvalentin (talk) 13:23, 29 September 2012 (UTC)
- Well dearest Richard, do you, with all your knowledge of the English language, understand what the fundamentally wrong idea behind the combining doors argumentation is? BTW: what do you think of the combining purses example? Nijdam (talk) 12:16, 29 September 2012 (UTC)
- Nijdam: I can see a lot wrong with your version of the combining doors argument, but I see no point whatsoever in writing out an argument which is obviously wrong. This is just like Morgan et al. actually changing Vos Savant's words in order to be able to claim a point and get a publication in a prestigious journal by saying she was wrong. No: Morgan et al showed their stupidity by not having the imagination to see that she was right, if interpreted in a constructive way. As some of the discussants of their paper pointed out.
- You say that your version is the combining doors argument, but we don't have to buy your version of it. Especially not, since it is wrong. It's a straw man, a characature.
- On the other hand I see nothing wrong with the combining doors solution in the form in which I presented it to you here, quoting moreover from a reliable source, who, I happen to know, wrote it for the express purpose of showing that Devlin was close to home with his argument - he simply made one step without motivation, and when people pressed him on it, he apparently got confused and decided it was safer to go a long way round instead of finishing his short, elegant, route to the summit. But he's not a probabilist or a statistician so I can imagine he lost his self-confidence at that point.
- As to the purses, I don't understand your combining purses remarks at all. If you think it has relevance you had better find a reliable source which explains it, and hopefully explains it better. If such a source doesn't exist you'ld better write one. I suspect that you have a somewhat narrow mathematician's notion of probability which doesn't always match well to what ordinary people mean when they use the language of probability in ordinary conversation and non-technical writing. Mathematicians don't have a monopoly on the use of English. Richard Gill (talk) 13:19, 29 September 2012 (UTC)
- Happily you admit there is a lot wrong with "my" version of the combining doors solution. Here is a quote from Devlin's article:
- Imagine you are the contestant. Suppose the doors are labeled A, B, and C. Let's assume you (the contestant) initially pick door A. The probability that the prize is behind door A is 1/3. That means that the probability it is behind one of the other two doors (B or C) is 2/3. Monty now opens one of the doors B and C to reveal that there is no prize there. Let's suppose he opens door C. (Notice that he can always do this because he knows where the prize is located.) You (the contestant) now have two relevant pieces of information:
- [1] The probability that the prize is behind door B or C (i.e., not behind door A) is 2/3.
- [2] The prize is not behind door C.
- Combining these two pieces of information, you conclude that the probability that the prize is behind door B is 2/3.
- Apparently you admit there is a lot wrong with Devlin's way of reasoning. Nijdam (talk) 14:08, 29 September 2012 (UTC)
- There is not a lot wrong in Devlin's way of reasoning. There is one missing step in Devlin's argument. Devlin admitted that there was a step missing. The missing step is easy to fill in. It has been done by yours truly, and no doubt by many others (it's easy to do). What's the point of talking about a wrong argument which is nearly right? Fix it first and then discuss whether or not it is useful in the popular early parts of the article. Let's talk about the article, not about everyone's personal favourite and personal most hated solutions. Richard Gill (talk) 14:25, 29 September 2012 (UTC)
- @Richard, please show me where "my" version of the combining doors diffesr, as you stated, from Devlin's. I would not brag much about fixing Devlin's argumentation. It is in fact no more than the complete solution to the problem, which is well known and of a very elementary level. Calling it fixing is something like showing a front tyre and the rear light of a bike and saying it's a bike, but only needs some fixing. Devlin does no more than stating two more or less given facts, coming down to: every door has 1/3 chance on the car and (surprisingly, but apparently not to Devlin), door 3, the opened one, has probability 0 on the car. To me it's a contradiction, instead of a brilliant idea, and I surely hope you do not use this way of reasoning yourself when explaining the MHP. Nijdam (talk) 15:31, 3 October 2012 (UTC)
Nijdam: If I get you right your position is this: even if the door numbers are elided from the problem and we have a "you choose a door, host opens another door, wanna switch to remaining door?" formulation, one should still condition on doors, because they are distinguishable to the player (e.g. left, middle, right door; or top, middle, bottom door). You do not condition on specific goats (e.g. label them A and B yourself and condition on B, just like you label the doors 1, 2, 3 and condition on 3), because the goats are indistinguishable. I am curious: how do you justify that view?
Surely the goats are visible to the player. The goats have a size (say, p times the average goat). If the host chooses randomly, then no matter what continuous size distribution you use for the goats, the revealed goat's size almost surely won't hit the median of the hidden goat's distribution, so "which goat is bigger?" will almost surely not be 50:50. You got information distinguishing the goats; you have the "probably smaller goat" and the "probably bigger goat". Might not goat size therefore matter in general (if you took Freud too seriously, you might believe the host wants to show the bigger goat..?), and need to be conditioned on? -- Coffee2theorems (talk) 07:40, 4 October 2012 (UTC)
(editing)
- @Coffee2theorems: I had the impression you know all the ins and outs of the MHP, so you will understand and support my objection to Devlin's combining doors, as being highly misleading as an explanation. What your question about my position concerns, I do not see the immediate connection with the above discussion about combining doors. If you mean, the audience, being informed about the rules of the game, and unaware of the door the player will choose, is asked in advance whether the player should switch or not after the host will show them a door with a goat, yes, even then the answer "yes, you should witch" will be motivated by considering all the conditional probabilities,m like: if the player chooses door 1, and the host opens door 3, then .... As for the goats, firstly we may just consider them as undistinguishable, or formulate the problem with two empty doors. I think most people accept the goats as no more than "bad luck". But you will know this, so your question must beef a more sophisticated nature. When the goats are distinguishable, we are stuck with two goats, from which we do not know how they are chosen. Clearly if a player wins a goat, she has to be replaced. However I see no difficulties, as long as the host, when applicable, chooses randomly between the door numbers. Is this what you're aiming at? (connection was broken)Nijdam (talk) 12:34, 4 October 2012 (UTC)
- I see Devlin's combined doors explanations as variants of the "condition on the event 'door 2 or door 3 was opened'" approach, and I don't see any actually wrong statements there. The question is whether he has given a convincing argument or not.
- That leads to the question of whether it is permissible to condition on the event "a door (= door 2 or 3) was opened, showing a goat (= goat A or B)", or whether you should condition also on one of "door 3", "goat B", or both. Essentially, Martin's Billy/Nanny argument; I just translated it into something observable (e.g. goat size), as otherwise it makes no sense to me.
- I agree that the problem may well be expressed without goats (I explained my views on that here (01:58, 2 October comment)). What I'm aiming at is that, while the idea of conditioning on goats is surprising (why should that matter! a goat is a goat!), conditioning on doors is just as surprising to others (why should that matter! a door is a door!). I can't help but notice the similarity! Consider that the person you are arguing with (Gill) is also quite competent in this field; to me that is evidence that perhaps the issue is not so cut-and-dried after all.
- The MHP can also be formulated without distinguishable doors. One way is to use a bag with a red marble and two blue marbles in it, instead of e.g. shells and peas like vos Savant's (goatless!) simulation. IIRC some years ago Gill opined that the former is still a simulation of "the MHP". I feel that it is not quite satisfactory; but less strongly than I used to. Is that purely a matter of opinion, or a matter with a clear-cut correct/incorrect answer, or something in between? That, I feel, is the core issue. Once you have a formal model instead of a fuzzy word problem, there's not going to be much disagreement among informed people; the issue is in how to get there.
- It's true that the "condition on a door" arguments don't work in the case of hosts who favor e.g. the right-hand door, and that that takes people by surprise (oh, door number can matter!). But the "condition on door 3" version also doesn't work for hosts who favor bigger goats, and I bet that would take people even more by surprise (oh, goat size can matter!). Either way, you've taken a real(?) situation, built a simplistic model, and are surprised when reality breaks out of it. If reality doesn't do that (lucky!), was your reasoning nevertheless wrong, because reality could have done so and you would have been surprised if it did - you just got lucky? Can you see how reasonable people might end up having a disagreement here, depending on the details? You might argue that including a door number is a second-order correction and something fuzzy like goat size is a third-order correction (effect limited by observation uncertainty), but by then you have admitted that both are approximations instead of Absolutely Correct One True Solution(s). The first-order model, with indistinguishable doors, already captures the main part of the phenomenon (2/3 vs. 1/2), so it's not entirely unreasonable to argue that it's a legitimate option to stop there ("good enough for physicist work!"). -- Coffee2theorems (talk) 18:59, 4 October 2012 (UTC)
- Well, look closer at Devlins (and others') way of reasoning (see above). Try to understand what he means when he says: combining these two pieces of Information. There is nothing to combine.there! And hence nothing is explained. It really is easy to see. Nijdam (talk) 19:44, 4 October 2012 (UTC)
- It's about a brain teaser that has been told in a story about a "one-time problem". In this one-time problem, the host either got the car and only one goat in 2 out of 3, being restricted to show his only goat then. – Or, in this one-time problem, the host got no car but both goats in the rest of 1 out of 3. Then – in this one-time problem – he cannot "show" any (for ever unknown) "preference". It is of no avail and therefore unnecessary to "assume" what you never will know, instead of trusting in that what you already know for sure, just from the outset.
And, just not to fall into the dangerous 50:50 trap, it is helping to "see" that in only 1 out of 3 his two doors hide just goats, but in 2 out of 3 he has got the only prize with one of those two goats. Not to be trapped, it is helping to distinguish the door first selected on the one side, and the group of those two host's doors on the other side. There is nothing wrong. And, although it is a one-time problem ("you are in a" game show, and not "you will be in ten game shows"), in only about 33 millions out of 100 millions staying will give you the prize, but in more than 66 millions out of 100 millions switching will give the prize, because of symmetry: "no matter at all, which one" of his two doors the host did open in that 100 millions. Gerhardvalentin (talk) 21:17, 4 October 2012 (UTC)
- It's about a brain teaser that has been told in a story about a "one-time problem". In this one-time problem, the host either got the car and only one goat in 2 out of 3, being restricted to show his only goat then. – Or, in this one-time problem, the host got no car but both goats in the rest of 1 out of 3. Then – in this one-time problem – he cannot "show" any (for ever unknown) "preference". It is of no avail and therefore unnecessary to "assume" what you never will know, instead of trusting in that what you already know for sure, just from the outset.
- To Nijdam: Falk says that conditioning on "which door" has been opened makes only sense "if the host IS biased" and that you KNOW about that bias. And I am adding: You of course CAN utilize a mathematically correct phantasmal cure-all, but then you must be aware of it's inexpedience to give any better advice than to "always switch". Thus: no necessity at all to give the correct answer for the MHP, but very suited and helpful to teach and to train conditional probability theory, see the plenitude of available textbooks on teaching conditional probability theory. Gerhardvalentin (talk) 21:51, 4 October 2012 (UTC)
- Imagine you are the contestant. You are given the choice of three miniature doors in a bag (like three marbles in a bag, really). Suppose they are labeled A, B, C; the labels are written in a secret compartment in each miniature. You blindly pick one from the bag (secretly, door A). The probability that the car is in the bag (in both senses!) is 2/3. The host looks in the bag and secretly peeks behind the doors, picking a goat door (secretly, door C), and opens it for you. As Devlin says, "he can always do this", where "this" must mean picking a goat door (he can't very well always pick door C, it might be the car door!). In other words, this is a sure event, and so the car is behind one of the host's doors (secretly, door B or C) still with probability 2/3. The car is not behind the opened door (secretly, door C). Combining these two pieces of information, you conclude that the probability the car is behind the door in the bag (secretly, door B) is 2/3. The car is probably in the bag! Switch!
- I think this is basically the same thought process, put slightly more clearly, perhaps with some unnecessary wrinkles smoothed out. ("he can always do this" is a dead giveaway, IMO) You can label the doors and talk about the labels without assuming that the contestant knows them or the distinctions they stand for. You can of course argue about clarity of phrasing things and the sensibility of a model with indistinguishable doors. (another possibility is a blind contestant told appropriate things, and that probably fits the story slightly better, but I like bags of marbles as a model better, being a classic and all; also, the A, B, C labeling here is actually entirely superfluous) -- Coffee2theorems (talk) 23:39, 4 October 2012 (UTC)
- Sorry, Coffee2theorems, often people come with alternative descriptions as if they would make the problem more understandable. As if the original setting is not simple enough as it is. Anyway, if you like to use an alternative setting, like yours, with tiny doors, etc, you firstly have to show it's equivalent to the MHP, and guess ... it isn't. That's often the point, someone gives an alternative description, from which they believe it is equivalent to the MHP, and then proves their different way of solving with this alternative description. Why are people that reluctant to admit Devlin's combining is nonsense? Nothing particularly difficult there. I will spell it out again. Devlin reasons: 1) the not chosen doors 2 and 3 have together probability 2/3 on the car (what he omits to mention, or simply doesn't realize, is that each has probability 1/3); 2) the opened door 3 has probability 0 on the car. To me this is a contradiction. And to you? Nijdam (talk) 06:53, 5 October 2012 (UTC)
- I'm not sure that Gerhard is against this. The use of the closed doors figure alone (with an explanation, to suggest the partition) at the beginning was actually his idea (10:27, 27 September 2012 comment above), I just copied it because it seemed good to me. It may of course be that I somehow misunderstood it, but I don't see how. -- Coffee2theorems (talk) 08:17, 29 September 2012 (UTC)
Proposed text for Solution section, take 2
Proposed text for Solution section, take 2
| ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
SolutionThe player should switch. Switching wins twice as often as staying. [many citations] The answer is easily verified experimentally. It has been verified countless times using computer simulations as well as simulations with human participants. [many citations] Simple explanationIf the player is resolved to always stick to their initial choice, they might as well not be offered the option to switch at all. Sticking wins exactly when the player initially picks the car door, which happens 1/3 of the time. Switching wins the other 2/3 of the time. This may be easier to grasp if the doors are grouped into player's doors (door 1) and host's doors (doors 2 and 3), as illustrated below. The player is basically given the choice of keeping what's behind their door, or taking everything behind the host's two doors. The host is saying in effect: "You can keep your one door or you can have the other two doors, one of which (a goat door) I'll open for you." No matter what the host does, a player who always switches gets all cars behind the host's two doors. (Adams 1990) The situation can also be analyzed by cases, as illustrated below. Switching loses in only one of the three equally likely cases (case 1), and wins in the other two. A player who always switches wins 2/3 of the time. (vos Savant 1990b; Krauss and Wang, 2003)
Many people find the situation intuitively easier to understand by considering the same problem with a million doors instead of just three. (vos Savant 1990; Krauss and Wang, 2003) In this case there are 999,999 doors with goats behind them, and the player's chances of picking the car door are one in a million. The game host goes down the line of doors, opening each one to show 999,998 goats in total, skipping over only the player's door and one other door. The host then offers the player the chance to switch to the only other unopened door. On average, in 999,999 out of 1,000,000 times (i.e. the times the player initially picked a goat) the other door will contain the prize. Explanation with door 3 openWhen first encountering the problem, most people consider only the situation where door 3 is open, leaving only two possibilities: the car is either behind door 1 or door 2. They then incorrectly conclude that the chances are 50:50 either way (Krauss and Wang, 2003). These are indeed the only two possibilities when door 3 is open, but they are not equally likely! This is illustrated in the alternative explanation below, with these two possibilities on the left side of the thick line.
The above illustration shows everything that can happen to players who pick door 1. On average, three in six end up in the exact situation described in the problem statement (door 3 is opened; left of the thick line). Two of the three win and one loses by switching; therefore the probability that switching wins in that situation is 2/3 (Chun 1991; Grinstead and Snell 2006; Morgan et al. 1991). | ||||||||||||||||||||||||||||
Comments on the proposed text
OK, I modified the proposal again to take some of the above comments in account, as well as other modifications. What do you think? -- Coffee2theorems (talk) 20:15, 29 September 2012 (UTC)
- Very well illustrated and professed, really a good assistance. Gerhardvalentin (talk) 21:33, 4 October 2012 (UTC)
A necessary and sufficient condition
As we seem to be getting nowhere again, I am going to suggest a completely different approach:
Suppose we give the vS/Whitaker problem statement with the following addition. 'It is generally assumed that the host takes no action and no other event occurs that changes the probability that the player has originally chosen the car'.
This innocuous statement covers all the angles, the host must offer the swap, he must always reveal a goat, and he must choose a legal door uniformly. It avoids the need for conditional probability since the posterior probability that the player has chosen the car is equal to the prior probability by definition.
We can then relax this condition to include the host opening an unchosen door randomly that happens to reveal a goat, the host having a preference for a specific door or goat, the host indicating by some other means where the car is, and the host only offering the swap when the player has chosen the car. The MHP and 10 years of argument in a nutshell. Martin Hogbin (talk) 00:06, 29 September 2012 (UTC)
- I'm really not sure if you're kidding or not. Assuming you're not, how would you reference this suggested statement? You're basically saying it is generally assumed the probability the car is behind the player's originally chosen door remains 1/3 (which it obviously is before the host opens a door) after the host opens a door. It seems to me this is the entire point of the problem, and if you simply assume this you're assuming the answer. Rather than argue about this, let's just say [[citation needed]. -- Rick Block (talk) 05:20, 29 September 2012 (UTC)
- I am sure that we could find a reference for this somewhere. We are writing an encyclopedia not a puzzle book, so if the problem statement starts to lead the reader in the right direction that is an advantage. Is my statement even contentious? Is there anyone who thinks that the problem is not generally (and intentionally) set up in such a way that host's action does changes the probability that the player has originally chosen the car? Martin Hogbin (talk) 09:09, 29 September 2012 (UTC)
- I did just give you a reference. RD Gill (2011). Let's approach MHP with the layman's notion of probability, which is the same as the notion of the founders of probability, Huygens, Pascal, Laplace, Boole... Probability is in your mind, it's about your knowledge or lack thereof, and if you have no reason to think otherwise, then alternative possibilities are equally likely. This is probability based on symmetry, which unfortunately is apparently a too difficult word for editors and readers of wikipedia. However probability in the classical sense is all about symmetry. Probability in our readers minds is all about symmetry. Symmetry is why everyone initially thinks that the chance the car is behind Door 1 and behind Door 2 must be the same. But at this stage of the problem, Door 1 and Door 2 are doors with two different roles: the door initially chosen by the competitor and the different door left closed by the host. Because these doors have different histories they no longer have the same probabilities to hide the car.
- Let's imagine being told the MHP story bit by bit and let's think about how our opinion changes as our knowledge grows. Initially the chance for us is 1/3 that the car is behind the competitor's door, Door 1 (symmetry). Then we are told that the host opens a different door revealing a goat, something which he always can do because he knows where the car is, and something he always does do. Our information about whether there's a goat or a car behind Door 1 hasn't changed. So for us the chance is still 1/3 that the car is behind Door 1. Finally we are told that the host in fact opened Door 3. We know he was going to open Door 2 or Door 3, and the number on the door which he opens is irrelevant to whether or not there is a car behind Door 1, since we have no information to the contrary (symmetry).
- Please delete the word symmetry everywhere from these remarks if it is too expensive for you. The solution I have just told you is published by R D Gill and it's a combining doors solution: it talks about the chance that the car is behind Door 1 versus the chance that the car is behind Door2 or Door 3. Richard Gill (talk) 09:26, 29 September 2012 (UTC)
- So we now have a reference. My suggestion is to make this point part of the problem statement, not part of the the solution. The problem was intentionally set up this way right from the start by Selvin. If doing things this way makes the solution easier, or even obvious, that we have achieved a great success. Martin Hogbin (talk) 09:32, 29 September 2012 (UTC)
- No Martin. MHP is solved by different authorities in fundamentally different ways. The choice of which route to take is free. I think there are three basic ways: (1) Some authorities solve MHP by strategic thinking (the location of the car is fixed but unknown, probability is in the choice of initial door by the competitor), "choose at random and switch" is the minimax solution. (2) It is solved by some authorities, e.g. Morgan et al., by frequentist probability, probability is used to model the actual long run behaviour of the quiz-show team and of the host. Assumptions as to what these long run probabilities are have therefore to be made explicitly. These "input" probabilities have to be part of the complete problem statement. (3) It is solved by other authorities using subjective probability and therefore symmetry. Invoking symmetry to get the subjective probabilities of this and that (thus: not how the team hides the car, and how the host makes his choice, but the facts that you, the problem solver, have no information about either process) is part of the subjectivist's solution. The probabilities are part of the solution, not part of the problem. Richard Gill (talk) 11:23, 29 September 2012 (UTC)
- Yes, the probabilities are part of the solution. That's why I think we should avoid potentially confusing "changing probabilities" in the initial Solution section, because we can. It can readily enough be read in a Bayesian way without shoving that interpretation down the reader's throat.
- Incidentally, you are wrong about subjective probability implying symmetry. It is only the objective Bayesian (the people who like reference priors and suchlike) who is forced to use a 50:50 prior; a subjective Bayesian may choose whatever prior they please. Perhaps they think that the doors are numbered from left to right and the host is probably right-handed and that right-handed people probably pick the right-hand door more often so the host probably favors door 3 vs door 2; in any case, if a subjectivist tells you they believe that and you disagree, they are not obliged to agree with you just because you claim your subjective prior is "objective" or "the right one" or whatever. If you want to have only one unambiguous subjective Bayesian solution, you must specify the prior; there's no way around that. -- Coffee2theorems (talk) 11:55, 29 September 2012 (UTC)
- I meant the objective subjective probability of Laplace, Boole and so on. And I reiterate that I think that this is the way most laypersons think about probability. — Preceding unsigned comment added by Gill110951 (talk • contribs) 12:07, 29 September 2012 (UTC)
- Exactly. Nobody is making a subjective guesses about the a priori right-handedness of Monty or how this might influence his choice of goats. The symmetry lies in applying the principle of indifference, i.e., the uninformative prior that uses symmetry when there is no knowledge indicating unequal probabilities.
There may be some terminological confusion about "objectivist Bayesian" and "subjectivist Bayesian", and even some debate about whether all Bayesianism is subjective at root; but in the course of discussions here, "subjective" has been used to contrast "Epistemic probability" with "frequentist statistics". In these pages, for the variant in which Monty's method of choosing goats is unspecified, the so-called "subjectivists" treat the absence of information about Monty's preference as an epistemological fact and calculate a "probability" expressing the state of ("subjective") knowledge; and the so-called "frequentists" treat Monty's preference as an ontological unknown and formulate a "probability" in terms of an open parameter to express a state of ("objective") reality. They really do not mean the same thing by the word "probability".~ Ningauble (talk) 15:48, 4 October 2012 (UTC)
- Exactly. Nobody is making a subjective guesses about the a priori right-handedness of Monty or how this might influence his choice of goats. The symmetry lies in applying the principle of indifference, i.e., the uninformative prior that uses symmetry when there is no knowledge indicating unequal probabilities.
- I meant the objective subjective probability of Laplace, Boole and so on. And I reiterate that I think that this is the way most laypersons think about probability. — Preceding unsigned comment added by Gill110951 (talk • contribs) 12:07, 29 September 2012 (UTC)
- The statement "It is generally assumed that the host takes no action and no other event occurs that changes the probability that the player has originally chosen the car" is not true; that is not generally assumed, but is often considered to be something to be shown. It is also very confusing to some people who are not familiar with belief update or probabilities changing or the Bayesian way of phrasing things. Consider e.g. these comments from the talk page of the Sleeping Beauty problem where a conditional/unconditional interpretation issue also arises:
- "What is your credence now for the proposition that our coin landed heads?" This could mean "What probability should she give to the coin actually landing heads?" and is definitely a question about her knowledge of the ratio of throws H:T that actually occur (or land). It appears to (erroneously) imply that this probability could vary which might explain why it is often interpreted as the quite different question "What probability should she give to her correctly guessing that the coin had landed heads?"
- and:
- The HALFERS define the Bernoulli trial as the the coin flip. The waking of Sleeping Beauty is a secondary event. When awakened, Sleeping Beauty is being asked to reflect on an event that occurred in the past. The halfers imagine the interviewer asking "Hey we flipped a coin on Sunday, what do you think the chances are that it came up heads?" Beauty will say 1 out of every 2 trials regardless of the number of times she was awakened.
- The THIRDERS define the Bernoulli trial as the waking of Sleeping Beauty. Sleeping Beauty is being asked about the present. The thirders imagine the interviewer asking "See that bowl there? What do you think the chances are that the coin under it reads heads?" Beauty will answer 1 out of every 3 trials. It could be argued that these trials are not truly independent.
- and further:
- The Sleeping Beauty problem is not a mathematical paradox. The two probabilities are the result of calculating probability in different ways, the unconditional probability being 1/2 and the conditional probability (given the condition that Sleeping Beauty be awake) being 1/3. Neither of these is "the right way"; both are valid approaches.
- If someone tossed a coin and asked me what my credence was for the proposition that the coin landed heads, I would respond 50% for obvious reasons. To me, "what is my credence" is just one of many ways of asking what the probability is. So I can see no reason why Sleeping Beauty should answer differently. The business with Mondays and Tuesdays and putting to sleep and amnesia-inducing drugs is just window dressing added by the problem's poser to mislead the solver into giving a false answer. It's not unusual to do that, and in fact considering how people normally try to solve this it's clear why the problem was posed that way.
- Try thinking of it like this. If the problem asked "What is your credence now for the proposition that the coin landed heads, given that you are awake?" the answer would clearly be 1/3. So why hasn't the poser asked it that way? My answer is, because that's not what he is asking for. He has deliberately added the trappings of a conditional probability problem in order to trick the reader into giving the wrong answer. You've fallen for his trick.
- How utterly confused is that? You are begging for the same kind of confusion here. People who think probability is immutable think that "the probability that the player has originally chosen the car" means the unconditional probability, no matter what happens afterwards. Suppose you are told which door the car is behind. To these people, the probability you speak of is still 1/3, because, you know, that's what it originally was and that's what it still is, (unconditional) probabilities don't ever change, this is mathematics, once something takes on some value it will forever be that value.. etc. -- Coffee2theorems (talk) 10:38, 29 September 2012 (UTC)
- Who says that all the probabilities are part of the solution and not part of the question? It was clearly Selvin's and vS/Whitakers intention that the action of the host should not change the probability that the car is behind door 1. If we state this as part of the problem then all solutions become much clearer. Martin Hogbin (talk) 13:25, 29 September 2012 (UTC)
- Perhaps you interpret Selvin/vS/Whitaker that way (though I don't really see how). Perhaps they even intended it that way. That doesn't really matter much. The assumption is not generally made; there are many who do not make it, and in many sources it is not something to be assumed but something to be proved.
- Aside from that, even if what you say were the case, it would be much clearer to state the assumption this way:
- It is generally assumed that when door 3 is opened, the probability that the car is behind door 1 remains unchanged.
- The argument against the 50:50 misconception then becomes very simple indeed: the probability that the car is behind door 1 was 1/3, and by assumption it still is so; therefore it is not 1/2. -- Coffee2theorems (talk) 14:04, 29 September 2012 (UTC)
- I agree with Coffee2theorems. Everybody who writes down some probability assumptions to solve the problem is solving the problem by introducing probability assumptions. Solving such a problem entails motivating some formal assumptions and then proceeding to use those assumptions (and just those assumptions) in a logically correct way to get to a formal conclusion, and then finally translating the formal conclusion back to a real world statement. In the academic context we perform each of these three steps explicitly. In a popular context ordinary people don't draw the boundaries between the three phases distinctly and may skip discussion of steps which everyone finds obvious. But if challenged, one must be prepared to make distinctions and one must be prepared to fill in "obvious" steps. Not everyone makes the same assumptions. That's why the article can't start by saying that these are the assumptions we have to make. It can start by saying that certain assumptions are very commonly made.
- In my opinion, most laypersons approach MHP using (symmetry driven) subjective probability. Thus without comment they automatically assume that, for them, the car is equally likely behind any of the three doors and that if the host has a choice of door to open it is equally likely, for them, that he opens either. This does not mean that the car is hidden by using an unbiased random generator and that the host chooses a door to open by using an unbiased random generator. It means that we don't know anything about how these tasks are performed, and hence that what we do know about it, is unaffected by renumbering the doors anyway we like. This implies that subjective probabilities of events involving numbered doors won't change if we renumber those doors. Therefore the subjective probability of winning by switching given any particular door initially chosen and any particular door opened by the host does not depend on what those particular door numbers happened to be. Therefore these subjective probabilities are all equal to the overall subjective probability of winning by switching, which anyone can quickly be convinced equals 2/3. OMG, what an ado about nothing.
- But many laypersons approach MHP with quite a different mindset. See The Economist for instance. Strategic thinking! The location of the car is fixed but unknown. The only randomness which we know about is in the choice of initial door by the competitor. Richard Gill (talk) 14:11, 29 September 2012 (UTC)
- As the famous story about a one-time problem has asked the question "is it to your favor to switch", the "behavior" of the host may not (since cannot) be misinterpreted. Doing it though, means forgetting about this one-time problem and creating another new story with quite another new different question. But the paradox might not "appear" in other quite different stories and questions. So N.Henze, in addressing the paradox, explicitly says that the host is "observing secrecy" regarding the door that hides the car. I see that to be a clear and logical consequence for that one-time problem. So: No maths in the problem description. Gerhardvalentin (talk) 14:26, 29 September 2012 (UTC)
- As to the MHP sources say that, under explicit suppositions, the conditional probability to win by staying can / may vary within the fixed range of 0 to max. 1/2, under all possible suppositions, with an average of 1/3. And they say that the conditional probability to win by switching can / may vary within the fixed range of at least 1/2 to 1, under all possible suppositions, with an average of 2/3. And sources say that simple solutions correctly give an overall probability to win by staying of 1/3, and correctly give an overall probability to win by switching of 2/3.
And sources say that the overall probability to win by switching of 2/3 "impossibly can be enhanced" by any "staying" on any single occasion. Sources say that, as a consequence, it never will be necessary to base the conditional probability to win by switching on "which" door has been opened by the host who even is "invited" to be biased. The door opened by the host may never be considered as a basis to your decision to stay or to switch, this would be a fallacy, as you know already from the very beginning that staying forever is definitively excluded. Excluded just from the outset. So the simple solution is fully correct in neglecting "which" door has been opened by the host. Regarding the MHP conditional probability, based on the door opened by the host, is once and forever unnecessary, as per the sources. Switching gives an overall success rate of 2/3 that cannot be augmented by any "staying".
So imo it is superfluous to try to reconsider the probability of the door first selected to hide the car, based on which one of his two doors has been opened by the host. Imo the article should base on reliable sources. Gerhardvalentin (talk) 00:42, 30 September 2012 (UTC)
- As to the MHP sources say that, under explicit suppositions, the conditional probability to win by staying can / may vary within the fixed range of 0 to max. 1/2, under all possible suppositions, with an average of 1/3. And they say that the conditional probability to win by switching can / may vary within the fixed range of at least 1/2 to 1, under all possible suppositions, with an average of 2/3. And sources say that simple solutions correctly give an overall probability to win by staying of 1/3, and correctly give an overall probability to win by switching of 2/3.
I think that I should clarify what I meant, 'that the host takes no action and no other event occurs that changes the probability that the player has originally chosen the car' is a necessary and sufficient condition for the simple solutions to be valid. If the condition is not fulfilled then the simple solutions can be criticised for requiring unstated assumptions. If the condition is satisfied the simple solutions are all perfectly correct. That is all I am saying.
Coffee2theorems, I do not see how Selvin's problem statement can be interpreted any other way that implying the above condition. Are you suggesting that Selvin envisaged that some action of the host would change the probability that the player had chosen the car? When pressed on that point he made it clear that he was not considering that possibility.
Vos Savant also made clear that she interpreted the question (that she actually formulated) in the same way. In both formulations the original intent is clearly that the host takes no action that changes the probability that the player has originally chosen the car. Martin Hogbin (talk) 22:49, 29 September 2012 (UTC)
- Your statement
- the host takes no action and no other event occurs that changes the probability that the player has originally chosen the car
- is already basically implied by the K&W assumptions, as is shown by the conditional solutions. The simple fact that the problem statement implies some thing X doesn't mean that we should incorporate X as a part of the problem statement. The problem statement also implies that the player should switch, and Selvin probably didn't envisage that staying would ever be better either. That doesn't mean that we should add "It is generally assumed that the player should switch." as a part of the problem statement. That would be a total cop-out. Likewise, anything that allows us to basically say
- the probability that the car is behind door 1 was 1/3, and by assumption it still is so; therefore it is not 1/2
- is a total cop-out. We proved that it's not 50:50 by assumption! I don't think anyone would accept that. That assumption is too strong in some vague cop-out sense (technically e.g. the assumption "the player should switch" is weaker than "the host is unbiased", but the former is stronger in this vague cop-out sense). You also can't escape this by obfuscating the assumption somehow; by doing that you merely replace the original MHP paradox by a new one that arises entirely from your choice of obfuscation method. The widely accepted obfuscation method (accepted to do no violence to the problem) is to say that the host chooses uniformly among his choices, and we shouldn't invent our own.
- I'm also not convinced that your assumption is necessary or sufficient for validity of the simple solutions. You could argue that it is not sufficient because it is not explicitly referred to by the solutions. You could argue that it is not necessary because it is obvious (given unbiased host / symmetric beliefs) that the optimal strategy must either be "always switch" or "always stay", and unconditional probability suffices to show that the former is better, and hence optimal.
- Be the result of such an argument as it may, the unconditional solutions are valuable because they intuitively resolve a part of the paradox: The fact that switching is optimal in a particular situation is not paradoxical or even the least bit surprising after you understand that always switching is twice better than always staying. Conditional solutions provide the rest of the resolution, showing why the 50:50 "argument" (if you can call it that) is wrong, as well as dotting the i's and crossing the t's for those who care. -- Coffee2theorems (talk) 02:15, 30 September 2012 (UTC)
- The condition is necessary for the simple solutions to be valid in that if it is not met, in other words if the host does do something which does change the probability that the player has chosen the car then the simple solutions are wrong, not just in that they might be considered incomplete but in that they give the wrong answer. The condition is the only one which guarantees an answer of 2/3. The arguments you give only apply if other conditions are met, for example that the host always offers the swap and the host always reveals a goat. My condition is actually at the core of the problem, without it the problem is actually insoluble. The conditions in K&W are in fact rather poor substitutes for my condition and do not, as I have shown here actually guarantee the right answer in all cases.
- I do understand that spotting the condition might be regarded as being a key part to solving the problem rather than an explicit part of the problem statement and if we were setting a puzzle for readers I would not add that condition because it might weaken the power of the MHP to confuse. However, we are writing an encyclopedia and therefore weakening the problem might actually be to our advantage. We want people to understand exactly what is going on and the key fact in understanding that is the assumption (I think obviously intended by both problem authors) that the host action does not change the posterior probability that the player has chosen the car. Martin Hogbin (talk) 09:19, 30 September 2012 (UTC)
- Martin: first of all you are restricting yourself to the K&W conditions or what one could call: solution by subjective probability, symmetric case (probability as expression of ignorance). Fine to concentrate on this case, but please remember it isn't the only way people approach MHP, whether academic of amateur. Secondly, IMHO, you are assuming what needs to be proved. Thirdly, your approach is completely novel. Or is it your idea that many amateur writers take this approach without making it explicit? Still, that's a novel interpretation of what went on in the mind of Vos Savant and other popular writers. Richard Gill (talk) 10:04, 30 September 2012 (UTC)
- I am restricting myself to every case, in which the initial probability that the player has chosen the car is 1/3 and to which the answer is 2/3. The answer is 2/3 iff the probability that the host has chosen the car remains 1/3, regardless of how the problem is set up, what model of probability is used, and what approach is used to calculate the answer. This is why I want include the condition in the problem statement not in any particular solution.
- I am not assuming quite what needs to be proved, which is that the probability that the player will win by switching is 2/3 but I do accept that I have moved some way in that direction. I am stating the one and only essential assumption for the answer to have the standard/conventional value of 2/3. It is the other assumptions that are not always necessary and generally not sufficient to ensure the correct answer. I agree that we are leading the reader by the nose by stating this essential assumption as part of the standard/conventional formulation of the problem but is that a bad thing here? We are supposed to be trying to help the reader not fool them. It would be very interesting to present people with the vS/W problem statement plus my condition and see how many get the right answer. My guess would be more than usual but far from everyone (even though the correct answer follows from a simple and obvious calculation).
- I think vS went some way towards stating my condition as a central assumption, as did Selvin. Whether what they said is clear enough to be used as a source I cannot say without reading what they wrote carefully again. Martin Hogbin (talk) 13:27, 30 September 2012 (UTC)
- So you are asking for the conditional probability (this is what you mean by "the answer"), or in less expensive words, you are asking that the probability does not depend on specific door numbers. You assume that the car is initially equally likely behind any of the three doors (this rules out the Economist's solution). What you call an assumption is what other people call a deduction. You are correct in noticing the mathematical fact that the logic works both ways. Your way: answer is 2/3 implies the host's choice is completely random. Other way: host's choice is completely random implies answer is 2/3. I think your observation is technically speaking OR, I did not see it in the literature.
- Selvin (1975a) assumes car location and initial choice are independent and completely random. He looks at 9 equally likely combinations. In essence he gives the combining doors solution. Given the location of the car and the initial choice, he compares "switching" with "staying". He doesn't differentiate which door is chosen by the host when the host has a choice since it doesn't make a difference to whether switching or staying wins or loses, in his table of 9 combinations. He ignores the possibility that one might like to make one's choice of switch or stay depend on which particular doors are involved in a particular case.
- Selvin (1975b) was written in response to many letters he got about his first article. One of the letters was from Monty Hall himself, who gave a short sharp version of the combining doors argument (the chance that the car is behind door 1 is not changed by subsequent events).
- Selvin (1975b) explicitly adds the assumption that the choice of the host is completely random and he states explicitly that his earlier solution is based on this assumption, even though was no mention of the assumption and no explicit use of the assumption in Selvin (1975a). He goes on to give a new solution by calculating the conditional instead of the unconditional probability of switching. The suggestion that he wants to give is that the two solutions are the same. A pedant could have avoided the explicit calculation but instead added the phrase, "the chance of winning by switching doesn't depend on which particular doors are chosen and opened (symmetry!) since the host is equally likely to open either door if he has the opportunity" to his first solution. (As discussants of Morgan et al. also did, later).
- Vos Savant is mainly concerned with preserving her image of being an immensely smart person who always gets it right. She does not waste ink getting into technical niceties. I don't think she ever explicitly said that she was silently assuming the host's choice as being completely at random, and I don't think she ever explicitly argued that this assumption was needed in order to solve the problem. (Discussants of Morgan et al. considered this a matter of taste). I do think that she implicitly did want us to assume complete symmetry, by using the words "say, Door 1" and "say, Door 3". This leads to a formal solution where one invokes symmetry at the outset to forget door numbers altogether. By symmetry, the only thing that interests us are the chances that the initially chosen door hides the car and the other closed door hides the car. These chances have to be the same as the conditional chances of the same events, given the specific door numbers, e.g. 1 and 2. But there is no particular interest in saying so. It can be added, for completeness, and if you do so it will please people like Nijdam. A matter of taste. Richard Gill (talk) 09:48, 1 October 2012 (UTC)
- As you know, I would rather say nothing at all about conditions. I have no objection to using the term 'conditional probability' but I see no reason why the door number opened by the host should be regarded as the only significant condition of the problem.
- Vos Savant is mainly concerned with preserving her image of being an immensely smart person who always gets it right. She does not waste ink getting into technical niceties. I don't think she ever explicitly said that she was silently assuming the host's choice as being completely at random, and I don't think she ever explicitly argued that this assumption was needed in order to solve the problem. (Discussants of Morgan et al. considered this a matter of taste). I do think that she implicitly did want us to assume complete symmetry, by using the words "say, Door 1" and "say, Door 3". This leads to a formal solution where one invokes symmetry at the outset to forget door numbers altogether. By symmetry, the only thing that interests us are the chances that the initially chosen door hides the car and the other closed door hides the car. These chances have to be the same as the conditional chances of the same events, given the specific door numbers, e.g. 1 and 2. But there is no particular interest in saying so. It can be added, for completeness, and if you do so it will please people like Nijdam. A matter of taste. Richard Gill (talk) 09:48, 1 October 2012 (UTC)
- It's a common way the word probability is used, to always understand "conditional on everything that you know at this point in time". When people ask "wnat is the probability", they mean "what is the probability, given what you know". As some history of events unrolls in time, "the probability" of anything in particular is always the probability relative to some observer, and hence it evolves in time as the observer gets more information. For Monty, the probability the car is behind door 2 is fixed at 1, or 0, at the start of the show. For the competitor it changes as his actions stimulate reactions from Monty, which give him more information. From decision theory, theory of dynamic programming, we know that if you want to maximize your overall succes-rate at some task, then at any point in time at which you have to make a choice, you shoukd make the choice which gives you the best conditional chance of success given what you know so far. Pretty intuitive, right? This is the reason why the conditionalists keep saying "you have to compute the conditional probability to solve the problem". They don't know the reason why, for them it is a dogma. But understanding why the dogma is actually sound wisdom, we see that we can do without it. If we can succeed with unconditional probability 2/3 by always switching, and if there is no way to do better, then there is no point at all in figuring out conditional probabilities. I think this is the reason why ordinary folk are completely satisfied with simple solutions. It's obvious you can't do better than 2/3, so no more needs to be said.Richard Gill (talk) 20:21, 1 October 2012 (UTC)
I think this "dogma" is generally taken as axiomatic to the Bayesian approach because it is just too dang obvious. People do not generally ask "Why should it be optimal to take into account everything I know when making a decision, and why should failing to do so generally not be optimal?". People also do not prove obviosities like this or the intermediate value theorem because they suspect they are false, but to check that there are no problems in the formalization and to get the precise range of applicability. Was there ever any doubt?!
I agree with you that the "strategy with best guarantees" result is very nice. That is perhaps the only kind of result that has any serious claim to objectivity (in a "the solution of tic-tac-toe" sense). But the 2/3 number in it is not the probability of winning by switching at any time after the player's initial choice (this would be a likely misconception). Those probabilities, as well as initial probabilities of car location, are completely unknown with so weak assumptions, but insisting that they are unknown is unlikely to go over well.
That solution is assuming that when nothing definite is known, you should not bother with beliefs, but take the guaranteed result. While it gives a good result here, that kind of thinking in general has its own problems, as it focuses solely on worst opponent performance, ignoring average opponent performance (I've heard that e.g. at poker that approach sucks; you do much better by exploiting people's tendencies, even if you don't have enough data on them to satisfy a frequentist). As a general approach, reliance on beliefs in the face of uncertainty has its strong points (understatement?), and it is only natural that complete rejection of the approach ("car location probabilities are completely unknown!") will appear ludicrous, even if it has a strong justification in this idealized case.
All in all, I think these are nicely complementary approaches. Also, if it's assumed that everyone except perhaps the particular player under consideration plays optimally under certain fairly natural adversarial conditions (read: "obviously the host/producer will want to maintain total secrecy!"), then even a frequentist would agree with the Bayesian (we get K&W that way). If you ask someone: "What is the probability that you win at tic-tac-toe?", they'll probably respond: "Against a good opponent? Zero." Same with the MHP: "Against a good opponent? 2/3." -- Coffee2theorems (talk) 12:15, 2 October 2012 (UTC)
- My condition is the one single condition which totally defines the MHP as the simple puzzle that it was intended to be. The only other thing required is that the probability that the player has originally chosen the car is 1/3. I do not,as you suggest above, require the car and goats to be uniformly placed. You say in your edit summary that, 'answer is 2/3 if and only if host's choice is random', but that is not true. The answer is not 2/3 if the host does not know where the car is or if the host only uses the word 'pick' if the player has originally chosen the car, or if the host only offers the swap if the player has originally chosen the car. All these things, and many others, are ruled out by my condition. It is the essential core of the problem statement, not part of the solution.
- Maybe my proposed condition is OR but I was rather hoping that you would see the benefits of using it and find a sources that might justify its inclusion. Martin Hogbin (talk) 15:20, 1 October 2012 (UTC)
- When I said "answer is 2/3 iff host's choice is random" I meant it to be understood, that all the other standard ingredients are present: the host must open a different door revealing a goat, and the car is initially equally likely to be anywhere. Since we are talking about MHP it is understood that the host must open a different door revealing a goat. And please distinguish the technical meaning of the word "conditional" in the expression "conditional probability", from the meaning of the word "condition" as in assumptions, initial conditions, and so on. No relation at all! Completely different things. ... But regarding your new discovery: no I am not aware of any sources which had this insight, before you. You may well be right. But still I see it as something to be deduced, not something to be assumed. You are close to saying: the answer is 2/3 if we assume the answer is 2/3. Impeccable logic, but not so interesting. Richard Gill (talk) 18:36, 1 October 2012 (UTC)
- Yes I do understand that some of the points I mentioned are part of the standard setup of the MHP but I still think that it is worthy of note that my condition ensures all that at a stroke. However, some of the points are not normally even mentioned. The possibility that the host gives the player a helping hand by changing his wording, for example, when the player has originally chosen the car. In a real game show that is a more likely scenario than the host's having a door preference.
- When I said "answer is 2/3 iff host's choice is random" I meant it to be understood, that all the other standard ingredients are present: the host must open a different door revealing a goat, and the car is initially equally likely to be anywhere. Since we are talking about MHP it is understood that the host must open a different door revealing a goat. And please distinguish the technical meaning of the word "conditional" in the expression "conditional probability", from the meaning of the word "condition" as in assumptions, initial conditions, and so on. No relation at all! Completely different things. ... But regarding your new discovery: no I am not aware of any sources which had this insight, before you. You may well be right. But still I see it as something to be deduced, not something to be assumed. You are close to saying: the answer is 2/3 if we assume the answer is 2/3. Impeccable logic, but not so interesting. Richard Gill (talk) 18:36, 1 October 2012 (UTC)
- By 'condition' I am referring to the bit in italics in say, P(C=1|Host reveals Nanny). Is that the correct terminology?
- If you want to compute a conditional probability, anything you want to condition on is called a condition, yes. If you think a problem should be solved by computing a probability then you also have to make up your mind whether it should be conditional on anything, and if so what. Part of your "solution" should be to motivate why you want to condition, in the technical probabilistic sense, on anything. I see MHP as a decision problem: should you switch, yes or no? Computing probabilities or conditional probabilities are a means to solving the problem, not the solution itself. So if you solve MHP by calculating some conditional probability you have to explain why this particular conditional probability. If you solve it by calculating some unconditional probabilty you have to explain why that was sufficient for your present purposes.
- Now, if you have to choose between doors 1 and 2 and you want to achieve the highest possible (unconditional / overall) chance of picking the door with the car, then you should condition on everything which you know and which can influence the chance that the car is behind door 1 or 2. Then you'll be guaranteed of the highest possible overall chance of getting the car. In MHP it's not difficult to see (given what we're told about the problem) that there's no way to get a better overall success chance than 2/3. We also know that "always switching" gives you overall success rate 2/3. So 2/3 is attainable. So no need to compute conditional probabilities: you know you are doing the best that can be done anyway.
- Alternatively you might like to argue, by symmetry, a priori, that the chance of winning by switching does not depend on the specific door numbers chosen and open. In that case there is no point in conditioning on them because you know this information doesn't alter the chances anyway.
- But OK, if you don't like either of the preceding two solutions, you can say that you'll compute the conditional probability the car is behind door 2 given everything which the player has seen so far, since if he bases his choice on this conditional probability, he's guaranteed of doing the best overall.
- I would say that imagining situations where information is revealed by seeing whether the goat behind door 3 is a boy goat or a girl goat is silly. When you tackle a problem like MHP you start by deciding what you're going to take account of, what not. Selvin and Vos Savant tell us only a few things and it's understood that we're only supposed to reason with the information we've been told, not to start building fantasy variant-problems where there is more information around or different information. Richard Gill (talk) 14:05, 2 October 2012 (UTC)
- Perhaps then you can explain to me why conditioning on the goat that is revealed is sillier than conditioning on the door that is opened. Martin Hogbin (talk) 22:35, 2 October 2012 (UTC)
- Because we're told about the door that is opened and we can't help but discuss door numbers in some way or another in setting up a mathematical model of the problem. We're not told anything about the goats and we're obviously not supposed to start imagining that there's a boy goat and a girl goat and this should make a difference. However we are told about the door numbers. Under K&W assumptions, they are irrelevant: their irrelevance can be deduced from those assumptions. So if you explicitly write out the complete K&W assumptions but just give a simple solution and don't explain why the specific numbers in a particular case are irrelevant, there's something strange going on: you're making an assumption but not showing where you used it in your argument. It's not a big deal: one word would be enough; but unfortunately there seems a lot of opposition here to use of the word "symmetry". This is sad. It's a fundamental insight into the problem (under K&W assumptions) that permuting the door numbers changes nothing, hence there is no need to evaluate strategies which depend on door numbers: the solution must be the same for all door numberings. I am not a supporter of blanket use of K&W, by the way. I think that the simple solutions are legitimate precisely because they give the consumer useful information while making less assumptions. Hence the simple solutions have wider applicability. Richard Gill (talk) 11:27, 4 October 2012 (UTC)
- Richard, I have replied to your original response in my user space to avoid logging up the discussion here. Martin Hogbin (talk) 11:40, 5 October 2012 (UTC)
- Because we're told about the door that is opened and we can't help but discuss door numbers in some way or another in setting up a mathematical model of the problem. We're not told anything about the goats and we're obviously not supposed to start imagining that there's a boy goat and a girl goat and this should make a difference. However we are told about the door numbers. Under K&W assumptions, they are irrelevant: their irrelevance can be deduced from those assumptions. So if you explicitly write out the complete K&W assumptions but just give a simple solution and don't explain why the specific numbers in a particular case are irrelevant, there's something strange going on: you're making an assumption but not showing where you used it in your argument. It's not a big deal: one word would be enough; but unfortunately there seems a lot of opposition here to use of the word "symmetry". This is sad. It's a fundamental insight into the problem (under K&W assumptions) that permuting the door numbers changes nothing, hence there is no need to evaluate strategies which depend on door numbers: the solution must be the same for all door numberings. I am not a supporter of blanket use of K&W, by the way. I think that the simple solutions are legitimate precisely because they give the consumer useful information while making less assumptions. Hence the simple solutions have wider applicability. Richard Gill (talk) 11:27, 4 October 2012 (UTC)
- You are suggesting that the answer is obvious if we include my condition in the problem statement but here is the thing - which part of the MHP is not obvious? Yet most people get it wrong. Despite K&W we still do not really know why people cannot answer what should be a very straightforward question. Why they still do not believe you when you carefully explain the correct answer. Including my condition in the problem statement would be an interesting way of helping readers to reach the right conclusion. We can then go back and explain the standard requirements for my condition to be true. Martin Hogbin (talk) 21:19, 1 October 2012 (UTC)
- Without a whole slew of references saying something fairly similar to what you're suggesting (enough to convincingly show that this is how the problem is generally interpreted) including your condition in the problem statement is prohibited WP:OR. -- Rick Block (talk) 01:02, 2 October 2012 (UTC)
OK, I proposed a new way of trying to improve the article but no one liked it. I am happy to discuss the subject further in my user space with anyone interested but this is probably enough for the MHP talk page. The original dispute rumbles on unresolved. Martin Hogbin (talk) 08:23, 2 October 2012 (UTC)
Symmetry
- For the record, notwithstanding my earlier wisecrack about a five-dollar word, I do not really object to using it. My only reservation is that, although the shorthand "by symmetry" speaks loud and clear to mathematicians, and although laypersons appreciate the concept, some laypersons might not readily associate the concept with the shorthand. Nevertheless, it is a fundamental and readily accessible insight that greatly simplifies matters. ~ Ningauble (talk) 16:39, 4 October 2012 (UTC)
- Since I have criticized the cryptic name-dropping of "symmetry" before, let me clarify: I'm not trying to ban that word from the English language or this article. It just seems to me that such cryptic name-dropping is sometimes proposed as a replacement for a proper explanation in cases where someone does not want the reader to actually understand something that is in the proposer's personal opinion too "academic".
- It's easy enough to understand how this impression can arise: for example, you just basically said that it is appropriate to reduce the explanation of a fundamental insight into one word! I don't think that's reasonable outside of Zen koans. -- Coffee2theorems (talk) 20:24, 4 October 2012 (UTC)
- I guess we need one of the non-mathematician editors to write a few sentences about the consequences of symmetry in words which other non-mathematicians will understand. I certainly don't use the word because I don't want the reader to understand something which I think is too academic! It's the complete opposite: I use the word because I do want the reader to understand something which is not academic at all; it's easy to understand, it's in fact so obvious that many take it for granted!
- Take MHP with the usual K&W conditions, as for instance when we take a classical Bayesian approach: probabilities refer to our knowledge about the world, are they are equal when we have no information to the contrary (probability from symmetry!). It's now clear that the answer (switch or stay) can't depend on whether Vos Savant says "say, door 1, and say, door 3", or if she says "say door 3, and say, door 2". Or whatever else. There are altogether six questions she could have posed. They must all have the same answer. So we only need to compare "always switching" with "always staying". We know that the difference between these two strategies is the famous 2/3 versus 1/3. Since 2/3 is the probability of winning by switching and because of the just mentioned symmetry this probability can't depend on the case at hand - the probability of winning by switching is is 2/3, in every one of the six "versions" of Vos Savant's question (and if you want to use an expensive word here, you could say "conditional probability". But I'm trying to avoid expensive words which the layman doesn't grasp! That's exactly why I want the notion of symmetry brought to the fore! Richard Gill (talk) 04:39, 5 October 2012 (UTC)
- We agree on a lot of things, then (also on avoiding the term "conditional probability" initially). However, what you have assumed here is not K&W but something different. I'd prefix your argument with: "If the problem is to have a unique answer at all..." Note that this implies K&W and the other way around (assuming figuring out the probability is a part of the answer, as is usually done). This assumption is not as obvious as it appears: see e.g. Bertrand paradox. Seeing where it leads and verifying that the result is consistent does provide one (partially) satisfying resolution to the paradox. Note that the point about consistency is not so obvious either: generally, one finds that "that a probability assignment can be made to respect some symmetry is trivial; that one can be made to respect all symmetries is contradictory". -- Coffee2theorems (talk) 07:35, 5 October 2012 (UTC)
- I think we'ld make progress if everyone tried to write attractive (popular) descriptions of other people's favourite approaches. For instance: let Martin understand the point of symmetry and use it to compose a simple solution which at the same time is complete.
- The choice is not between simple solutions which only talk about the chance of winning by switching, overall, and solutions which go through the motions of computing conditional probabilities by going back to the definition of conditional probability. The reason we are still quarelling here is because no-one sees that there are simple solutions which give conditional probabilities without even using the word "conditional". Instead, use the word "independent" or the word "symmetry". These are not expensive words - they are words connecting immediately to intuition. Richard Gill (talk) 04:39, 5 October 2012 (UTC)
- Well, if no-one(!) sees such solutions, how do we know they exist. If you mean that the editors who claim the solution is essentially in terms of conditional probability, insist on using the term "conditional", you must have been sleeping part of the time, and myabe there all your dreams stem from. Me, nor Rick, want to use the term "conditional" in the first explanation, but for the discussion here we have to use the term to make sure it is understood. Using words like `'independent" or "symmetry" seems to me also to be undesirable. Nijdam (talk) 09:44, 5 October 2012 (UTC)
- I'm convinced. Richard, you know very well all about the MHP. And, as you said above, the door numbers matter insofar, that there are six combinations that may be considered. all equivalent. Hence considering one is enough. And the symmetry (maybe we have to explain this in different wording) guarantees the answer is the same in all combinations. But just saying the overall chance on winning by switching is 2/3, is not enough as an explanation. In every combination the conditional (maybe we have to explain this in different wording) probabilities have the same value and hence have the same value as the overall chance. This would be a correct solution. Nijdam (talk) 11:14, 5 October 2012 (UTC)
- Richard, I do not think that just saying the word symmetry gets us very far. To the general reader this is likely only to confuse. Most people's understanding of the word is restricted visual symmetry and similar.
- I am not clear exactly what you mean by the word. We can take the W/vS statement to indicate symmetry with respect to door number and goat number by noting that no information is given which breaks this symmetry but this is just the Bayesian understanding of the problem, so why not just say that? Martin Hogbin (talk) 12:17, 5 October 2012 (UTC)
Focus on the article
While I'm sure all this debate is fascinating, could I remind everyone that This is the talk page for discussing changes to the Monty Hall problem article itself. Please place discussions on the underlying mathematical issues on the Arguments page.
You guys are all starting to sound like a bunch of turkeycocks in a dust up - and this page is not for trying to persuade each other that your own approach to the problem is the right one. Can we return focus on the article. Does it in fact need any changes? Where does it need changes? What changes would make it better. Or do most of the folks here just prefer to keep this endless argument going? --Elen of the Roads (talk) 12:31, 5 October 2012 (UTC)
- Wikipedia former featured articles
- Featured articles that have appeared on the main page
- Featured articles that have appeared on the main page once
- Old requests for peer review
- B-Class Statistics articles
- Mid-importance Statistics articles
- WikiProject Statistics articles
- B-Class mathematics articles
- Mid-priority mathematics articles
- Featured articles on Mathematics Portal
- B-Class game theory articles
- Mid-importance game theory articles
- Wikipedia requests for comment