Electron

For other uses, see Electron (disambiguation).

Electron

File:Schattenkreuzröhre-in use-lateral view-standing cross.jpg Experiments with Crookes tube first demonstrated the particle nature of electrons. In this illustration, the profile of the cross-shaped target is projected against the tube face at right by a beam of electrons.
Composition	Elementary particle
Family	LeptonFermion
Generation	First
Interactions	Gravity, Electromagnetic, Weak
Symbol	e− , β−
Antiparticle	Positron (also called antielectron)
Theorized	Richard Laming (1838–51), G. Johnstone Stoney (1874) and others.
Discovered	J.J. Thomson (1897)
Mass	9.10938215(45)×10−31 kg 5.485 799 0943(23) × 10−4 u 1⁄1822.88850204(77) u 0.510998910(13) MeV/c2
Electric charge	−1 e −1.602176487(40)×10−19 C
Magnetic moment	−1.001 159 652 181 11(74) μB
Spin	1⁄2

The electron is an elementary subatomic particle that carries a negative electrical charge. The concept of a quantum of electrical charge had been theorized on several occasions beginning in 1838, including by Irish physicist George Johnstone Stoney in 1874, who introduced the name electron in 1894. The electron was first identified in 1897 by J.J. Thomson and his team of British physicists. These charged particles, together with the protons and neutrons that comprise atomic nuclei, make up atoms. Electron–electron interaction between atoms is the main cause of chemical bonding. Electrons play an essential role in many physical phenomena such as electricity, magnetism, and thermal conductivity.

Electrons are believed to be point particles with no apparent substructure. They are identical particles that belong to the first generation of the lepton particle family. Each electron carries a negative elementary charge and participates in electromagnetic and weak interactions. The components of its spin, or intrinsic angular momentum, can have values of ±ħ⁄2, where ħ is the reduced Planck constant. For this reason electrons are classified as spin-1⁄2 particles. The mass of an electron is approximately 1⁄1836 of that of the proton.

The properties of the electron are determined by its interaction with other particles. The attractive Coulomb force between an electron and proton is what causes electrons to be bound into atoms. When an electron is in motion, it both generates a magnetic field and is deflected by external magnetic fields. Electrons have quantum mechanical properties of both a particle and a wave, so they can collide with other particles and be diffracted like light. While an electron is undergoing acceleration, it can absorb or radiate energy in the form of photons. It can be annihilated by a collision with a positron, the electron's antiparticle, or an electron–positron pair can be produced from gamma ray photons with a combined energy at least equal to the energy at rest of the particles.

Etymology

The ancient Greeks noticed that amber, a gemstone that is formed from the hardened sap of trees, attracted small objects when rubbed with fur; apart from lightning this phenomenon was man's earliest experience of electricity. In his 1600 treatise De Magnete, the English physician William Gilbert coined the New Latin term electricus, to refer to this property of attracting small objects after being rubbed. Both electric and electricity are derived from the Latin ēlectrum, which in turn came from the Greek word ēlektron (ήλεκτρον) for amber. The English name electron is a combination of the word electric and the suffix -on, with the latter now used to designate a subatomic particle such as a proton or neutron.

History

Main article: History of electromagnetism

As early as 1838–51, the British natural philosopher Richard Laming conceived the idea that an atom is composed of a core of matter surrounded by subatomic particles that had unit electrical charges. Beginning in 1846, German physicist William Weber theorized that electricity was composed of positively and negatively charged fluids, and their interaction was governed by the inverse square law. After studying the phenomenon of electrolysis in 1874, the Irish physicist George Johnstone Stoney suggested that there existed a "single definite quantity of electricity", the charge of a monovalent ion. He was able to estimate the value of this elementary charge e of by means of Faraday's laws of electrolysis. However, Stoney believed these charges were permanently attached to atoms and could not be removed. In 1881, German physicist Hermann von Helmholtz argued that both positive and negative charges were divided into elementary parts, each of which "behaves like atoms of electricity".

In 1894, Stoney coined the term electron to represent these elementary charges.

In this paper an estimate was made of the actual amount of this most remarkable fundamental unit of electricity, for which I have since ventured to suggest the name electron.

— Stoney, George Johnstone (1894). "Of the "Electron," or Atom of Electricity". Philosophical Magazine. 38 (5): 418–420. {{cite journal}}: Unknown parameter |month= ignored (help)

However, it was only at the end of the nineteenth century that these various concepts came together to form a unified theory based upon an electron as a fundamental component of matter.

Discovery

In the Crookes tube, electrons released from the cathode plate are accelerated down the tube to the left, towards the anode, by an electric potential.

During the 1870s, English chemist and physicist Sir William Crookes developed the first cathode ray tube to have a high vacuum inside. He then showed that the luminescence rays appearing within the tube carried energy and moved from the cathode to the anode. Furthermore, by applying a magnetic field, he was able to deflect the rays, thereby demonstrating that the beam behaved as though it were negatively charged. In 1879, he proposed that these properties could be explained by what he termed 'radiant matter'. He suggested that this was a fourth state of matter, consisting of negatively charged molecules that were being projected with high velocity from the cathode.

The German-born British physicist Arthur Schuster expanded upon Crookes' experiments by placing metal plates in parallel to the cathode rays and applying an electrical potential between the plates. The field deflected the rays toward the positive plate, providing further evidence that the rays carried negative charge. By measuring the amount of deflection for a given level of current, in 1890 Schuster was able to estimate the charge-to-mass ratio of the ray components. However, this produced such an unexpectedly large value that little credence was given to his calculations at the time.

In 1896, British physicist J.J. Thomson, with his colleagues John S. Townsend and H. A. Wilson, performed experiments indicating that cathode rays really were unique particles, rather than waves, atoms or molecules as was believed earlier. Thomson made good estimates of both the charge e and the mass m, finding that cathode ray particles, which he called "corpuscles," had perhaps one thousandth of the mass of the least massive ion known: hydrogen. He showed that their charge to mass ratio, e/m, was independent of cathode material. He further showed that the negatively charged particles produced by radioactive materials, by heated materials and by illuminated materials were universal. The name electron was again proposed for these particles by the Irish physicist George F. Fitzgerald, and it has since gained universal acceptance.

While studying naturally fluorescing minerals in 1896, French physicist Henri Becquerel discovered that they emitted radiation without any exposure to an external energy source. These radioactive materials became the subject of much interest by scientists, including New Zealand physicist Ernest Rutherford who discovered they emitted particles. He designated these particles alpha and beta, based on their ability to penetrate matter. In 1900, Becquerel showed that the beta rays emitted by radium could be deflected by an electrical field, and that their mass-to-charge ratio was the same as for cathode rays. This evidence strengthened the view that electrons existed as components of atoms.

The electron's charge was more carefully measured by American physicist Robert Millikan in his oil-drop experiment of 1909. This experiment used an electrical field to prevent a charged droplet of oil from falling as a result of gravity. This device could measure the electrical charge from as few as 1–150 ions with an error margin of less than 0.3%. Comparable experiments had been done earlier by Thomson's team, using a clouds of charged water droplets generated by electrolysis. However, oil drops, were more stable than water drops due to their slower evaporation rate, and thus more suited to precise experimentation over longer periods of time.

Around the beginning of the twentieth century, it was found that under certain conditions a charged particle caused a condensation of water vapor. In 1911, Charles Wilson used this principle to devise his cloud chamber, allowing the tracks of charged particles, such as fast-moving electrons, to be photographed. This and subsequent particle detectors allowed electrons to be studied individually, rather than in bulk as had been the case before.

Atomic theory

The Bohr model of the atom, showing quantized states of electron orbital energy. An electron dropping to a lower orbit emits a photon equal to the energy difference between the orbits.

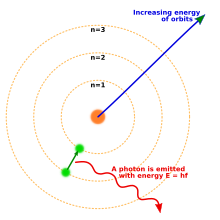
By 1914, experiments by physicists Ernest Rutherford, Henry Moseley, James Franck and Gustav Hertz had largely established the structure of an atom as a dense nucleus of positive charge surrounded by lower mass electrons. In 1913, Danish physicist Niels Bohr postulated that electrons resided in quantized energy states, with the energy determined by the angular momentum of the electron's orbits about the nucleus. The electrons could move between these states, or orbits, by the emission or absorption of photons at specific frequencies. By means of these quantized orbits, he accurately explained the spectral lines of hydrogen that were formed when the gas is energized by heat or electricity. However, Bohr's model failed to account for the relative intensities of the spectral lines and it was unsuccessful in explaining the spectrum of more complex atoms.

Chemical bonds between atoms were explained in 1916 by Gilbert Newton Lewis, as the interactions between their constituent electrons. As the chemical properties of the elements were known to largely repeat themselves according to the periodic law, in 1919 the American chemist Irving Langmuir suggested that this could be explained if the electrons in an atom were connected or clustered. Groups of electrons were thought to occupy a set of electron shells about the nucleus, providing the necessary clustering.

In 1924, Austrian physicist Wolfgang Pauli observed that the shell-like structure of the atom could be explained by a set of four parameters that defined every quantum energy state, as long as each state was inhabited by no more than a single electron. (This prohibition against more than one electron occupying the same quantum energy state became known as the Pauli exclusion principle.) However, what physicists lacked was a physical mechanism to explain the fourth parameter, which had two possible values. This was provided by the Dutch physicists Abraham Goudsmith and George Uhlenbeck when they suggested that an electron, in addition to the angular momentum of its orbit, could possess an intrinsic angular momentum. This property became known as spin, and it explained the previously mysterious splitting of spectral lines observed with a high resolution spectrograph; a phenomenon known as fine structure splitting.

Quantum mechanics

See also: History of quantum mechanics

During his 1924 dissertation Recherches sur la théorie des quanta, French physicist Louis de Broglie hypothesized that all matter possesses a wave–particle duality similar to photons: the de Broglie hypothesis. That is, under the appropriate conditions, electrons and other matter would show properties of either particles or waves. The wave-like nature of light occurs, for example, when light is passed through parallel slits and creates interference patterns. In 1927, a similar effect was demonstrated with a beam of electrons; by English physicist George Paget Thomson with a thin metal film and by American physicists Clinton Davisson and Lester Germer using a crystal of nickel.

In quantum mechanics, the behavior of an electron in an atom is described by an orbital, which is a probability distribution rather than an orbit. In the figure, the shading at a point indicates the relative probability of the particle in the lowest-energy orbital being at that point.

The success of de Broglie's prediction led to the publication, by Erwin Schrödinger in 1926, of the equation named after him that successfully describes how electron waves propagated. Rather than yielding a solution that determines the location of an electron over time, this wave equation gives the probability of finding an electron near a position. This approach became the theory of quantum mechanics, which provided an almost exact derivation to the energy states of an electron in a hydrogen atom.

In 1928, building on Wolfgang Pauli's work, Paul Dirac formulated the Dirac equation. This provided the wavefunction of an electron moving at velocities close to the speed of light. Once spin and the interaction between multiple electrons was also considered, this work allowed the configuration of electrons in atoms with higher atomic numbers than hydrogen to be successfully predicted. However, for atoms with multiple electrons, the exact solution to the wave equation is much more complicated, so approximations were often necessary.

Based upon his work, in 1930 Paul Dirac developed a model of the vacuum as an infinite sea of particles possessing negative energy. Known as the Dirac sea, this led him to predict the existence of a positron, the antimatter counterpart of the electron. This particle was discovered in 1932 by Carl D. Anderson. He proposed calling standard electrons negatrons, and using electron as a generic term to describe both the positively and negatively charged variants. This usage of the term 'negatron' is still occasionally encountered today, and it may be shortened to 'negaton'.

The first experimental discrepancy in this theory was discovered in 1947 by Willis Lamb, working in collaboration with graduate student Robert Retherford. They found that certain energy levels of hydrogen that should have the same value, were shifted relative to each other—the Lamb shift. About the same time, Polykarp Kusch, working with Henry M. Foley, discovered the anomalous magnetic dipole moment of the electron, which produced a larger than expected value for the magnetic moment. To resolve these issues, a refined version of the quantum electrodynamics theory was developed by Sin-Itiro Tomonaga, Julian Schwinger and Richard P. Feynman.

Particle accelerators

With the development of the particle accelerator during the first half of the twentieth century, physicists began to delve deeper into the properties of subatomic particles. The first successful attempt to accelerate electrons using magnetic induction was made in 1942 by Donald Kerst. His initial betatron reached energies of 2.3 MeV (million electron volts), while subsequent betatrons achieved 300 MeV. In 1947, synchrotron radiation was discovered with a 70 MeV electron synchrotron at GE. This radiation was caused by the acceleration of electrons, moving near the speed of light, through a magnetic field.

With a beam energy of 1.5 GeV, the first high-energy particle collider was ADONE, which began operations in 1968. This device accelerated electrons and positrons—the antiparticle of the electron—in opposite directions, effectively doubling the energy of their collision when compared to striking a static target with an electron. The Large Electron-Positron Collider (LEP) at CERN, which was operational from 1989 to 2000, achieved collision energies of 209 GeV and made important measurements for the Standard Model of particle physics.

Characteristics

Classification

Standard model of elementary particles. The electron is at lower left.

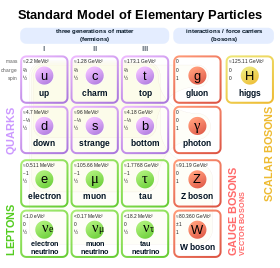
The electron belongs to the group of subatomic particles called leptons, which are believed to be fundamental particles. Electrons have the lowest mass of any electrically charged lepton. In the Standard Model of particle physics, the electron is the first-generation charged lepton.

If the spin of the electron is oriented in the same direction as its momentum, it is called a right-handed spin; otherwise it is left-handed. Thus the same electron can have left or right-handed spin, depending on its velocity with respect to an observer. The left-handed spin component of the electron forms a weak isospin doublet with the electron neutrino, which is an uncharged, first generation lepton with little or no mass. The right-handed component of the electron spin is an isospin singlet.

The electron is very similar to the two charged leptons of higher generations, the muon and the tau lepton, which are identical in charge, spin, and interaction, but are more massive. All members of the lepton group belong to the family of fermions. This family includes all elementary particles with half-odd integer spin; the electron has spin 1⁄2. Leptons differ from the other basic constituent of matter, the quarks, by their lack of strong interaction.

Fundamental properties

The mass of a stationary electron is approximately 9.109 × 10⁻³¹ kilograms, or 5.489 × 10⁻⁴ atomic mass units. Based on Einstein's principle of mass–energy equivalence, this mass corresponds to an energy of 0.511 MeV. The ratio between the mass of a proton and that of an electron is about 1836. This ratio is one of the fundamental constants of physics, and the Standard Model of particle physics assumes this and other constants are unchanging. Astronomical measurements show that the ratio has held the same value for at least half the age of the universe.

Electrons have an electric charge of −1.602 × 10⁻¹⁹ C, which is used as a standard unit of elementary charge for subatomic particles. Within the limits of experimental accuracy, the electron charge is identical to the charge of a proton, but with the opposite sign. As the symbol e is used for the constant of electrical charge, the electron is commonly symbolized by
e⁻
, where the minus sign indicates the negative charge. The positron is symbolized by
e⁺
because it has the same properties as the electron but with a positive rather than negative charge.

The electron is described as a fundamental or elementary particle. It has no known substructure. Hence, it is defined or assumed to be a point charge with no spatial extent; a point particle. Observation of a single electron in a Penning trap shows the upper limit of the particle's radius is 10⁻²² meters. The classical electron radius is 2.8179 × 10⁻¹⁵ m. This is the radius that is inferred from the electron's electric charge, by using the classical theory of electrodynamics alone and ignoring quantum mechanics.

There are elementary particles that spontaneously decay into different particles. An example is the muon, which decays into an electron and two neutrinos with a half life of 2.2 × 10⁻⁶ seconds. However, the electron is thought to be stable on theoretical grounds; an electron decaying into a neutrino and photon would mean that electric charge is not conserved. The experimental lower bound for the electron's mean lifetime is 4.6 × 10²⁶ years, with a 90% confidence interval.

Quantum mechanics

As with all particles, electrons can act as waves. This is called the wave–particle duality and can be demonstrated using the double-slit experiment. The wave-like nature of the electron allows it to pass through two parallel slits simultaneously, rather than just one slit as would be the case for a classical particle. In quantum mechanics, the wave-like property of an electron is described mathematically by a complex-valued function of the position, the wavefunction, often denoted by the Greek letter psi (ψ). When the absolute value of this function is squared, it gives the probability that an electron will be observed near a location—the electron density.

Example of an asymmetric wavefunction for a quantum state of two identical fermions in a box. If the particles swap position, the wavefunction inverts.

Electrons are identical particles because they can not be distinguished from each other by their intrinsic physical properties. In quantum mechanics, this means that a pair of interacting electrons must be able to swap positions without an observable change to their condition. The wave function of fermions, including electrons, is antisymmetric, meaning that it changes sign when two electrons are swapped; that is, ψ(r₁, r₂) = −ψ(r₂, r₁), where the variables r₁ and r₂ correspond to the first and second electrons, respectively. Since the absolute square is not changed by a sign swap, this corresponds to equal probabilities. Bosons, such as the photon, have symmetric wave functions instead.

In the case of antisymmetry, solutions of the wave equation for interacting electrons result in a zero probability that each pair will occupy the exact same location or state. This is responsible for the Pauli exclusion principle, which precludes any two electrons from occupying the same energy state. This principle explains many of the properties of electrons. For example, this causes groups of bound electrons to occupy different orbitals in an atom, rather than all overlapping each other in the same orbit.

Virtual particles

Physicists believe that empty space may be continually creating pairs of virtual particles, such as a positron and electron, which rapidly annihilate each other shortly thereafter. The net energy from this reaction is zero. The combination of the energy variation needed to create these particles, and the time during which they exist, fall under the threshold of detectability expressed by the Heisenberg uncertainty relation, ${\begin{smallmatrix}\Delta E\ \Delta t\ \geq \ \hbar \end{smallmatrix}}$. In effect, the energy needed to create these virtual particles, ΔE, can be "borrowed" from the vacuum for a period of time, Δt, such that their product is no more than the reduced Planck constant, ħ ≈ 6.6 × 10⁻¹⁶ eV·s. Thus, for a virtual electron, Δt is at most 1.3 × 10⁻²¹ s.

Virtual electron-positron pairs appearing at random near an electron (at lower left).

While an electron-positron virtual pair is in existence, the coulomb force from the ambient electrical field surrounding an electron causes a created positron to be attracted to the original electron, while a created electron experiences a repulsion. This causes the two charged virtual particles to physically separate for a brief period before merging back together, and during this period they behave like an electric dipole. The combined effect of many such pair creations is to partially shield the charge of the electron, a process called vacuum polarization. Thus the effective charge of an electron is actually smaller than its true value, and the charge increases with decreasing distance from the electron. This polarization was confirmed experimentally in 1997 using the Japanese TRISTAN particle accelerator.

A comparable shielding effect is seen for the mass of the electron. The equivalent rest energy consists of the mass-energy of the "bare" particle plus the energy of the surrounding electric field. In classical physics, the energy of the electric field is dependent upon the size of the charged object, which, for a dimensionless particle, results in an infinite energy. Instead, because of vacuum fluctuations, allowance must be made for an electron–positron pair appearing in the electric field and the positron annihilating the original electron; causing the virtual electron to become a real electron via the emitted photon. This interaction creates a negative energy imbalance that counteracts the radius-dependency of the electric field. The total mass is referred to as the renormalized mass, because a mathematical technique called renormalization is used by physicists to relate the observed and bare mass of the electron. This method replaces the terms used to compute the mass with the actual mass found experimentally, thereby avoiding problems with divergences in the formulas.

The electron has an intrinsic angular momentum of spin 1⁄2 as measured in units of ħ, and an intrinsic magnetic moment along its spin axis. The magnitude of the spin is √3⁄2ħ. A measurement of its component along any axis can only be ±ħ⁄2; this property is usually stated by referring to the electron as a spin-1⁄2 particle.

In classical physics, the angular momentum and magnetic moment of an object depends upon its physical dimensions. Hence, the concept of a dimensionless electron possessing these properties is unclear. A possible explanation lies in the formation of virtual photons in the electric field generated by the electron. These photons cause the electron to shift about in a jittery fashion (known as zitterbewegung), which results in a net circular motion with precession. This motion produces both the spin and the magnetic moment of the electron. In atoms, this creation of virtual photons explains the Lamb shift observed in spectral lines.

The magnetic moment associated with the orbital motion of an electron in an atom is expressed in terms of the Bohr magneton, which is a physical constant equal to 9.274 009 15(23) × 10^-24 J·T^-1. The intrinsic angular momentum of an electron is almost equal to one Bohr magneton, with the 0.1% difference being explained by interaction with virtual particles and antiparticles. The extraordinarily precise agreement of this predicted difference with the experimentally determined value is viewed as one of the great achievements of modern physics.

Interaction

An electron generates an electric field that exerts an attractive force on a particle with a positive charge, such as the proton, and a repulsive force on a particle with a negative charge. The strength of this force is determined by Coulomb's law. The Coulomb force between charged particles is mediated by photons, which are quanta of the electromagnetic field.

Here, Bremsstrahlung is produced by an electron e deflected by the electric field of an atomic nucleus. The energy change E₂ − E₁ determines the frequency f of the photon emission.

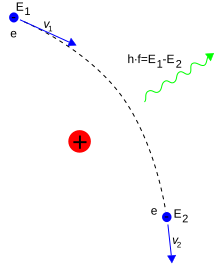
An isolated electron that is not undergoing acceleration is unable to emit or absorb energy via a photon; doing so would violate conservation of energy and momentum. Instead, virtual photons can transfer momentum (but no net energy) between two charged particles. It is this exchange of virtual photons that generates the Coulomb force. Energy emission can occur when a moving electron is deflected by a charged particle, such as a proton. The deceleration of the electron results in the emission of Bremsstrahlung radiation.

The outcome of an elastic collision between a photon and a solitary electron is called Compton scattering. This collision results in a transfer of momentum between the particles, which modifies the wavelength of the photon by an amount called the Compton shift. The maximum magnitude of this wavelength shift is h/mc, which is known as the Compton wavelength. For an electron, it has a value of 2.43 × 10⁻¹² m.

The relative strength of the electromagnetic interaction between two charged particles, such as an electron and a proton, is given by the fine structure constant. This value is a dimensionless quantity formed by the ratio of two energies: the electrostatic energy of attraction (or repulsion) at a separation of one Compton wavelength, and the rest energy of the charge. It is given by α = (7.29720±0.00003) × 10⁻³, which is approximately equal to 1⁄137. This constant appears frequently in the physics of atoms and in the theory of quantum electrodynamics.

When an electron is in motion, it generates a magnetic field. This magnetic field is related to the motion of one or more electrons (the "current") with respect to an observer by the Ampère-Maxwell law. It is this property of induction which supplies the magnetic field that drives an electric motor. The electromagnetic field of an arbitrary moving charged particle is expressed by the Liénard-Wiechert Potentials, which are valid even when the particle's speed is close to that of light (or relativistic velocities).

A charged particle q (at left) is moving with velocity v through a magnetic field B that is oriented perpendicular to the display. For an electron, q is negative so it follows a curved trajectory toward the top.

When an electron is moving through a magnetic field, it is subject to the Lorentz force that exerts an influence in a direction perpendicular to the plane defined by the magnetic field and the electron velocity. This causes the electron to follow a helical trajectory through the field at a radius equal to the Gyroradius. The curving motion creates a centripetal force on the particle, and this acceleration causes the electron to radiate energy called synchrotron radiation. The energy emission in turn causes a recoil of the electron, known as the Abraham-Lorentz-Dirac force, which creates a friction that slows the electron. This force is caused by a back-reaction of the electron's own field upon itself.

In the theory of electroweak interaction, the left-handed spin component of the electron forms a weak isospin doublet with the electron neutrino. This means that during weak interactions, electron neutrinos behave like electrons. Either member of this doublet can undergo a charged current interaction by emitting or absorbing a W boson and be converted into the other member. Charge is conserved during this reaction because the W boson also carries a charge, cancelling out any net change during the transmutation. Charged current interactions are responsible for the phenomenon of beta decay in a radioactive atom. Both the electron and electron neutrino can undergo a neutral current interaction via a Z⁰ boson exchange, and this is responsible for neutrino-electron elastic scattering.

When electrons and positrons collide, they annihilate each other, giving rise to two gamma ray photons emitted at roughly 180° to each other. If the electron and positron had negligible momentum, each gamma ray will have an energy of 0.511 MeV. On the other hand, high-energy photons may transform into an electron and a positron by a process called pair production, but only in the presence of a nearby charged particle, such as a nucleus.

Atoms

Main article: Atom

Probability densities for the first few hydrogen atom orbitals, seen in cross-section. The energy level of a bound electron determines the orbital it occupies, and the color shows the probability that the electron will be seen near a position.

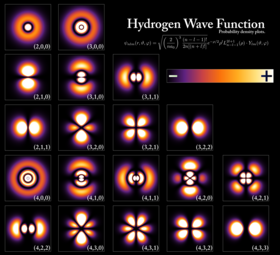
An electron can be bound to the nucleus of an atom by the attractive coulomb force. The wave-like behavior of a bound electron is described by a function called an atomic orbital. An orbital consists of a set of quantum states that have a particular energy, and only a discrete set of these orbitals exist around the nucleus. Electrons can transfer between different orbitals by the emission or absorption of photons with an energy that matches the difference in potential. Other methods of orbital transfer include collisions with particles, such as electrons, and the Auger effect. In order to escape the atom, the energy of the electron must be increased above the atom's binding energy. This occurs, for example, with the photoelectric effect, where an incident photon exceeding the atom's ionization energy is absorbed by the electron.

A bound electron gains a quantized angular momentum from its orbital state; this is analogous to the angular momentum of an orbit in classical mechanics. Because the electron is charged, this produces a magnetic moment that is proportional to the angular momentum. The net magnetic moment of an atom is equal to the vector sum of all its component orbital and spin magnetic moments. Pairs of electrons in an atom align their spins in opposite directions, giving them different spin quantum numbers that satisfy the Pauli exclusion principle. Thus the magnetic moments of an atom's paired electrons cancel each other out. The nucleus contributes a magnetic moment, but this is negligible compared to the effect from the electrons.

The chemical bond between atoms occurs as a result of electromagnetic interactions, as described by the laws of quantum electrodynamics. The strongest bonds are formed by the sharing or transfer of electrons between atoms, allowing the formation of molecules. Within a molecule, electrons move under the influence of the collective nuclei, and occupy molecular orbitals; much as they can occupy atomic orbitals in isolated atoms. A fundamental factor in these molecular structures is the existence of electron pairs. These are electrons with opposed spins, allowing them to occupy the same orbital without violating the Pauli exclusion principle. With high probability, a molecular system will contain pairs of electrons in localized regions of space.

Conductivity

Lightning is an example of the phenomena produced by triboelectricity.

A body has an electric charge when that object has more or fewer electrons than are required to balance the positive charge of the nuclei. (For a single atom or molecule, the object is termed an ion.) When there is an excess of electrons, the object is said to be negatively charged. When there are fewer electrons than protons, the object is said to be positively charged. When the number of electrons and the number of protons are equal, their charges cancel each other and the object is said to be electrically neutral. A macroscopic body can develop an electric charge through rubbing, by the phenomenon of triboelectricity.

Independent electrons moving in vacuum or certain media are termed free electrons. When free electrons move, they produce a net flow of charge called an electric current. A current of electrons acquires the cumulative electromagnetic properties of the individual particles, so it generates a magnetic field. Likewise a current can be created by a moving magnetic field. These interactions are described mathematically by Maxwell's equations.

At a given temperature, each material has an electrical conductivity that determines the value of electric current when an electric potential is applied. Examples of good conductors include metals such as copper and gold, whereas glass and Teflon are poor conductors. A material with metallic bonds has an electronic band structure that allows for delocalized electrons. These electrons are not associated with specific atoms, so when an electric field is applied, they are free to move like a gas through the material. However, unlike an atmospheric gas (which follows the Maxwell–Boltzmann distribution of energies), the states of this cloud of electrons obeys Fermi–Dirac statistics; hence the reason for the electron's family name, fermions.

Metals make relatively good conductors of heat, primarily because the delocalized electrons are free to transport thermal energy between atoms. However, unlike electrical conductivity, the thermal conductivity of a metal is nearly independent of temperature. This is expressed mathematically by the Wiedemann-Franz law, which states that the ratio of thermal conductivity to the electrical conductivity is proportional to the temperature. The thermal disorder in the metallic lattice increases the electrical resistivity of the material, producing a temperature dependence for electrical current.

Because of collisions between electrons and atoms, the drift velocity of electrons in a conductor is on the order of millimetres per second. However, the speed at which a current at one point in the material causes a current in other parts of the material, the velocity of propagation, is typically about 75% of light speed. This occurs because electrical signals propagate as a wave, with the velocity dependent on the dielectric constant of the material. In dielectric materials, the electrons remain bound to their respective atoms and the material behaves as an insulator. Semiconductors have a variable level of conductivity that lies between the extremes of conduction and insulation.

When cooled below a point called the critical temperature, materials can undergo a phase transition in which they lose all resistivity to electrical current; a process known as superconductivity. In BCS theory, this behavior is modeled by pairs of electrons entering a quantum state known as a Bose–Einstein condensate. These Cooper pairs have their motion coupled to nearby matter via lattice vibrations called phonons, thereby avoiding the collisions with atoms that normally creates electrical resistance. (Cooper pairs are separated by roughly 100 nm, so they can overlap each other.) However, the mechanism by which higher temperature superconductors operate remains uncertain.

Motion and energy

According to Einstein's theory of special relativity, as an electron's speed approaches the speed of light, from an observer's point of view its mass appears to increase thereby making it more and more difficult to accelerate it from within the observer's frame of reference. The speed of an electron can approach, but never reach the speed of light in a vacuum, c. However, when relativistic electrons are injected into a dielectric medium such as water, where the local speed of light is significantly less than c, the electrons temporarily travel faster than light in the medium. As they interact with the medium, they generate a faint light called Cherenkov radiation.

Lorentz factor as a function of velocity. It starts at value 1 and goes to infinity as v approaches c.

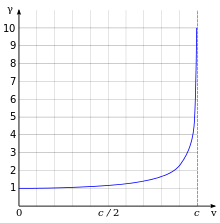
The effects of special relativity are based on a quantity known as the Lorentz factor γ, which is a function of the velocity v of the particle compared to c. The kinetic energy K_e of an electron moving with velocity v is:

${\begin{smallmatrix}K_{e}\ =\ \left(\gamma \ -\ 1\right)m_{e}c^{2}.\end{smallmatrix}}$

where m_e is the electron mass. For example, the Stanford linear accelerator can accelerate an electron to roughly 51 GeV. This gives a value of 100,000 for γ, since the mass of an electron is 0.51 MeV/c². The relativistic momentum of this electron is 100,000 times the classical momentum of an electron at the same speed.

Since an electron behaves as a wave, at a given velocity it has a characteristic de Broglie wavelength. This is given by λ_e = h/p where h is Planck's constant and p is the momentum. For the 51 GeV electron above, the wavelength is small enough to explore structures well below the size of an atomic nucleus.

Formation

Pair production caused by the collision of a photon with an atomic nucleus.

The big bang theory is the accepted scientific theory to explain the early stages in the evolution of the Universe. For the first millisecond of the big bang, the temperatures were over 10 billion kelvins and photons had mean energies over a million electron volts. These photons were sufficiently energetic that they could react with each other to form pairs of electrons and positrons,

${\begin{smallmatrix}\gamma \ +\ \gamma \ \leftrightharpoons \ e^{+}\ +\ e^{-}\end{smallmatrix}}$

where γ is a photon, e⁺ is a positron and e^- is an electron. Likewise, positron-electron pairs annihilated each other emitting energetic photons. An equilibrium between electrons, positrons and protons was maintained during this creation and destruction cycle. After 15 seconds had passed, however, the temperature of the universe dropped below the threshold where electron-positron formation could occur. Most of the surviving electrons and positrons annihilated each other, releasing gamma radiation that briefly reheated the universe.

For reasons that remain uncertain, during the process of leptogenesis there was an excess in the number of electrons over positrons. Hence, about one electron in every billion survived the annihilation process. This excess matched the excess of protons over anti-protons, a condition known as baryon asymmetry, resulting in a net charge of zero for the universe. The surviving protons and neutrons begin to undergo nucleosynthesis, forming isotopes of hydrogen and helium, with trace amounts of lithium. This process peaked after about five minutes. Any leftover neutrons underwent negative beta decay with a half-life of about a thousand seconds, releasing a proton and electron in the process,

${\begin{smallmatrix}n\ \Rightarrow \ p\ +\ e^{-}\ +\ {\bar {\nu }}_{e}\end{smallmatrix}}$

where n is a neutron, p is a proton, e^- is an electron and ${\begin{smallmatrix}{\bar {\nu }}_{e}\end{smallmatrix}}$ is an electron antineutrino. For about the next 300,000–400,000 years, the excess electrons remained too energetic to bind with atomic nuclei. What followed is a period known as recombination, when atoms were formed and the expanding universe became transparent to radiation.

Roughly one million years after the big bang, the first generation of stars began to form. Within a star, stellar nucleosynthesis results in the production of positrons from the fusion of atomic nuclei. These antimatter particles immediately annihilate with electrons, releasing gamma rays. The net result is a steady reduction in the number of electrons, and a matching increase in the number of neutrons. However, the process of stellar evolution can result in the synthesis of radioactive isotopes. Selected isotopes can subsequently undergo negative beta decay, emitting an electron and antineutrino from the nucleus. An example is the cobalt-60 (⁶⁰Co) isotope, which decays to form nickel-60 (⁶⁰Ni).

At the end of their lifetime, stars with more than about 20 solar masses can undergo gravitational collapse to form a black hole. According to classical physics, these massive stellar objects exert a gravitational attraction that is strong enough to prevent anything, including radiation, from escaping past the Schwarzschild radius. However, it is believed that quantum mechanical effects may allow Hawking radiation to be emitted at this distance. Electrons (and positrons) are thought to be created at the event horizon of these stellar remnants.

When pairs of virtual particles (such as an electron and positron) are created just inside the event horizon, the random spacial distribution of these particles may permit one of them to appear on the exterior; a process called quantum tunneling. The gravitational potential of the black hole can then supply the energy that transforms this virtual particle into a real particle, allowing it to radiate away into space. In exchange, the other member of the pair is given negative energy, which results in a net loss of mass-energy by the black hole. The rate of Hawking radiation increases with decreasing mass, eventually causing the black hole to evaporate away until, finally, it explodes.

An extended air shower generated by an energetic cosmic ray striking the Earth's atmosphere.

Cosmic rays are particles travelling through space with high energies. Energy events as high as 3.0 × 10²⁰ eV have been recorded. When these particles collide with nucleons in the Earth's atmosphere, a shower of particles is generated, including pions. More than half of the cosmic radiation observed from the Earth's surface consists of muons. This particle is a lepton which is produced in the upper atmosphere by the decay of pions. Muons in turn can decay to form an electron or positron by means of the weak force. Thus, for the negatively charged pion $\pi ^{-}$,

${\begin{smallmatrix}\pi ^{-}\ \Rightarrow \ \mu ^{-}\ +\ \nu _{\mu }\end{smallmatrix}}$

${\begin{smallmatrix}\mu ^{-}\ \Rightarrow \ e^{-}\ +\ {\bar {\nu }}_{e}\ +\ \nu _{\mu }\end{smallmatrix}}$

where $\mu ^{-}$ is a muon, $\nu _{\mu }$ is a muon neutrino and ${\begin{smallmatrix}{\bar {\nu }}_{e}\end{smallmatrix}}$ is an electron antineutrino.

Observation

Aurorae are typically the result of electron plasmas ejected by the Sun.

Remote observation of electrons requires the detection of their radiated energy. For example, in high energy environments such as the corona of a star, free electrons form a plasma that radiates energy due to Bremsstrahlung. Electron gas can undergo plasma oscillation, which are waves caused by synchronized variations in electron density, and these produce energy emissions that can be detected using radio telescopes.

In laboratory conditions, the interactions of individual electrons can be observed by means of particle detectors, which allow measurement of specific properties such as energy, spin and charge. The development of the Paul trap and Penning trap allows charged particles to be contained within a small region for long durations. This allows for very precise measurements to be made of the particle properties. For example, in one instance the Penning trap was used to contain a single electron for a period of 10 months. Measurements allowed the magnetic moment of the electron to be measured to a precision of eleven digits, which, in 1980, was a greater accuracy than for any other physical constant.

The first video images of an electron were captured by a team at Lund University in Sweden, February 2008. To capture this phenomena, the scientists used extremely short flashes of light. To produce this light, newly developed technology for generating short pulses from intense laser light, called attosecond pulses, allowed the team at the university’s Faculty of Engineering to capture the electron's motion for the first time.

The distribution of the electrons in solid materials can be visualized by angle resolved photoemission spectroscopy (ARPES). This technique uses the photoelectric effect to measure the reciprocal space, a mathematical representation of periodic structures that can be used to infer the original structure. ARPES can be used to determine the direction, speed and scattering of electrons within the material.

Applications

File:GPN-2000-003012.png

During a NASA wind tunnel test, a model of the Space Shuttle is targeted by a beam of electrons, simulating the effect of ionizing gases during re-entry.

Virtually every developed technology depends upon electrons. The chemical industry is based upon the chemical properties of atoms, which in turn depend on the interaction of bound electrons. Thus the thermodynamic properties for the solid, liquid and gaseous phases of matter are all decided by the interactions of electrons in atoms. In the electronics industry, electrical devices rely on the flow of electrons. Even technology that generates electromagnetic radiation, such as lasers, depend upon the electron.

Industry

There are specialized industrial applications that utilize free electrons. Electron beams are used in welding, lithography, scanning electron microscopes and transmission electron microscopes. Electron beam processing is used to irradiate products in order to change their material properties or sterilize medical and food products. LEED and RHEED are surface-imaging techniques that use electron diffraction.

Electrons are at the heart of cathode ray tubes, which are used extensively as display devices in laboratory instruments, computer monitors and television sets. In a photomultiplier tube, one photon strikes the photocathode, initiating an avalanche of electrons that produces a detectable current. Vacuum tubes used the flow of electron in a near vacuum to manipulate electrical signals, and they played a critical role in the development of electronics technology. However, vacuum tubes have been largely supplanted by solid-state devices such as the transistor.

Laboratory

In blue light, conventional optical microscopes have a diffraction-limited resolution of about 100 nm. By comparison, electron microscopes are limited by the de Broglie wavelength of the electron, which is equal to 0.0037 nm. For example, the TEAM electron microscope is capable of 0.05 nm resolution: small enough to resolve individual atoms. This makes the electron microscope a useful laboratory instrument for high resolution imaging. However, electron microscopes are expensive instruments that are costly to maintain. The high vacuum required to operate an electron microscope also prevents them from being used to observe living organisms.

Transmission electron microscopes function in a manner similar to optical microscopes, with a beam of electrons passing through a material. The magnifications range from 1,000× to 1,000,000× or better. Quantum effects of electrons are used in the scanning tunneling microscope to study features on solid surfaces with lateral-resolution at the atomic scale of around 0.2 nm.

Particle accelerators use electrical fields to propel electrons and their antiparticles to high energies. As these particles pass through magnetic fields, they can emit synchrotron radiation by changing their spin orientation, a process known as the Sokolov-Ternov effect. This causes the particles to self-polarize, which can be useful for various experiments. Synchrotron radiation can be used for radiation damping, which reduces the spread of the particles. Magnets are then used to increase the momentum of the particles in the desired direction. Once the particles have accelerated to the required energies, separate electron and positron beams are brought into collision. The resulting energy emissions are observed with particle detectors and used to study particle physics.

Other

In radiation therapy, electron beams are generated by linear accelerators for treatment of superficial tumors. Because an electron beam only penetrates to a limited depth before being absorbed, typically up to 5 cm for beams in the range 5–20 MeV, electron therapy is useful for treating skin lesions such as basal cell carcinomas. It is also used to supplement the treatment of areas that have been irradiated by X-rays.

In the free electron laser (FEL), a relativistic electron beam is passed through a laser cavity containing an array of magnetic fields that are oriented in alternating directions. The resulting synchrotron radiation from the electrons is emitted in a coherent form, creating a laser. FEL can emit a wide range of frequencies, from microwaves to soft X-rays. These devices are used for manufacturing, communication and various medical applications, such as soft tissue surgery.

See also

• Covalent bonding
• Electron bubble
• Exoelectron
• G-factor
• One-electron universe
• Spintronics

External links

• "The Discovery of the Electron". American Institute of Physics, Center for History of Physics. Retrieved 2006-08-10.
• "Particle Data Group". University of California. Retrieved 2008-11-17.
• Weisstein, Eric W. (2007). "Electron". Eric Weisstein's World of Physics. Wolfram Research. Retrieved 2008-11-17.
• Researchers Catch Motion of a Single Electron on Video